工业生产一直是能源消耗的主体,据2014年中国统计年鉴,2012年我国工业能源消费总量占全国可供消费能源总量的72.8%。由此可见,提高工业生产过程中能源利润率、降低工业能耗,对提升工业生产效益及改善环境有重要的意义。
在过去几十年里,对制造系统的研究主要集中在如何提高生产率和质量上,而对节能的研究相对较少,近几年的研究结果表明,制造系统存在巨大的节能潜能。Gutowski等[1]研究了大批量制造环境,发现超过85%的能源被消耗在与零件生产没有直接关联的方面。Drake等[2]研究结果显示机器开机和机器闲置需要消耗大量的能源。目前,大多数制造系统都没有能源管理功能,这意味着大量的能源消耗在机器的拥堵或饥饿时刻。
为了解决此类能源消耗问题,一些学者将节能分析与传统生产调度问题结合,试图从工件调度优化的角度寻找解决方法。Mouzon等 [3-4]通过调度单机以实现总的能源消耗最小,将非瓶颈机器关掉直到需要时再打开,避免非瓶颈机器处于闲置状态,结果表明可以节省80%消耗在闲置、开机、关机的能源。Liu等[5]则针对经典Job shop问题提出了考虑电力消耗和总权重延迟的双目标最小化的节能方法。
近几年,一些学者针对不同类型的串行生产线进行了节能分析。Guorong等 [6-8]研究了缓冲容量有限的串行生产线的节能方法,通过决策在一个生产周期内每个机器的开机时间和关机时间来实现节能。Chang等 [9-11]研究了考虑机器失效和修复的串行生产线的节能方法,利用非瓶颈机器与瓶颈机器之间缓冲区内的存储量提供的节能机会,以实现节能。
为了更有效地减少机器消耗在拥堵和饥饿时刻的能源,本文针对缓冲区容量有限、机器失效和修复服从指数分布的串行生产线,提出了一种基于可变缓冲区存储量的节能方法(energy saving method,ESM)。在保证一定产出量的前提条件下,机器根据自身状态以及其上下游缓冲区的存储量改变运行状态,在正常加工状态与节能状态之间切换,以避免出现闲置,由此实现最大化的节能。
1 问题描述与数学模型为了有效描述问题域,对串行生产线的做如下定义及假设。
1) B2,B3,…,Bk,…,BM表示缓冲区的最大容量;Ck(t)表示缓冲区k在时刻t的存储量,初始库存量为Ck(0)。
2) 每一台机器Sm的额定速度为1/Tm,m=1,2,…,M,其中Tm表示机器Sm加工一个工件的时间。当Sm不处于饥饿(starved),同时不处于拥堵(blocked)状态时,机器始终以额定速度运行。
3) 如果一台机器正在工作且它的上游缓冲区是空的,则这个机器处于饥饿状态。
4) 如果一台机器正在工作且它的下游缓冲区是满的,则这个机器处于拥堵状态。
5) 机器Sm无故障工作时间服从指数分布,失效率为λm,则平均无故障时间间隔MTTF为1/λm;机器Sm修复时间服从指数分布,修复率为μm,则平均修复时间MTTR为1/μm。
6) 当机器Sm正常运行时,单位时间的能耗为Pm;当机器Sm处于待机状态(即节能状态)时,单位时间的能耗为αmPm,0<αm<1。
7) 所有机器都可以在多个运行状态之间切换,切换时间为0,从待机状态调节至正常运行状态后,机器就可开始正常加工。
8) 当机器发生失效时,工件停留在机器上,当修复完成后,机器继续加工,且机器修复如新。
9) 缓冲区在存贮和传递工件的过程中是完全可靠的,不会出现故障。
为了实现对上述串行生产线的节能,提出基于可变缓冲区存储量的节能方法,考虑一个计划期T内的串行生产系统运行状态。
图 1所示串行生产线在初始时刻t=0的状态如下:

|
| 图1 M个机器、M-1个缓冲区的串行生产线 Figure 1 A serial production line with M machines and M-1 buffers |
| ${{S}_{m}}(0)\ne 1,1\le m\le M,0\le {{C}_{k}}(0)\le {{B}_{k}},2\le k\le M$ |
定义1 机器Sm在任意时刻t的状态用不同的数字表示如下:
| ${{S}_{m}}(t)=\left\{ \begin{align} & 0,表示机器处于节能状态 \\ & 1,表示机器处于正常加工状态 \\ & 2,表示机器处于失效修复状态 \\ \end{align} \right.$ | (1) |
其中0≤t≤T。
易知缓冲区k在时刻t的状态为
| $\begin{align} & {{C}_{k}}(t)={{C}_{k}}(0)+\frac{\sum\limits_{i=1}^{t}{(1-\left| {{S}_{(k-1)i}}-1 \right|)}}{{{T}_{k-1}}}- \\ & \frac{\sum\limits_{i=1}^{t}{(1-\left| {{S}_{ki}}-1 \right|)}}{{{T}_{k-1}}},0\le {{C}_{k}}(t)\le {{B}_{k}} \\ \end{align}$ | (2) |
式中:2≤k≤M,0≤t≤T。用C1(t)表示第一台机器的上游在t时刻的存储量,由于第一台机器永不会饥饿,因此,可以假设对于∀t∈[1,T],有C1(t)=∞;用CM+1(t)表示最后一台机器的下游在t时刻的存储量,由于最后一台机器永不会拥堵,因此,可以假设对于∀t∈[1,T],有CM+1(t)=0。
定义2 对于有M个机器,M-1个缓冲区的串行生产线,用一个M×4的矩阵A(Buffer State)表示不同机器运行状态转变所对应的上下游缓冲区的值:
| $A=\left[ \begin{matrix} {{A}_{11}} & \begin{matrix} {{A}_{12}} & {{A}_{13}} \\ \end{matrix} & {{A}_{14}} \\ {{A}_{21}} & \begin{matrix} {{A}_{22}} & {{A}_{23}} \\ \end{matrix} & {{A}_{24}} \\ \vdots & \vdots & \vdots \\ {{A}_{(M-1)1}} & \begin{matrix} {{A}_{(M-1)2}} & {{A}_{(M-1)3}} \\ \end{matrix} & {{A}_{(M-1)4}} \\ {{A}_{M1}} & \begin{matrix} {{A}_{M2}} & {{A}_{M3}} \\ \end{matrix} & {{A}_{M4}} \\ \end{matrix} \right]$ | (3) |
式中:Am1和Am3表示机器Sm上游缓冲区Bm的取值,Am2和Am4表示机器Sm下游缓冲区Bm+1的取值,并满足以下条件:
1) 对于∀m∈[2,M],0≤Am1≤Bm-1,1≤Am3≤Bm;
2) 对于∀m∈[1,M-1],1≤Am2≤Bm+1,0≤Am4≤Bm+1-1;
3) 对于∀m∈[1,M],Am3>Am1,Am2>Am4;
4) 对于∀m∈[1,M-1],Am2≥Am+13。
考虑最后一台机器在时间T内的产出量PV,显然,当A=A0时,即仅当机器的上游缓冲区为空或下游缓冲区满时机器才停止加工,该串行生产线可实现最大的产出量PVmax,其中A0可表述为
| ${{A}_{0}}=\left[ \begin{matrix} 0 & \begin{matrix} {{B}_{2}} & 1 \\ \end{matrix} & {{B}_{2}}-1 \\ 0 & \begin{matrix} {{B}_{3}} & 1 \\ \end{matrix} & {{B}_{3}}-1 \\ \vdots & \ddots & \vdots \\ 0 & \begin{matrix} {{B}_{M}} & 1 \\ \end{matrix} & {{B}_{M}}-1 \\ 0 & \begin{matrix} ∞ & 1 \\ \end{matrix} & ∞ \\ \end{matrix} \right]$ | (4) |
定义3 对于∀t∈[1,T],∀m∈[1,M],若机器Sm在时刻t不发生失效,且Sm(t-1)≠1,则:当Cm(t-1)≥Am,
定义4 对于∀t∈[1,T],∀m∈[1,M],若机器Sm在时刻t不发生失效,且Sm(t-1)=1,则:当Cm(t-1)≤Am,
为了在实现节能的同时,能够满足产出要求,将满足一定的产出比率β作为限制条件,即在某个A下,PV≥βPVmax,0<β<1,目标函数为最大化节能量ES:
| $\operatorname{maxES}=\sum\limits_{i=1}^{T}{\sum\limits_{j=1}^{M}{(1-{{\alpha }_{j}}){{P}_{j}}(\left| {{S}_{j}}(i)-1.5 \right|-0.5)}}$ | (5) |
由Guorong等[8]可知:线下获得的最优化策略往往对系统参数很敏感,在实践中常常出现错误。而此次研究的目的在于证明串行生产线的节能潜能,与所提策略的节能效果,因此采用下述迭代搜索算法来寻得较优解:基于贪婪算法和概率接受准则的演化迭代算法。算法的核心思想:在局部搜索中采用贪婪算法,同时,为了提高算法的搜索能力,引入模拟退火算法的概率接受准则来更新最优解。当产生一个新解时,首先计算新解和旧解的目标函数值,如果节能率之差ΔE=f(S′)-f(S) 为正,则接受新解作为最优解;否则以概率expΔE/T接受新解,其中T是随时间变化的温度参数。
为了实现对不同缓冲区值组合的搜索,定义变化规则C(I),其中I表示矩阵的第i列,具体操作如下:
1) 对于所有的j∈(1,M),有hj为一个M×4的矩阵,其中第i列第j行的值为d=D(D为正常数),其他为0,令并A′j=A+(-1)i-1hj。
2) 判断A′j的值是否满足定义2,如果满足,则计算ESj=ESA′j,PVj=PVA′j;如果不满足,则淘汰。
3) 定义集合E表示:对于所有j∈1,M,满足条件PVj>=βPVmax的A′j的集合;如果集合为空,则直接进入下一步骤;如果集合为非空,则根据贪婪算法,在集合E中选取对应ESj值最大的A′j,并令Abest′=A′j,ESbest′=ESj,PVbest′=PVj。
4) 判断ESbest′与ESbest的大小关系,如果ESbest′≥ESbest,则令ESbest=ESbest′,PVbest=PVbest′,A=Abest′;如果ESbest′<ESbest,则根据概率接受准则判断是否接受ESbest′,如果接受,则令ESbest=ESbest′,PVbest=PVbest′,A=Abest′,如果不接受,则不变。
具体算法步骤如下:
1) 初始化。设k=1,初始解为A0:
| ${{A}_{0}}=\left[ \begin{matrix} 0 & \begin{matrix} {{B}_{2}} & 1 \\ \end{matrix} & {{B}_{2}}-1 \\ 0 & \begin{matrix} {{B}_{3}} & 1 \\ \end{matrix} & {{B}_{3}}-1 \\ \vdots & \ddots & \vdots \\ 0 & \begin{matrix} {{B}_{M}} & 1 \\ \end{matrix} & {{B}_{M}}-1 \\ 0 & \begin{matrix} ∞ & 1 \\ \end{matrix} & ∞ \\ \end{matrix} \right]$ |
计算初始解的节能量ES0=ESA0和产出量PV0=PVA0,并令ESbest=ES0,PVbest=PVmax=PV0,A=A0;
2) 变化第四列的值。I=4,在经过变化规则C4后,可得对第四列的值变化后的A,以及对应的ESbest、PVbest;
3) 变化第二列的值。I=2,在经过变化规则C2后,可得对第四列的值变化后的A,以及对应的ESbest、PVbest;
4) 变化第三列的值。I=3,在经过变化规则C3后,可得对第四列的值变化后的A,以及对应的ESbest、PVbest;
5) 变化第一列的值。I=1,在经过变化规则C1后,可得对第四列的值变化后的A,以及对应的ESbest、PVbest;
6) 判断是否改变d。如果
7) 判断是否满足算法终止条件。k=k+1,如果k=K,则退出循环,否则,进入2)。
3 仿真实验分析为了评价算法的性能,首先从计算时间与收敛性能两个角度分析算法性能,然后针对一条具体的串行生产线运用所提演化迭代算法,分析其产出、能耗、与节能。定义如下评价指标:
| $ESR=\frac{ES}{OEC}$ | (6) |
式中:ESR、OEC分别表示能耗降低率、原始能耗,原始能耗指未运用ESM时的能源消耗,即当且仅当机器出现失效需要修复时处于停机状态能耗为0,其时间均处于正常加工状态,能耗正常。
| $ESRR=\frac{OEC-ECAESM}{OEC}$ | (7) |
式中:ECRR、ECAESM分别表示能耗降低率、实施ESM的后的能耗,即表示实施本文所提节能方法后,机器处于正常加工状态时的能耗。
算法用Matlab R2010b编程实现,并在主频为2.10GHz,内存为2.00GB的PC机上运行。
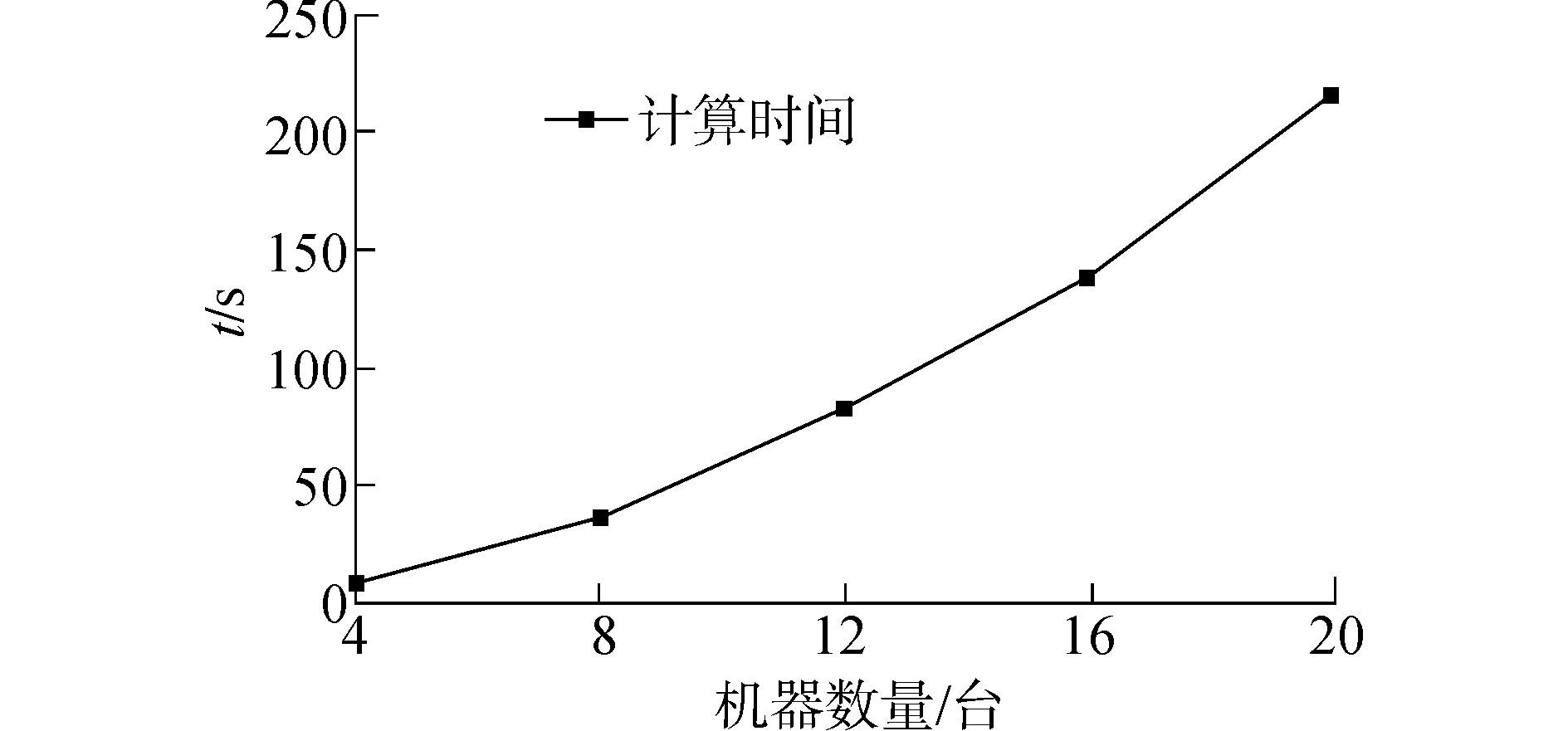
3.1 计算时间对机器数量的敏感性分析考虑机器数量分别为4、8、12、16、20,缓冲区容量服从[5, 10]的均匀分布,每台机器的单位加工时间服从[4, 8]的均匀分布,MTTF服从[30, 40]的均匀分布,MTTR服从[1, 10]的均匀分布,功率服从[100, 150]的均匀分布,αm=0.1,产出比率β=0.8,迭代次数K=20,在此情况下随机生成10个算例,经仿真运行后不同机器数量下的平均计算时间如图 2所示。
|
| 图2 机器数量对计算时间的影响 Figure 2 Number of machines versus the cumputing time |
由图 2可知,算法计算时间对机器数量的变化较为敏感,随着串行生产线机器数量的增加呈增加趋势。考虑到所提节能方法为事先决策,所以此计算时间在实际运用中是可以接受的。
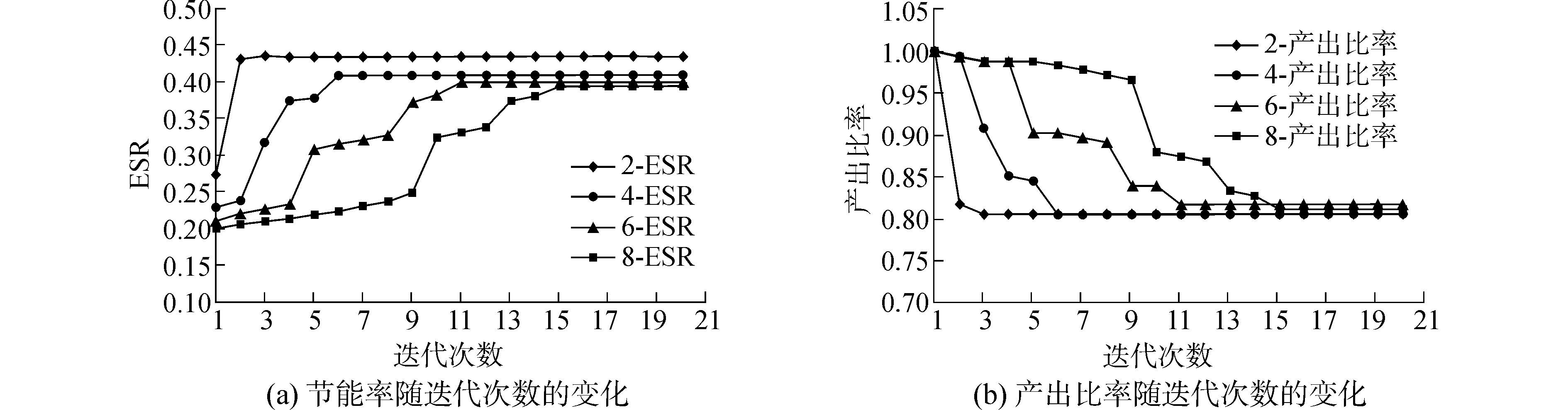
3.2 收敛性能对缓冲区容量的敏感性分析考虑缓冲区容量分别2、4、6、8,机器数量固定为5,每台机器的单位加工时间服从[4, 8]的均匀分布,MTTF服从[30, 40]的均匀分布,MTTR服从[1, 10]的均匀分布,功率服从[100, 150]的均匀分布,αm=0.1,产出比率β=0.8,迭代次数K=20,在此情况下随机生成10个算例,经仿真运行后不同缓冲区容量下的收敛情况如图 3所示。
|
| 图3 缓冲区容量对收敛性能的影响 Figure 3 Level of buffers versus the convergence performance |
由图 3可知,针对不同的缓冲区容量值,算法收敛所需迭代次数随缓冲区容量值的增大而增加,但均能在20次的迭代内实现收敛,且寻得较优解,说明该算法收敛速度快、寻优能力较强,对解决所提节能方法具有良好的适用性。
4.3 缓冲区容量对节能效果的影响为了分析本文所提节能方法对解决串行生产线节能问题的解决效果,针对表 1所示串行生产线,首先分析当不实施节能方法时,不同缓冲区容量下的产出量,然后在确定缓冲区容量的条件下运用ESM,分析其节能效果。
| 机器 | S1 | S2 | S3 | S4 | S5 |
| Tm | 5 | 6 | 4 | 5 | 7 |
| MTTF | 35 | 32 | 38 | 36 | 31 |
| MTTR | 2 | 8 | 6 | 5 | 5 |
| Pm | 112 | 128 | 102 | 107 | 126 |
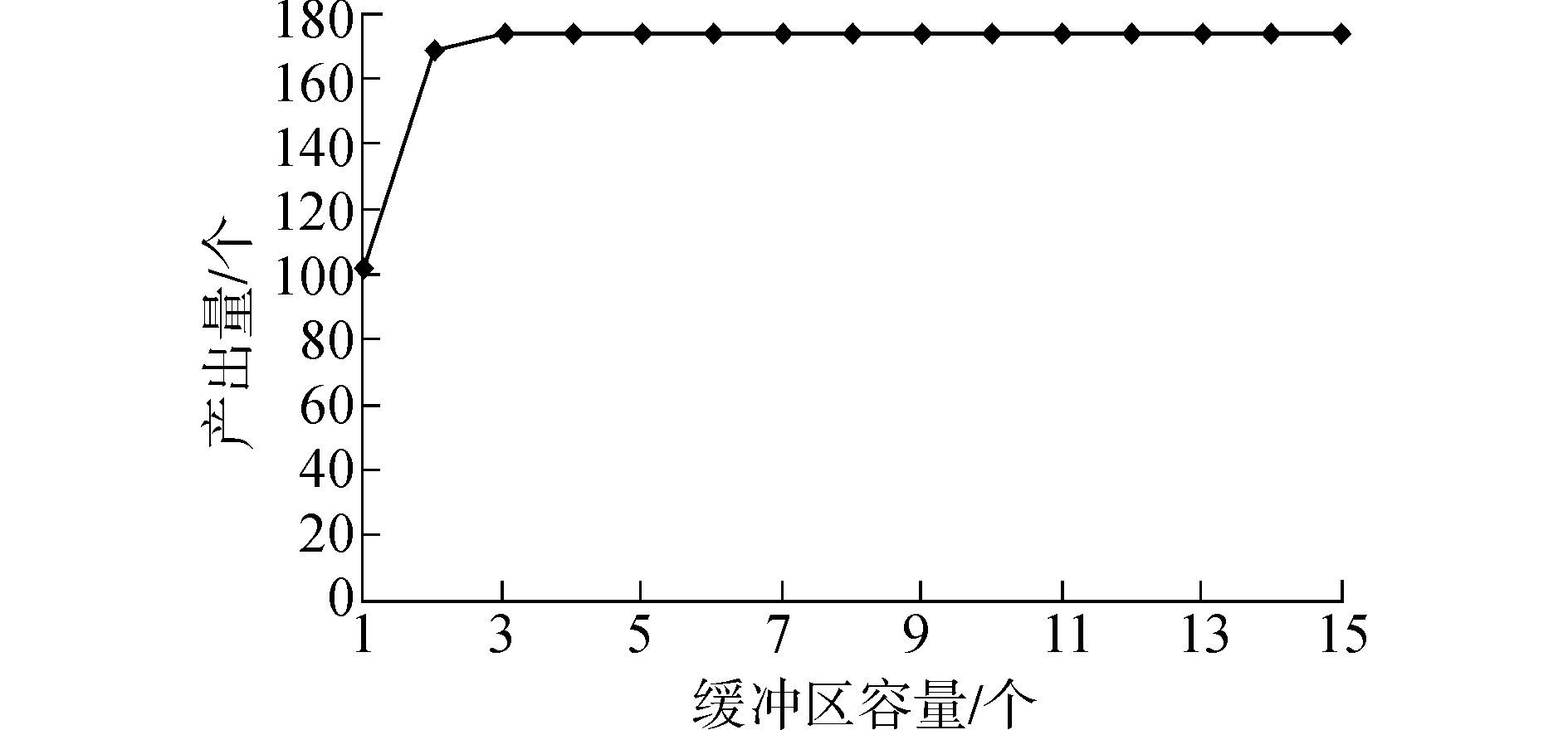
考虑每个缓冲区的容量相同,其值为1、2、3、4、5、6、7、8、9、10、11、12、13、14、15的情况,经仿真运行10次后,得到平均产出量随缓冲区容量变化的情况,如图 4所示。
|
| 图4 缓冲区容量对产出量的影响 Figure 4 Level of buffers versus the production volume |
由图 4可知,该串行生产线的产出量随缓冲区容量的增加而增加,当缓冲区容量值大于4时,该串行生产线的产出量开始趋于平稳,因此,选取6作为此生产线的缓冲区容量值。
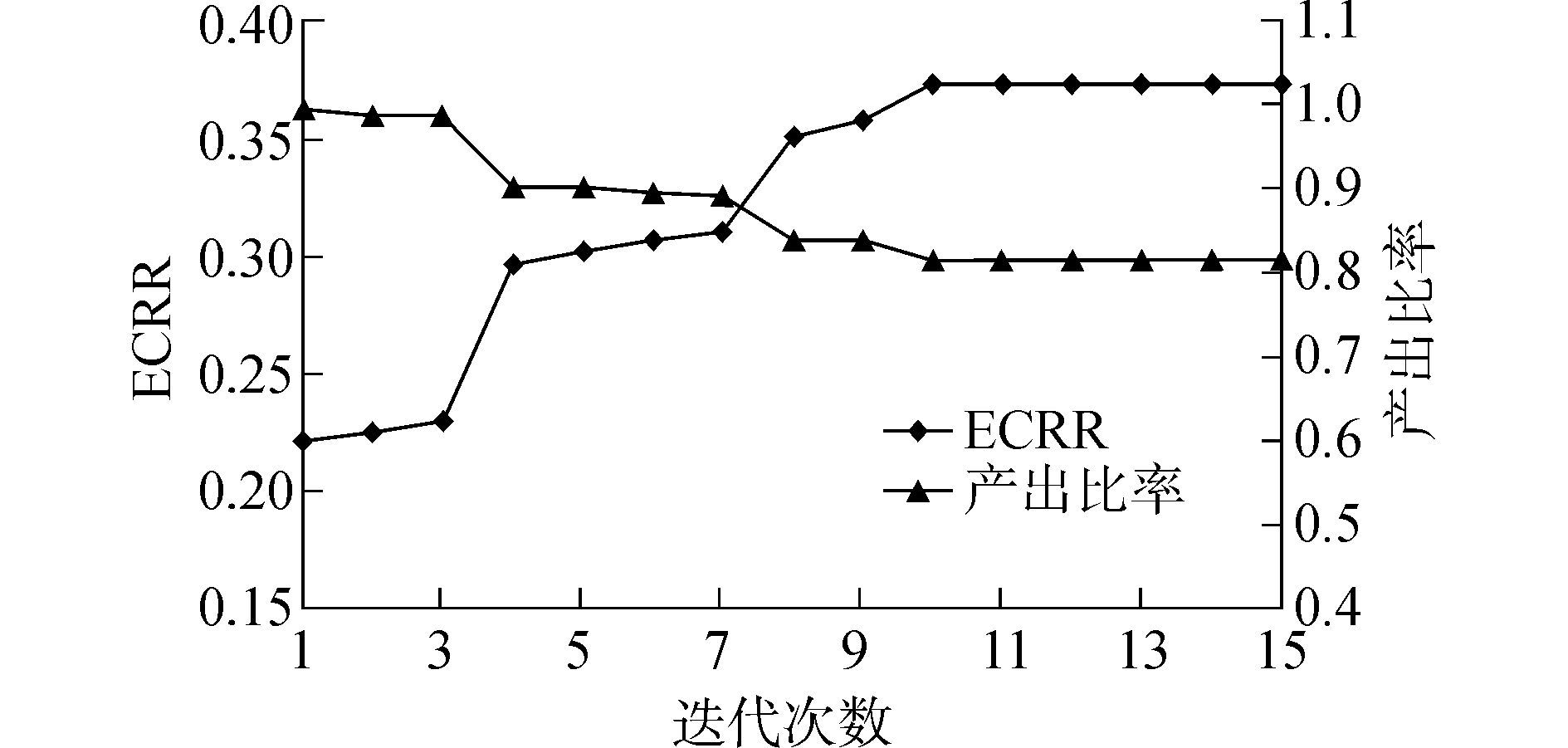
而后,分析此时生产线的能耗与产出量,并通过演化迭代算法寻找恰当的缓冲区容量组合A来实现节能。经15次迭代后,得到图 5,并将文献[8]中所提节能方法用于此生产线,得到图 6。
|
| 图5 节能效果 Figure 5 The performance of energy saving method |
|
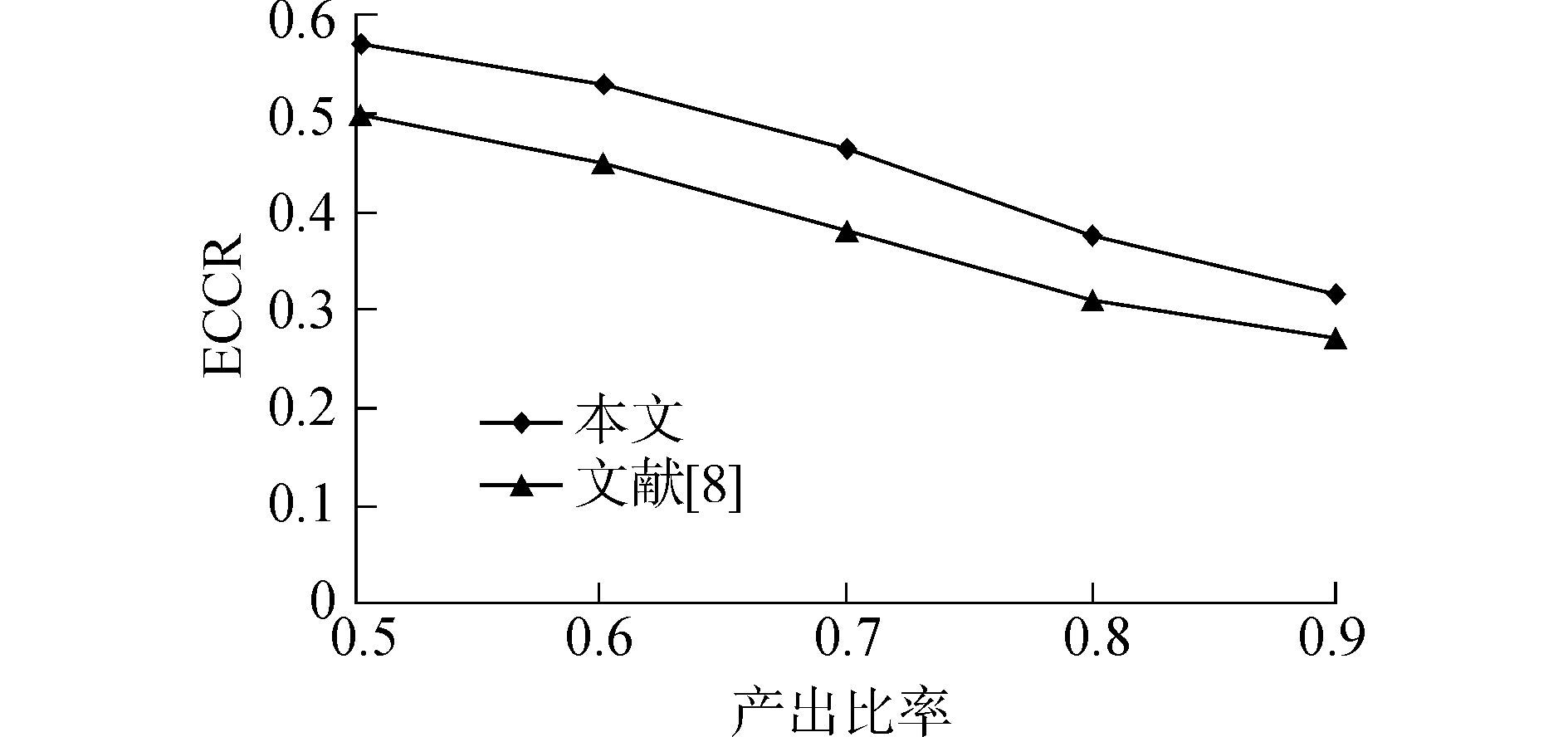
| 图6 产出比率对节能效果的影响 Figure 6 The proportion of production volume versus the energy saving performance |
由图 5可知,随着迭代寻优过程的递进,产出比率逐渐降低,能耗降低率逐步升高,最终可寻得产出比率为81.6%、能耗降低率为37.4%的较优解。由图 6可知,将本文所提节能方法与文献[8]中所提节能方法运用于同一串行生产线,在满足相同产出比率的条件下,前者均能得到较高的能耗降低率,实现较大的能源节省,且此方法不需要额外的资金投入,由此可见所提节能方法对解决实际生产过程中日益突出的能源问题具有较好的解决效果。
4 结论1) 通过分析不同问题规模下的ESM实施结果,表明所提节能方法在保证一定产出率的条件下,能有效降低消耗。
2) 并通过与其他节能方法对比,可知文中所提ESM能实现更好的节能效果。因此,基于可变缓冲区存储量的节能方法对解决制造过程中串行生产线的节能问题是可行的、有效的。
3) 基于贪婪算法和概率接受准则的迭代搜索算法寻得较优解所需迭代次数随着缓冲区容量值的增大而增加,但均能在较少的迭代次数内求得;且对于小、中、大规模问题,均能在可接受的时间内寻得此问题的较优解,具有良好的适应性。
| [1] | GUTOWSKI T C, MURPHY C, ALLEN D, et al. Environmentally benign manufacturing:observations from Japan, Europe and the United States[J]. Journal of cleaner produ-ction, 2005, 13(1): 1–17. |
| [2] | DRAKE R, YILDIRIM M B, TWOMEY J M, et al. Data collection framework on energy consumption in manufacturing[C]//Proceedings of the Industrial Engineering Research Conference, Institute of Industrial Engineers Annual Meeting. Orlando, FL, 2006. |
| [3] | MOUZON G, YILDIRIM M B, TWOMEY J. Operational methods for minimization of energy consumption of manufacturing equipment[J]. International journal of production research, 2007, 45(18/19): 4247–4271. |
| [4] | MOUZON G, YILDIRIM M B. A framework to minimise total energy consumption and total tardiness on a single machine[J]. International journal of sustainable engineering, 2008, 1(2): 105–116. |
| [5] | LIU Ying, DONG Haibo, LOHSE N, et al. An investigation into minimising total energy consumption and total weighted tardiness in job shops[J]. Journal of cleaner production, 2014, 65: 87–96. |
| [6] | CHEN Guorong, ZHANG Liang, ARINEZ J, et al. Energy consumption reduction in serial production lines via controlled machine startup[C]//Proceedings of ASME 2011 International Manufacturing Science and Engineering Conference. Corvallis, Oregon, USA:American Society of Mechanical Engineers, 2011, 2:155-161. |
| [7] | CHEN Guorong, ZHANG Liang, ARINEZ J, et al. Scheduling of machine startup and shutdown to reduce energy consumption in Bernoulli production lines[C]//Proceedings of ASME 2012 International Manufacturing Science and Engineering Conference collocated with the 40th North American Manufacturing Research Conference and in participation with the International Conference on Tribology Materials and Processing. Indiana, USA:American Society of Mechanical Engineers, 2012:1125-1131. |
| [8] | CHEN Guorong, ZHANG Liang, ARINEZ J, et al. Energy-efficient production systems through schedule-based operations[J]. IEEE transactions on automation science and engineering, 2013, 10(1): 27–37. |
| [9] | CHANG Qing, XIAO Guoxian, BILLER S, et al. Energy saving opportunity analysis of automotive serial production systems (march 2012)[J]. IEEE transactions on automation science and engineering, 2013, 10(2): 334–342. |
| [10] | BRUNDAGE M P, CHANG Qing, LI Yang, et al. Energy efficiency management of an integrated serial production line and HVAC system[J]. IEEE transactions on automation science and engineering, 2014, 11(3): 789–797. |
| [11] | BRUNDAGE M P, CHANG Qing, LI Yang, et al. Utilizing energy opportunity windows and energy profit bottlenecks to reduce energy consumption per part for a serial production line[C]//Proceedings of 2014 IEEE International Conference on Automation Science and Engineering (CASE). Taipei:IEEE, 2014:461-466. |



