2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin, 150001, China
作为海洋勘探不可缺少的技术装备,水下航行器已经越来越多的引起各国学者的关注。耐压壳结构是水下航行器主要结构之一,它不但是舱室内部各分类系统设备正常工作的重要保证,也在减少结构重量的同时为载体提供浮力储备。随着水下航行器下潜深度增加,耐压壳将会承受越来越大的深水压力。复合材料作为新型材料的一种代表,它具有比强度大、比刚度高、耐腐蚀性好、结构可设计性等多个性能特点。相比传统金属耐压壳结构,在相等强度、刚度条件下,重量大幅减轻,这对增加水下航行器有效载荷,提高续航力有重要意义。
由于复合材料结构设计中有大量的基体、纤维、铺层形式可供选择,单纯进行试验研究成本高昂,而数值模拟结合试验验证的研究方法不仅可以了解结构力学性能,还能以较低成本对结构进行优化设计,因此在工程中被广泛应用[1]。杨卓懿等[2]研究了复合材料潜器结构的强度分析方法,并完成了复合材料一体式潜水器多学科综合优化。李彬等[3]应用ANSYS软件对不同铺层形式复合材料层合板进行计算分析,并将计算数据与试验对比,验证了有限元分析软件预测复合材料结构性能的可行性。Al-Assaf 等人应用神经网络方法预测单向玻璃环氧复合材料的疲劳寿命,得到了误差小于20%的满意预测结果,Allan等[4]采用近似模型方法成功预测了聚丙烯纤维复合材料的性能。
耐压壳结构,特别是环肋圆柱壳有着利于内部舱室布置,加工简单,水中运动阻力小等特点,在水下航行器结构中应用广泛[5]。通常环肋圆柱壳采用截面惯性矩沿轴向等距均匀分布的环形肋骨加强,这样的结构布局能够降低加工难度。当环肋圆柱壳总体失稳时,圆柱壳中央部分径向失稳位移很大,从舱段总体稳定性方面考虑,均匀环肋结构形式并不完全合理。采用非均匀环肋结构布置方式,不但能降低结构总体重量,还能有效地提高耐压壳屈曲稳定性[6]。普通金属耐压壳通常采用外部环肋结构形式来提高耐压壳整体的稳定性。对于复合材料耐压壳结构来说,采用外部加环肋方式不利于加工,采用无肋骨方式需要增加单层厚度,使成本提高,直接影响经济性能[7]。
基于以上思想,本文结合复合材料细观力学刚度的材料力学分析方法,应用ANSYS有限元软件对水下航行器非均匀内部环肋复合材料耐压壳结构进行力学仿真分析。利用EBF椭圆基神经网络近似模型技术借助iSIGHT软件平台试验设计从细观层面对组分材料属性在非均匀内部环肋复合材料耐压壳性能中的影响进行了研究,为后续复合材料结构设计优化工作打下良好基础。
1 复合材料刚度的细观力学分析复合材料是由几种不同性质材料组合而成的新型材料。利用复合效应不但使得整体材料具有各组分材料所不具有的特性,同时可以保留原组分材料的某些主要性能。复合材料刚度的细观力学分析可采用材料力学分析方法根据复合材料中纤维体积分数确定单层复合材料整体力学性能[8]。
E1为纤维方向弹性模量。在确定E1时,认为纤维和基体组成一个并联模型,即假设纤维和基体在纤维方向上应变相等,即ε1=ε1m=ε1f,如两者都处于弹性状态,则应力为
| ${{\sigma }_{f}}={{E}_{f}}{{\varepsilon }_{1f}}={{E}_{f}}{{\varepsilon }_{1}},{{\sigma }_{m}}={{E}_{m}}{{\varepsilon }_{1m}}={{E}_{m}}{{\varepsilon }_{1}}$ | (1) |
式中:下标f表示纤维,m表示基体。平均应力σ1作用在横截面积A上,纤维应力σf作用在纤维横截面积Af上,基体应力σm作用在基体横截面积Am上,因此作用在复合材料体积单元上的合力为
| $P={{\sigma }_{1}}A={{\sigma }_{f}}{{A}_{f}}+{{\sigma }_{m}}{{A}_{m}}$ | (2) |
引入纤维体积分数
| ${{E}_{1}}={{E}_{f}}{{V}_{f}}+{{E}_{m}}{{V}_{m}}={{E}_{f}}{{V}_{f}}+{{E}_{m}}(1-{{V}_{f}})$ | (3) |
式中:Ef为纵向纤维弹性模量,Em基体弹性模量。
在确定E2时,假设纤维和基体承受相同的横向应力σ2,即认为纤维和基体组成一个串联模型,则总横向变形为
| $\Delta W=\Delta {{W}_{f}}+\Delta {{W}_{m}}$ | (4) |
复合材料横向总应变为
| ${{\varepsilon }_{2}}=\frac{\Delta W}{t}=\frac{{{\sigma }_{2}}}{{{E}_{2}}}$ | (5) |
纤维和基体横向应变分别为
| ${{\varepsilon }_{2f}}=\frac{\Delta {{W}_{f}}}{{{t}_{f}}}=\frac{{{\sigma }_{2}}}{{{E}_{2f}}},{{\varepsilon }_{2m}}=\frac{\Delta {{W}_{m}}}{{{t}_{m}}}=\frac{{{\sigma }_{2}}}{{{E}_{m}}}$ | (6) |
式中:t为复合材料厚度,E2f为横向纤维弹性模量,基体为各向同性材料,Em没有变化,且
| $\frac{1}{{{E}_{2}}}=\frac{{{V}_{m}}}{{{E}_{m}}}+\frac{{{V}_{f}}}{{{E}_{2f}}}$ | (7) |
| ${{E}_{2}}=\frac{{{E}_{2f}}{{E}_{m}}}{{{V}_{f}}{{E}_{m}}+(1-{{V}_{f}}){{E}_{2f}}}$ | (8) |
ν12定义为纤维方向受外力时横向应变与轴向应变的负比值,
| ${{\varepsilon }_{2}}t={{\varepsilon }_{2f}}{{t}_{f}}+{{\varepsilon }_{2m}}{{t}_{m}}$ | (9) |
纤维泊松比为
| $-{{\varepsilon }_{1}}{{\nu }_{12}}t=-{{\varepsilon }_{1f}}{{\nu }_{12f}}{{t}_{f}}-{{\varepsilon }_{1m}}{{\nu }_{12m}}{{t}_{m}}$ | (10) |
式(10)同时除以ε1和t,则泊松比为
| ${{\nu }_{12}}={{\nu }_{m}}{{V}_{m}}+{{\nu }_{f}}{{V}_{f}}={{\nu }_{m}}(1-{{V}_{f}})+{{\nu }_{f}}{{V}_{f}}$ | (11) |
假设纤维和基体所承受剪应力相等,即τ=τf=τm,且复合材料剪切特性是线性的,剪切变形符合串联模型,则有
| $\gamma =\frac{\tau }{{{G}_{12}}},{{\gamma }_{f}}=\frac{\tau }{{{G}_{f}}},{{\gamma }_{m}}=\frac{\tau }{{{G}_{m}}}$ | (12) |
式中:γf、γm分别表示纤维、基体剪应变,Gf、Gm表示纤维、基体剪切模量,则总剪切变形表示为
| $\delta ={{\delta }_{f}}+{{\delta }_{m}}$ | (13) |
| $\gamma t={{\gamma }_{f}}{{t}_{f}}+{{\gamma }_{m}}{{t}_{m}}$ | (14) |
由式(12)~(14)得到剪切模量:
| $\frac{1}{{{G}_{12}}}=\frac{{{V}_{f}}}{{{G}_{f}}}+\frac{{{V}_{m}}}{{{G}_{m}}}$ | (15) |
| ${{G}_{12}}=\frac{{{G}_{m}}{{G}_{f}}}{{{G}_{f}}1-{{V}_{f}}+{{G}_{m}}{{V}_{f}}}$ | (16) |
近似模型是通过数学模型方法构建一组输入变量与输出变量的响应关系。采用近似模型技术通过构造一个精度足够、计算消耗小的代理模型来代替耗费时间长的仿真分析,从而解决复杂系统分析计算代价高昂的问题。神经网络是对生物神经网络处理信息过程进行模拟的一种数学模型,其中神经元是神经网络进行信息处理的基本单元,神经元的连接方式不同,其构成的神经网络性质也不同[9]。目前,对于耐压壳结构研究常用的近似模型主要是径向基神经网络模型(radial basis functions,RBF),对于任意输入x,设第k个径向基神经元对应的输出为
| $R\left( x \right)=exp\left( \frac{-\|x-{{c}_{j}}{{\|}^{2}}}{2{{\sigma }^{2}}} \right)$ | (17) |
1993年,Kavuri等[10]根据模式识别问题的特点,提出了带有椭圆函数的神经网络模型。椭圆基神经网络模型(elliptical basis functions,EBF)与RBF神经网络的主要区别在于它是通过超椭圆来划分输入空间,根据输入样本数据距椭圆中心的距离以及与椭圆相对位置得出函数输出值,从而形成封闭且有界的样本激活区域,明确的划分了输入空间[11]。椭圆基神经网络模型也是由输入层、隐含层、输出层构成的一种前馈型网络模型,相同于RBF网络的结构,隐含层采用椭圆单元作用函数。其基本思想是以待测点与样本点之间的Mahalanobis距离为自变量,对于n维输入变量x1,x2,…,xN∈R,以椭圆函数gi=g‖x-xj‖m∈R,j=1,2,…,N为基函数,通过线性叠加的方式构造椭圆基神经网络模型,输入、输出层表达式分别为
| $f_{j}^{in}\left( x \right)=1-\sum\limits_{i=1}^{n}{\frac{{{\left( {{x}_{i}}-{{c}_{ji}} \right)}^{2}}}{b_{ji}^{2}}}$ | (18) |
| $f_{j}^{out}\left( x \right)=\frac{{{e}^{\beta }}+1}{{{e}^{\beta }}}\cdot \frac{1}{1+exp(-\beta f_{j}^{out}\left( x \right))}$ | (19) |
式中:cji、bji分别表示椭圆单元j在第i维上中心值及半轴长,引入eβ+1eβ为保证椭圆基函数的输出范围与径向基函数一致,β为sigmoid曲线斜率调节参数,β值越大,椭圆基函数单元输出值趋于零的速度越快。将各维的中心和半长轴写成向量形式为
| $E\left( x \right)=\frac{{{e}^{\beta }}+1}{{{e}^{\beta }}+exp\left( \beta {{\frac{\|x-{{c}_{h}}\|}{\|{{b}_{h}}{{\|}^{2}}}}^{2}} \right)}$ | (20) |
取cj=ch,2σ2=‖bh‖2,根据式(17)、(20)得到两种网络神经元输出关系对比如图 1所示。设
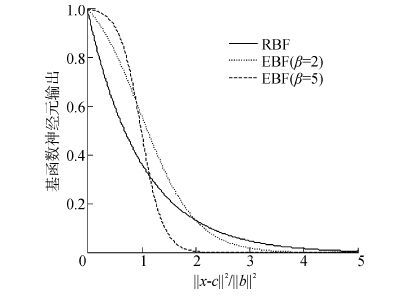
|
| 图1 基函数输出对比 Figure 1 Comparison of basis functions output |
本文选取70组复合材料耐压壳有限元分析数据样本对EBF神经网络模型优势进行验证。采用k-均值法对样本进行聚类,应用最小二乘法对隐含层到输出层的权值进行分析。分别对EBF和RBF神经网络模型隐含层含2、3、4个节点时进行准确度对比分析如表 1所示,可以看出EBF相比RBF准确度高。因此,相比较RBF神经网络模型,EBF神经网络模型具有更强的模式识别能力。
| 神经网络 | 2 | 3 | 4 |
| EBF | 0.919 9 | 0.934 4 | 0.984 2 |
| RBF | 0.908 0 | 0.909 2 | 0.964 4 |
为保证耐压壳结构的合理性及可靠性,本文应用ANSYS有限元软件APDL语言集编写命令流分别对非均匀环肋、均匀环肋及无肋骨复合材料耐压壳结构形式进行仿真分析。结构长度为1 080 mm,内径130 mm,金属内衬材料选用7075铝合金,厚度为10 mm,纤维增强复合材料采用环氧树脂作为基体,T800碳纤维作为增强纤维,单层厚度为1 mm,10层对称铺设,铺设角度为[0,45,-45,45,-45]sym。材料性能参数如表 2所示,三种方案肋骨尺寸如表 3所示,耐压壳剖面图如图 2所示。
|
| 图2 耐压壳剖面图 Figure 2 Profile of pressure hull |
| 材料 | 弹性模量/GPa | 剪切模量/GPa | 泊松比 | ||
| 纵向Ef | 横向E2f | ν12f | ν23f | ||
| 纤维 | 233 | 23.1 | 8.96 | 0.2 | 0.4 |
| 基体 | 4.62 | 8.27 | 0.36 | ||
| 金属内衬 | 71.7 | - | 0.33 | ||
| mm | ||||||
| 肋骨形式 | L1 | L2 | B1 | B2 | H1 | H2 |
| 均匀 | 216 | 216 | 8 | 8 | 10 | 10 |
| 非均匀1 | 150 | 249 | 8 | 8 | 10 | 10 |
| 非均匀2 | 60 | 270 | 10 | 8 | 15 | 10 |
表 4总结了四个算例的结果,其中σ1表示耐压壳体相邻肋骨中点处壳板的周向应力,σ2表示肋骨处壳板的轴向应力,σr表示肋骨应力,PE表示临界失稳压力,Fc表示失效指数,Fc <1则认为强度满足要求[8]。从表中可以看出,在满足强度要求前提下,非均匀环肋耐压壳稳定性优于无肋骨及均匀环肋耐压壳。因此,采用不等间距非均匀环肋耐压壳形式能够有效的提高结构性能。
| 肋骨形式 | σ1/MPa | σ2/MPa | σr/MPa | PE/MPa | Fc |
| 无肋骨 | - | - | - | 37.05 | 0.197 |
| 均匀 | 202.44 | 68.19 | 330.31 | 41.12 | 0.192 |
| 非均匀1 | 201.98 | 68.16 | 331.05 | 41.39 | 0.192 |
| 非均匀2 | 201.92 | 68.52 | 328.87 | 47.81 | 0.199 |
基于以上结论,本文耐压壳结构采用第二种非均匀环肋方案,金属内衬外部缠绕纤维增强复合材料结构形式,肋骨采用非均匀内部环肋布置方式,四根肋骨左右对称布置,截面尺寸及肋骨间距均不同。为了可以准确的分析各层间影响,选择SOLID185单元对结构进行网格划分。在编写参数化语言定义材料属性时根据材料弹性常数及铺层角计算材料刚度阵。虽然相比直接定义法计算量较大,但能够充分考虑到三个方向的应力状态。端面采用刚性固定约束,耐压壳结构工作深度为1 000 m,在设计工况下,铝合金内衬和复合材料层均未发生失稳和失效情况,耐压壳结构在弹性变形范围内。启动ANSYS后处理求解器,输出非均匀环肋复合材料耐压壳的肋骨中点处壳板周向应力,肋骨处壳板轴向应力,肋骨应力,临界失稳压力以及基于Tsai-Wu失效准则的失效指数,有限元计算结果如图 3所示。

|
| 图3 耐压壳结构计算图 Figure 3 Contour plots of pressure hull |
本文从细观层面研究组分材料属性对非均匀环肋复合材料耐压壳结构性能的影响。依照《潜水系统与潜水器入级建造规范》[13]中规定对承受外压的环肋圆柱耐压壳,要求壳体相邻肋骨中点处壳板的周向应力σ1,肋骨处壳板的轴向应力σ2,肋骨应力σr应小于结构要求许用应力。对于受外压的薄壳结构来说,稳定性也是需要重点考虑的因素之一。除此之外,复合材料具有各向异性的特点,工作应力的最大值不一定对应结构的最危险状态。它的失效准则与金属材料不同,不能只应用规范中的校核准则来判定结构是否发生破坏。目前,复合材料比较常用的失效准则包括最大应力理论,最大应变理论,Hill-Tsai强度理论,Tsai-Wu张量理论[8]。其中,Tsai-Wu张量理论相比其余三个强度理论不但考虑了应力分项间的耦合作用,而且区分了拉伸强度和压缩强度。因此,本文采用Tsai-Wu张量理论作为判定复合材料耐压壳失效的依据。对于平面应力下正交各向异性复合材料失效表面形式表示为
| ${{F}_{1}}{{\sigma }_{1}}+{{F}_{2}}{{\sigma }_{2}}+{{F}_{11}}{{\sigma }^{2}}_{1}+{{F}_{22}}{{\sigma }^{2}}_{2}+{{F}_{66}}{{\sigma }^{2}}_{6}+2{{F}_{12}}{{\sigma }_{1}}{{\sigma }_{2}}\ge 1$ | (21) |
式中:Fi和Fij称为应力空间的强度参数。当失效面公式值小于1时则认为结构满足强度要求。
综合以上考虑,在构建近似模型时将非均匀环肋耐压壳结构尺寸作为常量。将材料基体弹性模量Em,基体剪切模量Gm,纤维纵向弹性模量Ef,纤维剪切模量Gf以及纤维体积分数Vf作为输入参数。将耐压壳相邻肋骨中点壳板周向应力σ1,肋骨处壳板轴向应力σ2,肋骨应力σr,临界压力PE以及失效指数Fc作为影响耐压壳性能的输出参数。在编写APDL参数化语言时,将耐压壳结构材料工程常数表达成组分材料工程常数与组分体积分数的函数形式,采用拉丁超立方设计方法安排150次试验设计,依据参数样本响应值选取150个样本点构建基于EBF神经网络近似模型如下图所示,图 4表示当纤维体积分数分别与纤维、基体弹性常数一定时,基体弹性常数与临界失稳压力PE以及纤维弹性常数与失效指数Fc的近似模型三维图。
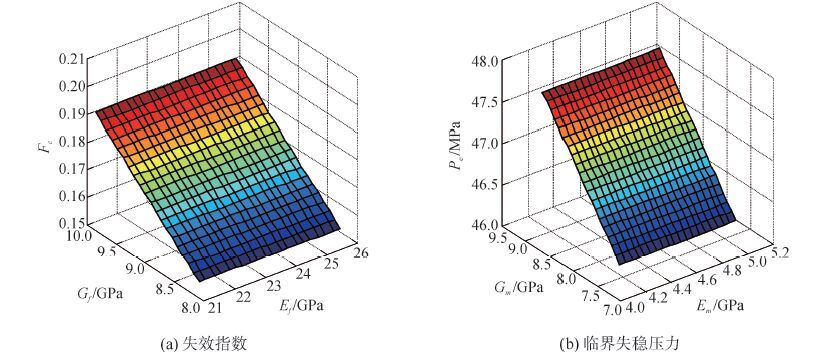
|
| 图4 弹性常数近似模型 Figure 4 Approximation of elastic constants |
复相关系数R2用来评估近似模型估计值与有限元计算真实值之间相符程度,R2值定义为
| ${{R}^{2}}=1-\frac{\sum\limits_{i=1}^{n}{{{(yi-{{y}^{i}})}^{2}}}}{\sum\limits_{i=1}^{n}{{{(yi-\bar{y})}^{2}}}}$ | (22) |
式中:n为样本点数,yi有限元计算真实值,${{\hat{y}}_{i}}$为近似模型估计值,y为真实值的平均值,R2越接近1表示模型精度越高。为预测近似模型精度,在设计空间内随机选取80个样本点进行误差分析,通过计算复相关系数可以得到所有输出参数包括相邻肋骨中点壳板周向应力,肋骨处壳板轴向应力,肋骨应力,临界压力以及失效指数的R2值均在99%以上。以肋骨应力和临界失稳压力为例展示近似模型与有限元计算对比如图 5所示。
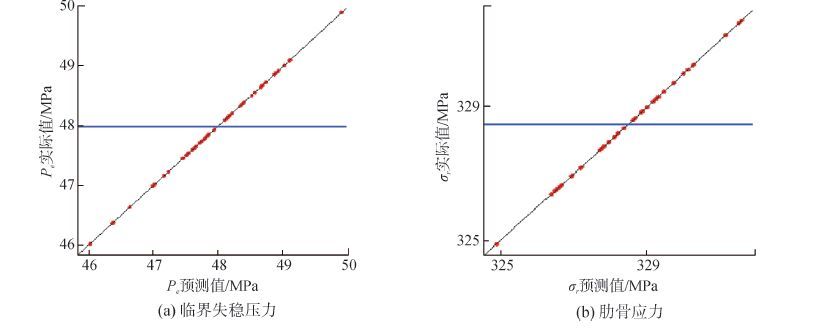
|
| 图5 近似模型误差分析 Figure 5 Error analysis of approximation |
图中各点表示与预测值对应的实际值。由图可以直观的看出各点均以极小误差落在直线y=x上,说明近似模型预测值与有限元计算值的重合度非常高,模型精度满足要求。因此,采用EBF神经网络模型能够在较少样本点的情况下得到高精度近似模型,这样既保证分析的准确性,又节约了计算成本。
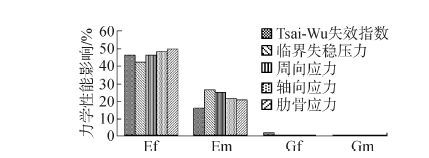
4.3 组分材料工程弹性常数对耐压壳力学性能影响借助iSIGHT平台集成ANSYS软件,采用拉丁超立方试验设计方法进行1000次迭代完成整个试验。通过试验得到组分工程常数对非均匀环肋复合材料耐压壳力学性能影响百分比如图 6所示。纤维弹性模量对耐压壳结构力学性能影响最大,均超过40%,其中对肋骨应力影响达到49.43%。其次是基体弹性模量。纤维和基体的剪切模量对各力学性能影响都很小。通过研究各单独组分材料属性对耐压壳整体力学性能的影响,不但可以对提高耐压壳力学性能方法进行预测,还可以在制备复合材料时对碳纤维及环氧树脂进行选型。
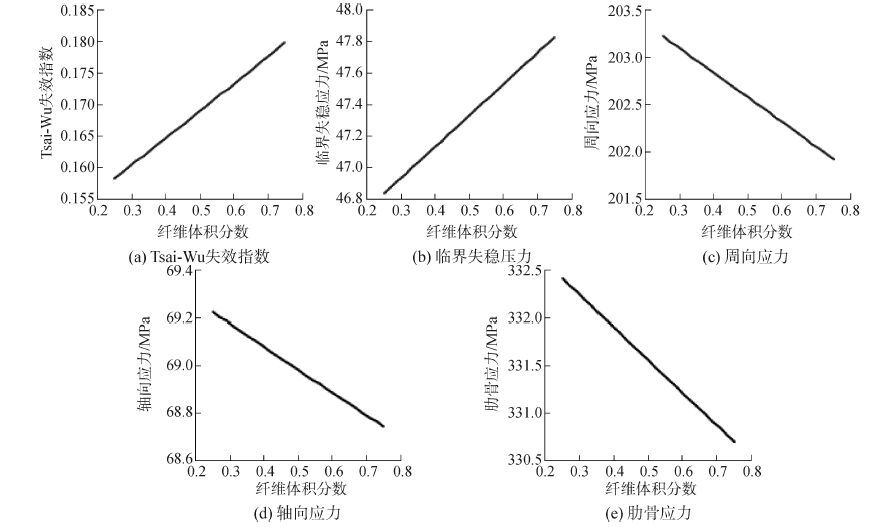
图 7为在材料选定情况下,组分含量对非均匀环肋复合材料耐压壳力学性能的影响。由各图曲线变化规律可知,纤维体积分数的增加导致Tsai-Wu失效指数和临界失稳压力有所提高,而周向应力、轴向应力和肋骨应力则随之降低。从结构强度及稳定性角度考虑,纤维体积分数增加能提高力学性能,具有积极作用。但是,从复合材料失效角度来看,随着纤维体积分数增加,将一定程度上促进失效提前发生。由此说明增加基体含量将一定程度上降低复合材料失效的可能。这是由于在纤维增强复合材料中,纤维和基体分别起不同作用,纤维具有高强度、高模量的特点,对复合材料力学性能有着直接的影响。而基体的主要作用是将纤维固结,虽然基体本身的力学性能较差,但它对复合材料结构整体性能有很大作用,如横向弹性模量、剪切强度、剪切模量、横向强度、压缩强度等。因此,为获得满足要求的复合材料耐压壳设计方案,需要解决组分含量以及各材料参数的最优化问题。
|
| 图6 组分材料属性影响百分比 Figure 6 Percentage effect on component material properties |
|
| 图7 纤维体积分数对耐压壳力学性能影响 Figure 7 The effect of fiber volume fraction on mechanical properties of pressure hull |
本文应用有限元理论对水下航行器非均匀内部环肋复合材料耐压壳结构进行力学仿真分析。采用拉丁超立方试验设计方法构建EBF椭圆基神经网络近似模型,从细观层面对组分材料在非均匀环肋复合材料耐压壳性能中的影响进行了研究,研究表明:
1) 近似模型技术以少量仿真计算结果拟合出反映整个设计空间属性的近似分析模型,在保证准确的同时很大程度上提高了分析效率。另外,相比RBF模型,EBF神经网络模型具有更强的模式识别能力,因此采用EBF近似模型得到的分析结构更为真实可靠。
2) 纤维和基体的弹性模量对耐压壳结构材料力学性能影响最大,剪切模量对各力学性能影响都很小。在耐压壳设计时,应将弹性模量作为组分材料选择的重要标准。
3) 在组分材料属性一定的情况下,随着纤维体积分数增加,Tsai-Wu失效指数和临界失稳压力有所提高,而相邻肋骨中点处壳板周向应力、肋骨处壳板轴向应力和肋骨应力随之降低。因此,在非均匀环肋复合材料耐压壳设计过程中可以重点考虑较大弹性模量以及适当纤维体积分数的组分材料。
非均匀内部环肋复合材料耐压壳结构新颖,计算数据缺乏,因此在未来同类耐压壳设计中有着十分广阔的应用前景。对于复合材料耐压壳设计分析,应结合结构强度、稳定性以及材料失效,充分考虑各方面限制要求。而传统的设计规范将无法完全适应复合材料耐压壳的力学性能特点,需要研究制定新的具有针对性的设计规范已达到结构最优化的目的。
| [1] |
赵丽滨, 秦田亮, 李嘉玺, 等. 复合材料结构三维有限元分析的材料参数[J].
北京航空航天大学学报, 2010, 36(7): 789–793.
ZHAO Libin, QIN Tianliang, LI Jiaxi, et al. Material parameters in 3D finite element analysis of composite structure[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(7): 789–793. |
| [2] |
杨卓懿. 无人潜器总体方案设计的多学科优化方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012: 108-119.
YANG Zhuoyi. A study on multidisciplinary design optimization method for scheme design of autonomous underwater vehicle[D]. Harbin: Harbin Engineering University, 2012: 108-119. http://cdmd.cnki.com.cn/article/cdmd-10217-1012518466.htm |
| [3] |
李彬. 复合材料潜器起吊工况结构强度及模态分析研究[D]. 哈尔滨: 哈尔滨工程大学, 2013: 23-39.
LI Bin. Strength and modal analysis of composite structure for underwater vehicle in lifting condition[D]. Harbin: Harbin Engineering University, 2013: 23-39. http://cdmd.cnki.com.cn/article/cdmd-10217-1014132501.htm |
| [4] | SAPUAN S M, MUJTABA I M. Composite Materials Technology Neural Network Applications[M]. Florida: CRC Press, 2010: 58 -60. |
| [5] | KIM K, KIM U, PARK J. A study on effects of initial deflection on ultimate strength of ring-stiffened cylindrical structure under external hydrostatic pressure[C]//Proceedings of the 13th International Offshore and Polar Engineering Conference. Hawaii: International Society of Offshore and Polar Engineers, 2003: 506-509. http://cn.bing.com/academic/profile?id=2185666931&encoded=0&v=paper_preview&mkt=zh-cn |
| [6] | SHANG Gaofeng, ZHANG Aifeng, WAN Zhengquan. Optimum design of cylindrical shells under external hydrostatic pressure[J]. Journal of ship mechanics, 2010, 14(12): 1384–1393. |
| [7] | PARK C M, YIM S J. Ultimate strength analysis of ring-stiffened cylinders under hydrostatic pressure[C]//Proceedings of the 12th Conference on OMAE. Glasgow: ASME, 1993: 399-404. |
| [8] | KAW A K. Mechanics of composite materials[M]. 2nd ed. Florida: CRC Press, 2006: 70 -71. |
| [9] |
胡寿松, 何亚群.
粗糙决策理论与应用[M]. 北京: 北京航空航天大学出版社, 2006: 218 -220.
HU Shousong, HE Yaqun. Rough decision theory and its application[M]. Beijing: Beihang University Press, 2006: 218 -220. |
| [10] | KAVURI S N, VENKATASUBRAMANIAN V. Using fuzzy clustering with ellipsoidal units in neural networks for robust fault classification[J]. Computers & chemical engineering, 1993, 17(8): 765–784. |
| [11] |
肖迪, 胡寿松. 一种基于粗糙K-均值的椭球基函数神经网络[J].
南京航空航天大学学报, 2006, 38(3): 321–325.
XIAO Di, HU Shousong. Ellipsoidal basis functional neural network based on rough K-Means[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2006, 38(3): 321–325. |
| [12] |
程妍雪, 庞永杰, 杨卓懿. 基于近似模型技术的复合材料耐压壳性能研究[J].
船舶工程, 2015, 37(4): 74–78.
CHENG Yanxue, PANG Yongjie, YANG Zhuoyi. Research on composite material pressure hulls based on approximation[J]. Ship engineering, 2015, 37(4): 74–78. |
| [13] |
中国船级社. 潜水系统和潜水器入级与建造规范[S]. 北京: 人民交通出版社, 1996: 27-59.
China Classification Society. Rules for classification and construction of diving systems and submersibles[S]. Beijing: China Communications Press, 1996: 27-59. |



