空间机械臂的末端位姿空间有6个变量,需要至少6个自由度以实现可达空间内的灵活控制。但是6自由度机械臂的一种末端位姿只对应有限组关节角空间的解,机械臂的操作灵活度不高[1-2]。相对于6自由度机械臂,冗余机械臂具有灵活度更高和避障性能更好的多方面的优点,但是逆运动学求解比较困难[3]。
在冗余机械臂的运动学解算问题已经进行了很多研究工作。文献[1]采用几何方法,运用特定的寻优指标,搜索与指定末端位姿对应的关节角空间最优解。文献[3]采用加权最小范数法,推导出一种避免计算雅克比矩阵伪逆的优化方法。文献[4-5]采用梯度投影算法,将机械臂之间的最大距离指标作为算法的优化目标函数。文献[6]采用矢量逼近的控制算法,对冗余机器人系统的灵活性进行了研究。文献[7]采用神经网络方法,该方法能够获得运动学逆解,但是计算量庞大,而且算法的收敛和实时性作业限制该方法的应用。文献[8]采用的几何方法虽然精度高、计算快,但是其求解复杂,而且仅针对其对应的机器臂构形不具有通用性。文献[9]以9自由度机器人为研究对象,提出了适于计算机迭代计算的冗余机器人在笛卡儿空间进行手爪姿态可变时的直线轨迹优化算法和手爪经过空间中任意不共线3点决定的平面内圆弧轨迹优化算法。文献[10]提出一种二次计算的方法,运用梯度投影和固定关节组合的方式,提高计算的精度,但是计算量较大。文献[11]利用改进的加权最小范数法求解冗余度机械臂的逆运动学。文献[12]采用扩展雅克比的方法,将空间轨迹作为主要操作任务,而空间的姿态作为次级任务进而实现冗余机器人的运动学解算。文献[13]采用了机器人位置和姿态进行分解方式,将7自由度的冗余机器人分解成4自由度的位置求解,再利用梯度投影法求解剩余关节的运动角度。但该方法损失了冗余机器人的灵活性能。文献[14]提出一种平面冗余度机器人运动学自动寻优方法。文献[15]采用萤火虫群优化算法求冗余机械臂运动学逆解,但该方法收敛速度慢。
本文针对冗余度机械臂的运动学求解方法进行研究,提出一种运用构形平面方法快速求解冗余机器人逆运动学方法,该方法不依赖机器人构形,形式简单,降低了求解的难度,减少计算量,能够按需要得到优化解,具有通用性和快速性。
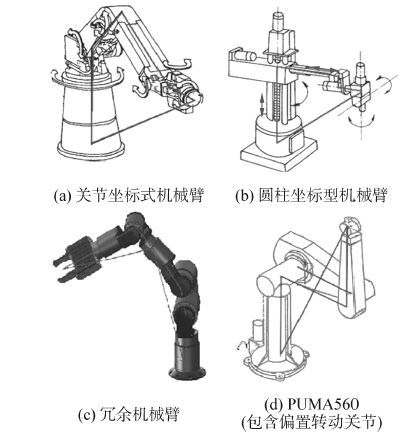
1 构形平面 1.1 机器人常用的工作构形串行形式的机器人具有结构简单、成本低、控制简单、运动空间大等优点,在生产生活中应用最为广泛。如搬运机器人、点焊机器人、喷涂机器人等。经典的串联机器人机构如图 1所示。
|
| 图1 典型的几种工业机器人 Figure 1 Several kinds of typical of industrial robots |
从机器人机构学的运动稳定性、机构的整体设计和力学优化等方面因素考虑,串联形式机器人连杆的中心轴线通常是共面的,如图 1(a)和图 1(b)所示。图 1(c)所示的机械臂,灵活度高,其工作构形的连杆中心轴线可拼成2~3个平面。图 1(d)所示的PUMA560的中心轴线平行于其他连杆组成的平面,这样使得机器人关节的工作范围变大。
1.2 构形平面的引入根据前文对机器人的工作构形特点分析,机器人三维空间机构可由机器人连杆中心轴线围成的空间平面组成,复杂的空间运动学问题可转化成二维平面构形问题。为此,在文献[16]的可重构机器人运动学中引入了构形平面的概念,解决了一些机器人构形的运动学求解问题。对于如图 1(d)引入虚拟构形平面的概念。
定义1 虚拟构形平面:串联机器人结构中若干个连杆的中心轴线组成一个空间几何平面,而其他的连杆的中心轴线平行该平面上,可以通过投影简化的方法进行等效结构处理,形成的空间几何平面称为虚拟构形平面。
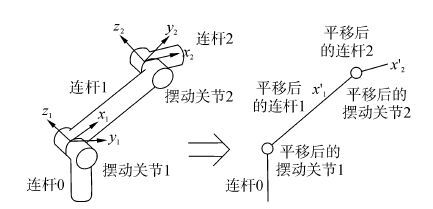
图 2(a)中的摆动关节1、2的关节轴线平行,连杆0和摆动关节1相连,摆动关节1、2之间是连杆1,把连杆1、2的中心轴线平移到连杆0所在的平面里(即虚拟构形平面处理),如图 2(b)所示。通过虚拟构形平面处理,使得构形平面变成统一的形式,便于进行构形平面的匹配。多角度连接关节的运动学模型如图 3所示。
|
| 图2 虚拟构形平面的平面化处理 Figure 2 Plane processing on virtual configuration plane |
|
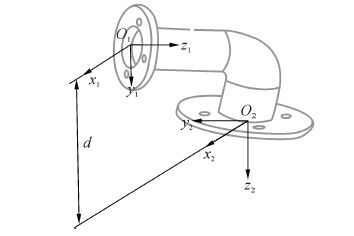
| 图3 多角度连接关节运动学模型 Figure 3 The kinematics model of link module with many connecting angles |
按照文献[16]中构形平面的定义,回转关节可作为机器人工作构形划分构形平面的依据。然而由于多角度连接关节的存在,使得机器人拓扑构形存在多样性,在构形平面划分时需要考虑这种连接关节。多角度形式的连接关节不具有运动能力,仅作为运动关节之间的连接,其运动学模型中没有变量,图 3所示的是一个连接面绕x轴顺时针转动α角度的连接关节,建立其运动学数学模型:
| ${T_{ang\_l}} = \left[ {\matrix{ 1 & 0 & 0 & 0 \cr 0 & {\cos \alpha } & { - \sin \alpha } & 0 \cr 0 & {\sin \alpha } & {\cos \alpha } & d \cr 0 & 0 & 0 & 1 \cr } } \right]$ | (1) |
式中d为多角度连接关节的结构参数。
1.3 构形平面的表达形式为便于构形平面匹配,需简化其运动学模型。构形平面以角度连接关节和回转关节进行区分。当角度连接关节的连接面的连接角度为0°或180°时,可通过虚拟构形平面的方式处理,使构形平面变成统一的形式,以便于进行构形平面的匹配;否则,该角度连接关节可以看作旋转角固定的回转关节,因此不能采用虚拟构形平面处理的方法,使得连杆在一个虚拟构形平面里。
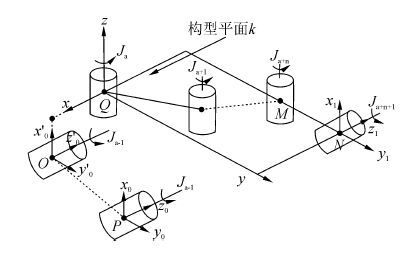
一个通用形式的构形平面如图 4所示,P为该构形平面的构形平面中心,O为工作构形通过虚拟构形平面处理后的构形平面中心;若无需进行虚拟构形平面处理,O与P重合;Q为该构形平面的第1个摇摆关节的起始点,O与Q之间存在连接面绕y轴顺时针转动90°的连接关节,M与N之间存在连接面绕y轴逆时针转动90°的连接关节,该构形平面由n+2个关节组成,Ja+i(i=0,1,…,n+1)为第i个关节的旋转轴线,其中Ja+i(i=0,1,…,n)为摇摆关节旋转轴线,与Q点坐标系的z轴平行;Ja+n+1为回转关节旋转轴线,与N点坐标系的z1轴平行。
|
| 图4 构形平面的运动学模型 Figure 4 Kinematics model of the configuration plane |
经过虚拟构形平面平面化处理后的附加转换矩阵:
| ${{T}_{ang\_l}}=\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & d \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$ | (2) |
该矩阵中px 、py、pz分别为构形平面化处理后的构形平面中心补偿的三维空间坐标值。
由式(1)可知,Q点和O点的连接面绕y轴顺时针转动90°的连接关节的数学模型用Tang_lOQ表示,d0为该连接关节的结构参数。
构形平面k中,旋转轴为Ja+i(i=0,1,…,n)的摆动关节或回转关节的运动学模型为
| ${T_{si}}\left[ {\matrix{ {\cos {\theta _i}} & { - \sin {\theta _i}} & 0 & 0 \cr {\sin {\theta _i}} & {\cos {\theta _i}} & 0 & 0 \cr 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & 1 \cr } } \right]$ | (3) |
式中θi(i=1,2,…,n+1)为转动关节或摆动关节的旋转角。
由于在构形平面k内的连杆关节是一般形式的连杆关节,即连接角度为0,则连杆i(i=1,2,…,n)数学模型用模型用Tli表示。构形平面内移动关节的数学模型用Tpi表示,di、li(i=1,2,…,n)分别是连接关节和移动关节的结构参数。
依次相连摇摆关节和移动关节组成的转换矩阵为
| $~{{T}_{s}}=\underset{i=1}{\overset{n}{\mathop{\prod }}}\,(\text{ }{{T}_{si}}\cdot \text{ }{{T}_{li}}\cdot \text{ }{{T}_{pj}})=\left[ \begin{matrix} \cos \beta & -\sin \beta & 0 & p_{x}^{'} \\ \sin \beta & \cos \beta & 0 & p_{y}^{'} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$ | (4) |
式中:β=θ1+θ2…+θn ,θi(i=1,2,…,n)为第i个摇摆关节转动角度,
p′x=-(dn-1+ln)sin(θ1+θ2+…+θn)-…-(d2+l2)sin(θ1+θ2)-(d1+l1)sin θ1p′y=(dn-1+ln)cos(θ1+θ2+…+θn)+…+(d2+l2)cos(θ1+θ2)+(d1+l1)cos θ1
当第i个摆动关节与其相连的下一个关节不是移动关节时,li=0。否则的话li不等于零。
M点与N点间的连接面绕y轴逆时针转动90°的连接关节的数学模型用Tang_lMN表示,p″y为该连接关节的结构参数。
定义
| $\begin{align} & {{T}_{H}}={}_{p}^{O}T\cdot {{T}_{ang\_lOQ}}\cdot {{T}_{s}}\cdot {{T}_{ang\_lMN}}= \\ & \left[ \begin{matrix} 1 & 0 & 0 & {{p}_{x}} \\ 0 & \cos \beta & -\sin \beta & {{p}_{y}}+p_{y}^{'}+p_{y}^{''}\cos \beta \\ 0 & \sin \beta & \cos \beta & {{d}_{0}}+{{p}_{z}}-p_{x}^{'}+p_{y}^{''}\sin \beta \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] \\ \end{align}$ | (5) |
构形平面k末端点在二维空间相对P点坐标运动学简化模型表达为
| ${{T}_{GXPMk}}={{T}_{H}}\cdot {{T}_{s(n+1)}}$ | (6) |
由式(6)可知,构形平面中,摆动关节、移动关节和连接关节完成构形平面的位置要求,摆动关节和回转关节完成构形平面的姿态要求。
2 基于构形平面的运动学求解方法 2.1 构形平面的划分根据文献[16]定义的构形平面和上述引入的虚拟构形平面的特点,我们知道在冗余机器人拓扑结构中,其工作构形由若干个构形平面组成,如图 5所示,其中关节a是回转关节,关节b是多角度连接关节。回转关节和多角度连接关节是区分构形平面的依据。组成机器人工作构形的构形平面的个数小于机器人的自由度数,通过对构形平面内和构形平面间的关节进行运动学分析,可以快速求得可冗余机器人的逆运动学解。
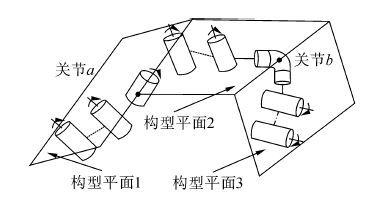
|
| 图5 构形平面组成的冗余机器人工作构形 Figure 5 The work configuration of redundant robot composed of configuration planes |
设目标点的位姿矩阵TS为
| ${{T}_{S}}={{T}_{GXPM1}}\cdot {{T}_{GXPM2}}\cdot {{T}_{GXPM3}}$ | (7) |
由式(6)可知,构形平面中的摆动关节、移动关节和连接关节完成构形平面的位置要求,构形平面终点在构形平面起点坐标系下的空间坐标为
| ${{P}_{GXPM}}=({{T}_{GXPM}}\left( 1,4 \right),{{T}_{GXPM}}\left( 2,4 \right),{{T}_{GXPM}}\left( 3,4 \right))$ | (8) |
目标点的空间坐标为
| ${{P}_{S}}=({{T}_{S}}\left( 1,4 \right),{{T}_{S}}\left( 2,4 \right),{{T}_{S}}\left( 3,4 \right))$ | (9) |
在位置解算时,首先把机器人构形看成一个构形平面,由式(7)可得
| $\|{{P}_{S}}\|=\|{{P}_{GXPM}}\|$ | (10) |
由式 (10)可以求得构形平面内的β(即所有摆动关节的转动角之和)的值。
采用如下的方法求θi(i=1,2,…,n-1) (即构形平面内第i个摆动关节的转动角)的值。
对于如图 6所示的一般形式的构形平面,采用基于矢量投影的方法进行自动求解,既满足:
| $\|p\|=\sum\limits_{i=1}^{n}{{{k}_{i}}}({{l}_{i}}+{{d}_{i}})$ | (11) |
式中:‖p‖为末端矢量的范数;ki为第i个关节杆臂在矢量p上投影与该关节杆臂的比值,由于矢量投影具有方向性,因此ki具有正负号,其表达式为
| ${{k}_{i}}=\cos \theta _{i}^{'}$ | (12) |
式中θ′i为第i个关节杆臂与目标点矢量p的夹角。
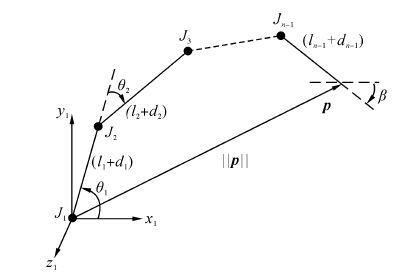
|
| 图6 构形平面的二维空间一般形式 Figure 6 Two-dimensional space of the general form ofthe configuration plane |
如果两个构形平面中有一个构形平面的工作空间固定,则这个构形平面的匹配点的空间坐标值就是一定的,经过构形转化后,可直接用矢量投影法求解构形平面内关节的关节变量。如果两个构形平面的工作空间都是不确定的,按照前一个构形平面承担位置要求,后一个构形平面进行位置补充的原则,进行构形平面的位置匹配。
在多构形平面的位置匹配上,关键是在各关节的运动范围内找到构形平面间的位置匹配点。按照构形平面工作空间的表示方法,在目标点和基坐标系原点连线的空间矢量上,找到构形平面间的匹配点,这样构形平面的位置匹配就确定了。
2.3 构形平面的姿态解算由于构形平面内的摆动关节和回转关节完成构形平面内的姿态要求,上文已完成构形平面的位置解算,因此在构形平面的运动学模型里只有一个参数是未知的,即回转关节的关节角。假如在冗余机械臂的拓扑结构中,存在多个构形平面,则需要进行多个构形平面的姿态匹配。把通过构形平面位置解算求得的摆动关节的关节角之和β代入式(5),则TH 为已知量。
设4个构形平面组成冗余机械臂的工作构形,由式(7)得
| $\begin{align} & {{T}_{S}}={{T}_{GXPM1}}\cdot {{T}_{GXPM2}}\cdot {{T}_{GXPM3}}\cdot {{T}_{GXPM4}}= \\ & {{T}_{H}}_{1}\cdot {{T}_{sn}}\cdot {{T}_{H}}_{2}\cdot {{T}_{sm}}\cdot {{T}_{H}}_{3}\cdot {{T}_{sk}}\cdot {{T}_{H}}_{4}\cdot {{T}_{sj}} \\ \end{align}$ | (13) |
在式(13)中,THi(i=1,2,3,4)是已知量,使得式(13)中等式两边矩阵的前三列前三行元素对应相等,即可求得回转关节的关节角,完成姿态解算。
值得说明的是,这里所求的各关节角值还需要进行校验,考查是否超出各关节角的运动范围,如超出,需在构形平面的位置解算部分重新计算,进而直接调整其他关节角。
实际计算中,由于三角函数计算存在多解的状态,需要进行选取确定。
3 实例验证 3.1 冗余机械臂数学建模以文献[3]设计的冗余机械臂作为研究对象,如图 7所示。该机械臂由3个运动关节组成:肩、肘、腕。具有7个自由度,肩关节由3个自由度,肘关节有2个自由度,腕关节也有2个自由度,按照人体构造设计。各关节运动范围如表 1所示。
由于冗余机械臂可简化成7自由度的连杆结构,杆件之间由旋转关节连接,每个旋转关节为一个独立自由度,完成单轴旋转运动[17]。采用模块化的建模方法,将各个关节进行分解成单自由度关节形式,模型如图 7所示。冗余机械臂的结构参数如表 1所示。
| 关节i | 运动范围θi | 连杆i | 连杆参数di/m |
| 1 | [-180°,180°] | 1 | 0 |
| 2 | [-90°,90°] | 2 | 0.2 |
| 3 | [-90°,90°] | 3 | 0.8 |
| 4 | [-90°,90°] | 4 | 0.8 |
| 5 | [-90°,90°] | 5 | 0.2 |
| 6 | [-90°,90°] | 6 | 0 |
| 7 | [-180°,180°] | 7 | 0.4 |
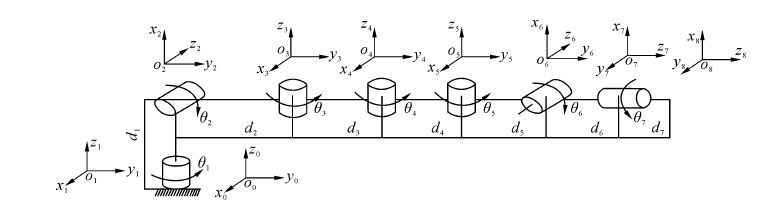
|
| 图7 冗余机械臂运动学模型 Figure 7 Kinematics model of redundant manipulator |
基于模块建模方法,各关节运动学模型如下:
| ${{T}_{i}}=\left[ \begin{matrix} {{\cos }_{{{\theta }_{i}}}} & -\sin {{\theta }_{i}} & 0 & 0 \\ \sin {{\theta }_{i}} & {{\cos }_{{{\theta }_{i}}}} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$ | (14) |
式中:θi是第i(i=1,2,…,7)个关节的关节变量,关节1和关节2之间是多角度形式的连杆,其运动学模型为
| ${{T}_{ang\_l12}}=\left[ \begin{matrix} 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & {{d}_{1}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$ | (15) |
关节2和关节3之间是多角度形式的连杆,其运动学模型为
| ${{T}_{ang\_l23}}=\left[ \begin{matrix} 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & {{d}_{2}} \\ -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$ | (16) |
关节3、4、5之间是一般形式的连杆,其运动学模型为
| ${{T}_{134}}=\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & {{d}_{3}} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$ | (17) |
| ${{T}_{l45}}=\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & {{d}_{4}} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$ | (18) |
关节5和关节6之间是多角度形式的连杆,其运动学模型为
| ${{T}_{ang\_l56}}=\left[ \begin{matrix} 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & {{d}_{5}} \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$ | (19) |
关节6和关节7之间是多角度形式的连杆,其运动学模型为
| ${{T}_{ang\_l67}}=\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & {{d}_{6}} \\ 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$ | (20) |
冗余机械臂末端的运动学模型为
| ${{T}_{8}}=\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & {{d}_{8}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$ | (21) |
冗余机械臂目标点的位姿矩阵如下:
| ${{T}_{S}}=\left[ \begin{matrix} 0.4294 & 0.7077 & -0.5610 & -0.6728 \\ 0.5489 & 0.2888 & 0.7844 & 1.9158 \\ 0.7172 & -0.6448 & -0.2664 & -1.1321 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$ | (22) |
根据冗余机械臂的工作构形参数可知,参数d1 和d6都为0,意味着O1和O2,O6和O7是两两重合的,而由于结构的原因,O1和O2相对机械臂原点坐标的位置是固定的,而O6和O7相对机械臂末端点的位置也是固定的。因此在进行机械臂运动学求解时,关节1、2、6、7主要承担机械臂末端的姿态要求。关节3、4和5的转动轴是相互平行的,其中心轴线组成一个二维空间的平面,因此这三个关节满足机械臂空间位置要求。
按照构形平面的定义,回转关节作为划分构形平面主要依据,而该机械臂的工作构形中还存在多角度连接关节,如连接关节12、23、56和67。把回转关节1看成构形平面1,连接关节12和关节2组成构形平面2,关节3、4、5、6和连接关节23、34、45、56组成构形平面3,连接关节67和关节7组成构形平面4。由式(6)得
| ${{T}_{GXPM1}}={{T}_{1}}=\left[ \begin{matrix} \cos {{\theta }_{1}} & -\sin {{\theta }_{1}} & 0 & 0 \\ \sin {{\theta }_{1}} & \cos {{\theta }_{1}} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$ | (23) |
| ${{T}_{GXPM2}}={{T}_{ang\_l12}}\cdot {{T}_{2}}=\left[ \begin{matrix} 0 & 0 & -1 & 0 \\ \sin {{\theta }_{2}} & \cos {{\theta }_{2}} & 0 & 0 \\ \cos {{\theta }_{2}} & -\sin {{\theta }_{2}} & 0 & {{d}_{1}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$ | (24) |
| ${{T}_{GXPM3}}={{T}_{H}}\cdot {{T}_{6}}$ | (25) |
| $\begin{align} & {{T}_{H}}={{T}_{ang\_l23}}\cdot {{T}_{3}}\cdot {{T}_{l34}}\cdot {{T}_{4}}\cdot {{T}_{l45}}\cdot {{T}_{5}}\cdot {{T}_{ang\_l56}}= \\ & \left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & \cos \beta & -\sin \beta & y \\ 0 & \sin \beta & \cos \beta & z \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] \\ \end{align}$ | (26) |
式(26)中
β=θ3+θ4+θ5 y=d2+d3cos θ3+d4cos(θ3+θ4)+d5cos β z=d3sin θ3+d4sin(θ3+θ4)+d5sin β
| $\begin{align} & {{T}_{GXPM4}}={{T}_{ang\_l67}}\cdot {{T}_{7}}= \\ & \left[ \begin{matrix} \cos {{\theta }_{7}} & -\sin {{\theta }_{7}} & 0 & 0 \\ 0 & 0 & 1 & {{d}_{6}} \\ -\sin {{\theta }_{7}} & -\cos {{\theta }_{7}} & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right] \\ \end{align}$ | (27) |
由式(7)可知:
| ${{T}_{S}}={{T}_{GXPM1}}\cdot {{T}_{GXPM2}}\cdot {{T}_{GXPM3}}\cdot {{T}_{GXPM4}}\cdot {{T}_{8}}$ | (28) |
由于d7是已知的,因此T8是已知的,设TG6=TS·T8-1,把式(22)代入式(28)得
| ${{T}_{G6}}=\left[ \begin{matrix} 0.4294 & 0.7077 & -0.5610 & -0.4484 \\ 0.5489 & 0.2888 & 0.7844 & 1.6020 \\ 0.7172 & -0.6448 & -0.2644 & -1.0263 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$ | (29) |
于是
| $\begin{align} & {{T}_{G6}}={{T}_{GXPM1}}\cdot {{T}_{GXPM2}}\cdot {{T}_{GXPM3}}\cdot {{T}_{GXPM4}}= \\ & {{T}_{GXPM1}}\cdot {{T}_{GXPM2}}\cdot {{T}_{H}}\cdot {{T}_{6}}\cdot {{T}_{GXPM4}} \\ \end{align}$ | (30) |
由于d1、d6为0,则O1、O2与O0重合,O6与O7重合,可知构形平面3承担冗余机械臂末端位置解算。
可知构形平面3的中点即点O6的空间坐标为
| ${{P}_{{{O}_{6}}}}=\left[ \begin{matrix} -0.4484 & 1.6020 & -1.026 \\ \end{matrix} \right]$ | (31) |
因此构形平面3的起点即O2到构形平面3的中点即点O6长度L为
| $L=\|{{P}_{{{O}_{6}}}}\|=1.9547$ | (32) |
在构形平面3中,已知L长度,按照矢量投影的方法,由于是多解的状态,也没有空间避障的要求,而且构形平面3中的3个关节角都没有超出运动范围,因采用3个关节运动角度相等的方式进行求解,易得
| ${{\theta }_{3}}={{\theta }_{4}}={{\theta }_{5}}=15.20{}^\circ $ | (33) |
把式(33)代入式(26),可得
| ${{T}_{H}}=\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 0.6997 & -0.7145 & 1.6620 \\ 0 & 0.7145 & 0.6997 & 0.6146 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]$ | (34) |
把式(34)代入式(30),在式(30)中,使得等式两边矩阵对应位置的元素相等,可依次求得各关节的关节变量。因此冗余机械臂的逆运动学解如下:θ1=-11.45°、θ2=34.72°、θ3=15.20°、θ4=15.20°、θ5=15.20°、θ6=-9.04°、θ7=17°。
该方法避免了冗余机械臂在逆运动学求解过程中出现的奇异值,而且采用半解析的方式,求解精度更高,求解速度更快。
4 结论1) 本文通过分析总结串联机器人工作构形的特点,引入虚拟构形平面的概念,并提出了构形平面理论。进而采用构形平面方法解决冗余机械臂的逆运动学问题。
2) 冗余机械臂的拓扑结构可分解为若干个构形平面,通过对构形平面进行建模和匹配,实现冗余机械臂工作构形的位置和姿态匹配。这钟方法使得复杂的机械臂拓扑结构简单化,而且得到的逆运动学解中避免了奇异解的产生。
3) 采用半解析的方式,使得该方法形式简洁,具有很高的精度和求解速度,因此具有很强的实用性和通用性。而且构形平面的方法为冗余机械臂的运动学优化、轨迹规划、空间避障任务奠定了基础。
| [1] |
陈鹏, 刘璐, 余飞, 等. 一种仿人机械臂的运动学逆解的几何求解方法[J].
机器人, 2012, 34(2): 211–216.
DOI:10.3724/SP.J.1218.2012.00211
CHEN Peng, LIU Lu, YU Fei, et al. A geometrical method for inverse kinematics of a kind of humanoid manipulator[J]. Robot, 2012, 34(2): 211–216. |
| [2] | PRIMROSE E J F. On the input-output equation of the general 7R-mechanism[J]. Mechanism and machine theory, 1986, 21(6): 509–510. |
| [3] |
阳方平, 李洪谊, 王越超, 等. 一种求解冗余机械臂逆运动学的优化方法[J].
机器人, 2012, 34(1): 17–21.
DOI:10.3724/SPJ.1218.2012.00017
YANG Fangping, LI Hongyi, WANG Yuechao, et al. An optimization method for solving the inverse kinematics of redundant manipulator[J]. Robot, 2012, 34(1): 17–21. |
| [4] |
马如奇, 王伟东, 董为, 等. 基于改进梯度投影算法的腹腔微创外科手术机器人系统术前摆位分析[J].
机器人, 2014, 36(2): 156–163.
MA Ruqi, WANG Weidong, DONG Wei, et al. Preoperative positioning analysis of the celiac minimally invasive surgery robotic system based on an improved gradient projection algorithm[J]. Robot, 2014, 36(2): 156–163. |
| [5] | DUBEY R V, EULER J A, BABCOCK S M. Real-time implementation of an optimization scheme for seven-degree-of-freedom redundant manipulators[J]. IEEE transactions on robotics and automation, 1991, 7(5): 579–588. |
| [6] |
张秋豪, 孙汉旭, 魏世民. 改善冗余度机器人灵活性的研究[J].
北京邮电大学学报, 2004, 27(4): 74–77.
ZHANG Qiuhao, SUN Hanxu, WEI Shimin. A new method for improving flexibility of redundant robot[J]. Journal of Beijing University of Posts and Telecommunications, 2004, 27(4): 74–77. |
| [7] | XIA Youshen, WANG Jun. A dual neural network for kinematic control of redundant robot manipulators[J]. IEEE transactions on systems, man, and cybernetics, part B:cybernetics, 2001, 31(1): 147–154. |
| [8] | MOHAMED H A F, YAHYA S, MOGHAVVEMI M, et al. A new inverse kinematics method for three dimensional redundant manipulators[C]//ICCAS-SICE. Fukuoka, 2009:1557-1562. |
| [9] |
贾庆轩, 褚明, 孙汉旭, 等. 9-DOF超冗余机器人轨迹规划优化算法[J].
北京邮电大学学报, 2008, 31(2): 20–25.
JIA Qingxuan, CHU Ming, SUN Hanxu, et al. Research on the optimal algorithm for trajectory planning of a 9-DOF hyper-redundant robot[J]. Journal of Beijing University of Posts and Telecommunications, 2008, 31(2): 20–25. |
| [10] |
祖迪, 吴镇炜, 谈大龙. 一种冗余机器人逆运动学求解的有效方法[J].
机械工程学报, 2005, 41(6): 71–75.
DOI:10.3901/JME.2005.06.071
ZU Di, WU Zhenwei, TAN Dalong. Efficient inverse kinematic solution for redundant manipulators[J]. Chinese journal of mechanical engineering, 2005, 41(6): 71–75. |
| [11] | JIA Qingxuan, HONG Lei, SUN Hanxu. An improved algorithm for inverse kinematics solution of redundant modular robots[C]//Proceedings of the International Technology and Innovation Conference. Hangzhou, 2006:2087-2092. |
| [12] |
谢宗武, 孙奎, 刘宏. 扩展雅克比方法的冗余度机器人逆运动学应用[J].
哈尔滨工业大学学报, 2009, 41(5): 34–37.
XIE Zongwu, SUN Kui, LIU Hong. Application study on inverse kinematics algorithm of redundant manipulator based on extended Jacobian method[J]. Journal of Harbin Institute of Technology, 2009, 41(5): 34–37. |
| [13] |
潘博, 付宜利, 杨宗鹏, 等. 面向冗余机器人实时控制的逆运动学求解有效方法[J].
控制与决策, 2009, 24(2): 176–180.
PAN Bo, FU Yili, YANG Zongpeng, et al. Efficient inverse kinematics solution for redundant robots to realtime control[J]. Control and decision, 2009, 24(2): 176–180. |
| [14] |
霍希建, 刘伊威, 姜力, 等. 平面冗余自由度机器人自寻优运动优化方法[J].
哈尔滨工程大学学报, 2015, 36(4): 528–533.
HUO Xijian, LIU Yiwei, JIANG Li, et al. Self-optimizing kinematic optimization method of planar redundant robots[J]. Journal of Harbin Engineering University, 2015, 36(4): 528–533. |
| [15] |
罗天洪, 陈才, 李富盈. 基于时变萤火虫群算法的冗余机器人手臂逆解[J].
计算机集成系统, 2016, 22(2): 576–582.
LUO Tianhong, CHEN Cai, LI Fuying. Inverse solution of redundant robot arm based on glowworm swarm optimization algorithm of time-varying[J]. Computer integrated manufacturing systems, 2016, 22(2): 576–582. |
| [16] |
魏延辉, 赵杰, 高延滨, 等. 一种可重构机器人运动学求解方法[J].
哈尔滨工业大学学报, 2010, 42(1): 133–137.
WEI Yanhui, ZHAO Jie, GAO Yanbin, et al. A solution method for kinematics of reconfigurable modular robots[J]. Journal of Harbin Institute of Technology, 2010, 42(1): 133–137. |
| [17] | ASFOUR T, REGENSTEIN K, AZAD P, et al. ARMAR-Ⅲ:An integrated humanoid platform for sensory-motor control[C]//Proceedings of the 6th IEEE-RAS International Conference on Humanoid Robots. Piscataway, NJ, USA, 2006:169-175. |



