2. Marine Engineering College, Dalian Maritime University, Dalian 116026, China
摩擦副磨合过程中产生的摩擦振动现象,蕴含着反映磨合状态的信息[1]。摩擦振动信号是微弱信号,往往埋没于背景噪声之中,未经处理的摩擦振动信号不能真实地反映摩擦振动特征[2]。因此,如何对获得的摩擦振动信号进行消噪,以及根据提取的有用信号找出摩擦振动信号的特征,是摩擦振动研究的关键问题。
经验模式分解(empirical mode decomposition, EMD)是美籍华人Huang等[3] 1998年提出的一种自适应数据驱动的信号处理方法,能清晰地分辨出非平稳非线性复杂数据的内蕴模式,但存在模式混叠问题[4]。Wu等[5]基于白噪声信号的统计特征,提出了总体经验模式分解(ensemble empirical mode decomposition, EEMD),解决了EMD模式混叠问题,该方法成功地应用于信号处理[6]、故障诊断[7-8]等的研究。多重分形去趋势波动分析(multifractal detrended fluctuation analysis, MFDFA)是Kantelhardt[9]于2002年提出的基于去趋势波动分析(detrended fluctuation analysis, DFA)的非稳态时间序列分析方法,可以有效地分析非线性非平稳信号的多重分形特征。该方法已被应用到地质学[10]、脑电波信号处理[11]、交通流分析[12]、金融市场[13]等领域,取得很好的效果。摩擦振动是摩擦副磨合磨损过程中产生的现象,其变化规律必然能反映系统摩擦学的状态和特征[14]。李国宾等[2]应用谐波小波提取摩擦振动的特征,黄朝明等应用时频谱图[15]研究了特征参数与摩擦振动的关系,孙迪等应用奇异值分解[16]和混沌吸引子[17]探讨了摩擦振动在磨合磨损过程中的变化规律,通过摩擦振动识别磨合磨损状态和特征。本文针对船用柴油机缸套—活塞环摩擦副摩擦磨损试验过程中获得的摩擦振动信号进行EEMD分解,获得若干个无模式混叠的IMF分量,根据摩擦振动信号的特点,选取包含摩擦振动信号特征的IMF分量重构摩擦振动特征信号。应用多重分形去趋势波动分析算法对摩擦振动特征信号进行分析,得到摩擦振动信号的Hurst指数、多重分形标度指数以及多重分形谱。并求取摩擦振动信号多重分形谱的宽度、极大值、维差以及驻点值,实现特征参数对摩擦副摩擦磨损状态的表征,为基于摩擦振动信号的机械摩擦副摩擦磨损行为的研究提供了新的途径。
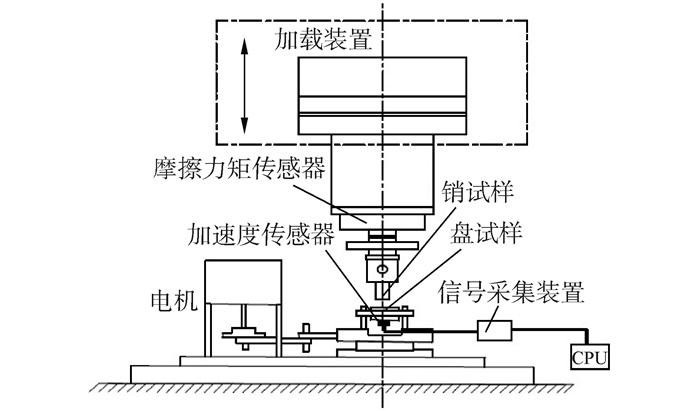
1 实验部分 1.1 试验材料与方法试验的设备采用CFT-I型摩擦磨损试验机(见图 1),采用销-盘摩擦副作为配副。试样均用线切割机从船用柴油机缸套和活塞环截取,盘试样作为下式样,取自船用柴油机的缸套,φ30 mm,原始表面粗糙度Ra=1.72 μm,材质为合金铸铁,硬度HV300~400;销试样作为上试样,取自和缸套配对的活塞环,矩形截面尺寸3 mm×4 mm, 原始表面粗糙度Ra=0.67 μm,材质为合金铸铁,硬度HV600~720。上试样用专用夹具固定不动;下试样由专用夹具固定在台架上,台架经电机驱动的偏心机构和连杆机构将回转运动转变为往复运动,运动行程5 mm,电机转速600 r/min,选用船用Mobilgard-412润滑油进行滴油润滑。载荷通过加载弹簧经销试样施加到盘试样上,施加的正压力为30 N,名义接触载荷2.5 MPa,试验时间600 min。
|
| 图1 CFT-I型摩擦磨损试验机原理图 Figure 1 Schematic diagram of CFT-I tester |
应用NI公司生产的PXIe-1071信号采集系统采集摩擦振动信号,采样频率25 600 Hz,采样点数4 096,采样间隔2 min,每次采样时间0.16 s。测量摩擦振动信号的传感器采用PCB PIEZOTRONICS公司生产的356A16型ICP三轴加速度传感器,灵敏度100 mV/g,量程50 g。加速度传感器水平安装在盘试样下方,随盘试样一起做往复运动。
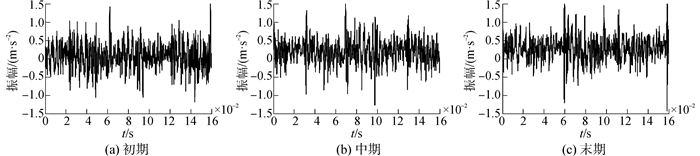
图 2为缸套活塞环摩擦副摩擦磨损试验在初期、中期、末期采集的摩擦振动信号时域波形。从图 2可以看出,试验获得的摩擦振动信号是非线性非平稳信号,微弱的摩擦振动信号埋没于背景噪声中,信号波动复杂,时域波形体现不出变化,如果直接采用此信号来分析,则无法提取正确的摩擦振动特征。
|
| 图2 摩擦振动信号的时域波形 Figure 2 Waveform of frictional vibration |
EEMD方法的本质是将待分析信号与高斯白噪声叠加,再进行多次EMD分解,利用具有频率均匀分布统计特性的高斯白噪声使待分析信号在不同尺度上具有连续性,从而降低各IMF分量的模式混叠程度。根据零均值高斯白噪声的特性,通过若干组IMF总体平均使加入的白噪声相互抵消,还原被分析信号。
EEMD算法归纳如下:
1)初始化EMD总体平均次数M和加入的白噪声幅值系数k,令m=1。
2)执行第m次EMD分解:
①对待分析信号x(t)加入一个给定幅度的高斯白噪声序列nm(t),得到第m次加噪后的信号xm(t):
| $ {x_m}\left( t \right) = x\left( t \right) + k \cdot {n_m}\left( t \right) $ | (1) |
②用EMD分解xm(t),得到一组IMFcj, m(j=1,2,…,I),其中,cj, m为第m次分解得到的第j个IMF;
③若m<M,则返回步骤2),m=m+1;
3)对M次分解得到的各IMF计算均值:
| $ \begin{array}{l} {{\bar C}_j} = \frac{1}{M}\sum\limits_{m = 1}^M {{c_{j,m}}} \\ j = 1,2, \cdots ,I;m = 1,2, \cdots ,M \end{array} $ | (2) |
4)输出Cj(j=1,2,…,I)作为EEMD分解得到的第j个IMF。
白噪声幅值系数k影响着信号的分解精度,通常k的取值范围是0.1~0.4。总体平均次数M影响着信号的消噪能力和计算时间,当M增大到一定值后,EEMD对信号的消噪效果增强不明显,但计算时间显著增加。
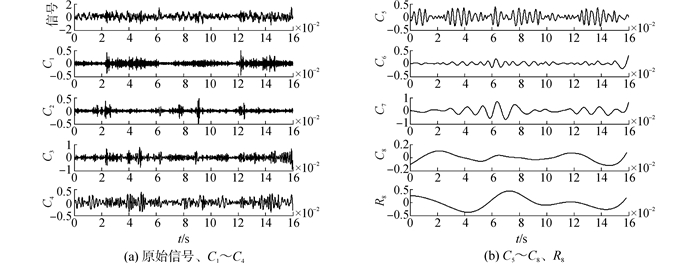
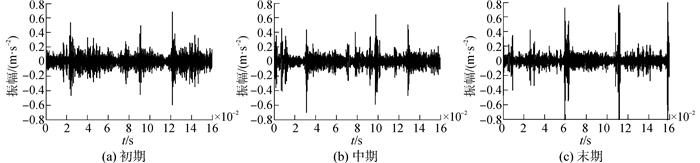
应用总体经验模式分解对摩擦振动信号进行分解,白噪声幅值系数k取0.1,总体平均次数M取100。图 3是缸套活塞环摩擦副摩擦磨损试验初期的摩擦振动信号EEMD分解结果, 分解得到8个IMF分量C1~C8和一个残差r8,限于篇幅,摩擦磨损试验中期、后期的摩擦振动EEMD分解结果图从略。从图 3可以看出,分解得到的IMF分量可使试验获得的原始摩擦振动信号在不同的分辨率下显现出来,摩擦振动信号具有频率高振幅小等特点[2],因此选择前两个分量C1、C2重新合成摩擦振动特征信号。图 4为选择的IMF分量重构得到的摩擦振动特征信号,可以看出IMF分量重构信号的振幅随着磨合的进行呈现明显的趋势变化,摩擦振动的冲击信息显著出现。
|
| 图3 试验初期摩擦振动信号EEMD分解结果 Figure 3 EEMD decomposition results of frictional vibration signal at the beginning of the test |
|
| 图4 IMF分量合成的摩擦振动特征信号 Figure 4 The recombined frictional vibration characteristic signal of IMF |
多重分形去趋势波动分析方法是Kantelhardt在去趋势波动分析的基础上提出的非稳态时间序列分析方法,MFDFA 算法步骤如下:
1)计算时间序列{xi}(i=1,2,…,N)的离差序列Y(i):
| $ Y\left( i \right) = \sum\limits_{k = 1}^i {\left( {{x_k} - \bar x} \right)} \left( {i = 1,2, \cdots ,N} \right) $ | (3) |
式中: x是均值。
2)将序列Y(i)划分成Ns=int(N/s)个区间,每个连续不重叠的区间均含有s个数据,当N不能整除s时,Y(i)会有数据剩余,为数据不丢失,再从序列反向开始重复这一分割过程,得到2Ns个等长小区间,包含序列的所有数据。
3)计算均方误差F2(s, v),以区间(v=1,2,…,2Ns)为例,进行k阶多项式拟合:
| $ {y_v}\left( i \right) = {a_1}{i^k} + {a_2}{i^{k - 1}} + \cdots + {a_{k + 1}}\left( {k = 1,2, \cdots } \right) $ | (4) |
对于区间(v=1,2,…,Ns):
| $ {F^2}\left( {s,v} \right) = \frac{1}{s}\sum\limits_{i = 1}^s {{{\left\{ {Y\left[ {v - 1} \right]s + i - {y_v}\left( i \right)} \right\}}^2}} $ | (5) |
对于区间(v=Ns+1,…,2Ns):
| $ {F^2}\left( {s,v} \right) = \frac{1}{s}\sum\limits_{i = 1}^s {{{\left\{ {Y\left[ {N - \left( {v - {N_s}} \right)s + i} \right] - {y_v}\left( i \right)} \right\}}^2}} $ | (6) |
4)计算q阶波动函数F(q, s):
| $ F\left( {q,s} \right) = {\left\{ {\frac{1}{{2{N_s}}}\sum\limits_{v = 1}^{2{N_s}} {{{\left[ {{F^2}\left( {s,v} \right)} \right]}^{q/2}}} } \right\}^{1/q}} $ | (7) |
式中,q为非0实数。
5)阶数q依次取某数值,尺度s取不同值,重复步骤2)~4),计算F(q, s)对q的双对数值,确定波动函数与尺度之间存在的幂率关系:
| $ F\left( {q,s} \right) \sim {s^{h\left( q \right)}} $ | (8) |
式中,h(q)为Hurst指数。
6)计算多重分形标度指数τ(q):
| $ \tau \left( q \right) = qh\left( q \right) - 1 $ | (9) |
7)计算多重分形参数α、f(α):
| $ \alpha = \tau \left( q \right),f\left( \alpha \right) = q\alpha - \tau \left( q \right) $ | (10) |
式中:α为奇异指数;f(α)表示由α确定的序列子集的维数,值越大表示时间序列分布越不均匀,分形强度越大。
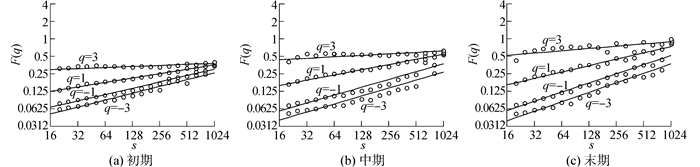
3.2 摩擦振动信号的多重分形去趋势波动分析应用多重分形去趋势波动分析算法分析摩擦振动特征信号,取尺度s为16~1 024均分的19个尺度,取阶数q分别-3、-1、1、3,图 5为分析摩擦振动初期、中期、末期信号得到的双对数回归线。尺度越小则取数据周期小,因此在不同阶数下,小尺度能够更明显区分各局部区域摩擦振动信号的小波动和大波动,而大尺度则区分不明显。从图 5可以看出,在不同的阶数q下,小尺度s计算得到的波动函数值比大尺度s计算得到的波动函数值差异更明显,回归线的斜率H(q)即Hurst指数[9]。图 5中摩擦振动初期、中期、末期信号不同阶数下的Hurst指数体现出渐进变化。如果0<H(q)<0.5,时间序列具有反持续性,即摩擦振动与之前的趋势相反,值越小反持续性越强;H(q)=0.5,时间序列可以用随机游走来描述;0.5<H(q)<1,时间序列具有持续性,即摩擦振动保持之前的趋势,值越大持续性越强。
|
| 图5 摩擦振动信号多重分形去趋势分析双对数回归线 Figure 5 Double logarithmic regression line of multifractal detrended fluctuation analysis of frictional vibration signal |
摩擦磨损试验摩擦副磨合初期,摩擦副表面粗糙度较大,磨合过程产生的能量较大,摩擦振动剧烈。随着试验的进行,摩擦副表面粗糙度逐渐减小,盘试样粗糙度从最初的1.72 μm降至1.21 μm,激发的摩擦振动强度减小,摩擦磨损逐渐趋于稳定。
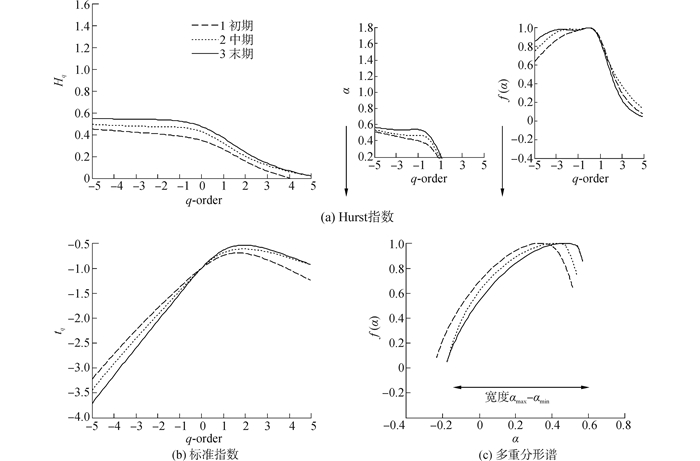
图 6(a)为由式(8)计算得到的摩擦振动信号在不同阶数q下的Hurst指数,使参数化时间序列的多重分形结构,其中阶数q取值-5~5均分的101个值,阶数q为-3,-1, 1, 3时的Hurst指数值见表 1;图 6(b)为由式(9)计算得到的多重分形标度指数τ(q),用于计算不同阶数下的奇异指数α、奇异维数f(α);图 6(c)即多重分形谱。从图 6可以看出,摩擦振动初期、中期、末期信号的分析结果在谱图中体现出渐进变化,表明随着摩擦振动试验的进行,获得的摩擦振动初期、中期、末期信号经EEMD重构去噪后,应用多重分形去趋势波动分析能够很好地反映摩擦副摩擦振动渐变过程,可以用MFDFA谱图及其参数表征摩擦振动信号的特征。
|
| 图6 摩擦振动信号多重分形去趋势分析谱图 Figure 6 Spectrogram of multifractal detrended fluctuation analysis of frictional vibration signal |
| 试验 | q=-3 | q=-1 | q=1 | q=3 |
| 初期 | 0.396 1 | 0.360 8 | 0.246 0 | 0.056 5 |
| 中期 | 0.470 4 | 0.448 3 | 0.300 6 | 0.107 5 |
| 末期 | 0.539 3 | 0.526 2 | 0.375 0 | 0.143 8 |
从表 1可以看出,随着摩擦振动试验的进行,摩擦振动特征信号的Hurst指数呈现逐渐增大,表明摩擦副的摩擦振动逐渐具有持续性,摩擦振动逐渐保持之前的趋势,也即摩擦振动逐渐趋于稳定。结合多重分形的物理意义[18],从表 2多重分形谱参数可以看出,随着摩擦振动试验的进行,分析得到的多重分形谱参数宽度∆α、驻点值αfmax呈现上升变化,表明摩擦副摩擦振动信号的振幅分布更为宽泛,强度减弱;维差∆f、极大值fmax表征摩擦振动信号各振幅分布数量上的差异,表明随着试验的进行,振幅分布小振幅的数量占优,强度减弱,摩擦磨损逐渐趋于稳定。
| 试验 | ∆α | ∆f | fmax | αfmax |
| 初期 | 0.654 1 | 0.581 3 | 0.998 8 | 0.311 5 |
| 中期 | 0.737 8 | 0.466 9 | 0.994 9 | 0.429 5 |
| 末期 | 0.767 3 | 0.856 2 | 0.998 5 | 0.495 4 |
上述分析表明,MFDFA谱图及其参数能体现摩擦振动的特征,反映摩擦副摩擦磨损过程中所处的摩擦振动状态。
4 结论摩擦振动蕴含着摩擦副磨合磨损的状态信息,本文利用总体经验模式分解和多重分形去趋势波动分析研究摩擦副摩擦磨损过程中的摩擦振动信号,结论如下:
1)应用总体经验模式分解对非线性非平稳的摩擦振动信号进行分解,适当选择本征模式分量来重构,可以获得反映摩擦振动特征的特征信号。
2)应用多重分形去趋势分析算法能有效地分析摩擦振动信号的多重分形特征,随着摩擦振动试验的进行,摩擦振动特征信号的Hurst指数呈现逐渐增大,表明摩擦副的摩擦振动逐渐具有持续性。MFDFA谱图及其参数能够反映摩擦副摩擦振动渐变过程,可以用MFDFA谱图及其参数表征摩擦振动信号的特征。
| [1] |
孙迪, 李国宾, 魏海军, 等. 磨合过程摩擦振动混沌吸引子演变规律[J].
振动与冲击, 2015, 34(6): 116–121.
SUN Di, LI Guobin, WEI Haijun, et al. Evolvement rule of frictional vibration chaos attractors in running-in process[J]. Journal of vibration and shock, 2015, 34(6): 116–121. |
| [2] |
李国宾, 任宗英, 王宏志, 等. 摩擦振动信号谐波小波包特征提取[J].
摩擦学学报, 2011, 31(5): 452–456.
LI Guobin, REN Zongying, WANG Hongzhi, et al. Characteristics extraction of friction vibration signal using harmonic wavelet packet transforms[J]. Tribology, 2011, 31(5): 452–456. |
| [3] | HUANG N E, SHEN Zheng, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceeding of the royal society A:mathematical, physical and engineering sciences, 1998, 454(1971): 903–995. DOI:10.1098/rspa.1998.0193 |
| [4] |
雷亚国, 孔德同, 李乃鹏, 等. 自适应总体平均经验模式分解及其在行星齿轮箱故障检测中的应用[J].
机械工程学报, 2014, 50(3): 64–70.
LEI Yaguo, KONG Detong, LI Naipeng, et al. Adaptive ensemble empirical mode decomposition and its application to fault detection of planetary gearboxes[J]. Journal of mechanical engineering, 2014, 50(3): 64–70. DOI:10.3901/JME.2014.03.064 |
| [5] | WU Zhaohua, HUANG N E. Ensemble empirical mode decomposition:a noise-assisted data analysis method[J]. Advances in adaptive data analysis, 2009, 1(1): 1–41. DOI:10.1142/S1793536909000047 |
| [6] | 郑旭, 郝志勇, 金阳, 等. 基于EEMD与广义S变换的内燃机噪声源识别研究[J]. 内燃机工程, 2011, 32(5): 68–73. |
| [7] | WANG Xia, LIU Changwen, BI Fengrong, et al. Fault diagnosis of diesel engine based on adaptive wavelet packets and EEMD-fractal dimension[J]. Mechanical systems and signal processing, 2013, 41(1/2): 581–597. |
| [8] | LEI Yaguo, HE Zhengjia, ZI Yanyang. Application of the EEMD method to rotor fault diagnosis of rotating machinery[J]. Mechanical systems and signal processing, 2009, 23(4): 1327–1338. DOI:10.1016/j.ymssp.2008.11.005 |
| [9] | KANTELHARDT J W, ZSCHIEGNER S A, KOSCIELNY-BUNDE E, et al. Multifractal detrended fluctuation analysis of nonstationary time series[J]. Physica A:statistical mechanics and its applications, 2002, 316(1/2/3/4): 87–114. |
| [10] | BARMAN C, CHAUHURI H, DEB A, et al. The essence of multifractal detrended fluctuation technique to explore the dynamics of soil radon precursor for earthquakes[J]. Natural hazards, 2015, 78(2): 855–877. DOI:10.1007/s11069-015-1747-1 |
| [11] | FIGLIOLA A, SERRANO E, ROSSO O A. Multifractal detrented fluctuation analysis of tonic-clonic epileptic seizures[J]. The European physical journal special topics, 2007, 143(1): 117–123. DOI:10.1140/epjst/e2007-00079-9 |
| [12] |
熊杰, 陈绍宽, 韦伟, 等. 基于多重分形去趋势波动分析法的交通流多重分形无标度区间自动识别方法[J].
物理学报, 2014, 63(20): 200504.
XIONG Jie, CHEN Shaokuan, WEI Wei, et al. Multi-fractal detrended fluctuation analysis algorithm based identification method of scale-less range for multi-fractal charateristics of traffic flow[J]. Acta physica sinica, 2014, 63(20): 200504. |
| [13] | MALI P, MUKHOPADHYAY A. Multifractal characterization of gold market:a multifractal detrended fluctuation analysis[J]. Physica A:statistical mechanics and its applications, 2014, 413: 361–372. DOI:10.1016/j.physa.2014.06.076 |
| [14] |
葛世荣, 朱华. 摩擦学复杂系统及其问题的量化研究方法[J].
摩擦学学报, 2002, 22(5): 405–408.
GE Shirong, ZHU Hua. Complicate tribological systems and quantitative study methods of their problems[J]. Tribology, 2002, 22(5): 405–408. |
| [15] |
黄朝明, 于洪亮, 关德林, 等. 摩擦振动时频图像特征提取[J].
振动与冲击, 2012, 31(7): 46–49, 62.
HUANG Chaoming, YU Hongliang, GUAN Delin, et al. Feature extraction of frictional vibration based on time-frequency image[J]. Journal of vibration and shock, 2012, 31(7): 46–49, 62. |
| [16] |
孙迪, 李国宾, 魏海军, 等. 磨合磨损过程中摩擦振动变化规律研究[J].
哈尔滨工程大学学报, 2015, 36(2): 166–170.
SUN Di, LI Guobin, WEI Haijun, et al. Study on variation rules of friction vibration in the process of friction and wear[J]. Journal of Harbin engineering university, 2015, 36(2): 166–170. |
| [17] | SUN Di, LI Guobin, WEI Haijun, et al. Experimental study on the chaotic attractor evolvement of the friction vibration in a running-in process[J]. Tribology international, 2015, 88: 290–297. DOI:10.1016/j.triboint.2015.03.033 |
| [18] | HARTE D. Multifractals:theory and applications[M]. Boca Raton: Chapman & Hall, CRC Press, 2001: 47 -50. |



