2. Engineering Company, Offshore Oil Engineering Co. Ltd., Tianjin 300451, China
2010年4月20日,英国石油公司在墨西哥湾的漏油事件,是石油与天然气史上最严重的灾难之一,造成了重大的财产损失,导致大量的人员受伤以及11名人员死亡,给人们留下苦难的回忆[1]。目前,人类正面临着能源危机,开采深海资源势在必行,因此,只能增加水下生产系统的安全性与可靠性,尽量减少发生事故的可能性。20世纪80年代,部分科研人员开始了水下生产系统的可靠性研究[2-3]。进入21世纪以后,随着水下生产系统的大量使用,人们越来越关注它的可靠性问题[4-8]。而水下管汇是水下生产系统的重要组成部分[9-10],担负着流体、化学药剂的分配,一旦发生故障,将严重影响油气开采进度,甚至可能会造成油气的大量泄漏,造成灾难性的后果。因此,研究水下生产系统管汇的可靠性问题具有实际的现实意义,不但可以给水下生产系统其他子系统的可靠性研究提供一定的参照,而且对制造生产和改进设计有一定指导和借鉴意义。另外,可靠性分析也是维修性和可用性分析的基础。
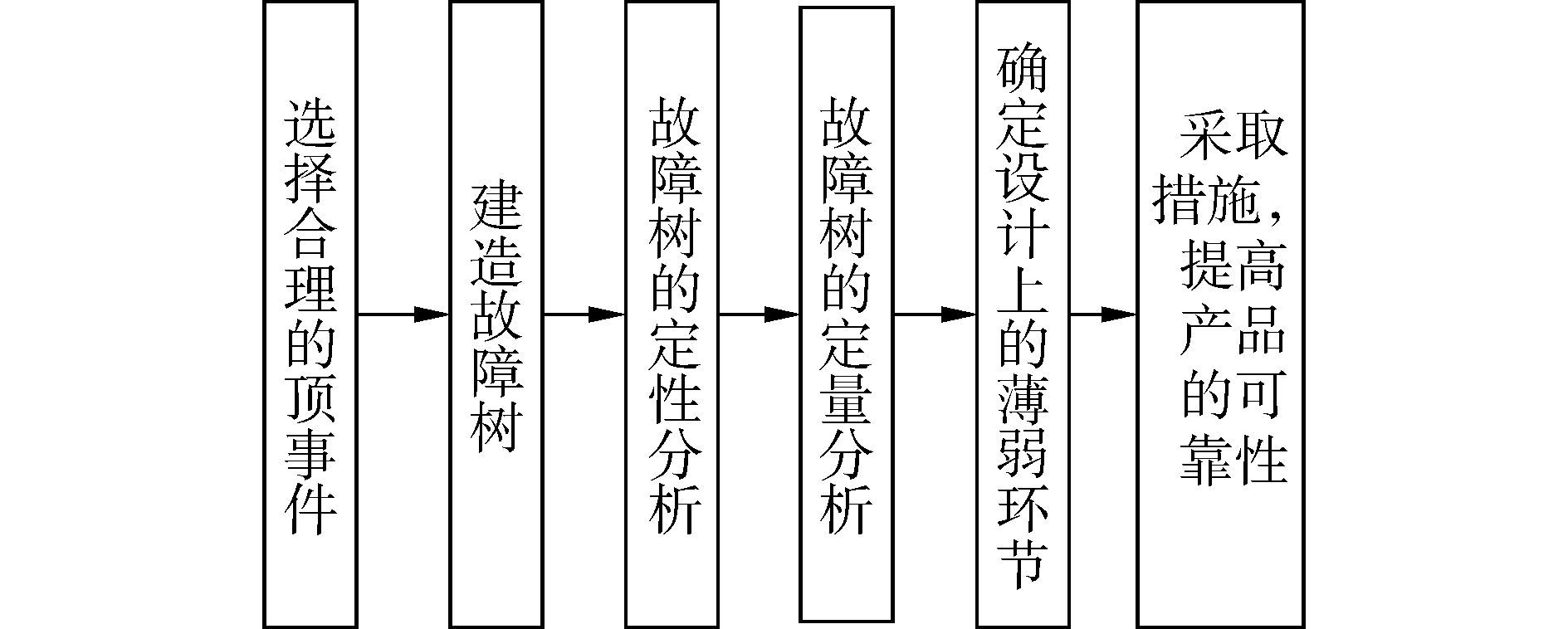
1 故障树分析理论方法1961年美国贝尔实验室在民兵导弹的发射控制系统可靠性研究中首次应用故障树分析(FTA)技术,并获得成功;1974年美国原子能委员会在核电站安全评价报告(WASH-1400)中主要应用的方法也是FTA技术[11]。随着计算机技术的发展,FTA技术已逐渐渗入到各工程领域,并逐步形成了一套完整的理论、方法和应用分析程序,如图 1所示。另外,基于FTA技术的故障树诊断也得到了广泛应用[12-13]。
|
| 图1 故障树的分析程序 Figure 1 Fault tree analysis procedure |
故障树指用来表明产品哪些部分的故障或外界事件或它们的组合将导致产品发生一种给定故障的逻辑图。故障树是一种逻辑因果关系图,构成的元素是事件和逻辑门。图中的事件用来描述系统或元部件故障的状态,逻辑门把事件联系起来,表示事件之间的逻辑关系。
2 水下生产系统管汇简介管汇是管道和阀门的排列布置,被设计用于联合、分配、控制盒监控流体流动[14]。以南海某水下生产系统的管汇为研究对象,建立管汇的可靠性模型。该管汇主要由管汇模块和管道模块两部分组成,进一步的结构组成划分见表 1。
| 名称 | 子系统 | 编号 | 部件 |
| 1 | 化学联轴器 | ||
| 2 | 连接器2 | ||
| 3 | 液压插头 | ||
| 4 | 管道2 | ||
| 管汇模块 | 5 | 保护性结构 | |
| 6 | 支持性结构 | ||
| 管汇 | 7 | 检测阀 | |
| 8 | 控制阀 | ||
| 9 | 进程隔离阀2 | ||
| 10 | 实用隔离阀 | ||
| 11 | 连接器1 | ||
| 管道模块 | 12 | 管道1 | |
| 13 | 进程隔离阀1 |
在建立管汇的故障树之前,假设:
1) 水下管汇及其组成单元只有故障与正常两种状态,不存在第三种状态;
2) 不同部件的故障概率之间是相互独立的;
3) 所有部件的故障率均是一常数。
水下生产系统管汇的可靠性数据都是在以往的试验和实际工程中测得并记录的数据,国内目前尚无水下管汇的可靠性数据。因此,在研究南海某水下生产系统管汇时,引用OREDA-Offshore Reliability Data Handbook(2015版)中的数据,如表 2所示。当然,这些故障数据和南海的实际情况可能会有一点误差,因为这些数据是OREDA在其他几个海域内的收集结果,而不同的海域间会有一些差别。
| 名称 | 平均故障率×10-6/h |
| 连接器 1 | 0.247 8 |
| 管道 1 | 0.364 3 |
| 进程隔离阀 1 | 0.418 4 |
| 化学联轴器 | 0.257 0 |
| 连接器 2 | 0.109 3 |
| 液压插头 | 0.059 1 |
| 管道 2 | 0.179 2 |
| 保护性结构 | 0.412 8 |
| 支持性结构 | 1.173 8 |
| 检测阀 | 0.453 4 |
| 控制阀 | 0.341 9 |
| 进程隔离阀 2 | 0.831 3 |
| 实用隔离阀 | 0.084 9 |
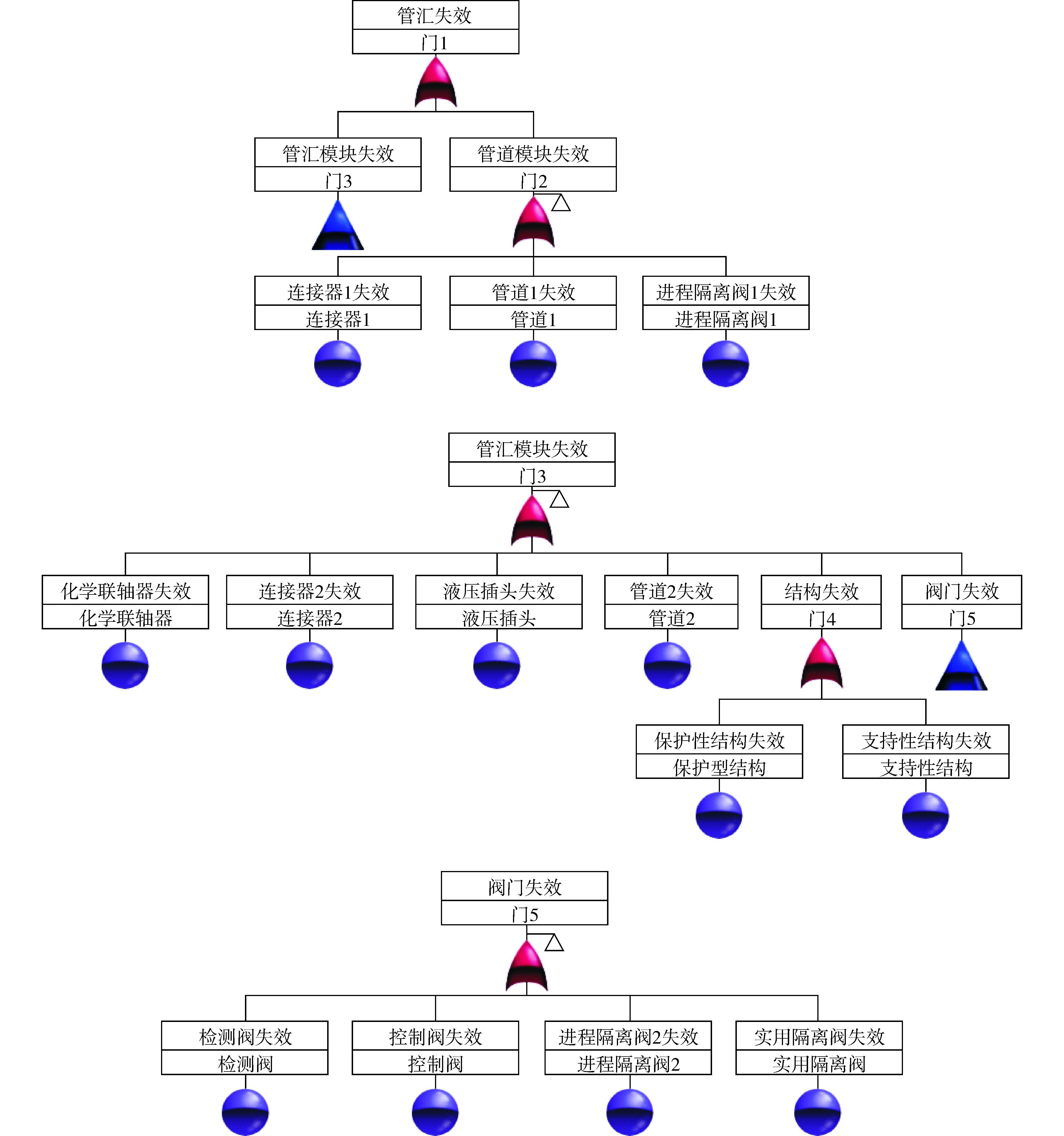
管汇可分为管汇模块和管道模块两部分。管汇模块主要由化学联轴器、连接器、液压插头、管道、保护性结构、支持性结构、检测阀、控制阀、进程隔离阀和实用隔离阀等部件组成;管道模块主要由连接器、管道和进程隔离阀等部件组成。取“管汇失效”作为顶事件,建立的故障树如图 2所示。
|
| 图2 管汇失效的故障树 Figure 2 Fault tree of manifold fails |
从管汇的故障树中,可以知道,顶事件“管汇故障”的最小割集有13个,分别为连接器2失效、 管道1失效、…、进程隔离阀1失效,即故障树的每个底事件。该结果与Windchill Quality Solutions软件的计算结果一致,软件的计算结果见图 3,Cut Sets即为最小割集。一个最小割集的发生就可以导致顶事件的发生,也可以称为导致“管汇失效”的一个主要故障模式,因此,“管汇失效”的主要故障模式有13个。

|
| 图3 管汇故障的最小割集 Figure 3 The minimum cut sets of manifold failure |
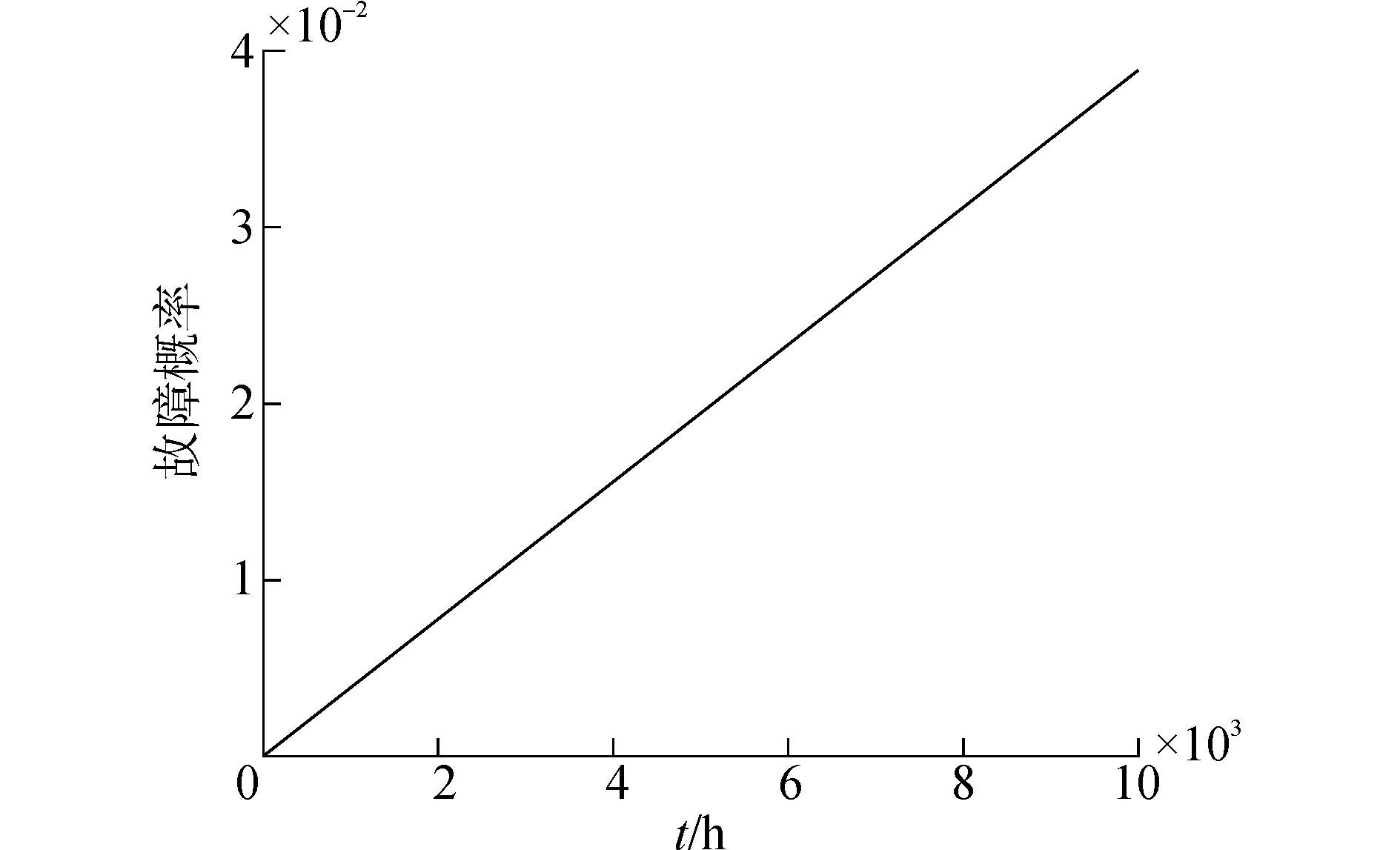
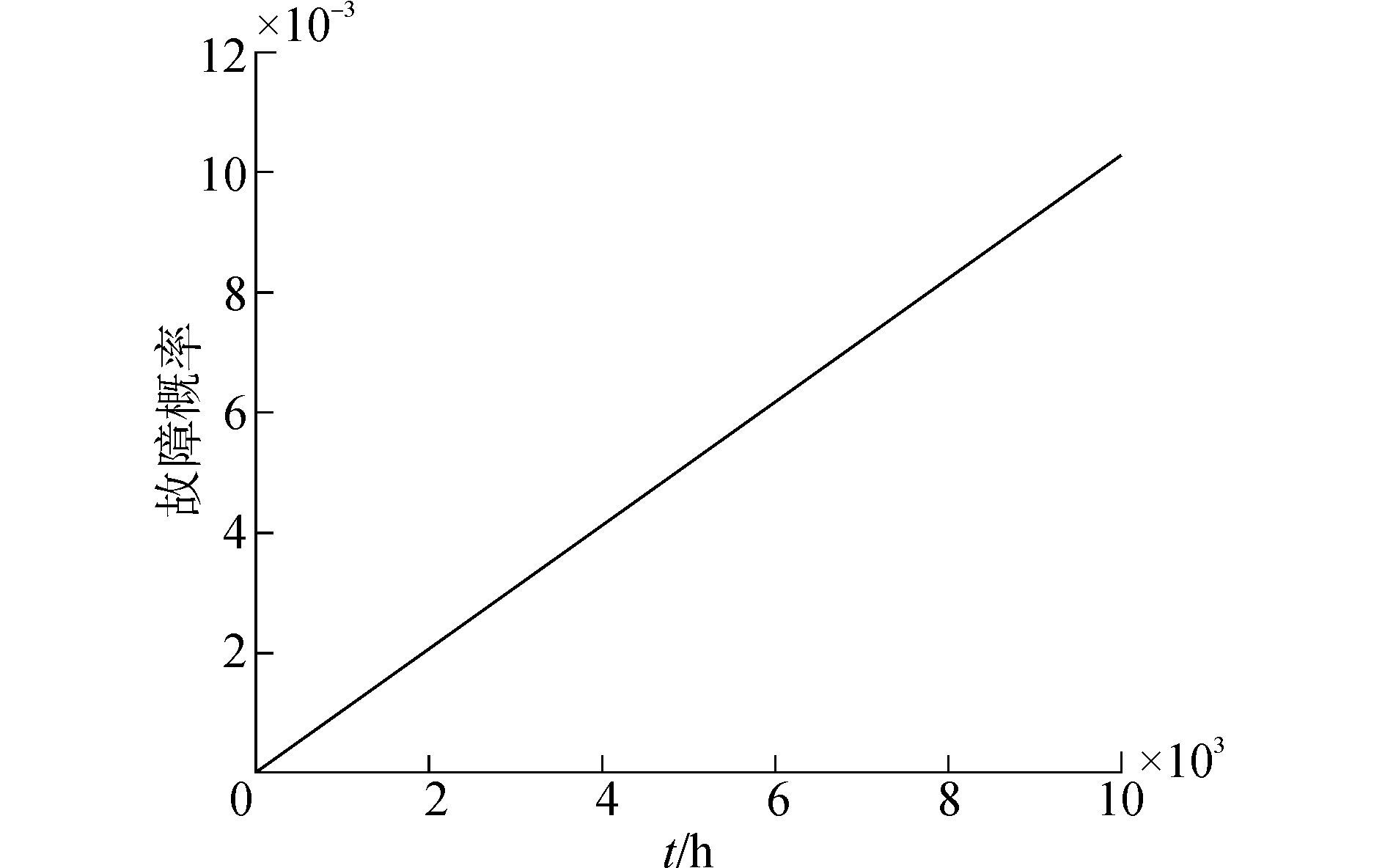
取计算时间t=10 000 h,代入表 2中数据,运用Windchill Quality Solutions软件中的故障树模块进行运算,可以得到管汇模块、管道模块以及管汇的故障概率随时间的变化曲线,依次如图 4、5和6所示。
|
| 图4 Manifold module的故障概率随时间的变化曲线 Figure 4 The change curve of manifold module failure probability with time |
|
| 图5 Pigging module的故障概率随时间的变化曲线 Figure 5 The change curve of pigging module failure probability with time |
|
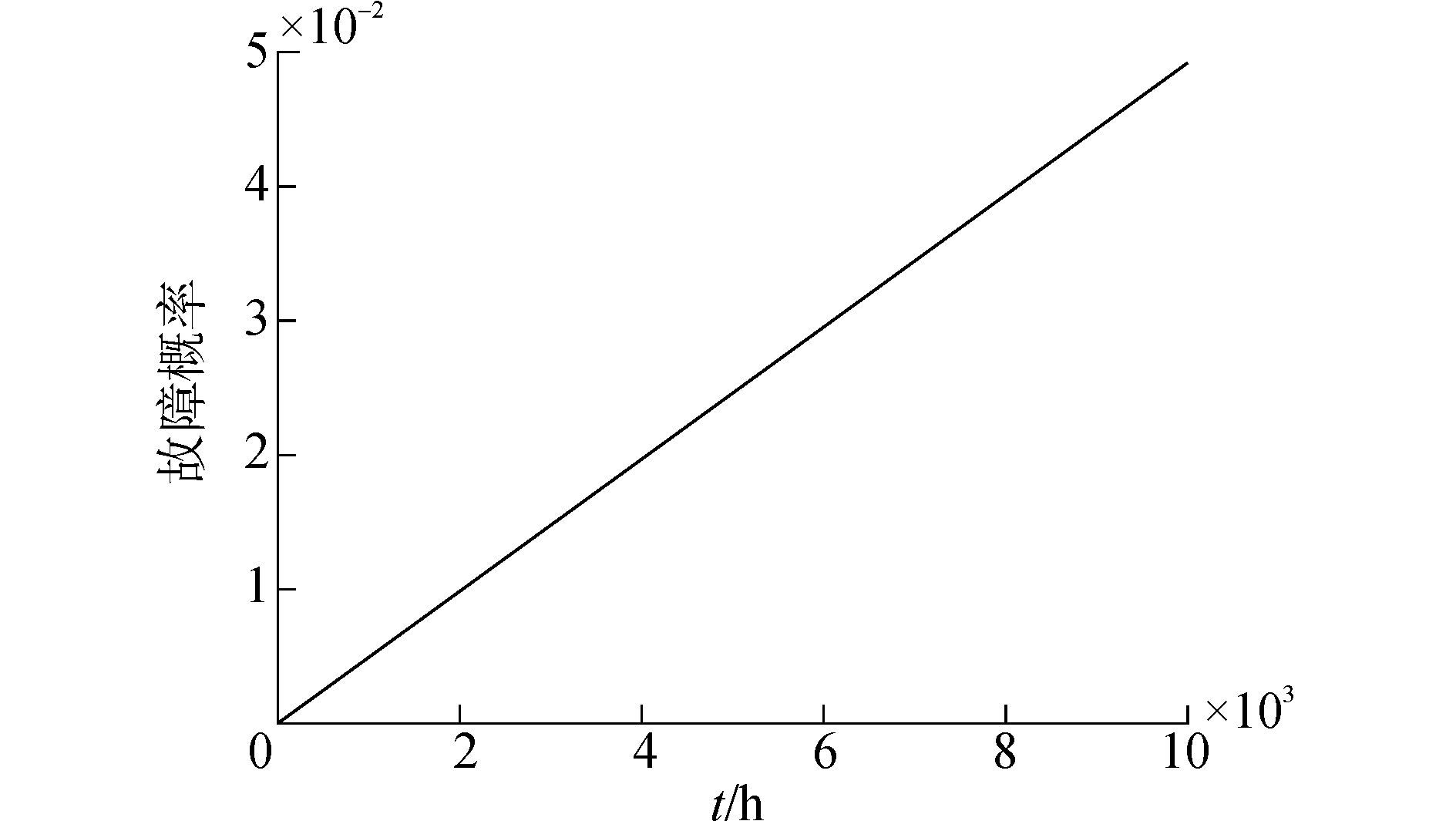
| 图6 管汇的故障概率随时间的变化曲线 Figure 6 The change curve of manifold failure probability with time |
当软件运行到10 000 h时,管汇的故障概率为0.049 2。通常,水下生产系统对水下管汇的可靠度都有一定的要求,即要求中心管汇的可靠度不低于一个值,假设该值为R0,这个值常称为最低门限值。根据最低门限值的大小,可以得到水下管汇的最大故障概率,再根据管汇的故障概率随时间的变化曲线,找到相对应的那个时刻t0,根据t0的值,就可以确定维修或保障的时间间隔(时间间隔小于t0),从而为制定维修和保障计划提供保证。
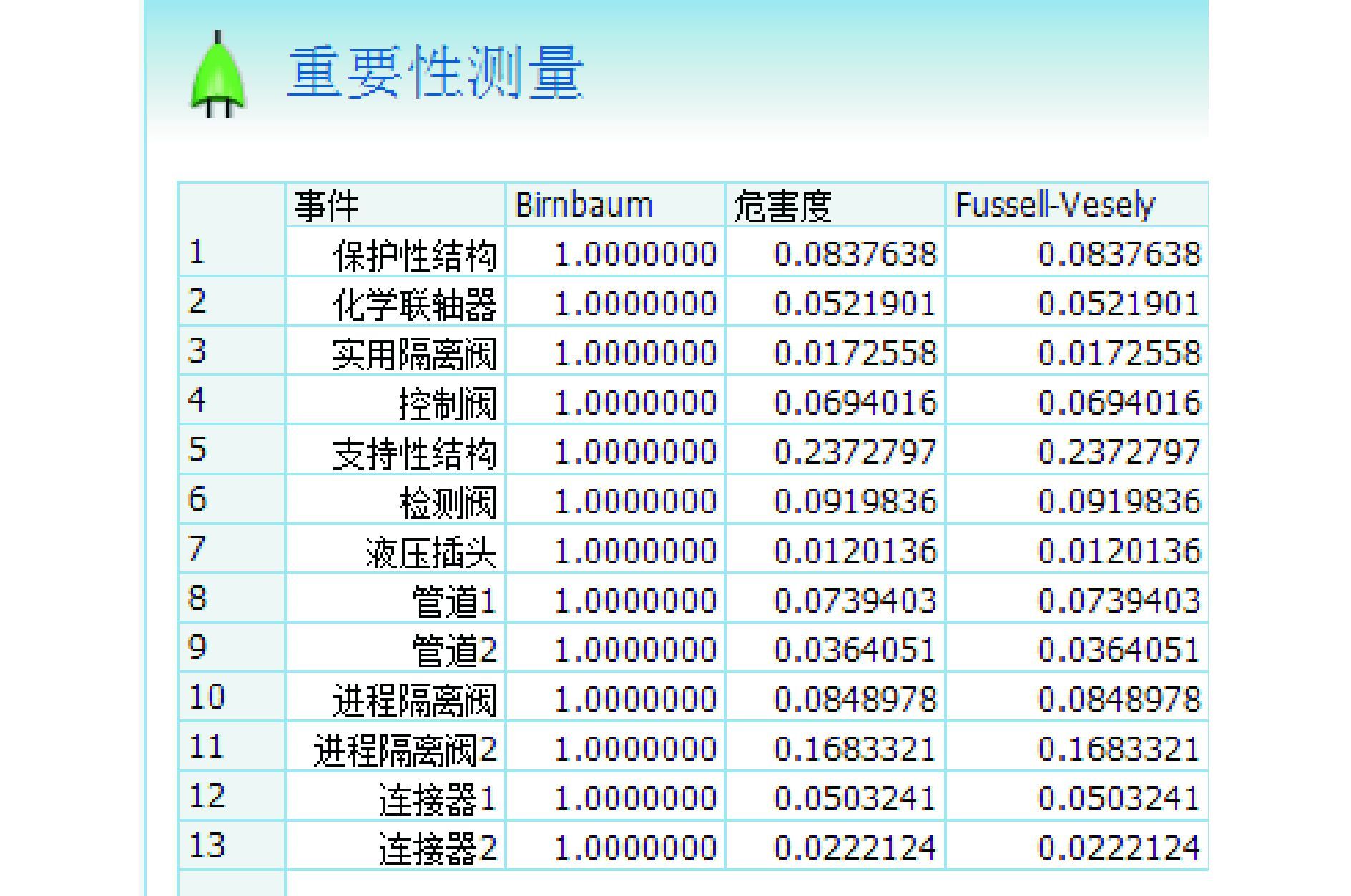
3.3 重要度分析水下管汇底事件的可靠性重要度计算结果如图 7所示。研究中用Windchill Quality Solutions软件,计算了底事件的3种可靠性重要度:Birnbaum重要度(常称为概率重要度),Criticality重要度(常称为关键重要度),Fussell-Vesely重要度(常称为割集重要度)。
|
| 图7 底事件可靠性重要度 Figure 7 Reliability importance measures of fault the basic events |
Birnbaum重要度,指的是一底事件发生时的顶事件概率减去该底事件不发生时的顶事件概率,即
| ${{I}_{g}}\left( A \right)=P\left( T|A \right)-P\left( T|\bar{A} \right)$ | (1) |
式中:A为底事件A发生,A-为底事件A不发生,T为顶事件,IBA为底事件A的Birnbaum重要度。
危害度的定义为
| ${{I}_{B}}{{I}_{C}}\left( A \right)={{I}_{B}}\left( A \right)\times \frac{P\left( A \right)}{P\left( T \right)}=\left( PT|A \right)-P\left. \left( T|\bar{A} \right) \right)\times \frac{P\left( A \right)}{P\left( T \right)}$ | (2) |
式中:ICA为底事件A的Criticality重要度。
Fussell-Vesely重要度的定义为
| ${{I}_{FV}}A=\frac{\sum P\left( {{C}_{i}} \right)}{P\left( T \right)}$ | (3) |
式中:Ci为包含底事件A的所有最小割集;IFVA为底事件A的Fussell-Vesely重要度。
根据图 7底事件可靠性重要度计算结果,底事件的排序为:
1)Birnbaum重要度顺序:13个底事件的地位一致,它们的Birnbaum重要度的值均为1。但在实际应用中,这13个底事件的Birnbaum重要度值并不等于1,而是非常接近于1,因此,软件把这些值都近似为1;
2)Criticality重要度顺序:支持性结构、进程隔离阀2、…液压插头;
3)Fussell-Vesely重要度顺序:支持性结构、进程隔离阀2、…液压插头;
由此可以知道,支持性结构的重要度最高,进程隔离阀2的重要度次之,这两个底事件的重要度大大高于其他的事件。即支持性结构故障发生的概率对顶事件的影响最大,进程隔离阀2次之,因此,降低支持性结构和进程隔离阀2的故障率能大大降低水下管汇的故障概率,在水下管汇的改进设计中,应该重点考虑。
4 结论1) 通过建立水下生产系统管汇的故障树模型,对管汇的可靠性进行研究,得到水下生产系统管汇的失效概率随时间的变化曲线,进而可以确定维修时间间隔t0。
2) 支持性结构和进程隔离阀2这两个部件的重要度远大于其他部件,在进行水下生产系统管汇的改进设计、维护以及保障计划的制定时,应该侧重考虑。
3) 此分析方法也可以为其他水下设备的可靠性研究提供参考。另外,可以在可靠性分析基础上进一步开展维修性和可用性分析,得到人们更加关心的生产率,对实际生产有一定的借鉴和指导意义。
| [1] | SAAD A ABBAS. Managing the reliability of a subsea production system[D]. Johor:University Teknologi Malaysia, 2014:8-11. |
| [2] | SIGNORET J P, LEROY A. Probabilistic caculations of the production of a subsea production cluster[C]//Safaty and Reliability Society Symposium 1985:Achievement of Reliability in Operating Plant. Southport, England, 1985:3.1-3.19. |
| [3] | HOKSTAD P. Assessment of production regularity for subsea oil/gas production systems[J]. Reliability engineering & system safety, 1988, 20(2): 127–146. |
| [4] | HARITONOV C M R, ROBERTSON N D, STRUTT J E. The design of subsea production systems for reliability and availability[R]. Paper OTC 20058. Huston, Texas, USA, 2009. |
| [5] | SHANKS E F, PFEIFER W, SAVAGE S, et al. Enhanced subsea safety critical systems[R]. Paper OTC 23480. Huston, Texas, USA:OTC, 2012. |
| [6] | BERG I A. Design for reliability-applied to development of subsea process systems[D]. Trondheim Norwegian:Norwegian University of Science and Technology, 2010:18-23. |
| [7] | AVEN T, PEDERSEN L M. On how to understand and present the uncertainties in production assurance analyses, with a case study related to a subsea production system[J]. Reliability engineering & system safety, 2014, 124: 165–170. |
| [8] | RAHIMI M, RAUSAND M. Prediction of failure rates for new subsea systems:a practical approach and an illustrative example[J]. Journal of risk and reliability, 2013, 227(6): 629–640. |
| [9] |
程寒生, 黄会娣, 周美珍, 等. 深水水下管汇设计研究[J].
石油机械, 2011, 39(5): 9–11.
CHENG Hansheng, HUANG Huidi, ZHOU Meizhen, et al. Research on the design of deep-water manifold[J]. China petroleum machinery, 2011, 39(5): 9–11. |
| [10] |
程寒生, 周美珍, 郭宏, 等. 水下管汇设计关键技术分析和设计原则研究[J].
中国海洋平台, 2011, 26(3): 30–32.
CHENG Hansheng, ZHOU Meizhen, GUO Hong, et al. Critical design techniques analysis and design principles study for subsea manifold[J]. China offshore platform, 2011, 26(3): 30–32. |
| [11] |
曾声奎.
可靠性设计与分析[M]. 北京: 国防工业出版社, 2011 .
ZENG Shengkui. Reliability design and analysis[M]. Beijing: National Defense Industry Press, 2011 . |
| [12] |
金鸿章, 徐雷, 綦志刚. 基于FTA的飞机液压刹车故障诊断专家系统[J].
应用科技, 2008, 35(8): 31–35.
JIN Hongzhang, XU Lei, QI Zhigang. FTA-based fault diagnosis expert system for hydraulic braking system of airplanes[J]. Applied science and technology, 2008, 35(8): 31–35. |
| [13] |
邱楚楚, 盖强, 马野. 基于故障树的无人机发动机点火系统维修性建模[J].
应用科技, 2011, 38(8): 5–7.
QIU Chuchu, GAI Qiang, MA Ye. Maintainability modeling of UAV engine ignition by fault tree[J]. Applied science and technology, 2011, 38(8): 5–7. |
| [14] |
白勇, 龚顺风, 白强, 等.
水下生产系统手册[M]. 哈尔滨: 哈尔滨工程大学出版社, 2012 .
BAI Yong, GONG Shunfeng, BAI Qiang, et al. The Manual of Subsea Production System[M]. Harbin: Harbin Engineering University Press, 2012 . |



