2. Department of Civil Engineering, Tianjin University, Tianjin 300072, China
对于海底管道轴向移动研究,Torne等[1]应用库伦管土摩擦模型建立有限元模型,得出管道内有效轴力的分布和管道轴向移动形态;Carr等[2]提出海底管道轴向移动的3个条件:立管连接端的张力、管道长度方向上海床的倾斜度、管道开启/关闭过程中的温度效应,进而提出管道轴向移动速率的解析方程;David等[3]研究了管土作用对管道轴向移动和侧向屈曲的影响;刘羽霄等[4]研讨了管道轴向移动和侧向屈曲的相互作用;Rong等[5]利用ABAQUS有限元软件,考虑了非线性管土摩擦与材料非线性建立埋地管道轴向移动模型,提出短管道更容易发生轴向移动现象的结论。
对于深海管道来说,在高温和高压环境下轴向膨胀现象和整体屈曲[6]尤为突出,并且由于经济技术原因,深海管道多是直接铺设于海床之上,其边界条件对于轴向移动的阻抗作用相比于埋地管道也更小,多种不利因素高温高压、直接铺设于平坦海床之上都大大加大轴向移动现象发生,因此本文研究背景为处于高温高压直接铺设于海床上环境条件下管道轴向移动现象的研究。
其次海底管道的开启/关闭的循环作用对于轴向移动起控制作用,但长直管道其沿管道长度方向温度梯度较小,且在使用寿命期内管道开启/关闭的次数较少,开启/关闭循环引起的管道轴向位移较小,可以控制在设计范围之内。因此,在深海高温高压平坦海床环境条件下,本文着重对短直管在多次开启/关闭循环轴向有效应力分布及各点轴向移动进行了分析详尽分析,最后对管土摩擦以及管道内压进行参数化分析,得到轴向移动现象的形成原因及发展规律。
1 管道膨胀产生原因引起海底管道膨胀的主要原因为以下3种:温度、内外压和材料泊松比,主要由以下几部分组成[7]:
1)端帽效应即由管道内部流体介质作用在管道端部面上从而产生的应变εp;
2)泊松比效应引起的管道压缩应变εv是由管道内压产生的环向应力引起的,导致管道在轴向方向上发生收缩;
3)管道安装和运营过程中温度的变化会引起管道温度应力的产生,在自由条件下,温度变化引起的温度应变为εt;
4)阻抗应变是由于管道和河床之间的摩擦阻力阻碍着管道轴向膨胀产生的应变εf。
管道的总的净应变εnet如下式:
| $ {\varepsilon _{net}}{\rm{ = }}{\varepsilon _t} + {\varepsilon _p} - {\varepsilon _v} - {\varepsilon _f} $ | (1) |
根据上式可以看出沿着管道长度方向有一个特定点净应变为零,此点称为锚固点,对于长直管道会出现两个锚固点,位于两个锚固点之间的管道处于完全约束状态,在这些管道的轴向应变为零的区域称为锚固段。对于短直管道,管道长度没有达到完全约束的位置,通常在管道靠近中点的位置有效轴力达到最大,同时形成虚拟锚固点。与长直管道不同的是,虚拟锚固点的位移为零,但是轴向应变不为零,管道的最大有效轴力远小于全约束轴向力。
2 短直管道轴向移动解析计算假设管道为均匀对称模型,且海床为刚性海床,考虑小变形和线弹性假设,温度引起的管道轴向荷载[8]fθ为:
| $ {f_\theta } = {A_s} \cdot E \cdot {\alpha _T} \cdot {q_\theta } $ | (2) |
| $ {q_\theta } = \frac{T}{L} $ | (3) |
式中: As为管道净截面面积,E为弹性模量,αT为热膨胀系数,T为管道内外温差,L为管道长度。
温度荷载作用下管道的轴向移动速率计算为
| $ {\Delta _\theta } = \frac{{{L^2}}}{{16{A_S}E}}\left( {\sqrt {24{f_\theta }f} - {f_\theta } - 4f} \right) $ | (4) |
| $ f = {\mu _a} \cdot {W_{sub}} $ | (5) |
式中: f管土摩擦阻力,μa为管道与海床的摩擦系数,Wsub为管道的淹没重量。
由式(5)可以看出管道轴向移动现象与管道海床之间的摩擦系数、管道重量等有关。本节对管道轴向移动速度的解析结果进行计算,以便验证后续的数值模拟结果,计算得到管道的轴向移动速度为0.059 m/循环,采取的主要计算参数见表 1。
| 参数 | 数值 |
| 管道规格 | API 5LX65 |
| 管道直径/mm | 323.9 |
| 管道壁厚mm | 12.7 |
| 热膨胀系数 | 1.17x10-5 |
| 管道淹没重量/(N·m-1) | 1 230 |
| SMYS/MPa | 448 |
| SMTS/MPa | 531 |
| 管道长度/m | 2 000 |
| 运营压力/MPa | 4.65 |
| 运营温度/℃ | 89 |
| 环境温度/℃ | 4 |
| 屈服强度预估下调值(设计温度89℃)/MPa | 23.4 |
在海底管道有限元分析中,由于建立的管道模型一般较长, 一个方向的尺寸(长度)远大于另外两个尺寸,并且以纵向应力为主,所以选择PIP31梁单元模拟海底管道,具体参数见表 1。管道材料采用Ramberg-Osgood本构关系来模拟管道的应力应变关系,其形式为:
| $ \varepsilon = \frac{\sigma }{E}\left[ {1 + \frac{3}{7}{{\left( {\frac{\sigma }{{{\sigma _{0.7}}}}} \right)}^{n - 1}}} \right] $ | (6) |
式中:n为材料的硬化系数,σ0.7为斜率为,0.7E的直线与材料应力应变曲线交点所对应的应力。
边界条件的模拟过程中,将海床模拟成刚性地基,由于海底管道发生轴向膨胀产生位移,管道与土体之间将会产生摩阻力,所克服的摩擦阻力与其轴向位移呈非线性关系,本文采用二折线模型模拟管土轴向相对作用[9]如图 1所示。
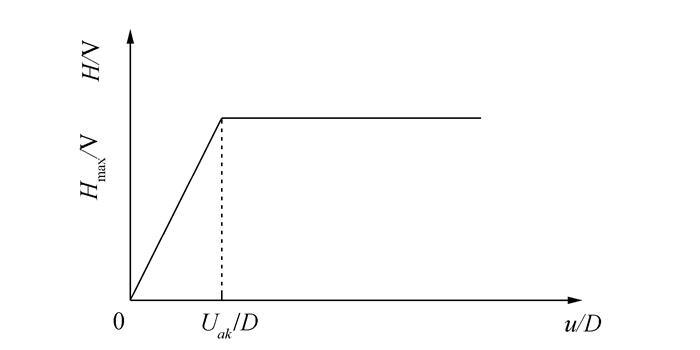
|
| 图1 管土相互作用两折线模型 Figure 1 Double line model of pipeline-soil interaction |
对于二折线模型中Ubk为管道滑移距离,进行管土侧向分析时取0.1倍管径,轴向分析时取0.01倍管径或0.005 m。H为摩擦阻力,V为管道淹没重量,两者有如下关系:
| $ \frac{{{H_{\max }}}}{V} = \mu $ | (7) |
在建模过程中,通过添加非线性弹簧单元来模拟管道与海床的摩擦接触,非线性弹簧单元含有两个节点,一个节点定义在管道外壁上,另一个节点定义在刚性海床上。通过定义弹簧变形量与弹簧受力之间的非线性关系,实现管道与海床间的非线性摩擦力模拟。
3.2 温度加载曲线管道在加热过程中,内外温差会引起内部流体温度损失,导致管道两端温度不一致,所以管道升温是一个非线性渐变的过程。与之相反,冷却过程发生在管道关闭之后,管道在失去温度荷载之后缓慢恢复到环境温度,是一个均匀线性降温的过程。在一个开启/关闭循环过程中,管道轴向移动现象通常发生在管道开启(非线性升温)过程中,并且在管道关闭(降温)过程中变形不可逆转,所以非线性的温度分布是造成管道轴向变形的主要因素。海底管道在多次开启/关闭循环过程中轴向变形产生积累,所以在每次循环时,管道所处的状态是不同的。图 2为管道一次开启过程中的温度变化曲线[10],每次开启过程分15步逐步升温。
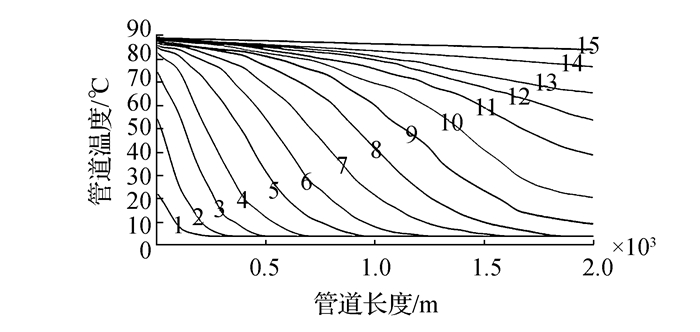
|
| 图2 管道加热温度曲线 Figure 2 Pipeline heating temperature curve |
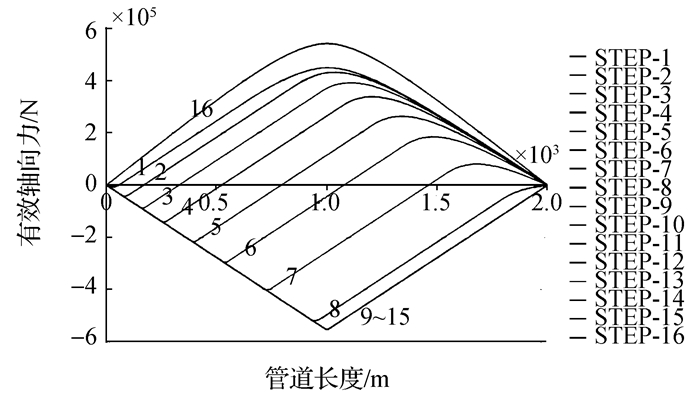
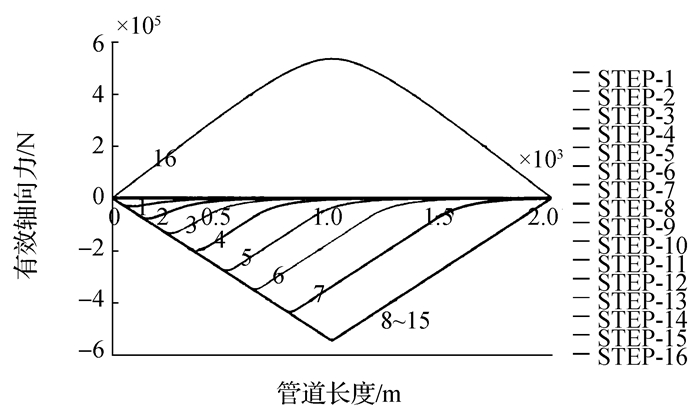
图 3为第一次开启/关闭循环过程中管道有效轴向力分布图。STEP 1~15代表15步升温加载过程,STEP-16代表降温过程。

|
| 图3 第一次循环加载有效轴向力分布图 Figure 3 Effective axial force distribution graph under the first cyclic loading |
管道在加热过程中膨胀产生轴向力,在第一次循环加载过程中,管道的虚拟锚固点伴随加热过程从管道加热端向中点移动,直到第8个加载步,管道虚拟锚固点位于管道中点,轴向力被完全激发。之后随着温度荷载的增加,管道会继续受热膨胀,但是管道有效轴向力沿管道分布形态几乎没有变化。在第16荷载步,管道降温到环境温度,管道收缩,导致摩擦力反向,管道的有效轴向力变为拉力,虚拟锚固点仍位于管道中部。
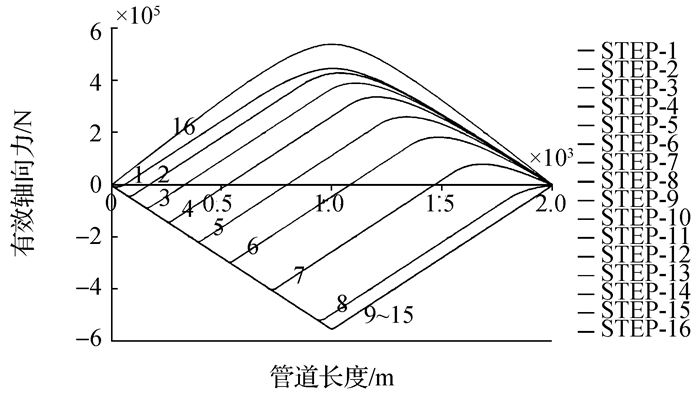
第二次和第三次开启/关闭循环过程中管道的有效轴向力分布如图 4、图 5所示,由于第一次降温过程中轴向摩擦产生管道残余轴向拉力,第二次循环及之后的循环的有效轴向力沿管长的分布与第一次循环是不同的。管道进行第一步加载后,产生两个虚拟锚固点,分别位于26 m和1 004 m处。随着管道持续升温,虚拟锚固点的位置分别向管道中点(1 000 m)和非加热端(2 000 m)移动。直至第9个加热步,管道膨胀被完全激发,虚拟锚固点位于管道中点,有效轴向力达到最大值(551 kN)并且分布趋于稳定。
|
| 图4 第二次循环加载有效轴向力分布图 Figure 4 Effective axial force distribution graph under the second cyclic loading |
|
| 图5 第三次循环加载有效轴向力分布图 Figure 5 Effective axial force distribution graph under the third cyclic loading |
图 6~8所示为管道在前三次开启/关闭过程中管道膨胀的累计位移分布图,随着温度的逐渐上升,管道会发生非均匀的膨胀作用,并倾向于由管道中部向两端膨胀。并且,在管道完全激发之后,管道非加载端的位移随着温度荷载的升高而急速增加。
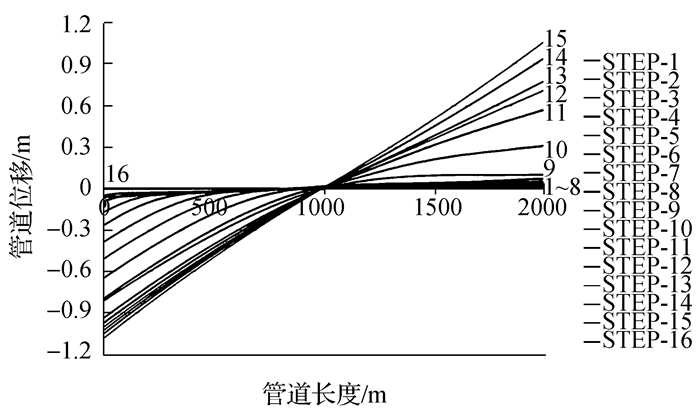
|
| 图6 第一次循环加载管道位移分布图 Figure 6 Pipeline displacement distribution under the first cyclic loading |
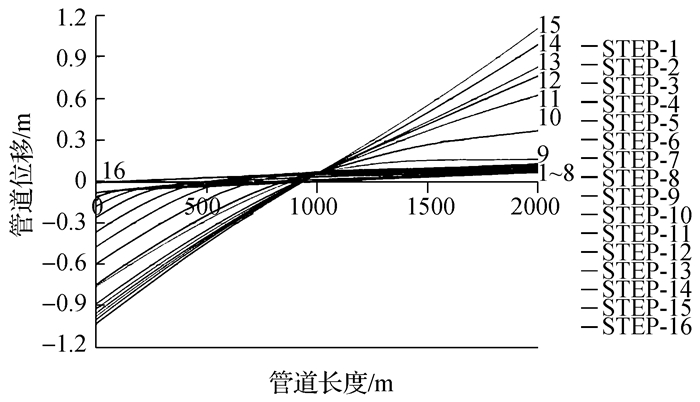
|
| 图7 第二次循环加载管道位移分布图 Figure 7 Pipeline displacement distribution under the second cyclic loading |
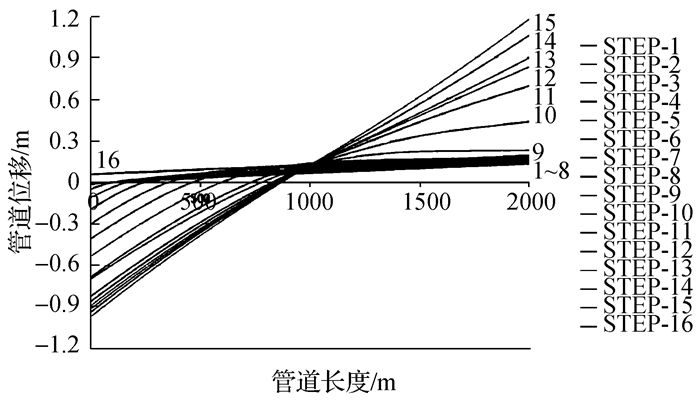
|
| 图8 第三次循环加载管道位移分布图 Figure 8 Pipeline displacement distribution under the third cyclic loading |
由前三次开启/关闭循环位移对比可看出,由于管道温度的不均匀升高,管道的整体趋势是由加热端向非加热端移动。
3.5 管道轴向移动现象 3.5.1 管道中点轴向移动由前三次开启/关闭循环过程中管道中点的轴向位移数据,绘制出管道中点轴向移动趋势图,见图 9。由图 9可见,随着温度荷载的升高,管道中点位移值逐步增加,并且是由管道加载端向非加载端移动。但是在管道被完全激发之后,由于管道非加热端温度的大幅度升高,管道中点位移会短暂下降,之后趋于稳定。管道中点轴向移动在第二次管道循环加热过程中开始发生,并且随着循环加载的进行,中点的轴向位移也逐渐增加。管道的轴向移动速度约为0.06 m/循环,与式(7)数值计算结果相似。
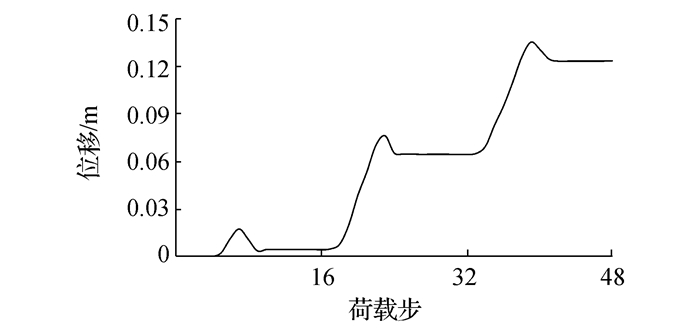
|
| 图9 管道中点轴向移动趋势图 Figure 9 Mid-point axial movement trend of the pipeline |
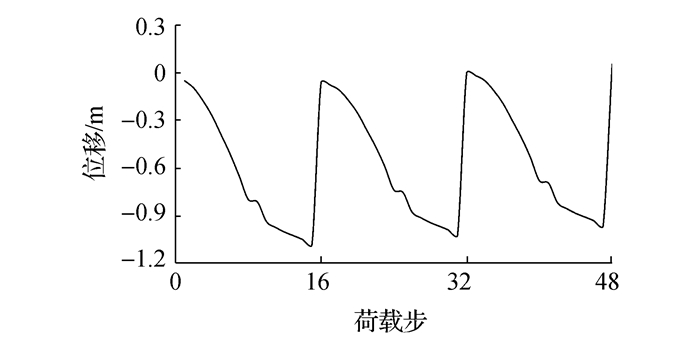
图 10为管道加热端在前三次升温降温循环过程中的轴向移动趋势图。如图 10所示,在首次循环荷载作用下,管道加热端的位移随着温度荷载的升高而快速增加,但在管道被完全激发之后,管道轴向位移值增加较缓,直至管道降温冷却收缩,管道位移迅速下降,但会存在部分残余变形。在随后的循环过程中,会继承之前管道的残余变形,重复之前的变形过程,进而发生管道加热端的轴向移动现象。
|
| 图10 管道加热端轴向移动趋势图 Figure 10 Axial movement of heated end of pipeline |
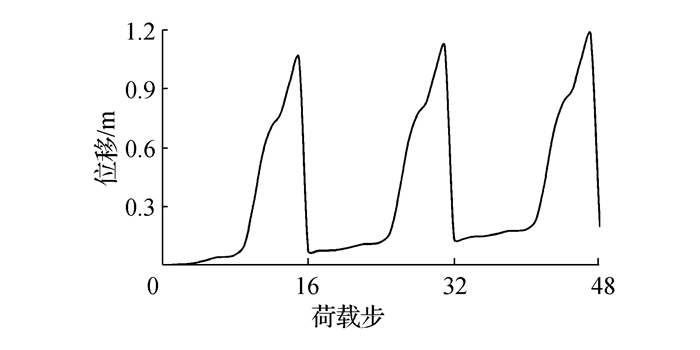
图 11为管道非加热端在前三次升温降温循环过程中的轴向移动趋势图。
|
| 图11 管道非加热端轴向移动趋势图 Figure 11 Axial movement of non-heated end of pipeline |
如图 11所示,在首次循环荷载作用下,管道被完全激发之前,管道非加热端的位移随着温度荷载的升高而增加,但位移变化很小。直至管道被完全激发,非加载端的轴向位移迅速增加,且由加载端向非加载端移动。在管道冷却过程中,端部位移会缓慢下降,但会有部分残余变形存在。在随后的循环过程中,会继承之前管道的残余变形,重新发生位移循环过程,进而发生管道非加热端的轴向移动现象。
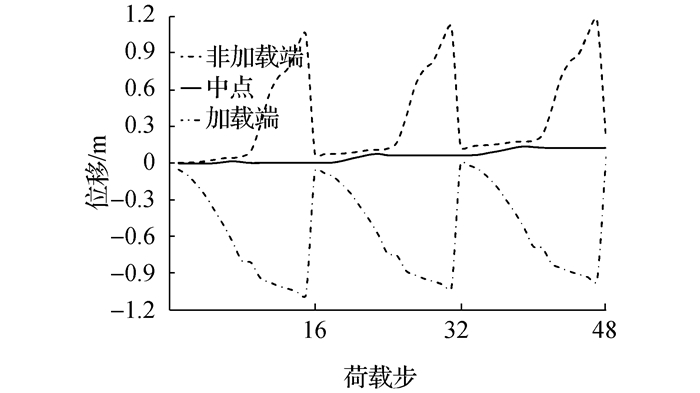
图 12为管道轴向移动趋势图。如图所示,在管道每次升温降温循环过程之后,管道都位于一个新的位置。这意味着,管道的轴向移动现象是多次循环荷载作用下轴向位移累积的结果。
|
| 图12 管道轴向移动趋势图 Figure 12 Axial movement trend of the pipeline |
综上所述,在非线性循环温度荷载作用下,管道有效轴向力将产生循环变化,从而发生管道轴向移动现象,且其方向为由管道加热端向非加热端移动。
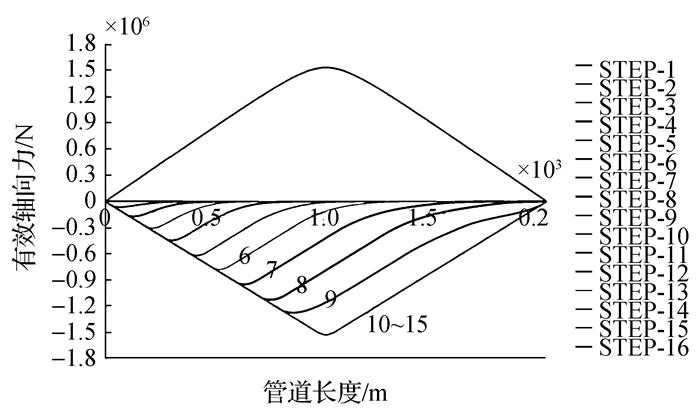
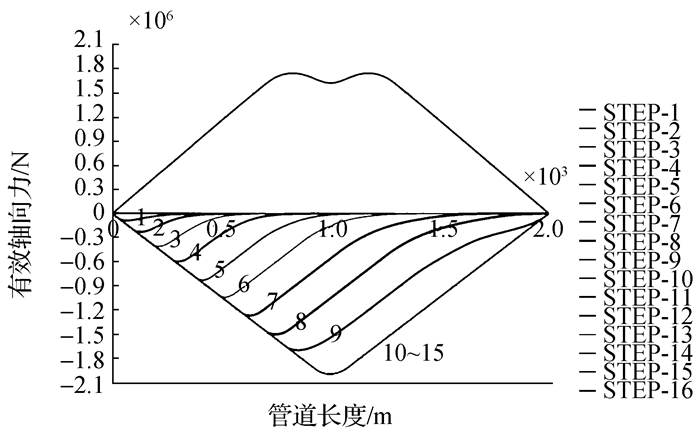
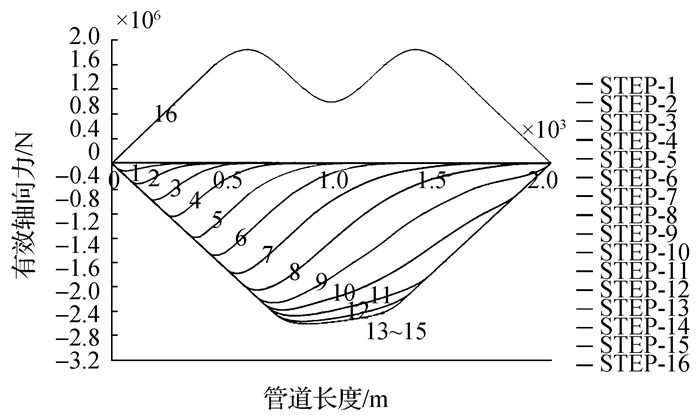
4 管土摩擦对管道轴向移动的影响 4.1 有效轴向力分布采用前文所述二折线管土相互作用模型,图 13~16为不同的管土摩擦系数下,管道的有效轴向力变化趋势,升温过程中管道中存在轴向压力,而在降温冷却过程中管道存在轴向拉力。如图所示,随着管道与海床摩擦力的增加,管道的有效轴向力逐渐增大。
|
| 图13 有效轴力分布图(μ=0.3) Figure 13 Distribution of effective axial force(μ=0.3) |
|
| 图14 有效轴力分布图(μ=0.9) Figure 14 Distribution of effective axial force(μ=0.9) |
|
| 图15 有效轴力分布图(μ=1.2) Figure 15 Distribution of effective axial force(μ=1.2) |
|
| 图16 有效轴力分布图(μ=1.8) Figure 16 Distribution of effective axial force(μ=1.8) |
当管土摩擦系数较小时,管道能够被完全激发,且在完全激发之后,管道的虚拟锚固点都位于管道中部,如图 13、14。
当管土摩擦系数增加到某一值时,此时由于管道升温产生的轴向力不足以抵消管土摩擦力,管道会在中间段产生虚拟锚固区域,并随着摩擦系数的增加,锚固区域扩大。在管道的虚拟锚固区域内管道没有被完全激发,这意味着在虚拟锚固区内,管土相互作用是发生在管土作用模型的弹性区域内的。因此,管道的有效轴向力不会从最大的压缩力变为最大的拉伸力。
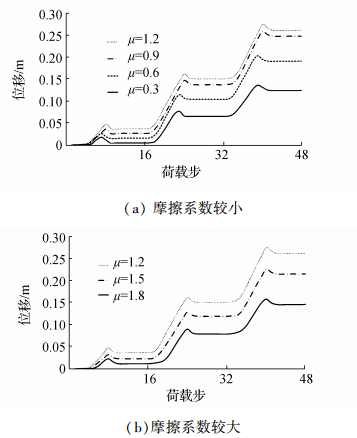
4.2 管道轴向移动速度根据不同的管土摩擦系数,建立模型计算管道前三次荷载循环作用下的轴向移动现象。得出不同摩擦系数下管道中点轴向位移值,如图 17所示。当管土摩擦系数较低时,随着管土摩擦系数的提高,管道中点处的位移也增加。但随着摩擦系数的继续提高,管道的中点位移反而下降。
|
| 图17 不同摩擦系数下管道中点轴向位移 Figure 17 Displacement of pipeline mid-point with different friction coefficient |
图 18显示了不同管土摩擦系数对管道轴向移动速率的影响。当管土摩擦系数较小时,管道再升温过程中会被完全激活,且随着管土摩擦系数的增大,管道的轴向移动速度也随之增加。但随着管土摩擦系数继续增大,管道的虚拟锚固区域逐渐增加,同时管道轴向移动速度开始下降。
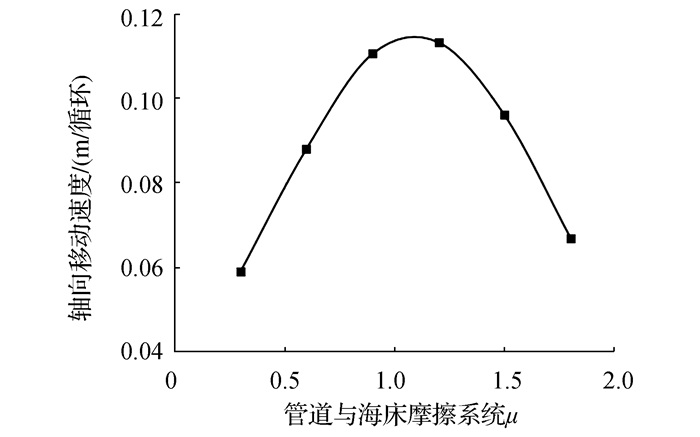
|
| 图18 管道轴向移动速度随管土摩擦系数变化曲线 Figure 18 Relationship between the pipeline-soil friction coefficient and velocity of axial movement of pipeline |
综上所述,管土之间轴向摩擦力的提高会使管道在中间段产生虚拟锚固区域,降低管道轴向移动速率。
5 管道内压对轴向移动的影响考虑恒定内压与循环内压两种方式下管道轴向移动。恒定内压加载方式为海底管道所受的压力荷载在整个温度循环过程种是恒定的,并在管道降温过程中下降为零;循环内压加载方式为在管道每一次温度循环过程中内压荷载也循环,并在降温荷载下,管道内压降低为零。
图 19为恒定内压条件下管道有效轴力分布,管道加热共分为15个加载步,第16步为降温加载步。由图中可以看出,在第一个加热步为管道施加内压荷载,在管道全长范围内有效轴向力增加,但在管道两端逐渐释放。此后加载步中有效轴向力的分布形态与无内压管道相同,但管道所达到的最大有效轴向力相较无内压管道有所增加。在降温加载步中,管道温度降低内压下降,管道收缩,摩擦力反向,管道有效轴力转变为拉力;循环内压条件下管道有效轴力分布与图 3相似,管道加热共分为15个加载步,每个荷载步中管道内压逐渐上升,第16步为降温加载步,此加载步中管道内压为零。在管道的每个升温加载步中,由于管道内压逐渐上升,管道内的有效轴向力也均匀上升。到第8个加载步时,管道被完全激发,虚拟锚固点位于管道中点。在此之后,虽然管道的虚拟锚固点不再变化,但管道有效轴向力还存在小幅升高。在降温加载步中,管道温度和内压逐渐下降,管道收缩,摩擦力反向,管道有效轴力转变为拉力。
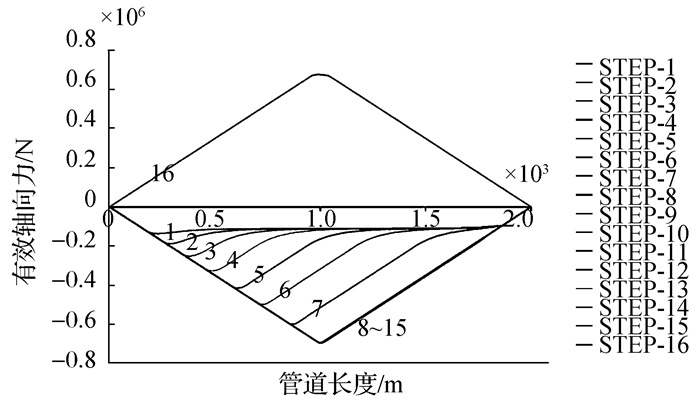
|
| 图19 恒定内压下管道有效轴力分布图 Figure 19 Distribution of effective axial force under constant inner pressure |
图 20所示为设计内压为10 MPa管道和无内压管道在循环温度荷载的作用下管道中点的轴向位移值。由图可知,在管道内压为10 MPa时,管道轴向移动速率约为0.081 m/循环,相较于无压力管道0.060 m/循环,增长了26%。由此可见,管道内压会加快管道的轴向移动速率。
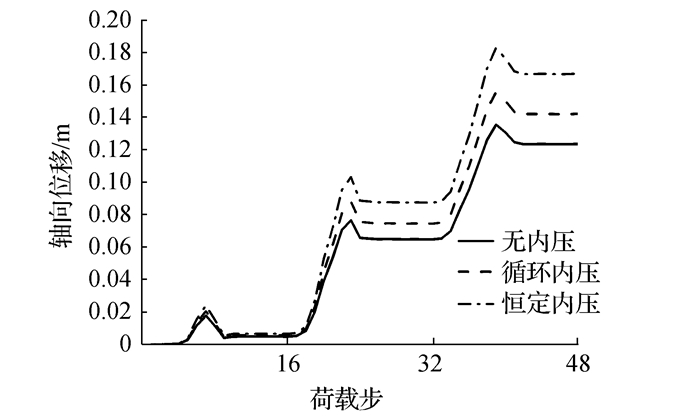
|
| 图20 管道中点轴向位移 Figure 20 Distribution of axial displacement of pipeline mid-point |
由图 20可知,内压循环管道的轴向位移值明显低于恒定内压管道。恒定内压管道和循环内压管道的中点轴向移动速率对比如表 2所示。由表可知,与恒定内压管道相比,循环内压管道对应的中点轴向移动速率降低了14.8%。由此可见,管道内压循环有益于降低管道的轴向移动速率。
| 恒定内压管道 | 循环内压管道 | |
| 轴向位移速率 | 0.081 m/循环 | 0.069 m/循环 |
综上所述,管道内压会提高管道在循环温度荷载下的轴向移动速率,但内压加载方式,管道轴向移动速率也不相同,相比于恒定内压的加载方式,循环内压方式有益于降低管道的轴向移动速率。
6 结论本文建立了循环温度荷载下平坦海床上直管道的非线性有限元模型,模型中考虑了非线性的温度加载梯度和高温对管道材料的影响。分析了短直管道轴向运动机理,考虑了管道内压加载方式对管道轴向移动现象的影响。通过研究得到如下结论:
1)短直管道在非线性循环温度荷载作用下更容易发生轴向移动现象,这是因为管道长度不足以使其达到完全约束状态,管道虚拟锚固点位于管道中点处。
2)管道的非线性温度循环使其产生由管道加热端向非加热端的轴向移动现象,因此管道端部的连接件可靠性尤为重要。
3)管土摩擦对管道轴向移动速率有很大影响,当管土摩擦系数大于某一范围后,管道轴向移动速率随着摩擦系数的增加而下降。
4)管道内压会提高管道在非线性循环温度荷载下的轴向移动速率,但内压加载方式,管道轴向移动速率也不相同,相比于恒定内压的加载方式,循环内压方式有益于降低管道的轴向移动速率。
| [1] | TORNES K, JURY J, OSE B. Axial creeping of high temperature flowlines caused by soil ratcheting[C]//Proceedings of the Conference on Offshore Mechanics and Arctic Engineering. ASME, (s.l.),2000. |
| [2] | CARR M, SINCLAIR F, BRUTON D. Pipeline walking-understanding the field layout challenges, and analytical solutions developed for the SAFEBUCK JIP[C]//Offshore Technology Conference, 2006. Houston, Texas:OTC, 2006. |
| [3] | BRUTON D A S, Bolton M, CARR M, et al. Pipe-soil interaction with flowlines during lateral buckling and pipeline walking-The SAFEBUCK JIP[C]//Offshore Technology Conference, 2008. Houston, Texas:OTC, 2008. |
| [4] | ZHOU Jing, LIU Yuxiao, LI Xin. Pipe walking-lateral buckling interaction[C]//Earth and Space 2010:Engineering, Science, Construction, and Operations in Challenging Environments. Honolulu, Hawaii, United States:American Society of Civil Engineers, 2010:3318-3327. |
| [5] | RONG Haicheng, INGLIS R, BELL G, et al. Evaluation and mitigation of axial walking with a focus on deep water flowlines[C]//Offshore Technology Conference 2009. Houston, Texas:OTC, 2009. |
| [6] |
王哲, 马克俭, 陈志华, 等. 深海管道整体屈曲研究综述[J].
天津大学学报:自然科学与工程技术版, 2014, 47(S): 17–23.
WANG Zhe, MA Kejian, CHEN Zhihua, et al. Overview of global buckling of deep-sea pipeline[J]. Journal Tianjin university:science and technology, 2014, 47(S): 17–23. |
| [7] | 《海洋石油工程设计指南》编委会. 海洋石油工程安装设计[M]. 北京: 石油工业出版社, 2007 . |
| [8] | TAYLOR N, TRAN V. Experimental and theoretical studies in subsea pipeline buckling[J]. Marine structures, 1996, 9(2): 211–257. DOI:10.1016/0951-8339(94)00021-J |
| [9] | American Petroleum Institute (API). API 2A, Recommended practice for planning, designing and constructing fixed offshore platforms-working stress design[S]. 21st ed. Washington:American Petroleum Institute, 2000. |
| [10] | CARR M, SINCLAIR F, BRUTON D. Pipeline walking-understanding the field layout challenges, and analytical solutions developed for the SAFEBUCK JIP[C]//Offshore Technology Conference 2006.Houston, Texas, 2006. |



