2. School of Economics and Management, Yanshan University, Qinhuangdao 066004, China
发展低碳经济已经成为我国加快转变经济发展方式、实现跨越式发展的重要引擎。我国明确了碳减排目标,并将其作为约束性指标纳入国民经济和社会发展中长期规划。一般地,碳减排主要手段包括结构减排、技术减排和消费减排,其中技术减排和消费减排主要集中于微观层面,其实质是结构减排的具体体现,这里的结构既包括产业结构,也包括能源消费结构[1]。
关于产业结构对碳排放的影响,有学者认为产业结构对碳排放增长起推动作用,中国当前的产业结构不利于碳减排[2-3]。也有学者持不同观点,认为产业结构对碳排放增长起抑制作用[4-5]。
关于能源结构对碳排放的影响。学术界前期主要依据历史统计数据进行因素分析[6-7];随着研究深入,开始关注区域碳排放特征与能源结构间的关系[8-9]。近年来,认识到进展迟缓的能源结构变化是造成碳排放增长无法实现大幅下降的关键因素,能源结构调整对实现碳减排目标的贡献潜力较大[10-11]。
以上研究均证实了产业结构与能源结构对碳排放的贡献,一致认为未来产业结构与能源结构变动对碳减排的贡献潜力较大,但忽略了产业结构与能源结构之间的相互关系。基于此,本文以低碳为切入点,探究河北省产业结构与能源结构的关联关系,以期为河北省实现低碳经济提供有建设性的能源规划和产业政策。
1 评价指标体系构建低碳化,狭义的理解就是碳生产能力的提高,即单位GDP碳排放的降低,广义的概念是指以低能耗、低污染、低排放为特征的可持续经济发展模式[12];产业结构与能源结构低碳关联是指在不影响社会经济发展目标的前提下,依靠技术进步和制度创新降低高碳产业部门在国民经济中的比重,转变产业能源利用方式,减少对高碳能源的需求,在促进清洁能源和新兴能源产业发展的同时进一步深化升级产业结构,实现产业结构与能源结构的协调发展,并最终形成以高增长、低能耗、低污染、低排放为特征的低碳经济发展模式。基于产业结构与能源结构低碳关联的内涵,参考国内外相关研究成果[13]及《“十二五”规划纲要》、《节能减排“十二五”规划》等,在系统性、科学性、可行性原则下构建低碳产业、低碳消耗、低碳能源和低碳排放四个准则层,包括11个具体指标的区域产业结构与能源结构低碳关联评价指标体系,如表 1所示。
| 评价目标 | 一级指标名称 | 二级指标 | |
| 指标名称 | 指标方向 | ||
| 产业结构与能源结构低碳关联A | 低碳产出B1 | 人均GDP增长率B11/% | (+) |
| 第一产业碳生产力B12/(万元·t-1) | (+) | ||
| 第二产业碳生产力B13/(万元·t-1) | (+) | ||
| 第三产业碳生产力B14/(万元·t-1) | (+) | ||
| 低碳消耗B2 | 能源消费总量B21/万吨标准煤 | (-) | |
| 第一产业能源强度 B22/(吨标准煤/万元) | (-) | ||
| 第二产业能源强度B23/(吨标准煤/万元) | (-) | ||
| 第三产业能源强度B24/(吨标准煤/万元) | (-) | ||
| 低碳能源B3 | 能源结构多元化系数B31 | (+) | |
| 能源效率B32 | (+) | ||
| 可再生能源消费比重B33/% | (+) | ||
| 低碳排放B4 | CO2排放B41/104t | (-) | |
| 化学需氧量排放B42/104t | (-) | ||
| SO2排放B43/104t | (-) | ||
| 注:(+) 表示正向指标,(-) 表示逆向指标。 | |||
正向指标的无量纲化公式为
| ${{X}_{ij}}=\frac{{{x}_{tj}}}{{{M}_{j}}-{{m}_{j}}}$ | (1) |
逆向指标的无量纲化公式为
| ${{X}_{tj}}=\frac{{{M}_{j}}-{{x}_{tj}}}{{{M}_{j}}-{{m}_{j}}}$ | (2) |
则为对应的无量纲值,Mj和mj分别表示第j个指标原始值中的最大值和最小值。
2.1.2 基于最小距离和最大熵原理的组合赋权[14]在以往的研究中,广泛应用的评价方法依据客观化程度可分为主观评价方法和客观评价方法,两类评价方法各有利弊,主观评价法可以充分发挥人的智慧和经验但容易受主观因素的影响,而客观评价法可以免除个人经验和主观意识的影响,具有相当的客观性但比较死板。本文尝试尽量避免评价方法的弊端,综合运用主观评价(AHP) 和客观评价(粗糙集理论和熵值法) ,保证评价结果的科学合理性。
设分别运用粗糙理论、熵值法和AHP确定第j个指标的权重为wfj,f=1,2,3,则第j个指标的组合权重为
| ${{w}_{j}}=\sum\limits_{f=1}^{F}{{{\lambda }_{f}}w_{j}^{f},\sum\limits_{f=1}^{F}{{{\lambda }_{f}}=1}}$ | (3) |
1) 基于最小广义距离的组合权系数
最小广义距离,即各年度加权得分与理想点广义距离最小,设广义距离为d,则
| $\min \sum\limits_{t=1}^{T}{{{d}_{t}}=\sum\limits_{t=1}^{T}{\sum\limits_{j=1}^{J}{\sum\limits_{f=1}^{F}{{{\lambda }_{f}}w_{j}^{f}\left( 1-{{x}_{tj}} \right) }}}}$ | (4) |
2) Jaynes最大熵原理,即保证各赋权结果差异最小,则
| $\max S=-\sum\limits_{f=1}^{F}{{{\lambda }_{f}}\ln {{\lambda }_{f}}}$ | (5) |
据此,构建目标函数:
| $\left\{ \begin{matrix} \min \sum\limits_{t=1}^{T}{\sum\limits_{j=1}^{J}{\sum\limits_{f=1}^{F}{{{\lambda }_{f}}w_{j}^{f}\left( 1-{{x}_{tj}} \right) }}}+ \\ \left( 1-\eta \right) \sum\limits_{f=1}^{F}{{{\lambda }_{f}}\ln {{\lambda }_{f}}} \\ \sum\limits_{f=1}^{F}{{{\lambda }_{f}}=1} \\ {{\lambda }_{f}}\ge 0 \\ \end{matrix} \right.$ | (6) |
式中:η(0≤η≤1) 为平衡系数。
构建拉格朗日函数求得
| ${{\lambda }_{f}}=\frac{\exp \left\{ -\left[ 1+\eta \sum\limits_{t=1}^{T}{\sum\limits_{j=1}^{J}{w_{j}^{f}\left( 1-{{x}_{tj}} \right) /\left( 1-\eta \right) }} \right] \right\}}{\sum\limits_{f=1}^{F}{\exp \left\{ 1+\eta \sum\limits_{t=1}^{T}{\sum\limits_{j=1}^{J}{w_{j}^{f}\left( 1-{{x}_{tj}} \right) /\left( 1-\eta \right) }} \right\}}}$ | (7) |
1) 确定最优向量G:
| $G=\left( {{g}_{1}},{{g}_{2}},\cdots {{g}_{J}} \right) =\left( {{x}_{11}}V{{x}_{21}}V\cdots V{{x}_{T1}},{{x}_{12}}V{{x}_{22}}V\cdots V{{x}_{T2}},\cdots {{x}_{1J}}V{{x}_{2J}}V\cdots V{{x}_{TJ}} \right) $ | (8) |
式中:xtj为无量纲化数据,V为取最大运算符。
2) 计算灰色关联系数:
| ${{R}_{t}}=\left( {{X}_{j}},G \right) =\frac{\underset{t}{\mathop{\min }}\,\underset{j}{\mathop{\min }}\,\left| {{x}_{tj}}-{{g}_{j}} \right|+\xi \underset{t}{\mathop{\max }}\,\underset{j}{\mathop{\max }}\,\left| {{x}_{tj}}-{{g}_{j}} \right|}{\left| {{x}_{tj}}-{{g}_{j}} \right|+\xi \underset{t}{\mathop{\max }}\,\underset{j}{\mathop{\max }}\,\left| {{x}_{tj}}-{{g}_{j}} \right|}$ | (9) |
式中:ξ(0≤ξ≤1) 表示分辨系数。
3) 计算关联度:
| $\xi \left( 0\le \xi \le 1 \right) $ | (10) |
依据科学性、可行性等原则,参考《中国统计年鉴》、《中国能源统计年鉴》以及《河北经济年鉴》,选取河北省2000-2012年各指标数据对河北省产业结构与能源结构低碳关联进行深入分析(2014《河北经济年鉴》尚未发布,因此2013、2014年相关数据无法获得) 。
3.1 指标数据计算1) 产业能源强度数据
根据2001-2013年《中国能源统计年鉴》中“河北能源平衡表(实物量) ”按行业分的终端能源消费量,本文参照国家统计局《三次产业划分规定》对三次产业的划分整理各产业原煤、洗精煤、其他洗煤、焦炭、原油、燃料油、汽油、煤油、柴油、液化石油气、炼厂干气、天然气、焦炉煤气、热力、电力等消费量(实物量) ,并根据“各种能源折标准煤参考系数”计算相应产业各种能源的消费量(标准量) ,汇总后得到2000-2012年河北省三次产业的能源消费量,进而计算各产业能源消费量与相应产业产值的比值得到产业能源强度数据。
2) 产业碳生产力数据
碳生产力,即单位CO2排放的经济产出,用GDP与CO2排放量的比值表示。对于三次产业碳排放的计算,借鉴王韶华等[16]对河北省三次产业碳排放量的估算方法。
3) 能源结构多元化系数数据
能源结构的多元化、均衡化是低碳经济发展的要求,也是衡量产业结构与能源结构关联的重要指标。本文用能源结构多元化系数反映河北省能源结构多元化均衡化程度,其计算公式为
| $SF=\sum \left( \frac{{{E}_{1}}}{{{E}_{1}}},\frac{{{E}_{2}}}{{{E}_{2}}}\cdots ,\frac{{{E}_{n}}}{{{E}_{1}}} \right) $ | (11) |
式中:SF表示能源结构多元化系数,Ei表示第i种能源的消费量,可通过2013年《河北经济年鉴》获得历年数据。
4) 能源效率数据
提高能源效率是促进低碳经济实现的核心举措,因此能源效率是衡量低碳经济发展水平的重要指标,也反映了产业结构与能源结构的关联程度,本文利用河北省GDP增速与能源消费增速的比值表示能源效率。其中河北省GDP和能源消费的历年数据均可通过2013年《河北经济年鉴》获得。
5) 其他指标数据
2000-2012年河北省的GDP、人均GDP、能源消费总量、可再生能源比重等指标数据均可通过《河北经济年鉴》获得,2000-2012年的CO2排放、化学需氧量排放,SO2排放等指标数据可通过《中国统计年鉴》获得。
2000-2012年河北省产业结构与能源结构低碳关联评价指标数据,如表 2所示。
| 年份 | B11 | B12 | B13 | B14 | B21 | B22 | B23 | B24 | B31 | B32 | B33 | B41 | B42 | B43 |
| 2000 | 10.85 | 0.960 5 | 0.124 0 | 0.327 5 | 11 195.71 | 0.209 6 | 1.999 1 | 0.950 3 | 1.099 6 | 0.61 | 0.05 | 8 186 | 70.7 | 132.1 |
| 2001 | 8.68 | 0.988 6 | 0.126 9 | 0.361 5 | 12 114.29 | 0.193 3 | 1.963 4 | 0.864 5 | 1.088 9 | 1.14 | 0.04 | 8 879 | 65.2 | 128.9 |
| 2002 | 8.59 | 0.878 7 | 0.120 8 | 0.394 8 | 13 404.53 | 0.202 1 | 2.086 9 | 0.777 8 | 1.097 5 | 0.85 | 0.03 | 9 809 | 64 | 127.9 |
| 2003 | 14.41 | 1.004 2 | 0.119 2 | 0.437 6 | 15 297.89 | 0.175 0 | 2.128 6 | 0.698 2 | 1.077 8 | 1.06 | 0.07 | 11 234 | 63.6 | 142.2 |
| 2004 | 21.81 | 1.211 3 | 0.131 5 | 0.463 6 | 17 347.79 | 0.141 2 | 1.924 3 | 0.655 2 | 1.097 2 | 1.68 | 0.1 | 12 687 | 65.8 | 142.8 |
| 2005 | 17.39 | 0.991 2 | 0.129 1 | 0.459 1 | 19 835.99 | 0.172 4 | 2.061 0 | 0.682 3 | 1.089 1 | 1.26 | 0.12 | 14 531 | 66.1 | 149.6 |
| 2006 | 13.8 | 0.986 3 | 0.137 8 | 0.53 | 2 0 21 794.09 | 0.151 3 | 1.987 1 | 0.563 4 | 1.091 8 | 1.47 | 0.1 | 15 958 | 68.8 | 154.5 |
| 2007 | 17.86 | 1.130 6 | 0.145 1 | 0.607 0 | 23 585.13 | 0.133 0 | 1.820 6 | 0.491 5 | 1.082 7 | 2.27 | 0.09 | 17 300 | 66.7 | 149.2 |
| 2008 | 16.91 | 1.206 1 | 0.160 9 | 0.545 | 2 24 321.87 | 0.137 9 | 1.618 3 | 0.513 3 | 1.083 3 | 5.66 | 0.08 | 17 831 | 60.5 | 134.5 |
| 2009 | 6.94 | 1.213 3 | 0.157 8 | 0.571 6 | 25 418.79 | 0.134 1 | 1.622 8 | 0.463 3 | 1.081 0 | 1.69 | 0.07 | 18 636 | 57 | 125.3 |
| 2010 | 16.63 | 1.325 6 | 0.176 9 | 0.576 6 | 27 531.11 | 0.133 | 3 1.436 7 | 0.466 1 | 1.105 6 | 2.21 | 0.74 | 19 974 | 54.6 | 123.4 |
| 2011 | 18.49 | 1.498 3 | 0.189 7 | 0.638 7 | 29 498.29 | 0.151 2 | 1.347 5 | 0.410 6 | 1.115 9 | 2.83 | 1.08 | 21 297 | 138.9 | 141.2 |
| 2012 | 7.7 | 1.613 4 | 0.199 8 | 0.584 | 3 30 250.21 | 0.159 4 | 1.296 2 | 0.395 4 | 1.126 1 | 3.3 | 1.56 | 21 699 | 134.1 | 134.9 |
粗糙集理论的原理就是在既定分类保持不变的基础上,通过指标约简,删除不重要的指标[17]。
1) 数据的离散化处理。本文借助SPSS16.0统计软件采用K-均值聚类分析(分类数设定为3) 对无量纲化数据进行离散化处理。
2) 指标约简:若ind(R) =U/ind(R-{R'}) ,则称R'为R中不必要的;否则称R'为R中必要的。
其中,R是由U上等价关系组成的集合,U称为论域,R'∈R,ind(R) 表示R上的不可区分关系,即∩R(R中所有等价关系的交集) 也是一个等价关系,U/ind(R-{R'}) 表示等价关系交集中删除一个等价关系后的所有等价类。
各指标的约简过程及结果如表 3所示,所有指标都是必要的,均被保留下来。
| 指标 | (U,R) | ∩P | U/ind(R-{R'}) |
| 低碳产出 | U={1,2,3,4,5,6,7,8,9,10,11,12,13} R={∩B11, ∩B12, ∩B13, ∩B14} | ∩B11 ={{1,4,6,7,8,9,11},{2,3,10,13},{5,12}} | {{1,2,3},{4,6},{5},{7},{8,10},{9},{11},{12,13}} |
| ∩B12 ={{1,2,3,4,6,7},{5,8,9,10,11},{12,13}} | {{1},{2,3},{4,6},{5},{7,9},{8},{10},{11},{12},{13}} | ||
| ∩B13 ={{1,2,3,4,5,6},{7,8,9,10},{11,12,13}} | {{1},{2,3},{4,6,7},{5},{8,11},{9},{10},{12},{13}} | ||
| ∩B14 ={{1,2,3},{4,5,6,7,9},{8,10,11,12,13}} | {{1,4,6},{2,3},{5},{7},{8,9},{10},{11},{12},{13}} | ||
| U/ ind(R) ={{1},{2,3},{4,6},{5},{7},{8},{9},{10},{11},{12},{13}} | |||
| 低碳消耗 | U={1,2,3,4,5,6,7,8,9,10,11,12,13} R={∩B21, ∩B22, ∩B23, ∩B24} | ∩B21 ={{1,2,3},{4,5,6,7,8},{9,10,11,12,13}} | {{1,2},{3},{4,6},{5,7},{8,9,10},{11,12},{13}} |
| ∩B22 ={{1,2,3},{4,6,13},{5,7,8,9,10,11,12}} | {{1,2},{3},{4,6},{5,7},{8},{9,10},{11,12,13}} | ||
| ∩B23 ={{1,2,5,7,8,9,10},{3,4,6},{11,12,13}} | {{1,2},{3},{4,6},{5,7},{8},{9,10,11,12},{13}} | ||
| ∩B24 ={{1,2},{3,4,5,6,7},{8,9,10,11,12,13}} | {{1,2},{3},{4,6},{5,7,8},{9,10},{11,12},{13}} | ||
| U/ ind(R) = {{1,2},{3},{4,6},{5,7},{8},{9,10},{11,12},{13}} | |||
| 低碳能源 | U={1,2,3,4,5,6,7,8,9,10,11,12,13} R={∩B31, ∩B32, ∩B33} | ∩B31 ={{1,2,3,5,6,7,11},{4,8,9,10},{12,13}} | {{1,2,3,4,5,6,7,10},{8},{9},{11,12},{13}} |
| ∩B32 ={{1,2,3,4,5,6,7,10},{8,11,12,13},{9}} | {{1,2,3,5,6,7},{4,8,9,10},{11},{12},{13}} | ||
| ∩B33 ={{1,2,3,4,5,6,7,8,9,10},{11,12},{13}} | {{1,2,3,5,6,7},{4,10},{8},{9},{11},{12,13}} | ||
| U/ ind(R) = {{1,2,3,5,6,7},{4,10},{8},{9},{11},{12},{13}} | |||
| 低碳排放 | U={1,2,3,4,5,6,7,8,9,10,11,12,13} R={∩B41, ∩B42, ∩B43, ∩B44} | ∩B41 ={{1,2,3},{4,5,6,7},{8,9,10,11,12,13}} | {{1,2,3},{4,5},{6,7,8},{9},{10,11},{12,13}} |
| ∩B42 ={{1,2,3,4,5,6,7,8},{9,10,11},{12,13}} | {{1,2,3},{4,5},{6,7},{8},{9,12,13},{10,11}} | ||
| ∩B43 ={{1,2,3,10,11},{4,5,9,12,13},{6,7,8}} | {{1,2,3},{4,5,6,7},{8},{9,10,11},{12,13}} | ||
| U/ ind(R) ={{1,2,3},{4,5},{6,7},{8},{9},{10,11},{12,13}} | |||
3) 属性重要性计算。设S=(U,R,V,f) 为一个知识表达系统,P,QR,则属性R'的重要性:
| ${{\mu }_{R'}}=\frac{\left| \left| Po{{s}_{p}}\left( Q \right) \right|-\left| Po{{s}_{p-\left| R' \right|}}\left( Q \right) \right| \right|}{U},j=1,\cdots ,J$ | (12) |
式中:P和Q为U中的等价关系,PosP(Q) 表示Q的P正域,指的是U中所有根据分类U/R'的信息可以准确地划分到关系Q的等价类中去的对象集合。
4) 对μ>0的指标的μ值进行“归一化”处理,得到各指标的权值wRj。
二级指标的重要性及单层权值、一级指标的重要性及权值,以及二级指标的综合权值,如表 4。
3.2.2 熵值法权重计算熵值法主要通过计算指标的信息熵,根据指标的相对变化程度对系统整体的影响来决定指标的权重[18]。
1) 数据的“归一化”处理:
| ${{s}_{tj}}=\frac{{{x}_{tj}}}{\sum\limits_{t=1}^{T}{{{x}_{tj}}}},j=1,\cdots ,J$ | (13) |
式中:stj表示第t年第j个指标的归一化值,xtj则为对应指标的原始值。
2) 熵值计算:
| ${{e}_{j}}=-\sum\limits_{t=1}^{T}{{{s}_{tj}}\ln \left( {{s}_{tj}} \right) /\ln T}$ | (14) |
式中:ej表示第j个指标的熵值,T为被评价年份的个数。
3) 权值确定:
| $w_{j}^{E}=\frac{1-{{e}_{j}}}{\sum\limits_{j=1}^{J}{\left( 1-{{e}_{j}} \right) }}$ | (15) |
式中:wEj表示运用熵值法确定的第j个指标的权值,J为指标的个数。
由式(13) ~(15) 可得到各指标的权重,如表 4。
| 一级指标 | 粗糙集理论权值 | AHP权值 | 二级指标 | 粗糙集理论权值 | 熵值法权值 | AHP 权值 | 组合权值 | ||||
| 重要性 | 权值 | 重要性 | 单层权值 | 综合权值 | 单层权值 | 综合权值 | |||||
| 低碳产出B1 | 0.417 0 | 0.253 5 | 0.387 3 | 人均GDP 增长率B11 | 0.538 5 | 0.368 4 | 0.093 4 | 0.061 5 | 0.445 9 | 0.172 7 | 0.124 4 |
| 第一产业碳生产力B12 | 0.153 8 | 0.105 2 | 0.026 7 | 0.066 4 | 0.120 2 | 0.046 8 | 0.043 1 | ||||
| 第二产业碳生产力B13 | 0.384 6 | 0.263 2 | 0.066 7 | 0.095 4 | 0.259 6 | 0.100 6 | 0.087 4 | ||||
| 第三产业碳生产力B14 | 0.384 6 | 0.263 2 | 0.066 7 | 0.043 3 | 0.170 7 | 0.066 2 | 0.062 3 | ||||
| 低碳消耗B2 | 0.254 4 | 0.154 7 | 0.198 1 | 能源消费总量B21 | 0.230 8 | 0.230 8 | 0.035 7 | 0.059 7 | 0.139 7 | 0.027 9 | 0.036 3 |
| 第一产业能源强度B22 | 0.230 8 | 0.230 8 | 0.035 7 | 0.042 6 | 0.198 2 | 0.039 5 | 0.038 7 | ||||
| 第二产业能源强度B23 | 0.307 7 | 0.307 6 | 0.047 6 | 0.081 1 | 0.387 3 | 0.076 7 | 0.066 9 | ||||
| 第三产业能源强度B24 | 0.230 8 | 0.230 8 | 0.035 7 | 0.036 6 | 0.274 8 | 0.054 5 | 0.044 6 | ||||
| 低碳能源B3 | 0.576 9 | 0.350 8 | 0.139 8 | 能源结构多元化B31 | 0.769 2 | 0.625 0 | 0.219 2 | 0.069 6 | 0.311 9 | 0.043 8 | 0.111 8 |
| 能源效率B32 | 0.307 7 | 0.250 0 | 0.087 7 | 0.082 4 | 0.197 6 | 0.027 8 | 0.059 1 | ||||
| 可再生能源比重B33 | 0.153 8 | 0.125 0 | 0.043 9 | 0.222 3 | 0.490 5 | 0.068 7 | 0.086 8 | ||||
| 低碳排放B4 | 0.396 5 | 0.241 0 | 0.274 8 | CO2排放B41 | 0.230 8 | 0.230 8 | 0.055 6 | 0.063 8 | 0.500 0 | 0.137 4 | 0.094 8 |
| 化学需氧量排放B42 | 0.230 8 | 0.230 8 | 0.055 6 | 0.032 0 | 0.250 0 | 0.068 7 | 0.057 5 | ||||
| SO2排放B43 | 0.538 5 | 0.538 4 | 0.129 8 | 0.043 3 | 0.250 0 | 0.068 7 | 0.086 3 | ||||
根据河北省产业结构与能源结构低碳关联评价指标的层次结构设计了AHP判断矩阵专家咨询表,并通过面谈和电子邮件相结合的方式发放给能源经济、产业经济、低碳经济等相关领域的专家学者,主要包括位于河北省、北京市和天津市等的10所高等院校以及2010年12月17日国家发展和改革委员会培训中心举办的“碳计量方法专题培训班”的学员等。问卷共计发放116份,共回收88份,回收率为75.86%,其中有效问卷81份,问卷的有效率为92.05%。通过和法求解判断矩阵,并进行一致性检验,得到一级指标和二级指标的权重,如表 4所示。
3.2.4 组合权重计算令η=0.5,将通过粗糙集理论、熵值法和AHP确定的各指标的权重代入式(7) ,可以得到三种评价方法的组合权系数,分别为0.361 9、0.176 1、0.462 0。
将三种方法确定的各指标权重与组合权系数代入式(3) ,可得到各指标的组合权重,见表 4。
由表 4可知,低碳产出中的人均GDP增长率、第二产业碳生产力以及低碳消耗中的第二产业能源强度等指标对河北省产业结构与能源结构低碳关联的影响较显著。目前,河北省处于并将长期处于工业化中期阶段,发展始终是第一要务,电力、冶金、化工、建材等原材料部门的快速增长导致碳排放和能耗总量不断上升,煤炭的廉价、可得性满足了河北省快速发展的需要,粗放式的经济增长方式使得单位产值的碳排放较大。因此,转变经济增长方式,逐渐由“又快又好发展”向“又好又快发展”过渡,以信息化改造传统工业,通过技术创新提升装备水平,大力发展高新技术产业,是优化低碳产出和低碳消耗的有效措施。
低碳能源中的能源结构多元化系数、可再生能源比重以及低碳排放中的CO2排放、SO2排放等指标对河北省产业结构与能源结构低碳关联的影响较显著。河北省能源结构极其不合理,煤炭所占比例过大(长期稳定在90%以上) 虽然在重化工业阶段一定程度上实现了河北省产业发展的过渡,但是带来了生态环境破坏、经济效率差等不良后果,阻碍了低碳经济的发展;随着河北省产业结构优化的深入,对高耗能行业的技术改造以及第三产业的不断壮大,加大了对落后产能的淘汰力度,对石油、天然气等清洁能源以及新能源、可再生能源等的需求增大。因此,科学制定能源发展规划,并以此为指导,加快调整能源结构,继续淘汰落后生产能力,大力发展新兴能源产业;加强能源综合利用,推进用能方式转变,提高能源利用效率,减少污染物排放,是形成以低能耗、低污染、低排放为特征的经济发展方式的关键。
3.3 河北省产业结构与能源结构低碳关联度计算将各指标的无量纲化数据代入式(8) ,得到最优比较序列:
| $G=\left( 1,1,1,1,1,1,1,1,1,1,1,1,1,1, \right) $ |
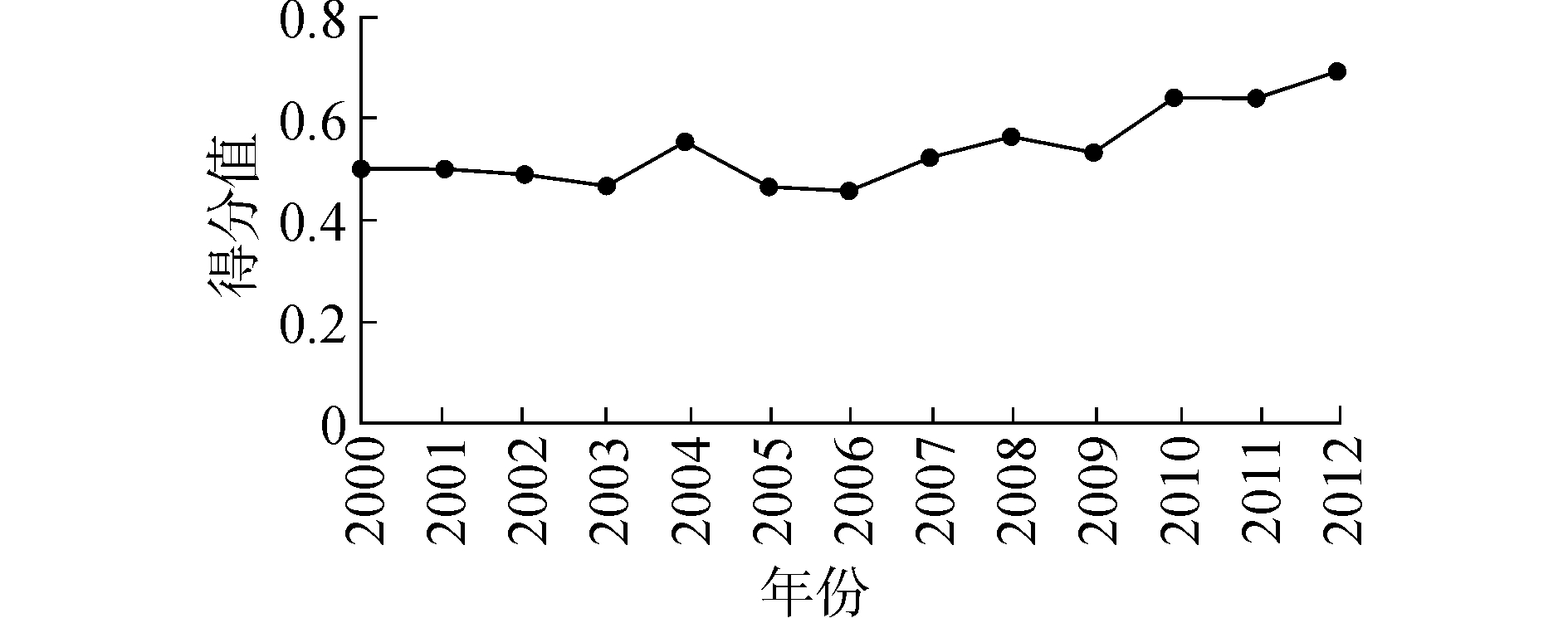
令ξ=0.5,将各指标的无量纲化数据及最优向量的元素数据依次代入式(9) 、(10) ,可得到2000-2012年河北省产业结构与能源结构低碳关联度,如图 1所示。
|
| 图1 年河北省产业结构与能源结构低碳关联分析 Figure 1 Analysis of low-carbon correlation between the industrial structure and energy structure between 2000 and 2012 in Hebei province |
由图 1可知,2000年以来,河北省产业结构与能源结构低碳关联度虽在不断波动,但总体上呈现上升态势,尤其是从2009年开始,我国在哥本哈根会议上做出了减排承诺并提出了低碳经济发展目标,河北省积极响应国家号召,制定了节能减排规划,以此为指导调整产业结构、优化能源结构,使得产业结构与能源结构关联度有了明显提升。
4 结论本文在界定产业结构与能源结构低碳关联的概念的基础上,通过参考和借鉴已有研究成果构建了区域产业结构与能源结构低碳关联评价指标体系,并对2000-2012年河北省产业结构与能源结构低碳关联度进行实证分析。结果表明:
1) 本文基于最小广义距离原理和Jaynes最大熵原理构建最优组合赋权模型,能够科学、合理地分配各评价方法所得结果在最终结果中所占的份额,保证评价结果的准确性。
2) 河北省产业结构与能源结构低碳关联水平主要由低碳能源、低碳产出、低碳排放、低碳消耗等四个方面综合反映。其中,人均GDP增长率、能源结构多元化系数、CO2排放、第二产业碳生产力、可再生能源比例、SO2排放等指标对河北省产业结构与能源结构低碳关联影响显著。
3) 利用灰色关联模型可以计算产业结构系统内每个指标和能源结构系统每个指标的关联程度,但是在划分关联度等级时主观性较强,这也是本文的一个不足,将在以后的研究中进行探讨。
| [1] |
张雷, 李艳梅, 黄园淅, 等. 中国结构节能减排的潜力分析[J].
中国软科学, 2011(2): 42–51.
ZHANG Lei, LI Yanmei, HUANG Yuanxi, et al. Analysis on character and potential of energy saving and carbon reducing by structure evolution in China[J]. China soft science, 2011(2): 42–51. |
| [2] |
徐成龙, 任建兰, 巩灿娟. 产业结构调整对山东省碳排放的影响[J].
自然资源学报, 2014, 29(2): 201–210.
XU Chenglong, REN Jianlan, GONG Canjuan. The influence of adjustment in industrial structures on carbon emissions in Shandong province[J]. Journal of natural resources, 2014, 29(2): 201–210. |
| [3] |
贾登勋, 黄杰. 门槛效应、经济增长与碳排放[J].
软科学, 2015, 29(4): 67–70.
JIA Dengxun, HUANG Jie. Threshold effect, economic growth and carbon emission[J]. Soft science, 2015, 29(4): 67–70. |
| [4] |
牛鸿蕾, 江可申. 中国产业结构调整碳排放效应的多目标遗传算法[J].
系统管理学报, 2013, 22(4): 560–566.
NIU Honglei, JIANG Keshen. Multi-objective genetic algorithm for optimizing carbon emission from industrial structure adjustment in China[J]. Journal of systems & management, 2013, 22(4): 560–566. |
| [5] |
李科. 中国产业结构与碳排放量关系的实证检验-基于动态面板平滑转换模型的分析[J].
数理统计与管理, 2014, 33(3): 381–393.
LI Ke. An empirical test on the relationship between industrial structure and carbon emission in China-an study based on dynamic panel smooth transition regression model[J]. Journal of applied statistics and management, 2014, 33(3): 381–393. |
| [6] |
徐国泉, 刘则渊, 姜照华. 中国碳排放的因素分解模型及实证分析:1995-2004[J].
中国人口·资源与环境, 2006, 16(6): 158–161.
XU Guoquan, LIU Zeyuan, JIANG Zhaohua. Decomposition model and empirical study of carbon emissions for China:1995-2004[J]. China population, resources and environment, 2006, 16(6): 158–161. |
| [7] |
林伯强, 蒋竺均. 中国二氧化碳的环境库兹涅茨曲线预测及影响因素分析[J].
管理世界, 2009(4): 27–36.
LIN Baiqiang, JIANG Zhujun. A forecast for China's environmental Kuznets curve for CO2 emission, and an analysis of the factors affecting China's CO2 emission[J]. Management world, 2009(4): 27–36. |
| [8] |
张雷. 中国一次能源消费的碳排放区域格局变化[J].
地理研究, 2006, 25(1): 1–9.
ZHANG Lei. A changing pattern of regional CO2 emissions in China[J]. Geographical research, 2006, 25(1): 1–9. |
| [9] |
王媛, 程曦, 殷培红, 等. 影响中国碳排放绩效的区域特征研究-基于熵值法的聚类分析[J].
自然资源学报, 2013, 28(7): 1106–1116.
WANG Yuan, CHENG Xi, YIN Peihong, et al. Research on regional characteristics of China's carbon emission performance based on entropy method and cluster analysis[J]. Journal of natural resources, 2013, 28(7): 1106–1116. |
| [10] |
王迪, 聂锐, 李强. 江苏省能耗结构优化及其节能与减排效应分析[J].
中国人口·资源与环境, 2011, 21(3): 48–53.
WANG Di, NIE Rui, LI Qiang. The optimization of energy consumption structure and its effects of energy saving and emission reduction for Jiangsu province[J]. China population, resources and environment, 2011, 21(3): 48–53. |
| [11] |
何立华, 杨盼, 蒙雁琳, 等. 能源结构优化对低碳山东的贡献潜力[J].
中国人口·资源与环境, 2015, 25(6): 89–97.
HE Lihua, YANG Pan, MENG Yanlin, et al. Contribution potential of optimizing energy structure to low carbon Shandong[J]. China population, resources and environment, 2015, 25(6): 89–97. |
| [12] | APERGIS N, OZTURK L. Testing environmental Kuznets Curve hypothesis in Asian countries[J]. Ecological indicators, 2015, 52: 16–22. |
| [13] | MAGAZZINO C. Economic growth, CO2 emissions and energy use in Israel[J]. International journal of sustainable development & world ecology, 2015, 22(1): 89–97. |
| [14] |
迟国泰, 齐菲, 张楠. 基于最优组合赋权的城市生态评价模型及应用[J].
运筹与管理, 2012, 21(2): 183–191.
CHI Guotai, QI Fei, ZHANG Nan. The city's ecosystem evaluation model based on optimal combination weights and its application[J]. Operations research and management science, 2012, 21(2): 183–191. |
| [15] | 邓聚龙. 灰理论基础. 武汉:华中科技大学出版社[M]. , 2002: 21 -36. |
| [16] |
王韶华, 于维洋, 张伟, 等. 基于产业和能源的河北省分产业碳强度因素分析[J].
经济地理, 2015, 35(5): 166–173.
WANG Shaohua, YU Weiyang, ZHANG Wei, et al. The decomposition analysis for Hebei's industrial carbon intensity based on industry and energy[J]. Economic geography, 2015, 35(5): 166–173. |
| [17] | PAWLAK Z, GRZYMALA-BUSSE J, SLOWINSKI R, et al. Rough sets[J]. Communications of the ACM, 1995, 38(11): 88–95. |
| [18] |
陈启明, 陈华友. 改进的熵值法在确定组合预测权系数中的应用[J].
统计与决策, 2011(13): 159–160.
CHEN Qiming, CHEN Huayou. The implication of improved entropy method in determining the weight coefficient of combination forecasting[J]. Statistics and decision, 2011(13): 159–160. |



