2. XEMC Windpower Co., Ltd, Xiangtan 411102, China
近年来,随着海上风电场逐步由浅滩向深水区域发展,对海上浮式风力机的研究已成为各国开发海上风能的热点工作。半潜型浮式风力机平台因其稳定性较好、适用水深范围广、安装运输方便而备受关注。稳定性是指浮式平台倾斜后恢复平衡位置的能力,是浮式平台主尺寸的主要影响因素。历史上曾发生多起浮式平台倾覆事件:1979年我国的“渤海2号”钻井平台因低干舷拖航等原因而翻沉,造成72人死亡[1];1982年美国的半潜型钻井平台Ocean Ranger号因恶劣天气导致倾覆而造成84人死亡[2]。可见稳定性对保证浮式风力机平台的安全至关重要。目前国内外对半潜型浮式风力机基础性能的研究大多集中在浮式平台的水动力性能和耦合动力分析等方面[3-5],对浮式平台稳定性的研究较少,而且与浮式风力机平台稳定性相关的规范基本上是借鉴海洋采油平台或船舶的相关规范。但浮式风力机属于高耸柔性结构,所受的风倾力矩较大,这与海洋采油平台或船舶差别很大。因此,有必要对半潜型浮式风力机平台进行专门深入的研究。
稳定性包括完整稳定性和破舱稳定性,本文主要研究前者。完整稳定性又分为初稳性和大倾角稳定性两部分,评价指标分别是初稳性高度和风倾力矩与回复力矩曲线图(以下简称力矩曲线图)。一方面,初稳性高度越大,平台抵抗倾覆的能力越强,但当其过大时平台的摇摆周期就会越短,很可能与波浪发生共振而影响机组的正常工作。浮式风力机平台的初稳性高度可参考船舶工程的相关规范,但是目前各相关规范对其限值的规定不一致。比如,中国船级社[6]规定船舶初稳性高度不小于0.15 m,而DNV-OS-J103[7]规范中规定深吃水浮体的初稳性高度不小于1.0 m,但并未规定半潜型浮体的初稳性高度。另一方面,对于力矩曲线图的研究目前主要侧重于验证某具体浮式风力机平台的力矩曲线图是否满足规范要求,而没有探究影响力矩曲线图(即稳定性)的因素。张亮等[8]对其课题组设计的一种半潜式风力机平台进行了稳定性分析,采用数值模拟的方法分别计算了该平台在不同工况下的力矩曲线,验证了其完整稳性和破舱稳性满足中国船级社规范的要求。唐友刚[9-10]针对5MW海上风力机,进行了半潜型浮式基础的概念设计,并验证了该平台的完整稳定性满足中国船级社规范的要求。Roddier[11]对Windfloat的水动力学和结构强度等技术性能进行了可行性研究,并简单地分析该平台在定常风作用下的稳定性。Collu[12]提出了一种改进的半潜型浮式风力机平台概念,并用Sesam软件对平台的完整稳定性和破舱稳定性做了分析,验证了平台的静平衡角均不超过限值。Mayilvahanan[13]针对某四浮筒式风力机平台的稳定性和耐波性进行了分析,并验证其初稳性高度和静平衡角均不超过限值。但他们均只是验算了平台的稳定性,并未深入探究影响稳定性的因素。
基于以上研究现状,本文将首先根据重心移动原理并考虑平台静平衡角和横摇周期等因素,提出适用于半潜型浮式风力机平台的初稳性高度限值计算公式。然后从进水角的角度分析大倾角稳定性中的最不利倾斜轴问题。最后采用Sesam软件对常见的三浮筒半潜型浮式平台进行数值模拟,探究浮筒间距、浮筒直径和干舷高度等因素对风力机平台稳定性的影响规律,为浮式风力机平台的稳定性设计提供参考。
1 初稳性分析 1.1 初稳性高度计算原理由船舶稳定性理论[14]可知:1)当船舶小角度(≤10°~15°)倾斜时,倾斜轴通过水面线的形心(即漂心);2)初稳性半径BM只与排水体积和水面线惯性矩有关,即:
| $\overline{BM}=\frac{{{I}_{T}}}{\nabla }$ | (1) |
| $\overline{GM}=\overline{BM}-\overline{BG}$ | (2) |
式中:IT为静水面线关于漂心轴的惯性矩,∇排水体积,G为重心位置,B为浮心位置,M为稳心位置。
以上结论同样适用于半潜型浮式风力机平台。一般情况下船舶结构的水面线为长方形,其与长边平行的形心轴惯性矩最小,因此船舶的稳定性主要研究横稳心高度以及横倾稳定性。目前半潜型浮式风力机大部分以正三角形布置的圆浮筒结构[11, 15]为主,此类平台的静水面线对任意轴线的惯性矩相等,所以半潜型浮式风力机平台对任意轴线的初稳性高度相等。
1.2 初稳性高度限值计算公式当风力机平台的初稳性高度越大,平台抵抗倾覆的能力越强,但当其过大时平台摇摆周期就会较短,很可能与波浪发生共振而影响机组的正常工作。为限制风力机平台的初稳性高度,可以从抗倾覆力和摇摆周期两个方面着手。在静水条件下,由定常风产生的稳定风压作用使处于静水中正浮状态的浮体开始横倾,复原力矩逐渐增大。当风倾力矩与复原力矩达到平衡,浮体将不再继续倾斜,此时对应的横倾角为静平衡角,该状态称为静平衡状态,平衡条件为
| ${{M}_{H}}={{M}_{R}}=\rho g\nabla \cdot \overline{GZ}=\rho g\nabla \cdot \overline{GM}\cdot {{\varphi }_{s}}$ | (3) |
式中:MH为风倾力矩;MR为回复力矩;φs为静平衡角;ρ为海水的密度,取1 025 kg/m3。
对于半潜型浮式风力机平台,其静平衡角φs应小于一个限值,一般认为小于10°[16]。所以可推导出GM的下限公式:
| $\overline{GM}\ge \frac{{{M}_{H}}}{\rho g\cdot \nabla \cdot {{\varphi }_{max}}}$ | (4) |
另外浮体结构的摇摆周期可表示为[17]
| $T=\frac{2\pi i}{\sqrt{g\cdot \overline{GM~}}}$ | (5) |
式中:T为结构摇摆周期,i为风力机结构关于倾斜轴的回转半径。
一般来说,半潜型浮式风力机平台的摇摆周期要稍大于波浪的谱峰周期[18]。为防止共振,应该控制风力机平台的摇摆周期不能太小,才能有效避开波浪的峰值周期Tp。这样可推导出GM的上限公式:
| $\overline{GM}\le \frac{4{{\pi }^{2}}{{i}^{2}}}{{{T}^{2}}_{p}g}$ | (6) |
式(4)、(6)中不仅包含了平台本身的参数——排水体积和结构关于倾斜轴的回转半径,还包含了与环境相关的参数——风倾力矩和波浪峰值周期。因此,本文提出的浮式风力机平台初稳性高度限值公式更加符合实际情况。浮式风力机平台的初稳性高度可根据式(4)、(6)判断是否合理。
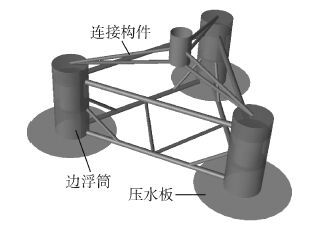
1.3 算例验证本文选取Collu[12]提出的半潜型浮式风力机平台模型,选取美国可再生能源实验室(NREL)的5 MW发电机组,以此为算例验算初稳性高度限值公式。风力机和平台的具体参数如表 1和表 2所示。(表 1中坐标系参考图 4所示,xy平面与平台底平面重合。)采用SESAM软件中GeniE模块建立浮式风力机的整体模型,平台数值模型如图 1所示。其中浮筒采用板单元模拟,连接构件采用梁单元模拟,利用HydroD模块进行稳性数值模拟。根据海洋环境采用指数风剪切模型,剪切指数取为0.14,再根据IMOD MODU规范定义各构件的风荷载系数,Sesam便可自行计算风荷载。设定海况水深100 m,作业工况下场地风速为11.4 m/s,波浪峰值周期为6 s,有义波高为3 m,此时风力机风轮转速为12.1 r/min,叶片桨距角为0°。自存工况下场地风速为44.1 m/s,波浪峰值周期为13 s,有义波高为11 m,此时风力机风轮停止转动,叶片顺桨。
|
| 图1 半潜型平台数值模型 Figure 1 Numerical model of the semi-submersible platform |
数值模拟之后得到以下结果:平台GM为13.79 m;最大风倾力矩分别是72 994 kN·m(作业工况)和59 812 kN·m(自存工况);排水体积为3 500 m3;结构关于倾斜轴的回转半径为40 m。
将数据代入式(4)和(6)得到:
作业工况:
| $\overline{GM}\ge \frac{72994\times {{10}^{3}}}{1025\times 10\times 3500\times 10/180\times 3.14}=11.63m;GM\le \frac{4\times {{3.14}^{2}}\times {{40}^{2}}}{{{6}^{2}}\times 10}=175m$ |
自存工况:
| $\overline{GM}\ge \frac{59812\times {{10}^{3}}}{1025\times 10\times 3500\times 10/180\times 3.14}=9.53m;GM\frac{\le 4\times {{3.14}^{2}}\times {{40}^{2}}}{{{13}^{2}}\times 10}=37.34m$ |
所以GM的上下限值分别是37.33 m和11.63 m。因此根据本文的计算方法可判定:Collu模型的初稳性高度是合理的。
| 构件参数 | 尺寸 |
| 吃水深度/m | 13.5 |
| 浮筒高度/m | 22.5 |
| 浮筒中心到三角形中心距离/m | 30 |
| 浮筒直径/m | 10 |
| 浮筒壁厚/m | 0.020 |
| 浮筒水平舱板厚/m | 0.015 |
| 水平连接构件/(m×m) | 直径1.5×0.02 |
| 斜向连接构件/(m×m) | 直径1.0×0.02 |
| 压水板/m | 直径26 |
| 重心位置 | (0,0,22.54) |
| 浮心位置 | (0,0,6.25) |
| 惯性矩/m4 | 105 374 |
| 构件属性 | 参数 |
| 整机型式 | 3叶片、上风向、水平轴 |
| 风轮,轮毂直径/m | 128、3 |
| 轮毂高度/m | 90(海平面以上) |
| 切入,额定,切出风速/(m·s-1) | 3、11.4、25 |
| 风轮质量/t | 110 |
| 机舱质量/t | 240 |
| 塔架质量/t | 347.46 |
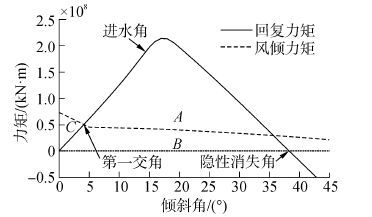
大倾角稳定性一般指倾角大于10°~15°或甲板边缘入水后的稳定性。当风力机平台大角度倾斜时,初稳性的结论不再适用,此时需要通过研究倾覆力矩和回复力矩曲线随倾角的变化规律来考查平台的大倾角稳定性。通过计算得到浮式风力机平台复原力矩与风倾力矩随倾角变化的曲线,如图 2所示。
|
| 图2 典型力矩曲线图 Figure 2 Typical moment curves |
通过分析曲线上的第一交角、进水角、稳性消失角和面积比等参数来评价大倾角稳定性。面积比指(A+B)/(B+C)的值,其中A、B、C分别为图 2所对应的面积。此面积比反映出回复力矩与风倾力矩做功的比值,是评价大倾角稳定性的主要指标。
2.1 最不利倾斜轴浮式风力机处于复杂的海洋环境之中,可能受到来自各方向的风荷载。当半潜型浮式平台受到不同方向的风荷载而发生倾覆时,平台抵抗倾覆的能力有差异,此时存在最不利的倾斜轴使平台的稳定性最差。为找到浮式平台的最不利倾斜轴,大多数学者采用先假定一组倾斜轴再数值计算验证的方法获得,比如王宁[19],但是他们并没有从理论解释最不利倾斜轴的问题。下面本文拟从理论分析的角度探究这个问题。由于浮式风力机平台关于任意形心轴的惯性矩相同(忽略连接构件对水线面的贡献)。由前面的推导可知,风力机在任意倾斜轴方向具有相同的初稳性高度,即相同的稳定性。因此,不论风向如何,平台必绕着垂直风向的形心轴倾覆。
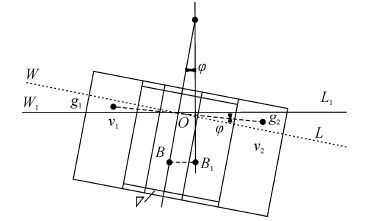
首先根据船舶重心移动原理可知,初稳性高度是由出入水体积决定,如图 3和式(7)、(8)所示。
| ${{v}_{1}}\cdot \overline{{{g}_{1}}o}+{{v}_{2}}\cdot \overline{o{{g}_{2}}}={{I}_{T}}\cdot tan\varphi $ | (7) |
| $\overline{GM}=\frac{{{v}_{1}}\cdot {{g}_{1}}o+{{v}_{2}}\cdot o{{g}_{2}}}{\nabla \cdot tan\varphi }-\overline{BG}=\frac{{{I}_{T}}}{\nabla }-BG$ | (8) |
|
| 图3 稳心高度示意图 Figure 3 Illustration of metacentric height |
式中:v1、v2分别为边缘进水前出入水体积,g1、g2分别为边缘进水前出入水体积的重心位置。
当风力机平台发生大倾角倾覆而导致边缘开始进水,水面线形状不再保持正三角形分布的圆形,水面线面积不再稳步增长,入水体积的增长速度跟不上出水体积的增长速度,导致漂心偏向出水方向,水面线形心位置也发生偏移。此时式(9)、(10)成立,因此稳心高度开始下降,即稳定性下降。由于对不同倾斜轴浮式平台的进水角不同,因此不同倾斜轴的稳定性不再相同。由于进水前各轴稳定性相同,进水之后稳定性开始下降,因此平台必先绕着最先进水之轴倾覆,即进水角最小之轴就是最不利倾斜轴。由几何知识可知,边缘距离倾斜轴越远时进水角越小,浮体绕该轴的稳心高度越低,此时对应的轴为最不利倾斜轴。
| $v{{\prime }_{1}}\cdot \overline{{{g}_{1}}o\prime }+v{{\prime }_{2}}\cdot \overline{og{{\prime }_{2}}}<{{I}_{T}}\cdot tan\varphi $ | (9) |
| $\overline{GM\prime }=\frac{v{{\prime }_{1}}\overline{\cdot {{g}_{1}}o\prime }+v{{\prime }_{2}}\cdot \overline{og{{\prime }_{2}}}}{\nabla \cdot tan\varphi }-\overline{BG}<\frac{{{I}_{T}}}{\nabla }-\overline{BG}=\overline{GM}$ | (10) |
式中:v′1、v′2分别为边缘进水后出入水体积,g′1、g′2分别为边缘进水后出入水体积的重心位置。
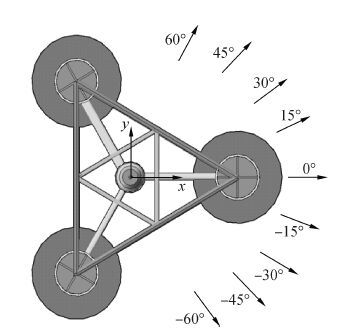
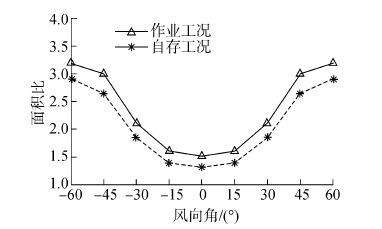
2.2 算例验证选用Collu的模型作为算例,计算参数和海况条件均参考1.3节描述。假定风力机的偏航系统可使风轮平面始终与风向垂直,由2.1节可知对应的倾斜轴均垂直风向。为探究风力机平台的最不利倾斜轴,选取如图 4所示-60°~60°等9个不同的风向,分别计算在作业工况和自存工况下浮式平台的稳定性。计算结果如图 5和表 3所示。从结果中可以发现,0°风向的确为最不利的方向,其对应的倾斜轴为最不利倾斜轴。由此证明2.1节的结论是合理的。
| 工况 | 风向角/(°) | 倾斜轴/(°) | 第一交角/(°) | 面积比 |
| -60 | 30 | 5.31 | 3.19 | |
| -45 | 45 | 5.30 | 3.00 | |
| -30 | 60 | 5.30 | 2.11 | |
| -15 | 75 | 5.29 | 1.60 | |
| 作业工况 | 0 | 90 | 5.29 | 1.51 |
| 15 | 105 | 5.29 | 1.60 | |
| 30 | 120 | 5.30 | 2.11 | |
| 45 | 135 | 5.30 | 3.00 | |
| 60 | 150 | 5.31 | 3.19 | |
| -60 | 30 | 6.30 | 2.91 | |
| -45 | 45 | 6.59 | 2.65 | |
| -30 | 60 | 6.59 | 1.85 | |
| -15 | 75 | 6.58 | 1.39 | |
| 自存工况 | 0 | 90 | 6.58 | 1.32 |
| 15 | 105 | 6.58 | 1.39 | |
| 30 | 120 | 6.59 | 1.85 | |
| 45 | 135 | 5.59 | 2.65 | |
| 60 | 150 | 6.60 | 2.91 |
|
| 图4 风荷载方向示意图 Figure 4 Illustration of wind headings |
|
| 图5 不同风向角的面积比 Figure 5 Area ratios at different wind headings |
为探究影响稳定性的因素,本文以浮筒间距、浮筒直径和干舷高度为变量研究稳定性的变化。采用Sesam软件进行数值模拟,以前文介绍的半潜型浮式平台为母模型,分别调整母模型的浮筒间距、浮筒直径和干舷高度等因素,一共建立了7个模型,以探究影响半潜型浮式风力机稳定性的因素,得到改进稳定性的措施。由于本文为探究性研究因此只计算作业工况下的稳定性,平台的倾斜轴均为对应的最不利倾斜轴。在此条件下计算浮式平台在不同倾角下复原力矩与风倾力矩的关系曲线。
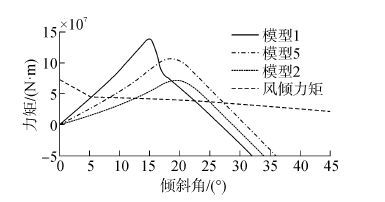
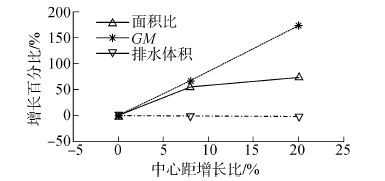
3.1 浮筒间距对稳定性的影响模型2、模型5和模型1的唯一区别在于浮筒中心距,其中心距依次为25、27和30 m。其他条件均不变,稳定性分析的计算结果如表 4和图 6所示。以具有最小中心距的模型2为参考,分别计算模型5和模型1两者的中心距、面积比、GM以及排水体积等指标相对模型2对应指标的增长率,并以中心距的增长百分比作为横坐标绘制图形,以研究中心距对稳定性的影响规律,如图 7所示。
| 模型 | 中心距/m | 第一交角/(°) | 进水角/(°) | 稳性消失角/(°) | 面积比 | GM/m | 排水体积/m3 |
| 2 | 25 | 12.57 | 16.70 | 28.77 | 0.87 | 5.04 | 3 440 |
| 5 | 27 | 8.34 | 15.72 | 30.95 | 1.35 | 8.44 | 3 470 |
| 1 | 30 | 5.29 | 14.42 | 26.74 | 1.51 | 13.79 | 3 500 |
|
| 图6 模型1、2、5的力矩曲线图 Figure 6 Moment curves of models 1,2 and 5 |
|
| 图7 相关指标随中心距的增长率 Figure 7 Growth rates of relevant parameters with the distance between pontoons |
由表 4、图 6和图 7可知,随着中心距的增大,第一交角变小,面积比和初稳性高度均变大,说明平台的稳定性随着中心距的增大而增强。这是因为随中心距的增大,水面线关于形心轴的惯性矩变大,导致平台GM变大,因此面积比增大而稳定性增强。从图 7可看出,GM几乎随中心距呈线性变化,而排水体积几乎不变。由式(1)可知,GM的增大是由水面线惯性矩增大而引起,所以改变中心距是以改变水面线惯性矩的方式影响GM,从而影响到平台稳定性。
由图 6发现,GM较大的模型1的稳性消失角反而较小,由图 7表现出来就是面积比的增长百分比斜率变缓,说明随倾角变大时,中心距较大平台的稳定性增长速度相对放慢。这是因为平台中心距越大,进水角就越小,由2.1节的解释可知,当平台边缘进水后回复力矩曲线将很快达到峰值并开始下降。因此中心距较大时,进水角对稳定性的不利影响也会更加显著。
因此,增大中心距能改善风力机平台的稳定性。此种措施的优点是:对平台的排水体积影响不大。而缺点是:当浮筒间距过大时,边缘进水角会减小而对稳定性产生不利影响;并且,初稳性高度会随浮筒间距增大而变大,从而导致横摇和纵摇的周期变短。
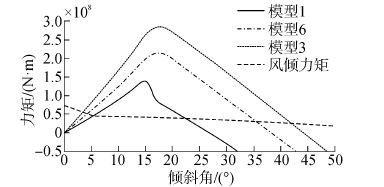
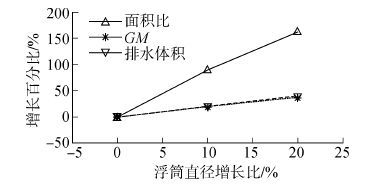
3.2 浮筒直径对稳定性的影响模型1、模型6和模型3的唯一区别在于浮筒直径,其浮筒直径依次为10、11和12 m,而其他条件均不变。稳定性分析的计算结果如表 5和图 8所示。以具有最小直径的模型1为参考,分别计算模型6和模型3两者的直径、面积比、GM以及排水体积等指标相对模型1对应指标的增长率,并以浮筒直径的增长百分比作为横坐标绘制图形,以研究浮筒直径对稳定性的影响规律,如图 9所示。
| 模型 | 筒径/m | 第一交角/(°) | 进水角/(°) | 稳性消失角/(°) | 面积比 | GM/m | 排水体积/m3 |
| 1 | 10 | 5.29 | 14.42 | 26.74 | 1.51 | 13.79 | 3 500 |
| 6 | 11 | 4.14 | 14.23 | 38.31 | 2.86 | 16.49 | 4 170 |
| 3 | 12 | 3.33 | 14.04 | 44.17 | 3.96 | 19.01 | 4 900 |
|
| 图8 模型1、3、6的力矩曲线图 Figure 8 Moment curves of models 1,3 and 6 |
|
| 图9 相关指标随浮筒直径的增长率 Figure 9 Growth rates of relevant parameters with the radius of pontoons |
由表 5、图 8和图 9可知,随着浮筒直径的增大,第一交角变小,稳定消失角、面积比和初稳性高度均变大,并且它们均随浮筒直径呈近似线性变化的关系。面积比的最大增大率达到160%,这说明增大浮筒直径可显著改善平台的稳定性。利用式(1)、(2),并研究水面线惯性矩和重心高度BG的变化可知:当浮筒直径在一定范围内增大时,水面线惯性矩和排水体积均增大而两者的比值增大不显著,所以导致GM增大的重要因素是重心高度的降低。由式(3)发现,GM和排水体积的共同增大导致回复力矩的显著增大,这就是增大浮筒直径会明显改善稳定性的原因。
因此,增大浮筒直径能显著提高浮式风力机平台的稳定性。但其缺点是:初稳性高度会随浮筒直径的增大而增大,从而导致横摇或纵摇周期变短,并且对平台重心高度、排水体积等产生显著影响。
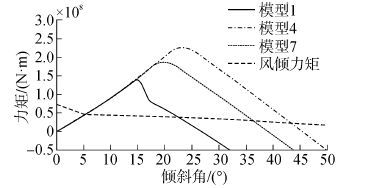
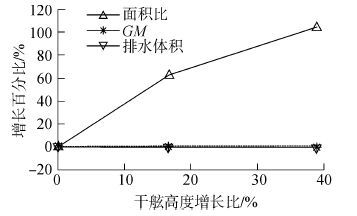
3.3 干舷高度对稳定性的影响模型1、模型4和模型7的唯一区别在于干舷高度,其干舷高度依次为9、10.5、12.5 m,而其他条件均不变。稳定性分析的计算结果如表 6和图 10所示。以具有最小干舷高度的模型1为参考,分别计算模型4和模型7两者的干舷高度、面积比、GM以及排水体积等指标相对模型1对应指标的增长率,并以干舷高度的增长百分比作为横坐标绘制图形,以研究干舷高度对稳定性的影响规律,如图 11所示。
| 模型 | 干舷高度/m | 第一交角/(°) | 进水角/(°) | 稳性消失角/(°) | 面积比 | GM/m | 排水体积/m3 |
| 1 | 9.0 | 5.29 | 14.42 | 26.74 | 1.51 | 13.79 | 3 500 |
| 4 | 10.5 | 5.24 | 16.71 | 39.01 | 2.46 | 13.92 | 3 500 |
| 7 | 12.5 | 5.26 | 19.66 | 45.42 | 3.09 | 13.89 | 3 500 |
|
| 图10 模型1、4、7的力矩曲线图 Figure 10 Moment curves of models 1,4 and 7 |
|
| 图11 相关指标随干舷高度的增长率 Figure 11 Growth rates of relevant parameters with the freeboard height |
由表 6、图 10和图 11可知,随着干舷高度的增大,第一交角、初稳性高度和排水体积几乎不变,稳性消失角、面积比均变大。其中当干舷高度增大38%时,面积比分别增大将近100%,说明增大干舷高度可明显提高平台的稳定性,并且不影响初稳性高度。由于干舷高度对排水体积的影响很小,且水线面面积不变,所以导致初稳性高度和第一交角几乎不变,只有平台进水角变大。因此稳性消失角和面积比增大进而平台稳定性增强。改变干舷高度是以控制进水角的方式影响平台的稳定性。
因此,增加干舷能够有效改善浮式风力机平台的稳定性。此种措施的优点是:增加干舷长度基本不影响初稳性高度,并且对排水体积影响较小。而其缺点是:影响浮筒的高度,对分舱造成影响。
4 结论本文首先对半潜型浮式风力机平台的初稳性问题进行了理论分析;然后分析了大倾角稳定性中的最不利倾斜轴问题;最后通过采用Sesam软件进行数值模拟,研究了半潜型浮式风力机平台稳定性的主要影响因素。得到以下结论:
1) 基于重心移动原理并考虑浮式风力机平台静平衡角和横摇周期等因素,提出了适用于半潜型浮式风力机的初稳性高度限值的计算公式。
2) 在风力机平台的边缘进水之前,对任意倾斜轴半潜型浮式平台的稳定性相同。进水之后稳定性迅速下降,因此导致最小进水角的形心轴为最不利倾斜轴。
3) 浮筒间距、浮筒直径和干舷高度等因素以不同的方式改变风力机的稳定性,同时会对初稳性高度、重心高度和排水体积等产生不同程度的影响。值得注意的是,较大的浮筒间距会减小进水角而对稳定性产生不利影响。设计者可根据具体情况选择不同的措施调整浮式风力机平台的稳定性。
值得说明的是,本文没有考虑浮筒之间的连接构件对稳定性的影响,同时研究内容没有涉及破舱稳定性,这将在今后进一步研究。
| [1] |
陈骥, 牛凤和. 渤海二号钻井船在拖航中翻沉[J].
报刊管理, 1999(6): 33–37.
CHEN Ji, NIU Fenghe. Bohai No. 2 drilling ship capsized in the towing[J]. Journal management, 1999(6): 33–37. |
| [2] | HEISING C D, GRENZEBACH W S. The ocean ranger oil rig disaster: a risk analysis[J]. Risk analysis, 1989, 9(1): 55–62. DOI:10.1111/risk.1989.9.issue-1 |
| [3] | JONKMAN J M. Dynamics modeling and loads analysis of an offshore floating wind turbine: TP-500-41958[R]. Colorado, United States: National Renewable Energy Laboratory, 2007. http://cn.bing.com/academic/profile?id=1562045875&encoded=0&v=paper_preview&mkt=zh-cn |
| [4] |
吴海涛, 张亮, 马勇, 等. 半潜式海上浮式风力机平台随机响应特性分析[J].
华中科技大学学报: 自然科学版, 2014, 42(5): 111–115.
WU Haitao, ZHANG Liang, MA Yong, et al. Stochastic response characteristics analysis of semisubmersible platform for floating offshore wind turbine[J]. Journal of Huazhong university of science and technology: natural science edition, 2014, 42(5): 111–115. |
| [5] |
朱航, 欧进萍. Truss-spar-buoy风机承载浮式平台的概念设计[J].
船舶力学, 2012, 16(11): 1267–1273.
ZHU Hang, OU Jinping. Conceptual design of a Truss-spar-buoy support platform for offshore wind turbine[J]. Journal of ship mechanics, 2012, 16(11): 1267–1273. |
| [6] |
中国船级社.
海上移动平台入级规范[M]. 北京: 人民交通出版社, 2012: 117 -182.
China Classification Society. Rules for Construction and Classification of Mobile Offshore Drilling Units[M]. Beijing: China Communications Press, 2012: 117 -182. |
| [7] | Det Norske Veritas. DNV-OS-J103 Design of floating wind turbine structures[S]. Norway: DNV, 2013. |
| [8] |
张亮, 邓慧静. 浮式风机半潜平台稳性数值分析[J].
应用科技, 2011, 38(10): 13–17.
ZHANG Liang, DENG Huijing. Numerical analysis on stability of the semi-submersible platform of floating wind turbines[J]. Applied science and technology, 2011, 38(10): 13–17. |
| [9] |
曹菡, 唐友刚, 陶海成, 等. 半潜型风机浮式基础设计及幅频运动特性研究[J].
海洋工程, 2013, 31(2): 61–67.
CAO Han, TANG Yougang, TAO Haicheng, et al. Design and frequency domain analysis of semi-submersible floating foundation for offshore wind turbine[J]. The ocean engineering, 2013, 31(2): 61–67. |
| [10] |
唐友刚, 桂龙, 曹菡, 等. 海上风机半潜式基础概念设计与水动力性能分析[J].
哈尔滨工程大学学报, 2014, 35(11): 1314–1319.
TANG Yougang, GUI Long, CAO Han, et al. Conceptual design and hydrodynamic performance of the semi-submersible floating foundation for wind turbines[J]. Journal of Harbin engineering university, 2014, 35(11): 1314–1319. |
| [11] | RODDIER D, CERMELLI C, AUBAULT A, et al. WindFloat: a floating foundation for offshore wind turbines[J]. Journal of renewable and sustainable energy, 2010, 2(3): 033104. DOI:10.1063/1.3435339 |
| [12] | LEFEBVRE S, COLLU M. Preliminary design of a floating support structure for a 5 MW offshore wind turbine[J]. Ocean engineering, 2012, 40: 15–26. DOI:10.1016/j.oceaneng.2011.12.009 |
| [13] | MAYILVAHANAN A C, SELVAM R P. Static and dynamic analysis of semi-submersible type floaters for offshore wind turbine[C]//Proceedings of MARTEC 2010: the International Conference on Marine Technology. Dhaka, Bangladesh, 2010: 101-106. |
| [14] |
盛振邦, 刘应中.
船舶原理[M]. 上海: 上海交通大学出版社, 2003: 105 -110.
SHENG Zhenbang, LIU Yingzhong. Shipping principle[M]. Shanghai: Shanghai Jiao Tong University Press, 2003: 105 -110. |
| [15] | HUIJS F, DE BRUIJN R, SAVENIJE F. Concept design verification of a semi-submersible floating wind turbine using coupled simulations[J]. Energy procedia, 2014, 53: 2–12. DOI:10.1016/j.egypro.2014.07.210 |
| [16] | WAYMAN E N, SCLAVOUNOS P D, BUTTERFIELD S, et al. Coupled dynamic modeling of floating wind Turbine systems[C]//Proceedings of 2006 Offshore Technology Conference. Houston, Texas, USA, 2006: 1583-1591. |
| [17] | COMSTOCK J P. Principles of Naval Architecture[M]. New York: Society of Naval Architects and Marine Engineers, 1967: 820 -830. |
| [18] |
王俊荣, 谢彬. 半潜式平台水动力性能及运动响应研究综述[J].
中国造船, 2009, 50(S): 255–61.
WANG Junrong, XIE Bin. Review of hydrodynamic performance and global motion prediction of semi-submeisibles[J]. Shipbuilding of China, 2009, 50(S): 255–61. |
| [19] |
王宁. 海上浮式风力机平台总体性能分析[D]. 哈尔滨: 哈尔滨工程大学, 2013: 40-45.
WANG Ning. Performance analysis of the offshore floating turbine foundation[D]. Harbin: Harbin Engineering University, 2013: 40-45. http://cdmd.cnki.com.cn/article/cdmd-10217-1014131937.htm |



