指定控制性能问题是近几年控制领域的一个热点研究问题。已有研究成果多将研究重点放在系统的稳态性能上,即证明闭环系统是稳定的,而对系统暂态性能的研究相对较少。文献[1]中给出了一种L2范数意义下关于跟踪误差与设计参数和初始状态之间的定量关系,首次关注系统的暂态性能。然而,该研究形式较为笼统,定量分析不够。文献[2]以单输入单输出线性系统为研究对象提出了一种自适应切换控制策略,是该类研究中早期较为典型的结果。该研究保证了跟踪误差的暂态和控制性能,以具体形式进行表达。为了进一步弥补上述研究中对象模型过于简单,难以推广到非线性系统的缺陷,Bechlioulis等[3-5]提出了一种具有指定性能的控制器设计方法,即在保证系统输出误差镇定到一个预先设定的、任意小的区域的同时,要保证收敛速率和超调量等性能的指定条件。近几年,该思想得到了广泛研究,并在机械臂系统中驱动力/位置控制[6]和高速飞行器姿态控制[7]等方面得到了有效应用。
船舶运动控制是控制理论应用于航海领域的一个重要研究课题,其最终目标是提高船舶自动化、智能化水平,保证船舶航行的安全性、经济性和舒适性[8-9]。海上行船不可避免存在很多未知不确定、航行危险以及风、浪、流等海洋干扰[10],这对船舶自动化技术发展和控制理论工程实现带来了更多困难。为了进一步改善船舶航向保持控制系统的控制性能,该研究在前人研究基础上提出了一种适用于一般不确定非线性系统的、考虑系统暂态/稳态控制性能的输出误差变换方法,并将其应用于船舶航向保持控制系统中。与已有研究对比,该算法进行了以下有针对性的考虑:1)暂态控制性能基于船舶初始状态设计,避免了针对不同误差符号进行分别讨论; 2)闭环控制系统实现一致最终有界稳定的同时,能够通过预先设计保证系统收敛速率和超调量等。
1 问题描述具有一般形式的严格反馈非线性系统:
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {f_1}\left( {{x_1}} \right) + {g_1}\left( {{x_1}} \right){x_2}\\ \vdots \\ {{\dot x}_i} = {f_i}\left( {{{\bar x}_i}} \right) + {g_i}\left( {{{\bar x}_i}} \right){x_{i + 1}}\\ \vdots \\ {{\dot x}_n} = {f_n}\left( x \right) + {g_n}\left( x \right)u\\ y = {x_1} \end{array} \right. $ | (1) |
式中:$ {\bar x_i} = {\left[{{x_1}\;\;\;{x_2} \cdot \cdot \cdot {x_i}} \right]^T} \in {R^i},x = {\left[{{x_1}\;\;\;{x_2} \cdot \cdot \cdot {x_n}} \right]^T} \in {R^n} $为系统状态变量,u∈R为控制输入,y∈R为系统输出,gi(·)、fi(·)分别为系统控制增益函数和系统漂移非线性部分,且fi(·)为未知连续函数。注意,本文不考虑增益函数的不确定性,即gi(·)视为已知函数。
控制任务不仅要求闭环系统最终收敛于一定区域内,同时对收敛速率和超调量存在一定要求。因此,控制目标详细描述如下:
1)系统输出y有效跟踪参考信号yr,满足一致最终有界条件且闭环系统中所有其他变量有界;
2)系统跟踪误差收敛情况满足一定的暂态和稳态控制性能。
为了保证系统设计顺利进行,首先引入以下假设和系统指定性能函数的定义。
假设1 对于不确定漂移项fi(·),存在参数向量θi和非线性函数向量ρi(x1…xi)(θi为未知参数向量,ρi(x1…xi)为已知函数向量),满足对于任意的($ {\bar x_i},$,t)∈(Ri,R+),当1≤i≤n时fi(·)=θiTρi(x1,x2…,xi)。
假设2 参考信号yr(t)及其n阶导数yr(n)(t)在t∈[0,$ \infty $]上连续且有界。
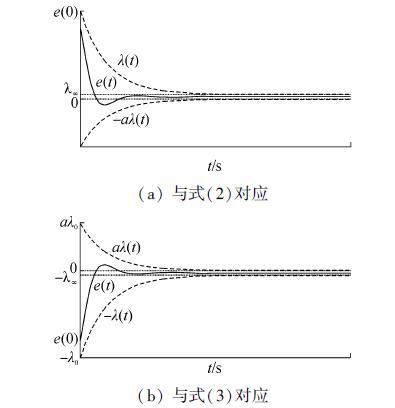
定义[4]连续函数λ:R+→R+为性能函数,满足:1)λ(t)是正的且严格递减;2)$ \mathop {\lim }\limits_{t \to \infty } (t) = {\lambda _\infty } > 0 $。其中,λ(t)为误差信号e(t)的预设界限。进一步可知,控制目标2)可以通过不等式(2)或(3)来设计:
| $ - a\lambda \left( t \right) < e\left( t \right) < \lambda \left( t \right),若e\left( 0 \right) > 0 $ | (2) |
或者
| $ - \lambda \left( t \right) < e\left( t \right) < \lambda \left( t \right),若e\left( 0 \right) < 0 $ | (3) |
式中:t∈[0,$ \infty $),a∈[0,1] 。λ(t) 为指定的性能函数,常数$ {\lambda _\infty } $ 为跟踪误差e(t)在稳态时的上限设计值。而且,λ(t)的衰减率即为系统误差信号e(t)收敛速率的下限,所以e(t)的最大超调量不会超过aλ(t)。
针对上述考虑,当取a=0时,e(t)为无超调的情况。因此,可视无超调的情况为普通有超调指定性能的特殊情况。
以上分析过程可由图 1给出的性能函数示意图进行说明。
|
| 图1 跟踪误差与指定性能函数的关系 Figure 1 Graphical representation for the tracking error and the prescribed performance function |
基于上述讨论,在进行控制器设计时选择式(4)所示的性能函数:
| $ \lambda \left( t \right) = \max \left\{ {\max \left[{\left( {1 + \Delta \% } \right){e_0} - sign\left( {{e_0}} \right){\lambda _\infty }} \right]\exp \left( { - lt} \right) + sign\left( {{e_0}} \right){\lambda _\infty },sign\left( {{e_0}} \right)\left[{\Delta \% {\lambda _\infty }\exp \left( { - lt} \right) + {\lambda _\infty }} \right]} \right\} $ | (4) |
式中:初始性能函数值λ0=(1+Δ%)e0,与系统初始跟踪误差关联;Δ由设计者根据需要进行确定。该性能函数的设计既考虑了初始跟踪误差e0=y(0)-yr(0)的大小,又考虑了其符号,避免了现有文献中针对不同初始跟踪误差需要重新设计控制器的缺陷,又可避免初始跟踪误差符号不同时分别进行讨论。max函数中的第2项针对的是初始跟踪误差已经处于指定稳态误差范围内(|e0|≤$ {\lambda _\infty } $ )时的情况,而该情况在已有研究中尚未进行讨论。
2 具有系统暂态/稳态性能设计的自适应控制分析可知,非线性系统(1)为受约束的被控制对象,利用传统Backstepping方法直接处理难以实现。为此,本节利用指定性能函数(4)进行系统输出转换,将被控对象(1)转化为不受约束的一般严反馈系统,将控制目标1)和目标2)统一化。
首先,引入如式(5)所示的输出误差转换函数:
| $ e\left( t \right) = \lambda \left( t \right)S\left( {{z_1}} \right) $ | (5) |
式中:z1为引入的变换误差变量,满足Lipchitz连续特性;S(·)为光滑、严格增函数,且具有以下特性:
| $ \left. 1 \right)\left\{ \begin{array}{l} - a < S\left( {{z_1}} \right) < 1,\;\;\;\;\;e\left( 0 \right) > 0\\ - 1 < S\left( {{z_1}} \right) < a,\;\;\;\;\;e\left( 0 \right) < 0 \end{array} \right. $ |
| $ \left. 2 \right)\left\{ \begin{array}{l} \mathop {\lim }\limits_{{z_{1 \to }} - \infty } S\left( {{z_1}} \right) = - a\\ \mathop {\lim }\limits_{{z_1} \to + \infty } S\left( {{z_1}} \right) = {1^{\;\;\;‘\;\;\;{\rm{e}}\left( 0 \right) > 0}}\;\;\; \end{array} \right. $ |
| $ \left. 3 \right)\left\{ \begin{array}{l} \mathop {\lim }\limits_{{z_1} \to - \infty } S\left( {{z_1}} \right) = - 1\\ \mathop {\lim }\limits_{{z_1} \to + \infty } S\left( {{z_1}} \right) = {a^{\;\;\;\;\;{’^{\;\;\;\;\;\;\;\;\;e\left( 0 \right) < 0}}\;\;\;\;}} \end{array} \right. $ |
选取S(·)函数为式(6):
| $ S\left( {{z_1}} \right) = \frac{{\exp \left( {{z_1} + r} \right) - a \cdot \exp \left[{ - \left( {{z_1}} \right) + r} \right]}}{{\exp \left( {z + r} \right) + \exp \left[{ - \left( {{z_1} + r} \right)} \right]}},r = \frac{1}{2}\ln a $ | (6) |
如果z1被有界镇定,那么当e(0)>0时,有 -a<S(z1)<1。 又因λ(t)>0,可得-aλ(t)< e(t)<λ(t)。同理,当e(0)<0时,有-1< S(z1)<a。因此,-λ(t)<e(t)<aλ(t) ,即 S(·) 函数的选取满足目标2)。
进一步,对S(z1)=e(t)/λ(t) 求逆可得式(7),z1为转换后系统输出误差。因此,若有效镇定变量 z1(t) ,则能保证同时完成控制目标1)和2)。
| $ {z_1} = {S^{ - 1}}\left( {\frac{{e\left( t \right)}}{{\lambda \left( t \right)}}} \right) $ | (7) |
基于上述分析,将原受限系统转化为等价不受约束的一般严反馈系统:
| $ \left\{ \begin{array}{l} {{\dot z}_1} = \frac{{\partial {S^{ - 1}}}}{{\partial \frac{{e\left( t \right)}}{{\lambda \left( t \right)}}}}\frac{1}{{\lambda \left( t \right)}} \cdot \\ \;\;\;\;\;\;\;\left( { - {{\dot y}_r} - \frac{{e\left( t \right)}}{{\lambda \left( t \right)}}\lambda \left( t \right) + {f_1}\left( {{x_1}} \right) + {g_1}\left( {{x_1}} \right){x_2}} \right)\\ {{\dot x}_2} = {f_2}\left( {{{\bar x}_2}} \right) + {g_2}\left( {{{\bar x}_2}} \right){x_3}\\ \;\;\;\;\;\;\;\;\; \vdots \\ {{\dot x}_n} = {f_n}\left( x \right) + {g_n}\left( x \right)u \end{array} \right. $ | (8) |
第1步:已知式(8)第一个子系统为ż1的动态方程,并定义误差变量z2=x2-α1,选取Lyapunov函数为
| $ {V_1} = \frac{1}{2}z_1^2 + \frac{1}{2}\tilde \theta _1^T{\Gamma _1}^{ - 1}{\tilde \theta ^1} $ | (9) |
结合式(8)所示的系统,对V1求导可得,
| $ {{V}_{1}}={{z}_{1}}\left( {{g}_{1}}\left( {{x}_{1}} \right){{x}_{2}}+{{f}_{1}}\left( {{x}_{1}} \right)-{{{\dot{y}}}_{r}}-\frac{e\left( t \right)}{\lambda \left( t \right)} \right)-\tilde{\theta }_{1}^{T}{{\Gamma }_{1}}^{-1}{{\dot{\hat{\theta }}}_{1}} $ | (10) |
因此,可以设计第1步中与状态变量x2对应的虚拟控制律为
| $ {\alpha _1} = \frac{1}{{{g_1}\left( {{x_1}} \right)}}\left( {\frac{{ - {k_1}{z_1}}}{\zeta } + {{\dot y}_r} + \frac{{e\left( t \right)}}{{\lambda \left( t \right)}}\lambda \left( t \right) - \hat \theta _1^T{\rho _1}\left( {{x_1}} \right)} \right) $ | (11) |
式(11)中,k1为设计参数,且
| $ \zeta = \frac{{\partial {S^{ - 1}}}}{{\partial \frac{{e\left( t \right)}}{{\lambda \left( t \right)}}}}\frac{1}{{\lambda \left( t \right)}} = \frac{1}{2}\left( {\frac{1}{{e + a\lambda \left( t \right)}} - \frac{1}{{e - \lambda \left( t \right)}}} \right) $ | (12) |
将式(11)代入式(10)中,整理后得到
| $ \begin{array}{*{35}{l}} {{{\dot{V}}}_{1}}=-{{k}_{1}}{{z}_{1}}^{2}+\tilde{\theta }_{1}^{T}{{\rho }_{1}}\left( {{x}_{1}} \right){{z}_{1}}-\tilde{\theta }_{1}^{T}{{\Gamma }_{1}}^{-1}{{{\dot{\hat{\theta }}}}_{1}}+ \\ {{z}_{1}}{{g}_{1}}\left( {{x}_{1}} \right){{z}_{2}}=-{{k}_{1}}z_{1}^{2}+{{\delta }_{1}}\tilde{\theta }_{1}^{T}\left( {{{\hat{\theta }}}_{1}}-{{{\hat{\theta }}}_{1}}\left( 0 \right) \right)+ \\ {{z}_{1}}{{g}_{1}}\left( {{x}_{1}} \right){{z}_{2}}\le -{{k}_{1}}z_{1}^{2}-\frac{{{\delta }_{1}}\tilde{\theta }_{1}^{T}{{{\tilde{\theta }}}^{1}}}{2}+ \\ \frac{{{\delta }_{1}}}{2}{{\left( {{\theta }_{1}}-{{{\hat{\theta }}}_{1}}\left( 0 \right) \right)}^{T}}\left( {{\theta }_{1}}-{{{\hat{\theta }}}_{1}}\left( 0 \right) \right)+{{z}_{1}}{{g}_{1}}\left( {{x}_{1}} \right){{z}_{2}} \\ \end{array} $ | (13) |
其中
| $ {{\dot{\hat{\theta }}}_{1}}={{\Gamma }_{1}}\left[ {{\rho }_{1}}\left( {{x}_{1}} \right){{z}_{1}}-{{\delta }_{1}}\left( {{{\hat{\theta }}}_{1}}-{{{\hat{\theta }}}_{1}}\left( 0 \right) \right) \right]$ | (14) |
第i步:对误差变量zi=xi-αi-1求导可得
| $ \begin{array}{l} {{\dot z}_i} = {{\dot x}_i} - {{\dot a}_{i - 1}} = {f_i}\left( {{{\bar x}_i}} \right) + {g_i}\left( {{{\bar x}_i}} \right){x_{i + 1}} + \\ \sum\limits_{j = 1}^{i - 1} {\frac{{\partial {\alpha _{i - 1}}}}{{\partial {x_j}}}\left( {{f_j}\left( {{{\bar x}_j}} \right) + {g_j}\left( {{{\bar x}_j}} \right){x_{j + 1}}} \right)} + \\ \sum\limits_{j = 0}^{i - 1} {\frac{{\partial {\alpha _{i - 1}}}}{{\partial {\lambda ^{\left( j \right)}}}}{\lambda ^{\left( {j + 1} \right)}} + \frac{{\partial {\alpha _{i - 1}}}}{{\partial {y_r}^{\left( {i - 1} \right)}}}{y_r}^{\left( i \right)}} = \\ Θ_i^T\phi \left( {{{\bar x}_i}} \right) + {g_i}\left( {{{\bar x}_i}} \right){x_{i + 1}} + \sum\limits_{j = 1}^{i - 1} {\frac{{\partial {\alpha _{i - 1}}}}{{\partial {x_j}}}{g_j}\left( {{{\bar x}_j}} \right){x_{j + 1}} + } \\ \sum\limits_{j = 0}^{i - 1} {\frac{{\partial {\alpha _{i - 1}}}}{{\partial {\lambda ^{\left( j \right)}}}}{\lambda ^{\left( {j + 1} \right)}} + \frac{{\partial {\alpha _{i - 1}}}}{{\partial y_r^{\left( {i - 1} \right)}}}y_r^{\left( i \right)}} \end{array} $ | (15) |
其中,Θi和Φi($ \bar x $i)用于描述系统中参数不确定项。具体表达为
| $ \begin{array}{l} {Θ_i} = {\left[{\theta _1^T,\theta _2^T,\cdots ,\theta _I^T} \right]^{\;\;T}},\\ {\phi _i}\left( {{{\bar x}_i}} \right) = {\left[{\frac{{\partial {\alpha _{i - 1}}}}{{\partial {x_1}}}\rho _1^T\left( {{x_1}} \right),\cdots ,\frac{{\partial {\alpha _{i - 1}}}}{{\partial {x_i}}}\rho _i^T\left( {{{\bar x}_i}} \right)} \right]^{\;\;T}} \end{array} $ |
选择Lyapunov函数为式(16)
| $ {V_i} = \frac{1}{2}z_i^2 + \frac{1}{2}\tilde Θ_I^T\Gamma _I^{ - 1}{\tilde Θ_i} $ | (16) |
对式(16)求导可得
| $ \begin{array}{*{35}{l}} {{V}_{i}}={{z}_{i}}\left[ \Theta _{i}^{T}\phi \left( {{{\bar{x}}}_{i}} \right)+{{g}_{i}}\left( {{{\bar{x}}}_{i}} \right){{x}_{i+1}}+\sum\limits_{j=1}^{i-1}{\frac{\partial {{\alpha }_{i-1}}}{\partial y_{r}^{\left( i-1 \right)}}{{g}_{j}}\left( {{{\bar{x}}}_{j}} \right){{x}_{j+1}}+} \right. \\ \left. \sum\limits_{j=0}^{i-1}{\frac{\partial {{\alpha }_{i-1}}}{\partial {{\lambda }^{\left( j \right)}}}{{\lambda }^{\left( j+1 \right)}}+\frac{\partial {{\alpha }_{i-1}}}{\partial y_{r}^{\left( i-1 \right)}}y_{i}^{\left( i \right)}} \right]-\widetilde{\Theta }_{i}^{T}\Gamma _{i}^{-1}{{\overset{.}{\mathop{\widehat{\Theta }}}\,}_{i}} \\ \end{array} $ | (17) |
选取第i步与xi+1对应的虚拟控制律为
| $ \begin{array}{l} {\alpha _i} = \frac{1}{{{g_i}\left( {{{\bar x}_i}} \right)}}\left[{ - {k_1}{z_1} - \sum\limits_{j = 1}^{i - 1} {\frac{{\partial {\alpha _{i - 1}}}}{{\partial {x_j}}}{g_j}\left( {{{\bar x}_j}} \right){x_{j + 1}}} } \right.\\ \sum\limits_{j = 0}^{i - 1} {\frac{{1\partial {\alpha _{i - 1}}}}{{\partial {\lambda ^{\left( j \right)}}}}{\lambda ^{\left( {j + 1} \right)}} - \frac{{\partial {\alpha _{i - 1}}}}{{\partial y_r^{\left( {i - 1} \right)}}}y_r^{\left( i \right)} - \hat Θ_i^T{\phi _i}\left( {{{\bar x}_i}} \right) - } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{g_{i - 1}}\left( {{{\bar x}_{i - 1}}} \right){z_{i - 1}}} \right] \end{array} $ | (18) |
式中:最后一项gi-1($ \bar x $i-1)zi-1的构建并不是基于式(17)进行补偿设计,其引入目的在于抵消第i-1步中$ \dot V $i-1放缩后的未处理项zi-1gi-1($ \bar x $i-1)zi。
将式(18)代入式(17)中,进一步整理后得到
| $ \begin{array}{l} {{\dot V}_i} = - {k_i}z_i^2 + {\delta _i}\tilde Θ_i^T\left( {{Θ_i} - {{\hat Θ}_i}\left( 0 \right)} \right) + {z_i}{g_i}\left( {{{\bar x}_i}} \right){z_{i + 1}} - \\ \;\;\;\;\;\;\;\;\;{z_{i - 1}}{g_{i - 1}}\left( {{{\bar x}_{i - 1}}} \right){z_i} \le - {k_i}z_i^2 - \frac{{{\delta _i}\tilde Θ_i^Tee{{\tilde Θ}_i}}}{2} + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{{\delta _i}}}{2}{\left( {{Θ_i} - {{\hat Θ}_i}\left( 0 \right)} \right)^T}\left( {{Θ_i} - {{\hat Θ}_i}\left( 0 \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{z_i}{g_i}\left( {{{\bar x}_i}} \right){z_{i + 1}} - {z_{i - 1}}{g_{{\rm{i}} - 1}}\left( {{{\bar x}_{i - 1}}} \right){z_i} \end{array} $ | (19) |
其中,参数向量Θi的自适应律设计为
| $ {\hat Θ_i} = {\Gamma _i}\left[{{Θ_i}\left( {{{\bar x}_i}} \right){z_i} - {\delta _i}\left( {{{\hat Θ}_i} - {{\hat Θ}_i}\left( 0 \right)} \right)} \right] $ | (20) |
第n步:对误差变量zn=xn-αn-1进行求导可得
| $ \begin{array}{l} {{\dot z}_n} = {{\dot x}_n} - {{\dot a}_{n - 1}} = \\ Θ_n^T{\phi _n}\left( x \right) + {g_n}\left( x \right)u + \sum\limits_{j = 1}^{n - 1} {\frac{{\partial {\alpha _{n - 1}}}}{{\partial {x_j}}}{g_j}\left( {{{\bar x}_j}} \right){x_{j + 1}} + } \\ \sum\limits_{j = 0}^{n - 1} {\frac{{\partial {\alpha _{n - 1}}}}{{\partial {\lambda ^{\left( j \right)}}}}{\lambda ^{\left( {j + 1} \right)}} + \frac{{\partial {\alpha _{n - 1}}}}{{\partial y_r^{\left( {n - 1} \right)}}}} {y_r}^{\left( n \right)} \end{array} $ | (21) |
其中,Θn、Φn($ \bar x $n)的具体表达式为
| $ \begin{array}{l} {Θ_n} = {\left[{\theta _1^T,\theta _2^T,\cdots ,\theta _n^T} \right]^{\;\;T}},\\ {\phi _n}\left( x \right) = {\left[{\frac{{\partial {\alpha _n}}}{{\partial {x_1}}}\rho _1^T\left( {{x_1}} \right),\cdots ,\frac{{\partial {\alpha _n}}}{{\partial {x_n}}}\rho _n^T\left( x \right)} \right]^{\;\;\;T}} \end{array} $ |
式中:Θn为未知参数向量,用于描述系统中参数不确定;u为系统的实际输入,通过设计为式(22)所示的形式:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;U = \frac{1}{{{g_n}\left( x \right)}}\\ \left[{ - {k_n}{z_n} - \sum\limits_{j = 1}^{n - 1} {\frac{{\partial {\alpha _{n - 1}}}}{{\partial {x_j}}}{g_j}\left( {{{\bar x}_j}} \right){x_{j + 1}} - \sum\limits_{j = 0}^{n - 1} {\frac{{\partial {\alpha _{n - 1}}}}{{\partial {\lambda ^{\left( j \right)}}}}{\lambda ^{\left( {j + 1} \right)}}} } } \right.\\ \left. {\frac{{\partial {\alpha _{n - 1}}}}{{\partial {y_r}^{\left( {n - 1} \right)}}}{y_r}^{\left( n \right)} - Θ_n^T{\phi _n}\left( x \right) - {g_{n - 1}}\left( {{{\bar x}_{n - 1}}} \right){z_{n - 1}}} \right] \end{array} $ | (22) |
选取Lyapunov函数为式(23):
| $ {V_n} = \frac{1}{2}z_n^2 + \frac{1}{2}Θ_n^T{\Gamma _n}^{ - 1}{\tilde Θ_n} $ | (23) |
对其求导,并代入式(22),进一步整理可得
| $ \begin{array}{l} {V_n} = - {k_n}z_n^2 - \frac{{{\delta _n}\tilde Θ_n^T{{\tilde Θ}_n}}}{2} + \frac{{{\delta _n}}}{2}{\left( {{Θ_n} - {{\hat Θ}_n}\left( 0 \right)} \right)^{\;\;\;T}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\left( {{Θ_n} - {{\hat Θ}_n}\left( 0 \right)} \right) - {z_{n - 1}}{g_{n - 1}}\left( {{{\bar x}_{n - 1}}} \right){z_n} \end{array} $ | (24) |
未知参数向量Θn的自适应律设计为
| $ {{\overset{.}{\mathop{\widehat{\Theta }}}\,}_{n}}={{\Gamma }_{n}}\left[ {{\phi }_{n}}\left( x \right){{z}_{n}}-{{\delta }_{n}}\left( {{\widehat{\Theta }}_{n}}-{{\widehat{\Theta }}_{n}}\left( 0 \right) \right) \right] $ | (25) |
定理1 对于误差系统(8),通过适当调整设计参数,利用本章提出的鲁棒λ调节技术所设计的控制律(11)、 (18)、(22)和参数自适应律(14)、(20)、(25)能够使闭环控制系统中所有信号一致最终有界,进而保证原系统(1)的输出误差动态满足指定的暂态/稳态性能要求。
证明 针对以上设计,对整个闭环控制系统选取Lyapunov函数V如式(26)所示:
| $ V = \sum\limits_{i = 1}^n {{V_i} = \sum\limits_{i = 1}^n {\left( {\frac{1}{2}{z_i}^2 + \frac{1}{2}\tilde Θ_i^T\Gamma _i^{ - 1}{{\tilde Θ}_i}} \right)} } $ | (26) |
对其进行求导运算,即将式(13)、(19)和(24)求和。求和运算过程中不同Lyapunov子函数之间zi-1gi-1($ \bar x $i-1)zi项相互抵消,最终可以化简为
| $ V = \sum\limits_{i = 1}^n {{{\dot V}_i}} \le - \sum\limits_{i = 1}^n {\left( { - {k_i}z_i^2 - \frac{{{\delta _i}\tilde Θ_i^T{{\tilde Θ}_i}}}{2}} \right)} + \rho $ | (27) |
式中:ρ为一小的正数,
| $ \rho = \sum\limits_{i = 1}^n {\frac{{{\delta _i}}}{2}{{\left( {{Θ_i} - {{\hat Θ}_i}\left( 0 \right)} \right)}^T}\left( {{Θ_i} - {{\hat Θ}_i}\left( 0 \right)} \right)} $ | (28) |
通过适当选取上述设计中的参数ki,δi,Γi,能够使式(29)成立:
| $ \dot V \le - k\sum\limits_{i = 1}^n {\left( {\frac{1}{2}z_i^2 + \frac{1}{2}\tilde Θ_i^T{\Gamma _i}^{ - 1}{{\tilde Θ}_i}} \right)} + \rho = - kV + \rho $ | (29) |
式中,
| $ \begin{array}{l} k = \min \left\{ {2{k_1},\cdots ,2{k_n},} \right.\\ \left. {\frac{{{\delta _1}}}{{{\lambda _{\min }}\left( {{\Gamma _1}^{ - 1}} \right)}},\frac{{{\delta _2}}}{{{\lambda _{\min }}\left( {{\Gamma _2}^{ - 1}} \right)}},\cdots ,\frac{{{\delta _n}}}{{{\lambda _{\min }}\left( {{\Gamma _n}^{ - 1}} \right)}}} \right\} \end{array} $ | (30) |
根据Lyapunov稳定性理论可以得出上述系统(8)是稳定的。因此,能够保证变换后的无约束系统一致最终有界。从而,由前面的变换系统分析可知,该控制策略能够实现原系统(1)满足暂态和稳态控制性能的要求。
3 仿真实例采用大连海事大学校实习船“育鲲”轮为仿真对象进行MATLAB仿真研究。操舵伺服系统考虑舵角幅值限制δmax=35°,执行速率限制$ \dot \delta $max=3.0°/s,以验证本章提出的考虑暂态/稳态控制性能的鲁棒λ调节控制的有效性。
| $ \left\{ \begin{array}{l} \dot \Psi = r\\ \dot r = - \frac{{{K_o}}}{{{T_0}}}\left( {{a_1}r + {a_2}{r^3}} \right) + \frac{{{K_0}}}{{{T_0}}}\left( {\delta + \Delta \left( t \right)} \right) \end{array} \right. $ | (31) |
式(31)为船舶航向保持控制系统数学模型[8, 12],K0=0.31,T0=62.0,a1=7.93,a2=4 100.46均为模型参数。利用所提出的控制算法,设计出针对船舶航向保持控制任务的控制律和自适应律分别为
| $ \begin{array}{l} {\alpha _1} = \left( {\frac{{ - {k_1}{z_1}}}{\zeta } + \frac{{\partial {\alpha _1}}}{{\lambda \left( t \right)}}\dot \lambda \left( t \right)} \right)\\ \delta = \frac{1}{b}\left[{ - {k_2}{z_2} - \frac{{\partial {\alpha _1}}}{{\partial \Psi }}\dot \lambda \left( t \right) - } \right.\\ \left. {\frac{{\partial {\alpha _1}}}{{\partial \lambda }}\dot \lambda \left( t \right) - \hat Θ_2^T{\phi _2}\left( r \right) - b{z_2}} \right] \end{array} $ | (32) |
| $ \begin{array}{l} {{\hat Θ}_2} = \left[\begin{array}{l} {{\hat \theta }_{21}}\\ {{\hat \theta }_{22}} \end{array} \right] = \left[\begin{array}{l} {\gamma _{21}}\;\;\;\;\;0\\ 0\;\;\;\;\;\;\;{\gamma _{22}} \end{array} \right]\left[{\left[\begin{array}{l} r\\ {r^3} \end{array} \right]} \right.{z_2} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {\left[\begin{array}{l} {\delta _{21}}\\ {\delta _{22}} \end{array} \right]\left( {{{\hat Θ}_2} - {{\hat Θ}_2}\left( 0 \right)} \right)} \right] \end{array} $ | (33) |
其中,转换误差变量$ \begin{array}{l} {z_1} = {S^{ - 1}}\left( {\frac{{e\left( t \right)}}{{\lambda \left( t \right)}}} \right) = \frac{1}{2}\ln \left( {e - a\lambda \left( t \right)} \right) - \\ \frac{1}{2}\ln \left( {\lambda \left( t \right) - e} \right) - \frac{1}{2}\ln a,e = \Psi - {\Psi _r},{z_2} = r - {\alpha _1},b = {K_0}/{T_0},\\ \zeta = 1/2\left( {1/\left( {e + a\lambda \left( t \right)} \right) - 1/\left( {\left. {\left. {e - \lambda \left( t \right)} \right)} \right)} \right.} \right. \end{array} $
仿真实验过程中,船舶初始航向为005°,初始转首角速度为-0.1°/s,参考航向命令为030°。因此,初始航向偏差为-25°。该仿真实例分2组进行:第1组仿真实验对系统暂态控制性能设计中要求-λ(t)<e(t)<aλ(t),a=0.1,保证船舶航向调节过程中尽量避免超调现象的发生。海洋环境干扰等效为Δ(t)=5+2sin(0.2t)+cos(0.5t)进行模拟[12];第2组实验增大暂态控制性能指定参数a=0.6,以验证本算法对考虑超调暂态性能指定的有效性,其他仿真实验条件与第1组相同。
针对以上实验方案,控制器参数设置为k1=0.5,k2=0.5,γ2,1=1.5,γ2,2=1.5,δ2,1=0.01,δ2,2=0.01,Δ=10,λ$ \infty $=3°,l=0.05;对于第2组仿真实验,由于指定暂态控制性能有所改变,为了获得较好的控制结果,控制器参数设置调整为k1=1.2,k2=0.8,γ2,1=1.5,γ2,2=1.5,δ2,1=0.01,δ2,2=0.01,Δ=10,λ$ \infty $=3°,l=0.05。
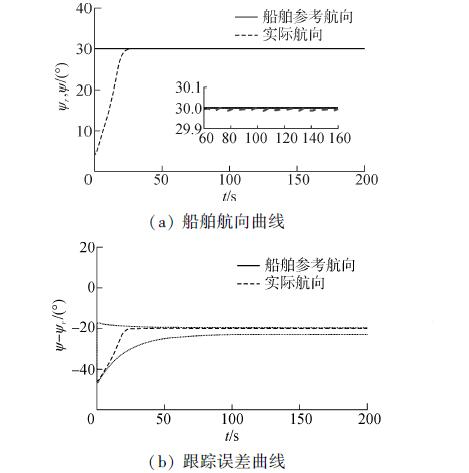
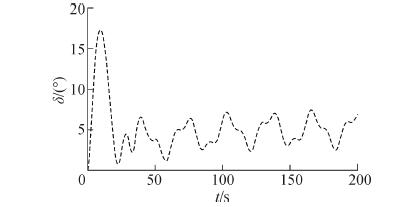
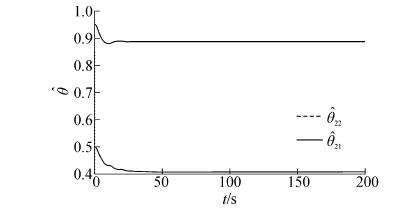
图 2(a)给出存在环境干扰条件下的船舶航向保持控制结果;图 2(b)为航向跟踪误差曲线。从实验结果可以看出,闭环控制系统受到外界环境干扰影响,暂态响应过程基本没有变化,但闭环控制系统进入稳定状态后,船舶实际航向在参考航向上下不断地微小摄动,控制精度较高。图 3表示考虑干扰时船舶控制舵角曲线。系统进入稳定状态后,控制舵角在较小的范围内上下抖动,目的在于合理补偿外界环境干扰与船舶系统相互作用产生的干扰力/力矩,为船舶控制工程实际所接受。图 4为考虑干扰时的自适应参数$ {\hat \theta _{2,1}} $、$ {\hat \theta _{2,2}} $值的变化。
|
| 图2 考虑干扰时的船舶航向及跟踪误差曲线(a=0.1) Figure 2 The course and tracking error with the environment disturbance (a = 0.1) |
|
| 图3 考虑干扰时船舶控制舵角曲线(a=0.1) Figure 3 The steering rudder angle with the environment disturbance (a = 0.1) |
|
| 图4 考虑干扰时自适应参数$ {\hat \theta _{2,1}} $、$ {\hat \theta _{2,2}} $的调节曲线(a=0.1) Figure 4 Estimation of the adaptive paraemeters $ {\hat \theta _{2,1}} $,$ {\hat \theta _{2,2}} $ with the environment disturbance (a=0.1) |
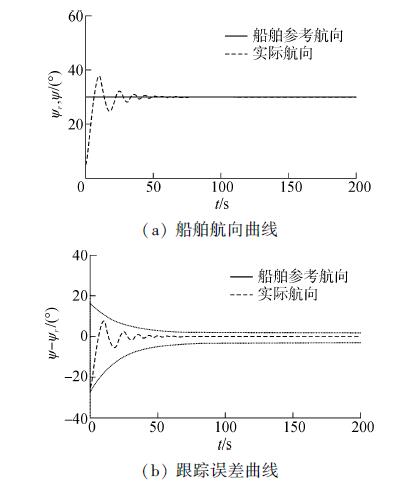
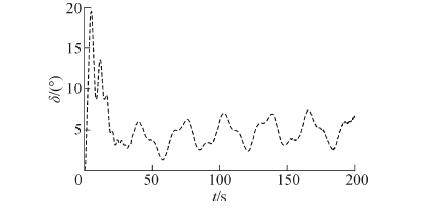
图 5~7给出了第2组实验结果。从图 5可以看出,实际航向和航向误差在暂态过程出现明显超调,但误差动态过程仍控制在性能指定界限以内,并最终趋于稳定,通过适当调整设计参数可以达到更好控制效果。图 6中控制舵角大幅度调节的时间相比图 3更长,当达到稳态时基本一致。实验结果验证了所提出的控制策略的鲁棒性。
|
| 图5 a=0.6时考虑干扰情况下的船舶航向及跟踪误差曲线 Figure 5 The course and tracking error with the environment disturbance (a=0.6) |
|
| 图6 a=0.6时考虑干扰情况下的船舶控制舵角曲线 Figure 6 The steering rudder angle with the environment disturbance (a = 0.6) |
|
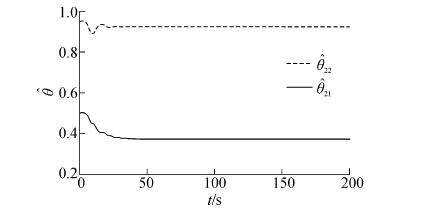
| 图7 a=0.6时考虑干扰情况下的自适应参数 $ {\hat \theta _{2,1}} $、$ {\hat \theta _{2,2}} $的调节曲线 Figure 7 Estimation of the adaptive paraemeters $ {\hat \theta _{2,1}} $, $ {\hat \theta _{2,2}} $ with the environment disturbance (a = 0.6) |
针对实际船舶控制工程需求,该研究在Backstepping方法的基础上,引入指定控制性能函数及系统变换,提出了一种易于工程应用的鲁棒λ调节控制技术。该算法主要具有以下优点:
1) 利用该算法能够保证系统输出最终收敛于一个预先设定的合理区域内;
2) 该算法可以通过调整设计参数保证系统收敛速度和超调量等暂态控制性能。将该算法应用于船舶航向保持控制系统,理论分析和实验结果验证了该方法的有效性。
| [1] | GE S S, HANG C C, ZHANG T. A direct method for robust adaptive nonlinear control with guaranteed transient performance[J]. Systems & control letters, 1999, 37(5): 275–284. |
| [2] | LIN Yan, LIU H, SUN Xiuxia. A variable structure MRAC with expected transient and steady-state performance[J]. Automatica, 2006, 42(5): 805–813. |
| [3] | DOULGERI Z, KARAYIANNIDIS Y, ZOIDI O. Prescribed performance control for robot joint trajectory tracking under parametric and model uncertainties[C]//Proceedings of the 17th Mediterranean Conference on Control and Automation. Thessaloniki: IEEE, 2009: 1313-1318. |
| [4] | BECHLIOULIS C P, ROVITHAKIS G A. Prescribed performance adaptive control of siso feedback linearizable systems with disturbances[C]//Proceedings of the 16th mediterranean conference on control and automation. Ajaccio: IEEE, 2008: 1035-1040. |
| [5] | BECHLIOULIS C, DOULGERI Z, ROVITHAKIS G. Prescribed performance adaptive control for robot force/position tracking[C]//Proceedings of 2009 IEEE control applications, (CCA) & intelligent control. St. Petersburg: IEEE, 2009: 920-925. |
| [6] | KARAYIANNIDIS Y, DOULGERI Z. Model-free robot joint position regulation and tracking with prescribed performance guarantees[J]. Robotics and autonomous systems, 2012, 60(2): 214–226. |
| [7] | GAI Wendong, WANG Honglun, ZHANG Jing, et al. Adaptive neural network dynamic inversion with prescribed performance for aircraft flight control[J]. Journal of applied mathematics, 2013: 452653. |
| [8] |
张显库.
船舶运动简捷鲁棒控制[M]. 北京: 科学出版社, 2012: 4 -11.
ZHANG Xianku. Ship motion concise robust control[M]. Beijing: Science Press, 2012: 4 -11. |
| [9] |
郭晨, 汪洋, 孙富春, 等. 欠驱动水面船舶运动控制研究综述[J].
控制与决策, 2009, 24(3): 321–329.
GUO Chen, WANG Yang, SUN Fuchun, et al. Survey for motion control of underactuated surface vessels[J]. Control and decision, 2009, 24(3): 321–329. |
| [10] |
刘正江, 吴兆麟, 李桢. 国际海事组织海事安全类公约的最新发展[J].
中国航海, 2012, 35(1): 61–65.
LIU Zhengjiang, WU Zhaolin, LI Zhen. Latest development of IMO maritime safety conventions[J]. Navigation of China, 2012, 35(1): 61–65. |
| [11] | FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. New York: Wiley, 2011: 48 -55. |
| [12] | LI T S, WANG D, FENG G, et al. A DSC approach to robust adaptive NN tracking control for strict-feedback nonlinear systems[J]. IEEE transactions on systems, man, and cybernetics, part b (cybernetics), 2010, 40(3): 915–927. |



