2. School of Transportation and Mechanical Engineering, Shenyang Jianzhu University, Shenyang 110168, China;
3. Dalian Huarui Heavy Industry Group Co., Ltd., Dalian 116013, China
全断面硬岩掘进机(TBM)将盘型滚刀挤压楔入岩体进行破岩,具有施工进度快、安全性高等特点,是装备制造业的标志性产品。随着我国对铁路、水利等基础设施建设工程需求的日益增加,TBM拥有广阔的市场前景[1]。
为了保证进度指标,当在坚硬岩层中施工时,TBM掘进推力维持在较高级别,平均到每把滚刀上的轴向载荷达到其额定值。由于刀盘重量、刀轴尺寸的限制及支撑形式的特点,各个滚刀承受的轴向载荷并不相同,部分滚刀过载将导致其密封失效或螺栓断裂,使刀具损坏。此外,因为轴向载荷、贯入度是影响刀圈磨损的主要因素[2],且贯入度与轴向载荷成正比关系[3],即轴向承载较大的滚刀其刀圈磨损量也将加剧。刀具损坏及刀圈磨损是更换刀具的主要原因,不仅增加了施工成本且频繁停机更换刀具严重影响施工效率[4-5]。因此,在保证硬岩环境施工进度的前提下,若能提高滚刀受载的均匀程度,不仅可以降低滚刀过载破坏的风险,还能提高刀圈的使用寿命。
国内外学者对破岩机理[6-9]、盘型滚刀受力及磨损[10-12]和滚刀布局[13-15]等相关问题进行了分析,为TBM的结构设计提供了基础,但研究中并未考虑刀盘刚度及其支撑直径(即主轴承中径)对滚刀受力的影响。本文基于理论及实验分析了刀盘支撑直径对滚刀轴向载荷分布规律的影响,得到了一些有意义的结论,为TBM刀盘驱动系统支撑结构的设计及主轴承的选型提供了基础。
1 主轴承中径的取值范围TBM的主轴承为三排滚柱式,在满足承载能力和使用寿命的基础上,还要考虑驱动源布置及啮合方式、护盾鞍架安装尺寸和排渣量等限制条件。此外,滚刀载荷分布均匀性也应作为其选型依据,以提高施工经济性及施工效率。
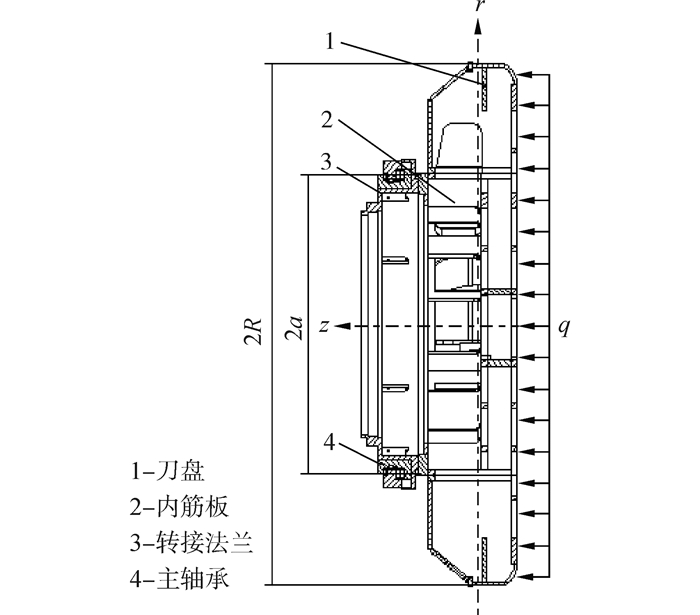
|
| 图1 TBM刀盘及主轴承 Figure 1 Structure of TBM cutter-head and main bearing |
虽然滚刀布置方案多种多样,但为了降低径向力的影响,基本均为绕回转轴对称布置,即对载荷分布均匀程度的考量可仅针对于径向。若假定刀间距相同且不考虑安装角度的影响,刀盘某一位置的轴向刚度较低则变形量较大,对应滚刀承受的载荷则较小。因此,为了使滚刀轴向载荷分布趋于均匀,即要求刀盘的轴向变形量也趋于均匀。而引起刀盘变形的主要载荷是轴向推力,可忽略径向及切向载荷的影响。初始掘进状态下,可认为每把正(中心)滚刀受到的轴向载荷均相同,且刀轴处刚度较低,则可将刀盘简化为受均载的弹性圆盘。设刀盘直径为Dc=2Rc,主轴承中径为Db=2Rb,则刀盘中面在柱坐标系下的弹性曲面微分方程为[15]:
| $D\left( {\frac{{{{\rm{d}}^2}}}{{{\rm{d}}{r^2}}} + \frac{1}{r}\frac{{\rm{d}}}{{{\rm{d}}r}}} \right)\left( {\frac{{{{\rm{d}}^2}w}}{{{\rm{d}}{r^2}}} + \frac{1}{r}\frac{{{\rm{d}}w}}{{{\rm{d}}r}}} \right) = q$ | (1) |
式中:r为径向; w为中面挠度函数; q为轴向外载; D=Et3/12(1-μ2)为刀盘抗弯刚度,t为等效刀盘厚度,E为弹性模量,μ为泊松比。考虑到dq/dr及dddr均为0,则式(1)的通解为:
| $w = {C_1}\ln r + {C_2}{r^2}\ln r + {C_3}{r^2} + {C_4} + {w_1}$ | (2) |
式中:C1~C4可根据边界条件确定。对于均布载荷其特解为:
| ${w_1} = \frac{{q{r^4}}}{{64D}}$ | (3) |
由于圆盘中心在任何情况下的挠度及内力均非无穷大,即:
| $\left\{ \begin{array}{l} {\left( w \right)_{r = 0}} \ne \infty \\ {\left( M \right)_{r = 0}} =-D\left( {\frac{{{{\rm{d}}^2}w}}{{{\rm{d}}{r^2}}} + \frac{\mu }{r}\frac{{{\rm{dw}}}}{{{\rm{d}}r}}} \right) \ne \infty \end{array} \right.$ | (4) |
当r→0时,
| $\left\{ \begin{array}{l} {\left( w \right)_{r = {R_b}}} = 0\\ {\left( {\frac{{{\rm{d}}w}}{{{\rm{d}}r}}} \right)_{r = {R_b}}} = 0 \end{array} \right.$ | (5) |
可得到C3和C4,代入式(2)可得:
| $w = \frac{q}{{64D}}{\left( {{r^2}-R_b^2} \right)^2}$ | (6) |
随着主轴承半径的变化,圆板中心点及边界点位置的挠度也发生变化。对于中心点及边界点:
| $\left\{ \begin{array}{l} w{\left( {{R_b}} \right)_{r = 0}} = \frac{{qR_b^4}}{{64D}}\\ w{\left( {{R_b}} \right)_{r = {R_c}}} = \frac{q}{{64D}}{\left( {R_c^2-R_b^2} \right)^2} \end{array} \right.$ | (7) |
由式(7)可知中面最大挠度必然位于中心或边界点上。在同样的推进力下,若要刀盘轴向变形量趋于均匀,则要求选定的支撑半径Rb可使w(Rb, r)max在Rb∈ 0, Rc 为最小值,即:
| $\begin{array}{c} \min \left\{ {w{{\left( {{R_b}, r} \right)}_{\max }}} \right\} = \\ \min \left\{ {\max \left\{ {w{{\left( {{R_b}} \right)}_{r = 0}}, w{{\left( {{R_b}} \right)}_{b = {R_c}}}} \right\}} \right\} \end{array}$ | (8) |
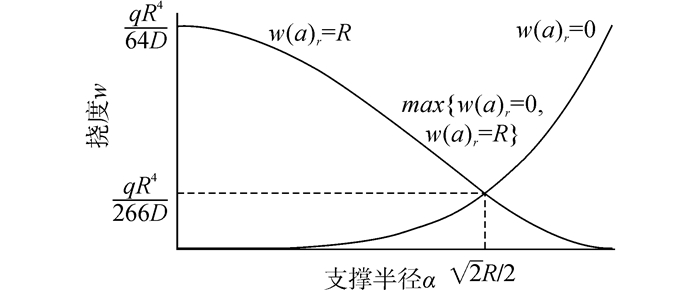
中心点与边界点的挠度函数单调性相反,则w(Rb, r)max的极小值位置必然位于w(Rb)r=0与w(Rb)r=Rc的交点(如图 2所示),根据式(7)可得:
| ${R_b} = 0.707{R_c}$ | (9) |
|
| 图2 刀盘中心及边缘的挠度与支撑半径的关系 Figure 2 Relationship between center and edge flection of cutter-head and support radius |
当考虑主轴承支撑条件为简支时,则边界条件为:
| $\left\{ \begin{array}{l} {\left( w \right)_{r = {R_b}}} = 0\\ {\left( {\frac{{{{\rm{d}}^2}w}}{{{\rm{d}}{r^2}}} + \frac{\mu }{r}\frac{{{\rm{d}}w}}{{{\rm{d}}r}}} \right)_{r = {R_b}}} = 0 \end{array} \right.$ | (10) |
得到简支条件下的常数C3和C4,则刀盘的挠度表达式为:
| $w =-\frac{{3 + \mu }}{{1 + \mu }}\frac{{qR_b^2}}{{32D}}{r^2} + \frac{{5 + \mu }}{{1 + \mu }}\frac{{qR_b^4}}{{64D}} + \frac{{q{r^4}}}{{64D}}$ | (11) |
在r∈(0, Rc)的区间内存在极值,则要求:
| $\frac{{{\rm{d}}w}}{{{\rm{d}}r}} =-\frac{{3 + \mu }}{{1 + \mu }}\frac{{qR_b^2}}{{16D}}r + \frac{{q{r^3}}}{{16D}} = 0$ | (12) |
对于Q345D材质,μ=0.3,则根据式(12)可得r=1.593Rb。因r≤Rc,即在Rb≤0.628Rc区间内仅存在一个极小值点, 若使变形趋于均匀,应使挠度函数的幅值A(ω)为最小,即
| ${\rm{min}}\left\{ {A\left( \omega \right)} \right\} = \min \left\{ \begin{array}{l} {\left( w \right)_{r = 0}}-{\left( w \right)_{r = 1.593{R_b}}}\\ {\left( w \right)_{r = {R_c}}}-{\left( w \right)_{r = 1.539{R_b}}} \end{array} \right\}$ | (13) |
而对于Rb>0.628Rc,式(12)为单调递减函数, 挠度幅值为:
| $A\left( \omega \right) = \frac{{qR_c^2}}{{64D}}\left( {\frac{{6 + 2\mu }}{{1 + \mu }}R_b^2-R_c^2} \right)$ | (14) |
由式(13)和式(14)可见,考虑刀盘为简支时支撑半径应位于区间内。为使刀盘挠度幅值为最小,则要求(w)r=0=(w)r=Rc,联立式(12)得:
| ${R_b} = 0.444{R_c}$ | (15) |
由于主轴承的自身刚度较弱且其与刀盘栓接,刀盘支撑的约束状态应介于夹支和简支之间,即要求:
| $\frac{{{D_b}}}{{{D_c}}} = \frac{{{R_b}}}{{{R_c}}} \in \left[{0.444, 0.707} \right]$ | (16) |
通过调研及查阅文献可知,目前国内外的TBM主轴承中径与刀盘的直径比均介于此范围内。
2 轴向载荷分布测量实验刀盘结构复杂,且内部布置了多块射线筋板,其结构抗弯刚度并不均等。为了进一步分析主轴承中径对滚刀轴向载荷的影响,基于相似理论建立了吉林引松供水工程某标段φ7.93 mTBM刀盘的缩尺结构,以荷重传感器及其等刚度立柱模拟正(中心)滚刀,与加载装置、反力架结构及安装平台组成了轴向载荷分布实验台,并测量在一定推力作用下的荷重传感器在不同支撑直径下所承受的轴向载荷。
考虑到刀盘属回转件及结构尺寸的限制,荷重传感器和等刚度立柱采用米字形对称布置,如图 4所示。其中1~8号为传感器测点,其布置半径随着编号的增加而增大;9号和10号为辅助测点,其布置半径分别与4号及7号相同,用以验证及调整结构受载的对称性。根据TBM对滚刀安装高度的累积误差要求及相似比,本实验中荷重传感器及等刚度立柱与刀盘挤压面的间隙需控制在0.3 mm以内。

|
| 图3 轴向载荷分布实验台 Figure 3 Axial load distribution test bed |

|
| 图4 传感器及等刚度立柱布置图 Figure 4 Distribution of sensors and equal stiffness columns |
实验中通过更换不同直径的法兰环以实现刀盘支撑直径的变化。考虑到工艺、结构尺寸的限制,法兰环直径与刀盘直径的比值除了采用前文分析所得到的极限值0.444和0.707外,还选取了0.516及0.667。
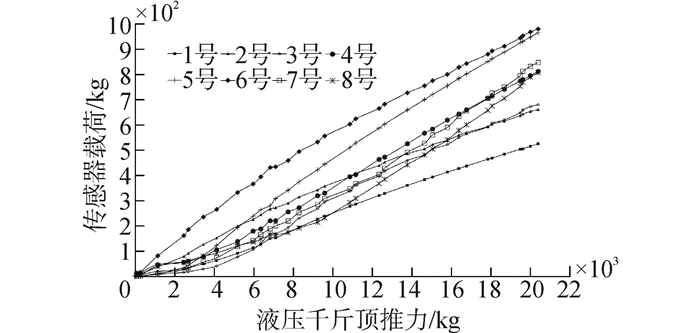
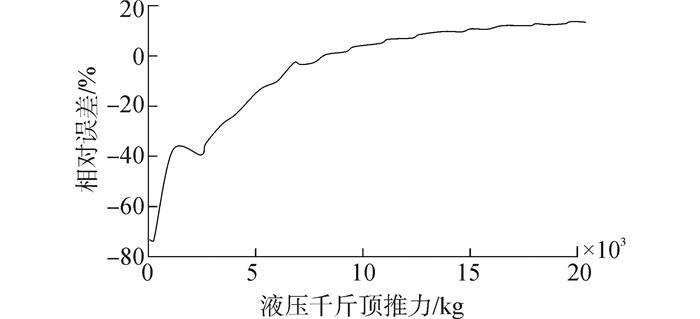
根据原型机推进力的相似转换及荷重传感器量程限制,液压千斤顶的推力上限为5 t。各传感器测量结果如图 5所示,其载荷均随液压千斤顶推力的增加而增大,但变化梯度并不相同。理想状态下,若各传感器(等刚度立柱)的挤压面初始闭合且处于同一平面,当推力较低时(小于5 t),由于刀轴尺寸相同且刚度相对较小,各个位置传感器承受的载荷差别较小,而加工及装配误差导致闭合面的初始间隙不同,2号、5号和6号传感器载荷值相对偏大,传感器载荷和值与其理论值的相对误差(图 6)为负且其绝对值较大;而当推力进一步增大时(大于5 t),各传感器载荷变化梯度及相对误差趋于平缓。实验过程中未对闭合间隙进行调整,因此4组测量值中2号、4号及7号传感器载荷均相对偏大,且推力较低时相对误差较大。由此可见,不论支撑直径如何变化,安装高度差始终对传感器的轴向载荷分布有着直接的影响。对于TBM而言,在安装及更换滚刀时,也需考虑刀刃高度差影响。
|
| 图5 直径比为0.516时传感器测量载荷值 Figure 5 Loads measured by sensors when diameter rate is 0.516 |
|
| 图6 传感器载荷和值与理论值的相对误差 Figure 6 Relative error between sensor resultant loads and theoretical loads |
| Db/Dc | 传感器载荷/kg | 载荷变异系数/% | |||||||
| 1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 | 8号 | ||
| 0.444 | 584.9 | 583.0 | 655.7 | 739.8 | 765.6 | 758.6 | 729.2 | 691.4 | 10.0 |
| 0.516 | 565.2 | 566.9 | 639.9 | 731.9 | 759.2 | 769.1 | 744.0 | 717.4 | 11.5 |
| 0.667 | 479.1 | 498.0 | 574.4 | 695.6 | 741.6 | 800.2 | 819.7 | 820.4 | 19.7 |
| 0.707 | 450.2 | 474.4 | 555.9 | 678.8 | 739.2 | 807.0 | 842.5 | 859.1 | 22.7 |
|
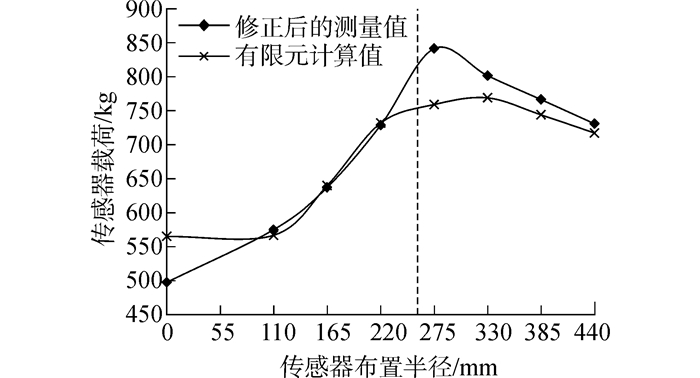
| 图7 20 t推力时传感器载荷与布置半径的关系 Figure 7 Relationship between sensor loads and layout radius when thrust is 20 t |
根据低负荷理想挤压状态下的均载特性计算传感器载荷的平均加权,并对后续测量值进行修正以降低初始闭合间隙不同带来的影响。修正后的测量值与有限元计算结果具有较高的吻合度,同时也验证了有限元算法的可行性。
|
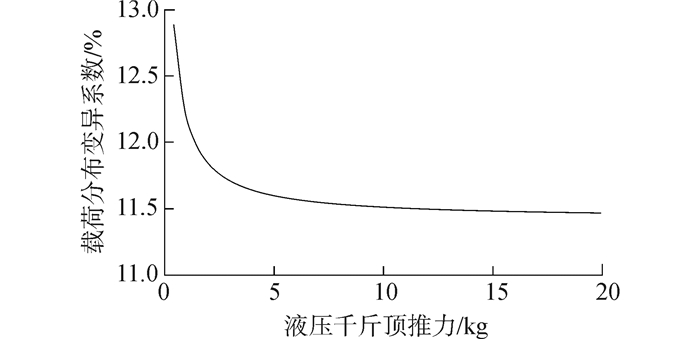
| 图8 推力对传感器载荷变异系数的影响 Figure 8 Effect of thrust on sensor load variation coefficient |
通过对测量载荷及有限元计算结果的分析可知,刀盘支撑直径的变化对滚刀载荷影响很大。在相同推力下,随着支撑直径增加,峰值载荷在不断增大,且峰值载荷的出现位置逐渐向边缘转移;1~5号的载荷在减小,而6~8号则增大,且中心(1号)及边缘(8号)位置的载荷变化最为明显。4种支撑直径下,靠近中心处的1号和2号载荷小于平均值,而5~8号载荷均大于平均值,且5号和6号的载荷始终维持在较高水平。若以支撑直径为分界线,其内部的传感器(对应中心滚刀及低号位正滚刀)受载相对较小,而其外部的传感器(对应边滚刀及高号位正滚刀)则相对较大,靠近支撑直径位置的传感器载荷始终较大。相同推力下传感器载荷变异系数也随着支撑直径的增加而增大。而对于同一支撑直径,推力变化时其载荷变异系数则变化较小,且当推力大于5 t时基本保持不变。
3 实例分析TBM刀盘的结构形式虽相似,但刚度及滚刀布置均存在差异。针对某一具体的刀盘结构及滚刀布置方案,可用有限元法分析主轴承中径与滚刀轴向载荷分布的关系,而如何建立刀盘与岩石间的联系是关键问题之一。对滚刀刚性约束将忽略岩石力学性能对边界刚度的影响,并不能反应两者之间的相互作用关系;而建立接触关系则需要考虑滚刀的细节特征及岩石失效准则,过多的单元数量及复杂的非线性本构关系将严重影响计算效率。采用非线性弹簧连接刀盘与岩石边界,通过设置弹簧刚度可以反映出岩石的力学参数对载荷分布的影响,并可提高模型的计算效率。根据CSM滚刀垂直力公式[3]得到弹簧等效刚度K的表达式为:
| $K = D_d^{\frac{1}{2}}\tan \frac{\theta }{2}\left[{2{P^{\frac{1}{2}}}{\sigma _c} + \tau \left( {{P^{-\frac{1}{2}}}S-6{P^{\frac{1}{2}}}\tan \frac{\theta }{2}} \right)} \right]$ | (17) |
式中:Dd为滚刀直径,P为贯入度,S为刀间距,θ为刀刃角,σc为岩石单轴抗压强度,τ为无侧限抗剪强度。由于边滚刀安装倾角φ的存在,滚刀临界应力随着φ的增加而增大[9]。安装倾角对滚刀受力的影响通过回归分析可等效转换为岩石单轴抗压强度的变化,即σc(φ)。对于不同类型的滚刀,由于其刀间距不同,因此其对应的弹簧刚度也不相同。
|
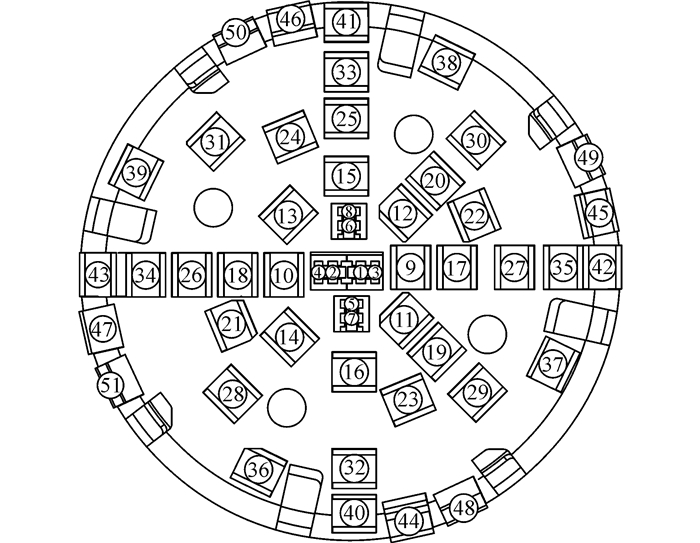
| 图9 刀具布置示意 Figure 9 Arrangement of cutter |
以实验台原型机TBM刀盘为分析对象,其盘面布置了4把17寸双刃中心滚刀(刀号1~8),32把19寸正滚刀(刀号9~40)及11把19寸边滚刀(刀号41~51)。围岩类型为花岗岩(100~250 MPa),且假定掘进面岩石力学性能一致。忽略径向力及扭矩的影响,且认为刀盘在任意时刻均处于准静态。由于滚刀布置、刀盘内筋板及排渣量的限制,且支撑直径变化过程中盘体结构尺寸并未改变,Db/Dc的取值下限为0.486。
| 中心刀直径/mm | 正滚刀直径/mm | 滚刀刀刃角/(°) | 单轴抗压强度/MPa | 无侧限抗剪强度/MPa |
| 432 | 483 | 30 | 160 | 30 |
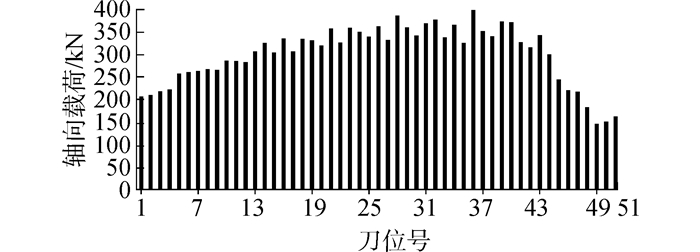
当有效掘进推力达到15 330 kN时(不考虑护盾及支撑等摩擦损耗),原结构支撑直径下各滚刀轴向载荷分布如图 10所示,多把滚刀载荷超过其极限承载值。由于刀盘结构刚度的不对称性及滚刀离散布置等特点,随着布置半径的增加滚刀载荷变化并不平滑,但整体趋势与实验测量结果一致。
|
| 图10 Db/Dc=0.606时滚刀轴向载荷分布 Figure 10 Axial loads distribution of cutters when Db/Dc=0.606 |
滚刀的最大载荷出现在28号位置,这是内筋板、刀盘分块尺寸及倾覆力矩共同作用的结果。边滚刀对应位置的岩石等效抗压强度虽有提高,但刀间距较小且对刚度的影响更为明显,使其承受的轴向推进载荷相对较小。考虑到边滚刀的安装倾角,将载荷转换到对应滚刀坐标系,则边滚刀承受的侧向载荷随刀号增加而增大。根据表 3所列不同样本空间计算结果可知,正滚刀及中心滚刀载荷分布受支撑直径的影响较大,且与直径比成正二次函数关系,最大载荷也随直径比增加而增大。若考虑刀盘中心块与支撑直径的尺寸对应关系,这种变化趋势将更加明显;边滚刀载荷相对较小且对支撑直径的变化并不敏感,使全滚刀样本的载荷变异系数基本不变。
| 直径比Db/Dc | 载荷分布变异系数/% | ||
| 正滚刀 | 正&中心滚刀 | 全滚刀 | |
| 0.486 | 8.20 | 14.72 | 21.45 |
| 0.499 | 8.26 | 14.78 | 21.37 |
| 0.516 | 8.51 | 15.10 | 21.40 |
| 0.532 | 8.70 | 15.34 | 21.43 |
| 0.547 | 9.08 | 15.72 | 21.40 |
| 0.561 | 9.29 | 16.00 | 21.49 |
| 0.576 | 9.59 | 16.32 | 21.46 |
| 0.591 | 10.01 | 16.71 | 21.61 |
| 0.606 | 10.33 | 17.03 | 21.65 |
| 0.621 | 10.69 | 17.43 | 21.73 |
| 0.636 | 11.05 | 17.82 | 21.91 |
| 0.651 | 11.40 | 18.17 | 21.99 |
| 0.667 | 11.89 | 18.66 | 22.16 |
| 0.687 | 12.53 | 19.31 | 22.45 |
| 0.707 | 13.09 | 19.85 | 22.65 |
1) 刀盘支撑介于简支和夹支之间,支撑直径与刀盘直径的理论比值应位于0.444~0.707的范围内。
2) 推力较低时,影响滚刀载荷的最主要因素是安装高度差;随着推力的增加,各滚刀载荷均增大但变化梯度各不相同,载荷变异系数基本保持不变。
3) 支撑直径的变化对正滚刀及中心滚刀的轴向载荷分布影响较大,对边滚刀影响相对较小。滚刀载荷变异系数、最大载荷及对应滚刀的布置半径与支撑直径成正比关系。
4) 在保证主轴承承载能力、寿命及排渣量需求的前提下适当降低支撑直径的尺寸以提高滚刀载荷的均匀程度。对于本文分析对象的TBM刀盘,直径比由0.606降至0.516时其正滚刀载荷均匀性提高1.82%。
| [1] |
夏毅敏, 罗德志, 周喜温. 盾构地质适应性配刀规律研究[J].
煤炭学报, 2011, 36(7): 1232–1236.
XIA Yimin, LUO Dezhi, ZHOU Xiwen. Study on the law of geology adaptability cutter selection for shield[J]. Journal of China coal society, 2011, 36(7): 1232–1236. |
| [2] | LI Fenghua, CAI Zongxi, KANG Yilan. A theoretical model for estimating the wear of the disc cutter[J]. Applied mechanics and materials, 2011, 90/91/92/93: 2232–2236. |
| [3] |
杨金强.盘形滚刀受力分析及切割岩石数值模拟研究[D].北京:华北电力大学(北京), 2007:11-19.
YANG Jinqiang. The force analysis and numerical simulation study on disk cutter cutting rock[D]. Beijing:North China Electric Power University (Beijing), 2007:11-19. http://cdmd.cnki.com.cn/article/cdmd-11412-2007083870.htm |
| [4] |
万治昌, 沙明元. 盘形滚刀的使用与研究(1):TB880E型掘进机在秦岭隧道施工中的应用[J].
现代隧道技术, 2002, 39(5): 1–11.
WAN Zhichang, SHA Mingyuan. Study on disk cutters for hard rock-application of TB880E TBM in Qinling Tunnel[J]. Modern tunnelling technology, 2002, 39(5): 1–11. |
| [5] |
万治昌, 沙明元. 盘形滚刀的使用与研究(2):TB880E型掘进机在秦岭隧道施工中的应用[J].
现代隧道技术, 2002, 39(6): 1–12.
WAN Zhichang, SHA Mingyuan. Study on disk cutters for hard rock (2)-application of TB880E TBM in Qinling Tunnel[J]. Modern tunnelling technology, 2002, 39(6): 1–12. |
| [6] |
谭青, 张旭辉, 夏毅敏, 等. 不同围压与节理特征下盘形滚刀破岩数值研究[J].
煤炭学报, 2014, 39(7): 1220–1228.
TAN Qing, ZHANG Xuhui, XIA Yimin, et al. Numerical study on breaking rock by disc cutter at different confining pressure and joint characteristics case[J]. Journal of China coal society, 2014, 39(7): 1220–1228. |
| [7] | CHANG S H, CHOI S W, BAE G J, et al. Performance prediction of TBM disc cutting on granitic rock by the linear cutting test[J]. Tunnelling and underground space technology, 2006, 21(3/4): 271. |
| [8] |
赵晓旭, 巩亚东. TBM滚刀在不同加载方式下的破岩机理研究[J].
中国工程机械学报, 2014, 12(5): 397–401.
ZHAO Xiaoxu, GONG Yadong. Mechanization study on rock fragmentation via TBM disc cutters under different loading modes[J]. Chinese journal of construction machinery, 2014, 12(5): 397–401. |
| [9] |
夏毅敏, 吴元, 郭金成, 等. TBM边缘滚刀破岩机理的数值研究[J].
煤炭学报, 2014, 39(1): 172–178.
XIA Yimin, WU Yuan, GUO Jincheng, et al. Numerical simulation of rock-breaking mechanism by gage disc cutter of TBM[J]. Journal of China coal society, 2014, 39(1): 172–178. |
| [10] | ROSTAMI J, OZDEMIR L, NILSON B. Comparison between CSM and NTH hard rock TBM performance prediction models[C]//Proceedings of Annual Technical Meeting of the Institute of Shaft Drilling Technology. Las Vegas:ISDT, 1996:1-10. |
| [11] |
谭青, 李建芳, 夏毅敏, 等. 盘形滚刀破岩过程的数值研究[J].
岩土力学, 2013, 34(9): 2707–2714.
TAN Qing, LI Jianfang, XIA Yimin, et al. Numerical research on rock fragmentation process by disc cutter[J]. Rock and soil mechanics, 2013, 34(9): 2707–2714. |
| [12] | GERTSCH R, GERTSCH L, ROSTAMI J. Disc cutting tests in Colorado Red Granite:implications for TBM performance prediction[J]. International journal of rock mechanics and mining sciences, 2007, 44(2): 238–246. DOI:10.1016/j.ijrmms.2006.07.007 |
| [13] |
霍军周, 杨静, 孙伟, 等. 不同模式下TBM刀群三维回转切削仿真与优化设计[J].
哈尔滨工程大学学报, 2014, 35(11): 1403–1408.
HUO Junzhou, YANG Jing, SUN Wei, et al. Simulation and optimization design of three-dimensional rotating cutting action of TBM cutter group with different modes[J]. Journal of Harbin engineering university, 2014, 35(11): 1403–1408. |
| [14] |
耿麒, 魏正英, 杜军, 等. 基于灰关联分析的全断面岩石掘进机滚刀布局优化方法[J].
机械工程学报, 2014, 50(21): 45–53.
GENG Qi, WEI Zhengying, DU Jun, et al. Cutters' layout optimization method of the Full-face Rock Tunnel Boring Machine based on grey relational analysis[J]. Journal of mechanical engineering, 2014, 50(21): 45–53. DOI:10.3901/JME.2014.21.045 |
| [15] |
徐芝纶.
弹性力学:下册[M].4版. 北京: 高等教育出版社, 2006: 26 -31.
XU Zhilun. Elasticity:volume Ⅱ[M].4th ed. Beijing: Higher Education Press, 2006: 26 -31. |
| [16] | OZDEMIR L, WANG F D. Mechanical tunnel boring prediction and machine design[R]. NSF/RA-790161, 1979. |



