面齿轮传动[1]是指圆柱齿轮与圆锥齿轮相啮合的新型传动,可用于两轮轴线相交或交错的场合。与锥齿轮传动相比,面齿轮传动最大优点在于主动小轮安装位置比较自由,不需要精确定位,此外还具有结构简单、动力分流效果好等诸多优点[2-4]。为改善面齿轮传动的啮合特性,国内外做了大量地研究。Litvin等[5]对齿条刀具的齿廓抛物线修形,得到了倾斜的接触路径。为进一步解决齿面偏载,Zanzi等[6]提出对面齿轮副中小轮进行双向修形。国内彭先龙等[7]提出用给定的啮合性能对面齿轮和小轮齿面进行重新设计的方法,郭辉[8]则提出采用修形的蜗杆砂轮展成修形小轮的方法。但是,以上研究都未能提供精确的修形曲面和修形齿面,且需反复试凑参数才能确定合理修形量,已不能充分满足航空领域高精度传动设计要求。另外,现今多轴联动的高性能数控机床技术[9],则为高精度修形齿面的加工提供了条件。
本文对面齿轮副中小轮进行拓扑修形,设计了齿廓、齿向修形曲线,将修形曲面与理论齿面叠加构造出精确的修形齿面,对所获得的局部共轭面齿轮副啮合性能进行分析,并进行试验研究。为简单起见,文中面齿轮由虚拟插齿刀展成得到。
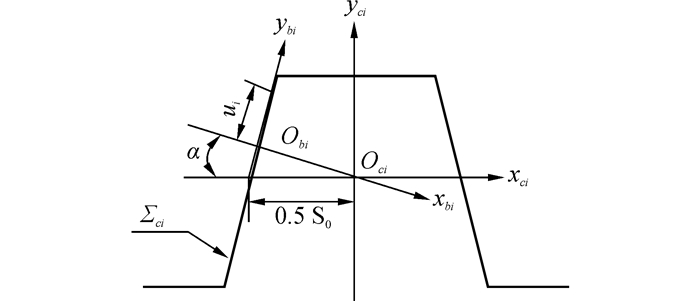
1 小轮和虚拟插齿刀理论齿面 1.1 齿条刀方程小轮和虚拟插齿刀齿面由齿条刀具展成得到,齿条刀具的端面齿廓见图 1。
|
| 图1 齿条刀具 Figure 1 Rack-cutters |
坐标系Sbi、Sci均是在齿条刀具端截面内,下脚标i=s、1分别表示展成虚拟插齿刀、小轮时的相关参数。S0=πm/2是齿条刀中线上的齿槽宽,α为端面压力角,设ui、li是曲面两个独立参数,则齿条刀齿面Σbi在坐标系Sbi、Sci中可以表示如下:
| ${\boldsymbol{R}_{bi}}\left( {{u_i}, {l_i}} \right) = {\left[{\begin{array}{*{20}{c}} 0&{{u_i}}&{{l_i}}&1 \end{array}} \right]^{\rm{T}}}$ | (1) |
| ${\boldsymbol{R}_{ci}}\left( {{u_i}, {l_i}} \right){\rm{ = }}{\boldsymbol{M}_{cibi}}{\boldsymbol{R}_{bi}}$ | (2) |
式中: Mcibi是坐标系Sbi到坐标系Sci的坐标变换矩阵。齿条单位法矢为:
| ${\boldsymbol{n}_{ci}} = \frac{{\partial {\boldsymbol{R}_{ci}}}}{{\partial {u_i}}} \times \frac{{\partial {\boldsymbol{R}_{ci}}}}{{\partial {l_i}}}/\left[{\frac{{\partial {\boldsymbol{R}_{ci}}}}{{\partial {u_i}}} \times \frac{{\partial {\boldsymbol{R}_{ci}}}}{{\partial {l_i}}}} \right]$ | (3) |
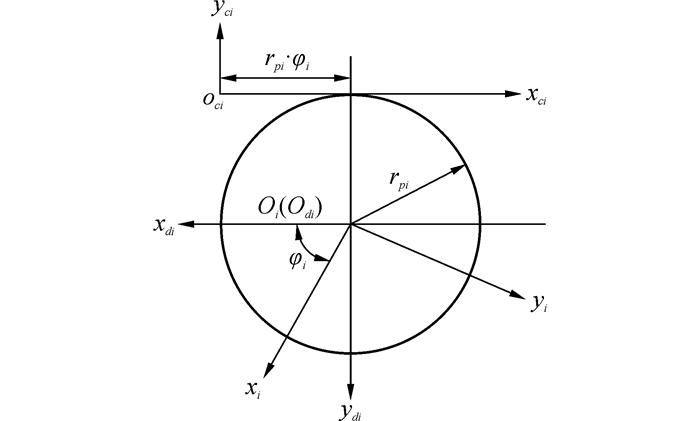
由齿条刀齿面Σb1、Σbs可分别包络得到小轮和虚拟插齿刀的齿面Σ1、Σs,见图 2。
|
| 图2 小轮和虚拟插齿刀展成坐标系 Figure 2 Coordinate systems for pinions and imaginary shaper cutters |
图中Si、Sci分别与齿轮、齿条刀固联,Sdi为固定坐标系。ψi、rpi分别为齿轮转角及分度圆的半径,ψirpi为齿条刀位移。小轮和虚拟插齿刀在Si中的理论齿面可由下式表示:
| $\left\{ \begin{array}{l} {\boldsymbol{R}_i}\left( {{u_i}, {l_i}, {\varphi _i}} \right) = {\boldsymbol{M}_{ici}}\left( {{\varphi _i}} \right){\boldsymbol{R}_{bi}}\left( {{u_i}, {l_i}} \right)\\ {f_i} = {\boldsymbol{n}_{ci}}\left( {{u_i}, {l_i}} \right){\boldsymbol{v}_{ic{i_{ci}}}}\left( {{u_i}, {l_i}, {\psi _i}} \right) = 0 \end{array} \right.$ | (4) |
式中: Mici为坐标系Sci到坐标系Si的变换矩阵,fi是齿条刀与齿轮的啮合方程,vciici为齿条刀齿面Σci与齿轮齿面Σi接触点在坐标系Sci中的相对速度。
理论齿面法矢为:
| ${\boldsymbol{n}_i}\left( {{u_i}, {l_i}, {\psi _i}} \right) = {\boldsymbol{L}_{ici}}\left( {{\psi _i}} \right){\boldsymbol{n}_{ci}}\left( {{u_i}, {l_i}} \right)$ | (5) |
式中: Lici为将矩阵Mici删除最后一行及最后一列得到。
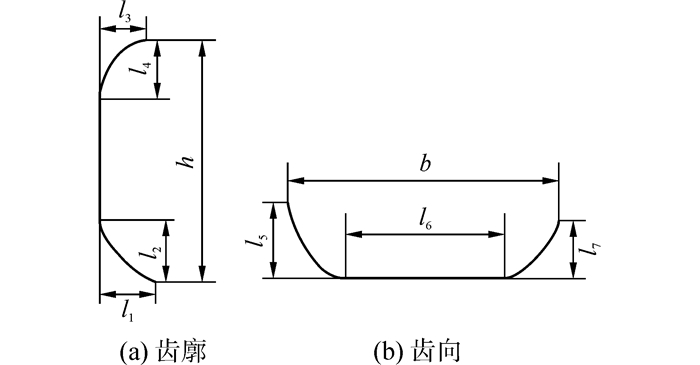
2 小轮拓扑修形齿面设计的修形曲线由2段抛物线与1段直线组成,见图 3,l1、l3与l2、l4为单独齿廓修形时齿廓两端最大修形量与对应修形长度,l5、l7与l6为单独齿向修形时齿向两端最大修形量与不修形长度,h、b为旋转投影面上的齿高、齿长,修形曲线用旋转投影面数据表示。旋转投影面表示为:
| $\left\{ \begin{array}{l} x = \sqrt {R_x^2 + R_y^2} \\ y = {R_z} \end{array} \right.$ | (6) |
式中:Rx、Ry、Rz是理论齿面位矢的坐标分量。
|
| 图3 设计修形曲线 Figure 3 Design curves of profile and longitudinal modification |
将旋转投影面沿轮齿齿高、齿长方向均匀划分成m×n个网格点阵,根据修形曲线计算网格节点的修形量δij(x, y),再由3次B样条对齿面网格节点数据拟合获得光滑的修形曲面。单独的齿廓、齿向修形为二维修形,拓扑修形可视为二者的叠加。将修形曲面与小轮理论齿面叠加,构造精确的拓扑修形齿面,其位矢和法矢表示如下:
| ${\boldsymbol{R}_{1r}}\left( {{u_1}, {l_1}} \right) = \delta \left( {x, y} \right){\boldsymbol{n}_1}\left( {{u_1}, {l_1}} \right) + {\boldsymbol{R}_1}\left( {{u_1}, {l_1}} \right)$ | (7) |
| ${\boldsymbol{n}_{1r}} = \left( {\frac{{\partial {\boldsymbol{R}_1}}}{{\partial {u_1}}} + \frac{{\partial \delta }}{{\partial {u_1}}}{\boldsymbol{n}_1} + \frac{{\partial {\boldsymbol{n}_1}}}{{\partial {u_1}}}\delta } \right) \times \left( {\frac{{\partial {\boldsymbol{R}_1}}}{{\partial {l_1}}} + \frac{{\partial \delta }}{{\partial {l_1}}}{\boldsymbol{n}_1} + \frac{{\partial {\boldsymbol{n}_1}}}{{\partial {l_1}}}\delta } \right)$ | (8) |
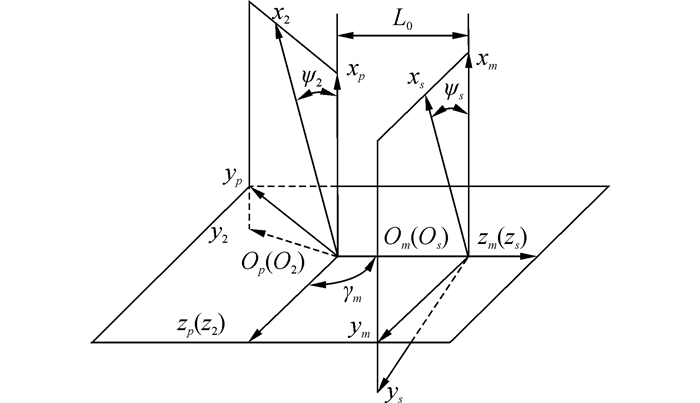
图 4所示为面齿轮的展成坐标系,坐标系Ss(Os, xs, ys, zs)、S2(O2, x2, y2, z2)分别与虚拟插齿刀和面齿轮固联,坐标系Sm(Om, xm, ym, zm)、Sp(Op, xp, yp, zp)与机架固联,为辅助坐标系,γm是面齿轮轴线z2与虚拟插齿刀轴线zs间的夹角,L0是面齿轮中径,ψs、ψ2分别是虚拟插齿刀和面齿轮的转角,两转角的关系为ψ2=ψs·m2s。面齿轮齿面Σ2s是曲面族R2s的包络,齿面方程由下式表示:
| $\left\{ \begin{array}{l} {\boldsymbol{R}_{2s}}\left( {{u_s}, {l_s}, {\psi _s}} \right) = s2{\boldsymbol{M}_{2s}}\left( {{\psi _s}} \right){\boldsymbol{R}_s}\left( {{u_s}, {l_s}} \right)\\ {f_{2s}} = {\boldsymbol{n}_s}\left( {{u_s}, {l_s}} \right){\boldsymbol{v}^s}\left( {{u_s}, {l_s}, {\psi _s}} \right) = 0 \end{array} \right.$ | (9) |
式中:f2s是虚拟插齿刀与面齿轮之间的啮合方程,vss2是表示在坐标系Ss中的两轮相对速度。理论齿面法矢为:
| ${\boldsymbol{n}_{2x}}\left( {{u_s}, {l_s}, {\psi _s}, x} \right) = {\boldsymbol{L}_{2x}}\left( {{\psi _s}} \right){\boldsymbol{n}_s}\left( {{u_s}, {l_s}, x} \right)$ | (10) |
式中: L2s为删除M2s的最后一行和最后一列得到。
|
| 图4 面齿轮展成坐标系 Figure 4 Coordinate systems for face gear |
齿面接触分析时采用的坐标系见图 5,坐标系S1、S2分别固联小轮、面齿轮,Φ1、Φ2为转角,齿面在固定坐标系Sf中切触。坐标系Sq、Se、Sd分别用来模拟轴向位移误差△q、偏置误差△E、轴夹角误差△γ,B为小轮与虚拟插齿刀分度圆半径之差,γf是实际安装轴夹角,γf=γm+△γ。面齿轮齿面位矢和法矢在Sf中表示为R2f和n2f,小轮拓扑修形齿面位矢和法矢在Sf中表示为R1f和n1f,则齿轮副在Sf中切触方程可表示为:
| $\left\{ \begin{array}{l} {R_{2f}}\left( {{\Phi _2}, {u_s}, {l_s}} \right) = {R_{1f}}\left( {{\Phi _1}, {u_1}, {l_s}} \right)\\ {n_{2f}}\left( {{\Phi _2}, {\mu _s}, {l_s}} \right) = {n_{1f}}\left( {{\Phi _1}, {u_1}, {l_1}} \right) \end{array} \right.$ | (11) |
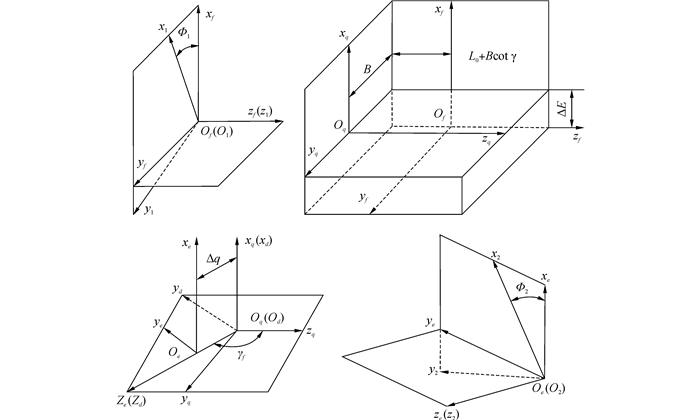
|
| 图5 面齿轮副啮合坐标系 Figure 5 Coordinate systems for gear meshing |
当以一定步长取Φ1为输入量求解上式,即可得到齿面啮合迹线、几何传递误差。
5 承载接触分析(LTCA)在TCA求得的准确齿面接触几何条件的基础上,可进一步确定两齿面接触间隙、沿接触椭圆长轴方向离散点的柔度矩阵,算法见文献[10-12],据此建立面齿轮副小轮拓扑修形后轮齿承载接触问题的数学规划模型:
| $\left\{ \begin{array}{l} \min \sum\nolimits_{j = 1}^{2n + 1} {{X_j}} \\ -Fp + Z + d + X = w\\ P = {e^{\rm{T}}}p + {X_{2n + 1}}\\ {\rm{S}}{\rm{.t}}{\rm{.}}\;{p_j} \ge 0, {d_j} \ge 0, {Z_j}, {X_j} \ge 0\\ {p_j} = 0\left\| {{d_j} = 0} \right. \end{array} \right.$ | (12) |
式中:Xj(j=1, 2, …2n+1)为人工变量,X=[X1 X2 …X2n]T,n维列向量,e的各元素均为1,w为弧线齿面齿轮齿面间n维初始间距矢量,p是齿面上的集中载荷,Z是轮齿变形后的法向位移。求解数学规划(12),由此可得承载传动误差、齿面载荷分布、齿间载荷分配系数等。
6 实例分析由上述推导编写MATLAB程序并设计了两组面齿轮传动,设计参数见表 1。实例1为传统面齿轮副,通过虚拟插齿刀与小轮齿数差实现局部共轭;实例2中虚拟插齿刀与小轮齿数相同,面齿轮副完全共轭,对安装误差非常敏感,需进行修形。
| 面齿轮传动参数 | 实例1 | 实例2 |
| 小轮齿数N1 | 30 | 30 |
| 虚拟插齿刀齿数Ns | 33 | 30 |
| 面齿轮齿数N2 | 360 | 360 |
| 端面压力角αt/(°) | 25 | 25 |
| 模数m/mm | 4.25 | 4.25 |
| 轴夹角γm/(°) | 90 | 90 |
| 面齿轮内径L1/mm | 745 | 745 |
| 面齿轮外径L2/mm | 785 | 785 |
设计小轮齿廓、齿向修形曲线见图 6,齿廓修形参数为l1=7.4 μm、l3=5 μm、l2=l4=m,齿向修形参数为l5=l7=20.8 T、l6=0。通过拟合得到小轮修形曲面见图 7,叠加齿廓、齿向修形可得拓扑修形齿根处最大修形量为28.2 μm,齿顶处最大修形量为25.8 T。
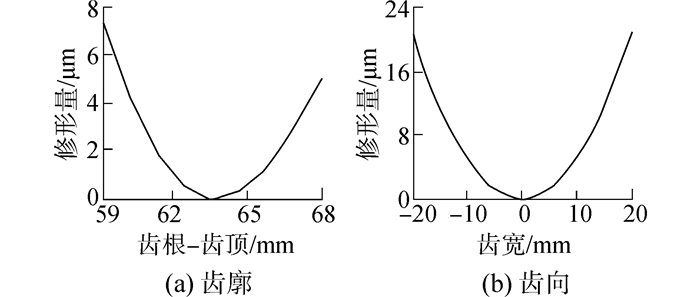
|
| 图6 修形曲线 Figure 6 Deviation curves |

|
| 图7 拓扑修形曲面 Figure 7 Deviation surface of topologically modified |
由图 8可知,无载时对准安装条件下,传统面齿轮副接触路径与齿根垂直,小轮拓扑修行后接触路径与齿根成一定角度倾斜,两者的接触印痕均大致位于轮齿的中部。经计算前者有效重合度为1.375,后者为1.5,提高了约10%,可见小轮拓扑修形能有效增大面齿轮副的有效重合度。
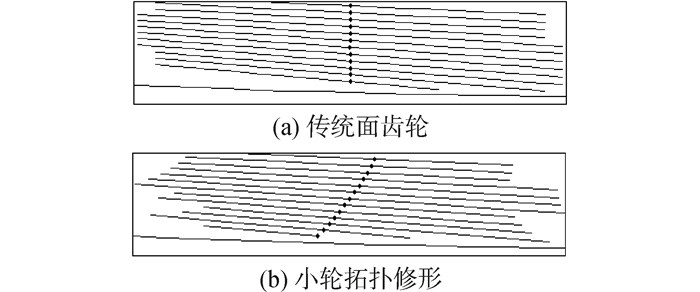
|
| 图8 无载时对准安装接触印痕 Figure 8 Contact patch without torque in case of no misalignment |
图 9表明无载对准安装时,传统面齿轮副几何传动误差为0,小轮拓扑修行获得了开口向下2阶对称抛物线几何传动误差,降低了安装误差敏感性,故允许最大安装误差变大,见表 2(由TCA获得),容差能力提高400%。图 9中Ⅰ、Ⅱ和Ⅲ分别对应载荷2 000、4 000、5 000 N·m时承载传动误差,可见小轮拓扑修形后获得了近似抛物线承载传动误差,误差波动幅值比传统面齿轮副明显减小,幅值分别由0.96"、1.82"、2.27"降到0.16"、1.03"、1.48",最大降幅83%,从而达到减振降噪的目的。
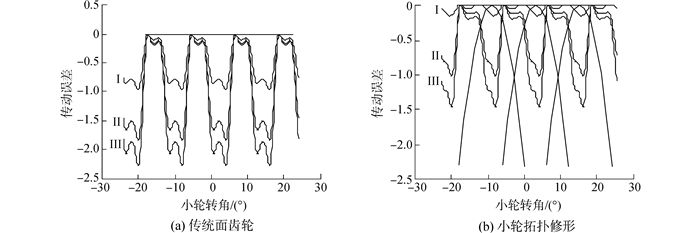
|
| 图9 对准安装时传动误差 Figure 9 Tansmission errors in case of no misalignment |
| 安装误差 | 小轮拓扑修形 | 传统误差 |
| △q/mm | 0.85 | 0.15 |
| △E/mm | 1.6 | 0.3 |
| △γ/(°) | 0.048 | 0.009 |
图 10表明传统面齿轮副在承载5 000 N·m时,每条接触椭圆长轴上的载荷都有较大突变,且齿轮副存在较严重边缘接触,而小轮拓扑修形后载荷从轮齿中部沿接触椭圆长轴向两端逐渐减小为零,仅齿根处接触椭圆长轴上的载荷有轻微突变,齿面载荷分布变化较均匀、平缓。
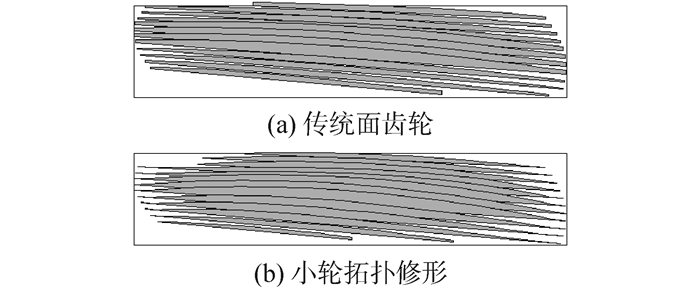
|
| 图10 承载5 000 N·m时对准安装载荷分布 Figure 10 Load distribution with a torque of 5 000 N·m in case of no misalignment |
面齿轮副承载时存在单、双齿啮合,因承载齿数变化导致齿间载荷分配系数有突变,见图 11,系数等于1时为单齿啮合,小于1为双齿啮合,小轮拓扑修形后双齿啮合时长比重增加,且轮齿进入和退出啮合时承受载荷减小50%,传动更加平稳。
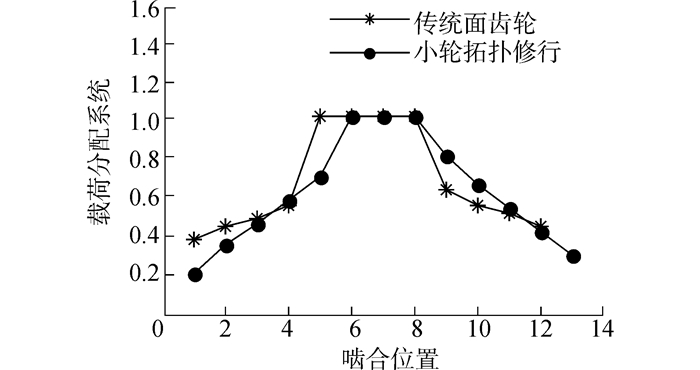
|
| 图11 承载5 000 N·m时对准安装载荷分配系数 Figure 11 Gear transverse load distribution factors with a torque of 5 000 N·m in case of no misalignment |
图 12为加工的面齿轮局部轮齿,参数见表 1中实例2。轮齿外端齿顶处无变尖,内端齿根处无根切,表明参数选取合理。

|
| 图12 面齿轮轮齿 Figure 12 The teeth of face gear |
根据图 6修形曲线,编制数控程序并完成小轮拓扑修形。滚检见图 13,涂有红丹粉的小轮轮齿区域与面齿轮充分啮合,获得的接触印痕见图 14、15,红丹粉被磨掉的部分即为接触区域。对准安装时齿面接触印痕位于齿宽中部,与对准安装TCA结果图 8(b)吻合,当轴向位移误差△q、偏置误差△E取正值时印痕向面齿轮外端移动,与未对准安装TCA结果图 16吻合,但存在一定误差,可能是由于修形量较小,齿顶、齿根没有完全脱开,另外,面齿轮加工精度和齿面质量不高也是造成误差的重要原因。

|
| 图13 滚检 Figure 13 The rolling tests |

|
| 图14 对准安装接触印痕 Figure 14 Contact patch in case of no misalignment |

|
| 图15 未对准安装接触印痕 Figure 15 Contact patch in case of misalignment |
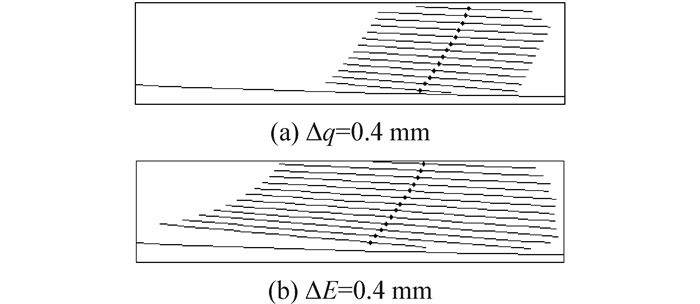
|
| 图16 无载时未对准安装TCA接触印痕 Figure 16 Contact patch of TCA without torque in case of misalignment |
1) 设计了小轮齿廓、齿向修形曲线,将修形曲面与小轮理论齿面叠加构造精确的拓扑修形齿面,建立了修形后面齿轮副传动的TCA、LTCA计算模型。
2) TCA表明小轮拓扑修形能获得开口向下2阶对称抛物线几何传动误差,接触路径与齿根倾斜,降低了安装误差敏感性,提高了面齿轮副的有效重合度及容差能力。
3) LTCA表明小轮拓扑修形较传统面齿轮副在优化承载传递误差、改善齿面载荷分布及避免边缘接触方面都具有优势。
4) 试验结果与TCA结果基本吻合,验证了TCA计算模型的正确性,但存在一定误差,须进一步完善试验条件并验证LTCA结果。
| [1] | KUIKEN H. Face gear transmission:US, 4744263[P]. 1988-05-17. |
| [2] | GABICCINI M, GUIGGIANI M, PUCCIO F D. Geometry and kinematics of face gears mating with a helical involute pinion[C]//Proceedings of the 11th World Congress in Mechanism and Machine Science. Tianjin:IFTOMM, 2004. |
| [3] | WU Canhui, CAO Ping. The application of tooth contact analysis in the shaper modification for face-gear[J]. Procedia engineering, 2015, 99: 94–100. DOI:10.1016/j.proeng.2014.12.512 |
| [4] | BOANTĂ C I, BOLOŞV. The mathematical model of generating kinematic for the worm face gear with modified geometry[J]. Procedia technology, 2014, 12: 442–447. DOI:10.1016/j.protcy.2013.12.512 |
| [5] | LITVIN F L, FUENTES A, HOWKINS M. Design, generation and TCA of new type of asymmetric face-gear drive with modified geometry[J]. Computer methods in applied mechanics and engineering, 2001, 190(43/44): 5837–5865. |
| [6] | ZANZI C, PEDRERO J I. Application of modified geometry of face gear drive[J]. Computer methods in applied mechanics and engineering, 2005, 194(27/28/29): 3047–3066. |
| [7] |
彭先龙, 胡锡文, 方宗德. 构造拓扑修形齿面的面齿轮传动主动设计[J].
航空动力学报, 2014, 29(5): 1216–1222.
PENG Xianlong, HU Xiwen, FANG Zongde. Active design of face gear drive for modifying ease-off topology flank[J]. Journal of aerospace power, 2014, 29(5): 1216–1222. |
| [8] | 郭辉.面齿轮滚齿加工方法及其啮合性能研究[D].西安:西北工业大学, 2009. |
| [9] | SHIH Y P, CHEN S D. Free-form flank correction in helical gear grinding using a five-axis computer numerical control gear profile grinding machine[J]. Journal of manufacturing science and engineering, 2012, 134(4): 041006. DOI:10.1115/1.4006096 |
| [10] |
赵宁, 郭辉, 方宗德, 等. 直齿面齿轮修形及承载接触分析[J].
航空动力学报, 2008, 23(11): 2142–2146.
ZHAO Ning, GUO Hui, FANG Zongde, et al. Modification and loaded contact analysis of spur face gears[J]. Journal of aerospace power, 2008, 23(11): 2142–2146. |
| [11] |
方宗德. 斜齿轮齿面柔度矩阵与修形的有限元计算[J].
航空动力学报, 1994, 9(3): 242–244.
FANG Zongde. Calculation on flexibility matrix and modification of helical gears by FEM[J]. Journal of aerospace power, 1994, 9(3): 242–244. |
| [12] |
方宗德. 齿轮轮齿承载接触分析(LTCA)的模型和方法[J].
机械传动, 1998, 22(2): 1–3, 16.
FANG Zongde. Model and approach for loaded tooth contact analysis (LTCA) of gear drives[J]. Journal of mechanical transmission, 1998, 22(2): 1–3, 16. |



