潮流能是一种由潮汐现象引起的海水流动动能,受月球影像周期性地改变其大小和方向。在世界范围内合理开发利用潮流能对解决当今能源短缺问题具有深远影响。潮流能开发的核心是水轮机,与水平轴水轮机相比,竖轴水轮机对来流方向没有要求,自启动性能好,能量利用率较高,成为潮流能开发利用的主要方向[2-3]。
水动力性能、结构强度与可靠性是评价水轮机综合性能的两个基本指标。国内外学者对潮流能水轮机水动力性能及其预测方法[4-5]、实验[6-7]、新型水轮机开发[8]等给予了充分的关注。水轮机工作在复杂海洋环境中,受到海洋潮流波浪、海洋暴风潮等自然环境影响,还存在海水腐蚀、微生物污染等。此外,水轮机转子系统还受到自身不平衡力、密封力、刹车力、电磁激励等影响,诸因素共同导致水轮机发电机组出现复杂的振动,降低其可靠性性,从而影响其服役寿命[9]。
关于潮流能水轮机强度和可靠性研究的文献较少。Mattias等[10]对水中悬臂结构的横向振动与水动力特性关系进行了分析,给出了水流力对结构作用影响的等效方式。王树杰等[11]研究了风浪流载荷下潮流能发电实验平台的稳定性,并进行了实际海洋环境测量。意大利Ponte diArchimede公司设计开发三叶片“Kobold”竖轴水轮机,在试验和海试时实现了水轮机转子扭矩和转速的实时监控。马勇等[12]设计并进行了竖轴水轮机静水拖航实验和波浪实验,为漂浮式竖轴潮流能水轮机发电装置的振动及工程应用提供参考。
而国内外普遍关注水动力性能而缺乏结构或转子动力学特性的研究工作,因而无法对水轮机转子系统的可靠性、稳定性进行预测,在结构设计、水轮机运行过程中缺乏必要的目标和指标[13],因此难以准确预估水轮机的健康状态和寿命。综上,针对潮流能水轮发电机组开展振动特性分析是水轮机设计的前提,具有重要的意义。
本文针对等臂长和变臂长水轮机转子系统,建立了其变结构回转体的转子动力学模型和流体激励模型,通过仿真和实验研究了潮流流体激励下转子系统振动特性。
1 竖轴水轮机流体激励所谓的等臂长水轮机,是竖轴水轮机的叶片支撑臂的长度在运行过程中保持不变;与之相对,变臂长水轮机是指假定支撑臂长度在运行过程中有规律的变化,使得每个叶片运行轨迹为椭圆形等非圆形轨迹,以期提高水轮机水动力性能。
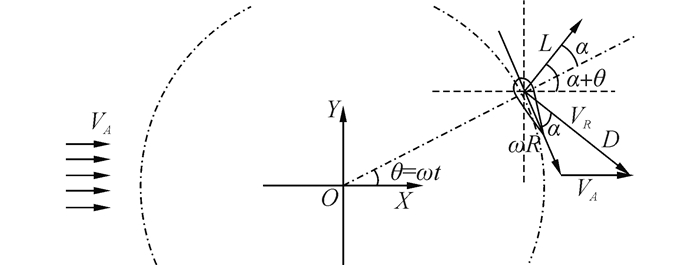
对于等臂长竖轴水轮机,垂直水轮机主轴的截面建立平面直角坐标系,主轴圆心为坐标原点。假设水轮机叶片的安装角为0°,叶片受力分析如图 1。
|
| 图1 等臂长水轮机叶片受力分析 Figure 1 The force analysis of vertical axis equal arm length turbine |
对每个象限,第z个叶片的速度三角形、攻角、升阻力及其导致的横向力、周向力等分别推导如下:
| ${V_R}\left( z \right) = \sqrt {{{\left( {\omega R} \right)}^2} + V_A^2 + 2\omega R{V_A}\sin \left[ {\theta + \frac{{2{\rm{\pi }}}}{3}\left( {z - 1} \right)} \right]} $ | (1) |
| $\alpha \left( z \right) = {\rm{arctan}}\frac{{{V_A}\cos \left[ {\theta + \frac{{2{\rm{\pi }}}}{3}\left( {z - 1} \right)} \right]}}{{{V_A}\sin \left[ {\theta + \frac{{2{\rm{\pi }}}}{3}\left( {z - 1} \right)} \right] + \omega R}}$ | (2) |
式中:VA代表水流速度,θ代表叶片转角,z代表计算的叶片序号
根据雷诺数定义:
| $Re\left( z \right) = \frac{{\rho {V_R}\left( z \right)c}}{\mu }$ | (3) |
式中:c是流场的特征长度,μ是流体运动粘性系数。
当水轮机叶片翼型确定以后,根据翼型理论,翼型在一定攻角、速度的流体流过时,产生的升力和阻力可以表示为:
| $\left\{ \begin{array}{l} L\left( z \right) = {C_l}\left( z \right)\left( {\alpha \left( z \right),{\mathop{\rm Re}\nolimits} \left( z \right)} \right) \cdot \frac{1}{2}\varepsilon V_R^2\left( z \right){L_0}c\\ D\left( z \right) = {C_d}\left( z \right)\left( {\alpha \left( z \right),{\mathop{\rm Re}\nolimits} \left( z \right)} \right) \cdot \frac{1}{2}\rho V_R^2\left( z \right){L_0}c \end{array} \right.$ | (4) |
将上述翼型的升力和阻力沿坐标方向分解,在水轮机横向(图 1中y向)的综合作用力即横向力为
| $\begin{array}{l} {F_x}\left( z \right) = L\left( z \right)\cos \left[ {\theta + \frac{{2{\rm{\pi }}}}{2}\left( {z - 1} \right) + \alpha \left( z \right)} \right] + \\ D\left( z \right)\sin \left[ {\theta + \frac{{2{\rm{\pi }}}}{3}\left( {z - 1} \right) + \alpha \left( z \right)} \right] \end{array}$ | (5) |
周向力为:
| ${F_\tau }\left( z \right) = L\left( z \right)\sin \alpha \left( z \right) - D\left( z \right)\cos \alpha \left( z \right)$ | (6) |
因此,水轮机旋转一周过程中,叶轮产生的横向力和周向力分别为
| $\left\{ \begin{array}{l} {{\bar F}_x} = \sum\limits_{z = 1}^n {{F_x}\left( z \right)} \\ {{\bar F}_\tau } = \sum\limits_{z = 1}^n {{F_\tau }\left( z \right)} \end{array} \right.$ | (7) |
上述横向力或周向力不能直接求解,因为来流速度VA尚不知,需要通过如下动量定理建立等式获得。
假设潮流均匀,速度为V0,作用在盘面处的流体速度是来流速度和盘面诱导速度的叠加:
| ${V_d} = \left( {1 - \kappa } \right){V_0}$ | (8) |
诱导速度满足:u=κV0,κ为诱导速度系数。
在叶轮盘面上下游分别运用Bernoulli方程,根据动量定理,盘面的受力为
| ${F_m} = \left( {P_d^ + - P_d^ - } \right){A_d} = 2\varepsilon {A_d}V_0^2\kappa \left( {1 - \kappa } \right)$ | (9) |
其中,Ad为水轮机垂直于来流的截面面积:Ad=2RL0。
根据动量定理,叶轮产生的横向力和盘面受的推力相等,即Fx=Fm。
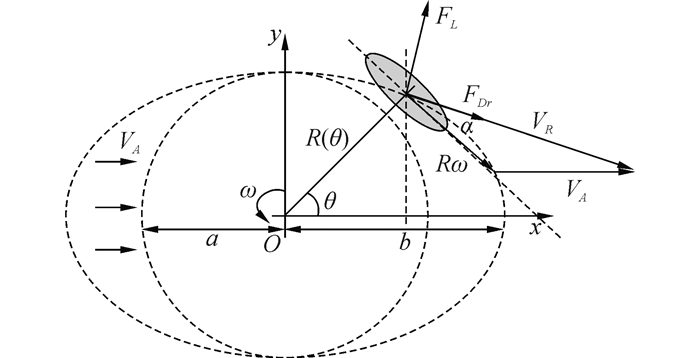
如果水轮机臂长按照椭圆轨迹变化,如图 2所示。假设叶片弦线方向始终垂直半径方向,垂直、平行于潮流方向的臂长分别为a、b。
|
| 图2 变臂长水轮机叶片受力分析 Figure 2 The force analysis of variable arm length turbine |
水轮机动态臂长:
| $R\left( {\theta ,z} \right) = \frac{{ab}}{{\left( {\sqrt {{a^2}{{\cos }^2}\left[ {\theta + \frac{{2{\rm{\pi }}}}{3}\left( {z - 1} \right)} \right] + {b^2}{{\sin }^2}\left[ {\theta + \frac{{2{\rm{\pi }}}}{3}\left( {z - 1} \right)} \right]} } \right)}}$ | (10) |
上述与臂长R相关的量,均随转角而变化。
2 竖轴水轮机转子动力学模型 2.1 等臂长水轮机转子系统动力学模型对水轮机转子系统进行合理简化,采用有限元法建立其动力学运动方程:
| $\boldsymbol{M}\ddot u + \boldsymbol{C}\mathop u\limits^ \cdot + \boldsymbol{K}u = f\left( t \right) + Q\left( t \right)$ | (11) |
式中:K为转子结构刚度矩阵,包含了滚动轴承支承刚度;f(t)为水轮机的激振力,如式(9)所示。Q(t)为水轮机的不平衡力,C为阻尼矩阵,采用工程中广泛应用的经典的Rayleigh阻尼模型; M为质量矩阵,由于臂长不变,且质量较轻,忽略其影响,只将叶片等效为轮盘处理。此外,因为水轮机一般工作转速较低,例如200 r/min以下,因而忽略转子的陀螺效应。为后面推导方便,将质量矩阵简记为
| $\begin{array}{l} \boldsymbol{M} = \frac{{\rho Al}}{{420}}\left[ {\begin{array}{*{20}{c}} {156}&{22l}&{54}&{ - 13l}\\ {22l}&{4{l^2}}&{13l}&{ - 3{l^3}}\\ {54}&{13l}&{156}&{ - 22l}\\ { - 13l}&{ - 3{l^2}}&{ - 22l}&{4{l^2}} \end{array}} \right] + \\ \frac{{\rho A{r^2}}}{{120l}}\left[ {\begin{array}{*{20}{c}} {36}&{3l}&{ - 36}&{3l}\\ {3l}&{4{l^2}}&{ - 3l}&{ - {l^2}}\\ { - 36}&{ - 3l}&{36}&{ - 3l}\\ {3l}&{ - {l^2}}&{ - 3l}&{4{l^2}} \end{array}} \right] \end{array}$ | (12) |
可以简化为:
变臂长水轮机为一个变结构回转体,将水轮机叶片简化成附加质量和附加转动惯量,为了计算方便,将NACA0018叶片截面形状简化为近似椭圆处理,椭圆长半轴为a',短半轴为b',则椭圆绕自身轴心旋转的转动惯量为:
| ${I_{z2}} = \frac{1}{4}m\left( {{{a'}^2} + {{b'}^2}} \right)$ | (13) |
由于水轮机臂长R(θ)随方位角θ变化,则单叶片的转动惯量为:
| ${J_d} = \frac{1}{4}m\left( {{{a'}^2} + {{b'}^2}} \right) + m{R^2}\left( \theta \right)$ | (14) |
当水轮机含有三个叶片时:
| $\begin{array}{c} {J_d}^\prime = \frac{1}{4}m\left( {{{a'}^2} + {{b'}^2}} \right) + \\ m\left[ {R{{\left( \theta \right)}^2} + R{{\left( {\theta + \frac{{2{\rm{\pi }}}}{3}} \right)}^2} + R{{\left( {\theta + \frac{{4{\rm{\pi }}}}{3}} \right)}^2}} \right] \end{array}$ | (15) |
考虑叶片的附加质量和附加转动惯量时会对原来水轮机的质量矩阵产生影响,叶片所处结点的质量矩阵变为:
| $\begin{array}{c} C_1^{11}{\;^\prime } = C_1^{11} + m;\;E_1^{11}{\;^\prime } = E_1^{11} + m;\\ C_1^{22}{\;^\prime }{\rm{ = }}C_1^{22}{\rm{ + }}{J_d};\;E_1^{22}{\;^\prime }{\rm{ = }}E_1^{22}{\;^\prime }{\rm{ + }}{J_d} \end{array}$ |
即设叶片对轴段施加影响的方程为:
| ${I_z} = \left[ {\begin{array}{*{20}{c}} m&0\\ 0&{{J_d}^\prime } \end{array}} \right]$ |
因此,考虑叶片以后,等臂长水轮机质量矩阵为:
| $\begin{array}{c} M' = \left( {\left[ {\begin{array}{*{20}{c}} {{C_1}}&{{C_2}}\\ {{D_1}}&{{D_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{I_z}}&0\\ 0&0 \end{array}} \right]} \right){\rm{ + }}\left( {\left[ {\begin{array}{*{20}{c}} {{E_1}}&{{E_2}}\\ {{F_1}}&{{F_2}} \end{array}} \right]{\rm{ + }}} \right.\\ \;\left. {\left[ {\begin{array}{*{20}{c}} {{I_z}}&0\\ 0&0 \end{array}} \right]} \right) = \left[ {\begin{array}{*{20}{c}} {{C_1} + {I_z}}&{{C_2}}\\ {{D_1}}&{{D_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{E_1} + {I_z}}&{{E_2}}\\ {{F_1}}&{{F_2}} \end{array}} \right] \end{array}$ | (16) |
通过推导可知,变臂长水轮机的刚度矩阵保持不变。
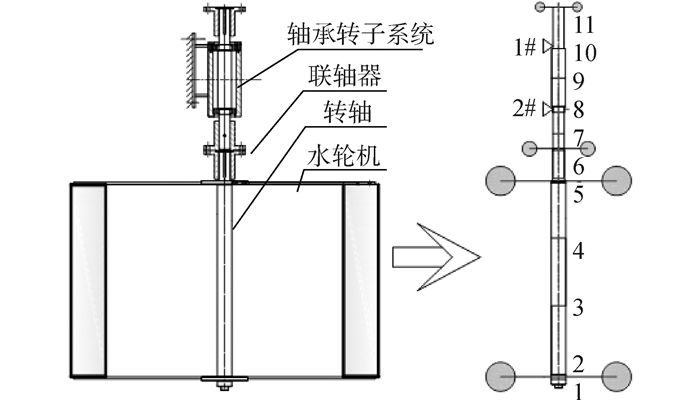
3 竖轴水轮机流体激励仿真 3.1 水轮机转子系统结构参数水轮机转子系统包括水轮机、转轴、联轴器、轴承转子系统等,如图 3所示。水轮机叶片采用铝合金,其余为45#钢,水轮机的结构参数如表 1。
|
| 图3 水轮机转子系统结构及有限元简化 Figure 3 Turbine rotor system structure and simplification by FEM |
| 类别 | 取值 |
| 叶片弦长/m | 0.12 |
| 叶片展长/m | 0.66 |
| 叶片数目 | 3 |
| 等臂长叶轮直径m | 1 |
| 主轴直径/m | 0.05 |
| 主轴长度/m | 0.717 |
| 转子-轴承系统长度/m | 0.6 |
| 转子-轴承系统直径/m | 0.045 |
| 工作转速/(r· min-1) | 60 |
| 水流流速/(m· s-1) | 2 |
| 叶片翼型 | NACA0018 |
| 轴承支承刚度/(MN· m-1) | 100 |
采用有限元法,将水轮机转子系统离散分为10个轴段,11个结点,轴承位于8和10结点,联轴器位于6和11结点。
变臂长水轮机的长、短径a、b或a/b不能无限制变化,椭圆周长越长、椭圆面积越大,水轮机可靠性低,成本越高。为研究变臂长水轮机转子系统的动力学特性,并与等臂长有一定的可比性,建立两个计算准则:等面积准则和等周长准则,变臂长水轮机计算方案如表 2所示。
| 臂长方案 | 方案名称 | 长半轴/m | 短半轴/m |
| 臂长方案 | 方案名称 | 长半轴/m | 短半轴/m |
| 等臂长 | 方案0 | 0.5 | 0.5 |
| 等面积变臂长 | 方案1 | 0.6 | 0.417 |
| 方案2 | 0.7 | 0.357 | |
| 方案3 | 0.8 | 0.312 5 | |
| 等周长变臂长 | 方案4 | 0.55 | 0.412 3 |
| 方案5 | 0.6 | 0.324 6 | |
| 方案6 | 0.65 | 0.236 8 |
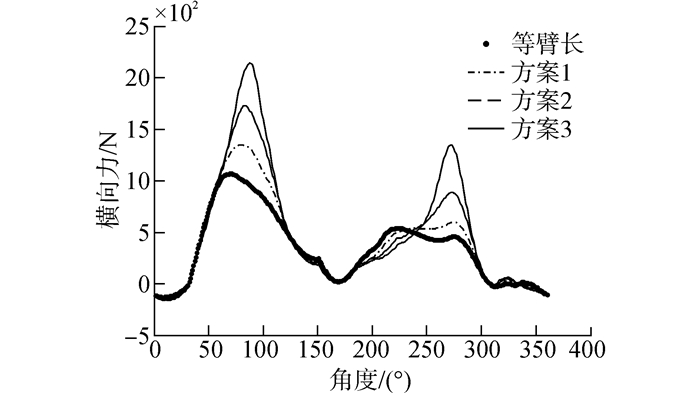
由于水轮机横向力是流体作用导致的一种横向冲击力,其对于转子结构的可靠性会产生重要影响,因而对该横向力进行详细仿真分析;由于本文主要关注水轮机的结构强度与可靠性,而影响水轮机效率、功率等水动力性能的其他指标如升力、周向力等暂不予以考虑。根据表 1所示的水轮机及叶片、翼型结构。变臂长水轮机横向力(式(7))分别如图 4、5。
|
| 图4 等面积变臂长水轮机横向力 Figure 4 Cross force of constant area rules scheme |
|
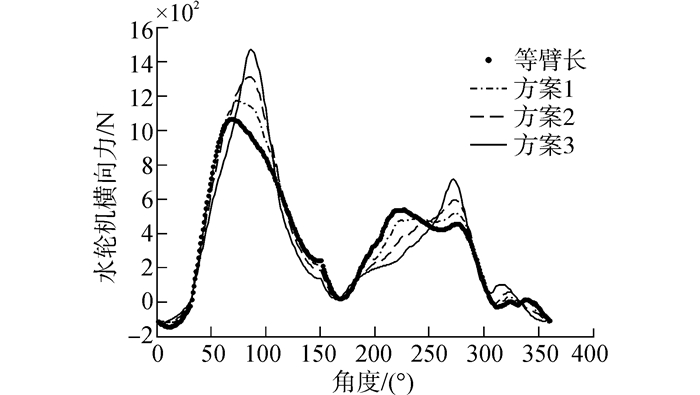
| 图5 等周长变臂长水轮机横向力 Figure 5 Cross force of constant perimeter rules scheme |
仿真结果表明:水轮机旋转一周,横向力存在3个波峰,波峰幅值依次减小。和等臂长相比,变臂长水轮机波峰幅值增加,a/b越大,即椭圆度越大,波峰幅值越大,方案3的横向力变化最为剧烈。由于横向力是引起转子振动、影响水轮机可靠性的关键因素,因此还需要研究横向力对水轮机转子系统的振动特性影响。
4 水轮机转子系统的振动特性水轮机转速、潮流流速同上,响应输出结点为6,即刚性联轴器所在结点。计算方案设置如表 3。
| 方案名称 | 变臂长 | 流体力 | 不平衡力情况 |
| 方案7 | 否 | 否 | 大小2.07 kg·m |
| 方案8 | 否 | 是 | 所在节点2 |
| 方案9 | 方案1 | 是 | 相位45° |
| 方案10 | 方案3 | 是 |
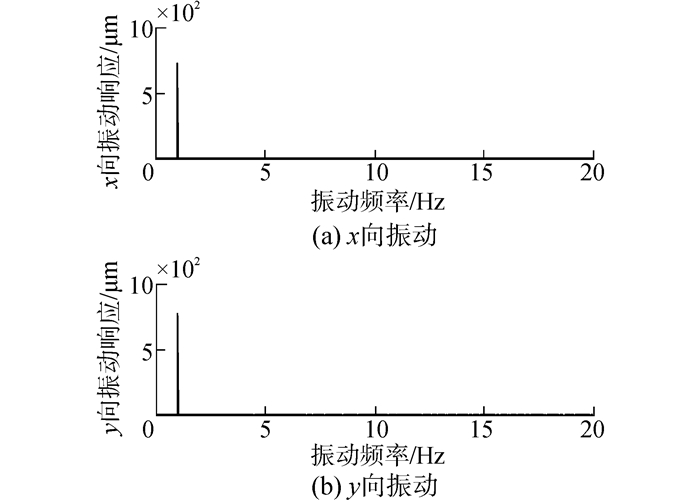
仿真结果表明,对于方案7,当不考虑流体激励时,等臂长水轮机轴心轨迹为一个圆,只存在不平衡力引起的工频振动,如图 6所示。
|
| 图6 方案7水轮机振动频谱图 Figure 6 Turbine spectrum of scheme 7 |
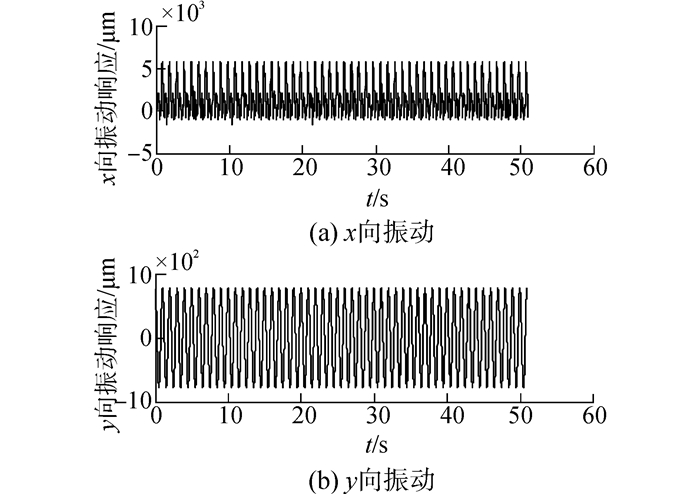
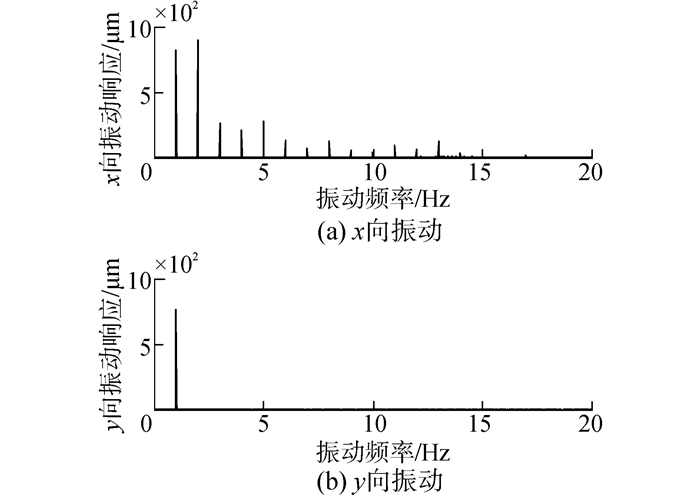
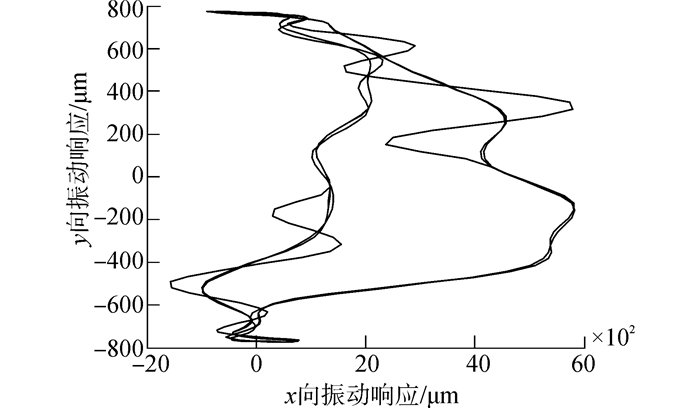
对于方案8,在方案1基础上考虑流体激励时,由于流体激振力位于x方向,因此y向振动保持不变,x方向不仅工频振动增大,而且存在2×-5×等倍频振动,且2×倍频振动略大于工频振动,工频振动约增大2.4倍,此外,还存在振幅较小的高倍频振动(如10×-13×)。由于1×、2×倍频振动均比较大,轴心轨迹为近似“8”字形,如图 7-9所示。
|
| 图7 方案8水轮机振动时间历程图 Figure 7 Turbine time history figure of scheme 8 |
|
| 图8 方案8水轮机振动频谱图 Figure 8 Turbine spectrum of scheme 8 |
|
| 图9 方案8水轮机振动轴心轨迹 Figure 9 Turbine axis center track of scheme 8 |
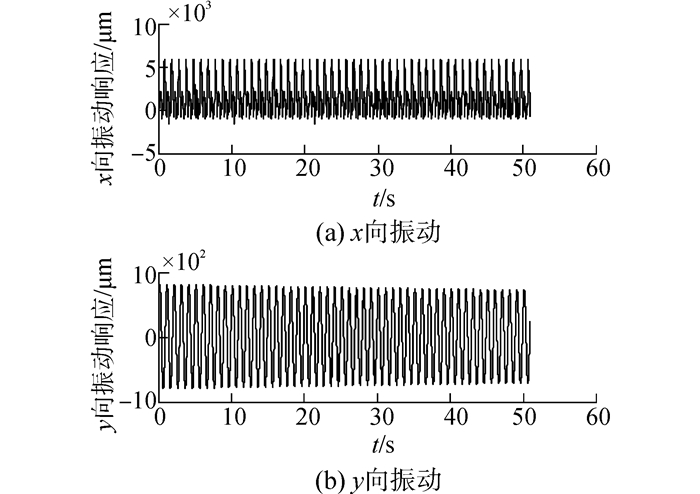
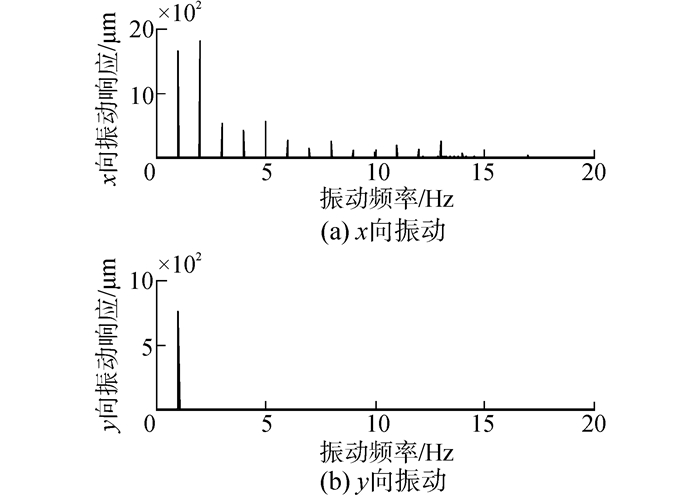
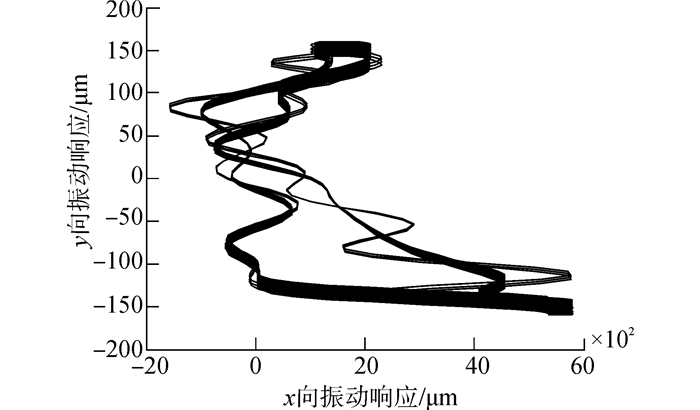
对于方案9和10,当水轮机为变臂长时,对结构质量矩阵和流体激励均有所影响。结果表明,和等臂长相比,变臂长水轮机导致y向基频振动降低,但对x向复杂倍频振动影响不大。其中1×、2×、3×倍频振动略有下降,4×倍频振动略有增加。如图 10-12所示。
|
| 图10 方案9水轮机振动时间历程图 Figure 10 Turbine time history figure of Scheme 9 |
|
| 图11 方案9水轮机振动频谱图 Figure 11 Turbine spectrum of scheme 9 |
|
| 图12 方案9水轮机振动轴心轨迹 Figure 12 Turbine axis center track of scheme 9 |
流体激励模型和转子动力学模型都是建立在一定的假设和简化之上,为对竖轴水轮机振动特性进行验证,搭建等臂长竖轴水轮机实验台,实验台包括水轮机本体(包括水轮机、联轴器、转子-轴承系统)、驱动及传动系统(电动机/发电机、齿轮箱)、测控系统(扭矩传感器、变频器、控制器、工控机)、支撑系统(拖车、浮桥、横梁支架)和振动测试系统(加速度传感器、动态数据采集仪、工控机)、船池拖车等,实验台实物图如图 13所示。

|
| 图13 竖轴水轮机结构振动实验台 Figure 13 Structure experiment rig of vertical axis turbine |
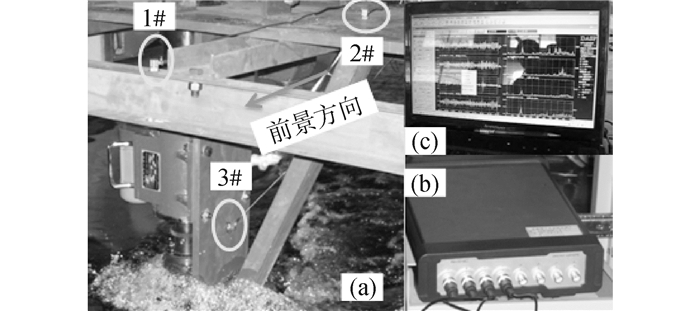
实验台主要结构同前述仿真参数。由于水轮机在水下工作,支撑结构常常在启动或停车阶段暴漏在水流冲刷之下,因而转子等旋转部件振动测试、信号传输存在困难,因此主要监测主框架的振动信号。振动测试系统实物图如图 14所示。
|
| 图14 实验台振动测试系统 Figure 14 The vibration test system |
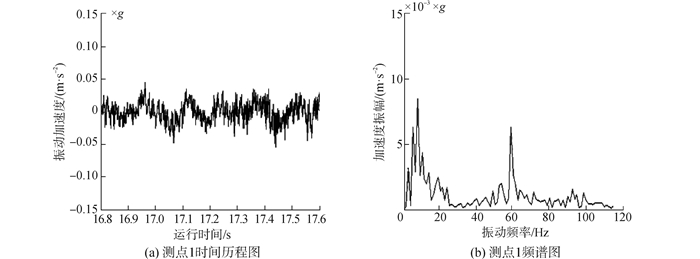
当拖车速度为2 m/s、水轮机转速为50 rpm时,水轮机主框架振动特性测量结果如图 15所示。其中(a)、(b)为测点1#的时间历程图和频谱图,(c)、(d)为测点2#的结果。
|
| 图15 水轮机结构振动特性测量结果 Figure 15 Test results of turbine structure vibration characteristics |
振动测试结果表明,水轮机结构振动比较复杂,不但有低倍频(1×-10×)振动,而且存在高倍频(11×-100×)振动,且高频振动中包含结构的共振成分,即高频振动中振幅较大的频率为结构共振频率。
低倍频振动与水轮机转速和叶片个数有关,分别为2.5、5、7.5、10 Hz,其中7.5 Hz振动最大。根据水轮机工作转速,其基频为0.833 Hz,由于是三个叶片,其3×倍频为2.5Hz。在水轮机工作工程中,在流体激励、转速激励、叶片数目等共同作用下,2.5 Hz的振动会出现复杂的倍频成分,即会出现5、7.5、10 Hz等各种倍频振动。因此从定性角度分析,水轮机结构振动存在1×、2×~12×倍频振动,且9×(7.5 Hz)振动相对较大,由于采样频率限制,0.833 Hz的低频振动无法分辨出来。
不同流速、转速工况测试表明,振动测量实验的可重复性强,定性的频率成分明显。从定性角度分析,实验测试和数值仿真出现的振动频率成分基本一致。因此不论等臂长还是变臂长水轮机,其结构振动以转速的倍频为主;流体激励不仅激起工频振动,还激起较大的倍频振动,由于倍频振动分布密集,还会导致结构共振的出现。
诚然,由于实际水轮机运行的不平衡力难以准确获取,螺栓连接较多,因而结构阻尼复杂,从定量角度计算和分析其振动特性存在较大困难。此外液体对水轮机模态会产生一定影响,还需要进一步深入研究。此外,在多次水轮机综合性能试验中,还发现众多结构振动和可靠性问题,简述如下:
1)水轮机叶片支撑臂螺栓脱落导致支撑臂一端与固定轮盘脱开;
2)水轮机支撑主横梁在水轮机转速大于90 rpm、潮流流速大于2.5 m/s以后出现结构共振;
3)船池采用深井淡水,水下工作的水轮机、主轴等45#材料均进行了“发黑”处理,经过10天水下试验后,45#材料出现了严重的锈蚀,铝合金叶片表面也出现了白色斑点,表面不在光滑。
实际海洋工况更加复杂,因此竖轴潮流能水轮机的可靠性不容忽视,还需要开展更深入的研究工作。
6 结论建立了等臂长和变臂长竖轴水轮机流体激励模型,并推导了水轮机转子系统横向振动动力学方程,研究了水轮机转子系统流体激励下的动力学响应,最后搭建了等臂长竖轴水轮机结构实验台,进行了振动特性测量,主要结论如下:
1)基于动量定理的流管法,建立了等臂长和变臂长水轮机的流体激励模型,水轮机旋转一周,流体激励的横向力存在三个波峰,波峰幅值依次减小。和等臂长相比,变臂长水轮机波峰幅值增加,臂长变化幅度越大,波峰幅值越大。
2)推导了等臂长竖轴水轮机转子系统的动力学模型,考虑臂长变化引起的叶片附加转动惯量影响,推导了变臂长水轮机的质量矩阵模型,这类变结构回转体对质量矩阵的影响不容忽视。
3)对于等臂长水轮机:水轮机的不平衡力只会激起转子的工频振动,流体激励的横向力只对本方向上的振动产生影响,不仅导致工频振动增大,而且会产生很大的2×倍频振动,此外还存在振幅较小的高频振动,轴心轨迹为复杂的“8”字形。对于变臂长水轮机:臂长变化会导致水轮机转子椭圆短径对应的方向振动降低,对流体激励所在方向的振动影响较小。
4)搭建了等臂长竖轴水轮机综合性能实验台,对振动特性进行了测试,结果表明,水轮机结构振动比较复杂,以倍频振动为主,不但有低倍频(1×-10×)振动,而且存在高倍频(11×-100×)振动。从定性角度,实验测试和数值仿真出现的振动频率成分基本一致。由于倍频振动分布密集、频带较宽,会导致结构共振的出现。
| [1] | 王传崑, 卢苇. 海洋能资源分析方法及储量评估[M]. 北京: 海洋出版社, 2009 . |
| [2] |
陈存福.潮流能水平轴水轮机叶片优化及水动力性能研究[D].青岛:中国海洋大学, 2012.
CHEN Cunfu. Study on blade optimization and hydrodynamic performance of horizontal axis marine current turbine[D]. Qingdao:Ocean University of China, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10423-1012504874.htm |
| [3] | SCHÖNBORN A, CHANTZIDAKIS M. Development of a hydraulic control mechanism for cyclic pitch marine current turbines[J]. Renewable energy, 2007, 32(4): 662–679. DOI:10.1016/j.renene.2006.02.004 |
| [4] | LI Ye. Development of a procedure for predicting power generated from a tidal current turbine farm[D]. Columbia:The University of British Columbia, 2008. https://doi.library.ubc.ca/10.14288/1.0066762 |
| [5] | NABAVI Y. Numerical study of the duct shape effect on the performance of a ducted vertical axis tidal turbine[D]. Columbia:The University of British Columbia, 2008. https://open.library.ubc.ca/handle/2429/14704 |
| [6] | RAWLINGS G W. Parametric characterization of an experimental vertical axis hydro turbine[D]. Columbia:The University of British Columbia, 2008. http://www.doc88.com/p-2905231916419.html |
| [7] | COIRO D P, NIEOLOSI F. Numerical and experimental analysis of kobold turbine[C]//Synergy Symposium on Vertical Axis Wind Turbine. Hangzhou, China, 1998. |
| [8] | COIRO D P, NICOLOSI F, DE MARCO A, et al. Dynamic behavior of novel vertical axis tidal current turbine:numerical and experimental investigations[C]//Proceeding of the 15th International Offshore and Polar Engineering Conference. Seoul, 2005. |
| [9] | KARLSSON M, AIDANPÄÄ J O. Dynamic behaviour in a hydro power rotor system due to the influence of generator shape and fluid dynamics[C]//Proceeding of ASME 2005 Power Conference. Chicago:ASME, 2005:905-913. |
| [10] | NÄSSELQVIST M, GUSTAVSSON R, AIDANPÄÄ J O. Case study of resonance phenomena in a vertical hydropower unit[C]//The 12th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery. Honolulu, Hawaii, 2008. |
| [11] | 王树杰, 尹克金, 李淑一, 等.风浪流联合载荷作用下潮流能发电实验平台稳定性研究[C]//第十四届中国海洋(岸)工程学术讨论会论文集.呼和浩特:中国海洋学会, 2009:370-374. |
| [12] |
马勇, 由世洲, 张亮, 等. 漂浮式潮流能发电装置振动与波浪响应试验研究[J].
振动与冲击, 2013, 32(2): 14–17.
MA Yong, YOU Shizhou, ZHANG Liang, et al. Tests for oscillation and wave response of a floating tidal power generation device[J]. Journal of vibration and shock, 2013, 32(2): 14–17. |
| [13] | LI Ye, ÇALIŞAL S M. A discrete vortex method for simulating a stand-alone tidal-current turbine:modeling and validation[J]. Journal of offshore mechanics and arctic engineering, 2010, 132(3): 031102. DOI:10.1115/1.4000499 |
| [14] |
郭嘉楠.竖轴潮流能水轮机转子系统动力学特性研究[D].大连:大连理工大学, 2013.
GUO Jianan. Study on dynamics of rotor system in vertical-axis tidal turbine[D]. Dalian:Dalian University of Technology, 2013. http://cdmd.cnki.com.cn/article/cdmd-10141-1013199721.htm |



