辽宁蓡窝水库位于辽阳市以东约40 km,属于大型综合利用水利工程,也是太子河流域骨干水利枢纽之一。最初水库按百年一遇洪水设计、千年一遇洪水校核[1 , 2]。1995年上游观音阁水库建成后的设计洪水标准提至300年一遇、校核洪水标准提到万年一遇。重力坝1970年开工、1974年竣工,主要由拦河坝、溢流坝、电站组成。拦河坝为混凝土重力坝,31个坝段,全长532 m、坝顶高程103.5 m、重力坝高50.3 m、坝顶宽6 m,挡水坝段长217.3 m、溢流坝段长274.2 m、电站坝段长40.5 m。溢流坝段位于拦河坝的中部,15个坝段,14个溢流表孔、6个底孔,表孔堰顶高程84.8 m、12 m×12 m弧型钢闸门控制、2×80 t固定卷扬启闭,闸墩分2个边墩、6个胖墩、7个瘦墩(胖墩与瘦墩间隔设置),6个底孔、检修门井、工作门井布置于胖墩中[1 , 2]。
重力坝裂缝较多且成因复杂。1975年大坝新建初期检测发现15个闸墩中11个出现裂缝且裂缝存在闸墩两侧并呈对称分布特征。运行期产生了较多新裂缝,截止2009年12月累计裂缝超过800条[1 , 2]。
20世纪60年代起,全球进入人类历史以来第5个岩石圈强烈运动与地震活动期,库区未来可能发生更大的强震作用。加之库区位于具有现代活动断层特征的太子河断裂与地震带,重力坝曾遭受5.4级强震袭击,坝体发生了一定程度地震损伤[3]。而且,闸墩大量发育的各种裂缝直接危害重力坝的抗震性能。因此,立足于当前裂缝状态,开展重力坝地震反应与稳定性评价,并对坝体安全性做出合理评价。为此,针对葠窝水库混凝土重力坝,考虑现有坝体真实裂缝状况,关注库水水位变化情况,进行溢流坝段地震反应分析,考察裂缝对坝体抗震性能的影响,评价坝体的强震安全性
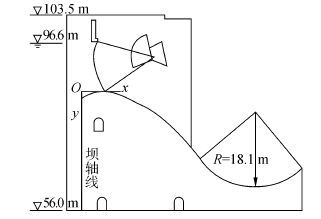
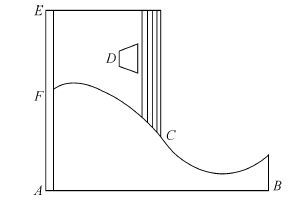
1 溢流坝段地震反应数值模型 1.1 几何模型选取葠窝水库混凝土重力坝中毗连的两个坝段作为研究对象。胖墩闸墩宽9 m(简称胖坝),瘦墩闸墩宽4 m(简称瘦坝),两者宽度均为18 m。溢流坝段的几何模型见图1。
|
| 图1 溢流坝段典型剖面图 Fig.1 Typical section of overflow dam |
模型几何参数根据《葠窝水库设计说明书》确定[2]。岩面高程56 m,堰顶高程84.8 m,坝顶高程103.5 m,溢流坝底宽60 m。滚水坝堰面曲线选用实用断面克-奥非真空曲线,溢流面曲线以1∶0.9之坡线和半径18.1 m的反弧与挑坎相接。尾部以半径18.1 m的反弧与挑坎相连,反弧半径21.1 m。挑坎高程64.5 m,挑角38°,溢流坝典型剖面见图1[2]。基岩为420 m×80 m×38 m(高度方向约坝高1.5倍,左右各取坝长2.5倍)。
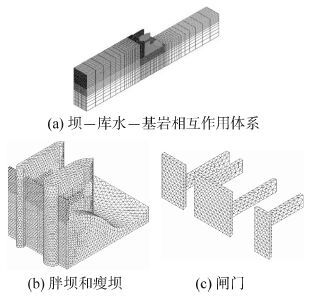
1.2 体系动力有限元模型与数值计算方法针对实际工程,建立强震下溢流坝段-库水-基岩动力相互作用分析有限元模型,见图2 。坝体和闸门有限元模型见图2 (b)。地震下,坝体与库水之间存在较强的流-固动力耦合作用。库水处理为无旋、无粘、均质的理想流体,模拟为势流体[2 , 3],并通过设置完全耦合的流-固动力耦合模型实现坝体-库水、库水-基岩的耦合作用[2]。采用瑞利阻尼( C=αM+βK,C为瑞利阻尼矩阵,M为质量矩阵,K为刚度矩阵,α、β 为系数)考虑坝体和基岩的耗能效应[2]。根据体系模态分析结果,结合线性体系识别方法,最终确定 α=0,β=1.85×10-3。
1.3 混凝土弥散裂缝本构模型采用Rashid提出的混凝土弥散裂缝本构模型[2, 4, 5, 6]。模型基于弹性损伤的概念和连续介质力学理论,描述混凝土“受拉开裂与受压等向硬化”的损伤开裂的弹塑性力学行为与动力特性。模型能够真实地刻画地震下坝体裂缝发展状态,反映坝体混凝土受压软化、受拉破坏与开裂后抗压强度、剪切刚度降低等典型动力特征。混凝土开裂破坏的具体过程:地震下混凝土单元达到开裂应力条件,单元发生开裂,裂缝均匀弥散于单元内部,整个单元进入开裂状态[2]。
|
| 图2 有限元模型 Fig.2 Finite element models |
根据已有研究坝体闸墩裂缝力学成因分析结果[1]:闸墩裂缝主要集中于牛腿上游附近的闸墩中部。为避免因坝体中无加强筋而导致不可预知的网格敏感性影响,混凝土拉伸破坏后力学行为由断裂能量破坏准则定义的“应力-位移曲线”取代“应力-应变曲线”表示,且假定混凝土因压缩破坏而导致刚度退化为零[1]。
1.4 计算参数闸门作为刚体。基岩模拟为线弹性模型。闸墩的裂缝区域,采用混凝土弥散裂缝本构模型模拟,并选用Kupfer建立的双轴压-压破坏准则[7 , 8]。
| 材料参数 | 基岩 | 混凝土 |
| 弹性模量/GPa | 1.2 | 2.8 |
| 泊松比 | 0.3 | 0.15 |
| 密度/(kg·m-3) | 2 630 | 2 500 |
| 初始压缩屈服应力/MPa | - | 13.0 |
| 最大压应力/MPa | - | 18 |
| 最大压应力对应应变 | - | 0.001 8 |
| 极限压应力/MPa | - | 10 |
| 极限压应力对应应变 | - | 0.004 |
| 最大主张应力/MPa | - | 2.0 |
| 断裂后刚度折减系数 | - | 0.000 1 |
| 断裂后剪力折减系数 | - | 0.5 |
基岩和坝体混凝土计算参数见表1,混凝土参数由现场回弹试验与室内材性试验检测结果[3 , 4]确定。库水计算参数见表2。
| 材料参数 | 取值 |
| 密度/kg·m-3 | 1 000 |
| 粘度/Pa·s | 0.001 |
| 水中纵波声速/m·s-1 | 1 483 |
| 体积模量/MPa | 23 000 |
闸门将库水压力传到牛腿上。闸门模拟为刚体,并设置整个闸门可绕连接处自由转动。相邻胖墩和瘦墩之间设置有伸缩缝,依据混凝土重力坝抗震设计规范基本假定[9],将重力坝每一段溢流坝段看作独立的悬臂结构,未施加任何边界条件。完全约束基岩底部3个方向的位移自由度;当在基岩底部沿着水平方向输入地震动时,完全释放基岩底部沿水平向的位移约束;在基岩前后侧面上,约束垂直于侧面的位移。此外,在基岩左右侧面设置粘-弹性人工边界[10],合理考虑基岩辐射阻尼效应。
水库边界分3种情况[2]:
1)库水表面。库水表面假定为自由水面:
p=0
(1)
2)坝体、基岩与库水接触面。这些面模拟为流-固耦合面,需要满足:
∂p/∂n=-ρün
(2)
3)其他三面。其他面处理为无限远边界面。依据无反射 Sommerfeld 辐射条件,得到
∂p/∂r=-1/c·∂p/∂t
(3)
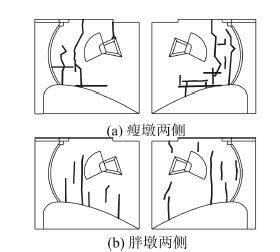
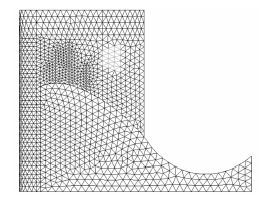
根据已有研究与现场调查[1 , 2],溢流坝典型坝面胖坝和瘦坝的闸墩裂缝分布见图3。为此,确定了3条控制性裂缝,见图4。
考虑坝体中实际存在的裂缝状态措施为[3]:将坝体中裂缝区取宽为10 cm(含裂缝宽度及周围影响区域总宽度)的长带状区域,采用薄层单元模拟,并确保裂缝区与周围混凝土之间具有连续性;然后,采用分离式裂缝单元剖分裂缝区域,单元宽度为3 mm;最后,设置出现裂缝后的混凝土弹性模量有所降低,且裂缝区混凝土弹性模量 E 与混凝土抗拉强度 ft 、网格单元的等效宽度 h 与断裂能 E 之间存在关系[2]:
$$E = {{f_t^2h} \over {2G}}$$
(4)
$$E = {{{f_t}h} \over w}$$
(5)
|
| 图3 闸墩裂缝分布示意图 Fig.3 Actual cracking on the spillway pier |
|
| 图4 有限元模型中闸墩混凝土裂缝分布 Fig.4 Concrete’s cracking in finite element modeling |
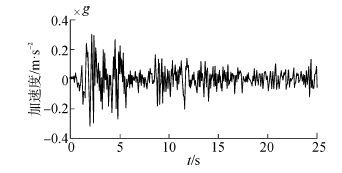
选取经典的El Centro(N-S)波作为沿着顺河向的基岩地震输入,峰值0.319g,加速度时程见图5。随后,考虑3种水位情况:高库水位:库水深39 m,用于表示水库丰水期水位;低库水位:库水深度20 m ,描述水库枯水期的水位;空库,相当于不考虑库水、坝体之间不存在流固耦合效应。
|
| 图5 El Centro波加速度时程 Fig.5 Time history of El Centro record |
图6表示坝体的关键部位: A~F 点分别为坝踵、坝趾、闸墩与溢流坝段面交汇处、闸门与坝体交汇处(牛腿)、坝顶,及迎水面中部。这些部位易发生应力集中现象。
|
| 图6 混凝土重力坝关键部位 Fig.6 Key positions in concrete gravity dam |
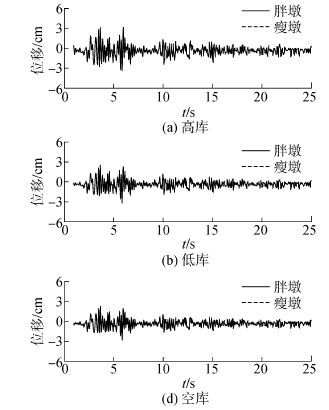
不同库水条件下胖墩、瘦墩坝顶( E 点)位移时程分别见图7(位移向上游一侧为正值,向下游一侧为负值)。可见,3种库水水位条件下,胖墩与瘦墩 E点动位移反应中曲线形状、峰值时刻及衰减规律基本保持一致。3.5~6.0 s 时段内,不同库水条件下坝体位移反应较其他时段反应要大,坝体处于最不利状态。E点峰值位移反应滞后地震波峰值发生时刻(2.2 s),并在5.9 s 时刻附近出现位移反应第2峰值,随后E点位移反应逐渐减弱且趋于稳定。高库水位下E点动位移最大,空库时E点峰值动位移最小,更多因库水与坝体动力耦合作用所致。[11]
|
| 图7 闸墩顶部动位移时程 Fig.7 Displacement time histories at the top of overflow dam under various water levels |
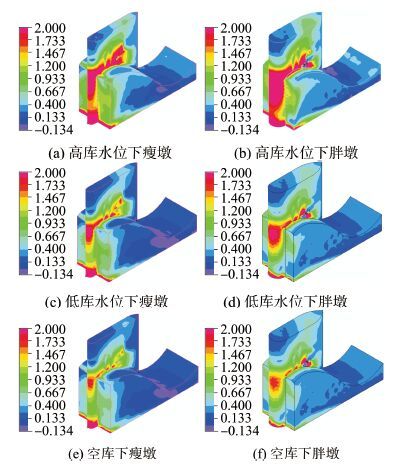
计算中,先获得大坝初始应力,即为坝体自重应力(即静应力)。随后,随时地震波进行坝体的地震反应分析,获得3种库水条件下胖墩和瘦墩第一主应力云图分别见图8。
|
| 图8 输入和输出的自功率谱 Fig.8 Power spectrums of input and output |
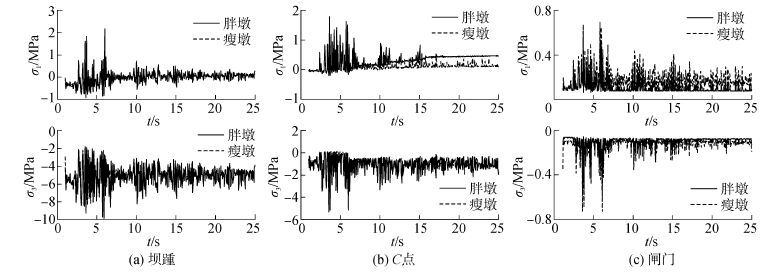
高库水条件下闸墩(胖墩、瘦墩)主应力时程分别见图9,其中,第一和第三主应力采用 σ1和σ3 表示。高库水位下,胖墩坝踵区拉应力6.02 s达到峰值2.15 MPa、压应力5.9 s达到峰值-9.93 MPa,瘦墩坝踵区拉应力6.02 s达到峰值2.09 MPa、压应力5.9 s达到峰值-9.88 MPa。闸墩与溢流堰交汇区,胖墩拉应力3.62 s达到峰值1.78 MPa、压应力3.54 s达到峰值-5.39 MPa,瘦墩拉应力3.62 s达到峰值1.73 MPa、压应力3.54 s达到峰值-4.5 MPa。
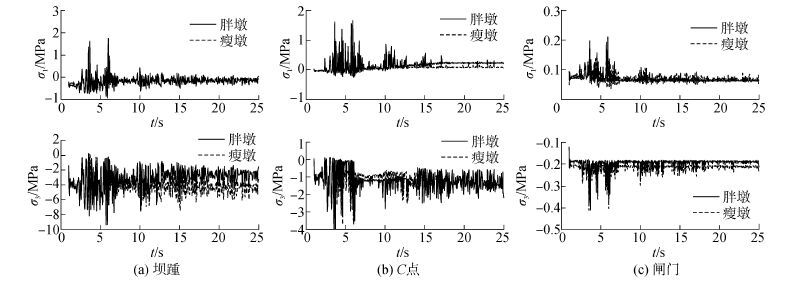
低库水条件下闸墩(胖墩、瘦墩)主应力时程分别见图10。低库水位条件下,胖墩坝踵区拉应力6.02 s达到峰值1.72 MPa、压应力5.74 s达到峰值-9.45 MPa,瘦墩坝踵区拉应力3.7s达到峰值1.62 MPa、压应力5.74 s达到峰值-9.26 MPa;胖墩闸墩与溢流堰交汇区峰值拉应力1.65 MPa、峰值压应力-4.9 MPa,瘦墩闸墩与溢流堰交汇区峰值拉应力1.51 MPa、峰值压应力-3.9 MPa。
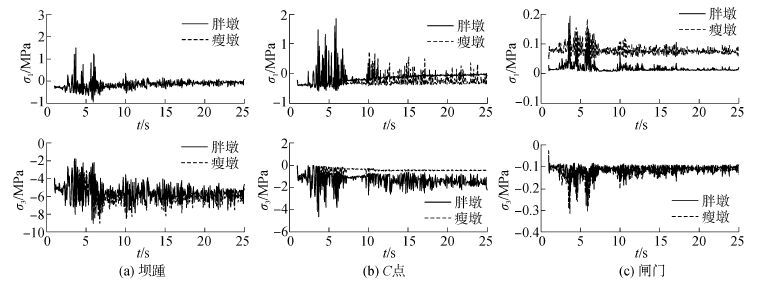
空库条件下闸墩(胖墩、瘦墩)主应力时程分别见图11。空库条件下,胖墩坝踵区拉应力在3.7 s时达到峰值1.46 MPa、压应力在5.94 s达到峰值-8.87 MPa,瘦墩的坝踵区拉应力在3.7 s达到峰值1.36 MPa、压应力5.9 s达到峰值-8.68 MPa;胖墩在闸墩与溢流堰交汇区峰值拉应力1.62 MPa、峰值压应力-4.66 MPa,瘦墩闸墩与溢流堰交汇区峰值拉应力1.49 MPa、峰值压应力-3.72 MPa。可见,地震下库水与坝体之间动力耦合作用更显著,使得高库水位较低库水位和空库条件下的闸墩动应力要大。高库水位、低库水位条件下瘦墩的坝趾区出现最大拉应力,空库条件下瘦墩最大拉应力出现在溢流堰与闸墩交汇区;胖墩、瘦墩不同部位峰值张拉应力出现时刻几乎与输入地震加速度峰值或第二峰值时刻保持一致。3种水位下,胖墩与瘦墩均于6.02 s达到峰值动应力且为拉应力。坝踵区、坝趾区、闸墩与溢流堰交汇区均属于较大应力区域。
|
| 图9 高库水位下闸墩主应力时程 Fig.9 The main stress time histories of the overflow dam under high water level |
|
| 图10 低库水位下闸墩主应力时程 Fig.10 The main stress time histories of the overflow dam under low water level |
|
| 图11 空库下闸墩墩主应力时程 Fig.11 The main stress time histories of the overflow dam with fat spillway pier under empty reservoir |
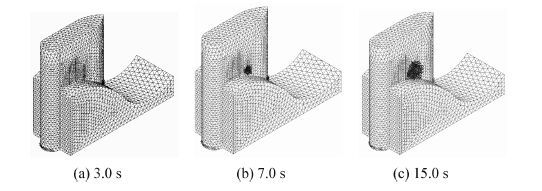
根据大坝地震应力模拟计算结果[2],高库水位条件坝体受到的地震应力较低库水位和空库条件所受的地震应力更大,因而将高库水位条件坝体地震开裂破坏过程作为分析对象。图12、图13分别给出了高库水位条件下胖墩和瘦墩地震开裂扩展过程的数值模拟结果,深黑色部分表示模拟的张开、闭合裂缝。
过去实践与研究表明,混凝土坝体基面刚度突变部位与上游、下游坝面坡折部位等区域均易出现较大拉应力(应力集中),这些区域属于坝体抗震薄弱部位。但是,由于模拟的坝体(胖墩与瘦墩)为已有先存裂缝(有的为贯通性裂缝)的旧坝,强震下容易在先存裂缝的两端产生高应力集中,使得这些先存裂缝进一步延伸扩展,并且在先存裂缝区域也易产生新的地震裂缝,故此胖墩、瘦墩地震开裂部位与过程的模拟结果并非上述的坝体基面刚度突变部位、上游坝面坡折部位、下游坝面坡折部位等区域,而是先存裂缝区域。由图12、13且结合坝体裂缝现场调查结果可见:强震下,首先在闸墩先存裂缝基础上发生开裂破坏(先存裂缝进一步延伸扩展,并在先存裂缝区产生新裂缝),随后裂缝迅速向四周扩展,约在地震输入3.5~5.0 s出现较大的裂缝区域且裂缝扩展至整个坝体厚度1/2左右,超过5.0 s裂缝区域快速扩展且发生严重贯通破裂。这主要由于闸墩因发育较多先存裂缝且混凝土老化、结构劣化而显著降低整体刚度、消弱局部强度、增大了地震反应,从而导致强震下闸墩很快发生开裂与裂缝快速扩展现象,由此造成坝体处于强震不安全状态[12]。
|
| 图12 强震下胖坝裂缝产生与发展过程 Fig.12 Generation and development of cracking at the overflow dam with fat spillway pier under strong earthquake |
|
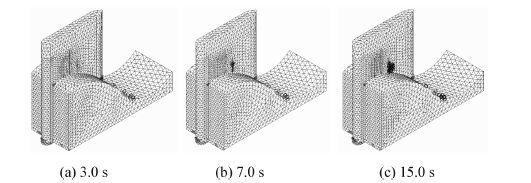
| 图13 强震下瘦坝裂缝产生与发展过程 Fig.13 Generation and development of cracking at the overflow dam with thin spillway pier under strong earthquake |
1)以实际的裂缝状态下的坝体(胖墩-瘦墩坝段,含溢流堰)为研究对象,考虑高库、低库、空库3种水位条件,采用“势流体”模拟库水,选择混凝土弥散裂缝本构模型模拟强震下坝体裂缝产生与破坏过程,借助流-固动力耦合分析的动力有限元方法,建立坝体-库水-基岩地震相互作用的三维动力有限元数值模型,输入水平0.319 g El Centro波,分析强震下溢流坝段动位移反应、应力反应与地震破坏过程,适当评价大坝强震安全性。
2)闸墩裂缝显著影响大坝(溢流坝段)地震反应与抗震安全性,主要对闸墩地震动位移与地震应力具有一定放大作用。强震中,胖坝、瘦坝中裂缝区域为坝体的薄弱部位,不仅使整个墩体地震变形大,而且在裂缝两端因发生高应力集中而导致裂缝快速扩展延伸,并且在先存裂缝区域更易产生新的地震裂缝,各种裂缝迅速向四周扩展且形成严重的贯通性裂缝,最终导致坝体开裂破坏,由此造成坝体处于强震不安全状态。
3)胖墩、瘦墩地震开裂部位与过程的模拟结果并非通常认为的坝体基面刚度突变部位、上游坝面坡折部位、下游坝面坡折部位等,而是先存裂缝区域。由于先存裂缝影响,坝踵区、坝趾区、牛腿区、闸墩与溢流堰交汇区均易产生新的地震裂缝而发生开裂破坏。
| [1] | 张东宇. 辽宁葠窝水库溢流坝段闸墩裂缝力学成因分析[D]. 哈尔滨:哈尔滨工业大学, 2012:46-48. HANG Dongyu. Mechanical reason analysis for crack on spillway pier of overflow dam in Shenwo reservoir, Liaoning[D]. Harbin:Harbin Institute of Technology, 2012:46-48. |
| [2] | 宋曰良. 辽宁葠窝水库溢流坝段裂缝状态下地震反应分析[D]. 哈尔滨:哈尔滨工业大学, 2013:35-38. SONG Yuliang. Seismic response of overflow dam with cracks in Shenwo reservoir, Liaoning[D]. Harbin:Harbin Institute of Technology, 2013:35-38. |
| [3] |
白象忠, 郝亚娟. 非线性流体弹性力学研究进展[J]. 力学进展, 2008, 38(5):545-560. BAI Xiangzhong, HAO Yajuan. Advances in nonlinear hydroelasticity[J]. Advances in Mechanics, 2008, 38(5):545-560. |
| [4] | 李正, 李忠献. 一种修正的混凝土弹性损伤本构模型及其应用[J]. 工程力学, 2011, 28(8):145-150.LI Zheng, LI Zhongxian. A modified elastic damage constitutive model of concrete and its applications[J]. Engineering Mechanics, 2011, 28(8):145-150. |
| [5] | 侯艳丽, 周元德, 张楚汉. 用3D离散元实现Ⅰ/Ⅱ型拉剪混合断裂的模拟[J]. 工程力学, 2007, 24(3):1-7. HOU Yanli, ZHOU Yuande, ZHANG Chuhan. Mode Ⅰ/Ⅱ-fracture simulation of concrete based on 3D distinct element method[J]. Engineering Mechanics, 2007, 24(3):1-7. |
| [6] | 张楚汉. 论岩石、混凝土离散-接触-断裂分析[J]. 岩石力学与工程学报, 2008, 27(2):217-235. ZHANG Chuhan. Discrete-concrete-fractural analysis of rock and concrete[J]. Chinese journal of Rock Mechanics and Engineering, 2008, 27(2):217-235. |
| [7] |
覃丽坤, 宋玉普, 陈浩然, 等. 高温后混凝土在双轴拉压下的强度和变形试验研究[J]. 工程力学, 2006, 23(1):112-116. QIN Likun, SONG Yupu, CHEN Haoran, et al. Experimental study of strength and deformation of concrete under biaxial tension-compression stress after high temperature[J]. Engineering Mechanics, 2006, 23(1):112-116. |
| [8] | 何振军, 宋玉普. 高温后高强高性能混凝土双轴压力学性能[J]. 力学学报, 2008, 40(3):364-374.HE Zhenjun, SONG Yupu. Mechanical properties of plain high-strength high-performance concrete under biaxial compression after exposure to high temperatures[J]. Chinese Journal of Theoretical and Applied Mechanics, 1900, 40(3):364-374. |
| [9] | 中华人民共和国水利部. SL 319-2005, 混凝土重力坝设计规范[S]. 北京:中国水利水电出版社, 2005. |
| [10] | 刘晶波, 王振宇, 杜修力, 等. 波动问题中的三维时域粘弹性人工边界[J]. 工程力学, 2005, 22(6):46-51.LIU Jingbo, WANG Zhenyu, DU Xiuli, et al. Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems[J]. Engineering Mechanics, 2005, 22(6):46-51. |
| [11] | EMAMZADEH S S, AHMADI M T, MOHAMMADI S, et al. Dynamic adaptive finite element analysis of acoustic wave propagation due to underwater explosion for fluid-structure interaction problems[J]. Journal of Marine Science and Application, 2015, 14(3):302-315. |
| [12] | BAI Xu, SUN Liping, QIN Wei, et al. Strength reliability analysis of stiffened cylindrical shells considering failure correlation[J]. Journal of Marine Science and Application, 2015, 13(1):49-54. |



