2. 大连理工大学 工业装备与结构分析国家重点实验室 工程力学系, 辽宁 大连 116024;
3. 中国船舶科学研究中心, 江苏 无锡 214082
2. State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics, Dalian University of Technology, Dalian, 116024, China;
3. China Ship Scientific Research Center, Wuxi, 214082, China
半潜平台(semi-submersible)是开采3 000 m水深石油资源的重要装备,其结构设计必须保证其在整个使用期的绝对安全[1-2]。上述严格的使用要求使得在设计半潜钻井平台时必须同时考虑以下3个方面:1)高精度的三维建模方法;2)考虑实体模型在不同波浪方向和频率作用下的水动力响应和波浪力计算方法[3-9];3)基于实体模型的全船有限元分析方法[11-13]。
进行全船结构有限元分析的前提是准确预报作用在海工结构物湿表面下的流体压力分布包括静水压力和运动响应引起的波浪压力,这些分布力需要准确投影到进行结构分析的有限元模型上。
半潜平台是一个复杂的空间结构,在波浪的作用下其六个方向的刚体运动都很明显,在计算波浪压力分布时,需要同时考虑半潜平台的辐射运动和绕射运动的影响,是一个极为复杂的大规模数值分析系统[14]。基于波浪辐射和绕射理论的边界元方法[15]是目前求解海洋工程波浪与结构物相互作用的重要方法,为了获得良好的考虑不同波向和频率作用下半潜平台波浪压力分布的稳定数值解,研究中采用了高阶边界元方法并考虑了物体的几何对称性[16-17]。
目前较先进的有限元建模软件包括GAMBIT, MSC Pastran和ANASYS等,这些软件可以根据不同的流体计算和结构分析的要求构建复杂的有限元模型;本研究中首次将半潜平台有限元建模、运动参数计算以及边界元数据输出统一成一个完整体系,同时发展了一个重要的新手段就是在半潜平台的几何奇异点处(角点或者物体表面相交的直角边处)按照几何连续性和物理连续性的概念布置双重和多重节点,在该位置处的节点具有不同的法向导数、属于不同的单元,但具有共同的位置坐标和速度势。数值实践表明,该方法极大的提高了波浪压力分析的准确性和数值稳定性,上述方法是实现半潜平台这种复杂空间结构波浪压力高精度结果的重要保证[18]。本文依据波浪辐射、绕射理论,通过有限元模型发展了新的边界元分析几何数据模型,同时引入高阶边界元方法对半潜平台湿表面的动波压力进行了研究。
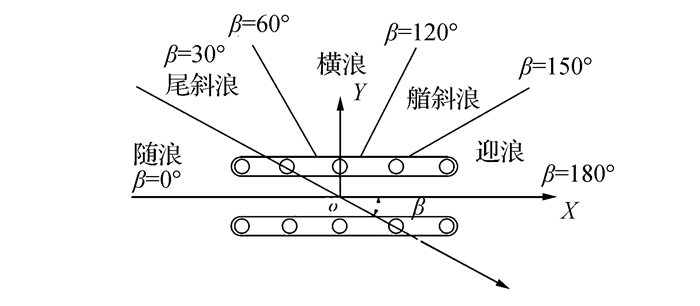
1 边界值问题 1.1 波浪辐射绕射基本理论定义如图 1所示笛卡尔坐标系,该坐标系相对于无扰动的自由表面和物体处于静止状态,原点取在自由表面上,z轴垂直向上为正。假定流体为无粘性、不可压缩并且运动是无旋的,则流体速度可表示为速度势Φ的梯度。在波浪作用下,半潜平台的运动可假定为一个简谐振荡系统,流体由于半潜平台的摇荡运动产生的速度势可设为Φ=Re(Φe-iωt),式中Re表示实部,ω为入射波浪频率,t为时间,Φ为与时间变量无关的空间速度势,一般也为复数。这样所有的边界值问题都可以用复速度势Φ来表示,最后的计算结果为复数变量与时间因子e-iωt的乘积。
|
| 图1 半潜平台计算示意图 Figure 1 Calculation sketch of Semi-submersible |
速度势Φ的求解为定常问题,在整个流体域内也满足拉普拉斯方程。
| $ {{\nabla }^{2}}\mathit{\Phi} =0 $ | (1) |
线性化的自由表面条件为
| $ {{\mathit{\Phi} }_{Z}}-K\mathit{\Phi} =0,z=0 $ | (2) |
式中:K=ω2/g为深水波数, g为重力加速度。波浪入射速度势可表示为
| $ {{\mathit{\Phi} }_{I}}=\frac{igA}{\omega }\frac{\cosh \left[ k\left( z+H \right) \right]}{\cosh kh}{{\text{e}}^{-\text{i}k\left( x\cos \beta +y\sin \beta \right)}} $ | (3) |
式中:A为入射波浪振幅,H为水深,β为入射波浪传播方向与x轴正向的夹角; 波数k为散射方程
| $ \left\{ \begin{align} & \mathit{\Phi} ={\mathit{{\Phi }}_{R}}+{\mathit{{\Phi }}_{S}} \\ & {{\mathit{\Phi} }_{R}}=-\text{i}\omega \sum\limits_{j=1}^{6}{{{\xi }_{j}}{{\mathit{\Phi} }_{j}}} \\ & {{\mathit{\Phi} }_{S}}={{\mathit{\Phi} }_{I}}+{{\mathit{\Phi} }_{D}} \\ \end{align} \right. $ | (4) |
式中:散射势(ΦS)包含入射势(ΦI)和绕射势(ΦD);ξj表示物体做辐射运动时在6个刚体自由度方向上的复数振幅;Φj为单位速度辐射势,ΦD为入射势作用在固定物体上时产生的绕射势。在静平衡位置上做简谐摇荡运动的物体,其边界条件一般可由总速度势的各个分量表示,其中辐射势和散射势应满足以下边界条件:
| $ \left\{ \begin{align} & {{\mathit{\Phi} }_{jn}}={{n}_{j}} \\ & {{\mathit{\Phi} }_{Sn}}=0 \\ \end{align} \right. $ | (5) |
(n1, n2, n3)=n, (n4, n5, n6)=x×n, x=(x, y, z),单位向量n沿法线方向指向物面为正,x为物面坐标。同时辐射速度势Φj(j=1, …, 6)和绕射势ΦD还必须满足波浪在无限远处传播的辐射条件:
| $ \left\{ \begin{align} & \underset{R\to \infty }{\mathop{\lim }}\,\sqrt{R}\left( \frac{\partial {{\mathit{\Phi} }_{j}}}{\partial R}-\text{i}k{{\mathit{\Phi} }_{j}} \right)=0 \\ & \underset{R\to \infty }{\mathop{\lim }}\,\sqrt{R}\left( \frac{\partial {{\mathit{\Phi} }_{D}}}{\partial R}-\text{i}k{{\mathit{\Phi} }_{D}} \right)=0 \\ \end{align} \right. $ | (6) |
总波压力$\mathop P\limits^ -$为:
| $ \begin{matrix} \overline{p}=-\rho gz-\rho \frac{\partial \left( \mathit{\Phi} {{\text{e}}^{-\text{i}\omega t}} \right)}{\partial t}=-\rho gz+\text{i}\rho \omega \mathit{\Phi} {{\text{e}}^{-\text{i}\omega t}}= \\ \ \ {{P}_{0}}+P{{\text{e}}^{-\text{i}\omega t}}={{P}_{0}}+\left( {{P}_{S}}+{{P}_{R}} \right){{\text{e}}^{-\text{i}\omega t}} \\ \end{matrix} $ | (7) |
式中:P0为静压,P为动压,而散射波压力PS为
| $ {{P}_{S}}=\text{i}\rho \omega \left( {{\mathit{\Phi} }_{I}}+{{\mathit{\Phi} }_{D}} \right) $ | (8) |
辐射波浪力PR为
| $ {{P}_{R}}=\text{i}\rho \omega \left( -\text{i}\omega \sum\limits_{j=1}^{6}{{{\xi }_{j}}{{\mathit{\Phi} }_{j}}} \right)=\rho {{\omega }^{2}}\sum\limits_{j=1}^{6}{{{\xi }_{j}}{{\mathit{\Phi} }_{j}}} $ | (9) |
上述关于物体表面的辐射和散射速度势的边界值问题(1)~(6)可通过格林定理在物面边界上建立积分方程式的方法求解。其中物面上的辐射势满足的积分方程为:
| $ \begin{matrix} {{\mathit{\Phi} }_{j}}\left( {{r}_{0}} \right)\left[ 1-K\int\limits_{{{S}_{{{f}'}}}}{G\text{d}s} \right]+ \\ \iint_{{{S}_{b}}}{\left[ {{\mathit{\Phi} }_{j}}\left( r \right)-{{\mathit{\Phi} }_{j}}\left( {{r}_{0}} \right) \right]}\frac{\partial G\left( r;{{r}_{0}} \right)}{\partial n}\text{d}s\text{=}\iint_{{{S}_{b}}}{{{n}_{j}}G\left( r;{{r}_{0}} \right)\text{d}s} \\ \end{matrix} $ | (10) |
而散射势满足的积分方程为
| $ \begin{matrix} {{\mathit{\Phi} }_{S}}\left( {{r}_{0}} \right)\left[ 1-K\int\limits_{{{S}_{{{f}'}}}}{G\text{d}s} \right]+ \\ \iint_{{{S}_{b}}}{\left[ {{\mathit{\Phi} }_{S}}\left( r \right)-{{\mathit{\Phi} }_{S}}\left( {{r}_{0}} \right) \right]}\frac{\partial G\left( r;{{r}_{0}} \right)}{\partial n}\text{d}s\text{=}\iint_{{{S}_{b}}}{{{\Phi }_{I}}\left( {{r}_{0}} \right)} \\ \end{matrix} $ | (11) |
式中:r=(x, y, z)表示域点, r0(ξ, η, ζ)表示源点, Sf'为物体内部水线面,Sb表示物体在静水中的湿表面,K为深水波数,格林函数G(r; r0)指的是波浪脉动源,它表示位于r0点的单位强度点源在r点处产生的速度势。格林函数满足自由表面和远场的波浪辐射条件,有限水深时格林函数可定义为:
| $ \begin{matrix} \ G\left( r;{{r}_{0}} \right)=-\frac{1}{4\text{ }\!\!\pi\!\!\text{ }}\left[ \frac{1}{r}+\frac{1}{{{r}''}}+ \right. \\ 2\int_{0}^{\infty }{\left. \frac{\left( k+K \right)\cosh k\left( z+H \right)\cos k\left( \zeta +H \right)}{k\sinh kH-K\cosh kH}{{\text{e}}^{-kH}}{{\text{J}}_{0}}\left( kR \right)\text{d}k \right]} \\ {{\left( {{r}''} \right)}^{2}}={{\left( x-\xi \right)}^{2}}+{{\left( y-\eta \right)}^{2}}+{{\left( z+\zeta +2H \right)}^{2}} \\ \end{matrix} $ | (12) |
式中:J0为零阶贝塞尔函数,k的积分路径取k值在实轴上的实根上半部分,从而满足波浪的远场辐射条件。格林函数的具体求解方法见文献[19]。
1.3 节点重置方法及方程离散求解半潜平台的空间结构是非常复杂的,当采用边界元方法求解时,针对半潜平台在面-面相交形成的大范围的直角边和角点的情况,研究中采用在该几何奇异位置布置双重和多重节点的方法,例如在原来直角边的一个控制点处再增加一个控制点,变成直角边同一位置具有两个控制点,对于三个面构成的角点位置可以增加两个控制点,变成三个控制点。这些新的节点具有相同的空间坐标和速度势,但是具有不同的法向导数并且属于不同的单元。同时研究中采用6节点三角形单元和8节点四边形单元对半潜平台湿表面进行剖分。与重节点方法相匹配,在进行高阶单元网格剖分时,单元不能跨越奇异边界和节点,必须逐面剖分[20]。由于半潜平台具有两个对称面,研究中引入了几何对称性的方法,提高了计算精度和矩阵的组装时间。空间复杂结构的波浪漂流力计算在短波时会有数值不稳定现象出现,研究中采用了Gauss直接方法求解高频波浪问题,而在其它波浪频率内采用LU分解方法。
2 半潜平台波浪压力分布研究波浪压力分布研究半潜平台是由立柱和浮箱组成的,长宽比适中具有透空间隔的极为复杂的三维大型结构物,它通常具有两个对称面(关于x和y轴对称)。研究中根据其几何对称性的特征,在迎浪β=180°至横浪β=90°的第一象限波浪入射区域内,沿15°角的间隔共假定了7个方向的波浪入射,在每个波浪入射方向上考虑了21个波浪频率,频率间隔为Δω=0.05 rad/s,这样的计算体系能够完全涵盖半潜平台的所有方向。表 1为研究中采用的ISSC型半潜平台的基本设计和工作参数,其中半潜平台各立柱的位置坐标如表 2所示。
| 参数 | 数值 |
| 排水量/m3 | 142 495.57 |
| 立柱间距/m | 60 |
| 立柱半径/m | 8 |
| 立柱高度/m | 20 |
| 箱体长度/m | 260 |
| 箱体宽度/m | 20 |
| 箱体高度/m | 10 |
| 箱体轴线间距/m | 80 |
| 平台吃水/m | 30 |
| 垂向重心距自由水面高度/m | 5.96 |
| 横向水平重心距船艏距离/m | 130 |
| 纵向重心距立柱中轴线距离/m | 40 |
| 纵摇惯性半径/m | 69.9 |
| 横摇惯性半径/m | 42.2 |
| 艏摇惯性半径/m | 69.9 |
| 工作水深/m | 325 |
| 名称 | X/m | Y/m | 名称 | X/m | Y/m |
| A1 | 120 | 40 | B1 | 120 | -40 |
| A2 | 60 | 40 | B2 | 60 | -40 |
| A3 | 0 | 40 | B3 | 0 | -40 |
| A4 | -60 | 40 | B4 | -60 | -40 |
| A5 | -120 | 40 | B5 | -120 | -40 |
本研究首先利用Gambit软件对半潜平台进行三维实体建模和网格剖分,并通过自主开发的fortran算法对Gambit所输出的三维体网格进行处理,以形成边界元计算所需的经双重及多重节点重置得到的结构湿表面网格,之后通过自有的边界元计算算法[21-23]对半潜平台波动压力进行计算。
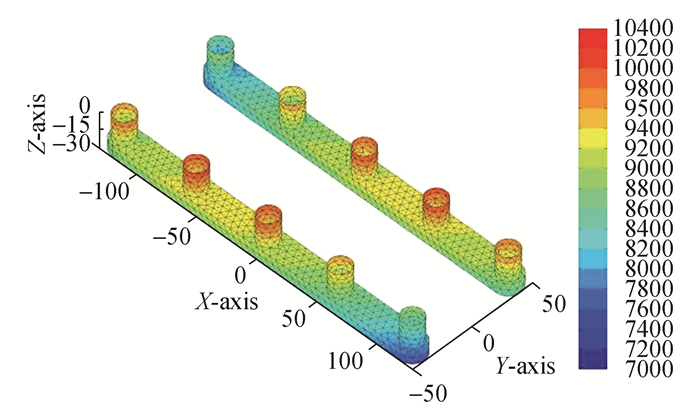
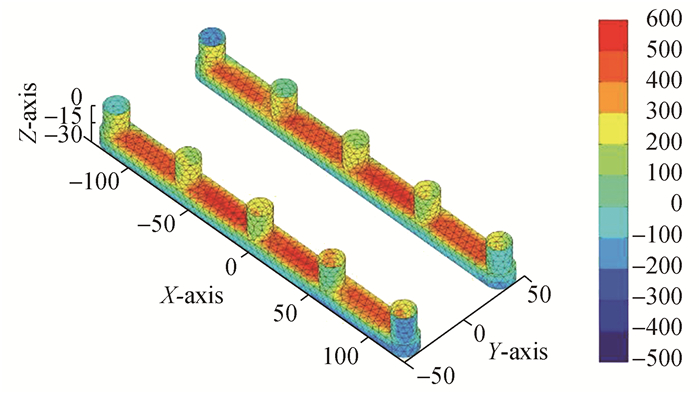
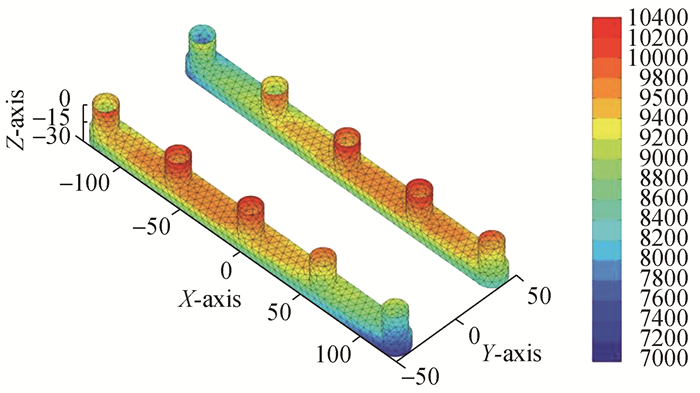
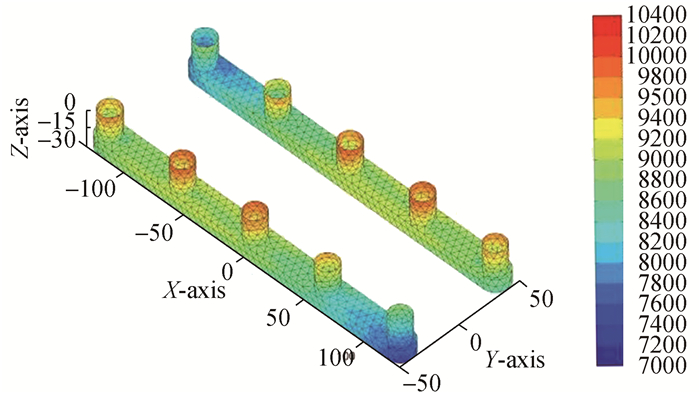
研究中选取了对运动响应和波浪力影响明显的波浪频率ω=0.2、0.9 rad/s以及波向β=135°、180°进行了比较分析。图 2~5为ω=0.2 rad/s, β=135°、图 6~9为ω=0.2、0.9 rad/s, β=180°时入射势(ΦI)、绕射势(ΦD)、散射势(ΦS)及总速度势(Φ)产生的动压分布图。由图 2~5可以发现,在长波ω=0.2rad/s及首斜浪β=135°情况下,总速度势产生的动压主要由入射势决定。总速度势(Φ)及入射势(ΦI)产生的动压均为正值,在立柱A2, A3及B3, B4处最大,其中入射势波压在立柱近自由表面处波压为(9 800~10 400 Pa),而总速度势产生的波压在立柱近自由表面处为(9 400~9 800 Pa),入射势和总速度势产生的波压在A5, B1处最小,沿浮箱底部至立柱,波压力变化范围为(7 600~8 800 Pa)。绕射势(ΦD)产生的波压最小并且有负压区产生,负压区主要分布在浮箱的底部、侧面以及立柱(A1, A4, A5)以及(B1, B2, B5)的背浪面。绕射势产生的最大正压区位于浮箱顶部,数值区间为(400~600 Pa),其余正压区位于立柱A3及B3表面及以其为中心的外传波浪与其他圆柱的迎浪面,数值区间为(100~300 Pa)。
|
| 图2 入射势产生的动压分布ΦI:ω=0.2 rad/s, β=135° Figure 2 Dynamic pressure distribution of incident potential ΦI:ω=0.2 rad/s, β=135° |
|
| 图3 绕射势产生的动压分布ΦD:ω=0.2 rad/s, β=135° Figure 3 Dynamic pressure distribution of diffraction potential ΦD:ω=0.2 rad/s, β=135° |
|
| 图4 散射势产生的动压分布ΦS:ω=0.2rad/s, β=135° Figure 4 Dynamic pressure distribution of scattering potential ΦS:ω=0.2 rad/s, β=135° |
|
| 图5 总速度势产生的动压分布Φ=ΦS+ΦR:ω=0.2 rad/s, β=135° Figure 5 Dynamic pressure distribution of total velocity potential Φ=ΦS+ΦR:ω=0.2 rad/s, β=135° |
|
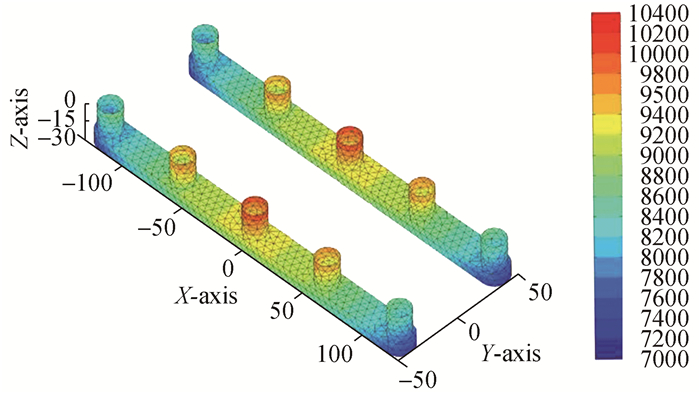
| 图6 入射势产生的动压分布ΦI:ω=0.2 rad/s, β=180° Figure 6 Dynamic pressure distribution of incident potential ΦI:ω=0.2 rad/s, β=180° |
|
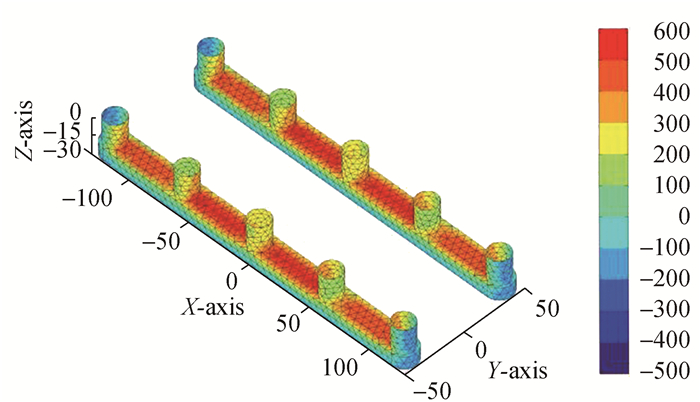
| 图7 绕射势产生的动压分布ΦD:ω=0.2 rad/s, β=180° Figure 7 Dynamic pressure distribution of diffraction potentialΦD:ω=0.2 rad/s, β=180° |
|
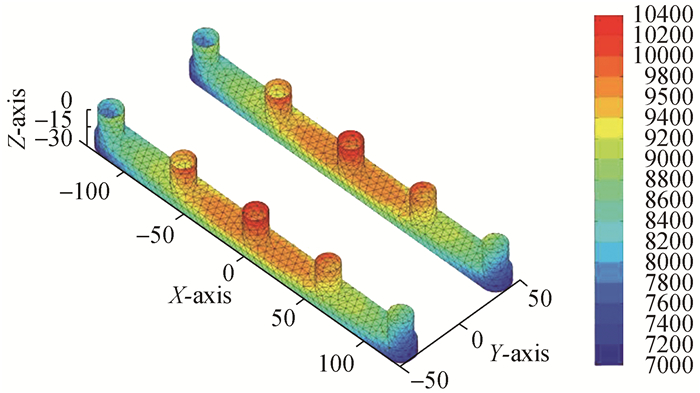
| 图8 散射势产生的动压分布ΦS:ω=0.2 rad/s, β=180° Figure 8 Dynamic pressure distribution of scattering potential ΦS:ω=0.2 rad/s, β=180° |
|
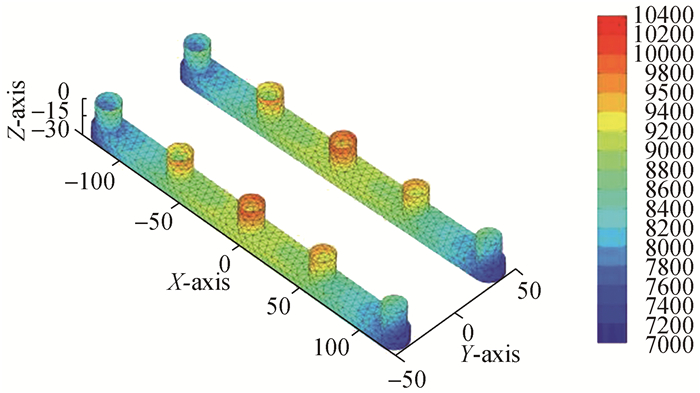
| 图9 总速度势产生的动压分布Φ=ΦS+ΦR:ω=0.2 rad/s, β=180° Figure 9 Dynamic pressure distribution of total velocity potential Φ=ΦS+ΦR:ω=0.2 rad/s, β=180° |
在迎浪β=180°情况下由图 6~9可以看到,在长波ω=0.2 rad/s时,总速度势产生的动压也是主要由入射势决定。总速度势(Φ)及入射势(ΦI)和散射势(ΦI+ΦD)产生的动压均为正值并且由于半潜平台的几何对称性,各速度势产生的压力分布也是对称的。波动压力在立柱A3及B3处最大,其中入射势波压在立柱A3及B3处为(9 800~10 400 Pa),而总速度势产生的波压在A3及B3处为(9 400~9 800 Pa)。入射势(ΦI)、散射势(ΦI+ΦD)和总速度势(Φ)产生的波压在(A1, A5), (B1, B5)处最小,沿浮箱底部至立柱,波压力变化范围为(7 000~8 400 Pa)。绕射势(ΦD)产生的波压最小并且有负压区产生,负压区主要分布在浮箱的底部、侧面以及立柱(A1, A5), (B1, B5)处,数值区间为(-500~0 Pa)。绕射势产生的最大正压区位于浮箱顶部,数值区间为(400~600 Pa),其余正压区位于立柱A3及B3表面及以其为中心的外传波浪与其余圆柱的迎浪面,数值变化区间为(200~400 Pa)。
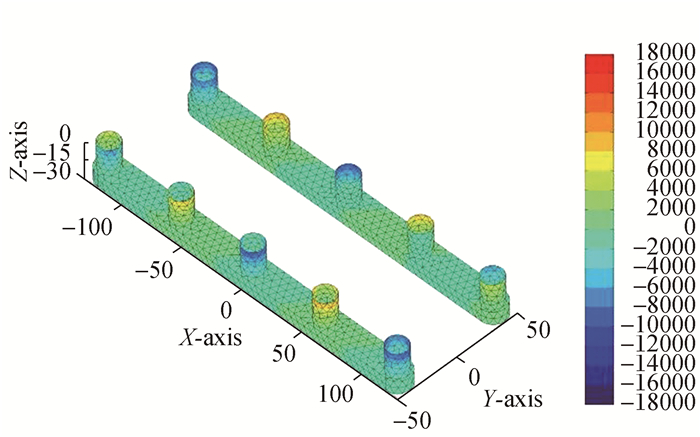
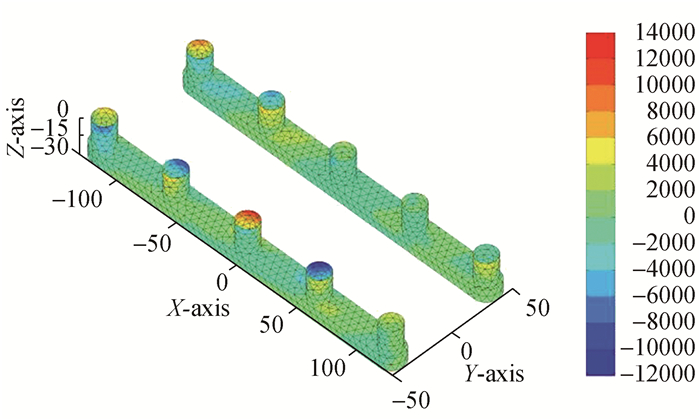
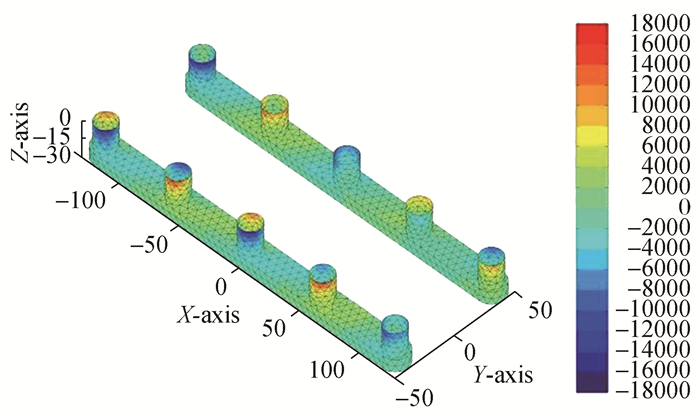
由图 10~13可以看到在首斜浪ω=0.9 rad/s, β=135°时,总速度势产生的动压主要由散射势(ΦI+ΦD)决定。总速度势(Φ)及入射势(ΦI)和散射势(ΦI+ΦD)产生的动压在半潜平台不同位置出现量级相当的正负压区域。入射势(ΦI)产生的压力变化区间(-18 000~18 000 Pa), 最大正压区位于(A2, A4), (B2, B4),而最小负压区位于(A1, A3, A5), (B1, B3)。绕射势(ΦD)产生的压力变化区间为(-12 000~14 000 Pa), 最大正压区位于(A5, A3),而最小负压区位于(B2, B4)。而总速度势(Φ)和散射势(ΦI+ΦD)产生的波压分布基本相同,在A4处均为正压,而在(A3, A1)处为负压区,在其余立柱表面会同时存在正负压分布区。总速度势(Φ)和散射势(ΦI+ΦD)在浮箱表面产生的波压力变化范围为(-400~400 Pa)。
|
| 图10 入射势产生的动压分布ΦI:ω=0.9 rad/s, β=135° Figure 10 Dynamic pressure distribution of incident potential ΦI:ω=0.9 rad/s, β=135° |
|
| 图11 绕射势产生的动压分布ΦD:ω=0.9 rad/s, β=135° Figure 11 Dynamic pressure distribution of diffraction potential ΦD:ω=0.9 rad/s, β=135° |
|
| 图12 散射势产生的动压分布ΦS:ω=0.9 rad/s, β=135° Figure 12 Dynamic pressure distribution of scattering potential ΦS:ω=0.9 rad/s, β=135° |
|
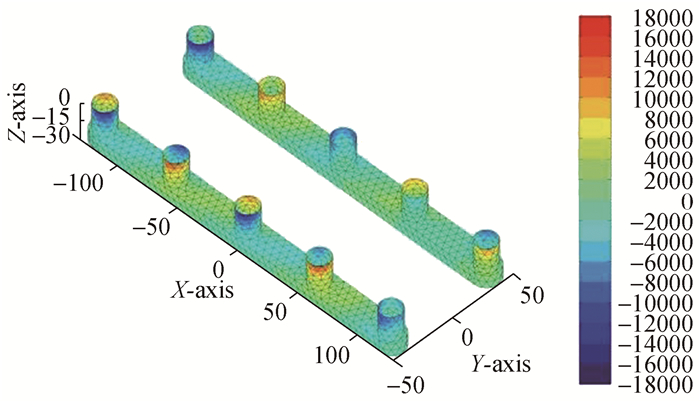
| 图13 总速度势产生的动压分布Φ=ΦS+ΦR:ω=0.9 rad/s, β=135° Figure 13 Dynamic pressure distribution of total velocity potential Φ=ΦS+ΦR:ω=0.9 rad/s, β=135° |
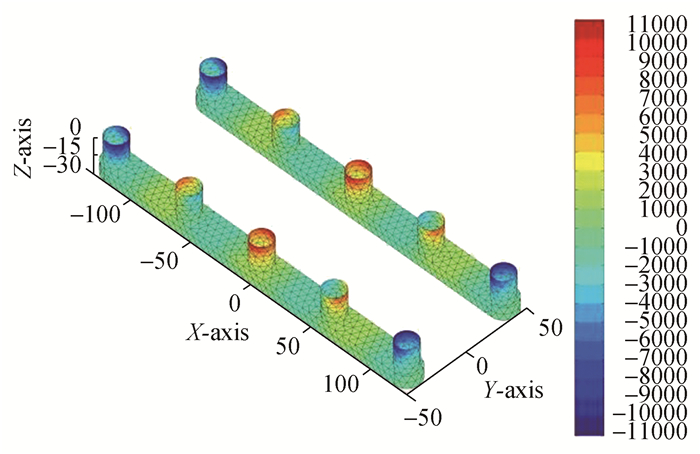
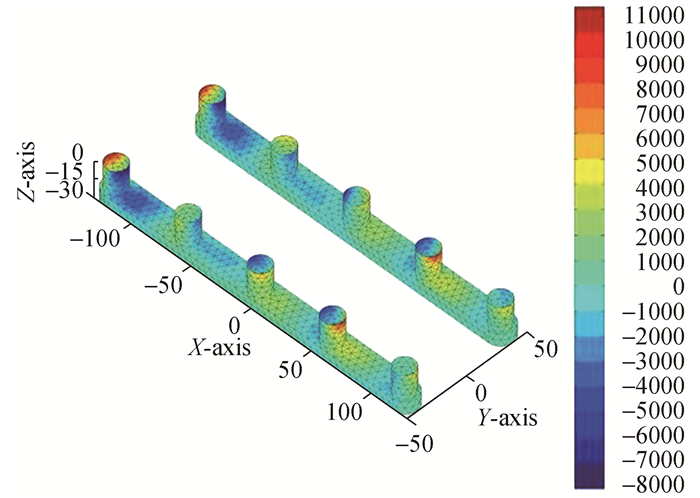
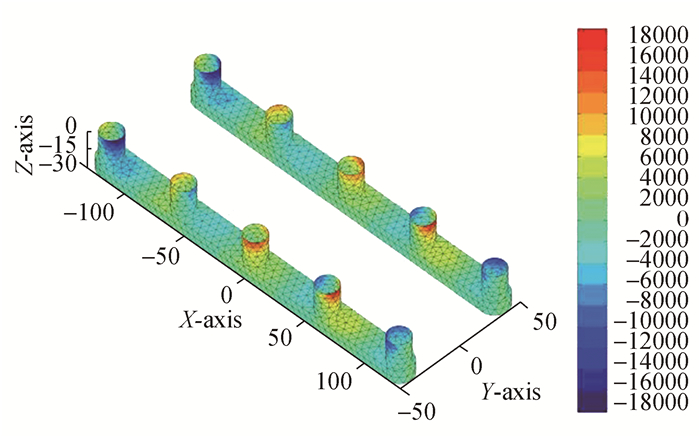
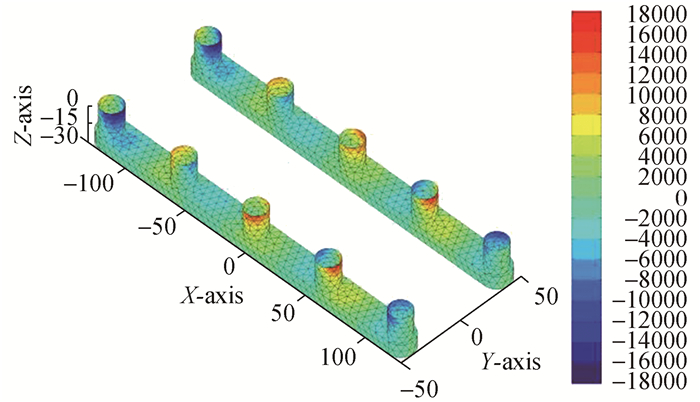
由图 14~17可以看到在迎浪ω=0.2 rad/s, β=180°时,总速度势产生的动压主要由散射势(ΦI+ΦD)决定。总速度势(Φ)及入射势ΦI和散射势(ΦI+ΦD)产生的动压在半潜平台A区及B区对称分布,正负压同时出现在不同位置但量级相当。入射势(ΦI)产生的压力变化区间(-11 000~11 000 Pa), 最大正压区位于(A1, B1),而最小负压区位于(A1, A5), (B1, B5)。绕射势(ΦD)产生的压力变化区间为(-8 000~11 000 Pa), 最大正压区和最小负压区同时位于立柱(A2, A5)和(B2, B5)处。总速度势(Φ)和散射势(ΦI+ΦD)产生的波压分布基本相同,压力变化区间为(-18 000~18 000 Pa),正压主要分布在立柱(A2, A3), (B2, B3)迎浪面,而负压区分布在(A1, B1)背浪面及(A5, B5)迎浪面。在其余立柱表面会同时存在正负压分布区。总速度势(Φ)和散射势(ΦI+ΦD)在浮箱表面靠近立柱(A5, B5)处有最小负压存在,波压变化范围为(-800~200 Pa)。
|
| 图14 入射势产生的动压分布ΦI:ω=0.9 rad/s, β=180° Figure 14 Dynamic pressure distribution of incident potential ΦI:ω=0.9 rad/s, β=180° |
|
| 图15 绕射势产生的动压分布ΦD:ω=0.9 rad/s, β=180° Figure 15 Dynamic pressure distributionof diffraction potential ΦD:ω=0.9 rad/s, β=180° |
|
| 图16 散射势产生的动压分布ΦS:ω=0.9 rad/s, β=180° Figure 16 Dynamic pressure distributionof scattering potential ΦS:ω=0.9 rad/s, β=180° |
|
| 图17 总速度势产生的动压分布Φ=ΦS+ΦR:ω=0.9 rad/s, β=180° Figure 17 Dynamic pressure distribution of total velocity potential Φ=ΦS+ΦR:ω=0.9 rad/s, β=180° |
为了提高半潜平台波压力的计算精度,本文研究中考虑了半潜平台的几何对称性并应用了双重和多重节点的重置方法去除速度势求解过程中的几何奇异性。研究发现:
1)半潜平台的波压力主要由散射势和辐射势两部分组成,其中散射势产生散射波浪力,辐射速度势所产生的动压与运动响应相关。
2)ω=0.2 rad/s时无论迎浪β=180°还是首斜浪β=135°产生的波压都是正值,而且在起控制作用的散射速度势中入射波浪速度势起决定作用,绕射势产生的波压幅值很小。
3)在ω=0.9 rad/s时迎浪β=180°和首斜浪β=135°产生的波压在半潜平台湿表面特别是立柱表面,同时出现正负压分布区域,而且量值相当。整体而言,对于双浮筒立柱结构的半潜平台,控制波浪频率在ω=0.9 rad/s附近。
| [1] |
缪泉明, 董慎言, 刘楚学. 半潜平台在波浪中的运动响应[J].
中国海洋平台, 1994(Z1): 344–356.
MIAO Quanming, DONG Shenyan, LIU Chuxue. Motion response of Semi-submersible in waves[J]. China offshore platform, 1994(Z1): 344–356. |
| [2] |
史琪琪, 杨建民. 半潜式平台运动及系泊系统特性研究[J].
海洋工程, 2010, 28(4): 1–8.
SHI Qiqi, YANG Jianmin. Research on hydrodynamic characteristics of a Semi-submersible platform and its mooring system[J]. The ocean engineering, 2010, 28(4): 1–8. |
| [3] | SÖYLEMEZ M, ATLAR M. A comparative study of two practical methods for estimating the hydro dynamic loads and motions of a Semi-submersible[J]. Journal of offshore mechanics and arctic engineering, 2000, 122(1): 57–63. DOI:10.1115/1.533726 |
| [4] | NEWMAN J N. Marine hydrodynamics[M]. Massachusetts: MIT Press, 1979 . |
| [5] | FALTINSEN O M. Sea loads on ships and offshore structures[M]. Cambridge, UK: Cambridge University Press, 1993 . |
| [6] | JOHN F. On the motion of floating bodies Ⅱ. Simple harmonic motions[J]. Communications on pure and applied mathematics, 1950, 3(1): 45–101. DOI:10.1002/(ISSN)1097-0312 |
| [7] | WEHAUSEN J V. The motion of floating bodies[J]. Annual review of fluid mechanics, 1971, 3: 237–268. DOI:10.1146/annurev.fl.03.010171.001321 |
| [8] | MEI C C. The applied dynamics of ocean surface waves[M]. London: World Scientific, 1989 . |
| [9] | NEWMAN J N, SCLAVOUNOS P D. The computation of wave loads on large offshore structures[C]//MOAN T, JANBU N, FALTINSEN O M. Conference on the Behaviour of Offshore Structures (BOSS"88). Trondheim:Tapir Publishers, 1988, 2:605-622. |
| [10] |
张少雄, 曾竞龙, 杨永谦. 某潜艇耐压壳结构强度和屈曲有限元分析[J].
海洋工程, 2004(5): 13–15.
ZHANG Shaoxiong, ZENG Jinglong, YANG Yongqian. Strength and buckling direct calculation for the pressure shell of a submarine[J]. Ship & ocean engineering, 2004(5): 13–15. |
| [11] |
朱胜昌, 陈庆强. 整船准静态分析的有限元模型自动加载及载荷修正技术[J].
船舶力学, 1999, 3(5): 47–54.
ZHU Shengchang, CHEN Qingqiang. Techniques of auto-loading and amending external node forces for whole hull model in F. E. M. strength calculation[J]. Journal of ship mechanics, 1999, 3(5): 47–54. |
| [12] | CABOS C, IHLENBURG F. Vibrational analysis of ships with coupled finite and boundary elements[J]. Journal of computational acoustics, 2003, 11(1): 91–114. DOI:10.1142/S0218396X03001821 |
| [13] |
张少雄, 杨永谦. 惯性释放在油船结构强度直接计算中的应用[J].
船海工程, 2004(4): 4–6.
ZHANG Shaoxiong, YANG Yongqian. Application of inertial relief in direct calculation of structural strength of tanker[J]. Ship & ocean engineering, 2004(4): 4–6. |
| [14] | NEWMAN J N, LEE C H. Boundary-element methods in offshore structure analysis[J]. Journal of offshore mechanics and arctic engineering, 2002, 124(2): 81–89. DOI:10.1115/1.1464561 |
| [15] | HESS J L, SMITH A M. Calculation of non-lifting potential flow about arbitrary three-dimensional bodies[J]. Journal of ship research, 1964, 8: 22–44. |
| [16] | TAYLOR R E, CHAU F P. Wave diffraction theory-some developments in linear and nonlinear theory[J]. Journal of offshore mechanics and arctic engineering, 1992, 114(3): 185–194. DOI:10.1115/1.2919970 |
| [17] | LIU Y H, KIM C H, LU X S. Comparison of higher-order boundary element and constant panel methods for hydrodynamic loadings[J]. International journal of offshore and polar engineering, 1991, 1(1): 8–17. |
| [18] |
王科, 贺大川, 张志强. 半潜式钻井平台波浪散射力与运动响应分析[J].
船舶力学, 2013, 17(5): 478–487.
WANG Ke, HE Dachuan, ZHANG Zhiqiang. Wave exciting force and motion response of Semi-submersible[J]. Journal of ship mechanics, 2013, 17(5): 478–487. |
| [19] | NEWMAN J N. Algorithms for the free-surface Green function[J]. Journal of engineering mathematics, 1985, 19(1): 57–67. DOI:10.1007/BF00055041 |
| [20] | WANG Ke, CHEN Zhi. An efficient FEM-BEM coupling method in wave radiation problem analysis of oil platforms with complicated geometry[J]. Engineering analysis with boundary elements, 2015, 58: 18–25. DOI:10.1016/j.enganabound.2015.02.011 |
| [21] |
王科, 张犀, 张志强, 等. FPSO型采油平台附加质量与阻尼力的分析研究[J].
船舶力学, 2011, 15(1/2): 40–47.
WANG Ke, ZHANG Xi, ZHANG Zhiqiang, et al. Numerical analysis of added mass and damping of FPSO type platform[J]. Journal of ship mechanics, 2011, 15(1/2): 40–47. |
| [22] |
王科, 张志强, 许旺. FPSO型采油平台波浪力与运动响应分析[J].
船舶力学, 2009, 13(5): 718–726.
WANG Ke, ZHANG Zhiqiang, XU Wang. Wave exciting force and motion response analysis of FPSO type platform[J]. Journal of ship mechanics, 2009, 13(5): 718–726. |
| [23] |
王科, 许旺. FPSO型采油平台波浪漂移力的分析研究[J].
哈尔滨工程大学学报, 2008, 29(12): 1261–1265.
WANG Ke, XU Wang. Study of wave drift forces affecting FPSO systems[J]. Journal of Harbin engineering university, 2008, 29(12): 1261–1265. |


