舰载机弹射系统是舰载机安全起飞的有力保障,目前普遍采用蒸汽弹射技术。现阶段,我国主要通过滑跃起飞方式完成舰载机出动,有关舰载机蒸汽弹射的实验和理论研究较少。
蒸汽弹射系统为弹射装置产生动力输出,它能将高温高压水蒸汽的能量可控地传给被弹射舰载机,并能通过水刹制动系统高效地吸收弹射结束时活塞的剩余动能[1]。蒸汽弹射系统主要由储汽筒、汽缸、各蒸汽管道和控制阀组成。
当前已公开的有关蒸汽弹射技术的文献资料很少,并且主要针对甲板上舰载机弹射起飞过程的研究,包括弹射拖拽动力学、起落架缓冲器突伸动力学、舰载机-舰-气流综合效应以及前起落架振动等方面[2]。C.B Lucas[3]对弹射起飞最小离舰速度限制以及滑跑过程中飞机姿态的变化进行研究。F.J Slavin[4]描述了蒸汽弹射器的结构及设计,分析了系统性能。赵险峰[5]在忽略储汽筒内闪蒸现象并在简化汽缸工作过程的前提下对舰载机弹射系统进行仿真研究。金长江等[6]研究了弹射起飞规律,对不同型号舰载机离舰后的下沉量进行了分析。Michael M. Wallace[7]对F/A-18E/F型舰载机弹射起飞的多次试验结果进行分析,得到了最小的舰载机弹射起飞速度。郑本武等[8]发现舰载机前起落架支柱的突伸对弹射起飞性能有明显影响,研究了这种情况下的弹射起飞过程。以上研究均很少涉及甲板下面的蒸汽弹射系统的工作机理和控制规律。
因此,建立一套较精确的蒸汽弹射系统模型是研究舰载机弹射起飞技术的基础。其中,汽缸负责向待起飞舰载机输出必要的弹射力,其控制效果直接影响蒸汽弹射系统性能,是蒸汽弹射系统的核心部分。但是,汽缸系统具有多输入、非线性和强耦合等特点,PID校正方法难以实现针对该系统的有效控制设计,导致发射阀开度大幅波动。本文在建立储汽筒、发射阀的数学模型,汽缸的热力学模型和舰载机六自由度运动模型的基础上,对汽缸部分进行了状态反馈线性化[9],实现汽缸有杆腔压力和活塞加速度解耦,完成蒸汽弹射系统的发射阀调节设计,以保证舰载机在规定时间和行程内获得弹射所需速度。
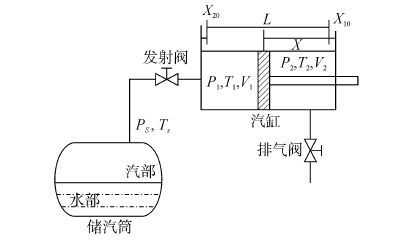
1 舰载机蒸汽弹射系统建模舰载机弹射系统主要由储汽筒、汽缸以及各蒸汽管道和控制阀组成。储存大量能量的储汽筒通过发射阀向汽缸供汽,推动汽缸活塞运动从而产生弹射力供舰载机弹射起飞。舰载机弹射系统组成如图 1所示。其中,Ps、Ts为储汽筒输出蒸汽的压力与温度,P1、T1、V1分别为汽缸有杆腔的压力、温度和体积,P2、T2、V2分别为汽缸无杆腔压力、温度和体积。X10是工作腔余隙的当量长度,X20为排气腔侧余隙的当量长度,L为活塞行程,X为活塞在t时刻时的位移量。
|
| 图1 舰载机弹射系统结构图 Figure 1 Catapult launch system structure of carrier-based aircraft |
储汽筒的结构类似于蒸汽蓄热器,是储存热水与蒸汽进行放热的定压力容器,容器的下部分为水空间,上部分为气空间[10]。其中储存着来自于增压锅炉燃烧所产生的大量蒸汽,在向汽缸放气的过程中,储汽筒内水蒸汽的质量和压力会随之下降,为了保证储汽筒出口的压力,储汽筒内会发生闪蒸现象,即高压饱和水部由于压力突然降低而迅速蒸发,补充流出的蒸汽。储汽筒内饱和水部闪蒸时满足能量守恒定律[11]:
| $\begin{align} & \Delta {{m}_{c}}{{h}_{in}}=({{m}_{v(i+1)}}{{u}_{v(i+1)}}+{{m}_{l(i+1)}}{{u}_{l(i+1)}}) \\ & -({{m}_{v(i)}}{{u}_{v(i)}}+{{m}_{l(i)}}{{u}_{l(i)}}) \\ \end{align}$ | (1) |
并且储汽筒体积恒定[11],因而有
| ${{m}_{v(i)}}{{v}_{v(i)}}+{{m}_{l(i)}}{{v}_{l(i)}}={{m}_{v(i+1)}}{{v}_{v(i+1)}}+{{m}_{l(i+1)}}{{v}_{l(i+1)}}$ | (2) |
式中:角标i、i+1分别表示闪蒸前后时刻;l、v分别表示水和水蒸汽;Δmc为闪蒸过程中充入过热蒸汽量,kg;u为单位质量的内能,kJ/kg;m为储汽筒内水或水蒸汽的质量;h为水或水蒸汽的焓值,kJ/kg;v为水或水蒸汽比容,kg/m3;V为储汽筒容积。根据热力学等熵关系:
| $C{{v}_{v(i)}}\times ln\frac{{{T}_{v(i+1)}}}{{{T}_{v(i)}}}+{{r}_{v(i)}}\times \frac{ln{{v}_{v(i+1)}}}{{{v}_{v(i)}}}=0$ | (3) |
式中:Tv为储汽筒内水蒸汽的温度;Cvv(i)为储汽筒内定容比热容;rv(i)为气体常数,在等熵过程的前后变化不大,在计算i+1时刻时储汽筒的压强仍使用i时刻的气体常数。
水蒸汽通过体积变化对外做功,传热过程[12]中的热量计算式如下:
| $Q={{U}_{i+1}}\times {{A}_{i+1}}\times ({{T}_{v(i+1)}}-{{T}_{w}})\times \Delta t$ | (4) |
式中:Ui+1为传热系数,Ai+1为储汽筒的内表面积,Tv(i+1)为储汽筒温度,Tw为储汽筒壁面温度,Δt为时间增量。
由式(5)计算热交换引起的汽体温度改变,等体积传热结束后,汽缸温度为式(6):
| $\Delta T=\frac{Q}{{{C}_{v(i+1)}}\times {{m}_{v(i+1)}}}$ | (5) |
| ${{T}_{v(i+2)}}={{T}_{v(i+1)}}+\Delta T$ | (6) |
根据等熵阶段得到储汽罐内水部的温度和压强,由IPAWS-IF97公式可得该温度、压强下的气体常数rv(i+1);考虑到质量和体积不变,比体积也取自等熵阶段,根据气体状态方程式(7),可求出储汽筒内汽部的压力变化:
| ${{p}_{v(i+2)}}\times {{v}_{v(i+1)}}={{r}_{v(i+1)}}\times {{T}_{v(i+2)}}$ | (7) |
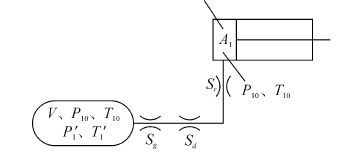
图 2为储汽筒放气模型:储汽筒容积V,初始温度T10,初始压力P10,t时刻储汽筒内温度P′1压力T′1;储汽筒出口面积Sg,气路进入汽缸前管道和空气处理元件简化面积为Sd,汽缸入口面积Sr;汽缸无杆腔初始温度和压力分别为P10、T10(常温常压)。放气过程是绝热放气,各状态量间的关系满足式(8)~(12) [13],式中:b1为临界压力比,一般取值(0.2~0.5),本文统一取0.46;Qm1为从储汽筒流入汽缸的蒸汽流量。
| $T{{\prime }_{1}}={{T}_{10}}{{\left( \frac{{{P}_{10}}}{P{{\prime }_{1}}} \right)}^{\frac{1-\kappa }{\kappa }}}$ | (8) |
| $\frac{dP{{\prime }_{1}}}{dt}=-\frac{\kappa RT{{\prime }_{1}}{{Q}_{m1}}}{V}$ | (9) |
| ${{Q}_{m1}}=\frac{SP{{\prime }_{1}}\sqrt{1-{{b}_{1}}}}{\sqrt{RT{{\prime }_{1}}}}{{\omega }_{e1}}$ | (10) |
| ${{\omega }_{e1}}=\left\{ \begin{matrix} \sqrt{1-{{\left( \frac{{{\sigma }_{1}}-{{b}_{1}}}{1-{{b}_{1}}} \right)}^{2}}~} & {{b}_{1}}~{{\sigma }_{1}}=\frac{{{P}_{1}}}{{{P}_{10}}}\le 1 \\ 1 & {{\sigma }_{1}}=\frac{{{P}_{1}}}{{{P}_{10}}}\le {{b}_{1}} \\ \end{matrix} \right.$ | (11) |
| $S=\frac{1.46\sqrt{1-{{b}_{1}}}}{\sqrt{\frac{1}{S_{g}^{2}}}+\frac{1}{S_{d}^{2}}+\frac{1}{S_{r}^{2}}}$ | (12) |
|
| 图2 储汽筒放气模型示意图 Figure 2 Steam accumulator discharge model |
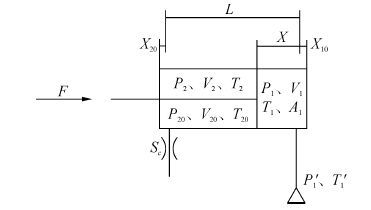
汽缸做功过程模型如图 3所示。气源压力T′1、温度P′1,汽缸有杆腔和无杆腔侧面积分别为A1和A2,初始压力P20、温度T20。工作腔的起始容积V10=A1X10,无杆腔容积等于工作腔余隙容积与活塞运动产生容积之和,F为外负载,Sc为气赶排气口面积。根据典型的双作用气压传动系统的动态特性研究[13],可得式(13)~(19),式中Qm2为从汽缸无杆腔流出的蒸汽流量。
| $\frac{d{{P}_{1}}}{dt}=\frac{\kappa RT{{\prime }_{1}}{{Q}_{m1}}}{{{A}_{1}}({{X}_{10}}+X)}-\frac{\kappa {{P}_{1}}}{{{X}_{10}}+{{X}_{1}}}\frac{dX}{dt}$ | (13) |
| ${{T}_{1}}={{T}_{10}}{{\left( \frac{{{P}_{1}}}{{{P}_{10}}} \right)}^{\frac{\kappa -1}{\kappa }}}$ | (14) |
| $\frac{d{{P}_{2}}}{dt}=\frac{\kappa {{P}_{2}}}{(S+{{X}_{20}}-X)}\frac{dX}{dt}-\frac{\kappa R{{T}_{2}}{{Q}_{m2}}}{{{A}_{2}}\left( S+{{X}_{20}}-X \right)}$ | (15) |
| ${{T}_{2}}={{T}_{0}}{{\left( \frac{{{P}_{2}}}{{{P}_{0}}} \right)}^{\frac{\kappa -1}{\kappa }}}$ | (16) |
| ${{Q}_{m2}}=\frac{{{S}_{2}}{{P}_{2}}\sqrt{1-{{b}_{2}}}}{\sqrt{R{{T}_{2}}}}{{\omega }_{e2}}$ | (17) |
| ${{\omega }_{e2}}=\left\{ \begin{matrix} 1-{{\left( \frac{{{\sigma }_{2}}-{{b}_{2}}}{1-{{b}_{2}}} \right)}^{2}} & {{b}_{2}}~ <{{\sigma }_{2}}=\frac{{{P}_{0}}}{{{P}_{2}}}\le 1 \\ 1 & ~{{\sigma }_{2}}=\frac{{{P}_{0}}}{{{P}_{2}}}\le {{b}_{2}} \\ \end{matrix} \right.$ | (18) |
| ${{S}_{2}}=1.46{{S}_{c}}\sqrt{1-{{b}_{2}}}$ | (19) |
|
| 图3 汽缸做功过程模型 Figure 3 The working process model of cylinder |
被弹射舰载机在汽缸作用下,以速度V向左运动,所受的总摩擦阻力为Ff,忽略弹射架质量,舰载机质量为M。根据牛顿第二定律可得舰载机和弹射装置未分离时的运动情况:
| $M\frac{{{d}^{2}}X}{d{{t}^{2}}}=\left\{ \begin{matrix} {{P}_{1}}{{A}_{1}}-{{P}_{2}}{{A}_{2}}-{{F}_{1}}-{{F}_{f}} & ~(X=0\cap {{P}_{1}}{{A}_{1}}\ge {{P}_{2}}{{A}_{2}}+{{F}_{1}}+{{F}_{f}})\cup \left( 0 <X<S \right) \\ 0 & (X=0\cap {{P}_{1}}{{A}_{1}}\ge {{P}_{2}}{{A}_{2}}+{{F}_{1}}+{{F}_{f}})\cup \left( X=S \right) \\ \end{matrix} \right.$ | (20) |
式中:Ff和F1分别表示汽缸活塞受到的摩擦力和弹射舰载机受到的附加推力。
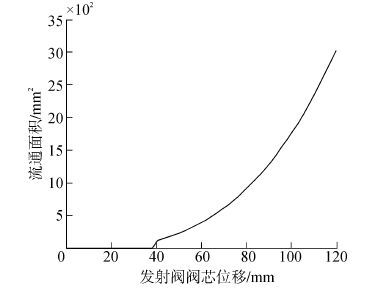
1.3 发射阀建模根据文献[14]得出一组关于蒸汽弹射器发射阀测量杆位移与流通面积相对应的一组数据。将其拟合为式(21)后可得关系曲线图 4,式中:Sl为阀芯通油面积,l(40 mm≤l≤120 mm)为阀芯位移。
| ${{S}_{l}}=0.002{{l}^{3}}+0.062\text{ }8{{l}^{2}}-4.885\text{ }9l+112.4125$ | (21) |
假设舰载机所受合力F在机体系Sb各轴分量为(Fxb,Fyb,Fzb),在地面系Sg各轴的分量为(Fxg,sFyg,Fzg),而舰载机航迹速度Vk在Sg各轴的分量为(Vk.xg,Vk.yg,Vk.zg),在Sb各轴的分量为(Vk.xb,Vk.yb,Vk.zb),并用(ωxb,ωyb,ωzb)表示舰载机的角速度ωp在Sb各轴的分量。综合机体运动学和动力学特性,可以得到舰载机的十二阶微分方程[15]:
| $\left\{ \begin{align} & \frac{d{{F}_{xg}}}{dt}={{V}_{k.xg}} \\ & \frac{d{{F}_{yg}}}{dt}={{V}_{k.yb}} \\ & \frac{d{{F}_{zg}}}{dt}={{V}_{k.zb}} \\ & \frac{d{{V}_{k.xb}}}{dt}=\frac{{{F}_{xb}}}{m}+{{\omega }_{zb}}{{V}_{k.yb}}-{{\omega }_{yb}}{{V}_{k.zb}} \\ & \frac{d{{V}_{k.yb}}}{dt}=\frac{{{F}_{yb}}}{m}+{{\omega }_{xb}}{{V}_{k.zb}}-{{\omega }_{zb}}{{V}_{k.xb}} \\ & \frac{d{{V}_{k.zb}}}{dt}=\frac{{{F}_{zb}}}{m}+V{{\omega }_{yb}}{{V}_{k.xb}}-{{\omega }_{xb}}{{V}_{k.yb}} \\ & \dot{\phi }={{\omega }_{xb}}+tan~\theta ({{\omega }_{yb}}sin\text{ }\phi +{{\omega }_{zb}}cos~\phi ) \\ & \dot{\theta }={{\omega }_{yb}}cos~\phi -{{\omega }_{zb}}sin\text{ }\phi \\ & \dot{\psi }=\frac{{{\omega }_{yb}}sin\text{ }\phi +{{\omega }_{zb}}cos~\phi }{cos~\theta } \\ & {{{\dot{\omega }}}_{xb}}=\frac{1}{{{I}_{x}}{{I}_{z}}-{{I}_{xz}}^{2}}\{{{I}_{z}}[({{I}_{z}}-{{I}_{y}}){{\omega }_{yb}}{{\omega }_{zb}}-{{I}_{xz}}{{\omega }_{xb}}{{\omega }_{yb}}+ \\ & {{M}_{L}}]+{{I}_{xz}}[({{I}_{y}}-{{I}_{x}}){{\omega }_{xb}}{{\omega }_{yb}}+{{I}_{xz}}{{\omega }_{yb}}{{\omega }_{zb}}+{{M}_{N}}]\} \\ & {{{\dot{\omega }}}_{yb}}=\frac{({{I}_{x}}-{{I}_{z}}){{\omega }_{zb}}{{\omega }_{xb}}-{{I}_{xz}}({{\omega }^{2}}_{xb}-{{\omega }^{2}}_{zb})+{{M}_{M}}+P}{{{I}_{y}}} \\ & {{{\dot{\omega }}}_{zb}}=\frac{1}{{{I}_{x}}{{I}_{z}}-{{I}^{2}}_{zx}}\{{{I}_{x}}[({{I}_{y}}-{{I}_{x}}){{\omega }_{xb}}{{\omega }_{yb}}+{{I}_{xz}}{{\omega }_{yb}}{{\omega }_{zb}}+ \\ & {{M}_{N}}]+{{I}_{xz}}[({{I}_{z}}-{{I}_{y}}){{\omega }_{yb}}{{\omega }_{zb}}-{{I}_{xz}}{{\omega }_{xb}}{{\omega }_{yb}}+{{M}_{L}}]\} \\ \end{align} \right.$ | (22) |
|
| 图4 发射阀阀芯位移与流通面积之间的关系 Figure 4 The relationship between launching valve displacement and flowing area |
其中,θ、Φ、φ分别为舰载机运动过程中的俯仰角、滚转角和偏航角,ML、MM、MN分别为舰载机在运动过程中所受俯仰力力矩、滚转力矩和偏航力矩。Fxb=Tsin θT+P,蒸汽弹射器输出的弹射力作为联系舰载机蒸汽弹射系统与舰载机弹射起飞系统之间的纽带,假设弹射杆的弹射角为θT,舰载机发动机推力为P。通过式(22)联合求解从而获得舰载机的纵向轨迹:
| $y={{y}_{0}}+\int {{V}_{k.yb}}dt$ | (23) |
式中:y0为初始条件下舰载机重心离海平面的高度,本文取13 m。
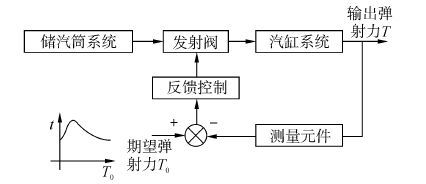
2 舰载机蒸汽弹射控制系统设计弹射控制系统结构图如图 5所示,分为储汽筒系统和汽缸系统,发射阀作为两者衔接的纽带,其开启时间与开度通过弹射力的实际输出值T与期望值T0的差来调节。本章对汽缸系统完成状态反馈线性化[16],为后面设计发射阀调节器做准备。
|
| 图5 弹射控制系统结构 Figure 5 The structure diagram of catapult launch control system |
汽缸中活塞的动力学方程可简化为式(24),而汽缸系统模型[17]可简化为式(25):
| $F={{P}_{1}}{{A}_{1}}-{{P}_{2}}{{A}_{2}}$ | (24) |
| $\left\{ \begin{align} & \dot{x}=f\left( x \right)+g\left( x \right)u \\ & y=h\left( x \right) \\ \end{align} \right.$ | (25) |
式中
| $\eqalign{ & x = {\left[ {\matrix{ X & {{P_1}} & {{P_2}} \cr } } \right]^{\rm T}} \cr & h\left( x \right) = {P_1}{A_1} - {P_2}{A_2} \cr & f\left( x \right) = \left[ \matrix{ {\dot X} \hfill \cr - {{\kappa {P_1}} \over {{X_{10}} + {X_1}}}{{dX} \over {dt}} \hfill \cr {{\kappa {P_2}} \over {(S + {X_{20}} - X)}}{{dX} \over {dt}} \hfill \cr} \right] \cr & g\left( x \right)u = \left[ \matrix{ {{\kappa RT{\prime _1}{Q_{m1}}} \over {{A_1}({X_{10}} + X)}} \hfill \cr {{ - \kappa R{T_2}{Q_{m2}}} \over {{A_2}(S + {X_{20}} - X)}} \hfill \cr} \right] \cr} $ |
h(x)关于向量场f(x)和g(x)的李导数分别为
| $\begin{align} & {{L}_{f}}h={{\left( \frac{\partial h}{\partial x} \right)}^{T}}\dot{x}=\frac{\kappa RT{{\prime }_{1}}{{Q}_{m1}}}{{{X}_{10}}+X}+ \\ & \frac{\kappa R{{T}_{2}}{{Q}_{m2}}}{S+{{X}_{20}}-X}-\kappa \dot{X}\left( \frac{{{P}_{1}}{{A}_{1}}}{{{X}_{10}}+X}+\frac{{{P}_{2}}{{A}_{2}}}{S+{{X}_{20}}-X} \right) \\ \end{align}$ | (26) |
| $\begin{align} & {{L}_{g}}hx={{\left( \frac{\partial h}{\partial x} \right)}^{T}}g\left( x \right)= \\ & \frac{\kappa RT{{\prime }_{1}}{{Q}_{m1}}}{{{X}_{10}}+X}+\frac{\kappa R{{T}_{2}}{{Q}_{m2}}}{S+{{X}_{20}}}-X\ne 0 \\ \end{align}$ | (27) |
显然,该仿射非线性系统的相对阶1,系统可反馈线性化的条件是Lfh=v有有界解[17],由式(10)和式(17)可知Lfh为单增函数,从而Lfh=v存在有界唯一解。可通过状态反馈变换式(29)得到输出y对新输入v的的一阶线性系统[18]。
| $\begin{align} & v={{L}_{f}}h=\frac{\kappa RT{{\prime }_{1}}{{Q}_{m1}}}{{{X}_{10}}+X}+\frac{\kappa R{{T}_{2}}{{Q}_{m2}}}{S+{{X}_{20}}-X}- \\ & \kappa \dot{X}\left( \frac{{{P}_{1}}{{A}_{1}}}{{{X}_{10}}+X}+\frac{{{P}_{2}}{{A}_{2}}}{S+{{X}_{20}}-X} \right) \\ \end{align}$ | (28) |
| $\begin{align} & u=\frac{1}{{{L}_{g}}h\left( x \right)}-{{L}_{f}}h\left( x \right)+v= \\ & \frac{v+\kappa \dot{X}\left( \frac{{{P}_{1}}{{A}_{1}}}{{{X}_{10}}+X}+\frac{{{P}_{2}}{{A}_{2}}}{S+{{X}_{20}}-X} \right)}{\Omega \left( {{S}_{u1}},{{P}_{1}} \right)-\Omega \left( {{S}_{u2}},{{P}_{2}} \right)}-~ \\ & \frac{\left[ \Omega \left( {{S}_{1}},{{P}_{1}} \right)-\Omega \left( {{S}_{2}},{{P}_{2}} \right) \right]}{\Omega {{\left( {{S}_{u1}},P \right)}_{1}}-\Omega \left( {{S}_{u2}},{{P}_{2}} \right)} \\ \end{align}$ | (29) |
式中
| $\left\{ \begin{align} & \Omega {{S}_{u1}},{{P}_{1}}=\frac{\kappa {{S}_{u1}}P{{\prime }_{1}}\sqrt{RT{{\prime }_{1}}}\sqrt{1-{{b}_{1}}}}{{{X}_{10}}+X}{{w}_{e1}} \\ & \Omega {{S}_{u2}},{{P}_{2}}=\frac{\kappa {{S}_{u2}}{{P}_{2}}\sqrt{R{{T}_{2}}}\sqrt{1-{{b}_{2}}}}{S+{{X}_{20}}-X}{{w}_{e2}} \\ & \Omega {{S}_{1}},{{P}_{1}}=\frac{\kappa {{S}_{1}}P{{\prime }_{1}}\sqrt{RT{{\prime }_{1}}}\sqrt{1-{{b}_{1}}}}{{{X}_{10}}+X}{{w}_{e1}} \\ & \Omega {{S}_{2}},{{P}_{2}}=\frac{\kappa {{S}_{2}}{{P}_{2}}\sqrt{R{{T}_{2}}}\sqrt{1-{{b}_{2}}}}{S+{{X}_{20}}-X}{{w}_{e2}}~ \\ \end{align} \right.$ |
其中,Su1、Su2、S1、S2分别为阀开口对应的阀流通面积,可由式(21)求得。令Xl=P1A1-P2A2,综合式(26)~(29)可得状态反馈线性化后的汽缸系统模型为
| $\left\{ \begin{align} & \dot{X}=\upsilon \\ & Y={{X}_{l}} \\ \end{align} \right.$ | (30) |
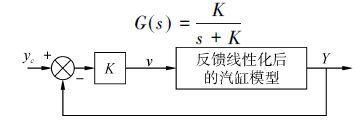
以上得到了系统的伪线性模型,由于系统经反馈线性化后已简化为积分环节,故系统可控,并且设计简单控制器就能使系统具有较好的动态性能[13],从而其闭环框图如图 6所示,其中yC为期望的输出,相应的传递函数为
| $G\left( s \right)=\frac{K}{s+K}$ | (31) |
|
| 图6 汽缸系统伪线性模型 Figure 6 The pseudo linear model of cylinder system |
根据上文建立的弹射系统汽缸及储汽筒模型,利用Matlab对弹射过程进行仿真。仿真条件如表 1所示。
| 仿真量 | 仿真取值 |
| 储汽筒初始压力/MPa | 5.3 |
| 储汽筒初始温度/K | 570 |
| 储汽筒容积/m3 | 69 |
| 储汽筒初始水质量/kg | 30 000 |
| 储汽筒初始水蒸汽质量/kg | 968.76 |
| 储汽筒内表面积/m2 | 0.159 |
| 管道等效流通面积/m2 | 0.000 107 287 650 7 |
| 汽缸有杆腔面积/m2 | 0.057 2 |
| 汽缸无杆腔面积/m2 | 0.159 |
| 活塞总冲程/m | 60 |
| 舰载机质量/kg | 33 000 |
| 弹射角/(°) | 30 |
| 发动机推力/N | 13 |
| 舰载机所受总摩擦阻力/N | 40 425 |
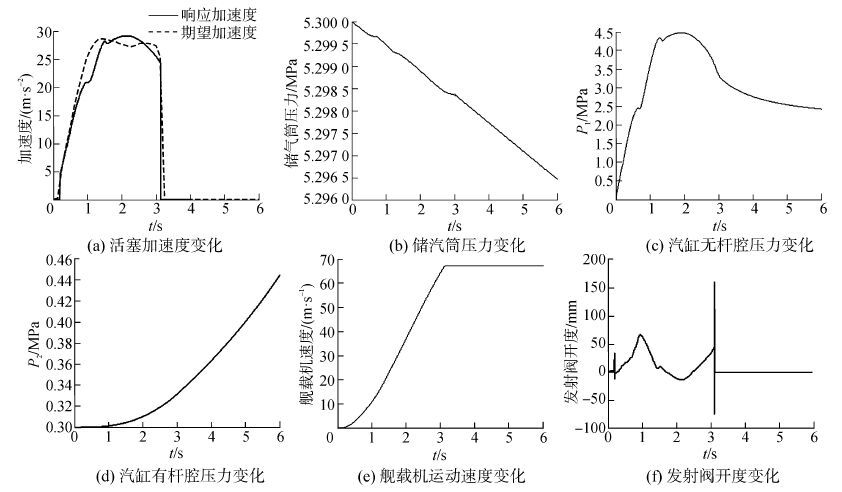
针对图 5中的反馈控制部分设计PID控制器。舰载机弹射时的期望加速度可由文献[4]获得,如图 7(a)中虚线所示。在利用Simulink响应最优化软件包对控制器参数进行调试的过程中发现,若发射阀控制器存在积分环节,发射阀将在弹射结束后,即3.1 s结束以后[7],仍然保持此刻的开度,继续向汽缸中供汽,而实际弹射过程中弹射结束后发射阀应该关闭,因此最终采取PD控制策略使发射阀动作符合实际规律。而利用check step response模块对系统进行阶跃响应的仿真,在设定超调量为5%,上升时间为0.5 s,调节时间为3.1 s,此标准是根据文献[7]中实际弹射需求所确定的,其中积分系数设定为0,模块经过多次仿真取得满足以上指标的最优比例系数10.78、微分系数0.001 46,图 7给出仿真结果。
|
| 图7 传统PID蒸汽弹射系统响应 Figure 7 Traditional PID steam catapult system response |
由于弹射时牵制杆的作用,活塞和舰载机在0.18 s后才运动,舰载机加速度在2 s时达到最大值28.6 m/s2,在3.1 s时达到68.4 m/s的速度而脱离弹射装置,活塞加速度也随即降为0,加速度和速度如图 7(a)和图 7(e)所示;由图 7(b)可知,储汽筒压力变化过程近似为线性,压降较小;汽缸无杆腔压力先增大再随着发射阀的关闭而减小,在弹射过程中存在小幅波动,而有杆腔压力刚开始增加较缓慢,而后增速变大;虽然实际弹射过程中发射阀开度有可能出现波动,但在开启和关闭时发生较剧烈的变化会降低发射阀的使用寿命,而图 7(f)表明在0.18 s和3.1 s附近发射阀的开度多次突变甚至出现负值,由于实际弹射过程中储气筒内流入汽缸的蒸汽压力会有所下降,加速度在2 s时会有一定的下降,因此发射阀需要相应关闭来实现加速度的跟踪,由于微分作用对偏差进行了超前控制,发射阀开度在2 s之前就开始减小,使发射阀产生了负向开度,但在发射阀最终关闭时,产生了约160 mm的正向开度,此开度超过了实际中发射阀的正常最大开度,,严重时不仅会损坏发射阀,而且影响舰载机的正常起飞。另一方面,由文献[7]中可知舰载机的最小起飞速度为69.5 m/s,在规定的时间内也未达到舰载机的起飞速度。由此可见,采用经典的PD控制方法难以使该弹射系统达到期望控制性能。
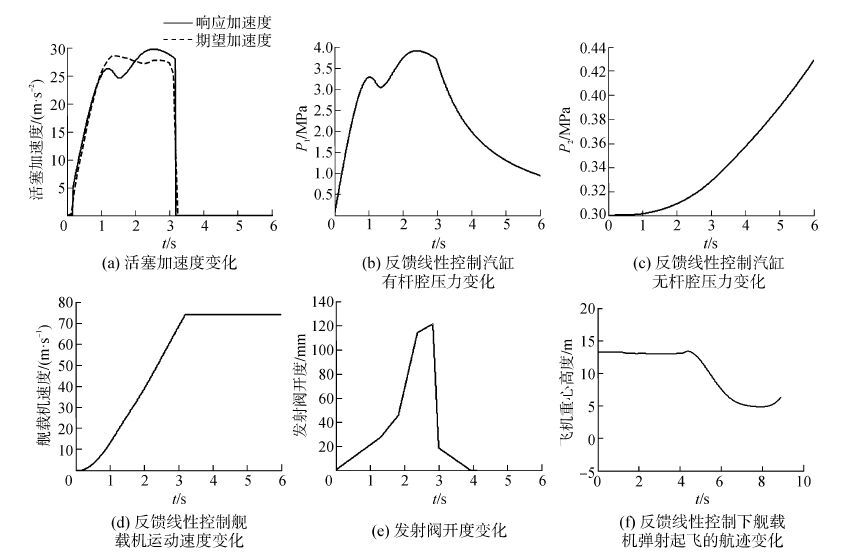
3.2 基于反馈线性化的发射阀调节器设计利用第2.1节中线性化后的系统(如图 6),通过调节参数K使活塞加速度逼近期望值。取K为30能获得相对较好的控制效果,仿真结果如图 8所示。
|
| 图8 反馈线性化蒸汽弹射系统响应 Figure 8 Feedback linearization steam catapult system response |
比较图 7和图 8 发现:相比经典PD控制方案下的系统仿真结果,采用反馈线性控制系统后,虽然活塞加速度的响应性能有所下降,但变化过程与期望值基本一致;并且,图 8(e)表明发射阀开度逐渐增加,在1.8 s时急速增加,最大至120 mm,随后急剧下降,整个过程中随时间连续变化,无剧烈波动和突变,由于采用反馈线性化的方法设计控制器,使汽缸内也未出现负值,因而更符合实际情况;而最终舰载机的速度能达到74.2 m/s,满足舰载机的最小起飞速度;图 8中其余系统状态的响应结果与图 7相差无几。
加入基于反馈线性化方法设计的控制器后,舰载机弹射起飞的纵向航迹如图 8(f)所示(不考虑甲板随机振荡),其中纵坐标值表示相对海平面高度。在规定的甲板段行程内舰载机轨迹平稳,离舰后先下沉然后迅速爬升,满足文献[19]中最小下沉量的安全起飞指标要求,这也表明了蒸汽弹射系统控制设计的有效性。
4 结论1) 在舰载机蒸汽弹射过程中,储汽筒内压降很小,可以忽略。
2) 基于经典控制理论设计的发射阀PD调节器控制效果不佳,主要表现在发射阀开度在弹射初期和结束时发生突变,甚至出现负值,与实际情况不符。
3) 利用精确线性化方法实现了汽缸内各状态量解耦,在此基础上设计的发射阀调节器能使发射阀稳定工作,符合设计要求。
| [1] |
程刚, 倪何, 孙丰瑞. 舰载蒸汽弹射系统建模与仿真研究[J].
武汉理工大学学报:交通科学与工程版, 2010, 34(2): 301–305.
CHENG Gang, NI He, SUN Fengrui. Modeling and simulation research on naval steam-power aircraft launch system[J]. Journal of Wuhan University of Technology:transportation science & engineering, 2010, 34(2): 301–305. |
| [2] |
聂宏, 房兴波, 魏小辉, 等. 舰载飞机弹射起飞动力学研究进展[J].
南京航空航天大学学报, 2013, 45(6): 727–738.
NIE Hong, FANG Xingbo, WEI Xiaohui, et al. Overview of carrier-based aircraft catapult launch dynamics[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(6): 727–738. |
| [3] | LUCAS C B. Catapult criteria for a carrier-based airplane[R]. AD0702814. 1968. |
| [4] | SLAVIN F J. Aircraft steam catapults[R]. A69-24068. 1969. |
| [5] |
赵险峰. 航母舰载机蒸汽弹射系统的数学仿真研究[J].
舰载武器, 1996(3): 45–53.
ZHAO Xianfeng. The mathematic simulation of aircraft carrier steam catapult system[J]. Carrier weapon, 1996(3): 45–53. |
| [6] |
金长江, 洪冠新. 舰载机弹射起飞及拦阻着舰动力学问题[J].
航空学报, 1990, 11(12): .
JIN Changjiang, HONG Guanxin. Dynamic problems of carrier aircraft catapult launching and arrest landing[J]. Acta aeronautica et astronautica sinica, 1990, 11(12): . |
| [7] | WALLACE M M. F/A-18E/F catapult minimum end airspeed testing[D]. Knoxville:The University of Tennessee, 2002. |
| [8] |
郑本武. 舰载飞机弹射起飞性能和影响因素分析[J].
飞行力学, 1992, 10(3): 27–33.
ZHENG Benwu. The catapulting performance of the carrier based airplane and the paramter study[J]. Flight dynamics, 1992, 10(3): 27–33. |
| [9] | HUANG C S, YUAN K. Output tracking of a non-linear non-minimum phase PVTOL aircraft based on non-linear state feedback control[J]. International journal of control, 2002, 75(6): 466–473. |
| [10] | STEVANOVIC V D, MASLOVARIC B, PRICA S. Dynamics of steam accumulation[J]. Applied thermal engineering, 2012, 37: 73–79. |
| [11] | SUN Baozhi, GUO Jiamin, LEI Yu, et al. Simulation and verification of a non-equilibrium thermodynamic model for a steam catapult's steam accumulator[J]. Intenational journal of heat and mass transfer, 2015, 85: 88–97. |
| [12] | THOMAS A, LEVENSON J. Steam catapult performance prediction program docu-mentation[R]. NAEC_ENC_7640. 1970. |
| [13] |
刘救世. 贮气瓶供气无人机弹射器弹射过程的研究[D]. 郑州:郑州大学, 2013.
LIU Jiushi. Study on the ejection process of the UAV catapult supplied by gas cylinder[D]. Zhengzhou:Zhengzhou University, 2013. |
| [14] |
周清和. 蒸汽弹射器速率阀研究[J].
液压与气动, 2003(4): 3–4.
ZHOU Qinghe. Study on the velocity valve for steam launching equipment[J]. Chinese hydraulics & pneumatics, 2003(4): 3–4. |
| [15] |
张智, 闻子侠, 朱齐丹, 等. 舰载机阻拦过程动力学仿真[J].
哈尔滨工程大学学报, 2014(5): 571–579.
ZHANG Zhi, WEN Zixia, ZHU Qidan, et al. Kinetic simulation of shipboard arresting system[J]. Journal of Harbin Engineering University, 2014(5): 571–579. |
| [16] |
赵志学. 基于反馈线性化的气动负载模拟器研究[D]. 哈尔滨:哈尔滨工业大学, 2007.
ZHAO Zhixue. Study of the pneumatic load simulator based on feedback linearization[D]. Harbin:Harbin Institute of Technology, 2007. |
| [17] | DA SILVA A L, PAGLIONE P, YONEYAMA T. Cruising autopilot for a flexible aircraft with an internal loop of model following[J]. Journal of aerospace engineering, 2014, 27(2): 202–214. |
| [18] | 胡跃明. 非线性控制系统理论与应用[M].2版.. 北京: 国防工业出版社, 2005 . |
| [19] |
严重中. 舰载飞机下沉量计算及影响因素分析[J].
飞行力学, 1993, 11(3): 42–49.
YAN Chongzhong. The calculation of sink and analysis of influence factors for a carrier based airplane[J]. Flight dynamics, 1993, 11(3): 42–49. |



