悬臂式离心泵作为离心泵应用最广泛的一种结构形式,其转子泵轴的两个支撑轴承均位于泵轴的一端,叶轮则安装在泵轴的另一端,处于自由悬臂状态。这种特殊结构,使得其工作状态参数(转速、外载荷)和实际结构参数(悬臂长度、支撑间距等)对转子动力特性的综合影响变得更为复杂。离心泵在高速旋转过程中,蜗壳内流场状态不断变化,势必造成叶轮所受载荷随之变化而产生流体激励力,继而引起悬臂式离心泵转子的振动。同时周期性的液力载荷又会引起叶轮及泵轴的动态变形,从而进一步影响流体的分布,直接导致离心泵运行效率低,甚至引发故障[1]。
悬臂式离心泵内部流动为复杂的三维非定常湍流流动,常伴有涡流、回流、汽蚀、水力振动等现象[2]。随着计算流体力学的发展,运用CFD研究离心泵内部流场已成为一种主流手段,在内流场与压力脉动的计算已经取得了一些成果[3-4]。Kelder等[5]通过势流理论和实验两方面研究了离心泵内外流场的特性。Kaewnai等[6]利用CFD研究不同湍流模型对离心泵外特性的影响。当前,在旋转机械中流固耦合问题已成为研究热点之一,如罗永要等[7]对混流式水轮机动载荷作用下的应力特性进行研究,结果表明动应力过大导致叶片产生裂纹。Young[8]对弹性的复合海洋螺旋桨进行研究,指出叶片的变形改变液体压力分布、空化程度,最终降低螺旋桨的效率。Brennen等[9]通过理论和试验分析了悬臂式离心泵流体诱导转子产生动应力,尝试在前盖板上增加沟槽或凸条以降低入口处涡流率,进而增加转子系统的稳定性,但效果并不明显。吴贤芳等[10]对离心泵关死点内部流场研究表明,流固耦合作用对扬程的影响较小,对压力脉动影响较大。Zhang等[11]基于流固耦合方法研究了不同叶片形状的瞬态振动性能。刘厚林等[12]对比分析单、双向耦合的叶轮静应力强度,指出单向耦合即可满足叶轮静应力分析。
泵轴结构参数是离心泵运行稳定性的重要因素,针对悬臂式离心泵的特殊结构,其悬臂比的设计对离心泵动力学特性有重要影响,但目前泵轴结构对转子动力学影响研究鲜有报道。采用单向流固耦合计算方法研究悬臂式离心泵静力学特性和转子动力学特性,分析悬臂比对离心泵稳定性的影响。
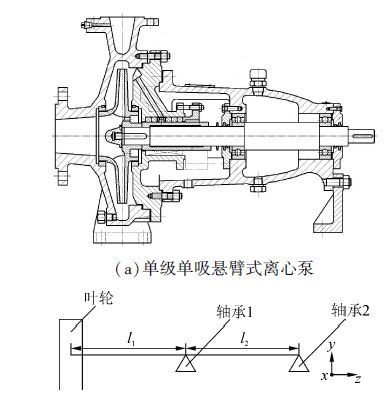
1 参数建模及数值计算方法 1.1 离心泵建模离心泵流固耦合特性研究过程中,以IS 80-50-250型号离心泵为研究对象,其结构示意图如图 1(a)。
|
| 图1 离心泵结构示意图 Figure 1 Structure diagram of centrifugal pump |
离心泵参数为:流量Q=50 m3/h,扬程H=80 m,转速n=2 900 r/min,进口直径D1=80 mm;叶轮为闭式叶轮,叶片数为5,叶轮外径D2=252 mm;叶轮材料选为HT200,密度ρ=7 200 kg/m3,弹性模量E=2.07×1011 Pa,泊松比γ=0.3;泵轴材料选为45,密度ρ=7 890 kg/m3,弹性模量E=1.1×1011 Pa,泊松比γ=0.28。离心泵悬臂比为泵轴伸出端与轴承支撑间距之比,如图 1(b)所示,则离心泵的悬臂比λ为
| $\lambda = l1/l2$ | (1) |
式中:l1为泵轴伸出端长度,l2为轴承支撑间距。
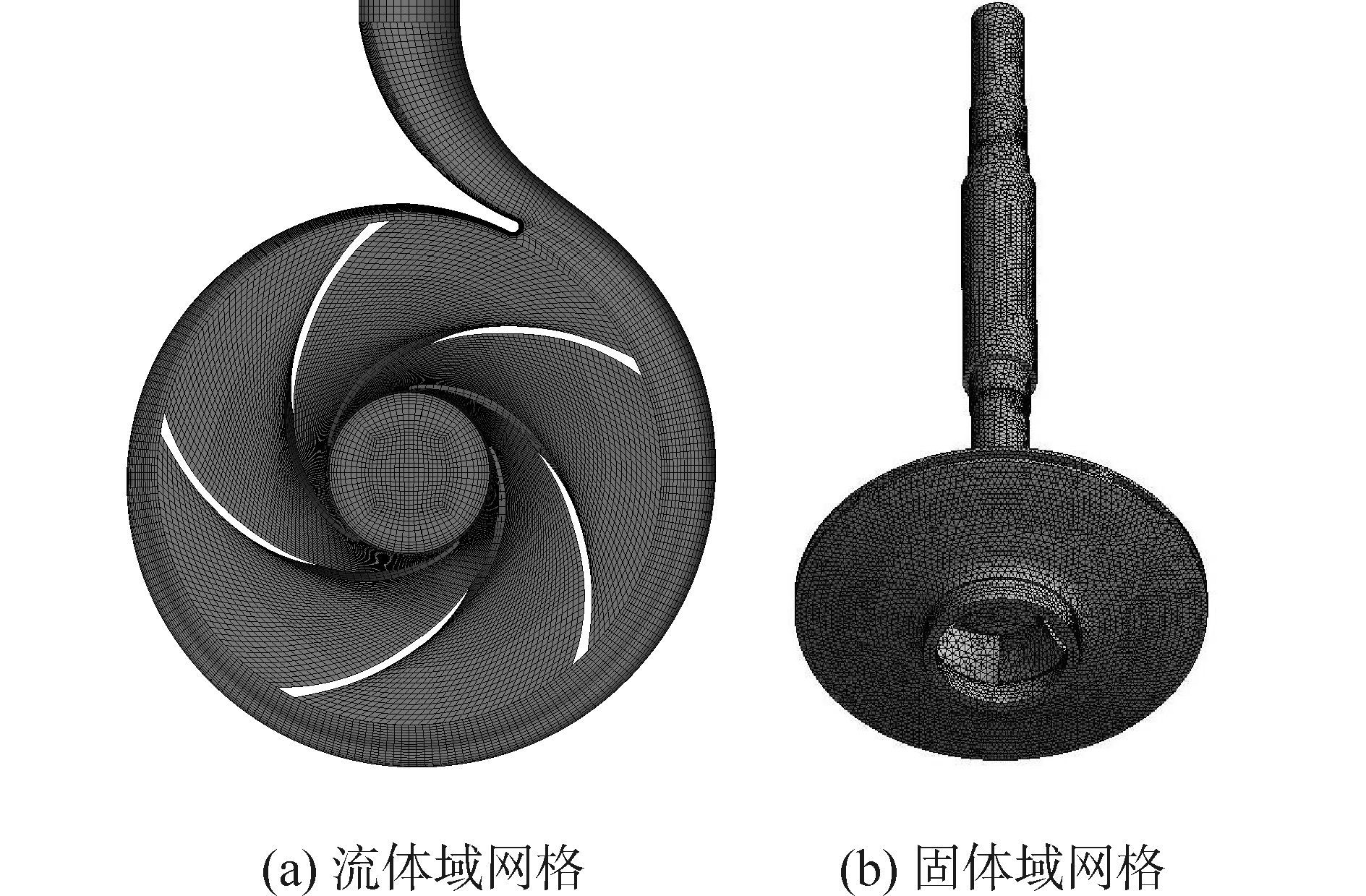
1.2 网格划分离心泵数值计算模型流体域包括进水管、叶轮水体、蜗壳水体和出水管4部分,采用网格划分软件ICEM对流体域进行网格划分。因叶轮和蜗壳水体结构复杂,造成离心泵非结构化网格单元数量多,进而带来数值计算量大、耗时长的问题,故采用拓扑映射法对流体域划分结构化六面体网格,使网格生成速度快、质量好、数据结构简单[13]。进水管与出水管部分,因其结构简单,对液体流入面和流出面进行O型划分,即得到高质量、正交性良好的结构化网格;叶轮水体部分,结构虽相对复杂,但呈现循环对称的特点,因此将叶轮平均分割成5个部分,只需建立其中一个周期的块并做出符合实际流体流向的六面体网格;蜗壳水体部分,其结构复杂部位集中在隔舌处,可将隔舌部位的六面体网格流向分为3个方向,分别是出水口方向、第一断面方向和第八断面方向,确保网格流向和实际流体流向相同,同时在隔舌处进行网格加密。在流体壁面的边界层节点应用linear排列方式,加密边界层使流固耦合交换信息误差减小。分别用4组不同尺度的网格对设计工况进行数值模拟,对比模拟扬程值来进行网格无关性验证,如表 1所示不同网格数量对应的模拟扬程,从表中可看出计算的扬程值与试验值间的误差较小,均在2%内。因此在满足计算精度的前提下考虑到节省时间,本文最终选用网格数量为110万左右。固体域包括固体叶轮和泵轴2部分,采用ANSYS自带网格划分软件对其进行非结构化网格划分,网格数为188 763,节点数为297 564。计算模型网格划分情况如图 2所示。
| 网格数×10-4 | 扬程模拟值/m | 与试验值的误差/% |
| 80 | 78.9 | 1.4 |
| 110 | 80.26 | 0.3 |
| 140 | 80.54 | 0.7 |
| 180 | 80.50 | 0.7 |
|
| 图2 网格模型 Figure 2 Grid model |
悬臂式离心泵在数值计算中,内部流体可视为等温不可压缩流体,内部流动近似为常密度流动。采用三维、稳态、不可压的连续性方程及RNG k-ε湍流方程进行求解[14]。其中连续方程为
| $\frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial {x_i}}} = 0$ | (2) |
动量方程为
| $\frac{{\partial {u_i}}}{{\partial t}} + {u_i}\frac{{\partial {u_i}}}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial \rho }}{{\partial {x_i}}} + \frac{1}{\rho }\frac{{\left( {\partial \rho {u_i}{u_j}} \right)}}{{\partial {x_j}}}$ | (3) |
式中:ρ为密度,ui为平均相对速度,xi为各坐标分量,t为时间。
悬臂式离心泵内部流线弯曲程度大,采用RNG k-ε湍流模型能很好地处理内部流动中旋转和旋流情况,在RNG k-ε湍流模型中湍动能k和湍流耗散率ε的方程为
| $\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_j}} \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\alpha _k}{\mu _e}\frac{{\partial k}}{{\partial {x_j}}}} \right) + \rho \left( {{P_k} - \varepsilon } \right)$ | (4) |
| $\begin{array}{l} \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_j}} \right)}}{{\partial {x_j}}} = \\ \frac{\partial }{{\partial {x_j}}}\left( {{\alpha _\varepsilon }{\mu _e}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right) + \rho \frac{\varepsilon }{k}\left( {C_{1\varepsilon }^{^*}{P_k} - {C_{2\varepsilon }}\varepsilon } \right) \end{array}$ | (5) |
式中:C1ε*=C1ε-η1-η/η0/1+βη3,
研究过程中分别选取0.6Q、0.8Q、1.0Q、1.2Q、1.4Q五种工况,采用ANSYS CFX中进行数值模拟,进出口分别设置为质量流量进口、自由流出口。叶轮采用旋转坐标系,蜗壳、进出水管采用静坐标系;定常计算时,动静交接面采用冻结转子。控制方程空间离散使用基于有限元体积法,对流项选择高分辨率,收敛目标设置为10-4。采用标准壁面函数处理近壁面,固体壁面设为无滑移。输送介质为常温常压条件下的清水。
1.5 单向耦合过程基于单向耦合方法,对离心泵λ分别为0.8、0.9、1.0、1.1、1.2、1.3等6种悬臂比下的叶轮应变应力分布情况进行分析。耦合过程在ANSYS Workbench中实现,为将离心泵内部流体力准确得传递到固体叶轮表面,需定义流固耦合面,将流体定常计算结果以压力载荷的形式施加到流固耦合面上,定义叶轮水体与固体所有接触面为流固耦合面,即前、后盖板面以及叶片表面[15];并对转子结构施加惯性载荷(重力载荷和离心载荷);假定轴承支承为刚性支承,其安装处添加圆柱约束,轴向和径向固定,切向自由。
离心泵结构强度计算的静力学方程[16]:
| $K\delta = F$ | (6) |
| $\sigma = DB\delta $ | (7) |
式中:K为刚度矩阵,D为弹性矩阵,B为应变矩阵,δ为位移,F为所受的力,σ为应力。
根据第四强度理论计算等效应力σe:
| ${\sigma _e} = \sqrt {\frac{1}{2}{{\left( {{\sigma _1} - {\sigma _2}} \right)}^2} + {{\left( {{\sigma _2} - {\sigma _3}} \right)}^2} + {{\left( {{\sigma _3} - {\sigma _1}} \right)}^2}} $ | (8) |
式中:σ1为第一主应力,σ2为第二主应力,σ3为第三主应力。
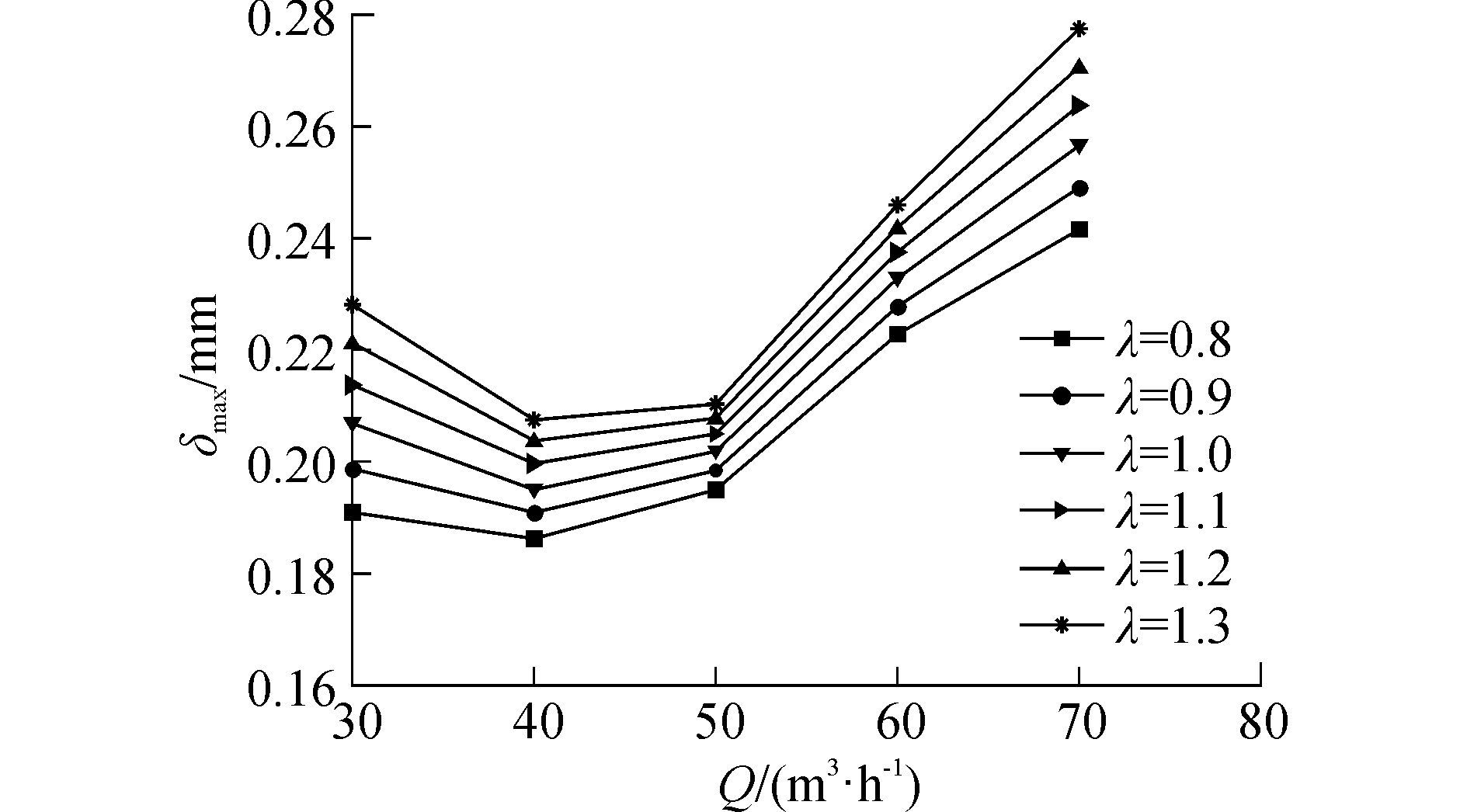
2 叶轮应变应力分析 2.1 叶轮应变分析图 3为不同悬臂比λ下叶轮的最大总变形随流量变化曲线图。由图 3可知,叶轮在离心泵径向力、轴向力和扭矩共同作用下发生应变,总变形的最小值和最大值分别处于λ=0.8在Q=40 m3/h和λ=1.3在Q=70 m3/h下。各个工况下,最大总变形量与悬臂比的大小呈正相关,悬臂比越小,叶轮变形越小。不同悬臂比的离心泵运行时,叶轮产生的最大总变形随工况的增大而呈现先下降后上升的变化趋势。这是因为不同工况下离心泵径向力、轴向力、扭矩都随流量而变,由离心泵定常计算结果可知,轴向力随流量增大而减小,径向力随流量先减小后增大,设计工况下径向力最小。扭矩随流量增大而增大,在三者综合载荷作用下叶轮总变形先下降后上升。从最大总变形的变化趋势可以看出,大悬臂比对不同工况的敏感程度更高,即改变运行工况时大悬臂比离心泵的叶轮变形梯度更大,小悬臂比的变形量较平缓。各个工况下,不同悬臂比的离心泵运转时叶轮产生的变形量方差依次为1.93×10-4、6.3×10-5、3.3×10-5、7.55×10-5、1.82×10-4。在设计工况点变形量较为集中,区间为0.19~0.21 mm;越偏离设计工况,叶轮最大变形量随悬臂比的改变发生的变化越大。故盲目增大悬臂比会加剧离心泵不稳定运行,内部流体激励力引起叶轮较大变形,反过来较大变形影响内部流场。为了保证叶轮运转过程中的刚度要求,避免选择较大的悬臂比,且避免悬臂泵在过大偏离设计工况点下运行。
|
| 图3 不同悬臂比不同载荷下叶轮的最大总变形 Figure 3 The maximum total deformation of impeller under different cantilever ratios and loads |
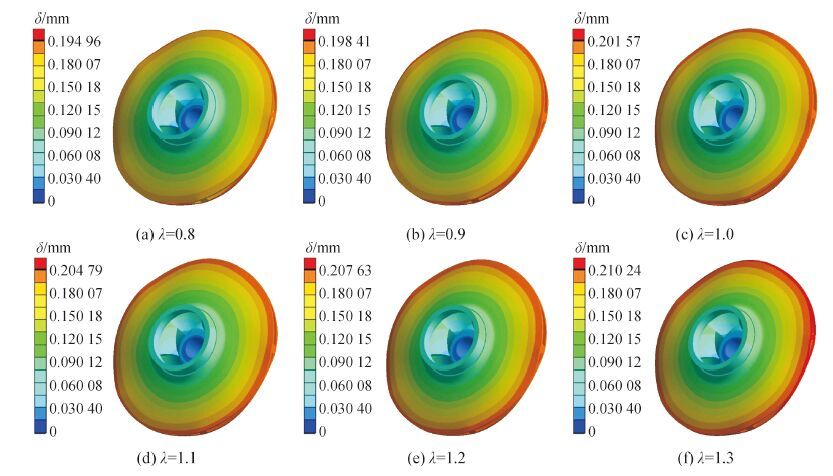
图 4 为在设计工况点不同悬臂比λ下叶轮的应变分布云图。可知,叶轮发生了弯曲变形,变形几乎成轴对称,并且沿着叶轮半径增大的方向逐渐增加。叶轮后盖板出口边缘中间流道处发生最大变形,此处压力最大,说明此处最有可能发生刚度破坏。改变悬臂比对叶轮产生最大总变形有较明显的影响。随着悬臂比增加,叶轮小变形区域逐渐减小,变形量逐渐增大。此外,悬臂比取大值时叶轮的最大应变明显高于悬臂比取小值,说明泵轴伸出端越短叶轮变形越小,离心泵运行过程越稳定;泵轴伸出端越长越容易引起叶轮后盖板边缘中间流道处的较大应变。
|
| 图4 设计工况下叶轮应变分布图 Figure 4 Distribution of impeller total deformation under design condition |
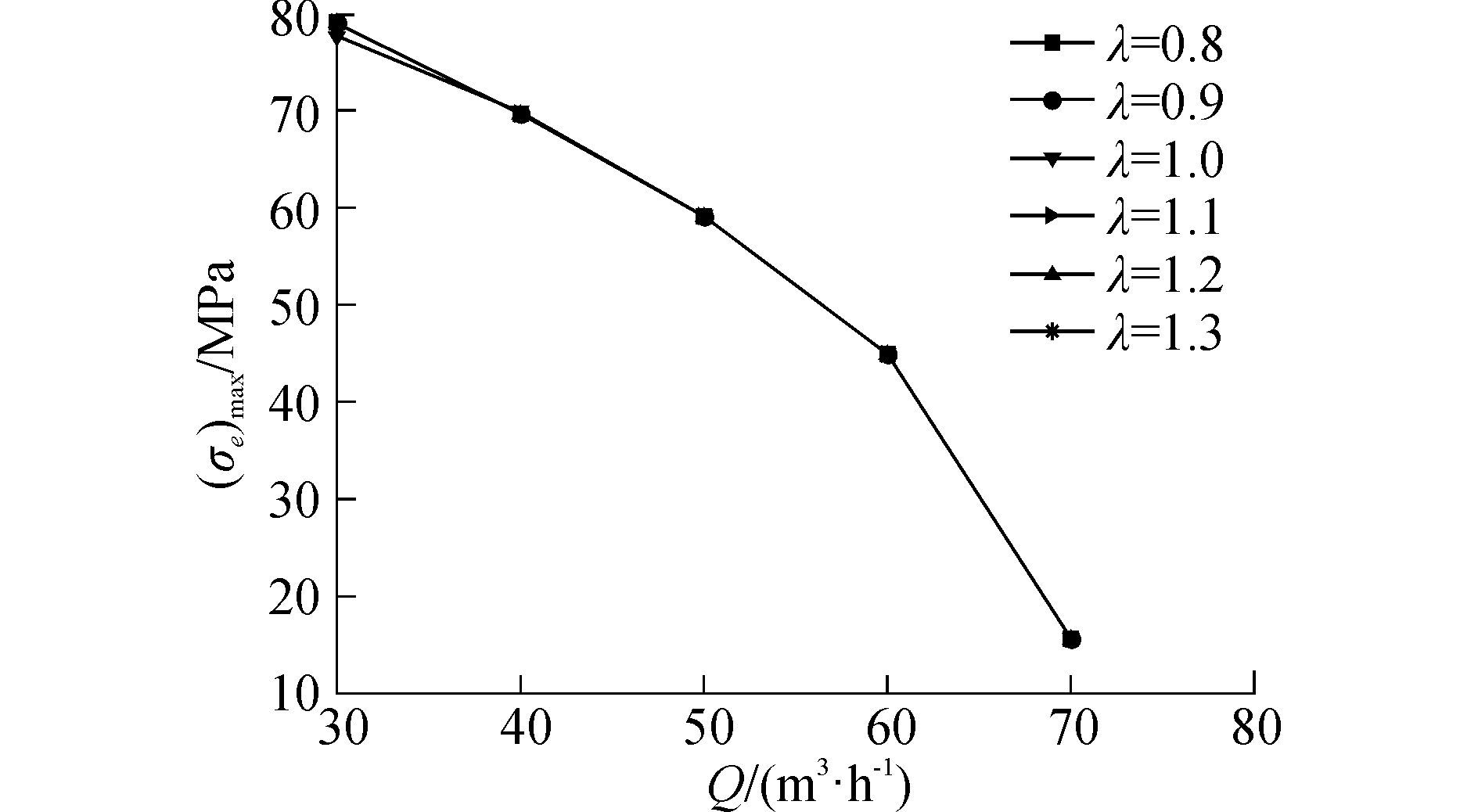
图 5为不同悬臂比λ下叶轮的最大等效应力随流量变化曲线图。由图 5可知,叶轮的最大等效应力均随流量的增加而降低,降低速度先缓后急。最大等效应力为78.958 MPa,小于叶轮材料HT200的许用应力200 MPa,说明叶轮的强度足够。在0.6Q工况下,叶轮的最大等效应力略有不同;当λ=1.0,最大等效应力最小,为77.73 MPa;当λ=1.3时,最大等效应力最大,为78.958 MPa,最大值与最小值相差1.2 MPa。悬臂比的改变并不会引起叶轮的最大等效应力出现明显变化,因此,对于悬臂式离心泵在小工况运转时,应充分考虑叶轮的强度要求。
|
| 图5 不同悬臂比不同载荷下叶轮的最大等效应力 Figure 5 The maximum equivalent stress of impeller under different cantilever ratios and loads |
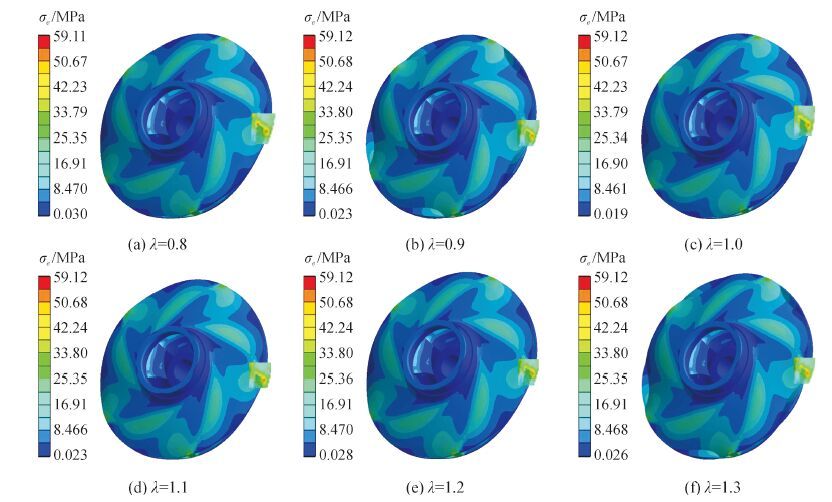
图 6 为在设计工况点不同悬臂比λ下叶轮的应力分布云图。由图 6可知,叶轮的等效应力呈循环对称分布,这与叶轮循环对称结构相符(如图中局部放大图所示最大等效应力集中在叶片背面出口边缘与前后盖板相交接的位置),此处前后盖板的压力载荷最大。最大等效应力在59.11~59.13 MPa,远小于叶轮的许用应力,且不同悬臂比下等效应力的最大值与最小值的相对偏差在1%以内,说明离心泵悬臂比对叶轮最大等效应力值的影响很小。
|
| 图6 设计工况下叶轮等效应力分布图 Figure 6 Distribution of impeller equivalent stress under design condition |
转子的稳定性限制了离心泵的高效运行范围,同时也影响了离心泵的安全可靠性。在静力学分析基础上,对不同悬臂比悬臂式离心泵进行有预应力模态分析,并将有预应力模态与自由模态的结果进行对比,其中预应力指的是内部流体计算的压力载荷、转子系统的惯性力和离心力。表 2为不同悬臂比下转子系统的前6阶固有频率。
| 阶数 | 预应力 | λ | |||||
| 0.8 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | ||
| 1 | 无 有 | 149.11 147.84 | 147.81 146.53 | 146.66 145.37 | 145.65 143.42 | 144.74 143.42 | 143.93 140.49 |
| 2 | 无 有 | 206.27 203.12 | 188.59 185.00 | 174.56 170.46 | 163.18 157.21 | 153.82 148.77 | 145.97 140.50 |
| 3 | 无 有 | 206.33 203.17 | 188.64 185.05 | 174.59 170.48 | 163.22 157.25 | 153.84 148.79 | 145.98 142.60 |
| 4 | 无 有 | 796.89 797.54 | 759.24 759.85 | 729.32 730.03 | 704.68 704.88 | 684.33 685.10 | 666.96 667.78 |
| 5 | 无 有 | 797.24 797.74 | 759.56 760.17 | 729.55 730.15 | 704.86 705.06 | 684.55 685.32 | 667.14 667.96 |
| 6 | 无 有 | 1283.2 1283.8 | 1273.1 1273.7 | 1264.1 1264.6 | 1256.0 1256.5 | 1248.6 1249.2 | 1242.0 1242.5 |
由表 2可知,随着λ的增大,叶轮的各阶固有频率逐渐减小,且减小幅度逐渐降低,说明泵轴结构的外形尺寸对固有频率有显著的影响。转子系统前3阶固有频率在有预应力的情况下明显低于无预应力情况,后三阶固有频率在两种情况几乎相等,因在无预应力时忽略了阻尼作用和附加质量,有预应力时考虑了离心泵的离心力和流体力,其中流体力相当于附着在固体叶轮表面的附加质量,在离心泵运转过程中固体叶轮与周围流体产生摩擦,同时内部流体也产生摩擦,引起能量消耗,增大了阻尼作用,从而降低了转子系统的固有频率。在有预应力、λ=1.3情况下,叶轮的第一阶固有频率最小,为140.49 Hz,远离叶片通过频率(zn/60=5×2 900/60=241.5 Hz),故悬臂式离心泵在运转过程中不会发生共振现象。
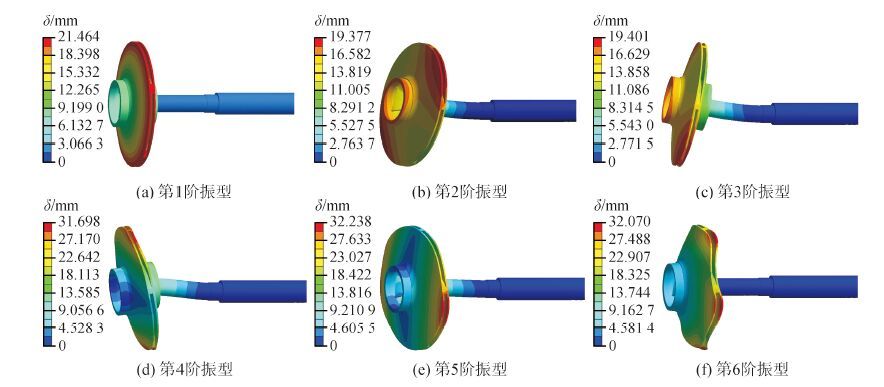
在有预应力、λ=0.8情况下离心泵转子系统前6阶振型如图 7所示。由图 7可知,前6阶振型表现为叶轮整体振动,叶轮较轴端振动较大。第1阶振型表现为绕z轴的扭转,振动出现节圆。第2阶和第3阶振型相同,但角度分布不同,分别沿y、x轴摆动。叶轮第4、5阶各出现1条节径,节径方向互相垂直,同时发生弯曲振动和扭曲振动。第6阶振型为沿z轴的伞形弯曲振动。转子系统的第2阶和第3阶、第4阶和第5阶振型相同固有频率相近,这种振型成对出现的现象与叶轮循环对称的结构有关,因循环对称结构具有重根模态。转子系统的振动幅度随着阶数的增加逐渐增长,阶数越高节径数越多,离心泵转子模态频率越大。无预应力下转子振型表现形式与有预应力时基本一致。
|
| 图7 有预应力下转子系统前6阶振型 Figure 7 The first six mode of vibration considering pre-stress |
1) 悬臂比与流量对叶轮应力应变有较大的影响,当流量一定时,悬臂式离心泵叶轮的应变随着悬臂比的增大而增大,最佳悬臂比为0.8;当悬臂比一定时,叶轮的应变随着流量的增加呈先减小后增大的变化趋势,叶轮应变沿着半径增大的方向逐渐增大,最大变形发生在叶轮后盖板中间流道处。
2) 悬臂比的改变并不会引起叶轮的最大等效应力出现明显变化,叶轮最大等效应力随流量的增加而减小,应力集中出现在叶片出口边缘与前、后盖板交接处。
3) 随着悬臂比的增加,叶轮固有频率逐渐减小,且减小幅度逐渐降低;流固耦合作用能够降低叶轮的固有频率,叶轮最小固有频率为140.49 Hz,不会发生共振现象。叶轮振型表现为扭曲、摆动、弯曲振动,且第2阶和第3阶、第4阶和第5阶振型相同固有频率相近。
| [1] | ZHANG Desheng, XU Yan, LIU Yang, et al. Effects on the performance and flow field of the axial flow pump hydraulic components with fluid-solid interaction[J]. Journal of food, agriculture & environment, 2013, 11(3/4): 2000–2004. |
| [2] | CHEAH K W, LEE T S, WINOTO S H. Unsteady analysis of impeller-volute interaction in centrifugal pump[J]. International journal of fluid machinery and systems, 2011, 4(3): 349–359. |
| [3] | LUCIUS A, BRENNER G. Unsteady CFD simulations of a pump in part load conditions using scale-adaptive simulation[J]. International journal of heat and fluid flow, 2010, 31(6): 1113–1118. |
| [4] |
率志君, 张权, 陈春来, 等. 多级离心泵整机流场三维非稳态湍流压力脉动特性分析[J].
哈尔滨工程大学学报, 2013, 34(3): 306–311.
SHUAI Zhijun, ZHANG Quan, CHEN Chunlai, et al. Characteristic analysis of three-dimensional unsteady turbulent pressure fluctuation in whole flow field of multi-stage centrifugal pump[J]. Journal of Harbin Engineering University, 2013, 34(3): 306–311. |
| [5] | KELDER J D H, DIJKERS R J H, VAN ESCH B P M, et al. Experimental and theoretical study of the flow in the volute of a low specific-speed pump[J]. Fluid dynamics research, 2001, 28(4): 267–280. |
| [6] | KAEWNAI S, CHAMAOOT M, WONGWISES S. Predicting performance of radial flow type impeller of centrifugal pump using CFD[J]. Journal of mechanical science and technology, 2009, 23(6): 1620–1627. |
| [7] |
罗永要, 王正伟, 梁权伟. 混流式水轮机转轮动载荷作用下的应力特性[J].
清华大学学报:自然科学版, 2005, 45(2): 235–237.
LUO Yongyao, WANG Zhengwei, LIANG Quanwei. Stress of francis turbine runners under fluctuant work conditions[J]. Journal of Tsinghua University:science and technology, 2005, 45(2): 235–237. |
| [8] | YOUNG Y L. Fluid-structure interaction analysis of flexible composite marine propellers[J]. Journal of fluids and structures, 2008, 24(6): 799–818. |
| [9] | BRENNEN C E, ACOSTA A J. Fluid-induced rotordynamic forces and instabilities[J]. Structural control and health monitoring, 2006, 13(1): 10–26. |
| [10] |
吴贤芳, 谈明高, 刘厚林, 等. 流固耦合作用对离心泵关死点内流的影响[J].
应用基础与工程科学学报, 2015, 23(1): 172–181.
WU Xianfang, TAN Minggao, LIU Houlin, et al. Effect of FSI on inner flow field in a centrifugal pump at shut off condition[J]. Journal of basic science and engineering, 2015, 23(1): 172–181. |
| [11] | ZHANG Yu, HU Sanbao, ZHANG Yunqing, et al. Optimization and analysis of centrifugal pump considering fluid-structure interaction[J]. The scientific world journal, 2014, 2014: 131802. |
| [12] |
刘厚林, 徐欢, 吴贤芳, 等. 基于流固耦合的导叶式离心泵强度分析[J].
振动与冲击, 2013, 32(12): 27–30.
LIU Houlin, XU Huan, WU Xianfang, et al. Strength analysis of a diffuser pump based on fluid-structure interaction[J]. Journal of vibration and shock, 2013, 32(12): 27–30. |
| [13] | LIN Hongwei, TANG Kai, JONEJA A, et al. Generating strictly non-self-overlapping structured quadrilateral grids[J]. Computer-aided design, 2007, 39(9): 709–718. |
| [14] |
谭磊, 曹树良, 桂绍波, 等. 带有前置导叶离心泵空化性能的试验及数值模拟[J].
机械工程学报, 2010, 46(18): 177–182.
DOI:10.3901/JME.2010.18.177
TAN Lei, CAO Shuliang, GUI Shaobo, et al. Experiment and numerical simulation of cavitation performance for centrifugal pump with inlet guide vane[J]. Journal of mechanical engineering, 2010, 46(18): 177–182. |
| [15] | CAMPBELL R L, PATERSON E G. Fluid-structure interaction analysis of flexible turbomachinery[J]. Journal of fluids and structures, 2011, 27(8): 1376–1391. |
| [16] | PEI Ji, YUAN Shouqi, YUAN Jianping. Dynamic stress analysis of sewage centrifugal pump impeller based on two-way coupling method[J]. Chinese journal of mechanical engineering, 2014, 27(2): 369–375. |



