2. College of Science, Chang'an University, Xi'an, 710061, China
形状记忆合金(shape memory alloy,SMA)材料是一种性能优良的智能金属感知、驱动材料,具有形状记忆效应和超弹性这两个独特的性能,为其在土木工程领域的应用创造了更优越的条件。然而,由于形状记忆合金材料力学性能变异性较大,受外界的影响因素较多,因此建立准确的数学本构模型十分困难。不同研究学者建立了不同的形状记忆合金本构模型[1]。目前,SMA材料本构模型主要有四类:Falk[2]基于Landau理论,考虑形状记忆效应材料的Helmholtz自由能函数F,建立了单晶理论本构模型; Abeyartane等[3] 从 Erieksen 应力诱发固—固相变的纯力学模型出发,提出的了SMA 材料的一维数学本构关系;Tanaka[4]和Brinson[5]提出了经典的唯象理论本构模型;Boyd等[6]提出了基于细观力学和热动力学并以能量耗散理论为依据的细观力学本构模型。由于不论上述哪一种本构模型,都是通过数学方法来模拟材料的力学行为,但是对于类似形状记忆合金的复合材料,影响其本构曲线的因素很多,不可能以数学模型精确表达出各影响因素对本构的影响程度,往往只能人为地进行简化与近似,这势必会造成局限性。另外,经典的Brinson本构模型虽能较为完整地反映SMA的力学性能,但是没有考虑加载频率对SMA超弹性性能的影响。近年来,随着智能算法研究的不断发展,智能算法在建立材料本构模型方面的作用日趋明显。人工神经网络智能算法是一种非线性建模的方法,该方法无需预知材料的本构形式,可以智能地分析各影响因素对本构的影响程度,从而可以建立非常精确的本构模型[7]。研究学者对神经网络本构做了如下研究:Peng等[8]提出了一种基于聚类径向基函数神经网络的弹塑性本构模型,为高精度的工程实践提供了可能性。李克钢等[9]利用神经网络建立了岩石本构模型。但是,神经元初始阀值和初始权值的变化对人工神经网络的结果影响较大。由此可知,有必要对BP网络神经元的初始阈值和权值进行优化,选择合适的阈值和权值。文中以材性试验结果作为BP网络的训练数据,利用遗传算法优化BP网络的初始权/阈值,建立了SMA遗传优化BP网络本构模型。
1 奥氏体SMA材性试验 1.1 试验设备与方案本次试验所用材料为西北有色金属研究院赛特金属材料开发有限公司生产的Ni-Ti SMA丝,该丝材化学成分为Ti-51at%Ni,直径规格为1.0 mm。相变温度如下:马氏体相变结束温度Mf为-420 ℃,马氏体相变开始温度Ms为-380 ℃,奥氏体相变结束温度Af为-60 ℃,奥氏体相变开始温度As为-20 ℃,由此可知该丝材常温下处于奥氏体状态。本次试验主要研究加/卸载速率对奥氏体SMA丝材的应力-应变曲线、特征点应力、耗能能力及等效阻尼比的影响,加/卸载速率分别为10、30、60、90 mm/min。试验中加载/卸载模式均采用定速率加载/卸载;每次循环均以丝材应变达到应变幅值作为加载的终止条件,应变幅值分别为3%、6%、8%;以丝材受轴向力小于5 N作为卸载的终止条件;每个加/卸载过程循环30圈。试验设备如图 1所示。

|
| 图1 试验设备 Figure 1 Test equipment |
对常温下为奥氏体的SMA丝进行加载/卸载循环试验,奥氏体SMA丝材的单圈相变过程和单圈典型应力-应变曲线如图 2所示。其中,相关力学性能参数定义如下:σMs、σMf分别表示马氏体相变开始应力和马氏体相变结束应力;σAs、σAf分别表示奥氏体相变开始应力和奥氏体相变结束应力;O-F段表示单圈残余应变;W表示单圈循环弹性势能,即B-D-E-F-G-B所围图形面积;ΔW表示SMA丝单位循环的耗能能力,即O-A-B-D-E-F-O所围的图形面积;Ks表示单位循环的等效割线刚度;ζa表示单位循环的等效阻尼比。其中,
| ${{K}_{s}}=\frac{{{\sigma }_{max}}-{{\sigma }_{min}}}{{{\varepsilon }_{max}}-{{\varepsilon }_{min}}},{{\zeta }_{a}}=\frac{\Delta W}{2\pi {{K}_{s}}{{\varepsilon }^{2}}}$ | (1) |

|
| 图2 奥氏体SMA典型应力-应变曲线 Figure 2 Typical stress-strain curve of austenitic SMA |
式中:σmax(εmax)、σmin(εmin)分别表示每次循环中的最大应力(应变)和最小应力(应变),ε表示幅值应变。
限于篇幅,现仅给出加/卸载稳定下应变幅值6%时,加/卸载速率对超弹性力学性能的影响,如图 3所示。随着加/卸载速率的增大,奥氏体SMA丝的应力—应变曲线的卸载段发生明显的变化,各相变应力和相变平台发生不同程度的变化:马氏体相变过程受加/卸载速率的影响较小,σMs基本没有变化,σMf有很小幅度的增大;而SMA卸载过程受加/卸载速率的影响较大,σAs增大了77.29 MPa,增幅达30.35%,而σAf变化较小。这说明在较大的加/卸载速率下,随着加/卸载速率的增大,近视水平的奥氏体相变“平台”逐渐向上倾斜,使近似矩形、菱形形状的应力-应变曲线变成近似梯形甚至较窄三角形形状,这从侧面反映出耗能能力的减弱。随加/卸载速率的增大,ΔW降低了2.18 MJ/m3,降低幅度达17.17%;当加/卸载速率大于30 mm/min时,随加/卸载速率的增大ζa逐渐减小,ζa降低了0.91%,降低幅度达14.56%。这主要是由于SMA丝加载过程中产生的热量引起相变过程中SMA试件温度升高,降低了其自身的耗能能力。
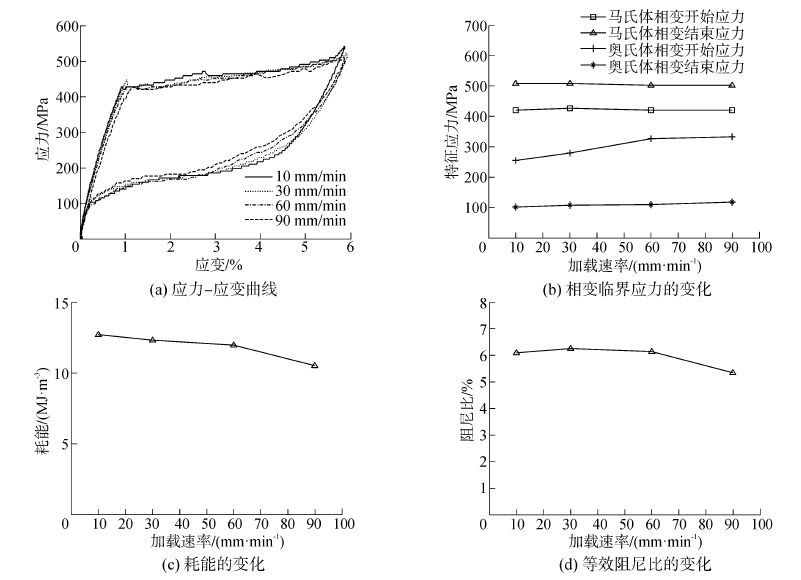
|
| 图3 加/卸载速率对奥氏体SMA丝力学性能的影响 Figure 3 Loading rate’s impact on mechanical properties of austenitic SMA wire |
BP网络即一种利用误差反向传播训练算法的神经网络,是一种由输入层、隐含层、输出层组成的多层前馈网络,其工作流程如图 4所示。BP网络以人工神经元作为基本单位,其工作过程主要分为两个阶段:第一阶段是学习阶段,此时各计算单元状态不变,各连接权上的权值可通过学习来修正;第二阶段是工作阶段,此时各连接权固定,计算单元变化,以达到某种稳定状态。BP网络因其较强的自学习能力得到广泛应用,但是在实际应用中存在网络收敛速度慢、容易震荡和陷入局部极小等问题[10-12],文中采用遗算法优化BP神经网络,从而提高网络收敛速度,避免震荡和陷入局部极小等问题。
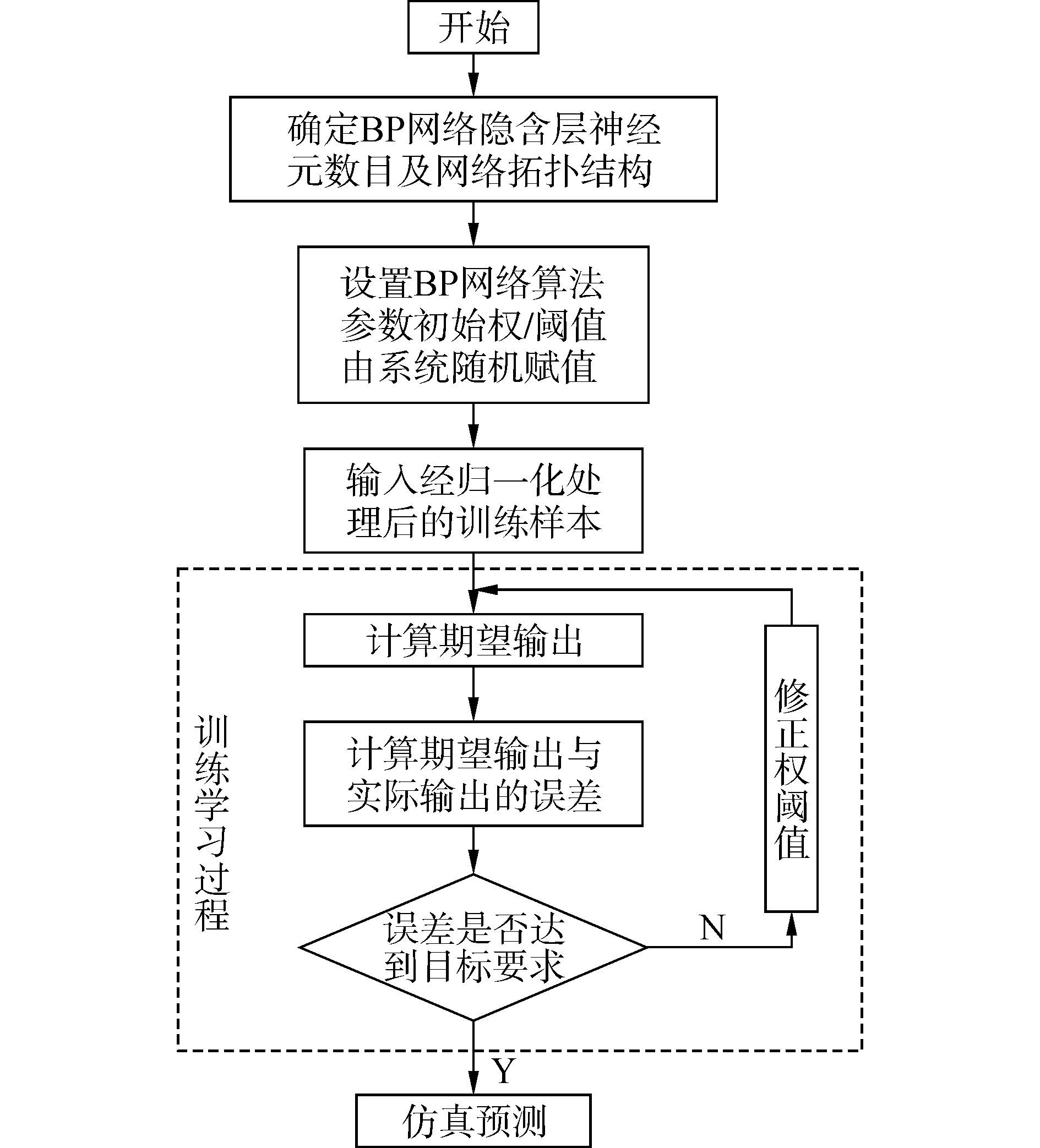
|
| 图4 BP网络算法流程 Figure 4 The process of BP network |
遗传算法采用以概率的并行全局搜索方式,而人工神经网络具有自学习的能力,为充分利用两者的优点,将两种算法结合使用,使新算法既有神经网络的鲁棒性和自学习能力,又具有遗传算法的全局搜索能力。因此文中利用遗传算法优化BP神经网络的初始权/阈值得到奥氏体SMA遗传优化BP网络本构模型。遗传算法优化BP网络初始权/阈值的流程图,如图 5所示。
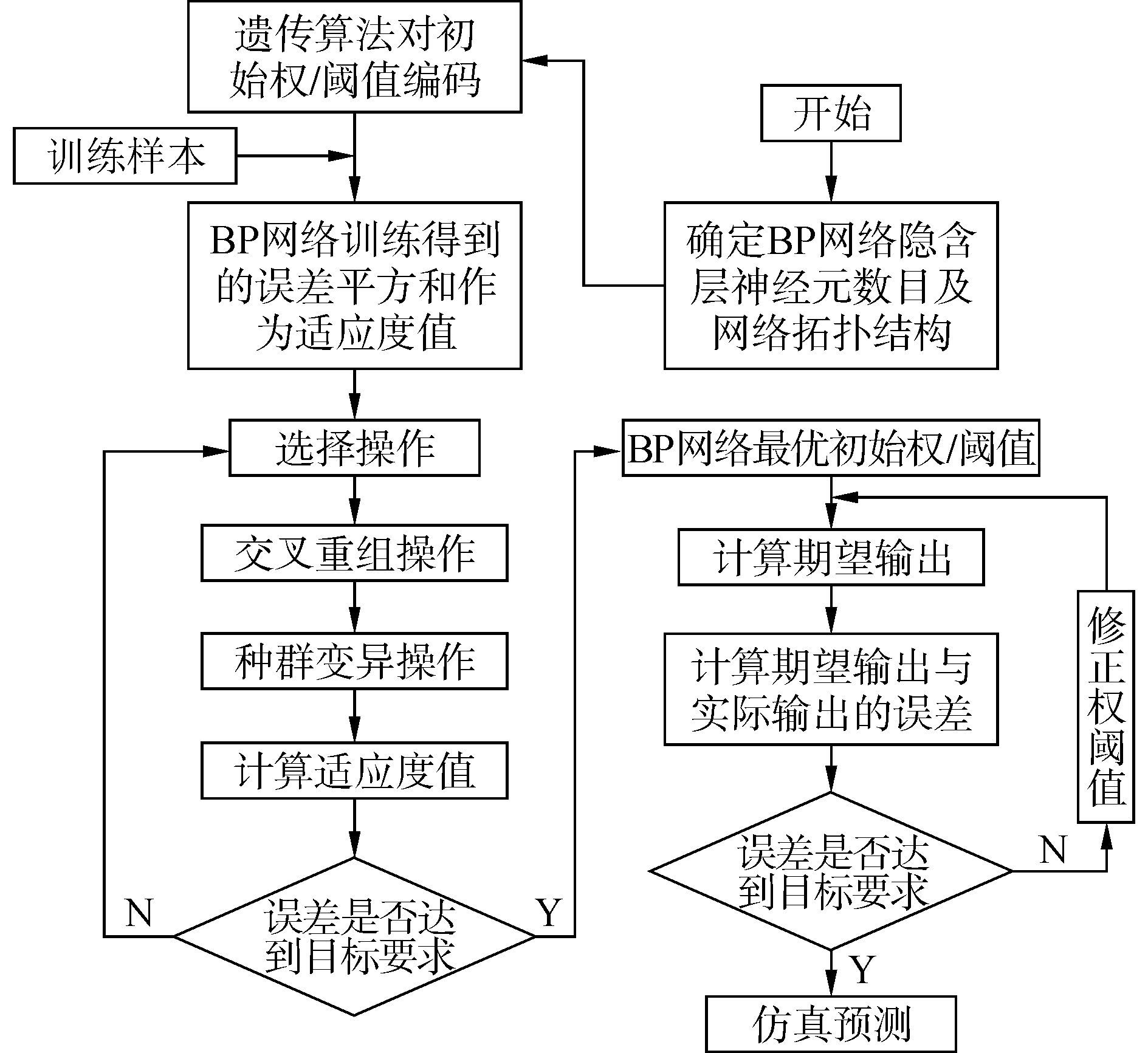
|
| 图5 遗传优化BP网络流程 Figure 5 The process of genetic BP network |
根据BP定理、Kolmogorov定理和Robert Hechi Nielson都证明了对于任何闭区间的一个连续函数,只要隐含层的神经元个数足够,可用一个隐含层的BP网络来实现任意精度的逼近。因此文中选用三层BP网络(即含一个输入层、一个输出层和一个隐含层)来建立奥氏体SMA神经网络本构模型。输入层神经元个数取为6个,分别为此时刻的加/卸载速率和应变,前时刻和前前时刻的应力、应变;输出层神经元为此时刻的应力;采用估算方法[12]隐含层神经元个数取为20个;隐含层神经元的激活函数选择为logsig,输出层神经元的激活函数为purelin。SMA本构模型的BP网络拓扑结构如图 6所示。
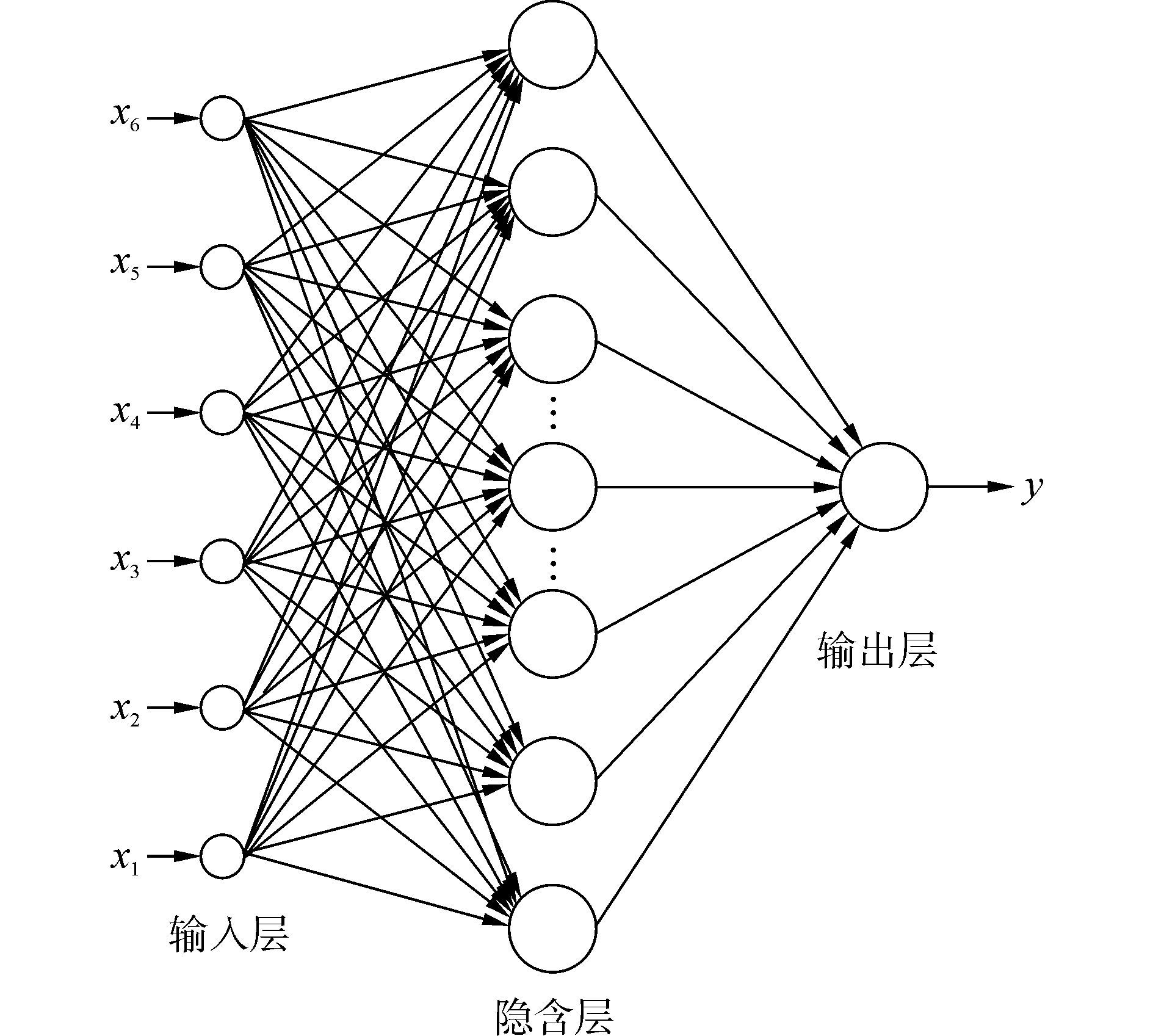
|
| 图6 BP网络本构的拓扑结构 Figure 6 The topological structure of BP network constitutive |
首先,由材性试验得到神经网络本构模型的训练数据。从12工况中选择应变幅值为6%对应的4个工况作为检验数据,其余8种工况作为训练数据。然后,将训练数据进行归一化处理得到训练BP网络所需的样本。
3.3 遗传算法优化参数确定未经优化BP网络的初始权/阈值,由系统随机分配;而经优化BP网络的初始权/阈值,由遗传算法寻优确定。由BP网路的结构可知,BP网络的待确定的权值有6×20+20×1=140个,待确定的阈值有20+1=21个,因此遗传算法的变量为所有权值和阈值,变量总数为161个。由于权/阈值取值可以是任意实数,为提高遗传算法的精度和效率,采用实值编码型遗传算法,则遗传算法染色体长度为161。目标函数为由训练样本输入所得期望输出与实际输出的误差平方和。遗传算法其他参数设置如下:初始种群数目为40;采用随机遍历采样选择函数,代沟为0.9;选择中间重组交叉算子;采用实值变异算子,变异概率为0.01;最大遗传代数为50代。
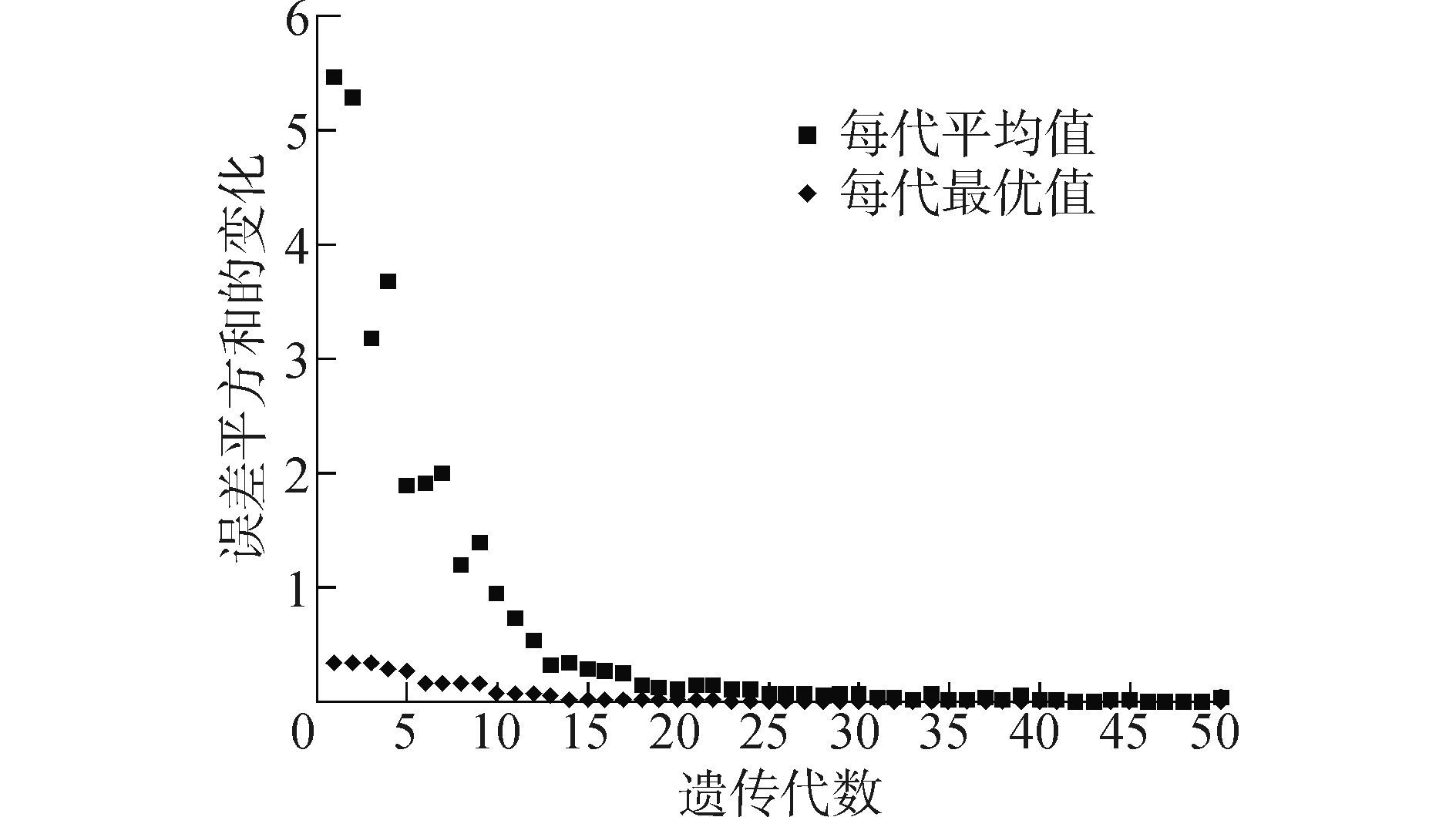
3.4 两种本构模型仿真结果比较利用Matlab建立奥氏体SMA本构的BP网络模型和经遗传优化的BP网络模型。遗传算法优化初始权/阈值过程如图 7所示,最小误差平方和为1.434 4。BP网络的训练函数选为trainlm,最大训练次数为1 000次,目标误差为10-5,学习速率为0.1,运行程序可得BP网络的拓扑结构如图 8所示。
|
| 图7 目标函数值随代数的变化 Figure 7 Changes in the value of the objective function |
|
| 图8 Matlab神经网络工具箱 Figure 8 The neural network toolbox of Matlab |
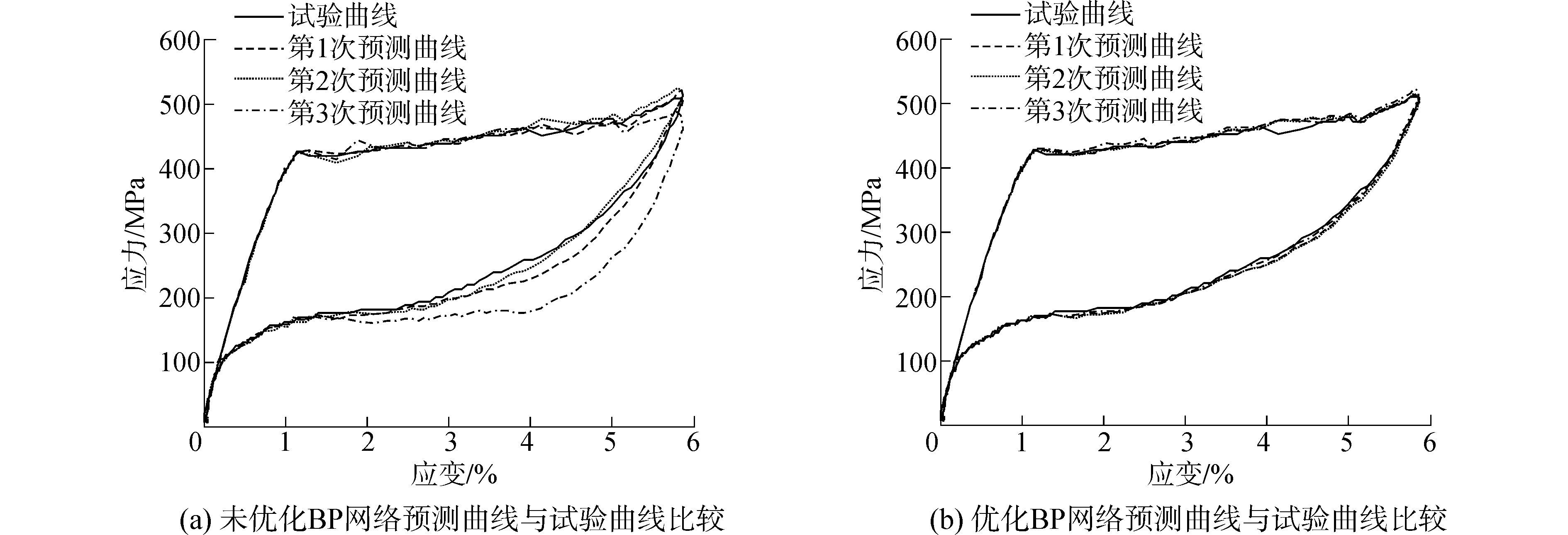
图 9为加/卸载速率为90 mm/min下3次应用未优化BP网络、遗传优化BP网络预测奥氏体SMA本构所得预测曲线与试验曲线的比较图。由图可知,未经遗传算法优化初始权/阈值的BP网络,由于初始权/阈值的随机性,使得每次训练学习后得到的BP网络具有较大差异,而经遗传优化后的BP网络算法能够得到稳定的BP网络本构模型。
|
| 图9 两种BP网络本构模型稳定性比较 Figure 9 The comparison of two BP network constitutive models′ stability |
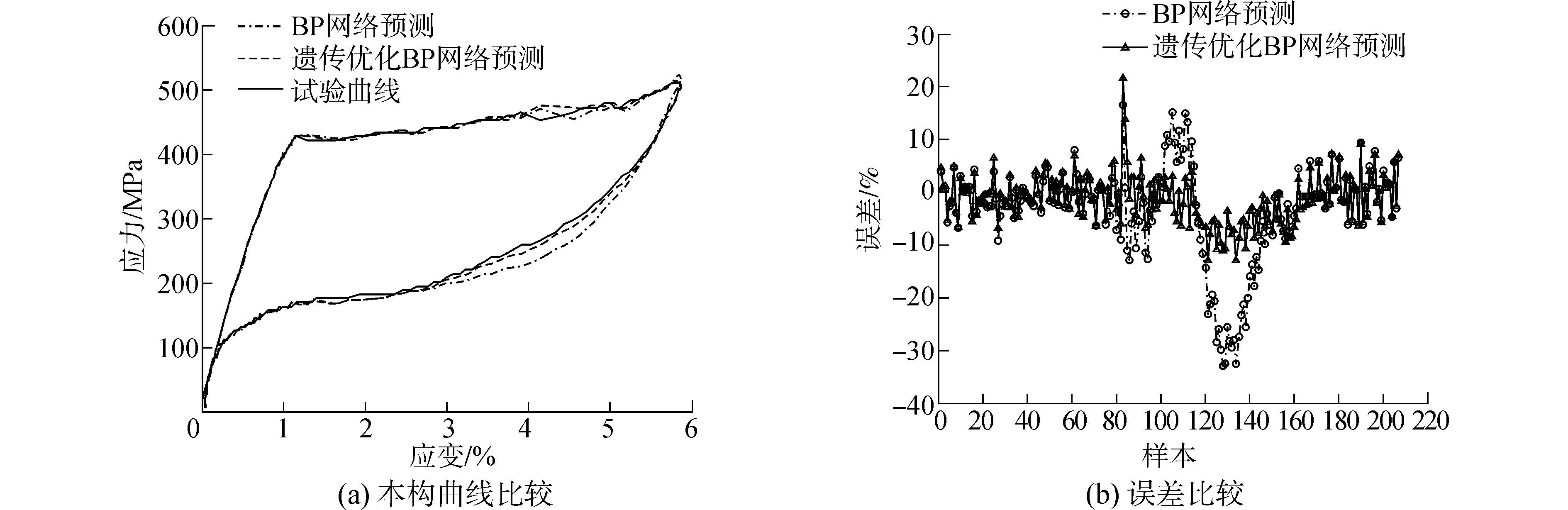
由于未优化BP网络每次运行的结构差异较大,此处选择预测结果较好的未优化BP网络与经优化的BP网络进行对比,加/卸载速率为90 mm/min下两种BP网络的预测比较如图 10所示,两种BP网络模型的预测平均绝对误差EP、EGP为
| ${{E}_{P}}=\frac{1}{n}\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\frac{\left| Y-{{Y}_{P}} \right|}{Y}=4.50%$ | (2) |
| ${{E}_{GP}}=\frac{1}{n}\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\frac{\left| Y-{{Y}_{GP}} \right|}{Y}=3.72%$ | (3) |
式中:Y为试验所测得的应力,YP为BP网络本构模型预测的应力,YGP为遗传算法优化的BP网络本构模型预测的应力。
由图 10可知,随奥氏体SMA丝加/卸载速率的变化,遗传优化的BP网络本构模型均能很好地预测SMA的受力行为,预测平均绝对误差仅为3.72%。尽管选取预测效果较好的未优化BP本构与遗传优化的BP本构比较,遗传优化的BP本构精度仍比未优化BP本构精度高。
|
| 图10 两种BP网络预测误差比较 Figure 10 The comparison of two BP networks′ prediction errors |
1) 由材性试验可知,SMA丝材的超弹性性能随着加载/卸载频率的增大而变化明显,应力-应变曲线奥氏体相变“平台”逐渐向上倾斜,奥氏体相变的开始应力明显增大,应力-应变形状从矩形、菱形逐渐过渡到梯形、较窄三角形,滞回曲线包围的面积逐渐减小,等效阻尼比逐渐减少,耗能能力也逐渐降低。
2) 相比未优化的BP网路,经优化的BP网络能得到稳定的本构模型,避免了每次运行BP网络算法所得模型的差异性,而且能避免由于权/阈值取值不当,引起的网络振荡而不收敛现象。
3) 遗传优化BP网络预测的本构曲线与试验曲线吻合很好,平均绝对误差很小,说明该模型能很好地反映加/卸载速率对SMA超弹性性能的影响,是一种精度较高的速率相关型超弹性本构模型。
| [1] |
王社良.
形状记忆合金在结构控制中的应用[M]. 西安: 陕西科学技术出版社, 2000 .
WANG Sheliang. Application of shape memory alloy in the structure control[M]. Xi'an: Press of Science and Technology of Shannxi, 2000 . |
| [2] | FALK F. One-dimensional model of shape memory alloys[J]. Arch mechanics, 1983, 35(1): 63–84. |
| [3] | ABEYARATNE R, KNOWLES J K. A continuum model of a thermoelastic solid capable of undergoing phase transitions[J]. Journal of the mechanics and physical solids, 1993, 41(3): 541–571. |
| [4] | TANAKA K. A thermomechanical sketch of shape memory effect:one-dimensional tensile behavior[J]. Res mechanica, 1986, 18(3): 251–263. |
| [5] | BRINSON L C, LAMMERING R. Finite element analysis of the behavior of shape memory alloys and their applications[J]. International journal of solids and structures, 1993, 30(23): 3261–3280. |
| [6] | BOYD J G, LAGOUDAS D C. A thermodynamical constitutive model for shape memory materials[J]. International journal of plasticity, 1996, 12(7): 843–874. |
| [7] |
任文杰, 李宏男, 王利强. 基于神经网络的超弹性形状记忆合金循环本构模型[J].
稀有金属材料与工程, 2012, 41(S2): 243–246.
REN Wenjie, LI Hongnan, WANG Liqiang. Cyclic model for superelastic shape memory alloy based on neural network[J]. Rare metal materials and engineering, 2012, 41(S2): 243–246. |
| [8] | PENG Xianghua, WANG Zhichao, LUO Tao, et al. An elasto-plastic constitutive model of moderate sandy clay based on BC-RBFNN[J]. Journal of central south university of technology, 2008, 15(S1): 47–50. |
| [9] |
李克钢, 郑东普, 黄维辉. 干湿循环作用下砂岩力学特性及其本构模型的神经网络模拟[J].
岩土力学, 2013, 34(S2): 168–173.
LI Kegang, ZHANG Dongpu, HUANG Weihui. Mechanical behavior of sandstone and its neural network simulation of constitutive model considering cyclic drying-wetting effect[J]. Rock and soil mechanics, 2013, 34(S2): 168–173. |
| [10] |
魏微, 高谦. 改进的BP神经网络模型预测充填体强度[J].
哈尔滨工业大学学报, 2013, 45(6): 90–95.
WEI Wei, GAO Qian. Strength prediction of backfilling body based on modified BP neural network[J]. Journal of Harbin Institute of Technology, 2013, 45(6): 90–95. |
| [11] | DING Shifei, Xu Xinzheng, ZHU Hong, et al. Studies on optimization algorithms for some artificial neural networks based on genetic algorithm (GA)[J]. Journal of computers, 2011, 6(5): 939–946. |
| [12] |
丛爽.
面向MATLAB工具箱的神经网络理论与应用[M]. 合肥: 中国科学技术大学出版社, 2009 .
CONG Shuang. Neural Network Theory and Applications Based on MATLAB Toolboxes[M]. Hefei: Press of University of Science and Technology of China, 2009 . |



