2. Department of Design, China Research and Development Academy of Machinery Equipment, Beijing 100089, China
将固体火箭发动机用于深水高速航行推进装置不仅具有机动性和灵活性的优势,而且更加有利于长期战备执勤[1]。唐嘉宁等[2]将球形气泡模型的计算结果与CFD计算结果进行对比,发现球形气泡模型结构简单,计算速度快,并能有效反映发动机点火瞬间的推力峰值特性。但由于该模型假设气体在整个射流过程中以单一气泡形态存在,并沿径向等速无限膨胀,没有考虑水-气的相互作用,因此在了解微观结构上需要进一步研究。王乐勤等[3]采用基于VOF方法的两相流模型结合动网格的方法模分析了气体喷射形成的复杂流场结构,发现在射流过程中气液两相流内形成了压缩和膨胀波以及涡旋运动。朱卫兵等[4-5]采用VOF模型对水下等温高速气体射流和热体射流进行了气水耦合数值求解,模拟出了气泡的形成、发展、断裂和融合过程,揭示了气泡中压力和马赫数等流场参数的变化规律。虽然Lindau等[6]对考虑空泡作用下的高速超空化水下推进过程进行了数值研究,提出了空泡的两相流计算模型,但没有对水下推进过程中的流动特性和发动机工作性能做进一步分析。唐嘉宁等[7-8]建立了水下超音速气体射流数学模型, 并将数值计算结果与实验结果进行对比,验证了该模型的合理性和准确性。由于气体射流数值模拟的研究还比较少,并且主要集中在对射流两相初期流场流动特性的模拟。从现有的水下高温燃气射流研究情况来看,基本都是采用气-液两相流进行建模,很少采用气-液-蒸汽具有相变过程两相进行研究,无法解决燃气射流在复杂环境下的流动过程。因此,建立了一套能够适应复杂环境的相变模型,对解决现有的工程实际中的有相变的流动问题非常有必要。
1 物理模型 1.1 真实气体模型及多相流气体处理方法固体火箭发动机水下射流流场中除燃气外,还存在液态水汽化而来的水蒸汽以及初始时刻的少量空气。将压强小于20 MPa、温度大于1 400 K时,可将燃气和空气作理想气体处理,由于水蒸汽离液态不远时,有必要将水蒸汽作真实气体考虑[9]。对水蒸汽应用Soave-Redlich-Kwong真实气体模型[10-12]为
| $ p = \frac{{RT}}{{V - b}} - \frac{{a\left( T \right)}}{{{V^2} + bV}} $ | (1) |
其中
| $ a\left( T \right) = {a_0}{\left\{ {1 + n\left[ {1 - {{\left( {\frac{T}{{{T_c}}}} \right)}^{\frac{1}{2}}}} \right]} \right\}^2} $ | (2) |
| $ n = 0.48 + 1.574\omega - 0.17{\omega ^2} $ | (3) |
该模型需要提供3个参数,即临界温度Tc、临界压力Pc、偏心因子ω。
将各相气体视为不同组分,利用多相流组分输运方程进行处理。不考虑流场中的化学反应,组分输运模型中第i组分守恒方程统一形式[13]为
| $ \frac{\partial }{{\partial t}}\left( {\rho {Y_i}} \right) + \nabla \cdot \left( {\rho v{Y_i}} \right) = - \nabla \cdot {J_i} + {S_i} $ | (4) |
| $ \sum\limits_{i = 1}^N {{Y_i} = 1} $ | (5) |
计算时,需要求解前N-1种组分的守恒方程,而第N种组分的质量分数可由式(5)求得。当把式(4)应用于多相流模型中,对q相的第i种组分,式(4)变为
| $ \begin{array}{l} \frac{\partial }{\partial }\left( {{\rho ^q}{a^q}Y_i^q} \right) + \nabla \cdot \left( {{\rho ^q}{a^q}{{\rm{v}}^q}Y_i^q} \right) = \\ - \nabla \cdot {a^q} \cdot J_i^q + {a^q}{S_i} + \left| {\sum\limits_{p = 1}^n {\left( {{{\dot m}_{{p^i}{q^j}}} - {{\dot m}_{{p^j}{q^i}}}} \right)} } \right| \end{array} $ | (6) |
式中:aq为q相的体积分数,ṁpiqj为由q相第j组分到p相第j组分的质量转移源项,ṁpiqj依此类推。
1.2 气液两相不平衡传热模型水温度如果不等于饱和温度,则认为燃气-水、蒸汽-水两相处于不平衡状态,相间将发生热交换。燃气-水、蒸汽-水两相界存在一层交界面。由于气液界面厚度很薄,假设两相交界面内的工质对两相的热流密度无影响[14],则:
| $ {Q_{VL}} = {Q_{VL}} = Q $ | (7) |
式中:Q为界面传热率;QVL为蒸汽向蒸汽-水交界面的传热率;QLV为水向蒸汽-水交界面的传热率。QVL、QLV分别由下式计算:
| $ {Q_{VL}} = A{h_{VL}}\left( {{T_V} - {T_{SAT}}} \right) $ | (8) |
| $ {Q_{VL}} = A\frac{{{k_L}}}{X}\left( {{T_V} - {T_{SAT}}} \right) $ | (9) |
式中:hVL为蒸汽-界面的传热系数;kL/X为水和界面的传热系数;X为传热界面的厚度;A为相间换热面积;TSAT为饱和温度;TV、TL分别为蒸汽、水液相温度。各相与两相间界面的热流密度qVL″和qLV″分别用下式计算[14]:
| $ {q_{VL}}^{\prime \prime } = \frac{{{Q_{VL}}}}{A} = {h_{VL}}\left( {{T_V} - {T_{SAT}}} \right) $ | (10) |
| $ {q_{VL}}^{\prime \prime } = \frac{{{Q_{VL}}}}{A} = \frac{{{k_L}}}{X}\left( {{T_L} - {T_{SAT}}} \right) $ | (11) |
根据水的饱和温度计算水的汽化率,对计算域中各个网格内的气相和液相流体分别求解。当混合相温度大于水的饱和温度,水吸收能量汽化为水蒸汽;当混合相温度小于水的饱和温度时,水蒸汽释放能量凝结为液态水[15]。液态水汽化公式:
| $ {{\dot m}_L} = \left\{ {\begin{array}{*{20}{l}} {{\lambda _L}{a_L}{\rho _L}\frac{{\left| {{T_L} - {T_{SAT}}} \right|}}{{{T_{SAT}}}},}&{{T_L} \ge {T_{SAT}}}\\ {0,}&{{T_L} < {T_{SAT}}} \end{array}} \right. $ | (12) |
水蒸汽凝结公式:
| $ {{\dot m}_V} = \left\{ {\begin{array}{*{20}{l}} {0,}&{{T_V} \ge {T_{SAT}}}\\ {{\lambda _V}{a_V}{\rho _V}\frac{{\left| {{T_V} - {T_{SAT}}} \right|}}{{{T_{SAT}}}},}&{{T_V} < {T_{SAT}}} \end{array}} \right. $ | (13) |
式中:ṁL、ṁV为液相的汽化率和气相的凝结率;λ为时间松弛因子;aL、aV为液相和气相的体积分数;其中TSAT根据当地压力查饱和水与饱和蒸汽表得到。某一单元格内液态水的净汽化率为
| $ \dot m = {{\dot m}_L} - {{\dot m}_V} $ | (14) |
水汽化造成的能量变化为
| $ {S_h} = - {Q_{LAT}}\dot m $ | (15) |
式中:Sh为水汽化吸收的能量或水蒸汽凝结释放的能量,当ṁ为正,表示当前单元格内总体表现为液态水汽化吸热,流场能量降低,Sh为负,反之亦同;QLAT为水的汽化潜热。
1.4 水的汽化冷凝过程为了考虑射流气体作用下一部分水的汽化和凝结过程。水的热力学面在p-T图反映了水的各相之间的转换关系,其中汽化线代表了汽化及冷凝过程。水的汽化和凝结主要取决于水的压力和温度,为了研究相变的转换过程,需要得到水的汽化线的方程即水的饱和蒸汽压与温度的关系以及汽化过程中能量的变化[16]。水蒸汽的临界温度为647.15 K,临界温度以下的饱和蒸汽压方程为[17]
| $ \ln {p_{SAT}} = 24.08 - \frac{{4651}}{{{T_{SAT}}}} $ | (16) |
用饱和蒸汽压强表示饱和温度为
| $ {T_{SAT}} = \frac{{4651}}{{24.08 - \ln {p_{SAT}}}} $ | (17) |
式中:pSAT为水的饱和蒸汽压,Pa。水的汽化潜热与水的汽化温度的关系如下:
| $ {Q_{LAT}} = - 2016{{\rm{e}}^{0.01006{T_{SAT}}}} + 3.007 \times {10^6}{{\rm{e}}^{ - 0.007291{T_{SAT}}}} $ | (18) |
式中:QLAT为水的汽化潜热, J/kg。
2 蒸汽相变过程实现采用的是有限体积方法,即求解过程中不断的对质量方程、动量方程、能量方程和体积输运方程进行迭代,具体方程[18]如下
| $ \frac{{\partial \left( {{\rho _m}} \right)}}{{\partial t}} + \frac{{\partial \left( {{\rho _m}{u_i}} \right)}}{{\partial {x_i}}} = {S_{\varphi 1}} $ | (19) |
| $ \begin{array}{l} \frac{{\partial \left( {{\rho _m}{u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {{\rho _m}{u_i}{u_j}} \right)}}{{\partial {x_j}}} = \\ - \frac{{\partial p}}{{\partial {x_i}}} + \frac{{\partial y}}{{\partial {x_j}}}\left[ {{u_m}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right] + {S_{\varphi 2}} \end{array} $ | (20) |
| $ \begin{array}{l} \frac{{\partial y}}{{\partial t}}\sum\limits_{k = L,g} {\left( {{a_k}{\rho _k}{E_k}} \right) + \frac{\partial }{{\partial {x_j}}}{u_j}} \sum\limits_{k = L,g} {\left[ {{a_k}\left( {{\rho _k}{E_k} + p} \right)} \right]} = \\ \frac{\partial }{{\partial {x_j}}}\left( {{k_{eff}}\frac{{\partial T}}{{\partial {x_j}}}} \right) + {S_{\varphi 3}} \end{array} $ | (21) |
| $ \frac{\partial }{{\partial t}}\left( {{a_g}{\rho _g}} \right) + \frac{\partial }{{\partial {X_i}}}\left( {{a_g}{\rho _g}{u_i}} \right) = 0 $ | (22) |
式中:ρ为密度;m为混合相;ui为速度分量;L下标为水,g为气体;Sφ1、Sφ2、Sφ3分别为质量源项、动量源项和能量源项;keff为有效热传导率(keff=kt+k);kt为湍流热传导率;T为绝对温度。源项方程写为[19]
| $ {S_\varphi } = A + B\varphi $ | (23) |
式(23)中A为显性部分;B为隐性部分,并且A、B分别为[19]
| $ A = {S^*} - {\left( {\frac{{\partial S}}{{\partial \varphi }}} \right)^*}{\varphi ^*} $ | (24) |
| $ B = {\left( {\frac{{\partial S}}{{\partial \varphi }}} \right)^*} $ | (25) |
水下发动机所涉及到的水-蒸汽相变过程是一种传热传质的物理过程,其中并没有涉及到化学反应。从而利用fluent用户自定义函数(User-Defined Function, UDF)只对与该物理过程相关的流体力学求解方程源项进行修改根据式(12)、(13)将水-蒸汽相变中水和蒸汽相的质量传递S*φ1、∂Sφ1/∂φ1*方程为
| $ \begin{array}{l} S_{{\varphi _1}}^* = \left[ { - k\frac{{\left( {{T_c} - {T_{SAT}}} \right)}}{{\left| {\left( {{T_c} - {T_{SAT}}} \right)} \right|}}} \right].\\ \left[ {\frac{{{C_1}{V_c}{R_c}\left| {\left( {{T_c} - {T_{SAT}}} \right)} \right|}}{{{T_{SAT}}}}} \right] \end{array} $ | (26) |
| $ \begin{array}{c} {\left( {\frac{{\partial {S_{{\varphi _1}}}}}{{\partial {\varphi _1}}}} \right)^*} = \left[ { - \frac{{\left| {\left( {{T_c} - {T_{SAT}}} \right)} \right| - k\left( {{T_c} - {T_{SAT}}} \right)}}{{2\left| {\left( {{T_c} - {T_{SAT}}} \right)} \right|}}} \right].\\ \left[ {\frac{{C \cdot {V_c} \cdot \left| {\left( {{T_c} - {T_{SAT}}} \right)} \right|}}{{{T_{SAT}}}}} \right] \end{array} $ | (27) |
式中:当k=1时表示S*φ1、∂Sφ1/∂φ1*是水的质量传递方程;当k=-1时表示S*φ1、(∂Sφ1/∂φ1)*是蒸汽的质量传递方程;-k(Tc-TSAT)/(Tc-TSAT)和-[|(Tc-TSAT)|-k·(Tc-TSAT)]/[2·|(Tc-TSAT)|]表示质量传递的方向。当Tc≥TSAT时,液相向汽相的质量转移;Tc < TSAT时,汽相向液相的质量转移。根据式(18)水-蒸汽相变的能量传递S*φ3、∂S*φ3/∂φ3*方程为
| $ S_{{\varphi _3}}^* = S_{{\varphi _1}}^*{Q_{LAT}} $ | (28) |
| $ {\left( {\frac{{\partial {S_{{\varphi _3}}}}}{{\partial {\varphi _3}}}} \right)^*} = \left[ { - 1 \cdot \frac{{\left( {{T_c} - {T_{SAT}}} \right)}}{{\left| {\left( {{T_c} - {T_{SAT}}} \right)} \right|}}} \right]\left[ {\frac{{{C_1} \cdot {V_c}}}{{{T_{SAT}}}}} \right] $ | (29) |
式中:-1·(Tc-TSAT)/|(TC-TSAT)|表示能量传递的方向。当Tc≥TSAT时,物质向外界放出热量;Tc < TSAT时,物质从外界吸收热量,最终能量达到平衡。式中Tc是网格单元温度;Vc是网格单元体积;RC网格单元密度;C1为质量转换系数,一般取值在0.1~0.2,也可选温度的一次函数来对求解过程进行加速,由式(8)~(11)可以知道能量最终会达到热平衡状态,采用文献[20]中的最小值作为整个相变过程中的转换系数,在此基础上通过减少时间步长来进行计算从而实验对瞬态结果进行描述;TSAT是网格单元中蒸汽的汽化冷凝温度,见式(17)所示;QLAT是网格单元中水汽化潜热,见式(18)所示。如果混合区的单元温度高于蒸发温度,质量转移由液相向汽相转移,进行吸热;相反,质量转移由汽相向液相转移,进行放热。把式(24)~(27)代入(23)可求出了质量方程的源项Sφ1;同理,把式(28)、(29)、(24)、(25)代入(23)可得出能量方程源项Sφ3。
3 模型有效性分析 3.1 实验对照模型水的饱和蒸汽压实验是在恒温恒压箱内进行。改变给定温度和给定压强条件后看是否发生蒸汽相变,由此来确定饱和蒸汽压强与温度的关系[20]。为了对水-蒸汽相变模型的有效性验证,建立一个简单模型(见图 1所示)。模型是一个长宽0.01 m,高0.005 m的长方形,全部使用结构网格划分。模型四周采用压力入口边界。

|
| 图1 水-蒸汽相变验证模型 Figure 1 Validation model of phase transition between water and vapor |
根据实验得到一些典型的饱和蒸汽压强与温度的关系数据, 如表 1所示[21]。
| 序号 | 1 | 2 | 3 | 4 |
| 温度/K | 323.15 | 373.15 | 423.15 | 473.15 |
| 压强/kPa | 12.3 | 101.3 | 476.2 | 1 554.8 |
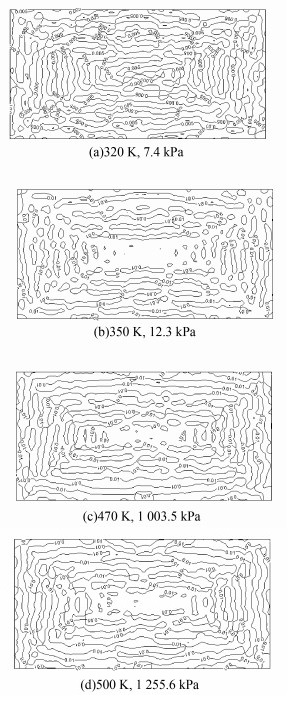
图 2为在饱和蒸汽压强与温度关系实验数据中选取的一组分别对温度和压强进行偏置后仿真结果。从图 2可以看出,运用提出的蒸发-冷凝相变模型进行计算,改变相应的工作条件具有以下规律:1)相同温度下减小压强会产生蒸汽;2)相同压强下增加温度会产生蒸汽;3)相同温度下增加压强蒸汽会消失;4)相同压强下减小温度会蒸汽消失。因此,该相变模型可以运用于复杂环境的仿真处理过程中,在改变仿真条件时,模型会根据本地条件自动给出相应的汽化-冷凝的相变温度及能量转换的热焓值,与以往的查表方式比较既快捷又准确还可以显示出不同区域的相变情况。
|
| 图2 不同条件下蒸汽相分布仿真结果 Figure 2 Distribution of vapor phase in different condition |
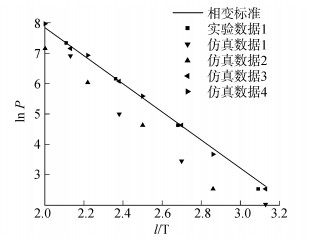
图 3将仿真数据与实验数据[21]进行比较,图中数据为对饱和蒸汽压强表数据进行偏置后的仿真结果,其中仿真数据3、4代表没有发生相变,仿真数据1、2代表发生相变。从图 3可以看出曲线走势一样,而发生仿真发生相变的饱和蒸汽压和温度的关系曲线必然在3、4和1、2之间与实验数据非常接近,并且趋势一样,通过夹逼原理可知,用于仿真的相变过程曲线与实验曲线非常吻合,能够很好地反应真实状态下的相变现象。由此可以证明该设计的水-蒸汽相变模型具有很高的有效性,可以解决工程实践中存在的相变现象,并且通过改变饱和汽化标准可以得到更加广泛的运用。
|
| 图3 仿真数据与实验数据对照图 Figure 3 Comparison of simulation data and experimental data |
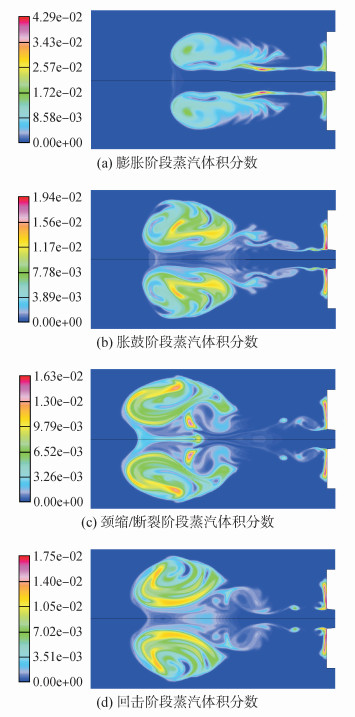
为了能够很好地说明该模型能够应用于现有的工程实际问题,对水下高温燃气射流中存在的相变问题进行分析。图 4为水下有相变的水下射流的过程。从图中可以看出有相变的射流过程仍然存在膨胀、胀鼓、颈缩/断裂和回击4个典型过程。在膨胀阶段(如图 4(a)所示),水下射流气体由于受到前段水的惯性阻力的作用下会在前端产生一个高压区,气体受到高压区的作用形成回流,回流在气泡内旋转形成两个涡区,由于涡区速度较高,压强较低,因此蒸汽在涡区具有驻留作用。在胀鼓阶段(如图 4(b)所示),由于喉部在激波系的作用下形成了高低压交互出现,在这里热量、质量交换比较剧烈,蒸汽量开始增加并随着高温燃气向前运动直至到涡区驻留。在缩颈/断裂阶段(如图 4(c)所示),气泡在水的挤压作用下形成两个气泡,新生气泡在水的惯性作用下会在气泡前段也会形成一个高压区,在高压区后方由于气泡处于过膨胀状态,气泡内压强较低,并且在燃气作用下形成两个回流区,这时这个区域较容易产生蒸汽。回击阶段(如图 4(d)所示),两个气泡融合成一个气泡,蒸汽在高压作用下被推向前方,气泡长度增长较快。气泡后端的回流区重新形成一个涡,由于涡区压强低,所以停留了大量蒸汽。射流将不断重复这4个典型过程。
|
| 图4 水-蒸汽-燃气流动典型过程仿真结果 Figure 4 Simulation results of typical processes in water-vapor-gas flow |
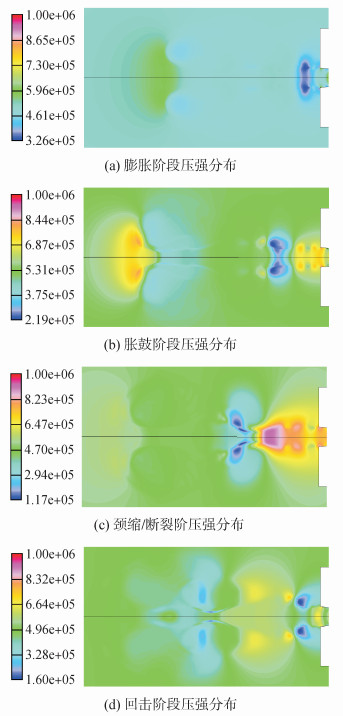
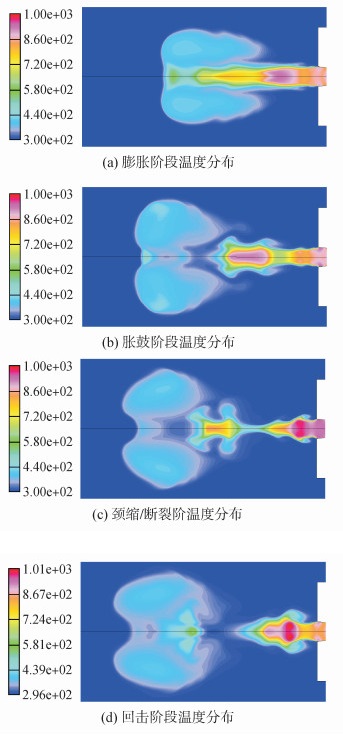
图 5为水下高温燃气射流4个典型过程中压强分布云图,图 6为水下高温燃气射流4个典型过程中温度分布云图。从图 5、6上可知,在燃气射流4个典型过程中产生了压强及温度的分布不均匀,并且压强和温度的工作作用下决定了蒸汽的产生及分布规律,如图 4所示。其中压强及温度变化趋势同图 4中解释相同。
|
| 图5 射流典型过程中的压强分布 Figure 5 Pressure distribution of typical processes for jets underwater |
|
| 图6 射流典型过程中的温度分布 Figure 6 Temperature distribution of typical processes |
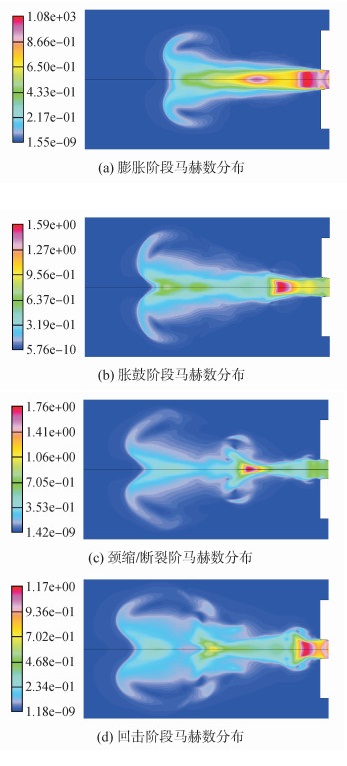
图 7为燃气射流四个典型过程中的马赫数分布云图。对比图 5、图 7可知,压力和马赫数之间满足伯努利方程。对比图 6、图 7可知,射流速度对温度分布具有影响,速度越大温度越小,反之既然。从图 7可知,图 7(a)到图 7(b)过程中,射流激波从正激波向斜激波转换,并且在斜激波的作用下产生了间歇性胀股,在能量聚集到一定程度后形成了缩颈。在缩颈阶段,由于气体通道变窄形成了二次加速,如图 7(c)所示。回击阶段通过图 5(d)和图 7(d)可知,气体反向运动,并与后来气体向后作用下分开从两侧向壁面运动完成回击过程。
|
| 图7 射流典型过程中的马赫数分布 Figure 7 Mach number distribution of typical processes |
通过采用VOF多相流模型的基本原理和蒸汽相变过程的基本理论设计了一种可以适用于复杂环境的蒸汽-水相变模型。
1) 该模型能够根据环境参数的变化自判断是否发生相变,并找到当地转换热焓值;
2) 设计了一套恒温恒压条件的仿真验证实验,仿真结果与实验结果进行对比发现两者数据非常吻合,验证了该模型具有较高的可靠性和实用性;
3) 把该蒸发-冷凝相变模型运用到了水下发动机有相变的燃气射流过程当中,对射流的四个典型过程中正蒸汽的产生与运动进行了分析。通过高温燃气射流对比分析,可以说明该模型比无相变过程的两相流模型更加优越,很好的解决工程实践中存在相变过程的射流问题。
| [1] |
甘晓松, 贾有军, 鲁传敬, 等. 水下燃气射流流场地数值研究[J].
固体火箭技术, 2009, 32(1): 23–26.
GAN Xiaosong, JIA Yonjun, LU Chuanjing, et al. Research on numerical simulation of combustion gas jet under water[J]. Journal of solid rocket technology, 2009, 32(1): 23–26. |
| [2] | TANG Jianing, LI Sipeng, WANG Ningfei, et al. Flow structures of gaseous jet injected into liquid for underwater propulsion[C]//46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. Nashville, IN:AIAA, 2010. |
| [3] |
王乐勤, 郝宗睿, 吴大转. 水下气体射流初期流场的数值研究[J].
工程热物理学报, 2009, 30(7): 1132–1135.
WANG Leqin, HAO Zongrui, WU Dazhuan. Numerical simulation of initial flow field of underwater gas jet[J]. Journal of engineering thermophysics, 2009, 30(7): 1132–1135. |
| [4] |
朱卫兵, 于洋, 王革, 等. 超音速欠膨胀多喷管燃气射流的数值模拟[J].
弹箭与制导学报, 2004, 24(3): 49–52.
ZHU Weibing, YU Yang, WANG Ge, et al. Numerical simulation of the supersonic under-expanded jet flow[J]. Journal of projectiles, rockets, missiles and guidance, 2004, 24(3): 49–52. |
| [5] |
徐琴华.水下发射燃气射流初期流场的数值研究[D].哈尔滨:哈尔滨工程大学, 2007:5-6.
XU Qinhua. Numerical study on the initial stage flow of gas jet for launch underwater[D]. Harbin:Harbin Engineering University, 2007:5-6. http://cdmd.cnki.com.cn/article/cdmd-10217-2008029078.htm |
| [6] | LINDAU J, VENKATESWARAN S, KUNZ R, et al. Multiphase computations for underwater propulsive flows[C]//16th AIAA Computational Fluid Dynamic Conference. Orlando, Florida:AIAA, 2013. |
| [7] | TANG Jianing, WANG Ningfei, WEI S. Flow structures of gaseous jets injected into water for underwater propulsion[J]. Acta mechanica sinica, 2011, 27(4): 461–472. DOI:10.1007/s10409-011-0474-4 |
| [8] |
唐嘉宁, 李世鹏, 王宁飞. 水下固体火箭发动机的负推力现象研究[J].
固体火箭技术, 2012, 35(3): 325–329, 343.
TANG Jianing, LI Shipeng, WANG Ningfei. Study on the negative thrust of the underwater solid rocket engines[J]. Journal of solid rocket technology, 2012, 35(3): 325–329, 343. |
| [9] | 赵险峰, 王俊杰. 潜地弹道导弹发射系统内弹道学[M]. 哈尔滨: 哈尔滨工程大学出版社, 2001: 31 -32. |
| [10] |
康玉东, 孙冰. 燃气非平衡流再生冷却流动传热数值模拟[J].
推进技术, 2011, 32(1): 119–124.
KANG Yudong, SUN Bing. Numerical simulation of regeneraive cooling flow and heat transfer with nonequilibrium flow[J]. Journal of propulsion technology, 2011, 32(1): 119–124. |
| [11] | 佘守贤. 真实气体与气液相变[M]. 北京: 人民教育出版社, 1964: 50 -51. |
| [12] | SOAVE G. Equilibrium constants from a modified Redlich-Kwong equation of state[J]. Chemical engineering science, 1972, 27(6): 1197–1203. DOI:10.1016/0009-2509(72)80096-4 |
| [13] |
刘伯伟, 姜毅. 汽化效应对燃气蒸汽式弹射气液两相流场的影响[J].
固体火箭技术, 2014, 37(2): 156–160.
LIU Bowei, JIANG Yi. Influence of vaporization effect on gas-liquid two-phase flow field of ejection in combustion gas and vapor mode[J]. Journal of solid rocket technology, 2014, 37(2): 156–160. |
| [14] |
孔夏明, 王苇, 孟海波, 等. 蒸汽排放系统蒸汽冷凝器动态特性仿真研究[J].
原子能科学技术, 2013, 47(12): 2272–2276.
KONG Xiaming, WANG Wei, MENG Haibo, et al. Simulation study on dynamic characteristic of steam condenser for steam discharge system[J]. atomic energy science and technology, 2013, 47(12): 2272–2276. |
| [15] | LEE W H. A pressure iteration scheme for two-phase flow modeling[M]//VEZIROGLU T N. Multiphase Transport Fundamentals, Reactor Safety, Applications, Vol 1.Washington:Hemisphere Publishing, 1980:407-431. |
| [16] | ANDERSON Jr J D. Fundamentals of aerodynamics[M]. 2nd ed. New York:McGraw-Hill, Inc., 1991:80-81. http://www.studfiles.ru/preview/461732/ |
| [17] | ZHANG Xiaoyuan, TANG Yunlong, LI Shipeng, et al. Impact of phase transitions on the flow structure of gaseous jets injected into water[C]//51st AIAA/SAE/ASEE, Joint Propulsion Conference. Orlando, Florida:AIAA, 2015. |
| [18] |
董师颜, 张兆良.
固体火箭发动机原理[M]. 北京: 北京理工大学出版社, 1996: 24 -25.
DONG Shiyan, ZHANG Zhaoliang. Principles of solid rocket motor[M]. Beijing: Beijing Institute of Technology Press, 1996: 24 -25. |
| [19] | 韩占中. Fluent:流体工程仿真计算实例与分析[M]. 北京: 北京理工大学出版社, 2009: 30 -31. |
| [20] | 何涛. 《工程热力学》课程实验指导书[M]. 北京: 北京交通大学, 2005: 14 -15. |
| [21] | 叶学群. 热工与流体力学基础(制冷和空调设备运用与维修专业)[M]. 北京: 高等教育出版社出版, 2004: 175 -176. |



