2. 中电科海洋信息技术研究院有限公司, 北京 100041;
3. 大连理工大学 海洋科学与技术学院, 辽宁 盘锦 124221;
4. 大连理工大学 计算机科学与技术学院, 辽宁 大连 116024
2. CETC Ocean Co., Ltd., Beijing 100041, China;
3. School of Ocean Science and Technology, Dalian University of Technology, Panjin 124221, China;
4. Department of Computer Science and Technology, Dalian University of Technology, Dalian 116024, China
海洋结构受恶劣的海洋环境荷载作用,定位性能是其结构与作业安全的保障。顺应式系泊系统由于出色的力学性能和经济效益,是目前应用最为广泛的定位系统[1]。顺应式系泊系统通常由锚链、钢缆或尼龙缆绳等多种成分构成,空间尺度巨大,通常被认为是与环境荷载和被系浮体强烈耦合的非线性时变动态系统,利用自身重力或者预张力提供浮式结构所需回复力。对系泊系统张力与动态响应特性的准确分析,是系泊系统结构设计与安全保障中的关键问题。
水动力分析和室内模型实验是系泊系统研究的主要方法。然而,随着系泊系统使用水深的增加,对深海海洋环境认识不足导致目前数值分析方法与室内模型试验方法在海洋结构分析方面存在局限性与不确定性[2]。因此,相关学者提出利用在位服役的结构上开展原型测量,可以获得真实环境荷载条件与同步的结构响应信息,以此开展海洋结构的动态行为研究。目前,原型测量已经作为重要的研究方法在服役的系泊系统上广泛的开展[3-7]。
目前系泊系统的测量方法主要有三类:
1) 顶端直接测量,利用loadcell等测力装置,在锚链止链器位置对系泊张力开展直接测量。同时,为了获得系泊力的水平与竖直分量,需要对系泊缆的入水角度进行测量。顶端直接测量具有易于开展、高精度和低成本的优点,是目前应用最为广泛的测量方法[8-10]。然而,由于系泊缆与平台之间存在接触,会导致顶端系泊张力测量结果动态响应较实际结果偏低。另外,测量系统的安装与维护需要脱缆操作,对于永久固定式系泊系统和老龄平台系泊系统并不适用;
2) 预置传感器测量,采用在系泊缆中预置光纤或应变片等测量传感器,开展系泊结构在位响应的测量。文献[11]介绍了一种利用预置聚合物光纤对系泊缆开展测量的方法,实现了对系泊缆疲劳寿命的测量;文献[12]开发了一种基于应变片的系泊缆测量系统,能够在系泊缆上端对系泊缆的张力和弯矩开展测量。预置测量方法对系泊缆的动态响应测量效果出色。另外可以对较长跨度的系泊缆开展连续的测量。然而由于工艺复杂和安装困难等缺点,并不适合广泛的应用;
3) 水下测量,利用开发的特殊传感器对在位系泊系统开展结构测量。文献[13]讨论了一种利用横向变形获得锚链张力的测量装置。然而该装置仅适合无肋锚链测量,且对安装精度有很高的要求;文献[14]介绍了一种水下系泊检测机器人,利用光学校准器精确的获得系泊缆的形状参数;文献[15]介绍了一种利用主动激励,通过对结构振动响应分析检测系泊结构完整性的装置。以上两种装置均无法获得系泊缆的张力信息。
目前的系泊系统测量方法和测量装置难以实现系泊测量系统长期性、准确性、稳定性和经济性的需求。尤其是对老龄平台系泊系统难以开展原型测量。为此,本文基于集中质量法提出了一种系泊缆的测量策略,利用数值分析中边界条件的变换,将难以获得的参量转化为水下易于高精度测量的物理量,以此解决目前研究工作中对在位系泊缆无法开展张力测量的问题。同时基于自容式技术设计了一套新型水下监测系统,并在我国南海开展了实际应用。为了证明监测系统的可靠性和可行性,对长期数据和短期数据样本分别开展了分析。
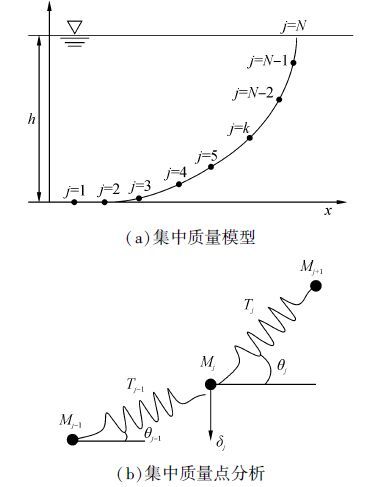
1 系泊缆张力测量策略图 1(a)为系泊缆的集中质量模型,图 1(b)为集中质量节点分析。系泊链集中质量点的运动方程:
| $({{M}_{j}}+{{m}_{j}})\times {{\ddot{u}}_{j}}={{f}_{j}}$ | (1) |
|
| 图1 系泊缆集中质量模型分析 Figure 1 The lumped mass model of mooring line |
式中:Mj为质量阵,mj为附加质量阵,
第j节点荷载包括自身重力δj,张力Tj,下一节点的张力Tj-1,等效节点流体拖曳力fdxj和fdzj,因此,运动方程可以表达为
| $\begin{align} & \left( {{M}_{j}}+{{A}_{nj}}si{{n}^{2}}{{{\bar{\theta }}}_{j}}+{{A}_{tj}}co{{s}^{2}}{{{\underset{\scriptscriptstyle\centerdot}{\theta }}}_{j}} \right){{{\ddot{x}}}_{j}}+\left( {{A}_{tj}}- \right. \\ & \left. {{A}_{nj}} \right){{{\ddot{z}}}_{j}}sin{{{\bar{\theta }}}_{j}}cos{{{\bar{\theta }}}_{j}}={{T}_{j}}cos{{{\bar{\theta }}}_{j}}-{{T}_{j-1}}cos{{\theta }_{\bar{j}-1}}-{{f}_{dxj}} \\ \end{align}$ | (2) |
| $\begin{align} & \left( {{M}_{j}}+{{A}_{nj}}co{{s}^{2}}{{{\bar{\theta }}}_{j}}+{{A}_{tj}}si{{n}^{2}}{{{\bar{\theta }}}_{j}} \right){{{\ddot{z}}}_{j}}+\left( {{A}_{tj}}- \right. \\ & \left. {{A}_{nj}} \right){{{\ddot{x}}}_{j}}sin{{{\bar{\theta }}}_{j}}cos{{{\bar{\theta }}}_{j}}={{T}_{j}}cos{{{\bar{\theta }}}_{j}}-{{T}_{j-1}}cos{{{\bar{\theta }}}_{j-1}}-{{f}_{dxj}}-{{\delta }_{j}} \\ \end{align}$ | (3) |
| ${{{\bar{\theta }}}_{j}}=\frac{1}{2}({{\theta }_{j}}+{{\theta }_{j+1}})$ | (4) |
式中:Anj、Atj为法向和切向的附加质量,θj和θj+1为第j点和第j+1点处的角度。
流体拖曳力可以由Morrison方程获得
| $\left[ \matrix{ {f_{dxj}} \hfill \cr {f_{dzj}} \hfill \cr} \right] = \left[ \matrix{ - {\rho \over 2}{D_c}l({C_{dn}}sin{{\bar \theta }_j}\left| {{u_{nj}}} \right|{u_{nj}} - {C_{dt}}cos{{\bar \theta }_j}\left| {{u_{tj}}} \right|{u_{tj}}) \hfill \cr {\rho \over 2}{D_c}l({C_{dn}}cos{{\bar \theta }_j}\left| {{u_{nj}}} \right|{u_{nj}} - {C_{dt}}sin{{\bar \theta }_j}\left| {{u_{tj}}} \right|{u_{tj}}) \hfill \cr} \right]$ | (5) |
| $\left[ \matrix{ {u_{nj}} \hfill \cr {u_{tj}} \hfill \cr} \right] = \left[ \matrix{ - ({{\dot x}_j} - {c_j})sin{{\bar \theta }_j} + {{\dot z}_j}cos{{\bar \theta }_j} \hfill \cr ({{\dot x}_j} - {c_j})cos{{\bar \theta }_j} + {{\dot z}_j}sin{{\bar \theta }_j} \hfill \cr} \right]$ | (6) |
式中Cdn和Cdt为切向和法向的拖曳系数。
系泊缆集中质量模型运动方程的数值求解,通常利用Houbolt差分格式,以上端点位移作为边界条件,获得系泊缆的动态张力。
| ${{x}_{0}}\left( t \right)={{x}_{0}},\text{ }{{z}_{0}}\left( t \right)={{z}_{0}}$ | (7) |
| ${{x}_{N}}\left( t \right)={{x}_{N}},\text{ }{{y}_{N}}\left( t \right)={{z}_{N}}$ | (8) |
| ${{x}_{i}}\left( 0 \right)=x_{i}^{0},\text{ }{{y}_{i}}\left( 0 \right)=z_{i}^{0}$ | (9) |
由于浮式平台远离陆地,缺少固定参照物,因此很难获得准确的位移响应信息。精度达到分米级的DGPS是应用广泛的测量装置。然而测量结果无法满足系泊缆张力分析需求。因此,本文提出一种利用两倾角测量反算系泊力的测量方法。
第N节点在时间步长n+1上的几何边界条件为
| $\left\{ \begin{align} & x_{N}^{n+1}=x_{N}^{n}+x \\ & z_{N}^{n+1}=z_{N}^{n}+z \\ \end{align} \right.$ | (10) |
式中:x和z是节点N的位移量;xNn和zNn是节点N在时间步长n上的位置量。
x和z可以利用几何关系获得
| $\left\{ \begin{align} & x=\sum\limits_{1}^{N}{{}}l_{k}^{n+1}cos\theta _{k}^{n+1} \\ & z=\sum\limits_{1}^{N}{{}}l_{k}^{n+1}sin\theta _{k}^{n+1} \\ \end{align} \right.$ | (11) |
式中:lkn+1是节点k和k-1之间的长度,θkn+1是节点k与水平方向的夹角。
原型测量中,无法获得所有节点的角度信息。根据悬链线几何关系可知,系泊缆上部角度变化更为明显。因此,如果获得上部两个已知位置的角度变化信息,可以利用迭代方法获得系泊缆顶部位移信息。
| $\left\{ \begin{align} & \Delta x_{N}^{n+1\left( 0 \right)}=l_{N}^{n}cos(\theta _{N}^{n+1}-\theta _{N}^{n})+l_{N-1}^{n}cos(\theta _{N-1}^{n+1}-\theta _{N-1}^{n}) \\ & \Delta z_{N}^{n+1\left( 0 \right)}=l_{N}^{n}sin(\theta _{N}^{n+1}-\theta _{N}^{n})+l_{N-1}^{n}sin(\theta _{N-1}^{n+1}-\theta _{N-1}^{n}) \\ \end{align} \right.$ | (12) |
| $\left\{ \begin{align} & \Delta x_{N}^{n+1(i)}=l_{N}^{n+1\left( i \right)}cos(\theta _{N}^{n+1}-\theta _{N}^{n+1\left( i \right)})+ \\ & l_{N-1}^{n+1\left( i \right)}cos(\theta _{N-1}^{n+1}-\theta _{N-1}^{n+1\left( i \right)}) \\ & \Delta z_{N}^{n+1\left( i \right)}=l_{N}^{n+1\left( i \right)}sin(\theta _{N}^{n+1}-\theta _{N}^{n+1\left( i \right)})+ \\ & l_{N-1}^{n+1\left( i \right)}sin(\theta _{N-1}^{n+1}-\theta _{N-1}^{n+1\left( i \right)}) \\ \end{align} \right.$ | (13) |
式中:ΔxNn+1(i)和ΔzNn+1(i)是第i次迭代时的位移增量,lNn+1(i)和lN-1n+1(i)是第i次迭代时节点之间的长度,θNn+1(i)和θN-1n+1(i)是第i次迭代时节点与水平方向夹角。 选择Houbolt差分格式,获得系泊缆的位移边界条件:
| $\eqalign{ & \left\{ \matrix{ \ddot x_j^{n + 1}\left( {2x_j^{n + 1} - 5x_j^n + 4x_j^{n - 1} - x_j^{n - 2}} \right)/\Delta {t^2} \hfill \cr \dot x_j^{n + 1} = (11x_j^{n + 1} - 18x_j^n + 9x_j^{n - 1} - 2x_j^{n - 2})/\Delta {t^2} \hfill \cr} \right. \cr & \left( {2 \le j \le N} \right) \cr} $ | (14) |
| $\eqalign{ & \left\{ \matrix{ \ddot z_j^{n + 1} = (2z_j^{n + 1} - 5z_j^n + 4z_j^{n - 1} - z_j^{n - 2})/\Delta {t^2} \hfill \cr \dot z_j^{n + 1} = (11z_j^{n + 1} - 18z_j^n + 9z_j^{n - 1} - 2z_j^{n - 2})/\Delta {t^2} \hfill \cr} \right. \cr & \left( {2 \le j \le N} \right) \cr} $ | (15) |
补充几何边界条件:
| $\begin{align} & \phi _{j}^{n+1}=(x_{j}^{n+1}-x_{j-1}^{n+1})2+(z_{j}^{n+1}-z_{j-1}^{n+1})2- \\ & {{l}^{2}}{{(1+T_{j-1}^{n+1}/EA)}^{2}}=0\text{ }\left( 2\le j\le N \right) \\ \end{align}$ | (16) |
由以上条件,可以获得第n+1时间步上第i次迭代时系泊缆的张力TNn+1,节点间长度lkn+1和与水平方向夹角变化量θkn+1。当θkn收敛时,即获得第n+1时间步的系泊信息。因此利用系泊缆水下两个已知位置角度的测量获得系泊缆张力的方法是可行的。此外,通过水下系泊缆角度测量也能获得系泊缆动态响应信息,对系泊缆动态行为研究也具有重要意义。
2 监测系统设计为了实现水下系泊结构角度测量,本文设计了一种水下自容式姿态测量传感器。基于此传感器构建了水下系泊缆监测系统。
2.1 自容式传感器设计自容式传感器是一类无缆的独立工作传感器,具有独立的信息采集、数据存储和电源供应,不需要外界支持即可完成结构信息测量。由于传感器具有独立工作的能力,易于开展防护,因此非常适合用于海洋环境测量。基于海洋结构测量需求,在传感器设计中应当开展了长期性设计和可靠性设计。
2.1.1 低功耗设计传感器依靠自身电力供应工作,为了获得足够长的工作时间,设计中对传感器功耗的控制尤为重要。自容式传感器主要由微处理单元、传感单元、A/D转换单元、数据存储、时钟和电力管理单元构成。为了满足使用中低功耗的需求,所有单元均采用低功耗元件设计。其中功耗较大的处理单元采用MSP430F149单片机,在满足处理速度的同时有效的控制了功耗。最终传感器工作状态电流为8 mA,待机状态仅为0.39 mA。选用两节19 Ah电池供电情况下,系统可以最少持续工作3个月。
2.1.2 模块化设计为了提高传感器的稳定性和可扩展性,自容式传感器硬件电路采用模块化设计,通过总线对实现独立模块之间的通信。采用模块化设计的硬件也易于实现小型化设计。
2.1.3 完全事件激发工作模式传感器系统采用完全事件激发工作模式。在无事件激发情况下,系统处于待机状态;当发现事件激发时,CPU被迅速唤醒,同时系统转换为工作模式。当事件处理完成,系统会再次转换为待机模式等待下一次的时间激发。
2.1.4 电源管理系统为了有效节能,传感器采用双电源芯片分别为微处理单元和电路供电。系统处于待机状态时,电路供电被关闭,仅供微处理单元处于休眠模式所需电力。此外,充分利用了电源芯片的使能,最大限度的节约电力供应。传感器最终设计指标如表 1,电路结构如图 2。
| 参数 | 数值 |
| 测量范围/(°) | ±90 |
| 采样频率/Hz | 1~10 |
| 精度/(°) | 0.01 |
| 分辨率/(°) | 0.002 5 |
| 工作时间 | 3个月 |

|
| 图2 自容式传感器电路结构图 Figure 2 Integration of circuits of the self-contained inclinometer |
水下结构监测的工程应用难点在于系统防护和系统的安装/回收。
2.2.1 水下防护传感器应用于水下,需要考虑长期工作中防水性与抗海水、水生物腐蚀的能力,同时系统也应当具有足够的强度抵抗各种类型的意外冲击。本文设计了专用密封桶传感器硬件和电源的防护装置。为了满足水下应用需求,密封桶采用了高等级316 L不锈钢设计。防护桶尺寸210 mm×60 mm(高度×半径),重量2.2 kg带传感器与电池)。尺寸设计满足水下系泊测量轻量化设计需求。防护桶设计可用于水下200 m,为了证明其防水性,进行了加压保压测试,结果证明传感器可抵抗不小于4 MPa瞬时压力,可抵抗不小于2 MPa的长期压力。
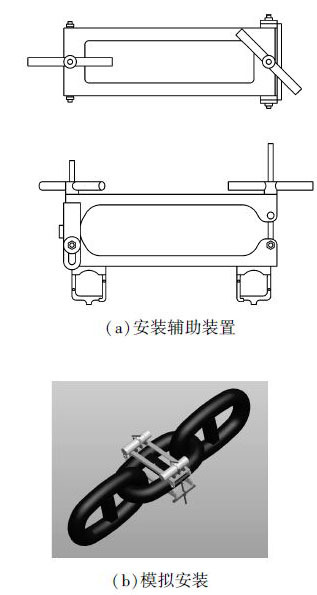
2.2.2 水下安装/回收水下安装/回收是水下监测的瓶颈问题。水上安装后投放是应用广泛的方式,但是不适用于在位结构的监测。为了解决这一问题,本文针对自容式传感器设计潜水员安装——水下机器人(ROV)回收的应用模式,并设计了水下安装辅助装置,解决了对于在位系泊结构的水下测量安装问题。图 5(a)为辅助装置设计图,图 5(b)为模拟安装图。

|
| 图3 自容式传感器样机 Figure 3 Self-contained inclinometer with water-resistant cover |

|
| 图4 加压测试实验 Figure 4 Waterproof performance test |
|
| 图5 自容式传感器安装辅助装置及模拟安装 Figure 5 Specially designed clamp and simulation installation of sensor |
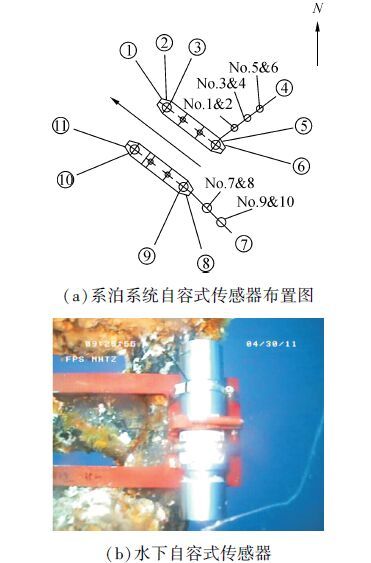
为了验证监测系统的可行性,在我国南海一座半潜式平台“南海挑战号”FPS上开展了实测。该平台采用十一根非对称系泊结构,选择其中4号和7号两条系泊缆开展了监测工作。监测系统共布置5套10个传感器,包含连续工作,采样频率1 Hz和每小时工作20 min,采样频率5 Hz两类传感器。图 6(a)为系泊系统与传感器布置图,图 6(b)为传感器在位工作图。
|
| 图6 水下系泊监测系统 Figure 6 Underwater monitoring system for mooring lines |
监测工作自2011年5月起至2011年10月,表 2例举了传感器的工作方式与工作时间。可以发现,连续工作的传感器工作时长为3个月;间断工作的传感器工作时间超过5个月。实现了监测传感器长期性设计要求。
| No.1 | No.2 | No.3 | No.4 | No.5 | No.6 | No.7 | No.8 | No.9 | No.10 | |
| 工作方式 | 连续 | 间断 | 连续 | 间断 | 连续 | 间断 | 连续 | 间断 | 连续 | 间断 |
| 采样频率/Hz | 1 | 5 | 1 | 5 | 1 | 5 | 1 | 5 | 1 | 5 |
| 工作天数 | 90 | 174 | 86 | 174 | 74 | 174 | * | * | 72 | 127 |
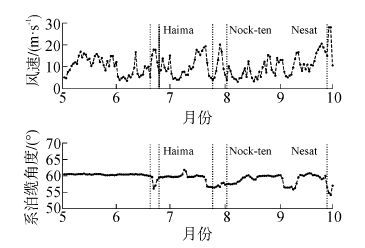
图 7为测量期间每日最大风速与No.1号自容式传感器测量到的每日最大角度。从图中可以看出,自容式传感器具有良好的持续工作能力。在测量期间也捕获了比较典型的台风天气环境与系泊响应信息。
|
| 图7 测量期间每日最大风速与系泊缆角度 Figure 7 Daily maximum values of wind and inclination angle during measurement period |
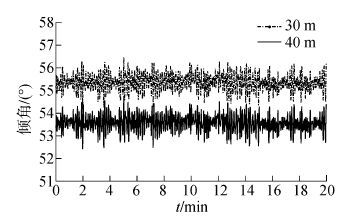
为了进一步对监测系统测量得到的信息进行验证,选择7月28日洛坦台风期间,22:00~22:20之间20 min的实测数据进行深入分析。实测的水下系泊角度信息如图 8所示。从图中可以看出,安装在不同深度的传感器测量结果具有比较好的同步性。
|
| 图8 4号锚链自容式传感器测量系泊缆角度变化 Figure 8 Inclination angle variations measured by sensors installed at mooring line No.4 during selected periods |
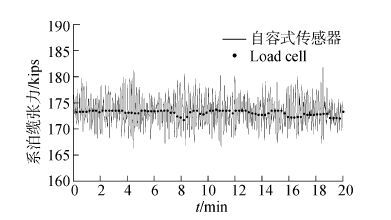
利用第1章介绍的集中质量法,获得监测系统测量得到的系泊缆张力。同时选择被测系泊缆顶部称重式压力传感器(Load cell)测量得到的系泊力作为比较结果。图 9为比较结果。统计结果如表 3所示。
|
| 图9 监测系泊缆张力与压力传感器测量结果比较 Figure 9 Comparison results of mooring line tension measured by self-contaied sensor and Load cell |
| 最大值/kips | 最小值/kips | 平均值/kips | 方差 | |
| 监测系统结果 | 181.8 | 166.3 | 173.3 | 2.5 |
| Load ell测量结果 | 173.7 | 171.7 | 173.1 | 0.48 |
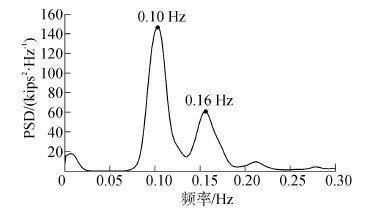
从结果可以看出,测量得到的系泊力与理论结果均值相近。但是监测系统测量有明显的波动性,可以获得更多频率上的系泊变化。图 10对监测系统获得的系泊缆张力开展了谱分析,结果显示在台风天气下,监测系统可以捕捉到系泊缆张力在波频和高频表现出来的能量波动,结果对与极端天气下系泊缆动态响应分析具有重要的意义。
|
| 图10 系泊缆张力谱分析 Figure 10 PSD result of mooring line tension measured by self-contained sensors |
对浮式平台系泊系统开展现场监测是开展动态行为研究和安全保障的重要手段。为了解决目前现役系泊结构缺少有效测量手段和测试设备的问题,本文开展了水下系泊系统测量方法和监测系统的研究工作。
1) 通过将传统集中质量模型求解中位移边界条件转换为水下易于高精度测量的角度信息,提出了一种通过对两已知位置角度信息测量进而获得深水系泊系统张力信息的测量方法。解决了在位水下系泊结构难以开展在位监测工作的问题;
2) 针对系泊结构水下测量需求,设计了低功耗自容式倾角传感器,解决了水下缺少成熟测量设备的问题。同时设计了水下安装辅助装置,能够实现潜水员安装、ROV回收的水下安装模式,突破了水下结构监测中安装/回收的技术瓶颈;
3) 在我国南海进行了5个月的连续应用,证明了本文设计的监测系统具有长期应用的可靠性。通过对20 min样本数据的分析,证明了本文提出的测量方法能够有效的获得系泊系统的张力信息。
本文设计的系泊缆监测系统适用于深水水下结构的现场监测,可为我国南海深水装备设计提供数据参考与安全保障。
| [1] | CHAKRABARTI S. Handbook of Offshore Engineering (2-Volume Set)[M]. Amsterdam: Elsevier, 2005 . |
| [2] | STANSBERG C T, ORMBERG H, ORITSLAND O. Challenges in deep water experiments:hybrid approach[J]. Journal of offshore mechanics and arctic engineering, 2002, 124(2): 90–96. |
| [3] | DU Yu, WU Wenhua, WANG Yanlin, et al. Prototype data analysis on LH11-1 semisubmersible platform in South China Sea[C]//Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering. San Francisco, California, USA:American Society of Mechanical Engineers, 2014. |
| [4] | WU Wenhua, WANG Yanlin, TANG Da, et al. Design, implementation and analysis of full coupled monitoring system of FPSO with soft yoke mooring system[J]. Ocean engineering, 2016, 113: 255–263. |
| [5] | WANG Yanlin, FAN Zheliang, DU Yu, et al. Security assessment of soft yoke moored FPSO for the hinge point problems[C]//Proceedings of the 25th International Ocean and Polar Engineering Conference. Hawaii, USA:International Society of Offshore and Polar Engineers, 2015. |
| [6] |
樊哲良, 王延林, 岳前进, 等. 软刚臂监测的设计验证[J].
哈尔滨工程大学学报, 2016, 37(3): 306–312.
FAN Zheliang, WANG Yanlin, YUE Qianjin, et al. Design and verification of the soft yoke mooring system[J]. Journal of Harbin Engineering University, 2016, 37(3): 306–312. |
| [7] |
杜宇, 武文华, 岳前进, 等. 深水浮式平台原型监测技术[J].
上海交通大学学报, 2016, 50(3): 448–455.
DU Yu, WU Wenhua, YUE Qianjin, et al. Prototype monitoring technique for deep water floating platform[J]. Journal of Shanghai Jiaotong University, 2016, 50(3): 448–455. |
| [8] | COLBOURNE D B, ALLEN J H. Observations on motions and loads in aquaculture cages from full scale and model scale measurements[J]. Aquacultural engineering, 2001, 24(2): 129–148. |
| [9] | GERNER M B, PERRYMAN S R, GEYER J F, et al. Marine monitoring of gulf of Mexico deepwater floating systems[C]//Proceedings of the Offshore Technology Conference. Houston, Texas:Offshore Technology Conference, 2007. |
| [10] | PRISLIN I, GOLDHIRSH M. Operational supports for offshore platforms:from system integrity monitoring to marine assurance and safety[C]//Proceedings of the ASME 200827th International Conference on Offshore Mechanics and Arctic Engineering. Estoril, Portugal:American Society of Mechanical Engineers, 2008. |
| [11] | SMITH D B, WILLIAMS J G. Direct measurement of large strains in synthetic fiber mooring ropes using polymeric optical fibers[C]//Proceedings of the Offshore Technology Conference. Houston, Texas:Offshore Technology Conference, 2002. |
| [12] | VAN DEN BOOM H, KONING J, AALBERTS P. Offshore monitoring; Real world data for design, engineering, and operation[C]//Proceedings of the Offshore Technology Conference. Houston, Texas:Offshore Technology Conference, 2005:171-172. |
| [13] |
杜宇, 武文华, 岳前进. 深海无肋锚链张力测量技术研究[J].
中国海洋平台, 2013, 28(5): 25–28.
DU Yu, WU Wenhua, YUE Qianjin. Method for tensile measurement of stud-less mooring chain[J]. China offshore platform, 2013, 28(5): 25–28. |
| [14] | HALL A D. Cost effective mooring integrity management[C]//Proceedings of the Offshore Technology Conference. Houston, Texas:Offshore Technology Conference, 2005. |
| [15] | BROWN M G, HALL T D, MARR D G, et al. Floating production mooring integrity JIP-key findings[C]//Proceedings of the Offshore Technology Conference. Houston, Texas:Offshore Technology Conference, 2005. |



