噪声控制是发展鱼雷隐身技术的关键,而涡轮气动噪声是鱼雷热动力装置噪声的主要来源之一。国外学者在涡轮噪声产生机理和控制水平方面开展了一系列研究。20世纪60年代末,Royce-Rolls公司的Smith和Bushell注意到了涡轮噪声问题的重要性,并给出了涡轮噪声预测的经验关联公式[1]。Clemons等发展了喷气发动机中涡轮单音噪声的声学控制-声衬技术,通过实验研究给出了不同消声系统的声阻抗和传播损失[2]。近年来,国外学者针对涡轮噪声产生机理开展深入研究。MTU的Broszat等[3]以1.5级低压涡轮实验件STTF为研究对象,得到了涡轮出口导叶(TEC)与末级转子轴向间距、倾斜TEC等对干涉单音噪声的影响。2012年Broszat等[4-5]又提出了基于Tyler & Sofrin规则的“Inverse Cut-off”设计,通过选择更多数目的TEC,进场工况下不仅末级转子/TEC干涉单音被截止,降低了两种单音噪声级。Traub等[6]基于气动声学一体化声学需求,应用基于Lowson理论的半经验方法和线化欧拉方程求解的CFD方法,改进了某六级低压涡轮的末级涡轮转静叶片数与叶片间距,重新选择了出口导向叶片的数目,使得涡轮级噪声减小了5~7 dB。相比之下,国内针对涡轮噪声开展的相关研究还比较少。
此外,国内外学者目前主要针对航空发动机常规涡轮的气动噪声开展研究[7-11],对鱼雷上采用超高膨胀比涡轮气动噪声的研究还未见于公开文献。超高膨胀比涡轮具有结构简单、体积小、单级焓降大的特点。涡轮一般采用冲击式涡轮的形式,反力度很小,使喷嘴出口的马赫数很高,流体在动叶和喷嘴之间形成复杂的波系[12-14]。这些结构和设计上的特点都会使超高膨胀比涡轮在气动噪声机理方面和表现特征与常规涡轮有所不同。
基于上述分析,目前国内外学者针对超高膨胀比涡轮气动噪声控制方法的研究还比较少。由于超高膨胀比涡轮内部复杂的流动特征,用于常规涡轮的气动噪声控制方法能否用于超高膨胀比涡轮有待进一步分析。本文以某单级超高膨胀比涡轮为研究对象,从流动特征的角度入手探讨了超高膨胀比涡轮气动噪声的产生机理,并有针对性地提出几种超高膨胀比涡轮气动噪声的控制改进措施,在此基础上对原型涡轮进行改进。
1 超高膨胀比涡轮气动噪声产生机理分析涡轮的气动噪声主要是由叶片通道内的非定常压力脉动引起的。Goldstein[15]给出了考虑运动固体表面影响的气动声学基本方程——Ffowes Williams-Hawkings方程(1),是研究叶轮机械内部噪声的基础。
| $p\prime {{x}_{i}},t=\frac{1}{4\pi }\frac{{{\partial }^{2}}}{\partial {{x}_{i}}\partial {{x}_{j}}}\underset{V}{\mathop{\int }}\,\left[ \frac{{{q}_{ij}}}{r\left| C \right|} \right]dV{{\eta }_{i}}-\frac{1}{4\pi }\frac{\partial }{\partial {{x}_{i}}}\underset{S}{\mathop{\int }}\,\left[ \frac{{{f}_{i}}}{r\left| C \right|} \right]dS{{\eta }_{i}}-\frac{1}{4\pi }\frac{\partial }{\partial {{x}_{i}}}{{\underset{V}{\mathop{\int }}\,}_{c}}\left[ \frac{{{\rho }_{0}}{{b}_{i}}}{r\left| C \right|} \right]dV{{\eta }_{i}}+\frac{1}{4\pi }\frac{{{\partial }^{2}}}{\partial {{x}_{i}}\partial {{x}_{j}}}{{\underset{V}{\mathop{\int }}\,}_{c}}\frac{{{\rho }_{0}}{{W}_{i}}{{W}_{j}}}{r\left| C \right|}dV{{\eta }_{i}}$ | (1) |
式中:fi为固体边界作用在流体上的力,r为声源点到观测点的距离,C为多普勒因子,ηi为转动坐标系下声源的坐标,W和b分别代表固体壁面的速度和加速度。
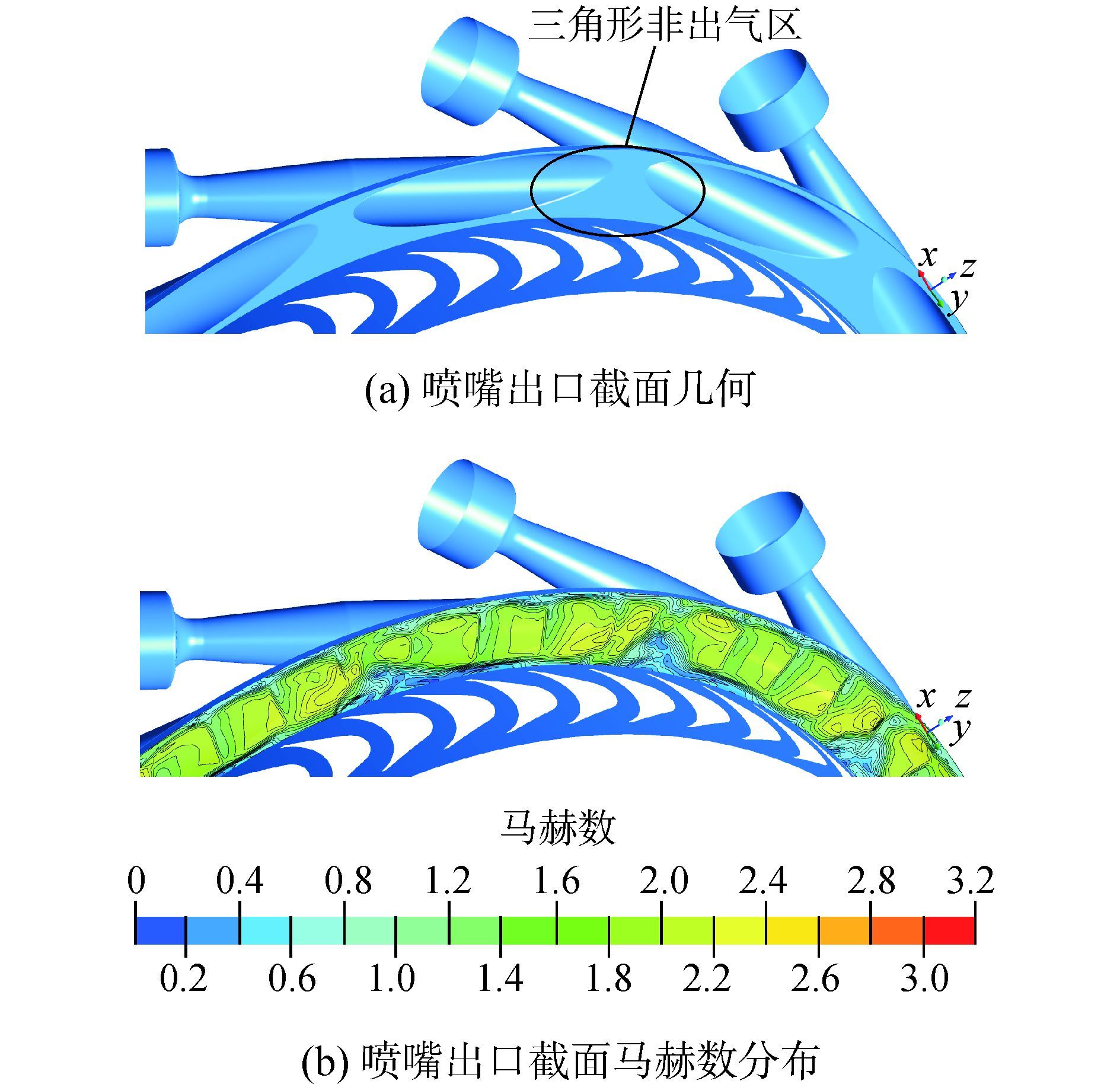
结合涡轮内部的流动特点分析式(1)右边各项可知,涡轮的气动噪声主要包括进气湍流、上游粘性尾迹与动叶的相互作用、非定常气动力作用下动叶叶片的振动等。与常规涡轮相比,超高膨胀比涡轮的气动噪声问题更加复杂。首先,考虑到加工方便等因素,超高膨胀比涡轮通常采用钻孔喷嘴代替涡轮导叶[16]。如图 1所示为某单级超高膨胀比涡轮钻孔喷嘴出口形式和喷嘴出口下游10%轴向弦长处S3截面马赫数分布云图。可以看出,由于钻孔喷嘴的出口截面为椭圆形,相邻喷嘴与流道之间会形成三角形的非出气区域,向下游发展形成低速区,使流向下游气流具有较宽的尾迹,与常规涡轮相比加剧了出口截面气流的不均匀性。喷嘴出口参数的不均匀性越强,则动叶内气流参数的波动越大。这种不均匀的气流与下游动叶相互作用,使下游叶片排噪声很强。此外,由于超高膨胀比涡轮的特点,基于出功最大的考虑,涡轮通常采取小反力度设计,使得喷嘴出口马赫数较高,流体在动叶和喷嘴之间形成复杂的波系,加剧了气流对动叶的冲击作用,由式(1)可知这种强烈的势场作用会增加涡轮的单音气动噪声。
|
| 图1 喷嘴出口的三角形非出气区域 Figure 1 The non-outlet triangle area of nozzle outlet |
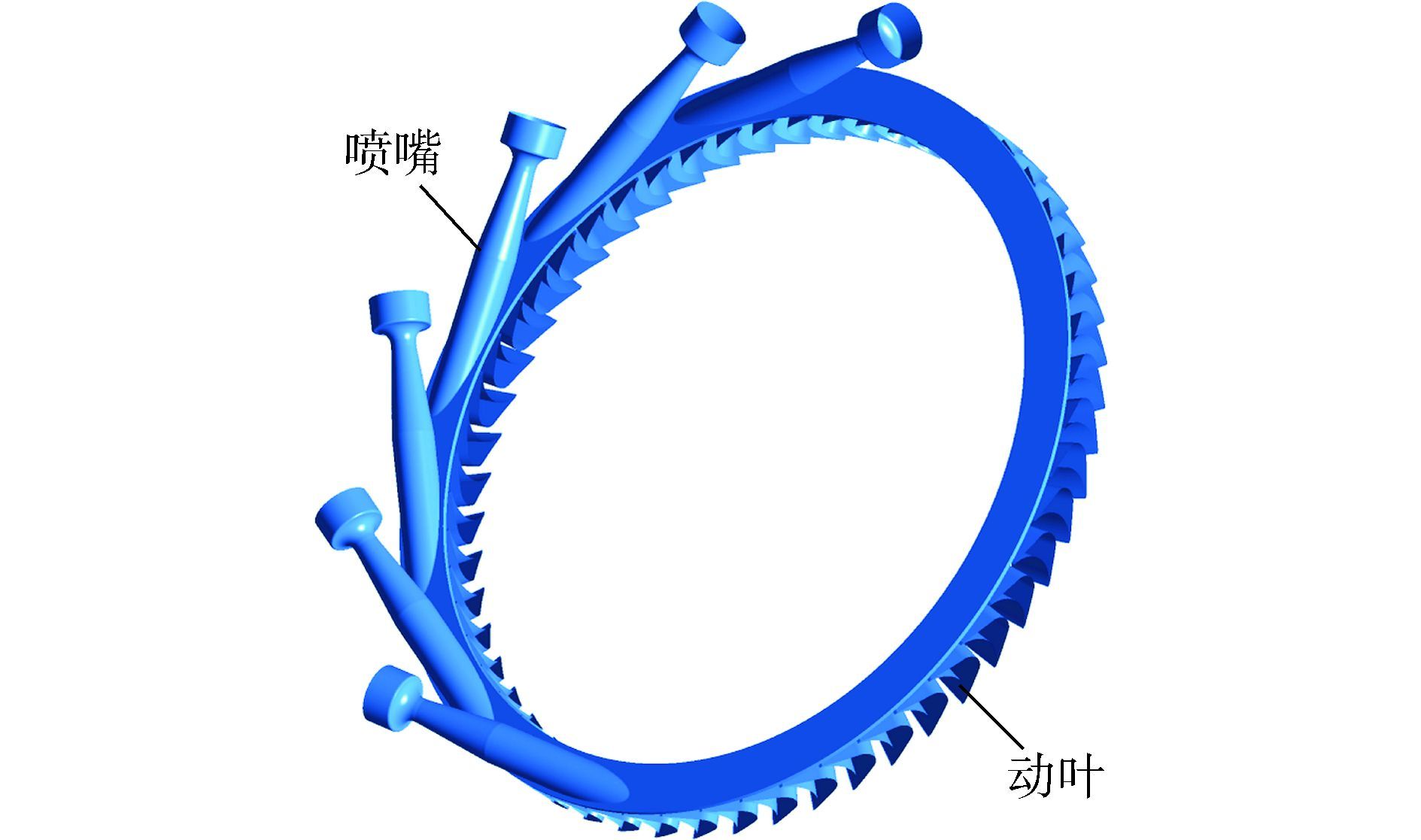
另一方面,由于超高膨胀比涡轮流量较小且喷嘴出口马赫数较高,在整圈上布置钻嘴会导致每个钻嘴的流道尺寸太小,使涡轮效率大大降低。因此,超高膨胀比涡轮采用部分进气式设计[17],即只在周向上一部分区域内布置喷嘴(图 2)。转子转动过程中,动叶交替经过有喷嘴区和无喷嘴区,加剧了流动的周向不均匀性,增加了涡轮的气动噪声。
|
| 图2 部分进气式的超高膨胀比涡轮 Figure 2 Partial admission of ultra-high expansion ratio turbine |
此外,超高膨胀比涡轮反力度小,气流在动叶通道内折转角较大,且几乎不膨胀,叶尖间隙泄漏流动比较明显。喷嘴出口的高速气流撞击到动叶叶冠前部,在自身流动惯性的作用下进入叶顶间隙,当外端壁没有安置气封齿时,气流跨过叶冠顶部各齿的过程中,速度降低幅度较小,到接触外缸后壁面时,速度仍然较大,最后以一定的横向冲击方式进入动叶后部的流动空间,对动叶出口后主流区域内的流体形成明显扰动,其下游区域也出现大尺度分离涡系,不稳定的分离流动结构内,气动参数是波动的,容易形成噪声向外辐射。
2 超高膨胀比涡轮气动噪声控制方案气动噪声主要是指由于流体的脉动引起的辐射声场,不是结构的振动产生的,而由第1节分析可知,气动噪声主要来源于流体内部由于流速不均匀或流体表面的压力脉动。针对上述分析提出的几种主要的气动噪声源,本文提出三种控制气动噪声的方法,包括:1)增加轴向间距:通过增加转子与静子之间的距离,喷嘴后面的流体由于进入动叶前,不均匀流层之间依靠流体自身特有的耗散作用进一步均化,以削弱周向不均匀性对动叶的冲击作用;2)喷管下俯、双侧修型、尾缘吹气(图 3):采用双侧修型后,沿径向喷管的尾迹变薄;将喷管入口相对抬高,可将轮毂附近三角形低速、低压区的流体团控制在靠近动叶下端部的区域,有利于改善动叶内部流动和降低动叶内的压力波动;在轮毂附近的低速区域,采用引流吹气的方法,提高低压气团流体的压力。提高过膨胀区域内的压力,减弱周向不均匀性,减弱尾迹宽度,提高轮毂附近三角形非出气区域内的压力;3)叶尖间隙流动控制:适当减小动叶叶尖间隙。

|
| 图3 喷嘴修形方案 Figure 3 Shape modification scheme of nozzle |
为验证本文提出的超高膨胀比涡轮气动噪声控制方案的可行性,本文采用上述方法对某单级超高膨胀比涡轮进行优化。具体如下:1)将转静之间轴向间距由原来的0.32倍动叶轴向弦长调整为0.8倍轴向弦长;2)喷嘴下俯2°、双侧修型、并在三角形非出气区域布置吹气孔(图 3);3)将叶尖间隙由原来的9%动叶叶高调整为4.5%动叶叶高。
为验证改进效果,在本文的研究中,首先使用CFX软件进行整圈数值模拟计算流场,然后在声学计算软件LMS virtual lab中导入CFD结果,设置声学网格和场点网格,预处理生成声学网格包络,将压力脉动映射到声学网格上,并进行傅里叶变换转换到频域内,采用直接边界元法计算场点上的噪声信息。根据流场的计算结果进一步计算声场。
网格质量会对数值模拟计算结果形成一定的影响。因此,在本文针对原型和改进涡轮流场的数值模拟计算中,由于喷嘴的几何结构比较复杂,故该部分结构采用非结构化网格;动叶通道采用结构化网格,以保证较好的壁面网格质量(图 4)。喷嘴部分的网格采用商用软件ICEM生成,动叶通道部分的网格采用AUTOGRID V5生成。为保证数值模拟结果的可靠性,采用总网格数不同的几套网格进行网格无关性验证,最终选取的喷嘴和动叶通道的网格数列于表 1。
| 参数 | 喷嘴 | 动叶 |
| 流道数 | 6 | 52 |
| 单流道网格数/万 | 43.07 | 7.79 |
| 网格/万 | 258.42 | 404.90 |
| 总网格数/万 | 663.32 |

|
| 图4 喷嘴和动叶通道的网格 Figure 4 Mesh of nozzle and rotor passage |
表 2为对某型超高膨胀比涡轮数值模拟的结果。采用CFX商用软件对超音速涡轮进行定常全三维数值模拟计算,求解三维粘性的雷诺平均N-S方程。计算格式采用时间推进的有限体积法。为获得较好的计算精度,空间项的离散采用二阶迎风格式,时间项的离散使用二阶后差欧拉格式。考虑到涡轮通道内流动可能十分复杂,湍流模型选取能较好的预测逆压力梯度和边界层分离SST模型。由于涡轮采用局部进气的设计方案,故数值模拟时涡轮转静交界面采用CFX提供的Frozen Rotor模式,该模式进行平均参数传递的同时,兼顾了流动的周向不均匀性。从表 2结果可以看出,改进后涡轮的落压比和绝热效率略有下降,但下降程度不大,因此可认为采用本文的方法控制气动噪声对涡轮的气动性能影响不大。
| 参数 | 原型 | 改进 |
| 流量(kg·s-1) | 0.652 | 0.652 |
| 落压比 | 10.29 | 10.28 |
| 绝热效率ηN | 0.625 | 0.619 |
| 喷管出口绝对马赫数 | 2.39 | 2.31 |
| 动叶入口相对马赫数 | 1.79 | 1.72 |
| 动叶出口绝对马赫数 | 1.07 | 1.12 |
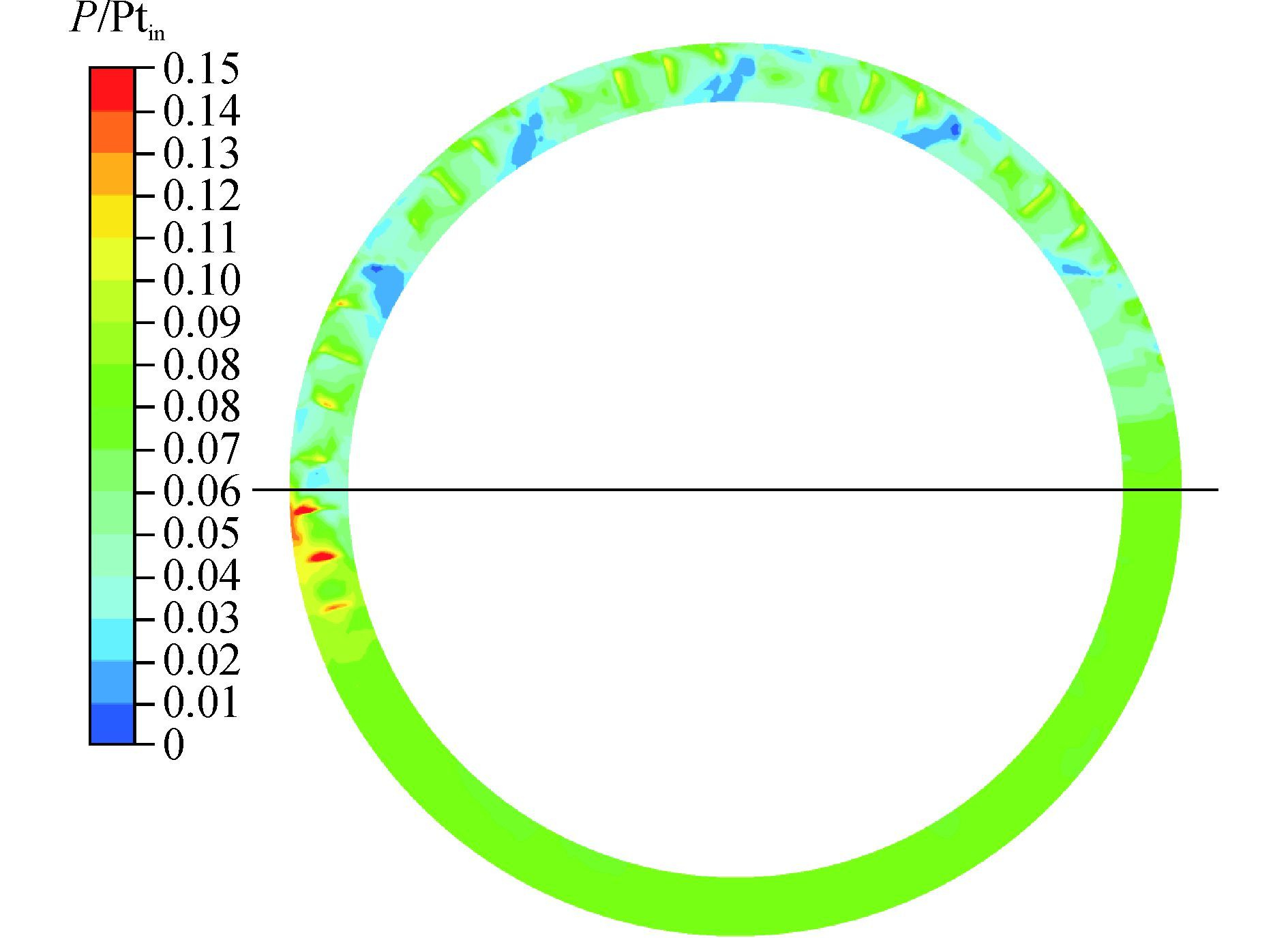
图 5给出了原型涡轮喷嘴出口截面的静压分布(其中P/Ptin为当地静压除以喷嘴进口总压),由于涡轮级采用局部进气式设计,气流流经喷嘴,在喷嘴壁面,新生成的附面层发展并使壁面附面层增厚;采用钻孔喷管后,相邻的两个喷嘴流道之间形成的尾迹区域比一般的叶栅流道要大的多;因此在尾缘处脱落形成以一定周期性出现的尾迹流动,随尾迹一起运动的气体,压力、速度、温度等参数与势流区内的气流不一致,旋转的动叶按照一定的规律不断的经过静叶的尾迹区和势流区,形成动叶流道内流动参数的周向波动。
|
| 图5 喷嘴出口截面的静压分布云图 Figure 5 Contour of static pressure of nozzle outlet |
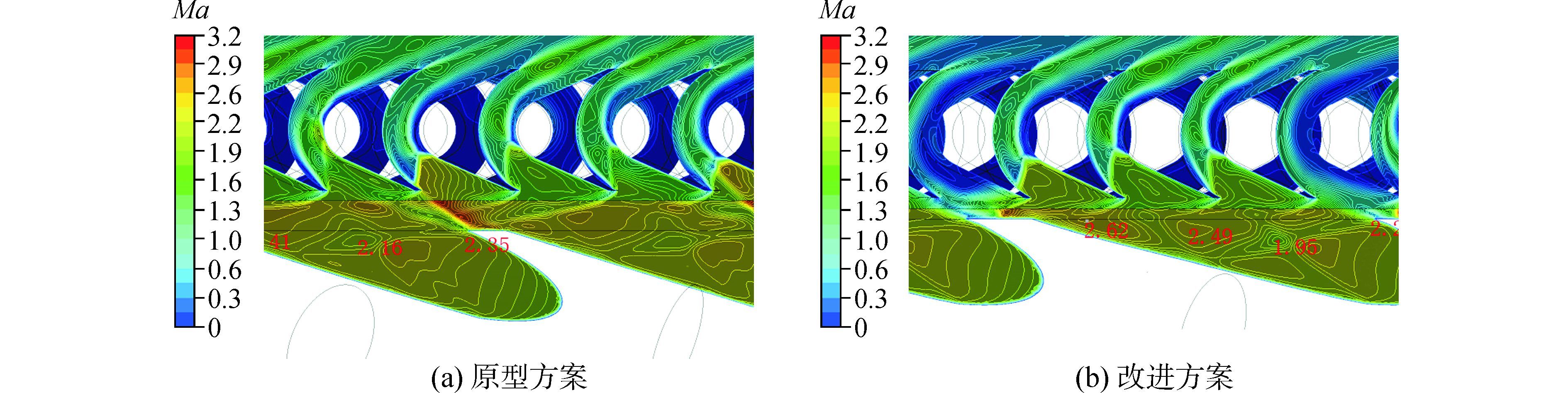
图 6给出原型和改进涡轮50%叶高S1截面Ma数分布云图。可以看出,原型涡轮动静叶间隙较小,喷嘴出口马赫数平均值相对较高,动叶入口形成明显的斜激波分布,该激波对喷嘴斜切部分的流动形成一定的扰动作用。喷嘴出口燕尾波直接与动叶叶片发生强烈的作用,使得动叶受到极大的非定常力。而增大转子与静子的轴向间距之后,燕尾波与动叶进口弓形激波以及喷嘴尾迹相互作用,流体在进入动叶通道之前进一步掺混,降低了进入动叶通道气流的周向不均匀性,减弱了动叶表面的非定常冲击作用,有利于控制涡轮的气动单音噪声。
|
| 图6 50%叶高S1截面Ma数分布云图 Figure 6 Contour of Mach number of 50% span |
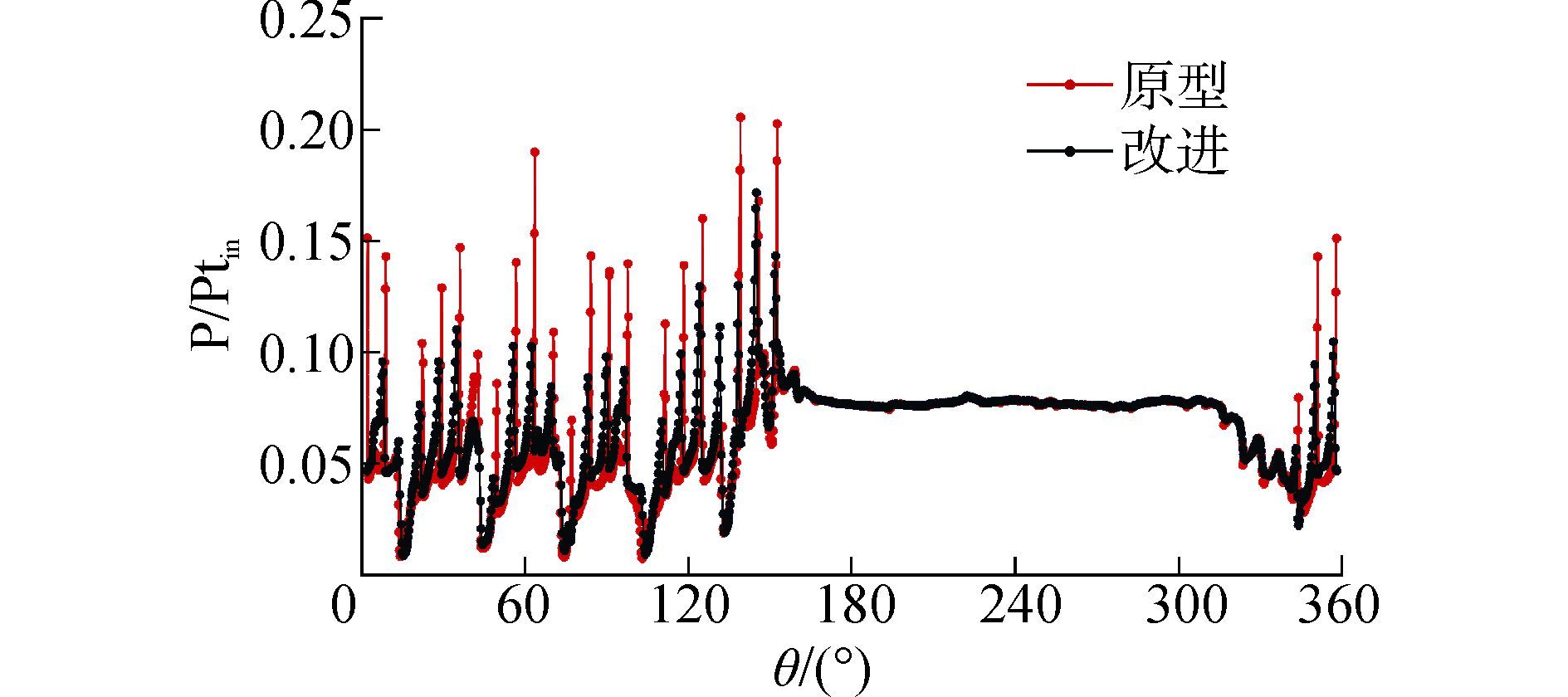
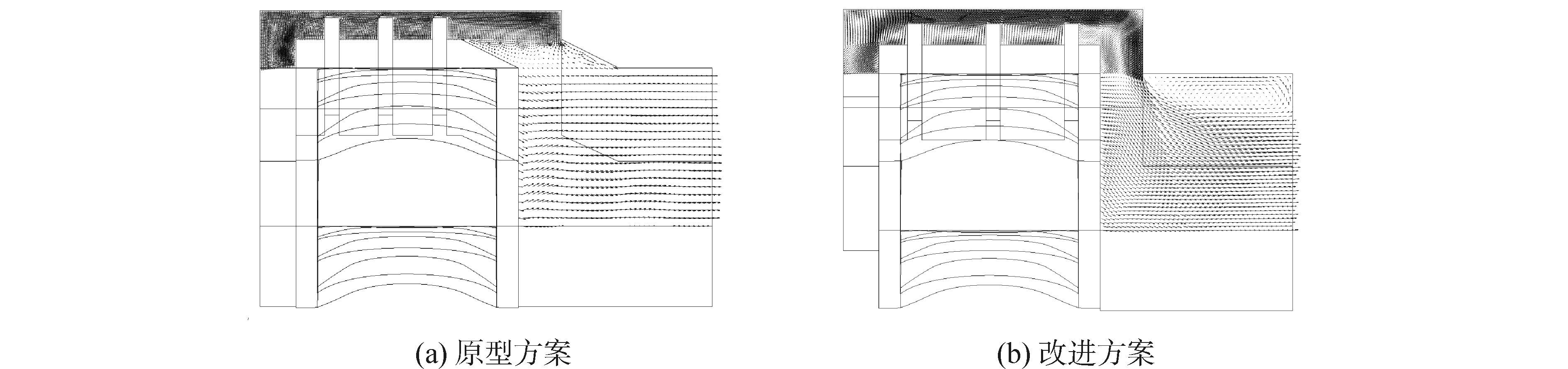
图 7给出了50%叶高S1截面动叶上游5%轴向弦长处的压力分布,其中P/Ptin为当地静压除以喷嘴进口总压。可以看出,由于改进方案进行了喷嘴出口双侧修型并增大了转静之间的轴向间隙,喷嘴出口的主流与尾迹气流在进入动叶通道前充分掺混,降低了气流的不均匀性,从而抑制涡轮的气动噪声。图 8给出了动叶叶尖间隙为4.5%和9%叶高的情况下,动叶通道子午流面的速度矢量图。从图中可以清晰地看到,减小间隙尺寸和在动叶叶尖间隙侧进行适当修型处理,可削弱或消除由动叶叶尖间隙泄漏流带来的大尺度分离涡系,控制了气动噪声。
|
| 图7 动叶上游5%轴向弦长处的周向压力分布(50%叶高S1截面) Figure 7 Circumferential pressure distribution of 5% axial chord upstream of rotor (50% span) |
|
| 图8 不同叶尖间隙条件下动叶通道子午流面流场 Figure 8 Meridional flow under conditions of different tip clearance |
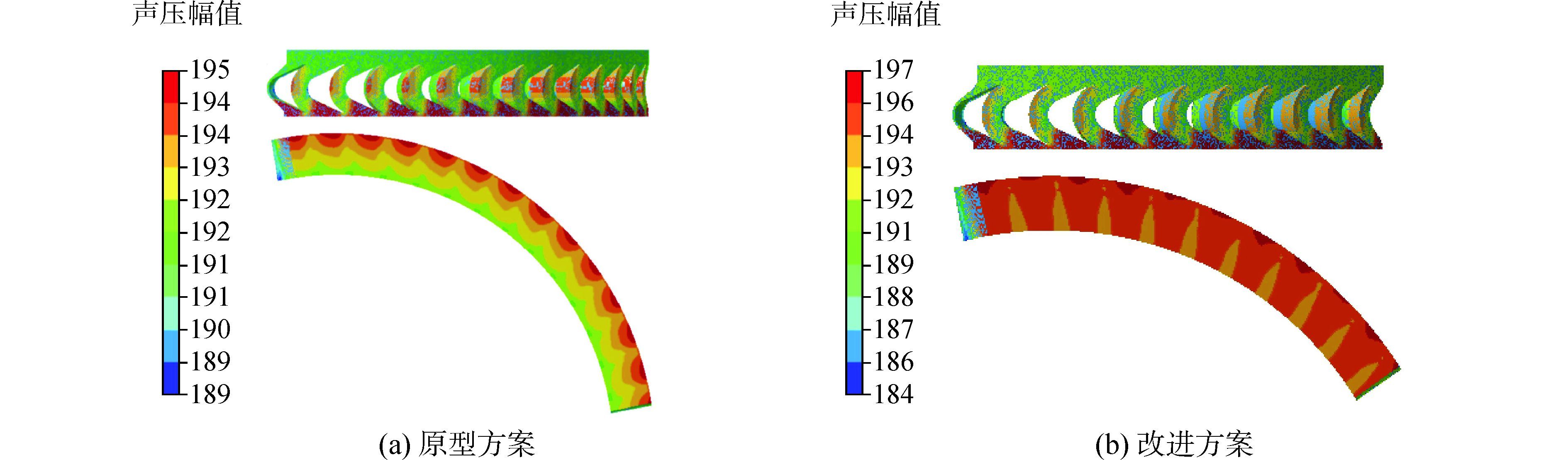
图 9给出了原型和改进方案涡轮声源声压云图。两种方案的观测点都是喷管出口处的场点。考虑到气动噪声源于流场的非定常脉动,喷管尾迹与动叶相互作用是涡轮中的非定常脉动的主要成因之一,所以在比较两种改进方案的时候首先考虑与喷嘴通过频率相对应的噪声。对比两种方案,改进方案比原型涡轮噪声降低3 dB以上。比较其他频率成分的噪声,改进方案对应于叶片组(由若干个喷嘴和对应的动叶组成)通过频率基频的噪声,相对于原型减少值在3 dB以上,降噪效果非常明显。
|
| 图9 原型和改进方案涡轮声源声压云图 Figure 9 Pressure contours of sound source of the original and optimized case |
对比涡轮动叶下游出口处的所有观测点的噪声取平均值的结果,原型涡轮噪声为161.9 dB,而采用本文的方法对叶形改进以后,涡轮动叶下游出口处观测到的噪声水平下降为148.6 dB。采用本文所提出的控制方法,在对涡轮效率影响不大的情况下,可使涡轮的气动噪声降低10 dB以上,从而验证了本文提出的超高膨胀比涡轮气动噪声控制方法的可行性。
3 结论本文基于超高膨胀比涡轮的流场特点,从流动特征的角度提出了三种适用于超高膨胀比涡轮的气动噪声控制方法,包括:增加转静之间轴向间距,喷管下俯、双侧修型、尾缘吹气,以及叶尖间隙流动控制。利用上述气动噪声控制方案对某单级超高膨胀比涡轮进行改进,结果表明,采用本文提出的改进方法降噪效果明显。
1) 增加涡轮转静之间的轴向间隙,使得主流和尾迹区的气流充分掺混,减弱转静之间的激波系强度,从而控制超高膨胀比涡轮的气动噪声。
2) 对喷嘴出口段进行双侧修型,可以缩小因喷嘴出口非出气区引起的宽尾迹,使转静之间区域的压力分布趋于一致,抑制气动噪声。
3) 控制叶尖间隙宽度,适当减小叶尖间隙,可以削弱由动叶叶尖间隙泄漏流带来的大尺度分离涡系,控制了气动噪声。
在后续工作中将进一步探讨3种噪声控制方法单独应用或两两组合情况下对超高膨胀比涡轮气动噪声的影响规律,及其与涡轮气动参数的相互联系,从而为考虑气动噪声控制的涡轮气动设计提供参考依据。
| [1] | 赵寅生. 鱼雷涡轮机原理[M]. 西安: 西北工业大学出版社, 2002 . |
| [2] | GREATREX F B, BRIDGE R. The evolution of the engine noise problem:an examination of the sources of engine noise and of the design concepts adopted to alleviate the problem[J]. Aircraft engineering and aerospace technology, 2013, 39(2): 6–10. |
| [3] | BROSZAT D, KORTE D, TAPKEN U, et al. Validation of turbine noise prediction tools with acoustic rig measurements[C]//Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference. Miami, Florida:AIAA. |
| [4] | BROSZAT D U, SELIC T, MARN A. Verification of the inverse cut-off effect in a turbomachinery stage part 1-numerical results[C]//Proceedings of the 18th AIAA/CEAS Aeroacoustics Conference. Colorado Springs, CO:AIAA. |
| [5] | BROSZAT D U, SELIC T, MARN A. Verification of the inverse cut-off effect in a turbomachinery stage-part 2-comparison to experimental results[C]//Proceedings of the 19th AIAA/CEAS Aeroacoustics Conference. Berlin, Germany:AIAA. |
| [6] | TRAUB P, KENNEPOHL F, HEINIG K. Active control of noise from turbomachines-A numerical simulation[C]//Proceedings of INTER-NOISE and NOISE-CON Congress and Conference. The Hague, The Netherlands:Institute of Noise Control Engineering, 2001:1824-1829. |
| [7] | SMITH M J T, HOUSE M E. Internally generated noise from gas turbine engines[J]. Journal of engineering for power, 2011, 89(2): 177–185. |
| [8] | 马志乐, 王雷, 乔渭阳, 等. 民机涡轮噪声的产生机理和抑制技术[C]//第十五届中国科协年会第13分会场:航空发动机设计、制造与应用技术研讨会论文集. 贵阳:中国科学技术协会, 2013. |
| [9] | XIAO Zhixiang, LIU Jian, LUO Kunyu, et al. Investigation of flows around a rudimentary landing gear with advanced detached-eddy-simulation approaches[J]. AIAA journal, 2013, 51(1): 107–125. |
| [10] |
王科俊, 杨晓飞. 采用改进结构特征度度量分析的噪声标准差估计算法[J].
智能系统学报, 2015, 10(2): 255–260.
WANG Kejun, YANG Xiaofei. The contourlet denoising algorithm based on modified noise variance estimation[J]. CAAI transactions on intelligent systems, 2015, 10(2): 255–260. |
| [11] | CHEN Bao, WEI Qingkai, SHAO Tianshuang, et al. Aeroacoustic imaging experiments of Air-frame noise in lined wall closed-section wind tunnel[J]. Journal of aerospace engineering, 2014, 28(4): 1943–5525. |
| [12] | REMILLIEUX M C, CAMARGO H E, RAVETTA P A, et al. Novel Kevlar-walled wind tunnel for Aeroacoustic testing of a landing gear[J]. AIAA journal, 2012, 46(7): 1631–1639. |
| [13] | DORNEY D J, GRIFFIN L W, GUNDY-BURLET K L. Simulations of the flow in supersonic turbines with straight centerline nozzles[J]. Journal of propulsion and power, 2000, 16(2): 370–374. |
| [14] | GRIFFIN L W, DORNEY D J. Simulations of the unsteady flow through the Fastrac supersonic turbine[J]. Journal of turbomachinery, 2000, 122(2): 225–233. |
| [15] | GOLDSTEIN M E. Aeroacoustics[M]. New York: McGraw-Hill International Book Co, 1976: 305 . |
| [16] | HOFFREN J, TALONPOIKA T, LARJOLA J, et al. Numerical simulation of real-gas flow in a supersonic turbine nozzle ring[J]. Journal of engineering for gas turbines and power, 2002, 124(2): 395–403. |
| [17] | HE L. Computation of unsteady flow through steam turbine blade rows at partial admission[J]. Proceedings of the institution of mechanical engineers, part A:journal of power and energy, 1997, 211(3): 197–205. |



