2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
水声定位技术利用声波测量水下声源的位置,广泛应用于海洋资源勘探、科学考察以及潜器自主导航等领域[1-3]。采用水声同步定位系统可以对水下合作目标进行定位跟踪。当目标运动速度较高时,如某些水中兵器或航行器的航速可能达到几十节甚至上百节[4],为了获得足够的轨迹采样点数来描绘其运动过程,定位系统需要采用较高的帧率,通常在百毫秒量级。一般地,按照基线长度,水声定位系统可以分为长基线系统、短基线系统和超短基线系统。对于在较大范围内高速运动的目标,工程上常采用长基线高帧率水声定位系统对其进行高精度定位跟踪。声速和系统同步周期的乘积称为非模糊距离,以信号发射周期为0.2s为例,若声速取1500m/s,则当目标距离定位阵元超过300m时,信号传播时延大于0.2s,而接收系统记录的时延值仍在0.2s以内,即与真实的时延值相差周期的整数倍,导致定位结果具有多值性,称为距离模糊问题[5]。针对距离模糊问题,许多学者提出了解决方法。信号设计类方法[6-7]通过设计区分不同同步周期的脉冲参数,间接增大了非模糊距离。但是需要对声源进行改造,且信号处理算法较复杂。事后处理类方法的实时性较低。软件逻辑判断类方法[8-10]主要对定位参量进行处理,例如举手表决法是利用冗余阵元的信息从所有可能的模糊解中判断真解,是在定位解算之后抗距离模糊的方法,计算量较大,且需要有足够多的冗余信息注入;参考位置标示法需要获取目标的初始位置,并且对目标运动轨迹的连续性要求较高;时延/时延差组合定位法利用三元阵时延差被动测距得到的目标距离作为参考值估计模糊周期,要求目标距离较近,时延测量精度较高。另外,现有的抗距离模糊方法通常采用基于几何结构的位置线或位置面交叉[11]的方法对目标进行定位。在工程实现中,定位参量的测量误差可能导致所有独立位置线或面无法相交于一点;另一方面,交叉定位方法无法充分利用诸如参量测量误差的统计特性、水声信道条件等冗余信息,定位精度受到限制。考虑到方位参量的测量不受距离模糊的影响,本文提出基于差分进化和时延方位融合的解距离模糊方法,将抗距离模糊问题转化为方位约束条件下非线性优化问题,并采用差分进化算法[12-13]进行随机、并行的全局搜索,得到的全局最优解即为无模糊的目标位置估计值。
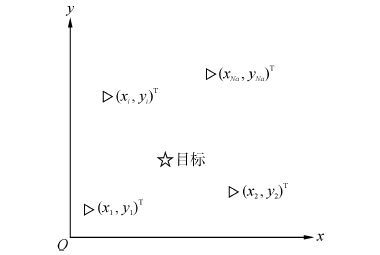
1 基于参量融合的同步定位解距离模糊优化方法 1.1 定位模型和距离模糊问题在不影响对问题讨论的情况下,本文考虑二维平面定位的情况。采用具有-Na-个阵元的分布式水声同步定位系统对水下目标进行定位,如图 1所示。
|
| 图1 分布式定位系统示意图 Figure 1 Diagram of the distributed positioning system |
在笛卡尔坐标系中,目标的位置坐标为-x=x,yT∈
| ${{{\hat{\theta }}}_{i}}={{\theta }_{i}}+{{\varepsilon }_{i}}=ta{{n}^{-1}}(\frac{y-{{y}_{i}}}{x-{{x}_{i}}})+{{\varepsilon }_{i}}$ | (1) |
式中,θi为方位真值,εi为方位测量误差。测量的信号传播时延为
| ${{{\hat{t}}}^{i}}+{{n}_{i}}T={{t}_{i}}+{{\xi }_{i}}=\frac{\left\| x-{{x}_{i}} \right\|}{c}+{{\xi }_{i}}$ | (2) |
式中,ti为信号传播时延真值,ξi为时延测量误差,c为水中声速。当‖x-xi‖>cT时,ti>T,ni为
当Rmax<cT时,定位系统不受距离模糊的影响。假设各个测量量都是无噪声的,采用两个阵元的时延测量值通过球面交汇定位算法一般可得到目标位置的两个解[5],需要结合目标与两阵元的相对位置做进一步判断。为了获得目标位置的唯一解,至少需要三个观测阵元,且阵元不能位于同一条直线上。
当Rmax≥cT时,定位问题的未知量包括目标位置坐标及各阵元对应的模糊周期数。仅采用时延信息定位时,未知量的个数始终比观测方程数多两个,理论上无法直接求得唯一解。而方位信息仅与目标和阵元的相对位置有关,不包含模糊周期信息。因此,可以将时延和方位信息加以融合,优化利用多冗余观测信息,从而实现对目标的无模糊定位。
1.2 基于参量融合的解模糊算法原理时延方位融合定位的本质是根据系统观测的时延和方位信息以及阵元位置信息对目标位置进行非线性估计。最大似然(maximum-likelihood,ML)估计量是使似然函数最大的渐进无偏估计量。本文根据观测误差的概率模型,建立最大似然准则下的定位优化模型,求得使似然函数最大的估计量即为目标位置最优估计值。
1.2.1 优化模型的构建假设式(1)和(2)中的方位和时延观测误差均服从零均值的高斯分布,并且各个误差统计独立,即εi~N(0,σεi2),ξi~N(0,σξi2),其中,σεi2和σξi2分别为第i个阵元的方位和时延测量方差。
定义时延真值向量和方位真值向量分别为t=t1,t2,…,tNaT和θ=[θ1,θ2,…,θNa]T,对应的观测矢量为
| $\hat{t}+NT=t+\xi $ | (3) |
| $\hat{\theta }=\theta +\varepsilon \text{ }$ | (4) |
式中,N=n1,n2,…,nNaT为模糊周期数向量,ξ=ξ1,ξ2,…,ξNaT和ε=ε1,ε2,…,εNaT分别为时延和方位观测误差向量,对应的协方差矩阵分别为Cξ和Cε,且Cξ=diagσξ12,σξ22,…,σξNa2,Cε=diagσε12,σε22,…,σεNa2。定义X=[xT,NT]T,其维数为向量x和N的维数之和,即2+Na,则似然函数为
| $\begin{align} & \Lambda \left( X \right)=p\left( \hat{t},\hat{\theta }|X \right)=p\left( \hat{t}|X \right)p\left( \hat{\theta }|X \right)= \\ & Cexp[-\frac{1}{2}\Psi \left( X \right)\text{ }\!\!]\!\!\text{ } \\ \end{align}$ | (5) |
其中,C为与变量X无关的常数。
| $\begin{align} & \Psi \left( X \right)={{[\hat{t}-g\left( X \right)]}^{T}}{{C}_{_{\xi }}}^{-1}[\hat{t}-g\left( X \right)]+ \\ & {{[\hat{\theta }-h\left( X \right)]}^{T}}{{C}_{\varepsilon }}^{-1}[\hat{\theta }-h\left( X \right)] \\ \end{align}$ | (6) |
式中,g:
| $\begin{align} & (ML):{{{\hat{X}}}^{=}}arg\underset{X\in {{\mathbb{R}}^{2+{{N}_{a}}}}}{\mathop{max}}\,\Lambda (X)= \\ & arg\underset{X\in {{\mathbb{R}}^{2+{{N}_{a}}}}}{\mathop{max}}\,\{-\ln \left[ \Lambda (X) \right]\}=arg\underset{X\in {{\mathbb{R}}^{2+{{N}_{a}}}}}{\mathop{max}}\,\Psi (X) \\ \end{align}$ | (7) |
模型(7)中优化变量X同时含有连续元素和整数离散元素,分别为目标位置坐标x和模糊周期向量N,且通常N的维数高于x的维数,属于混合整数非线性规划问题(mixed integer nonlinear programming,MINLP)。MINLP是一类 NP (nondeterministic polynomial) 完全问题,计算量随着变量维数的增加急剧增大。考虑到在实际应用中,一般只需要估计目标位置,不需要求模糊周期数。因此,将x直接作为待估计量,用取余数运算代替N,可以得到如下优化模型
| $\begin{align} & \hat{x}=arg\underset{x={{\mathbb{R}}^{2}}}{\mathop{min}}\,{{[\hat{t}-{{g}_{1}}\left( x \right)]}^{T}}{{C}_{_{\xi }}}^{-1}[\hat{t}-{{g}_{1}}\left( x \right)]+ \\ & {{[\hat{\theta }-{{h}_{1}}\left( x \right)]}^{T}}{{C}_{_{\varepsilon }}}^{-1}[\hat{\theta }-{{h}_{1}}\left( x \right)\text{ }\!\!]\!\!\text{ } \\ \end{align}$ | (8) |
其中,g1:
模型(8)的目标函数同时含有时延和方位信息,时延信息的周期模糊性导致目标函数具有多个局部极小值,而方位信息不受距离模糊的影响。工程实际中,通常采用矢量水听器或水听器阵列等进行方位估计。在系统硬件平台、软件算法复杂度等应用成本受到限制时,一般难以达到较高的方位估计精度。因此,当方位估计精度较低时,模型(8)中目标函数主要由时延信息决定,方位信息的影响较小,难以对距离模糊起到抑制作用。为了充分利用方位信息的无模糊性,将其作为约束条件,并根据目标距离进行适当松弛,得到优化模型如下
| $\begin{align} & \underset{x\in {{\mathbb{R}}^{2}}}{\mathop{min}}\,[\hat{t}-{{g}_{1}}{{(x)}^{T}}C_{\xi }^{-1}[\hat{t}-{{g}_{1}}(x)] \\ & \begin{matrix} s.t. & [\hat{\theta }-{{h}_{1}}(x) \\ \end{matrix}{{]}^{T}}{{C}_{r}}[\hat{\theta }-{{h}_{1}}(x)]\le \delta \\ \end{align}$ | (9) |
其中,Cr是以目标距离平方为元素的对角矩阵,即Cr=diag‖x-x1‖2,‖x-x2‖2,…,‖x-xNa‖2,δ为约束因子。模型(9)中约束条件的物理意义是对各个阵元的方位测量误差导致的目标位置误差进行约束,进而对目标真实位置即目标函数的全局最小点所在邻域进行限定,从而有效抑制距离模糊。设非模糊距离为R0=cT,一般地可以取δ=αR02,其中,比例系数α可以根据实际定位区域的大小,系统同步周期、阵元数等条件进行预先设定。
1.2.2 算法步骤优化模型(9)的目标函数是非凸、不光滑的,且多个局部极小值的存在容易使基于梯度下降的传统优化算法陷入局部最优,对搜索全局最优解造成了严重的干扰。差分进化(differential evolution,DE)算法是一种采用浮点矢量编码的智能优化算法,具有内在的并行性,采用种群搜索的方式对解空间的多个区域同时进行循环迭代寻优。实际应用中,分布式水声定位系统需要对一定区域内的目标进行定位,距离模糊问题可能会导致DE算法产生早熟收敛,降低了其在整个解空间的全局寻优能力。而模型(9)的方位约束函数可以进一步限定DE算法的搜索空间,降低算法陷入局部最优解的危险,提高其寻优效率及稳健性,从而获得较强的全局搜索能力。
基于差分进化和时延方位融合的解距离模糊方法 (range ambiguity resolution based on DE and TOADOA fusion,RARDEF)的具体实现步骤如下:
1) 建立最大似然准则下的时延方位融合定位优化模型。
2) 种群初始化。在满足定位区域边界约束的条件下随机选择一组位置坐标作为第一代种群向量。
3) 个体评价。将优化模型中的目标函数作为差分进化算法的最小化适应度函数,计算种群中每个个体对应的实数适应值,进而根据适应值大小及是否满足方位约束条件对个体的优劣进行评价。
4) 进化操作。根据种群中个体评价结果,采用DE/local to best/2/bin方式对当代种群执行变异(mutation)、交叉(crossover)和选择(selection)操作,得到下一代种群。
5) 重复执行步骤3)和4),直到满足终止条件,则最终得到的适应值最小的个体即对应目标位置矢量的最优估计值。
1.3 抗模糊性能及定位误差分析RARDEF算法的实质是通过数值搜索的方式对非线性定位观测方程进行优化求解,从而得到最大似然准则下的全局最优解。其解距离模糊性能主要受到系统阵元数、目标与阵元的位置关系、方位约束条件等因素的影响。对于系统阵元数,当Na=2时,一般情况下可以得到目标位置的无模糊解。但是,当目标位于两阵元连线附近时,方位约束函数难以有效限定目标所在区域,可能无法抗距离模糊。因此,至少需要三个阵元才可能实现对整个测量区域的无模糊定位。另一方面,在观测量质量一定的条件下,适当增加观测量的个数,即增强系统冗余有利于提高定位系统抗距离模糊的稳健性。因此,工程实际中,通常考虑在阵元数有冗余(即Na≥4)的条件下对目标进行无模糊定位。
对于一个测量系统,间接测量量Y理论上可以写成直接测量量Pi(i=1,2,…,m)的函数的形式,
| $Y=f({{P}_{1}},{{P}_{2}},\ldots ,{{P}_{m}})+\Delta $ | (10) |
其中,m为直接测量量个数,Δ为测量误差。在水声定位系统中,目标位置坐标是间接测量量,直接测量量一般是时延、方位、声速、阵元位置等,且二者之间的函数关系是非线性的。假设各直接测量量互不相关,根据误差传递规律,间接测量量Y的方差可以近似表示为
| ${{\sigma }_{_{Y}}}^{2}={{\sum\limits_{i=1}^{m}{\left( \frac{\partial f}{\partial {{P}_{i}}} \right)}}^{2}}{{\sigma }^{2}}_{{{P}_{i}}}$ | (11) |
式(11)说明定位精度同时受到各个观测量的精度以及误差传递关系的影响。由于RAR-DEF算法优化模型表达式较复杂,难以直接获得定位误差的解析表达式,因此,下面通过仿真实验对RAR-DEF算法的抗距离模糊性能及定位精度进行分析。
2 同步定位解模糊性能仿真实验考虑采用六阵元分布式水声同步定位系统对在半径r=800m的圆形区域内运动的水下目标进行定位。目标运动速度为60节,约为30m/s。通过仿真实验,对本文方法的抗距离模糊性能进行分析,并将其定位精度与基于方位测量的直线交汇定位方法[11]以及基于时延测量的球面交汇算法的定位精度进行比较。
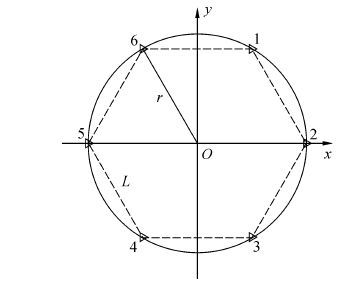
定位系统的几何布局如图 2所示,以测量区域中心为原点建立直角坐标系,系统的六个阵元用三角形符号表示,分别位于边长L=800m的正六边形的顶点。系统最大水声作用距离Rmax=1600m,同步周期T=0.2s,水中声速 c=1500m/s。信号方位及传播时延测量误差统计独立,且满足εi~N(0,σεi2),ξi~N(0,σξi2)。
|
| 图2 定位系统布局 Figure 2 Layout of the positioning system |
定位系统非模糊距离R0=300m,则最大传播周期Nmax=6。当采用球面交汇定位算法时,每个阵元测量的时延
采用RAR-DEF算法对目标进行定位,建立优化模型如下,设各阵元的方位和时延测量误差的标准差分别为σεi=σε=1°,σξi=σξ=0.1ms,i=1,2,…,6。
| $\begin{align} & \underset{x\in {{\mathbb{R}}^{2}}}{\mathop{\min }}\,{{[\hat{t}-{{g}_{1}}(x)]}^{T}}C_{\xi }^{-1}[\hat{t}-{{g}_{1}}(x)] \\ & \begin{matrix} s.t. & [\hat{\theta }-{{h}_{1}}(x) \\ \end{matrix}{{]}^{T}}{{C}_{r}}[\hat{\theta }-{{h}_{1}}(x)]\le \delta \\ \end{align}$ | (12) |
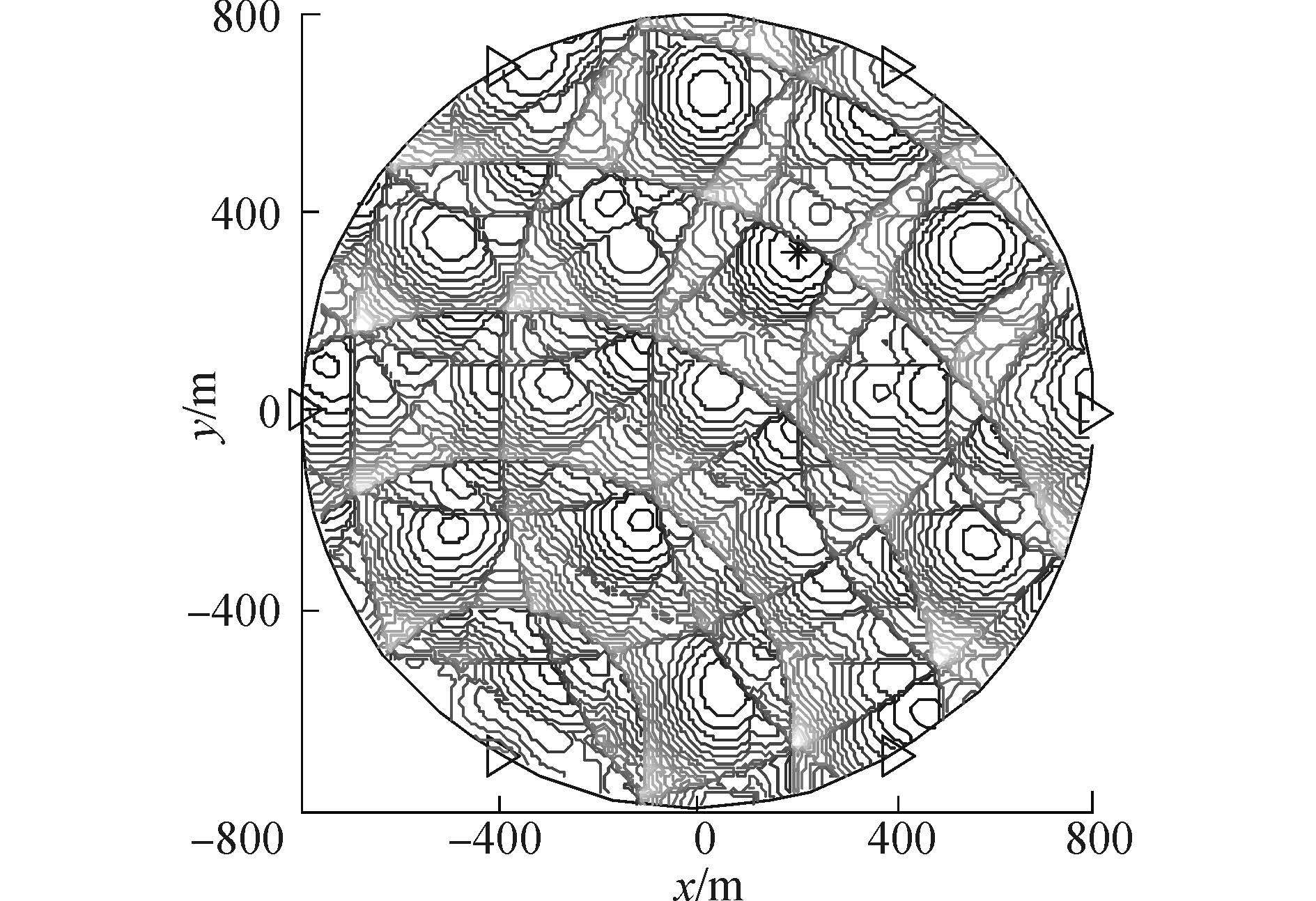
式中,δ=R02,Cξ=σξ2INa。 以目标位于[200, 320]Tm处为例,RAR-DEF算法优化模型(12)中目标函数的等高线图及约束条件所限定的区域如图 3所示。其中,星号表示目标,实线圆形代表定位区域的边界,其内部的虚线圆形表示通过方位约束条件限定的目标邻域的边界。由图 3可见,模型(12)的性能曲面有多个局部极小值,对应于由距离模糊导致的多个伪目标,而真实目标位于约束条件限定的虚线边界区域内。
|
| 图3 优化模型示意图 Figure 3 Diagram of proposed optimization model |
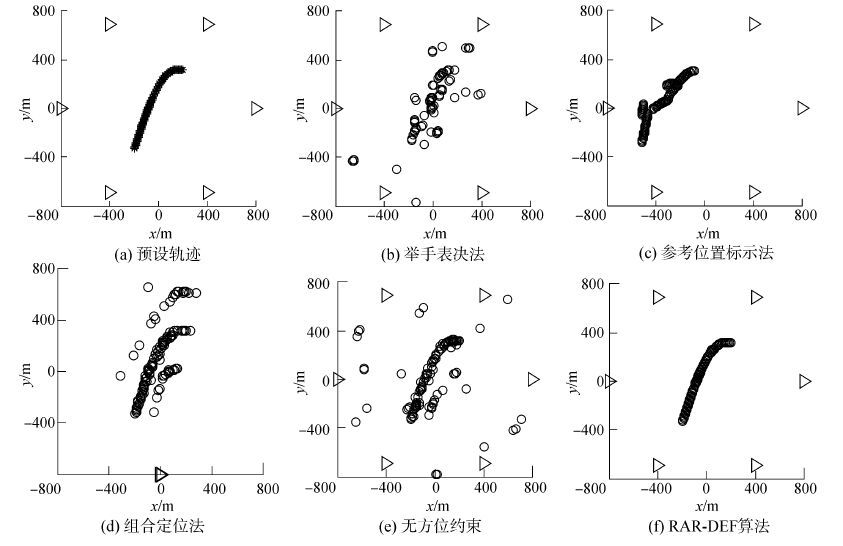
图 4给出了目标预设运动轨迹及RAR-DEF算法的定位结果,并与几种常用的抗距离模糊方法进行了对比。目标预设运动轨迹如图(a)所示,图(b)给出了采用举手表决方法[8]抗距离模糊的定位结果。在测量区域内随机选取一点作为目标初始位置,得到采用参考位置标示法[8]的定位结果,如图(c)所示。图(d)给出了采用间距为7.5m的三元阵组合定位抗距离模糊[10]的结果,其中,相邻阵元间时延差测量误差服从均值为0,标准差为5us的高斯分布。将模型(12)中的方位约束条件去掉,对应的定位结果如图(e)所示,采用本文方法得到的定位结果如图(f)。
由图(b)可见,距离模糊严重时,穷举得到的大量伪目标对真实目标的判决产生严重的干扰,导致举手表决法抗距离模糊性能下降。由图(c)可见,当目标初始位置未知时,参考位置标示法无法得到最初的无模糊传播时延,导致后续周期均无法有效抗距离模糊。图(d)结果表明,当目标距离远大于基阵孔径时,三元阵被动测距误差可能超过参考距离误差容限,从而无法实现无模糊定位。由图(e)可见,无方位约束条件时,距离模糊可能导致DE算法的早熟收敛,因此只有部分位置能够得到无模糊定位结果,且定位精度较低。图(f)中RAR-DEF算法定位结果与预设轨迹基本一致。综合以上结果可见,方位约束函数有效地限定了真实目标所在区域,降低了DE算法陷入局部最优解的危险。对于分布式高帧率定位系统,本文方法无需目标初始就位点,即可实现对大范围测量区域内运动目标的高精度稳健无模糊定位。
2.2 定位精度分析目标位于[200, 320]Tm处,假设声速、阵元位置等可以精确测量,各阵元方位测量误差标准差σε=1°。
|
| 图4 不同方法抗距离模糊性能对比 Figure 4 Performance comparison of different ambiguity resolving methods |
进行200次Monte Carlo实验,统计当时延测量误差标准差σξ在0~1ms范围内变化时,RAR-DEF算法和球面交汇算法[5] (spherical intersection,SI)的定位均方根误差(root mean square error,RMSE)的变化情况。
| $RMSE=\sqrt{E\{{{\left\| \hat{x}-x \right\|}^{2}}\}}$ | (13) |
采用基于时延测量的定位克拉美-罗界[14](Cramer-Rao bound,CRB)作为二者定位性能的评价标准。
| ${{\sigma }^{2}}={{c}^{2}}{{\sigma }_{_{\xi }}}^{2}{{N}_{a}}{{\left[ {{\sum\limits_{i=2}^{{{N}_{a}}}{\sum\limits_{j=i+1}^{{{N}_{a}}+1}{\left( \frac{{{d}_{1\bot i,j}}{{d}_{i,j}}}{{{d}_{1,i}}{{d}_{1,j}}} \right)}}}^{2}} \right]}^{-1}}$ | (14) |
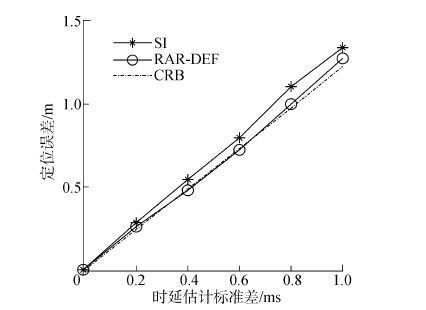
式中: σ 为标准差下界, d1⊥i,j 为目标到阵元i,j间的距离,d1,i和d1,j分别为目标到阵元i,j的距离。统计结果如图 5所示,需要说明的是,SI算法本身不具有抗距离模糊的能力,因此,图 5中SI算法的统计结果是利用无模糊的时延信息得到的,而本文方法仍是在存在距离模糊的条件下进行定位。
|
| 图5 定位误差随时延估计标准差的变化 Figure 5 Positioning error versus TOA standard error |
由图 5可见,随着时延估计误差的增大,RAR-DEF算法的定位误差始终接近CRB,精度稍高于SI算法。 另一方面,由各个阵元的方位交汇对目标进行定位。通过200次Monte Carlo实验统计得到的定位均方根误差约为11.5m。可见,本文方法的定位精度远高于方位交汇定位精度。
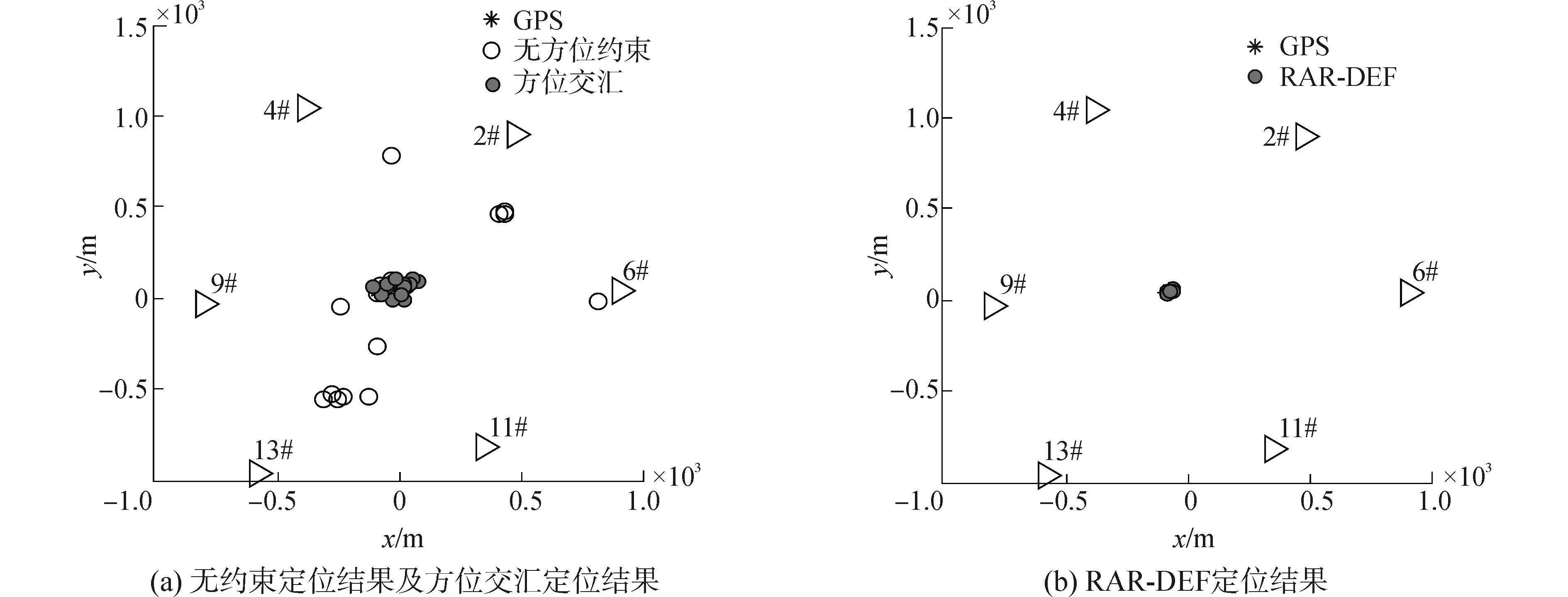
3 高帧率同步定位系统海试结果2015年在大连旅顺海域进行了分布式浮标阵水声定位系统的海上试验,RAR-DEF算法得到进一步验证。试验中水下6个浮标构成边长约1km的六边形测量阵,如图 6所示,其中,三角形符号表示浮标,右边为其编号。目标船停机漂泊,模拟声源发射换能器吊放于目标船上,其位置由目标船携带的GPS提供。系统同步周期0.2s,实测声速1515.47m/s。图 6(a)给出了系统在无方位约束条件下仅利用时延信息得到的目标定位结果及方位交汇的定位结果。采用RAR-DEF算法得到的定位结果如图 6(b)所示,统计得到其定位均方根误差为5.70m。由图 6可见,仅利用时延信息对目标进行定位存在模糊问题,仅利用方位信息定位精度较低,而本文方法将时延和方位信息融合优化求解,有效地克服了距离模糊问题,并且保证了系统定位精度。
|
| 图6 系统海试阵型及定位结果 Figure 6 Array shape and positioning result of sea trial |
针对高帧率水声同步定位系统所面临的距离模糊问题,提出了基于差分进化和时延方位融合的解距离模糊方法。建立了最大似然准则下时延方位融合定位优化模型,并采用差分进化算法求解。上述研究和试验数据分析结果表明:
1) 对于分布式高帧率定位系统,本文方法利用方位信息对目标所在区域进行了有效限定,同时约束了差分进化算法的搜索空间,具有较强的全局搜索能力;无需目标初始就位点,即可实现对大范围测量区域内运动目标的稳健无模糊定位。
2) 在各阵元时延测量误差统计特性相同时,本文方法定位精度与球面交汇算法精度相当,且克服了利用时延参量定位存在的模糊问题以及利用方位参量定位精度较低的问题。
| [1] | CARROLL P, MAHMOOD K, ZHOU Shengli, et al. On-demand asynchronous localization for underwater sensor networks[J]. IEEE transactions on signal processing, 2014, 62(13): 3337–3348. |
| [2] | DIAMANT R, LAMPE L. Underwater localization with time-synchronization and propagation speed uncertainties[J]. IEEE transactions on mobile computing, 2013, 12(7): 1257–1269. |
| [3] | PAULL L, SAEEDI S, SETO M, et al. AUV navigation and localization:A review[J]. IEEE journal of oceanic engineering, 2014, 39(1): 131–149. |
| [4] |
张木. 水下高速航行体超空泡减阻的大涡模拟与实验研究[D]. 南京:南京理工大学, 2013:2-5.
ZHANG Mu. Large eddy simulation and experimental study of the supercavity drag reduction of underwater high-speed navigation body[D]. Nanjing:Nanjing University of Science and Technology, 2013:2-5. |
| [5] | 田坦. 水下定位与导航技术[M]. 北京: 国防工业出版社, 2007: 54 -57. |
| [6] | KORSHUNOV A Y, FRIDMAN L B, SINITSIN E A. Effectiveness of range ambiguity mitigation in primary radars when using signals with high pulse-repetition frequency[C]//Proceedings of the 23rd international conference on microwave and telecommunication technology. Washington DC, 2013:1154-1155. |
| [7] | RIEGER P. Range ambiguity resolution technique applying pulse-position modulation in time-of-flight scanning lidar applications[J]. Optical engineering, 2014, 53(6): 061614. |
| [8] |
梁国龙, 杨春, 陈晓忠, 等. 同步水声跟踪定位系统软件抗距离模糊技术研究[J].
应用声学, 2005, 24(5): 300–304.
LIANG Guolong, YANG Chun, CHEN Xiaozhong, et al. On resolving range ambiguities by software in synchronous underwater acoustic tracking system[J]. Applied acoustics, 2005, 24(5): 300–304. |
| [9] |
于平, 谢胜. 水声定位实时抗距离模糊方法[J].
舰船电子工程, 2012, 32(1): 118–120.
YU Ping, XIE Sheng. A real-time anti-fuzzy distance method of acoustic positioning[J]. Ship electronic engineering, 2012, 32(1): 118–120. |
| [10] |
惠娟, 梁国龙. 组合定位抗距离模糊技术及性能分析[J].
哈尔滨工程大学学报, 2007, 28(6): 665–668.
HUI Juan, LIANG Guolong. Technology of resolving range ambiguities of active spherical positioning model combined with passive hyperboloid ranging model[J]. Journal of Harbin engineering university, 2007, 28(6): 665–668. |
| [11] |
田孝华, 周义建.
无线电定位理论与技术[M]. 北京: 国防工业出版社, 2011: 7 -69.
TIAN Xiaohua, ZHOU Yijian. Theory and technology of wireless location. Beijing:National Defense Industry Press[M]. , 2011: 7 -69. |
| [12] | PRICE K V. Differential evolution a fast and simple numerical optimizer[C]//Proceedings of 1996 biennial conference of the North American fuzzy information processing society. New York, 1996:524-527. |
| [13] | STORN R, PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization, 1997, 11(4): 341–359. |
| [14] | PATWARI N, HERO A O, PERKINS M, et al. Relative location estimation in wireless sensor networks[J]. IEEE transactions on signal processing, 2003, 51(8): 2137–2148. |


