圆柱绕流的分离控制方法较多[1],近年来,利用旋转来控制圆柱表面流体分离与涡脱落已渐被重视。初步研究表明[2-6],对于一定雷诺数圆柱绕流,当圆柱旋转速度达到一定值时旋涡脱落消失,同时因产生马格努斯力而使升力增加,然而,一定条件下还可能产生负马格努斯力效应。另外,圆柱绕流在亚临界区时圆柱体上分离的剪切层开始向不规则的湍流状态转变[7],呈现出三维效应,到了超临界区,尾流的流动状态则变得非常混乱,已经无法辨认涡街。由于随雷诺数的增加圆柱绕流呈现不同的绕流特性,而关于高雷诺数旋转圆柱绕流的数值模拟更为复杂且相关研究较少。因此,相关现象仍需进一步研究。
关于低雷诺数旋转圆柱绕流的相关研究较多,Kang等[2]研究了层流旋转圆柱绕流,发现粘性均匀流中的旋转圆柱可修正尾迹和旋涡脱落,能够降低激流振荡。Ingham等[3]采用有限差分法对雷诺数分别为5和20,转速区间为0~0.5的圆柱绕流进行了求解。Kang[4]对Re分别为40、60、100、160,转速区间为0~2.5时圆柱绕流进行了数值模拟,得出了60≤Re≤160时使流体稳定的最大转速。Mittal等[5]对雷诺数为200、Padrino等[6]分别对雷诺数为200、400、1 000时的旋转圆柱绕流进行计算,分析了升力系数、阻力系数以及压力系数的变化规律,证明当圆柱旋转速度达到一定值时旋涡脱落消失。中等雷诺数(Re>103)的圆柱绕流在求解时更为困难,因为存在三维效应且湍流效应也变得显著,Badr等[8]针对103≤Re≤104转速区间为0.5~3的流场进行了模拟,得出了使旋涡脱落消失的临界转速与雷诺数有关且其值约为2的结论。Chew等[9]采用混合涡方法对Re =103,转速为0~6进行了数值计算,结果表明,当转速超过临界值且接近2的时候旋涡脱落消失。对于高雷诺数圆柱绕流,由于尾流或边界层内流体基本为湍流,因而流场呈现三维特性,导致相关数值模拟非常复杂。目前许多高雷诺数圆柱绕流的研究均为非旋转。Breuer[10]采用大涡模拟(LES)对亚临界雷诺数Re=1.4×105的圆柱绕流进行了探讨,发现LES对高雷诺数圆柱绕流的模拟结果具有很高的准确性,并与实验结果非常吻合。Catalano等[11]采用LES方法对Re分别为5.0×105、1.0×106、2.0×106进行了数值模拟,其结果与非稳态雷诺平均N-S(URANS)、雷诺平均(RANS)以及实验数据进行了对比。高雷诺数条件下旋转圆柱绕流的研究主要由Karabelas[12]采用LES方法模拟了Re=1.4×105,转速为0~2的圆柱绕流,结果表明当旋转速度超过1.3时流体达到稳定。
为了进一步研究高雷诺数圆柱的旋转速度与尾流流场及受力的变化规律,本文选取不可压流雷诺数Re分别为3 900、1.4×105、1.0×106,转速α分别为1、2、3、4(其中α=θ·D/2U0,θ·为旋转角速度,U0为自由来流速度,D为圆柱直径,逆时针方向为正)。其中Re分别为3 900、1.4×105为亚临界区,Re=1.0×106为超临界区。通过对非旋转的圆柱绕流进行数值验证后,分析了不同雷诺数和转速条件下圆柱绕流的流场结构特点以及旋转对分离控制过程中圆柱受力变化。
1 数值方法与计算模型采用大涡模拟(LES)方法,其基本思想是通过滤波方法将湍流中瞬时脉动运动分解为大尺度和小尺度部分,大尺度运动通过求解网格尺度的三维N-S方程直接得到,小尺度运动对大尺度的作用通过亚格子尺度模型模拟。本文选用Smagorinsky亚格子模型,关于时间推进则用二阶R-K隐式格式,取时间步长dt=0.000 1。
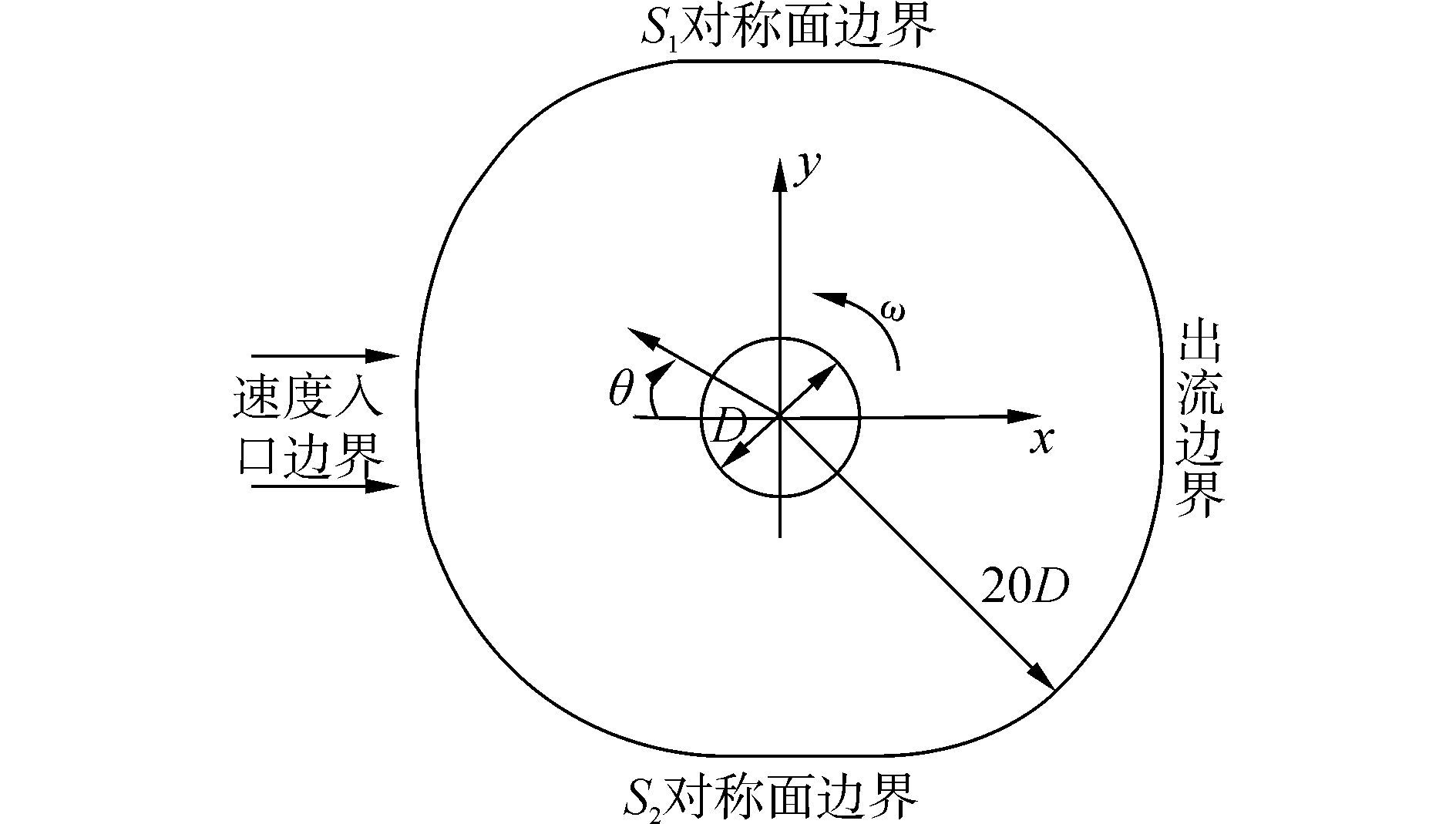
圆柱几何模型和边界条件如图 1 所示,左边为速度入口边界,右边为出流边界,远离圆柱的上下两个面采用对称面边界。本文采用的网格与文献[6]相同,为O型网格(图 2),并且自外层向圆柱表面网格被加密。外层网格与圆柱中心的距离为20D,其中D为圆柱直径。圆柱体展向长度与Breuer[10]中的算例相同,取Z=2D。圆柱表面的第一层网格与圆柱表面非常贴近,对于Re分别为3 900、1.4×105、106的流动,y+值均为1左右。
|
| 图1 模型在xOy面上的投影和边界条件 Figure 1 Computational domain projection on xOyand the boundary conditions |

|
| 图2 全局网格和局部放大网格 Figure 2 Global grid and local grid |
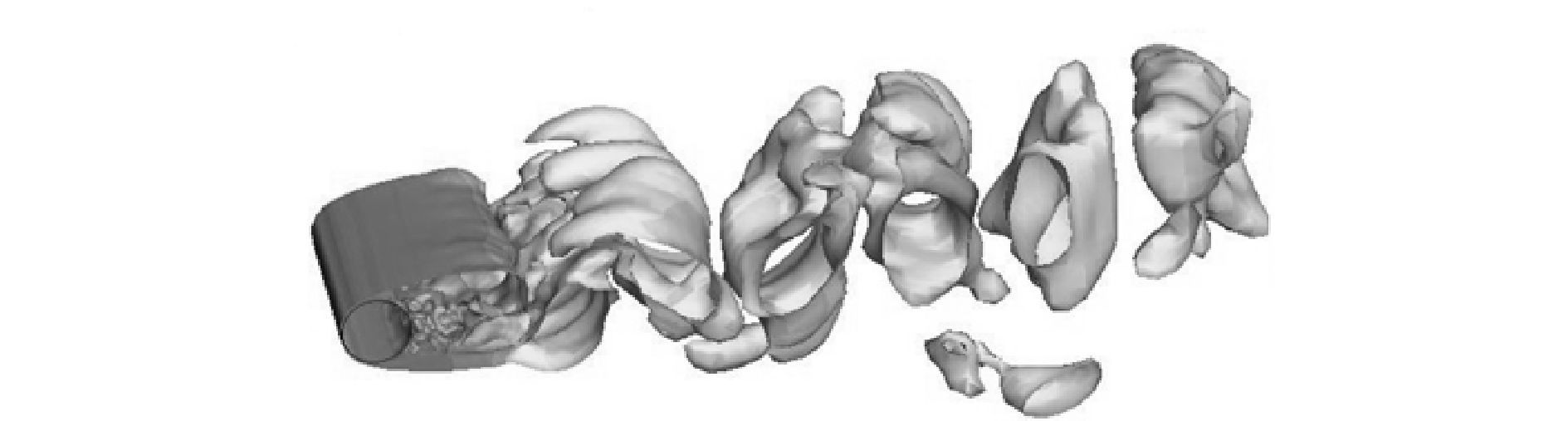
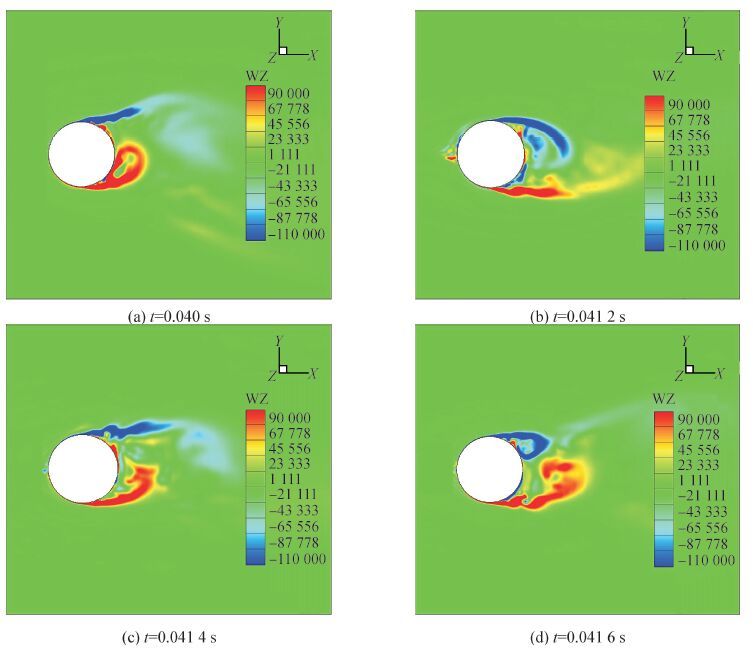
首先以非旋转的三维圆柱绕流作为算例对上述数值方法进行验证。图 3为Re=3 900时,圆柱绕流涡脱落的涡量等值分布。图 4为Re=1.0×106时圆柱尾涡周期脱落的涡量变化等值分布。
|
| 图3 圆柱绕流涡脱落的涡量变化等值图(Re=3 900) Figure 3 Vorticity contour for vortex shedding of flow past a cylinder(Re=3 900) |
可知,此时圆柱表面仍为层流,而圆柱尾流涡街则转捩为湍流,属于亚临界区。在该雷诺数条件下其尾流并不像层流中的经典卡门涡街那样有序,但仍可以看出旋涡在圆柱尾部的上、下表面流动发生了分离,然后向后运动逐渐脱离壁面,形成脱落旋涡,下部脱落旋涡向上运动、上部脱落旋涡向下运动,形成周期性交替脱落涡街。
表 1为两雷诺数条件下,圆柱Strouhal数与平均阻力系数的数值结果与相关实验结果及数值结果的对比。可知,Re=1.4×105时本文计算得到的涡脱离频率Strouhal 数为0.24,与Breuer[10]的计算结果和Zdravkovich[13]的实验结果较为吻合,平均阻力系数为1.26,与Zdravkovich[13]以及Cantwell[14]实验结果也较为吻合,最大偏差仅为4.76%,而与Tutar[15]的数值模拟结果偏差较大,达到11.1%;Re=1×106时Strouhal数为0.29,与实验结果吻合较好,时均阻力系数为0.302,与Catalano[11]的LES数值模拟吻合。
|
| 图4 Re=1×106时,圆柱尾部涡周期脱落的涡量等值分布 Figure 4 Vorticity contour for Periodic vortex shedding of flow past a cylinder at Re=1×106 |
| 相关文献及雷诺数 | Str | Cd |
| 本文计算结果, Re=1.4×105 | 0.24 | 1.26 |
| Exp. Zdravkovich[13], Re=1.4×105 | 0.2 | 1.2 |
| Exp. Cantwell et al.[14], Re=1.4×105 | 0.179 | 1.237 |
| LES, BReuer[10], Re=1.4×105 | 0.202 | 1.286 |
| Tutar et al.[15], Re=1.4×105 | 0.184 | 1.4 |
| 本文计算结果, Re=1.0×106 | 0.29 | 0.302 |
| Exp. Zdravkovich[13], Re=1.0×106 | 0.18~0.5 | 0.17~0..4 |
| Exp. Shih et al.[16], Re=1.0×106 | 0.22 | 0.24 |
| LES Catalano[11], Re=1.0×106 | 0.35 | 0.31 |
| RANS Catalano[11], Re=1.0×106 | 0.39 | - |
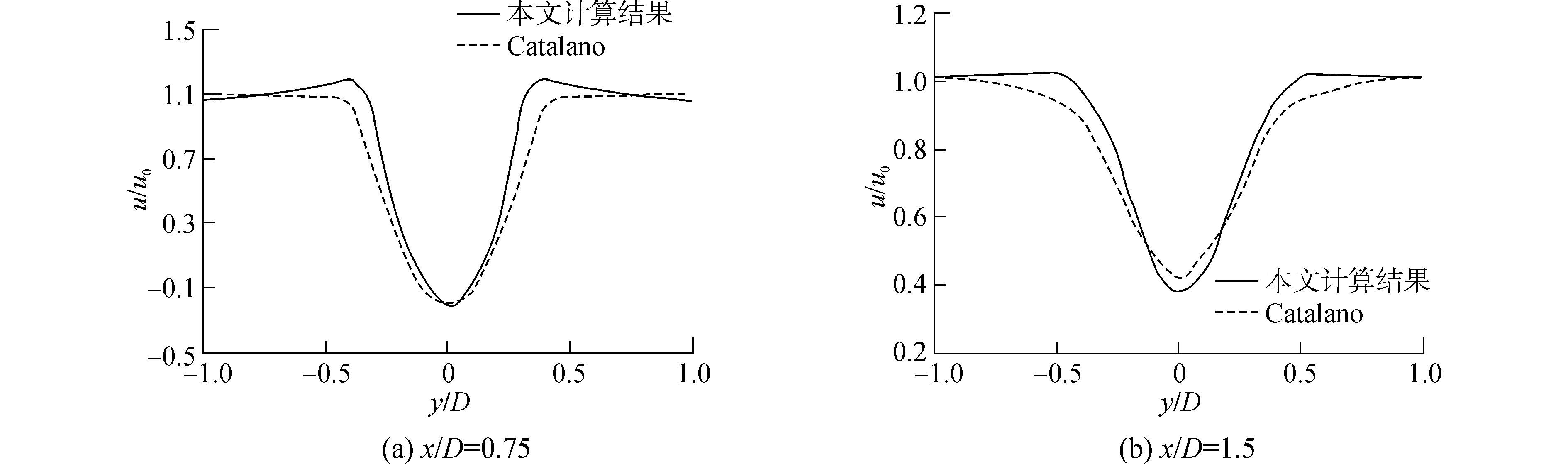
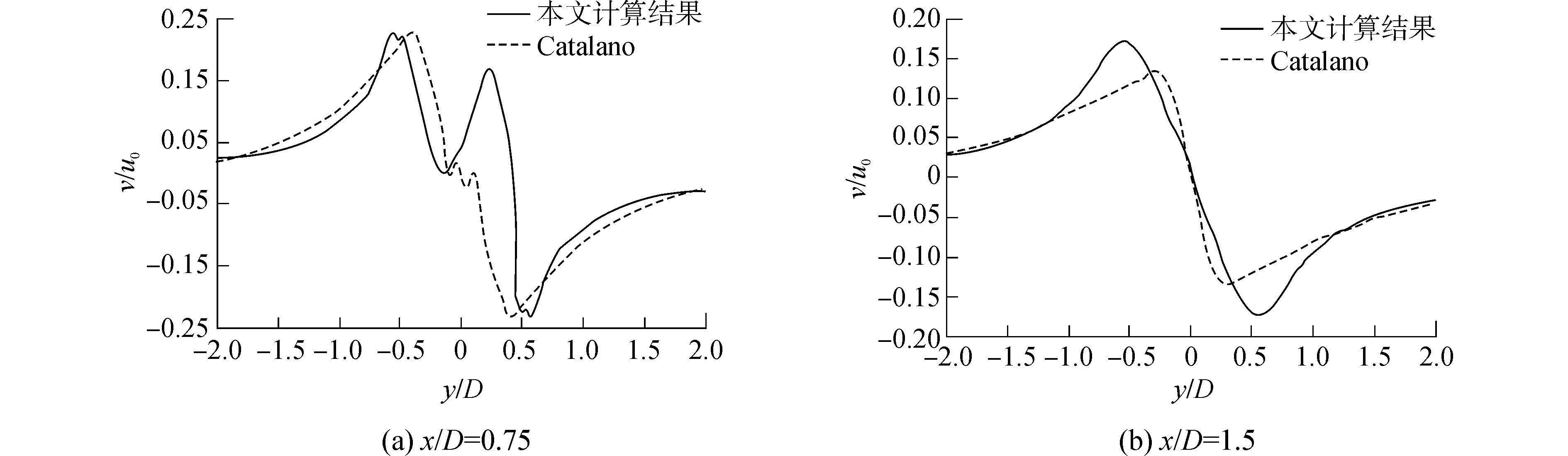
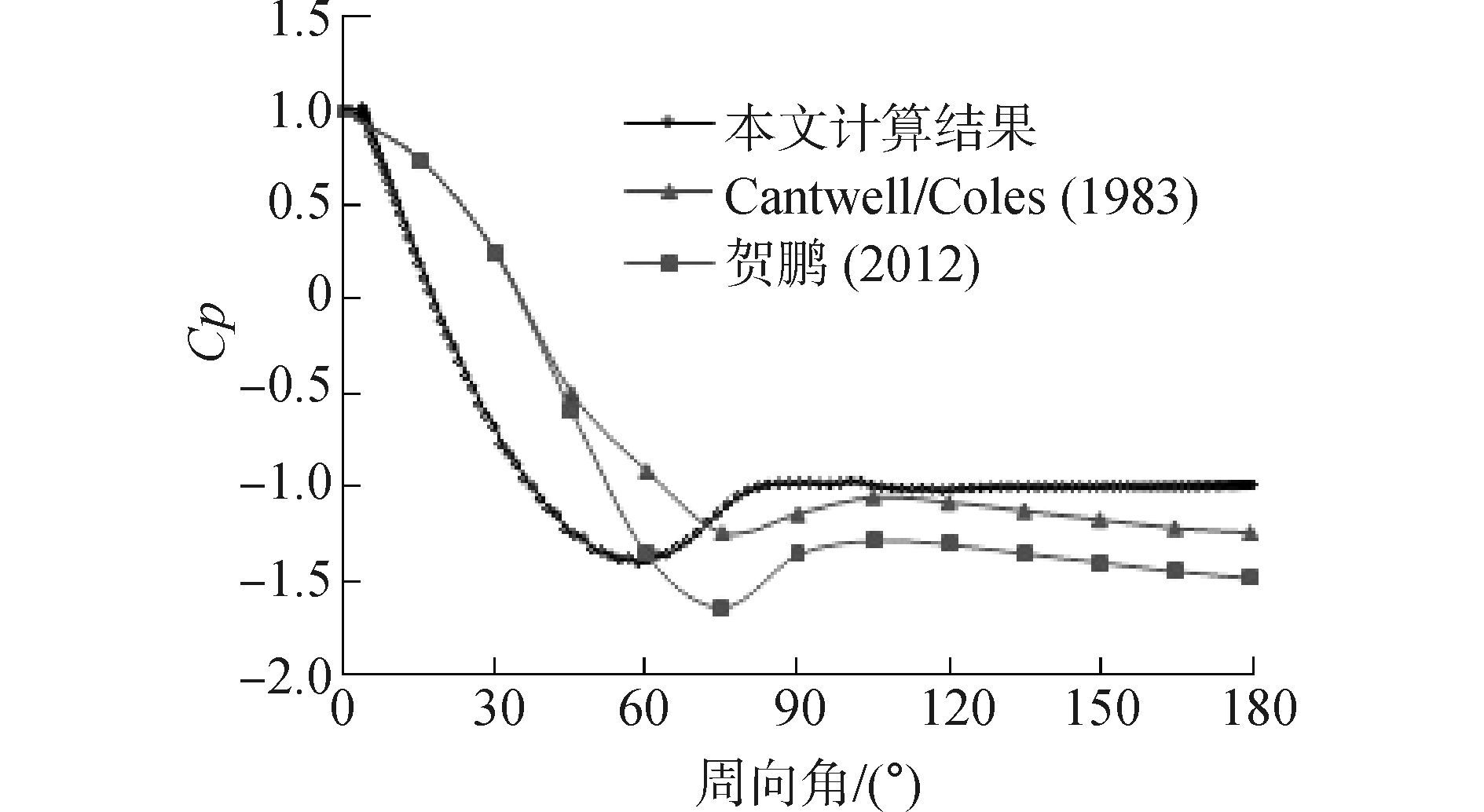
图 5和图 6分别为Re=1.0×106时沿直线x=0.75D,x=1.5D上顺气流方向(x轴方向)和垂直方向(y轴方向)的无量纲时均速度分布,可以看出本文计算结果与Catalano[11]的计算结果总体趋势基本相同。图 7为Re=1.4×105条件下时均稳态压力系数
|
| 图5 不同截面上沿x轴方向的平均速度分布 Figure 5 Time-averaged streamwise velocity u along the different line |
|
| 图6 不同截面上沿y轴方向的平均速度分布 Figure 6 Time-averaged streamwise velocity v along the different line |
|
| 图7 Re=1.4×105时压力系数周向分布的实验结果和数值结果对比 Figure 7 Experimental and numerical results compared to the present ones of the Pressuercoeffcient along the cylinder’s surface at Re=1.4×105 |
利用上述数值方法,分别对雷诺数Re为3 900、1.4×105、106,旋转速度α为0、1、2、3、4的圆柱绕流进行数值模拟。图 8为各不同雷诺数与转速条件下圆柱绕流的时均流线分布。可知,当α=0(无旋)时,流体在圆柱顶端分离,圆柱上、下表面的分离点S1和S2的时均位置与分离涡的时均大小基本相同。随着雷诺数的增加,分离点沿圆柱表面向下游移动,分离角增大,而涡变小。α=1时,圆柱下游的两个涡不再对称,上表面分离点S1稍有前移,而下表面S2点则向下游移动。这是因为下表面边界层内的流体因与旋转圆柱表面切向速度相同而被加速,因而导致逆压梯度的出现后移。同时,受圆柱逆时针旋转影响,分离产生的涡开始向尾部偏上区域发展。

|
| 图8 Re分别为3 900、1.4×105、 1.0×106条件下转速α分别为0、1、2、3、4的时均流线图 Figure 8 Streamlines of time-averaged velocity field for spin ratios αof 0, 1, 2, 3, 4 at Re=3 900, 1.4×105, 1.0×106 |
随圆柱转速的增加,圆柱下表面流体圆周速度进一步加大。当α=3时下涡因分离点的后移,以及受上涡空间压制而基本消失。同时,前、后驻点(A和B)均向上移动,且点A与S1之间的距离随着转速增加而变小。α=4时,圆柱边界旋转速度远大于自由来流速度,圆柱下表面分离点则向圆柱尾部转移,接近后驻点位置才从壁面脱落,而圆柱上表面分离同样变得不明显,且尾部回流区域变小。
从整体趋势来看,旋转圆柱的流场对雷诺数的变化不敏感,但其下表面分离点S2均随雷诺数增加而后移,且下表面尾涡均在α≥3时消失。
图 9为转速α分别为0、1、2、3、4时,圆柱附近的湍流动能时均等值分布。可知,低雷诺数时,圆柱表面附近基本为层流,随着涡街的脱落,在圆柱下游出现一个高湍动能区域。随着雷诺数的增加,湍流动能值增大,最大值出现位置更靠近圆柱。对于不旋转圆柱,其尾部附近的湍流动能基本对称,随着圆柱转速的增加,圆柱尾部湍流区域开始变小,并随涡的上移而上移,另外,湍流动能值随圆柱旋转速度的增加而变小。由此可知,圆柱旋转可有效抑制圆柱表面边界层的分离,降低分离涡的大小以及抑制尾部湍流的产生。

|
| 图9 Re分别为3 900、1.4×105、 1×106,转速α分别为0、1、2、3、4的湍流动能时均等值分布 Figure 9 Contours of the total resolved kinetic energy of the fluctuations for spin ratios α of 0, 1, 2, 3, 4 at Re=3 900, 1.4×105, 1×106 |
图 10为Re=1.0×106时,不同转速的圆柱阻力和升力系数随时间的变化曲线。可知,在α≤1时升力系数在整个监测时间内都以高幅值多周期振荡,随着转速的增加,其绝对值逐渐增加;α=2时,在一段时间内波动幅值不规律,流体依然是非稳态的,经过一个短暂的过渡时间后升力系数和阻力系数都变小,α>3以后升(阻)力系数在整个时间内都趋于稳定,表明此时圆柱表面涡的脱落呈现稳定的单周期性。

|
| 图10 Re=1.0×106时不同转速的圆柱阻力系数和升力系数随时间变化曲线 Figure 10 Time histories of the drag and lift coefficient for different spin raito at Re=1.0×106 |
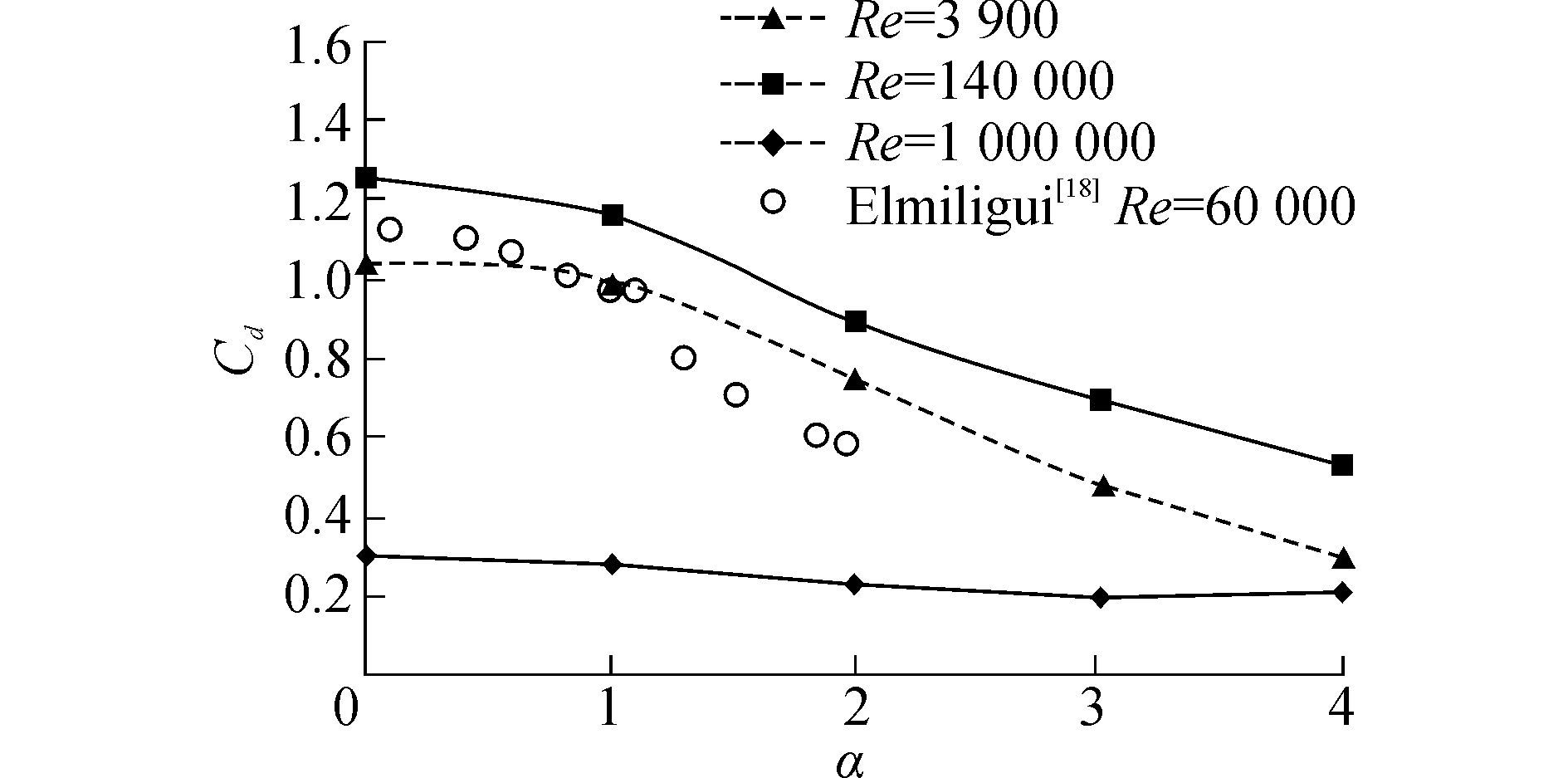
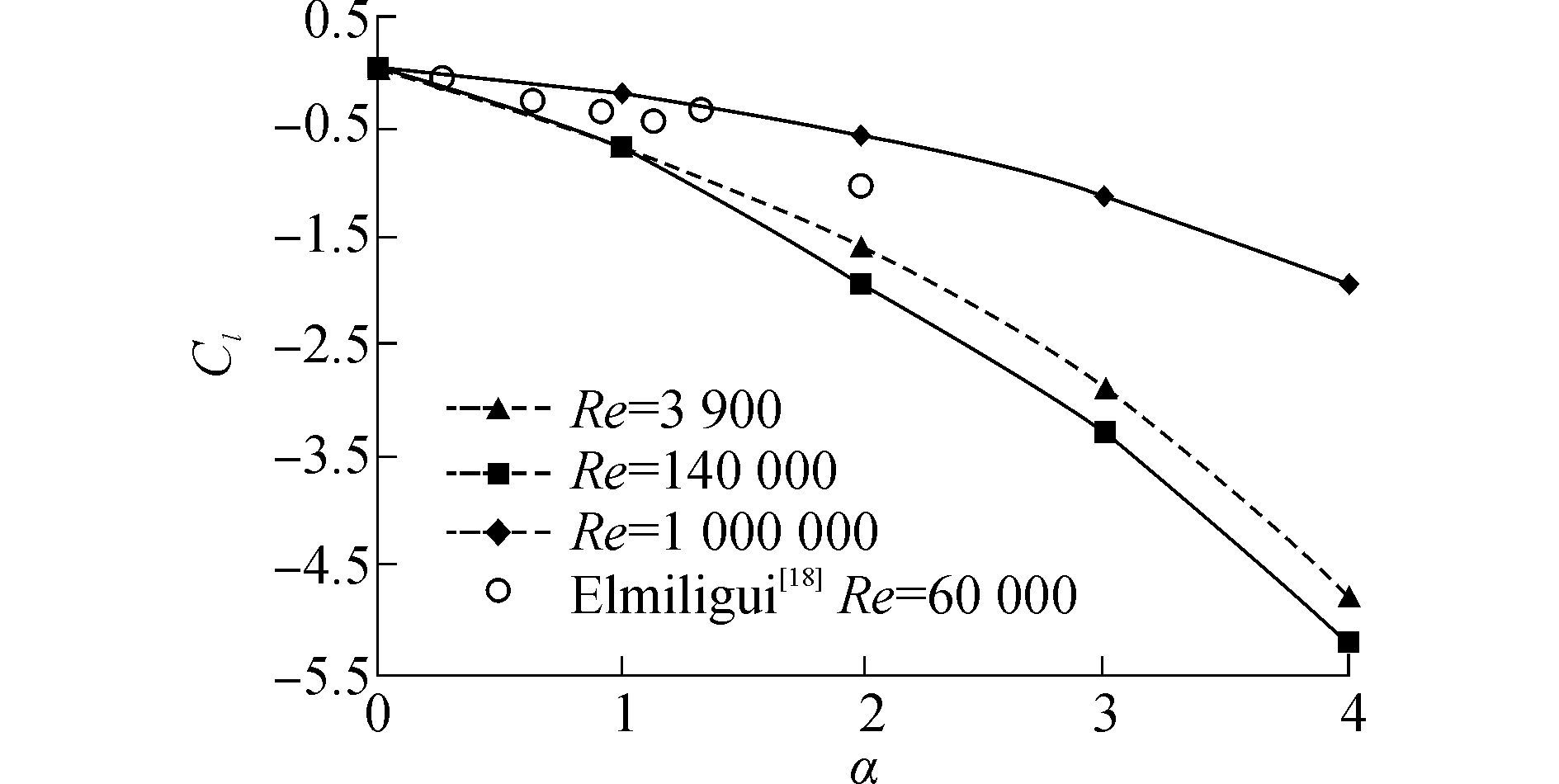
图 11为不同Re条件下,时均阻力系数随α的变化曲线。可知,阻力系数随转速的增大而降低,在亚临界条件下雷诺数越大,阻力系数也越大,随着转速的增大下降梯度增大,转速大于3以后,下降梯度变缓。在超临界雷诺数Re=1×106条件下,圆柱边界层以及尾流全部为湍流,因此圆柱前后压差阻力变小,从而导致总阻力系数减小,且随转速增大下降梯度很小;图 12为不同Re条件下时均升力系数随α的变化曲线,可知,转速为0时,由于圆柱上下表面的压力变化的平均值基本对称,所以时均升力为0,圆柱逆时针旋转时,下表面边界层内速度增加,而上表面速度减小,导致圆柱上表面压力大于下表面的压力,从而产生向下的侧向力(负升力),且随着转速增加,升力系数绝对值增大,曲线变陡。在亚临界条件下雷诺数越大圆柱受到的升力则越大,且其变化梯度较超临界雷诺数时陡,超临界时升力系数随转速的变化趋势缓慢。
|
| 图11 阻力系数随转速变化曲线 Figure 11 Mean drag coefficient versus spin raito |
|
| 图12 升力系数随转速变化曲线 Figure 12 Mean lift coefficient versus spin raito |
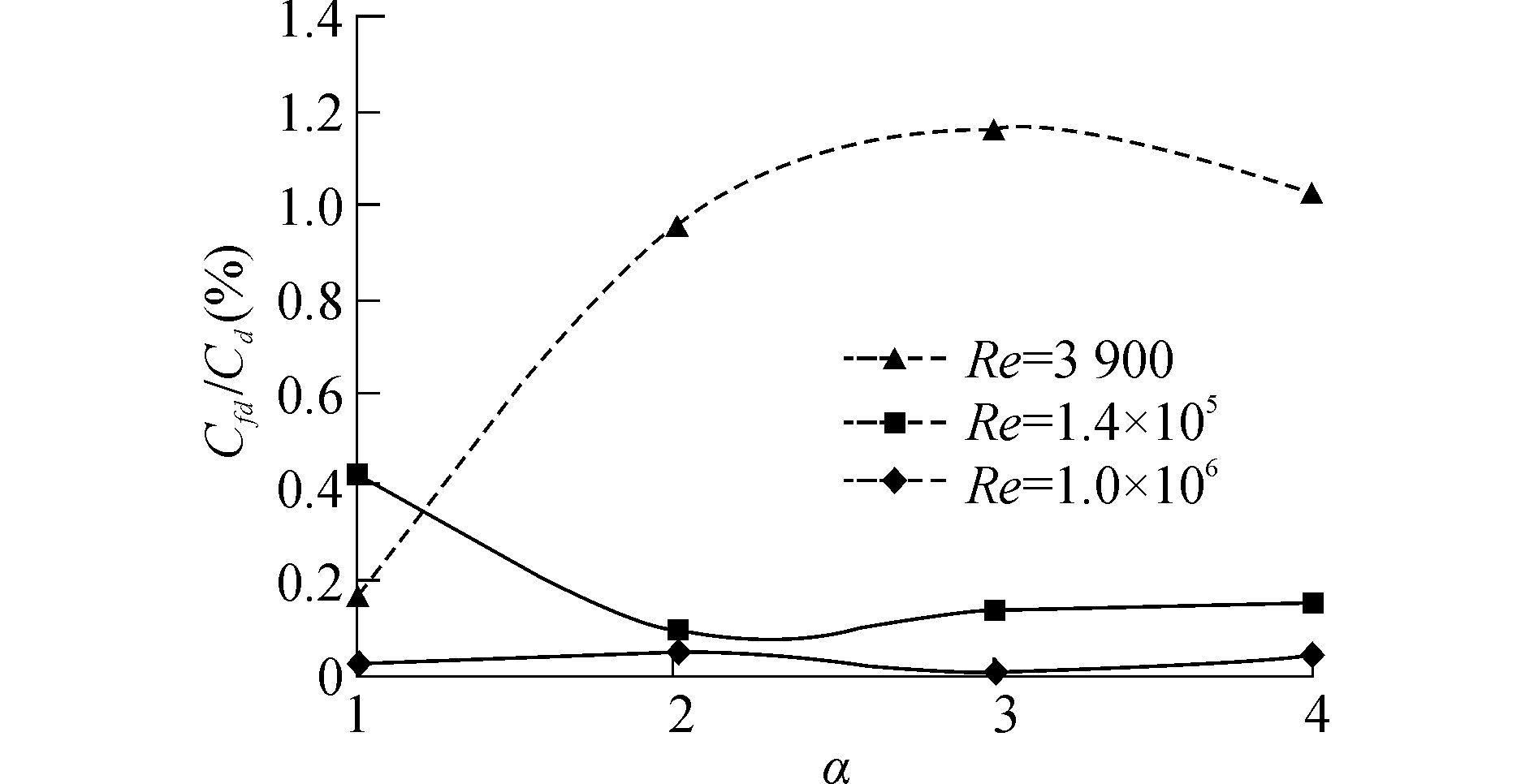
图 13为摩擦阻力占总阻力百分比随转速的变化曲线。由图 11可知,随着转速增大,圆柱总阻力均减小,而由图 13可知,摩擦阻力随转速增加而在总阻力中所占的比重增大。另外,Re为1.4×105 、1.0×106条件下,摩擦阻力所占总阻的比重几乎一致,而小雷诺数Re=3 900,摩阻比重增加。图 14为摩擦升力占总升力百分比随转速的变化曲线。从图中可以看出,高雷诺数Re=1.0×106时圆柱摩擦升力所占比重非常小,约为0.04%,而Re=1.4×105时除了在转速α=1时为0.4%,其余值在0.15%附近,因而高雷诺数条件下的粘性升力很小,可忽略。同样对于小雷诺数Re=3 900,摩擦升力所占比重有所上升,为1%左右。

|
| 图13 摩擦阻力占总阻力百分比 Figure 13 Viscous drag with the total drag |
|
| 图14 摩擦升力占总升力百分比 Figure 14 Viscous lift with the total lift |
本文在对非旋转圆柱绕流数值验证的基础上,采用LES方法对不同雷诺数Re分别为3 900、1.4×105、1.0×106,转速0≤α≤4的自由流圆柱绕流进行了三维数值研究,得出结论如下:
1) 旋转效应可以有效抑制圆柱表面流体的分离与旋涡脱落。随着转速的增加,圆柱下表面的分离点向尾部转移,涡街向上偏移。同时,分离涡随着转速和雷诺数的增大而变小。
2) 圆柱尾部的湍能区域以及湍能值都随转速的增大而减小,表明圆柱旋转能够有效抑制尾部湍流的产生。
3) 亚临界区雷诺数条件下,阻力系数随着转速的增大而减小;而在超临界区,阻力系数受转速影响不大。另外,较低雷诺数(Re=3 900) 时阻力系数中的摩擦力分量更大。
4) 升力系数随着转速的增大而减小,其中亚临界雷诺数条件下减小幅度更大,而超临界区雷诺数条件下的升力系数曲线变化平缓。同时,雷诺数越大,摩擦升力占总升力百分比越小,当Re=106时其值约为0.04%,可以忽略。
| [1] | YOON J, KIM J, CHOI H. Control of laminar vortex shedding behind a circular cylinder using tabs[J]. Journal of mechanical science and technology, 2014, 28(5): 1721–1725. |
| [2] | KANG Sangmo, CHOI H, LEE S. Laminar flow past a rotating circular cylinder[J]. Physics of fluids, 1999, 11(11): 3312–3321. |
| [3] | INGHAM D B, TANG T. A numerical investigation into the steady flow past a rotating circular cylinder at low and intermediate Reynolds numbers[J]. Journal of computational physics, 1990, 87(1): 91–107. |
| [4] | KANG Sangmo. Laminar flow over a steadily rotating circular cylinder under the influence of uniform shear[J]. Physics of fluids, 2006, 18(4): 047106. |
| [5] | MITTAL S, KUMAR B. Flow past a rotating cylinder[J]. Journal of fluid mechanics, 2003, 476: 303–334. |
| [6] | PADRINO J C, JOSEPH D D. Numerical study of the steady-state uniform flow past a rotating cylinder[J]. Journal of fluid mechanics, 2006, 557(6): 191–223. |
| [7] | BADR H M, COUTANCEAU M, DENNIS S C R, et al. Unsteady flow past a rotating circular cylinder at Reynolds numbers 103 and 104[J]. Journal of fluid mechanics, 1990, 220(7): 459–484. |
| [8] | CHEWY T, CHENGM, LUOS C. A numerical study of flow past a rotating circular cylinder using a hybrid vortex scheme[J]. Journal of fluid mechanics, 1995, 299: 35–71. |
| [9] | BREUER M. A challenging test case for large eddy simulation:high Reynolds number circular cylinder flow[J]. International journal of heat and fluid flow, 2000, 21(5): 648–654. |
| [10] | CATALANO P, WANG M, IACCARINO G, et al. Numerical simulation of the flow around a circular cylinder at high Reynolds numbers[J]. International journal of heat and fluid flow, 2003, 24(4): 463–469. |
| [11] | KARABELAS S J. Large eddy simulation of high-reynolds number flow past a rotating cylinder[J]. International journal of heat and fluid flow, 2010, 31(4): 518–527. |
| [12] |
何颖, 杨新民, 陈志华, 等. 旋转圆柱绕流的流场特性[J].
船舶力学, 2015, 19(5): 501–508.
HE Ying, YANG Xinmin, CHEN Zhihua, et al. Flow field characteristics of flow past a rotating cylinder[J]. Journal of ship mechanics, 2015, 19(5): 501–508. |
| [13] | ZDRVKOVICH M M. Flow Around Circular Cylinders[M]. Oxford: Oxford University Press, 1997 . |
| [14] | CANTWELL B, COLES D. An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder[J]. Journal of fluid mechanics, 1983, 136: 321–374. |
| [15] | TUTAR M, HOLDØ A E. Computational modelling of flow around a circular cylinder in sub-critical flow regime with various turbulence models[J]. International journal for numerical methods in fluids, 2001, 35(7): 763–784. |
| [16] | SHIH W C L, WANG C, COLES D, et al. Experiments on flow past rough circular cylinders at large Reynolds numbers[J]. Journal of wind engineering and industrial aerodynamics, 1993, 49(1/2/3): 351–368. |
| [17] |
赫鹏, 李国栋, 杨兰, 等. 圆柱绕流流场结构的大涡模拟研究[J].
应用力学学报, 2012, 29(4): 437–443.
HAO Peng, LI Guodong, YANG Lan, et al. Large eddy simulation of the circular cylinder flow in different regimes[J]. Chinese journal of applied mechanics, 2012, 29(4): 437–443. |
| [18] | ELMILIGUi A, ABDOL-HAMID K S, MASSEY S J, et al. Numerical study of flow past a circular cylinder using RANS, hybrid RANS/LES and PANS formulations[C]//22nd Applied Aerodynamics Conference and Exhibit. Rhode Island:ARC, 2004. |



