教与学优化算法(teaching learning based optimization,TLBO)是2011年由Rao等提出的一种新型群智能优化算法[1]。该算法模拟了以班级为单位的教学和学习的过程,通过老师对学生的教学以及学生之间的相互学习两个阶段来达到提高班级整体平均成绩的目的。由于TLBO算法参数设置少、计算简单,目前已在处理函数优化[2]、工程参数优化[3]、多目标优化[4]等问题上得到了广泛的应用。
文献[1]已经证明TLBO在收敛精度和收敛速度上明显优于粒子群优化算法、人工蜂群进化算法、差分进化算法等。但是该算法在搜索过程中仍然存在着易陷入局部最优以及收敛速度慢的问题。为此,许多学者对其进行了改进。文献[5]将自适应学习因子取代原有学习因子,提出一种改进的教与学优化算法。文献[6]将差分算法与教与学优化算法结合,提出了一种带有交叉操作的教与学优化算法。文献[7]将整个种群分成若干小组进行教与学两个过程,提出了一种基于分组的的教与学优化算法。上述的改进方法在一定程度上降低了算法陷入局部最优的可能,但是算法收敛精度与收敛速度仍有提升的空间。
为此,本文提出一种基于混合策略的自适应教与学优化算法(self-adaptive teaching learning based optimization with mixed-strategy,MSTLBO)。采用综合交叉学习策略代替原有学习机制,增强算法对解的搜索能力,加快收敛速度;提出一种具有一定方向性的扰动策略,增强算法跳出局部最优的能力,避免陷入局部最优。
1 教与学优化算法的基本理论TLBO算法模拟了班级中以提高平均学习成绩为目的的教师教学和学员之间相互学习这两个阶段。在教阶段,教师(适应度值最好的学员)将自己的知识全部传授给其他学员,所有学员向教师学习,逐步减小与教师之间的差距;在学阶段,学员之间互相取长补短、相互学习、共同进步。TLBO算法的主要步骤包括:教阶段和学阶段[1]。
1.1 教阶段教阶段模拟教师向学员传授知识的过程,学员通过平均值与教师之间的差异性进行学习,逐步提高学员学习成绩。具体实现过程如下:
1) 计算教师与平均值之间的差距。
| $difference={{r}_{i}}\cdot ({{X}_{teacher}}-{{T}_{f}}\cdot mean)$ | (1) |
式中:Xteacher为教师(适应度值最好的学员);mean=
2) 学员利用差异性进行学习。
| ${{X}_{new}}^{i}={{X}^{i}}+difference$ | (2) |
式中:Xi代表第i个学员教学前的值,Xnewi代表第i个学员经教学后的值。 学员Xi的学习成绩通过其适应度值f(Xi)进行衡量,即f(Xi)反映了Xi的学习成绩。f(Xi)越大则Xi成绩越好,反之Xi成绩越差。教学完成之后进行个体更新,如果f(Xinew)>f(Xi),则接受新个体,即Xi=Xnewi,否则个体不变。 教阶段学员通过向老师学习来提升自身学习成绩。
1.2 学阶段学阶段模拟学生之间类似于互相讨论、研究、演讲等相互交流的学习方式,通过向成绩更好的学员学习进而提高学员的自身成绩。 对于学员Xi,随机抽取与之不同的学员Xj进行交流学习。通过比较二者适应度值,对学习进行调整:
| ${{X}_{new}}^{i}=\left\{ \begin{matrix} {{X}^{i}}+r\cdot \left( {{X}^{i}}-{{X}^{j}} \right) & f({{X}^{i}})>f({{X}^{j}}) \\ {{X}^{i}}+r\cdot ({{X}^{j}}-{{X}^{i}}) & f({{X}^{i}})<f({{X}^{j}}) \\ \end{matrix} \right.$ | (3) |
式中:r=rand(0,1)代表每个学员的学习因子,取值0~1的随机数,这是因为在一个班级中,每个学员的学习能力有所差异,所以每个学员拥有不同的学习因子,可以更好地模拟现实中的学习情况。
学习完成之后进行个体更新,如果f(Xnewi)>f(Xi),则接受新个体,即Xi=Xnewi,否则个体不变。
学阶段通过学生之间的交流学习提升学员学习成绩。
TLBO算法流程图如图 1所示。
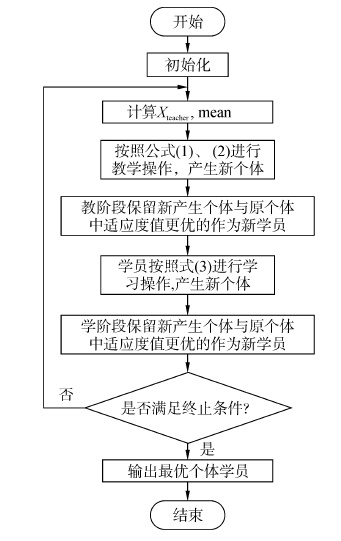
|
| 图1 TLBO算法流程图 Figure 1 The flow char of TLBO |
TLBO算法因其具有较强的收敛能力以及参数设置少等优点被广泛应用,但是通过深入研究发现TLBO算法仍存在易陷入局部最优以及收敛速度慢等缺点。为此,本文首先在文献[7]的基础上将学员分成若干小组进行教学与学习,而后从两方面进行改进,提出一种基于混合策略的自适应教与学优化算法,下面分别进行详细介绍。
2.1 自适应综合交叉学习策略的提出在TLBO算法学阶段,过分注重全局性探索的学习方式,使得在搜索过程中局部开发能力较差,对解的搜索速度较慢。事实上为更好地平衡TLBO算法全局搜索与局部开发能力,进化的不同阶段需要不同的学习方式。进化前期注重加强学员之间的信息交流,保证种群多样性,增大搜索范围,降低算法陷入局部最优的可能;进化后期注重群体进化的方向性,加快算法收敛速度,提高收敛精度。据此,本文提出将随机性学习与有向性学习融合的自适应综合交叉学习策略,即根据进化的不同阶段自适应的选择学习方式。两种学习方式在进化过程中起到不同的作用,较好的平衡了算法的全局搜索能力和局部开发能力。
随机性学习方式与标准TLBO学阶段学习方式相同,将学员Xi经随机性学习后得到的新解表示为Xnew1i:
| ${{X}_{new1}}^{i}=\left\{ \begin{matrix} {{X}^{i}}+r\cdot \left( {{X}^{i}}-{{X}^{j}} \right) & f({{X}^{i}})>f({{X}^{j}}) \\ {{X}^{i}}+r\cdot ({{X}^{j}}-{{X}^{i}}) & f({{X}^{i}})<f({{X}^{j}}) \\ \end{matrix} \right.$ | (4) |
这种随机性的学习方式保证了每个学员可以获得多元化的信息,增大种群的多样性。但是这种方式过分地注重全局搜索,具有一定盲目性,导致在进化后期算法在对解空间搜索时,收敛速度过慢,局部开发能力较差。基于以上分析,本文采用一种有向性学习方式用以弥补随机性学习在搜索过程中存在的不足。在有向性学习方式中,对于已完成分组后的学员Xi,不再是随机向学员Xj学习,而是向Xi所在学习小组内适应度值最优的XGroupteacher学习,令较优解参与进化产生新解,使得进化具有一定的方向性,总是向着较好的方向进行,逐渐向着最优值逼近,从而提高算法收敛速度与收敛精度。有向性学习方式:
| ${{X}_{new2}}^{i}={{X}^{i}}+r\cdot \left( {{X}_{Groupteacher}}-{{X}^{i}} \right)$ | (5) |
式中:r=rand(0,1),XGroupteacher为学员Xi所在学习小组内适应度值最好的学员即小组老师。Xnew2i为学员Xi向所在小组老师学习后产生的新解。 考虑到算法进化的过程中,前期侧重全局探索后期更加注重局部开发,故结合以上两种学习方式的优点,提出将这两种学习方式融合的自适应综合交叉学习策略为
| ${{X}_{new}}^{i}=c\cdot \left( 1-\frac{t}{{{T}_{max}}} \right)\cdot {{X}_{new1}}^{i}+\left( \frac{t}{{{T}_{max}}} \right)\cdot {{X}_{new2}}^{i}$ | (6) |
式中:t为当前迭代次数,Tmax为算法最大迭代次数,Xnew1i通过式(4)得到,Xnew2i通过式(5)得到,经过大量实验证明当c=1/2时效果最好。公式中两种学习方式的权重随着迭代次数t的变化而改变,进化前期Xnew1i系数较大,算法更加注重随机性学习,保证种群多样性,增大有效搜索范围,降低算法陷入局部最优的可能。进化后期随着迭代次数t的增大,Xnew1i的系数逐渐减小,Xnew2i的系数逐渐增大,学习方式慢慢侧重于有向性学习,加快对最优解的搜寻速度。基于以上分析,本文提出的自适应综合交叉学习策略教与学优化算法较好的平衡了全局搜索能力和局部开发能力,提高算法收敛速度与收敛精度。
2.2 自适应扰动策略的提出学阶段的分组教学方式为种群多样性做出了一定贡献,但是随着进化进行,种群仍然会出现“趋同”现象[8-9],尤其到了进化后期,粒子逐渐聚集到某一点(非全局最优值点),进化几乎停滞,种群处于一种相对平衡状态,易陷入局部最优。针对这种情况,本文提出一种自适应扰动策略:算法进化前期,学员比较分散多样性较好,为提高种群的局部搜索能力,围绕当前粒子进行扰动以期得到更优个体。随着迭代进行,学员逐渐聚集,种群多样性逐渐变差,种群陷入局部最优的可能逐渐增加,此时应逐渐增大最优个体对当前个体的影响力度,进而增大种群多样性,扩大种群的搜索空间,增强算法跳出局部最优的能力。基于以上分析,本文在文献[10]的基础上进行改进,提出扰动公式为
| ${{X}_{new}}^{i}={{(1-\frac{t}{Tmax})}^{2}}\cdot {{X}^{i}}+{{(\frac{t}{Tmax})}^{2}}\cdot {{X}_{teacher}}+2\cdot \left( r-0.5 \right)\cdot ({{X}_{teacher}}-{{X}^{i}})$ | (7) |
式中:t为当前迭代次数,Tmax为最大迭代次数,r=rand(0,1),Xi为当前迭代第i个学员,Xteacher为当前迭代适应度最好学员,Xnewi为第i个学员经扰动后得到的值。进化前期,Xi的系数较大,Xteacher的系数较小,扰动围绕着当前粒子。随着进化的进行,Xi的系数逐渐减小,Xteacher的系数逐渐增大,即最优个体的影响力度逐渐增加,从而增大了种群多样性,扩大了探索区域。Xi与Xteacher之间的差异性保证了扰动是朝着好的方向进行,提高了算法的搜索效率。加入扰动策略后可避免种群因陷入局部最优而导致的整个群体处于停滞状态的情况,增强了算法的局部开采能力。
2.3 MSTLBO算法执行步骤综合以上两个方面的改进措施,本文提出的MSTLBO算法具体步骤如下:
1) 初始化班级中学员数目(NP),变量维数 d,小组成员数目m,动态分组频率p;
2) 将所有学员分组[7],计算每个小组的XGroupteacher;
3) 教阶段,每个小组学员按照式(1)、(2)产生新个体,如果新个体适应度值优于未更新个体,则保留更新后的个体;
4) 学阶段,学员Xi按照式(4)进行学习,得到新解Xnew1i;
5) 学员Xi按照式(5)进行学习,得到新解Xnew2i ;
6) 按照式(6),产生自适应综合交叉学习后的新学员;
7) 学员按照式(7)进行扰动,将扰动后得到的新个体与扰动前的个体进行比较,保留适应度值较好的个体;
8) 如果mod(t,p)==0,则返回2),否则返回3),t=t+1;
9) 若满足终止条件,输出当前最优个体,算法结束。
3 实验结果与分析为验证本文所提出算法的整体性能,在10个典型 Benchmark 函数[11]上进行测试,并与TLBO算法[1]以及目前改进效果较好的ITLBO算法[5]、CTLBO算法[6]、DGSTLBO算法[7]进行对比。Benchmark 函数的取值范围以及理论最优值已经在表 1中给出。根据函数性质将其分为单峰和多峰两大类,其中函数f1~f6为复杂连续型单峰函数,主要用来测试算法的寻优精度,考察算法的执行性能。f 7~f10是非线性多峰函数,具有多个局部极值点,一般算法很难找到全局最优值因此可用来测试算法的全局搜索性能和避免早熟的能力[12]。
| 函数名 | 函数表达式 | 搜索空间 | 最优解 |
| Sphere | [-100,100] | 0 | |
| Sumsquare | [-10,10] | 0 | |
| Quadric | [-100,100] | 0 | |
| Schwefel2.2 | [-10,10] | 0 | |
| Schwefel1.2 | [-100,100] | 0 | |
| Schwefel2.1 | [-100,100] | 0 | |
| Ackley | [-32,32] | 0 | |
| Grienwank | [-600,600] | 0 | |
| Rastrigin | [-5.12,5.12] | 0 | |
| Zakharov | [-10,10] | 0 |
仿真实验在Intel(R).Pentium(R).CPU G260@2.60GHZ.2G内存的计算机上进行,开发环境为Matlab 2011a。
3.1 实验参数设置所有算法的种群大小为50,决策变量维数为30,所有测试函数上的最大迭代次数为1000次。本文算法中两个参数m=5,p=5。其他所有对比算法中涉及到的参数均与对比文献中相同。为避免偶然因素的影响,每个测试函数的寻优实验都独立运行30次。通过测试结果的最优值、最差值、平均值,标准差、函数评价次数、运行时间以及成功率来评价函数的寻优性能。
3.2 实验仿真与结果分析为验证本文算法中两点改进的有效性以及MSTLBO算法的整体性能,将从以下两方面进行仿真实验。
3.2.1 自适应综合交叉学习策略的有效性测试为验证本文提出的自适应综合交叉学习策略的有效性,选取单峰函数f1以及非常难找到全局最优值的多峰函数f7进行测试。得到的均值、方差,达到求解精度的函数评价次数以及成功率已在表 2中给出,各算法均独立运行30次。其中,TLBO-m代表本文提出的基于自适应综合交叉学习策略的TLBO改进算法。
| 测试函数 | 算法 | 平均值 | 方差 | 函数评价次数 | 成功率 |
| f1 | TLBO | 1.028×10-18 | 2.434×10-18 | 4058 | 100 |
| TLBO-m | 0 | 0 | 1006 | 100 | |
| f7 | TLBO | 3.908×10-15 | 1.136×10-15 | 7210 | 100 |
| TLBO-m | 3.553×10-187 | 1.592×10-186 | 1778 | 100 |
从表 2中可以看出,对于单峰函数f1 ,TLBO-m算法收敛到理论最优值,相比于TLBO算法得到了更小的平均值和方差,函数评价次数也较少,说明改进的算法在收敛精度和收敛速度上都有提升。对于多峰函数f7,虽然TLBO-m算法没有收敛到理论最优值但是相对于TLBO算法也得到了较小的均值、方差、函数评价次数。以上实验结果表明,本文提出的自适应综合交叉学习策略是有效的。
3.2.2 自适应扰动策略的有效性测试为验证本文提出的自适应扰动策略的有效性,在测试函数f5和f9上将加入扰动策略的TLBO算法与TLBO算法进行对比,其中TLBO-s代表加入扰动后的算法。为了更直观的表现两算法的对比结果,将其进化曲线图表示如图 2,其中横坐标代表进化代数,纵坐标代表每代最优适应度值的对数。
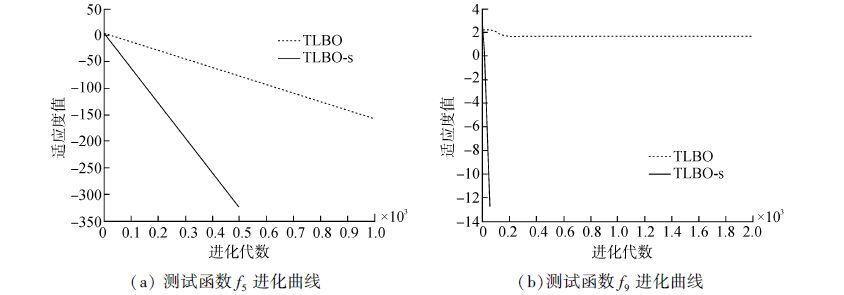
|
| 图2 改进的扰动策略效果图 Figure 2 Result of improved disturbance strategy |
从图 2中可以看出在对单峰函数f5以及多峰函数f9的寻优过程中,改进后的算法在收敛速度和收敛精度两方面都优于对比算法。尤其在多峰函数f9的寻优上,标准TLBO已陷入局部最优,而TLBO-s较快的收敛到最优值,寻优精度和收敛速度有较大提升,从而证明了本文提出的自适应扰动策略的有效性。
3.2.3 MSTLBO算法整体性能测试为验证本文所提出MSTLBO算法的整体性能,现与TLBO算法、CTLBO算法、ITLBO算法以及DGSTLBO算法进行对比,各算法均独立运行30次。对比算法性能的考察将从以下两个方面进行:通过结果中最优值、最差值、平均值、标准差来评价寻优精度;通过运行时间,函数评价次数以及成功率来评价算法收敛速度。各函数求解精度为VTR=10-8。算法性能对比结果如表 3所示,表中空白处代表对应算法未收敛到规定求解精度。 从表 3所得结果可以得出以下结论:
| 测试函数 | 算法 | 最优值 | 最差值 | 平均值 | 标准差 | 运行时间 | 函数评价次数 | 成功率 |
| f1 | TLBO | 6.784×10-19 | 7.010×10-18 | 1.028×10-18 | 2.434×10-18 | 63.72 | 4598 | 100 |
| ITLBO | 4.398×10-192 | 1.862×10-190 | 2.562×10-191 | 3.457×10-192 | 52.34 | 2356 | 100 | |
| CTLBO | 1.943×10-193 | 4.373×10-193 | 3.256×10-193 | 4.343×10-193 | 43.24 | 1479 | 100 | |
| DGSTLBO | 0 | 0 | 0 | 0 | 7.68 | 1730 | 100 | |
| MSTLBO | 0 | 0 | 0 | 0 | 6.16 | 556 | 100 | |
| f2 | TLBO | 3.553×10-15 | 7.106×10-15 | 3.908×10-15 | 1.136×10-15 | 91.85 | 3124 | 100 |
| ITLBO | 3.552×10-15 | 5.334×10-15 | 4.331×10-15 | 2.397×10-15 | 93.46 | 2820 | 100 | |
| CTLBO | 3.512×10-15 | 4.121×10-15 | 3.989×10-15 | 4.001×10-15 | 76.37 | 2516 | 100 | |
| DGSTLBO | 0 | 0 | 0 | 0 | 34.39 | 1724 | 100 | |
| MSTLBO | 0 | 0 | 0 | 0 | 34.12 | 556 | 100 | |
| f3 | TLBO | 1.053×10-115 | 1.323×10-109 | 2.124×10-110 | 1.460×10-109 | 45.37 | 4200 | 100 |
| ITLBO | 1.464×10-115 | 3.193×10-110 | 2.861×10-111 | 2.313×10-111 | 44.16 | 4120 | 100 | |
| CTLBO | 4.832×10-186 | 7.424×10-184 | 7.508×10-184 | 3.545×10-184 | 33.28 | 4486 | 100 | |
| DGSTLBO | 0 | 1.380×10-320 | 2.300×10-312 | 0 | 18.62 | 2400 | 100 | |
| MSTLBO | 0 | 0 | 0 | 0 | 21.49 | 558 | 100 | |
| f4 | TLBO | 3.127×10-80 | 7.258×10-78 | 2.178×10-79 | 1.974×10-78 | 14.04 | 3140 | 100 |
| ITLBO | 2.114×10-80 | 3.478×10-79 | 2.673×10-79 | 1.467×10-79 | 14.36 | 2454 | 100 | |
| CTLBO | 3.268×10-81 | 4.323×10-80 | 3.242×10-80 | 2.976×10-80 | 13.32 | 2186 | 100 | |
| DGSTLBO | 5.175×10-199 | 2.4528×10-188 | 2.453×10-189 | 0 | 8.41 | 2410 | 100 | |
| MSTLBO | 0 | 0 | 0 | 0 | 8.13 | 1044 | 100 | |
| f5 | TLBO | 5.463×10-16 | 4.481×103 | 1.435×102 | 2.364×102 | 17.28 | — | — |
| ITLBO | 1.649×10-6 | 1.217×103 | 1.094×102 | 2.083×102 | 16.36 | — | — | |
| CTLBO | 5.667×10-134 | 2.232×10-134 | 3.582×10-134 | 1.398×10-134 | 17.23 | 1830 | 100 | |
| DGSTLBO | 8.818×10-237 | 1.553×10-225 | 1.598×10-226 | 0 | 12.51 | 2324 | 100 | |
| MSTLBO | 0 | 0 | 0 | 0 | 10.24 | 564 | 100 | |
| f6 | TLBO | 1.4433×10-305 | 1.077×10-297 | 1.004×10-298 | 0 | 15.55 | 3146 | 100 |
| ITLBO | 6.232×10-305 | 3.808×10-301 | 4.471×10-302 | 0 | 13.41 | 2186 | 100 | |
| CTLBO | 0 | 0 | 0 | 0 | 17.82 | 2530 | 100 | |
| DGSTLBO | 0 | 0 | 0 | 0 | 10.22 | 1480 | 100 | |
| MSTLBO | 0 | 0 | 0 | 0 | 11.58 | 814 | 100 | |
| f7 | TLBO | 3.553×10-15 | 7.106×10-15 | 3.908×10-15 | 1.136×10-15 | 16.46 | 6934 | 96.67 |
| ITLBO | 3.552×10-15 | 5.334×10-15 | 4.331×10-15 | 2.397×10-15 | 14.66 | 7210 | 100 | |
| CTLBO | 3.512×10-15 | 4.121×10-15 | 3.989×10-15 | 4.001×10-15 | 18.47 | 5430 | 96.67 | |
| DGSTLBO | 0 | 0 | 0 | 0 | 9.37 | 216 | 100 | |
| MSTLBO | 0 | 0 | 0 | 0 | 10.85 | 66 | 100 | |
| f8 | TLBO | 2.872×10-16 | 9.301×10-16 | 3.981×10-16 | 2.463×10-16 | 15.75 | 1490 | 100 |
| ITLBO | 8.362×10-34 | 4.232×10-33 | 3.389×10-33 | 1.567×10-33 | 14.93 | 1066 | 100 | |
| CTLBO | 7.325×10-28 | 2.768×10-28 | 4.292×10-28 | 3.893×10-28 | 17.36 | 1286 | 100 | |
| DGSTLBO | 2.987×10-198 | 3.876×10-196 | 2.789×10-197 | 0 | 9.02 | 116 | 100 | |
| MSTLBO | 3.474×10-196 | 8.386×10-196 | 4.983×10-196 | 0 | 8.46 | 40 | 100 | |
| f9 | TLBO | 0 | 28.854 | 4.378 | 9.293 | 17.55 | — | — |
| ITLBO | 0 | 11.441 | 3.358 | 5.328 | 16.18 | — | — | |
| CTLBO | 3.782×10-17 | 8.438×10-16 | 6.383×10-16 | 4.857×10-17 | 15.62 | — | — | |
| DGSTLBO | 0 | 0 | 0 | 0 | 10.79 | 144 | 100 | |
| MSTLBO | 0 | 0 | 0 | 0 | 13.24 | 34 | 100 | |
| TLBO | 2.998×10-80 | 1.393×10-78 | 2.769×10-79 | 1.618×10-78 | 15.62 | 4386 | 73.37 | |
| f10 | ITLBO | 1.590×10-80 | 1.348×10-79 | 9.804×10-79 | 1.346×10-79 | 14.49 | 3812 | 96.67 |
| CTLBO | 7.891×10-189 | 1.776×10-188 | 4.838×10-188 | 9.382×10-188 | 17.36 | 3720 | 96.67 | |
| DGSTLBO | 7.659×10-262 | 2.777×10-251 | 2.805×10-252 | 0 | 9.34 | 2946 | 100 | |
| MSTLBO | 0 | 3.864×10-309 | 0 | 0 | 10.78 | 552 | 100 |
1) 寻优精度:在对复杂连续型单峰函数f1、f2的寻优过程中,MSTLBO算法和DGSTLBO算法收敛到了理论最优值。对于函数f3~f5,MSTLBO算法相较于TLBO、ITLBO、CTLBO、DGSTLBO算法收敛到了理论最优值而且具有较好的稳定性。对于函数f6,只有MSTLBO算法、CTLBO算法以及DGSTLBO算法收敛到了理论最优值。以上结果表明MSTLBO算法在寻优精度上具有较大优势。 对于具有多个局部极值点的多峰函数f7~f10而言,由于这些函数的自身特点很容易陷入局部最优而较难搜索到最优值。由表 3可知,对于多峰函数f7~f10,TLBO、ITLBO、CTLBO算法过早陷入局部最优并没有搜索到理论最优值,而DGSTLBO算法只在函数f7、f9上收敛到理论最优值,而本文提出的MSTLBO算法在函数f7、f9、f10上都收敛到了理论最优值。但是对于函数f8,MSTLBO算法收敛精度略次于DGSTLBO,但是相对于TLBO、ITLBO、CTLBO算法收敛精度大幅度改善。所以本文提出的MSTLBO算法几乎都可以收敛到理论最优值且算法稳定性较好,收敛精度相对于对比算法有较大提高。
2) 收敛速度:所得结果中函数评价次数较小的算法说明其收敛速度较快,成功率较高说明其达到规定收敛精度成功次数较多。由表 3可知,对于函数f1、f2、f4、f5,MSTLBO相较于TLBO、ITLBO、CTLBO以及DGSTLBO运行时间和函数评价次数均较少,成功率较高。对于函数 f3、f6、f7、f9、f10,MSTLBO相较于TLBO、ITLBO、CTLBO运行时间和函数评价次数均较少,但是较DGSTLBO运行时间较多,这是由于MSTLBO计算复杂度对比于DGSTLBO算法略有提高,使得单次收敛速度也有上升,但由于MSTLBO的函数评价次数较少使得总的计算效率与DGSTLBO相差不大。对于多峰函数f7、f9、f10,MSTLBO较TLBO、ITLBO、CTLBO、DGSTLBO函数评价次数大大减小,说明本文所提算法不易陷入局部最优且可以快速收敛到理论最优值。对于函数f8虽然MSTLBO的收敛精度略差于DGSTLBO但是函数评价次数以及运行时间均较小。总体上本文提出的MSTLBO算法收敛速度相对于对比算法有较大提高。
综合以上分析,本文提出的MSTLBO算法在收敛速度以及收敛精度两方面优于其他对比算法,尤其对于多峰函数寻优效果更为明显,有效避免了算法陷入局部最优的现象,较好地平衡了全局探索以及局部开发能力。
4 结论1) 本文提出了一种自适应综合交叉学习策略,从而加快算法对最优解的搜索速度;
2) 本文提出的自适应扰动策略,增强了种群多样性,从而降低种群陷入局部最优的可能。
3) 本文所提出算法具有较好的收敛精度和收敛速度,尤其在多峰函数的寻优上效果更佳,具有较好的推广价值。
| [1] | RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization:a novel method for constrained mechanical design optimization problems[J]. Computer-aided design, 2011, 43(3): 303–315. |
| [2] | RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization:an optimization method for continuous non-linear large scale problems[J]. Information sciences, 2012, 183(1): 1–15. |
| [3] | RAO R V, PATEL V. Multi-objective optimization of heat exchangers using a modified teaching-learning-based optimization algorithm[J]. Applied mathematical modelling, 2013, 37(3): 1147–1162. |
| [4] | RAO R V, PATEL V. Multi-objective optimization of two stage thermoelectric cooler using a modified teaching-learning-based optimization algorithm[J]. Engineering applications of artificial intelligence, 2013, 26(1): 430–445. |
| [5] | RAO R V, PATEL V. An improved teaching-learning-based optimization algorithm for solving unconstrained optimization problems[J]. Scientia iranica, 2013, 20(3): 710–720. |
| [6] |
高立群, 欧阳海滨, 孔祥勇, 等. 带有交叉操作的教与学优化算法[J].
东北大学学报:自然科学版, 2014, 35(3): 323–327.
GAO Liqun, OUYANG Haibin, KONG Xiangyong Y, et al. Teaching-learning based optimization algorithm with crossover operation[J]. Journal of northeastern university:natural science, 2014, 35(3): 323–327. |
| [7] | ZOU Feng, WANG Lei, HEI Xinhong, et al. Teaching-learning-based optimization with dynamic group strategy for global optimization[J]. Information sciences, 2014, 273: 112–131. |
| [8] | LI Jianping, BALAZS M E, PARKS G T, et al. A species conserving genetic algorithm for multimodal function optimization[J]. Evolutionary computation, 2002, 10(3): 207–234. |
| [9] | LI Xiaodong. Efficient differential evolution using speciation for multimodal function optimization[C]//Proceedings of the 7th Annual Conference On Genetic and Evolutionary Computation. New York, USA, 2005:873-880. |
| [10] |
伍大清, 郑建国. 基于混合策略自适应学习的并行粒子群优化算法[J].
控制与决策, 2013, 28(7): 1087–1093.
WU Daqing, ZHENG Jianguo. Improved parallel particle swarm optimization algorithm with hybrid strategy and self-adaptive learning[J]. Control and decision, 2013, 28(7): 1087–1093. |
| [11] | YAO Xin, LIU Yong, LIN Guangming. Evolutionary programming made faster[J]. IEEE transactions on evolutionary computation, 1999, 3(2): 82–102. |
| [12] | OMRAN M G H, ENGELBRECHT A P, SALMAN A. Self-adaptive barebones differential evolution[C]//Proceedings of the IEEE Congress on Evolutionary Computation. Singapore, 2007:2858-2865. |



