目前航运业每年CO2排放量超过12亿吨,约占全球碳排放总量的4%。如果不采取合理有效的措施,全球航运业的CO2排放将在2050年翻番。欧盟在2013年拟将航运业纳入欧盟碳排放交易体系,通过征收“航海碳税”对航运业的CO2排放进行限制。在全球低碳生成的大背景下,船公司在营运时必须考虑碳税征收成本,并通过CO2总量控制手段,将碳排放量控制在某一确定的范围内[1]。因此,产生了对船舶营运CO2排放量进行定量估算的需要。IMO于2009年7月通过和批准了包括《能效营运指数自愿使用导则》在内的四个导则,在导则中,提出了船舶能效营运指数(ship energy efficiency operational index,EEOI)的概念,并将其作为一种评估船舶温室气体排放水平的指标。
由于影响EEOI的因素非常多,对其进行足够精度的定量估算存在难度。目前对船舶EEOI预测和分析的研究主要有两个方向:1)船舶营运的统计数据,结合如灰色预测[2]、人工神经网络[3]、蒙特卡洛仿真[4]等方法,建立数据驱动的EEOI预测模型。 这类方法需要大量统计数据作为建模基础,普遍并不考虑气象和航线因素,或对环境因素简化处理。2)通过对船体、螺旋桨、主机、传动系统分别建模模型,对船舶CO2的排放进行计算[5-6]。这类研究目前停留在对假设航线进行仿真。由于航线假设,因此环境因素和操舵的控制信号也是假设,和船舶实际营运状况差别较大。
本文通过建立推进系统-船体运动-环境的联合数学模型,结合实际气象数据、目标船的设计参数(船体型线图、主机型号、螺旋桨设计参数、舵设计参数)和实验数据(船模实验、试航报告、螺旋桨敞水试验)、目标航线,在地球的球面坐标系下对船舶的整个营运过程进行动力学仿真。据此分析推进系统能量消耗过程,并对实际海况影响下的船舶EEOI进行预测。
1.1 建模基础导则中对一个航次的EEOI定义如下[7]:
| $EEOI=\frac{\sum jF{{C}_{j}}\times C{{F}_{j}}}{{{m}_{cargo}}\times D}$ | (1) |
式中:j为燃油类型,FCj为一个航次某类燃油的消耗量,CFj为燃油j的燃油量与CO2量转换系数,mcargo货物为客船所载货物(吨)或所作的功(标箱或乘客数量)或总吨,D 为对应于所载货物或所作的功的距离(海里)。根据导则所定义,3个因素影响船舶EEOI计算:1)船舶的载货量;2)船舶航程;3)完成航次船舶的总燃油消耗。
当船舶的载货量mcargo改变时,直接通过EEOI计算公式的分母直接影响到EEOI的计算结果。同时,还会导致船舶吃水改变,进而改变了水下船体的几何形状,影响到船体受力。虽然吃水增加会导致船舶阻力的增加,mcargo对EEOI计算的影响更为显著[8]。船舶完成一个航次的航程在航线选定后就已经基本确定。虽然航线越短,理论上EEOI越低。但是在实际营运过程中,航线还影响到船舶航行所经过海域。由于环境的不同,可能会出现短航线遭遇较为恶劣海况,总油耗反而上升的情况发生。
在对船舶EEOI进行计算时,最重要的工作是统计全船的燃油消耗。船舶的燃油消耗是一个能量的消耗过程,该过程存在于船舶营运的每一个方面。如推进系统、照明、供热、通风及空调,其中最主要的为船舶推进系统所消耗的能量[9]。船舶推进系统的燃油消耗不但占的比例较高,而且受环境干扰的影响大。对EEOI进行预测计算的重点,是建立环境影响下的推进系统模型,计算主机负荷及油耗。
1.2 坐标系及气象数据在建立船舶运动模型时,为便于分析问题,往往采用平面直角坐标系,因此船舶坐标和航迹是建立在大地平面坐标系之内的,如图 1(a)所示为船舶三自由度运动的大地平面直角坐标系。当从船舶整个营运过程分析时,由于地球为椭球体,船舶的位置由经度和纬度来标示如图所示;同时,船舶航行海域风浪数据也是以经纬度定位的。因此,需将大地平面直角坐标系坐标转化至经纬度坐标,方法为
| ${{b}_{lo}}={{a}_{lo}}+\frac{180\Delta {{x}_{0}}}{\pi Rcos({{a}_{la}}\cdot \pi 180)}$ | (2) |
| ${{b}_{la}}={{a}_{la}}+\frac{180\Delta {{y}_{0}}}{\pi R}$ | (3) |

|
| 图1 大地坐标系 Figure 1 Ground based coordinate system |
式中:A(alo,ala)为起点经纬度坐标,Δx、Δy为大地平面直角坐标上的位移,B(blo,bla)为终点经纬度坐标,R为地球半径。
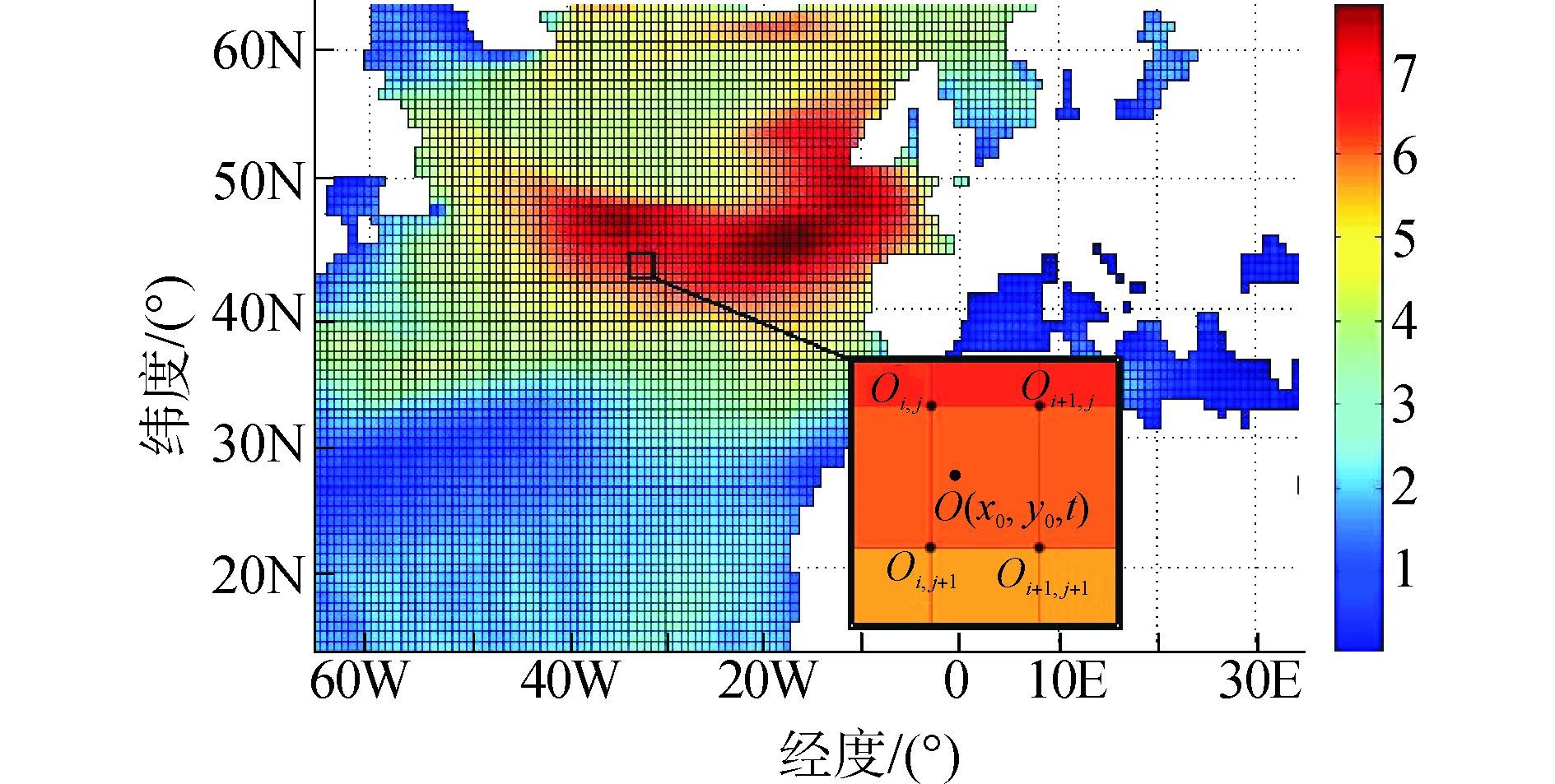
风浪等气象数据以等长经纬度格点作为地理单位存储;风浪数据格点连成的形状近似为梯形;在仿真过程中,船舶位置不会精确处于网格点上,因此需要根据船舶实际位置对网格点数据进行曲面插值。如图 2所示,以ECMWF提供的某时段局部海洋气象数据分布图为例,Ox0,y0代表坐标为(x0,y0)点的物理量,Oi,j、Oi+1,j、Oi,j+1、Oi+1,j+1为(x0,y0)点所在格点四个角点的物理量,则Ox0,y0根据当前坐标到四个角的相对位置和物理量通过三维线性插值得到。
|
| 图2 气象数据提取示意图 Figure 2 Diagram of meteorological data extraction |
船舶在海面上航行时,船体做六个自由度的运动。其中,纵摇、横摇、垂荡对船舶的燃油消耗影响较小,因此仅对船体的纵向速度u、横向速度v和艏摇速度r进行计算[5]。船舶在任一时刻,船舶的状态都是用纵向速度u、横向速度v、艏摇速度r、横向坐标x、纵向坐标y、船舶航向ψ、主机转速n、舵角θ这8个变量表示。本文将船体运动和推进系统作为一个动力系统,通过对船舶推进系统和运动状态参数的循环迭代,计算出航次过程中推进系统状态参数的连续变化。船舶状态迭代方程:
| $\left[ \begin{matrix} {{u}_{t+1}} \\ {{v}_{t+1}} \\ {{r}_{t+1}} \\ {{x}_{t+1}} \\ {{y}_{t+1}} \\ {{\psi }_{t+1}} \\ {{n}_{t+1}} \\ {{\theta }_{t+1}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{u}_{t}} \\ {{v}_{t}} \\ {{r}_{t}} \\ {{x}_{t}} \\ {{y}_{t}} \\ {{\psi }_{t}} \\ {{n}_{t}} \\ {{\theta }_{t}} \\ \end{matrix} \right]+\left[ \begin{matrix} {{{\dot{u}}}_{t}} \\ {{{\dot{v}}}_{t}} \\ {{{\dot{r}}}_{t}} \\ {{u}_{t}} \\ {{v}_{t}} \\ r \\ {{{\dot{n}}}_{t}} \\ \theta {{\cdot }_{t}} \\ \end{matrix} \right]$ | (4) |
在式(4)的8个变量中,u、v、r和x、y、ψ属于运动参数。在对面运动状态计算时,采用MMG模型,并推导出船舶运动微分方程,具体公式如下:
| $\dot{u}=\frac{{{X}_{H}}+{{X}_{P}}+{{X}_{R}}+{{X}_{D}}+\left( m+{{m}_{y}} \right)vr}{\left( m+{{m}_{x}} \right)}$ | (5) |
| $\dot{v}=\frac{{{Y}_{H}}+{{Y}_{P}}+{{Y}_{R}}+{{Y}_{D}}-\left( m+{{m}_{x}} \right)ur}{\left( m+{{m}_{y}} \right)}$ | (6) |
| $\dot{r}=\frac{{{N}_{H}}+{{H}_{P}}+{{H}_{R}}}{\left( {{I}_{zz}}+{{J}_{zz}} \right)}$ | (7) |
式中:m为船舶在某一吃水时的质量,mx和my为船舶分别在X方向和Y方向上的附加质量。XH、XP、XR、XD分别代表X方向上的流体、螺旋桨、舵和环境干扰的作用力;YH、YP、YR、YD分别代表Y方向上的流体、螺旋桨、舵和环境干扰的作用力;NH、HP、HR代表围绕着Z轴的流体,螺旋桨,舵的扭矩。Izz代表船舶绕Z轴的转动惯量,Jzz代表附体转动惯量。
在以上参数中,附加质量根据周昭明方法进行计算;附体转动惯量根据Clarke方法进行计算;3个自由度的水动力导数根据贵岛模型计算,其中静水阻力根据船模实验的结果换算得出;某一吃水时的船舶质量和转动惯量根据型值表在Maxsurf建模计算;舵力根据舵的设计参数和经验公式进行计算;螺旋桨的特性则根据螺旋桨敞水实验和自航实验的结果获得。环境干扰力主要考虑风和浪的作用,需要获风速、风向、浪高、浪向、浪周期这5个海洋环境数据作为计算基础。在计算环境干扰力时,根据文献[10-11]中的方法,获得环境干扰力在三个自由度上的影响。
式(4)中,n属于推进系统参数。在船舶正常航行时,一般采用定转速航行。由于干扰因素存在,转速会动态变化,其变化量为
| $\dot{n}=\frac{{{M}_{E}}-{{M}_{P}}-{{M}_{T}}}{2\pi I}$ | (8) |
式中:ME为主机输出扭矩,当转速变化时,调速器通过PID调节油门刻度pos来控制循环供油量gc,进而调整ME以保持主机转速稳定[12]。调速器控制原理如图 3(a)所示,中间系数根据实验报告进行拟合。MP为螺旋桨接收到的扭矩,MT为摩擦力矩,I为螺旋桨、轴系及附体的总转动惯量。

|
| 图3 调速器控制和航迹控制原理图 Figure 3 The control chart of governor and ship track keeping |
船舶还需要通过操作舵角θ来控制船舶的航线。当航线偏移一定距离时,即执行航迹保持策略,从伺服模块中输出舵角变化量θ·[13]。舵的控制策略如图 3(b)所示。
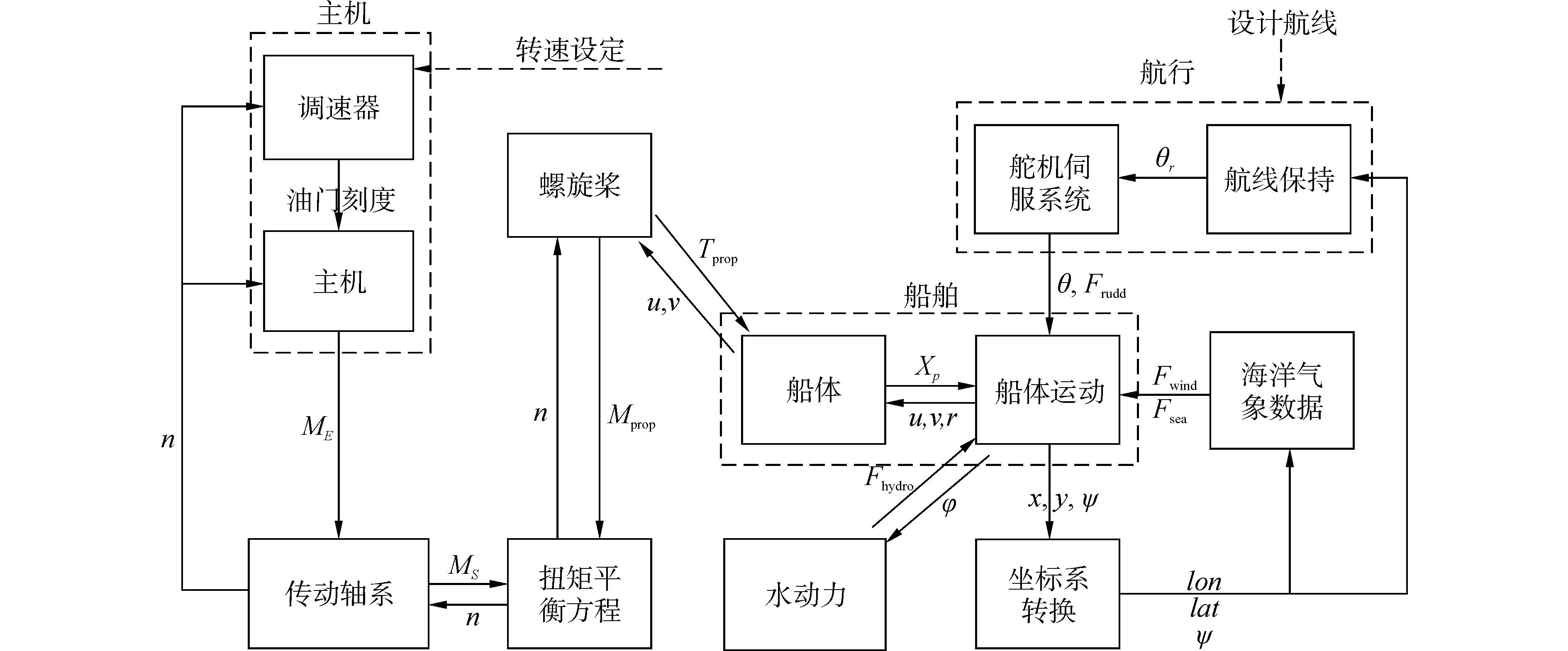
1.4 推进系统-船体运动-环境联合数学模型综合2.1和2.2节的研究内容,建立如图 4所示的推进系统-船体运动-环境联合数学模型。模型输入为主机设定转速和目标航线(一系列的经纬度坐标点)。在设定状态初值之后,首先计算当前初值情况下船体的受力情况,根据式(5)~(8)和转速、舵角的PID调节算出8个状态参数的变化量,和初值相加,作为下一个计算循环的初始值,直至航行位置达到航线的最终点。
|
| 图4 推进系统-船体运动-环境联合数学模型 Figure 4 The mathematical joint model of propulsion system,ship motion and sailing environment |
推进系统-船体运动-环境联合数学模型在循环迭代过程中,还可以获得其他中间变量的连续变化数据,如:流体、螺旋桨、舵和环境干扰的对船体作用力。对各种作用力的定量计算为推进系统能量耗散分析提供了数据条件。主机所输出的轴功率是船舶动力的能量源,轴系和螺旋桨将主机输出的旋转形式的能量转换为推力,克服各类阻力的合力,以推动船舶前进。在这一过程中,除螺旋桨及轴系输出有效功过程中的能量损失外,其他能量损耗主要是由于在船舶航行方向上的增阻造成的,对于这部分因素则根据式(9)进行计算:
| ${{E}_{{{R}_{i}}}}=\frac{{{R}_{i}}cos{{\theta }_{i}}}{{{R}_{T}}cos{{\theta }_{T}}}\times {{E}_{eff}}$ | (9) |
式中:ERi为克服第i项阻力所消耗的能量,Ri为第i项阻力的大小,θT为第i项阻力的方向和船舶运动方向的夹角,RT为船舶在航行时受到的除螺旋桨推力外的合力,θT为作用于船体的总阻力和船舶运动方向的夹角,Eeff是指船体收到有效功。
为计算EEOI还需对船舶燃油总消耗进行计算。对于主机总油耗,根据循环供油量gc、主机转速n和航行时间计算。对于辅机的燃油消耗,认为副机功率和主机功率有比例关系,再结合副机油耗率进行计算。
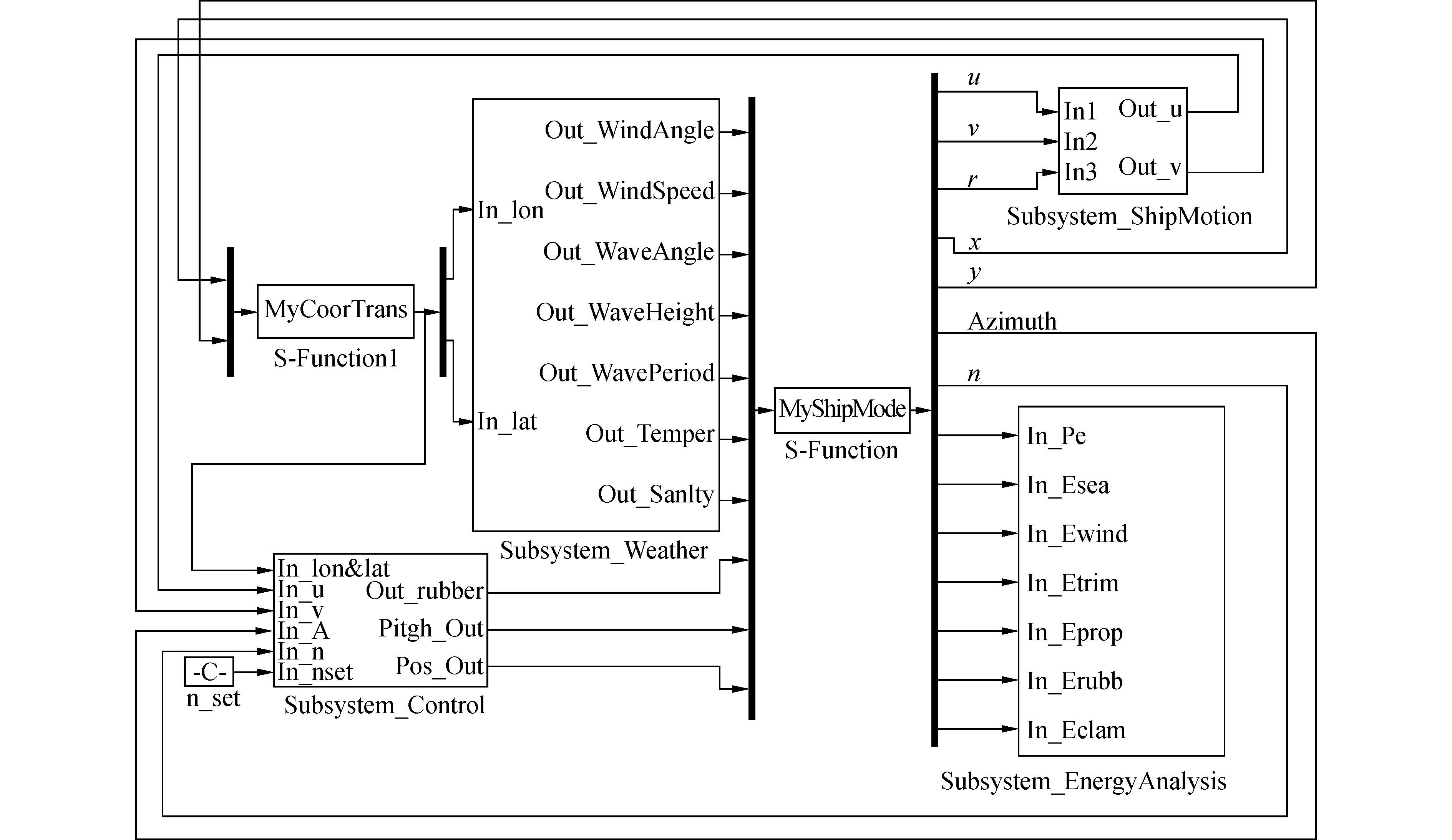
基于以上工作,使用Matlab/Simulink建立EEOI预测模型,该模型如图 5所示。
|
| 图5 EEOI预测分析仿真模型 Figure 5 Forecasting and Analysis simulation model of EEOI |
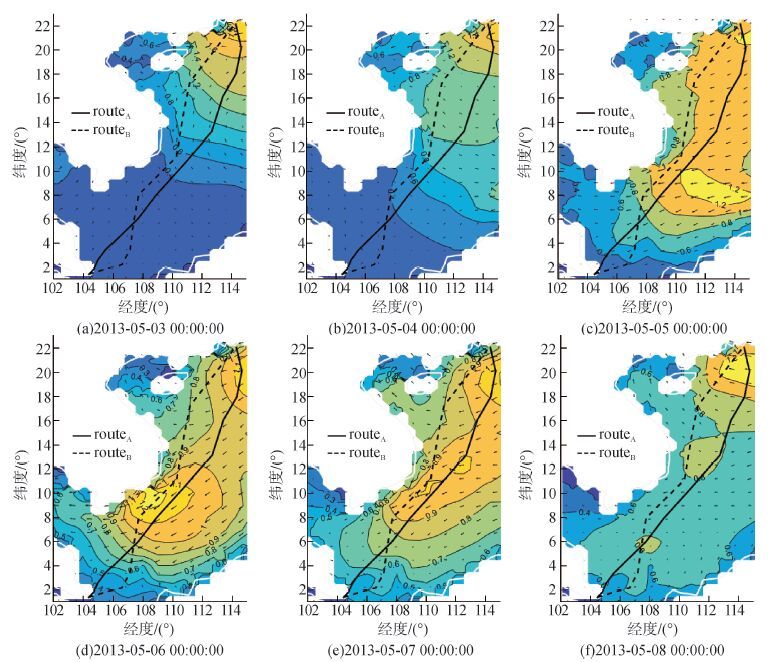
|
| 图6 航线及海况信息 Figure 6 The route and sea condition |
本文选取46000DWT油轮为目标船,对其在2013年5月3日在新加坡-香港航线航行过程进行了仿真。仿真航线及气象信息如图 5所示。图中的气象数据为每日0点~6点的6 h平均值,网格精度为0.25°×0.25°,其中风场以矢量形式显示,浪高以云图形式显示。采用了ECMWF的ERA-Interim数据源[15]的GRIB格式的气象文件。
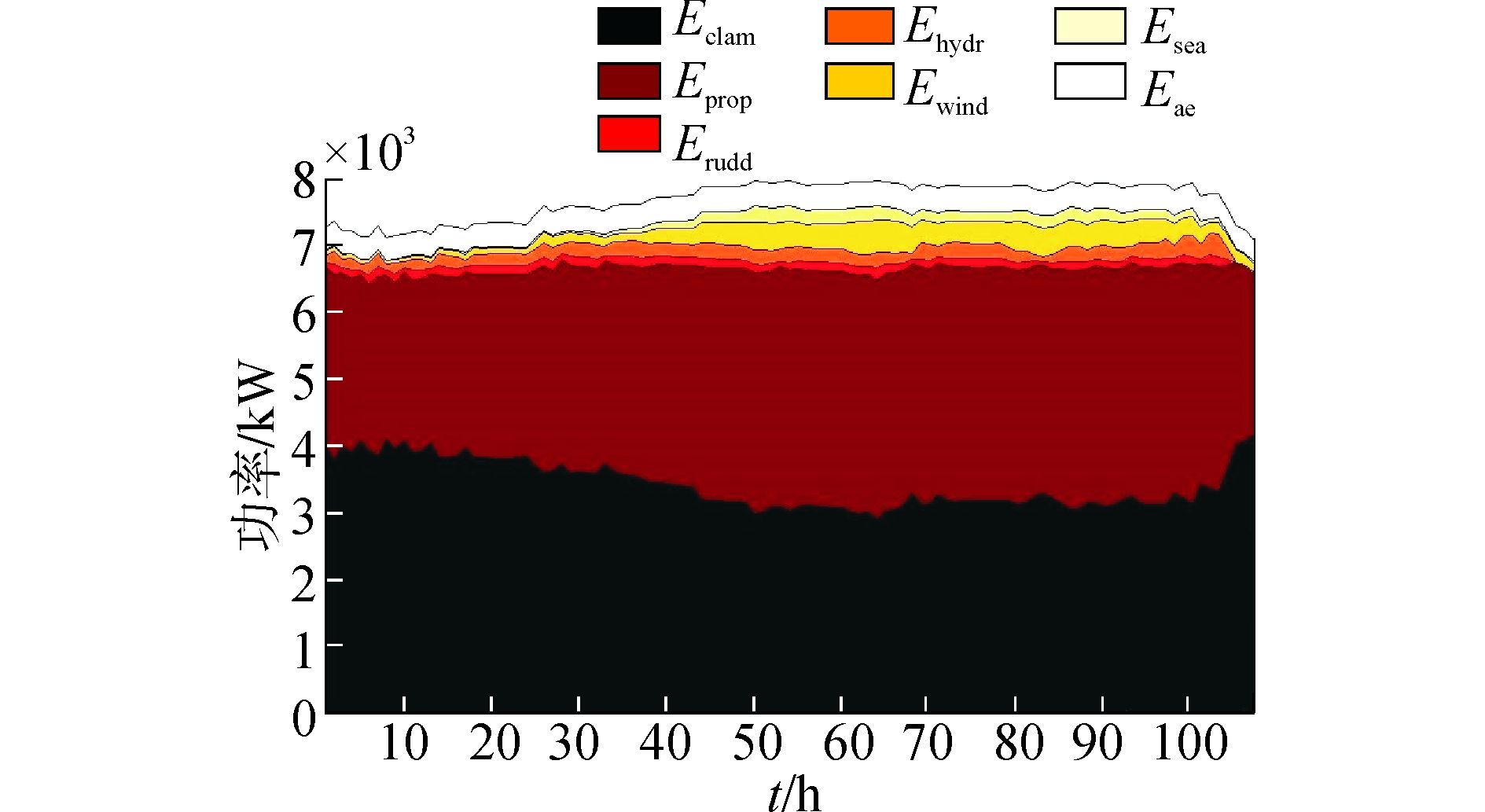
在主机设置转速n为115 r/min,对航线A进行仿真。仿真选择了定步长0.4,并在进行388 545步后完成,获得了推进系统能量耗散的分布历时曲线。结合估算的辅机功率,获得了如图 7所示的目标船能量耗散分布图。Eclam、Eprop、Erudd、Ehydr、Ewind、Esea、Eae分别代表了由于静水阻力、螺旋桨推进效率、操舵、漂角、风、海况和辅机的能量消耗。可以看出,在整个航次过程中,Eclam和Eprop导致的能量消耗虽然随着时间均有波动,但是整体之和基本保持恒定。而Ewind、Esea和Erudd、Ehydr在30~50 h逐渐增加,并在50~90 h保持稳定。从图 5中可以看出在3月3日至3月6日风场逐步增强,同时5日、6日的风场方向基本和航向相反。此时,在环境的影响下,船舶航速减缓,Eclam降低;但是船舶降速导致了螺旋桨能量效率的下降,Eprop上升。在100 h后,出现了顺浪、顺风的情况,此时环境对船体的偏航作用基本消失,由于Erudd和Ehydr基本为0,同时出现了整体能量消耗下降的趋势。
|
| 图7 主机转速n=115 r/min能量耗散仿真结果 Figure 7 The composition of propulsion system′s energy consumption in the case of 115 r/min |
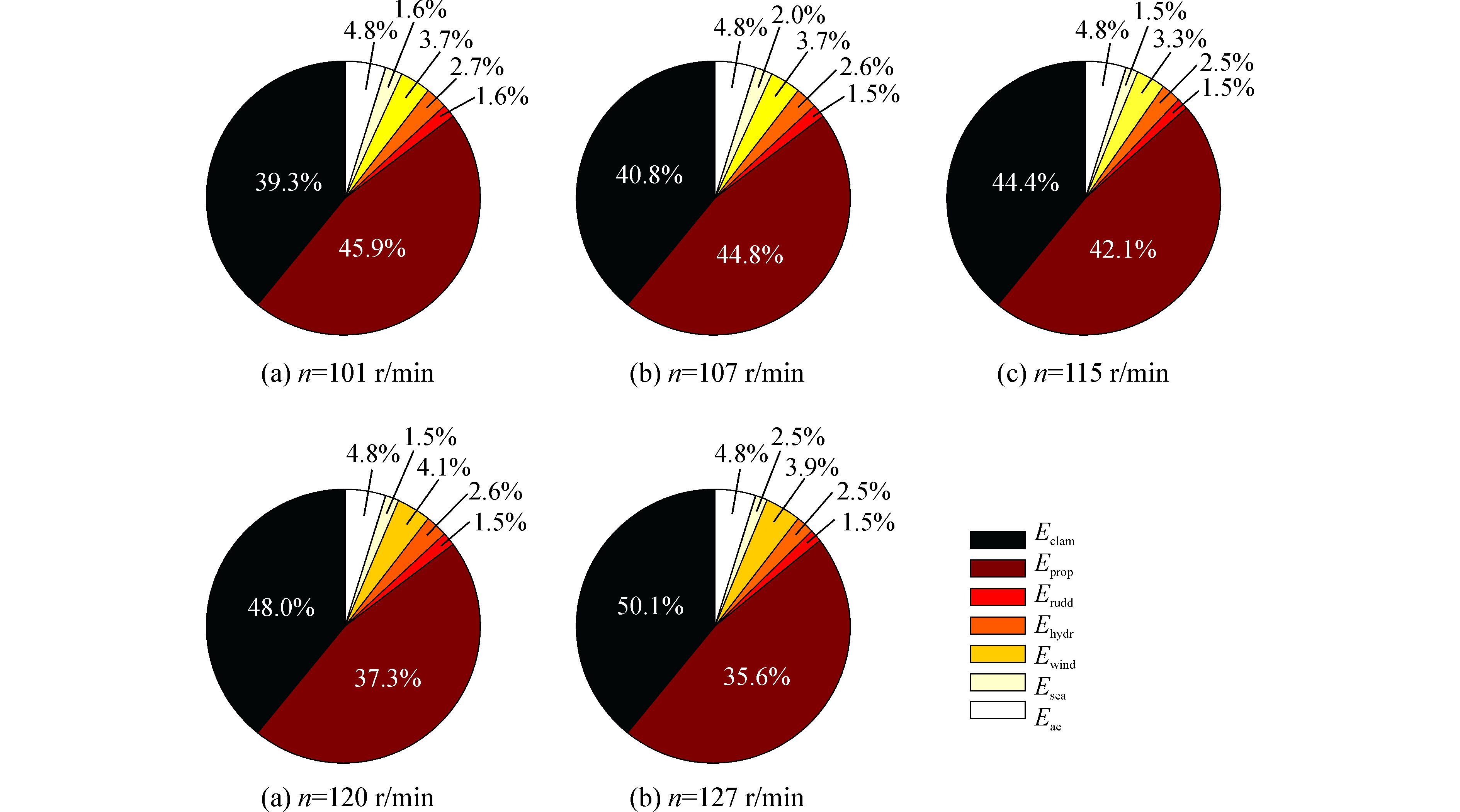
为了研究主机转速设定的不同对于能耗组成的影响,对航线A进行了5次仿真,分别取主机转速n为101、107、115、120和127 r/min,并做出能量消耗组成的饼形图,具体如图 8所示。
|
| 图8 不同转速能量耗散比例示意图 Figure 8 The composition of propulsion system′s energy consumption in different engine speed |
从图 8中可以看出,当主机设置转速提高时,最主要的是对Eclam和Eprop产生的影响。转速从101 r/min增至127 r/min,由于静水阻力的增大,Eclam所占比例从39.3%上升至50.1%,增加27.5%;同时,螺旋桨的效率升高,Eprop所占比例从45.9%下降至35.6%,降低22.4%。
在高转速时,通过清洁船体等方式降低静水阻力的节能效果比低转速时更加显著。在转速为101 r/min和107 r/min时,Eprop分别为45.9%和44.8%,大于Eclam的39.3%和40.8%。并且随着转速降低,Eprop所占比例升高,根据这一数量关系,认为低速时Eprop为更主要的能耗因素,因此在低速时提高螺旋桨的效率对船舶能效的提高更为显著。
Erudd和Ehydr在不同转速设定下都保持基本稳定,可见当船舶当保持航迹的操舵算法不变时,在同一海况下,由于漂角和操舵导致的能量消耗比例基本不变。
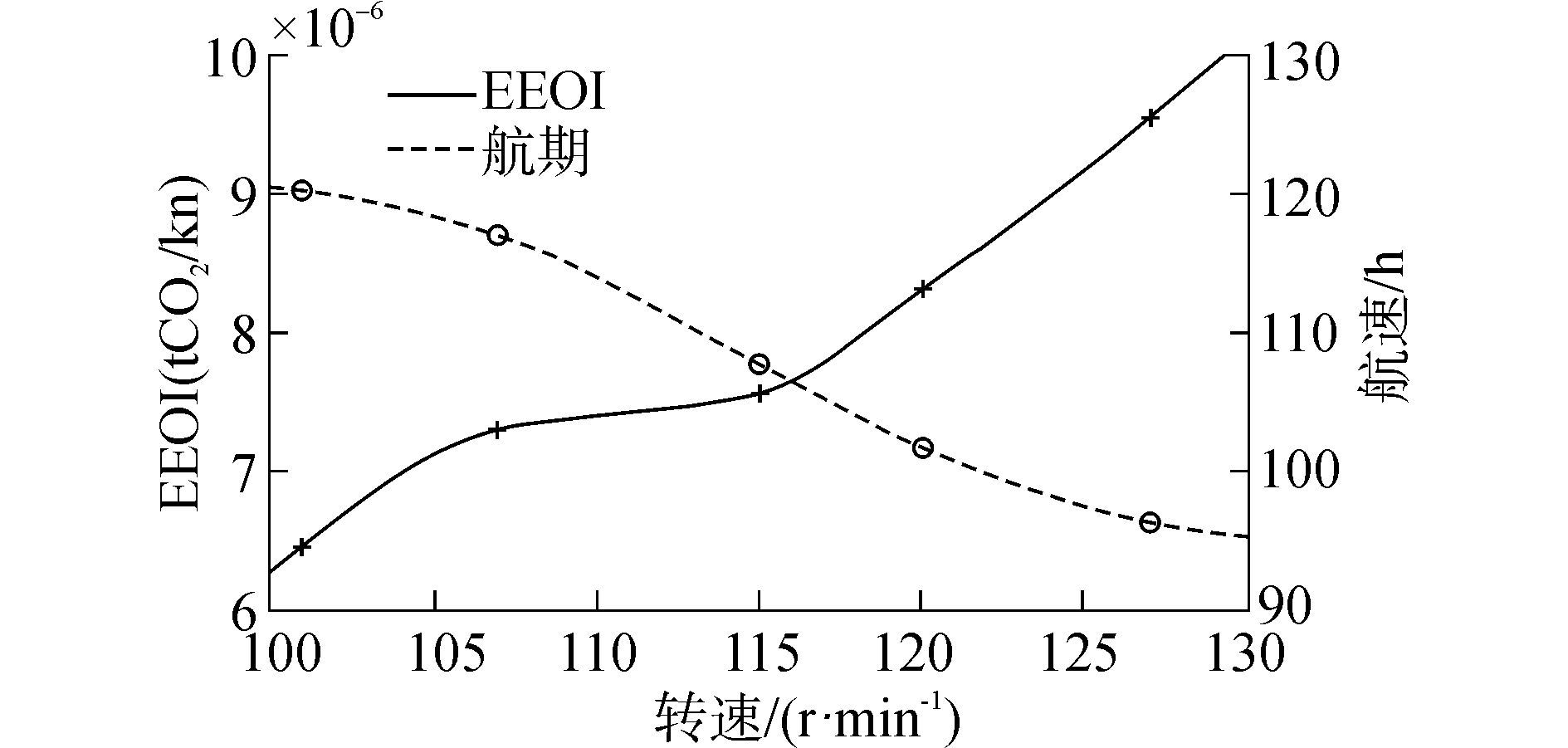
2.3 仿真结果分析根据不同主机转速下的仿真结果,计算出对应的EEOI及航行时间,如图 9所示。图 9给出了目标船在2013年3月3日完成香港-新加坡A航线时,主机转速和EEOI、航行时间的预测关系。从图 9中可以看出,在主机转速在107~115 r/min时,提高主机转速能够显著减少航行时间,但是EEOI的增长比较缓慢。因此当主机转速在该区间内时,可以适当提高转速以减少航期。根据关系图,可以对任一主机转速下的EEOI和航行时间进行读取。
|
| 图9 EEOI及航行时间随主机转速变化的关系图 Figure 9 The change trend of EEOI and voyage with the change of engine speed |
船舶主机转速降低,必然会带来总油耗的减少。但是由于航期及其他营运成本,速度不可能无限度的降低。EEOI预测模型可以计算出转速-EEOI-航行时间之间的定量关系,作为优化主机转速(优化整体营运成本)的依据和参考。实际的优化效果还需借助营运成本计算来获得。
对航线B在主机转速n=115 r/min时的仿真结果显示,航线B的航行时间为110.8 h,EEOI为7.798×10-6,相比同转速下的航线A,航行时间增加2.68%,EEOI升高2.82%,因此对于2013年3月3日至8日的海况环境下,航线A的能效水平要高于航线B。
在航线优化过程中对在原始航线和优化后航线进行仿真计算,可能存在4种结果:1)优化航线航行时间、EEOI小于原航线;2)优化航线航行时间小于原航线,EEOI大于原航线;3)优化航线航行时间大于原航线,EEOI小于原航线;4) 优化航线航行时间均大于原航线。对于第1)种结果,优化航线优于原航线;对于第4)种结果,则认为优化失败;第2)、3)种结果,需要根据实际需求(时间最短/EEOI最低)再进行决策。
3 结论本文以主机油耗作为研究重点,利用ECMWF所发布的气象数据,结合目标船的设计及实验参数对其EEOI进行了仿真计算,其仿真结果表明:
1) 推进系统-船体运动-环境联合数学模型可结合航线、设定转速、气象信息,对目标船的营运过程进行计算,并分析能耗组成;并据此指出在不同主机转速设定下,提高能效的方法。
2) EEOI预测模型可以通过仿真,定量的研究船舶速度、航线变化对航期及EEOI所带来的影响,该模型结合气象预数据可以为航线、速度设计的综合决策提供依据。
建立船舶能效营运指数仿真预测模型是定量研究船舶营运能效的理论,该模型在实际应用中需结合目标船实际营运数据对模型进行修正并验证分析结果。
| [1] |
叶德亮, 黄有方, 胡坚堃. 低碳模式下班轮航线配船问题研究[J].
华中师范大学学报:自然科学版, 2015, 49(2): 322–326.
YE Deliang, HUANG Youfang, HU Jiankun. Study on fleet deployment question for liners with low carbon pattern[J]. Journal of Huazhong Normal University:natural sciences, 2015, 49(2): 322–326. |
| [2] | MA Fongyuan. Analysis of energy efficiency operational indicator of bulk carrier operational data using grey relation method[J]. Journal of oceanography and marine science, 2014, 5(4): 30–36. |
| [3] | BEŞIKÇI E B, ARSLAN O, TURAN O, et al. An artificial neural network based decision support system for energy efficient ship operations[J]. Computers & operations research, 2016, 66: 393–401. |
| [4] | CORADDU A, FIGARI M, SAVIO S. Numerical investigation on ship energy efficiency by Monte Carlo simulation[J]. Proceedings of the institution of mechanical engineers, part M:journal of engineering for the maritime environment, 2014, 228(3): 220–234. |
| [5] | SHI W, GRIMMELIUS H T, STAPERSMA D. Analysis of ship propulsion system behaviour and the impact on fuel consumption[J]. International shipbuilding progress, 2010, 57(1/2): 35–64. |
| [6] | SHI WEI, STAPERSMA D, GRIMMELIUS H. Simulation of the influence of ship voyage profiles on air emissions[C]//Proceedings of ASME International Mechanical Engineering Congress and Exposition. Boston, Massachusetts, 2008, 14:165-174. |
| [7] | MEPC.1/Circ.684. Guidelines for voluntary use of the ship energy efficiency operational indicator (EEOI)[R]. London:IMO, 2009. |
| [8] |
刘伊凡. 基于蒙特卡罗方法的船舶能效建模仿真及研究[D]. 大连:大连海事大学, 2013.
LIU Yifan. Simulation and research of ship energy efficiency based on Monte Carlo method[D]. Dalian:Dalian Maritime University, 2013. |
| [9] |
中国船级社. GD18-2014, 船舶能量消耗分布与节能指南[S]. 北京:中国船级社, 2014.
China Classification Society. GD18-2014, Ship energy consumption distribution and energy saving guideline[S]. Beijing:China Classification Society, 2014. |
| [10] | 贾欣乐, 杨盐生. 船舶运动数学模型[M]. 大连: 大连海事大学出版社, 1999 . |
| [11] | ISO 15016, Ships and marine technology-guidelines for the assessment of speed and power performance by analysis of speed trial data[S]. ISO, 2002. |
| [12] |
李通. 风翼助航系统对船舶柴油机动力扰动特性研究[D]. 大连:大连海事大学, 2011.
LI Tong. Study on the output fluctuation characteristics of main engine of sail-assisted ships[D]. Dalian:Dalian Maritime University, 2012. |
| [13] |
李文魁, 田蔚风, 陈永冰, 等. 船舶运动混合智能控制评述[J].
武汉理工大学学报:交通科学与工程版, 2009, 33(3): 466–470.
LI Wenkui, TIAN Weifeng, CHEN Yongbing, et al. Review of ship motion hybrid intelligent control[J]. Journal of Wuhan University of Technology:transportation science & engineering, 2009, 33(3): 466–470. |
| [14] | ROH M. Determination of an economical shipping route considering the effects of sea state for lower fuel consumption[J]. International journal of naval architecture and ocean engineering, 2013, 5(2): 246–262. |



