2. College of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China
全断面岩石掘进机(tunnel boring machine,TBM)是一种用于隧洞全断面开挖的大型工程机械,广泛用于水利水电隧洞、铁路公路交通隧道、城市地下铁道和煤矿巷道等岩石地下工程的施工。全断面岩石掘进机施工的关键部件是刀盘以及支撑刀盘掘进的主轴承,刀盘承受较大的不平衡载荷矩易引起主轴承损坏、主轴承联接螺栓断裂的故障。刀盘倾覆力矩和径向载荷等力学性能的优劣会影响隧道掘进机的施工效率、施工成本及施工安全,因此对刀盘力学性能分析建模与评价的研究具有很大的工程意义,国内外学者在相关领域作了大量理论和实验研究工作。
在TBM盘形滚刀破岩载荷研究方面,科罗拉多矿业学院等[1-3]对滚刀破岩过程进行了大量实验研究和数值模拟分析,并提出了相应的力学计算模型,其中科罗拉多学院提出的CSM模型应用较为广泛。在刀盘力学性能研究方面,ZHAO J[4-5]等分析了刀盘的静态和动态特性;张照煌等[6]提出了掘进机破岩工作时的刀盘受力平衡理论,建立了刀盘径向载荷计算模型以及倾覆力矩计算模型;霍军周等[7-9]采用数学优化模型和遗传算法相结合的方法,对比分析了滚刀多螺旋线布局、星形布局和随机布局三种布局方案的性能优势和不足,提出以滚刀的极径与极角作为设计变量的TBM 刀具布置优化设计方法;耿麒等[10]对TBM平面刀盘与两级刀盘的整体力学性能进行了对比分析,提出两级刀盘的力学性能要优于平面刀盘。
综上所述,国内外学者在刀盘力学性能的研究方面取得了不少进展,但还少见对上软下硬地质、部分刀具磨损等工况下典型TBM刀盘力学性能的对比分析。本文主要针对理想工况、上软下硬工况以及部分刀具磨损三种不同工况下,对刀盘倾覆力矩和径向载荷等力学性能展开研究。
1 刀盘力学性能分析建模 1.1 单把滚刀三向破岩阻力计算TBM在硬岩地质条件下施工,刀盘需要安装盘形滚刀来切削岩体,盘形滚刀承受的垂直力与滚动力,采用科罗拉多提出的CSM模型[1]计算如下:
| ${F_V} = {F_t}cos\left( {\frac{\phi }{2}} \right){\rm{ }} = C\frac{{\phi RT}}{{1 + \psi }}{\left[ {\frac{{S{\sigma _c}^2{\sigma _t}}}{{\phi \sqrt {RT} }}} \right]^{\frac{1}{3}}}cos\left( {\frac{\phi }{2}} \right)$ | (1) |
| ${F_R} = {F_t}sin\left( {\frac{\phi }{2}} \right){\rm{ }} = C\frac{{\phi RT}}{{1 + \psi }}{\left[ {\frac{{S{\sigma _c}^2{\sigma _t}}}{{\phi \sqrt {RT} }}} \right]^{\frac{1}{3}}}sin\left( {\frac{\phi }{2}} \right)$ | (2) |
式中:Ft为滚刀受到的合力;R为滚刀半径;T为滚刀刀尖宽度;φ为滚刀与岩石接触角,φ=arccos((R-h)/R);h为滚刀贯入度(刀盘旋转一周所推进的深度);ψ为刀尖压力分布系数,-0.2≤ψ≤0.2;S为两滚刀刀间距;σc为岩石的抗压强度;σt为岩石的抗剪强度;C为无量纲系数,C≈2.12。
侧向力采用中南大学[11]提出的计算式:
| ${F_{si}} = \frac{{{\sigma _t} \cdot {\rm{arcsin}}\frac{{\sqrt {2Rh - {h^2}} }}{{{R_i}}}\left[ {{{\left( {S - T} \right)}^2}(cos{\beta _1} + cos{\beta _2}) + 2{R_i}\left( {S - T} \right)(cos{\beta _1} - cos{\beta _2})} \right]}}{{cos{\beta _1}cos{\beta _2}}}$ | (3) |
式中:Ri为第i把盘形滚刀在刀盘上的安装半径,β1为滚刀与其内侧滚刀间因相位差造成的岩面倾角, β2为所讨论滚刀与其外侧滚刀间的岩面倾角。
1.2 刀盘倾覆力矩计算刀盘倾覆力矩可分为因刀具受载产生的倾覆力矩和刀盘自重引起的倾覆力矩两部分,刀具受载产生的倾覆力矩是刀具破岩阻力相对刀盘中心轴的矢量和。刀具布置与受力情况如图 1所示,刀盘因刀具受载产生的倾覆力矩主要由滚刀垂直力FVi和滚刀侧向力Fsi两种载荷影响。
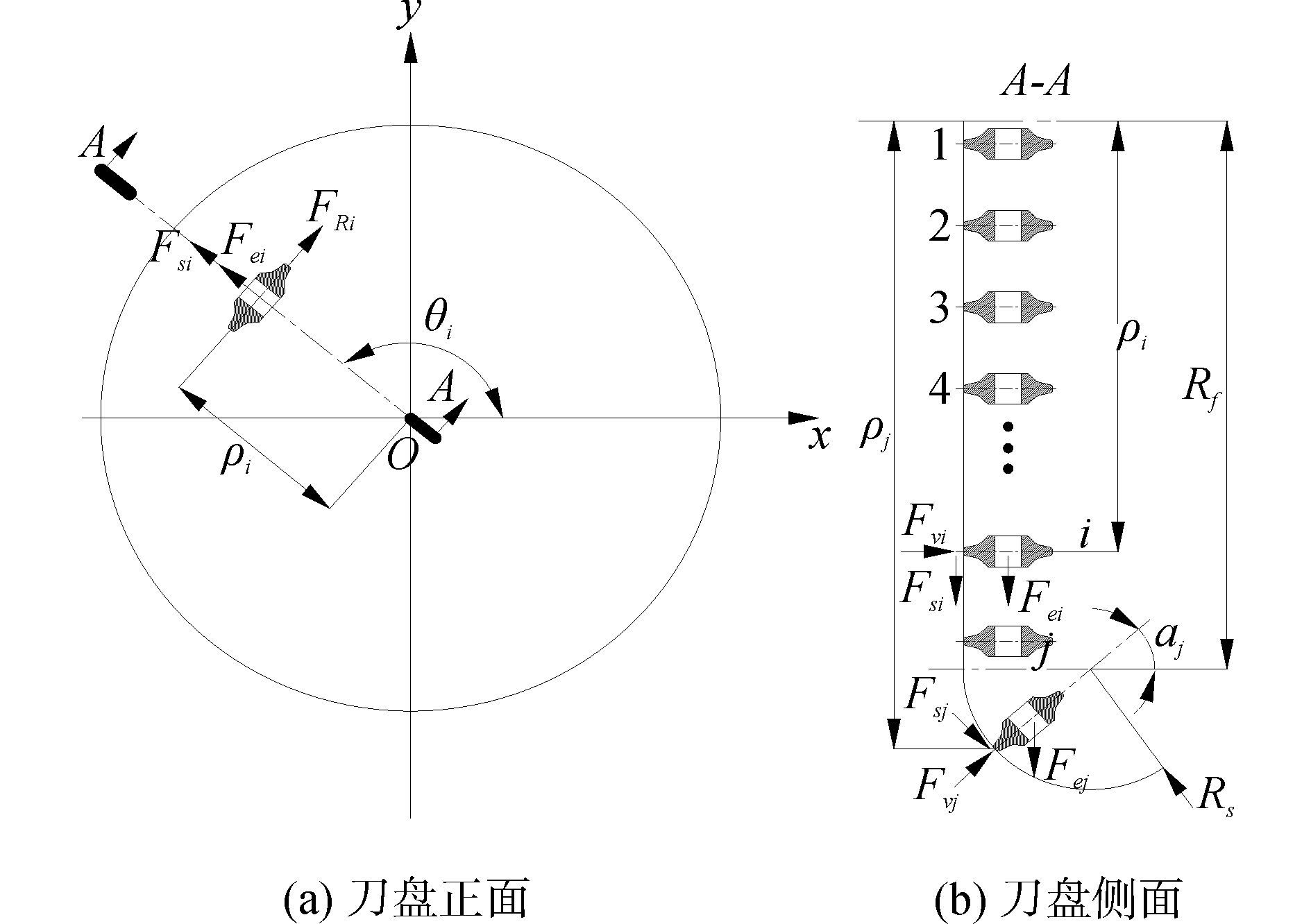
|
| 图1 刀具布置与力学参数 Figure 1 Cutters layout and mechanical parameters |
刀具受载产生的倾覆力矩表达式为
| $\left\{ {\begin{array}{*{20}{c}} {{M_X} = \sum\limits_{i = 1}^n {\left( {{F_{Vi}}{\rho _i}{\rm{cos}}{\alpha _i}{\rm{sin}}{\theta _i} + {F_{si}}{\rho _i}{\rm{sin}}{\alpha _i}{\rm{sin}}{\theta _i}} \right)} }\\ {{M_Y} = \sum\limits_{i = 1}^n {\left( {{F_{Vi}}{\rho _i}{\rm{cos}}{\alpha _i}{\rm{cos}}{\theta _i} + {F_{si}}{\rho _i}{\rm{sin}}{\alpha _i}{\rm{cos}}{\theta _i}} \right)} }\\ {M = \sqrt {{M_X}^2 + {M_Y}^2} } \end{array}} \right.$ | (4) |
为获得不同区域刀具受载产生的倾覆力矩情况,依据所在滚刀安装半径,将刀具分为中心刀,正面滚刀,边缘滚刀三部分,计算各部分刀具受载产生的倾覆力矩:
| $\begin{array}{l} {M_X} = \sum\limits_{i = 1}^l {{F_{Vi}}{\rho _i}sin{\theta _i} + } \sum\limits_{j = 1}^n {{F_{Vj}}{\rho _j}sin{\theta _j} + } \\ \sum\limits_{k = 1}^m {\left( {{F_{Vk}}{\rho _k}sin{\theta _k}cos{\alpha _k} + {F_{sk}}{\rho _k}sin{\theta _k}sin{\alpha _k}} \right)} \end{array}$ | (5) |
式中:l为中心滚刀的数量,n为正滚刀的数量,m为边滚刀的数量,ρ为滚刀的安装半径,θ为滚刀的初始角度(x轴为0°),φ为转动角度,α为滚刀的安装倾角。
刀盘每旋转一个角度φ,可以获得倾覆力矩X方向分量MX的变化,计算刀盘旋转一周的各部分刀具受载产生的倾覆力矩MX的变化,得到刀具受载产生的倾覆力矩的大小与方向的分布情况:
| $\begin{array}{l} {M_X} = \sum\limits_{i = 1}^l {{F_{Vi}}{\rho _i}sin} \left( {{\theta _i} + \varphi } \right) + \sum\limits_{j = 1}^n {{F_{Vj}}{\rho _j}sin} \left( {{\theta _j} + \varphi } \right) + \\ \sum\limits_{k = 1}^m ( {F_{Vk}}{\rho _k}sin\left( {{\theta _k} + \varphi } \right)cos{\alpha _k} + {F_{sk}}{\rho _k}sin\left( {{\theta _k} + \varphi } \right)sin{\alpha _k}) \end{array}$ | (6) |
刀盘自身重力引起的倾覆力矩为
| ${M_G} = {G_D} \times {S_D}$ | (7) |
式中:GD为刀盘重力,SD为刀盘质心到法兰与主轴承结合面的距离。刀盘总倾覆力矩为
| ${M_t} = {M_G} + M$ | (8) |
刀盘径向载荷是刀盘掘进面上因刀具破岩受载等引起刀盘径向承受载荷的矢量和。如图 1所示,刀盘的径向载荷由三种力决定,分别是滚刀滚动力FRi,滚刀侧向力FSi,滚刀牵连惯性力Fei。
| ${F_{si}} = \frac{\tau }{2}(r\varphi ){\rm{sin}}\frac{{r\varphi }}{{2{\rho _i}}}$ | (9) |
| ${F_{ei}} = m{\omega ^2}{\rho _i}$ | (10) |
刀盘所受径向载荷为
| $\left\{ {\begin{array}{*{20}{c}} {{F_x} = \sum\limits_{i = 1}^n {\left( {{F_{si}}cos{\alpha _i}cos{\theta _i} + {F_{Ri}}sin{\theta _i} + m{\omega ^2}{\rho _i}cos{\theta _i}} \right)} }\\ {{F_y} = \sum\limits_{i = 1}^n {({F_{si}}cos{\alpha _i}sin{\theta _i} - {F_{Ri}}cos{\theta _i} + m{\omega ^2}{\rho _i}sin{\theta _i})} }\\ {F = \sqrt {{F_x}^2 + {F_y}^2} } \end{array}} \right.$ | (11) |
式中:n为滚刀的数量,FX为刀盘的径向力合力在X轴方向的分力,FY为刀盘的径向力合力在Y轴方向的分力,F为刀盘受到的径向力合力。
刀盘每旋转一个角度φ,可以获得径向载荷X方向分量FX的变化,计算刀盘旋转一周的其径向载荷的大小与方向的分布情况:
| $\begin{array}{l} {M_X} = \sum\limits_{i = 1}^l ( {F_{si}}cos{\alpha _i}cos\left( {{\theta _i} + \varphi } \right) + \\ {F_{Ri}}sin\left( {{\theta _i} + \varphi } \right) + m{\omega ^2}{\rho _i}cos({\theta _i} + \varphi )) \end{array}$ | (12) |
两个刀盘刀具详细布置情况如图 2所示,两个刀盘直径相同,都为8.53 m大直径刀盘。A刀盘上安装53把刀具,全部为19寸盘形滚刀,其中包括8把中心滚刀、21把正面滚刀以及13把边缘滚刀。A刀盘刀具布置采用双螺旋线布置方法,中心滚刀的刀间距为100 mm,正刀的刀间距为90 mm;B刀盘上安装53把刀具,包括8把17寸中心滚刀、21把19寸正滚刀以及13把19寸边缘滚刀;其刀具布置采用米字型布置,中心刀的刀间距为101.5 mm,正刀的刀间距为84 mm。
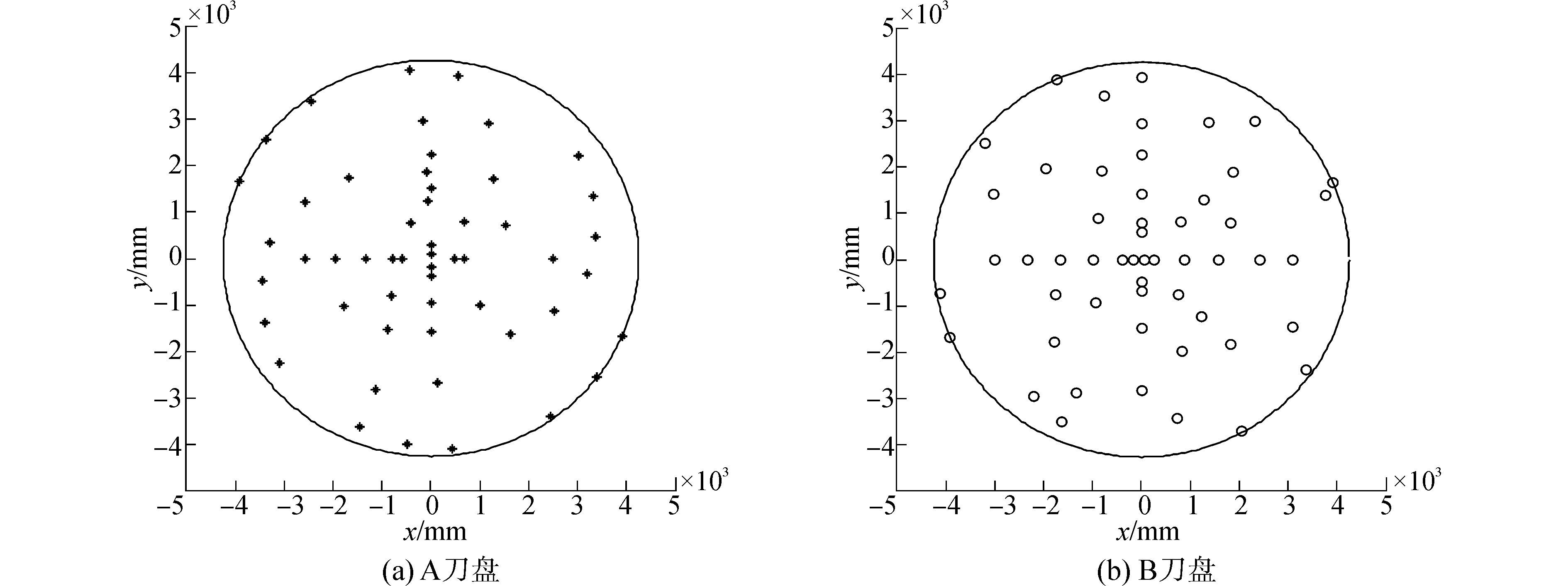
|
| 图2 某工程A刀盘与B刀盘刀具布置 Figure 2 Cutters layout of A and B cutterhead in a project |
根据刀盘三维建模质量特性测量,得到A刀盘质心偏移量为13.7 mm,B刀盘质心偏移量为2.35 mm,A刀盘质心偏移量较大,米字型布置刀盘刀具分布对称性优于双螺旋线布置刀盘。
2.2 不同工况下刀盘力学性能对比分析 2.2.1 理想工况1) 刀盘不平衡载荷计算。
在理想工况下,针对典型花岗岩地质,其主要力学参数如表 2所示,假设刀盘掘进的地质工况相同,所有刀具磨损等情况都相同。根据式(6) 以及表 1的刀具布置参数,计算得到两个刀盘刀具受载产生的倾覆力矩Mx随刀盘逆时针旋转的变化规律,如图 3所示。A刀盘的最大倾覆力矩达到MmaxX.A=1 048 kN·m,在刀盘旋转105°~285°时出现;B刀盘的最大倾覆力矩为MmaxX.B=814.4 kN·m,在刀盘旋转25°~205°时出现。A刀盘的最大倾覆力矩是B刀盘的1.3倍,米字型布置刀盘B刀具分布对称性优于双螺旋线布置刀盘A,所以A刀盘的最大倾覆力矩大于B刀盘。
| 刀号 | A刀盘 | B刀盘 | |||||
| 安装半 | 安装角 | 安装倾 | 安装半 | 安装角 | 安装倾 | ||
| 径/mm | 度/(°) | 角/(°) | 径/mm | 度/(°) | 角/(°) | ||
| 1 | 80 | 90 | 0 | 68.5 | 360 | 0 | |
| 2 | 180 | 270 | 0 | 170 | 180 | 0 | |
| 3 | 280 | 90 | 0 | 271.5 | 360 | 0 | |
| 4 | 380 | 270 | 0 | 373 | 180 | 0 | |
| 5 | 480 | 360 | 0 | 474.5 | 270 | 0 | |
| 6 | 580 | 180 | 0 | 576 | 90 | 0 | |
| 7 | 680 | 360 | 0 | 677.5 | 270 | 0 | |
| 8 | 780 | 180 | 0 | 779 | 90 | 0 | |
| 9 | 870 | 119 | 0 | 877 | 360 | 0 | |
| 10 | 960 | 270 | 0 | 975 | 180 | 0 | |
| 11 | 1 050 | 49 | 0 | 1 065 | 315 | 0 | |
| 12 | 1 140 | 225 | 0 | 1 151 | 45 | 0 | |
| 13 | 1 230 | 93 | 0 | 1 235 | 135 | 0 | |
| 14 | 1 320 | 180 | 0 | 1 320 | 225 | 0 | |
| 15 | 1 410 | 315 | 0 | 1 404 | 90 | 0 | |
| 岩石类型 | 体积密度/(kg·m-3) | 弹性模量/GPa | 单轴抗压强度/MPa | 抗拉强度/MPa | 内摩擦角/(°) |
| 花岗岩 | 2550 | 10.11 | 80 | 7.2 | 78 |
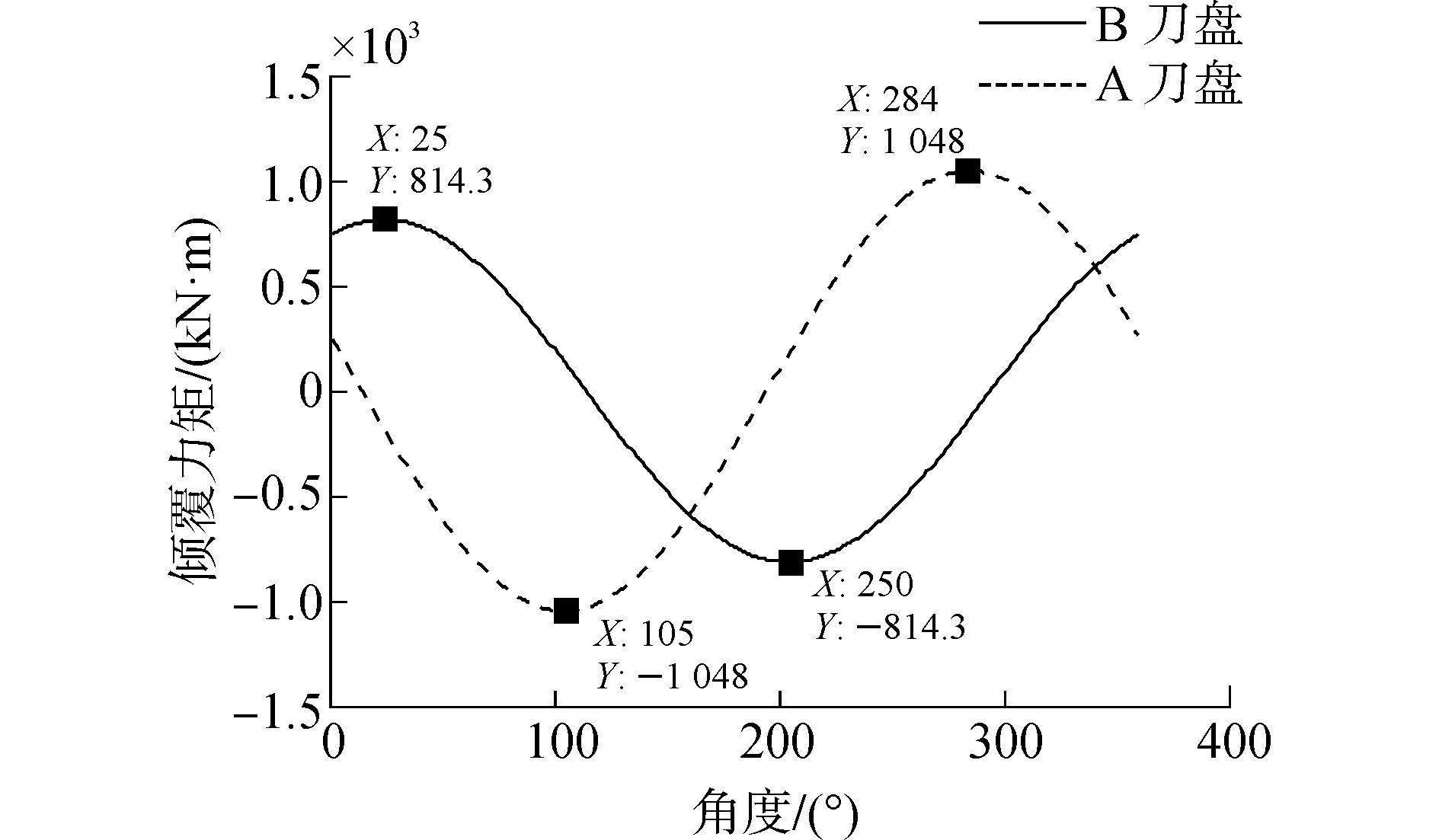
|
| 图3 刀具受载产生的倾覆力矩MX分布 Figure 3 Distribution of overturning moment MXcaused by cutters loading |
考虑刀盘自重引起的倾覆力矩,刀盘总倾覆力矩为
| $\begin{array}{l} {M_A} = {M_G}^A + M_{_{X.A}}^{max} = 1{\rm{ }}713.4 + 1048 = 2{\rm{ }}761.4kN.m\\ {M_B} = {M_G}^B + M_{_{X.B}}^{max} = 1{\rm{ }}677.5 + 814.4 = 2{\rm{ }}491.9kN.m \end{array}$ |
根据式(12) 以及表 1的刀具布置参数,计算得到两个刀盘径向载荷分布,如图 4所示。A刀盘的最大径向载荷65.3 kN,出现在刀盘旋转118°~298°时,即作用在62°~242°方向上;B刀盘的最大径向载荷为44.7 kN,作用在142°~332°方向上。在理想工况下,两刀盘的最大径向载荷都低于65 kN,对刀盘整体性能影响较小,其中A刀盘的最大径向载荷是B刀盘的1.42倍。
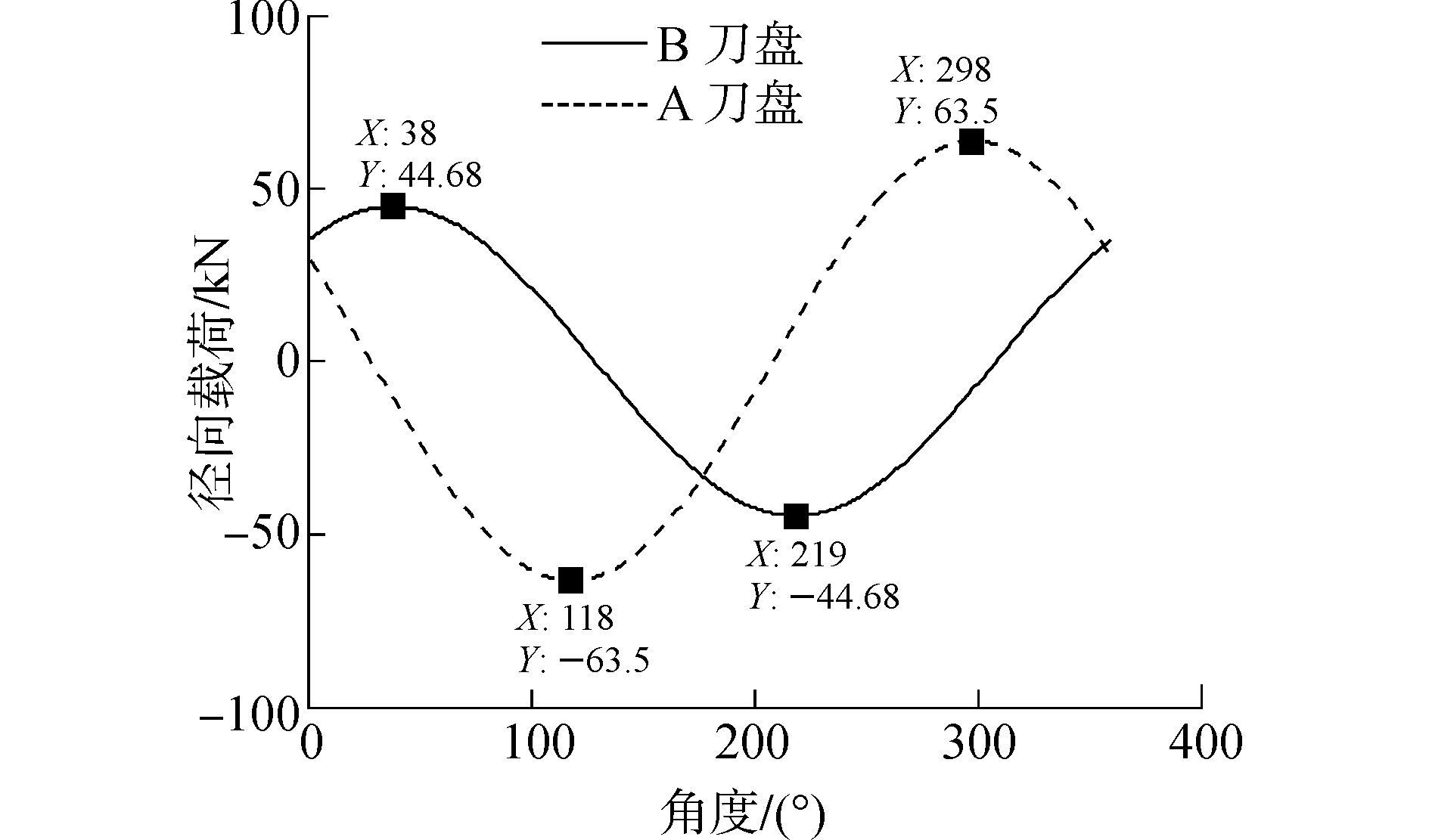
|
| 图4 刀盘的径向载荷FX分布 Figure 4 Distribution of cutterhead’s radial loadFX |
两刀盘总倾覆力矩在2 400 kN·m以上,刀盘的径向载荷远小于刀盘最大倾覆力矩,可见刀盘倾覆力矩对刀盘性能的影响远大于径向载荷。
2) 三部分刀具不平衡载荷计算。
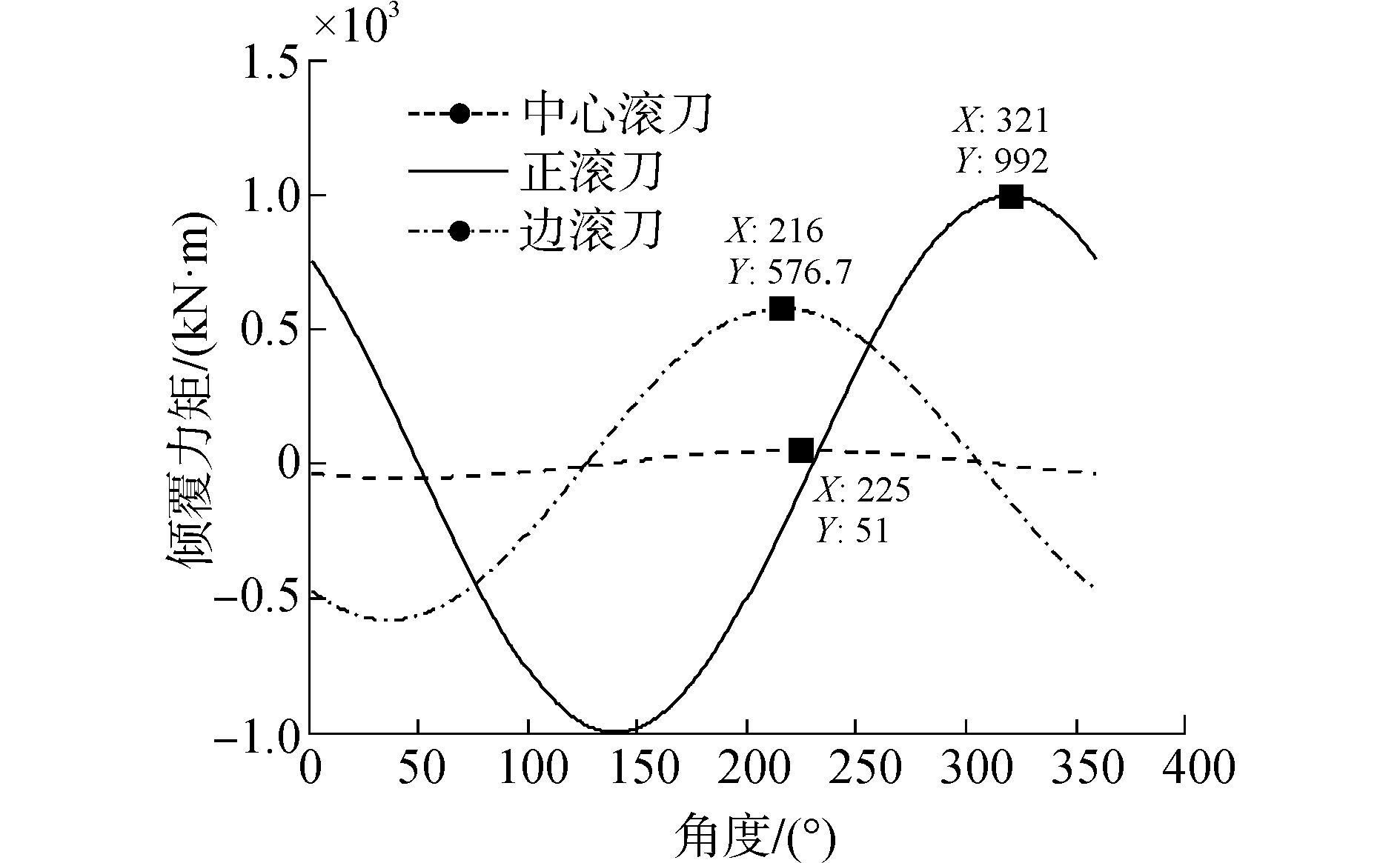
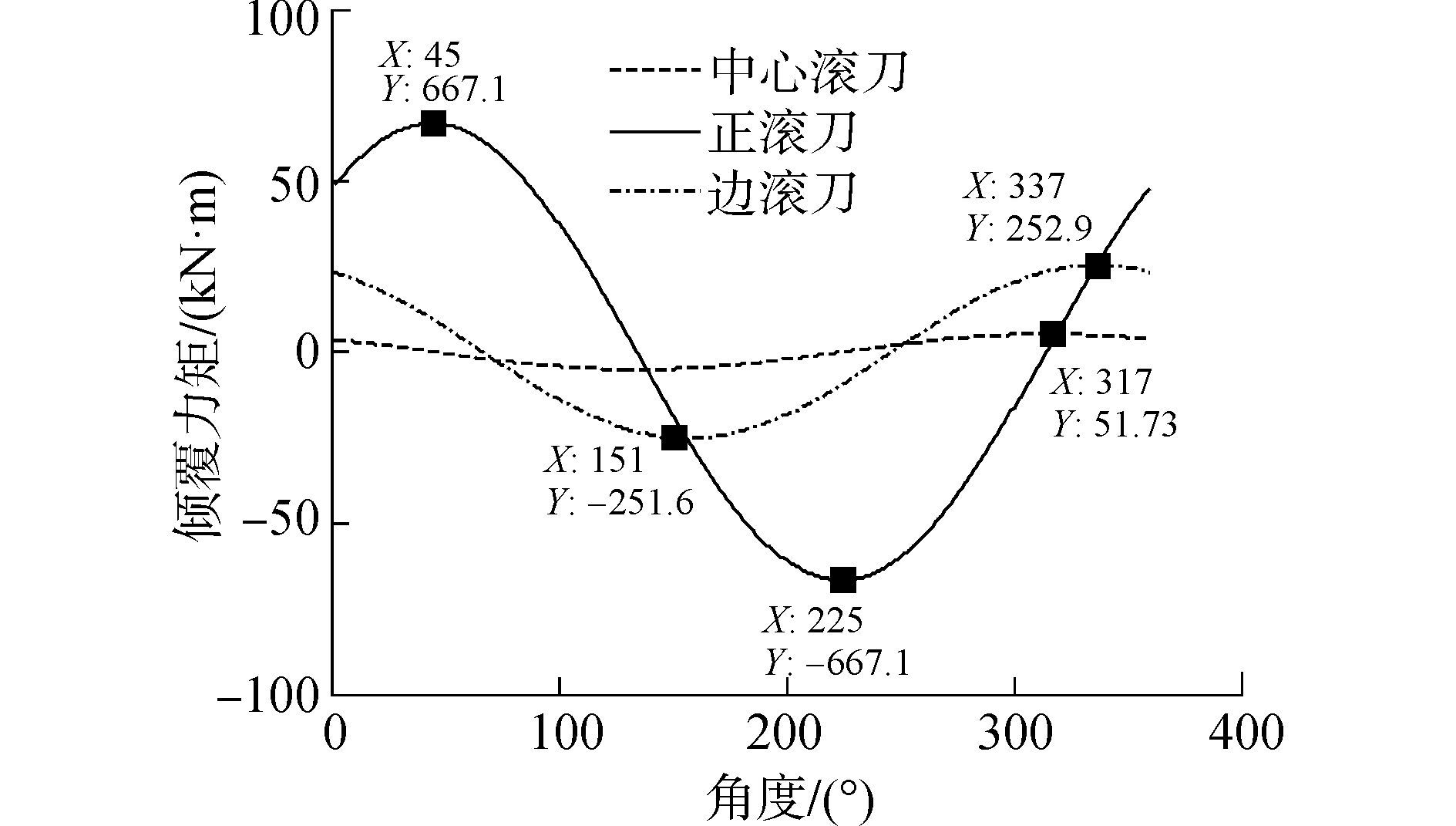
根据式(6) 以及表 1的刀具布置参数,计算得到盘旋转一周过程中,中心刀、正面滚刀和边缘滚刀三部分刀具受载产生的倾覆力矩MX的分布情况。如图 5和6所示,中心刀具数量少且安装半径小,其倾覆力矩数值很小;正面滚刀数量多,在三部分刀具中其倾覆力矩数值最大,A刀盘正面滚刀最大倾覆力矩达到992 kN·m,B刀盘正面滚刀最大倾覆力矩为667.1k N·m;边缘滚刀数量少而其安装半径最大,其倾覆力矩峰值与刀盘最大倾覆力矩的比值超过50%。
|
| 图5 A刀盘因刀具受载产生的倾覆力矩MX分布 Figure 5 Distribution of A cutterhead overturning moment MX caused by cutters loading |
|
| 图6 B刀盘因刀具受载产生的倾覆力矩MX分布 Figure 6 Distribution of B cutterhead overturning moment caused by cutters loading |
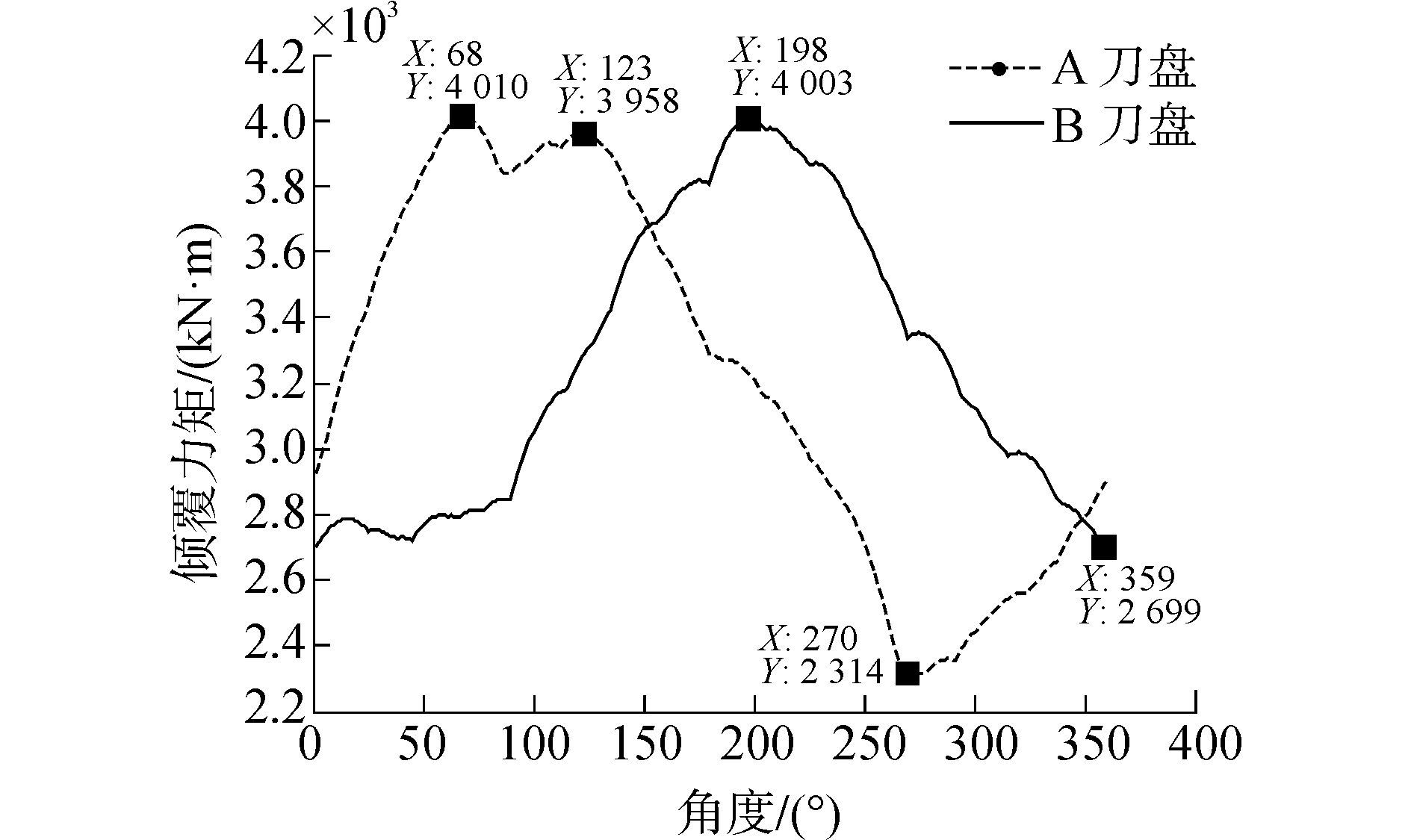
在岩石上软下硬工况下,假设刀盘下半部分地质参数如表 2,上半部分岩石强度为下半部分岩石的一半,这种极限工况下刀盘倾覆力矩会大大增加。根据式(6) 以及刀具布置参数,通过计算得到刀盘因刀具受载产生的倾覆力矩Mx分布,如图 7所示。A刀盘的倾覆力矩随刀盘360°逆时针旋转呈先增大后减小再增大的趋势,其中最大倾覆力矩达到MmaxX.A=4 010 kN·m,出现在刀盘旋转68°时,作用在292°方向上; B刀盘的倾覆力矩也呈先增大后减小的趋势,最大倾覆力矩为4 003 kN·m,出现在刀盘旋转198°时,作用在162°方向上。
|
| 图7 上软下硬工况下倾覆力矩MX分布 Figure 7 Distribution of overturning moment under soft upper and hard under stratum |
考虑刀盘自重引起的倾覆力矩,上软下硬工况下刀盘总倾覆力矩为
| $\begin{array}{l} {M_A} = {M_G}^B + M_{X.A}^{\max } = 5723.4kN.m\\ {M_B} = {M_G}^B + M_{X.B}^{\max } = 5679.5kN.m \end{array}$ |
TBM掘进过程中,刀圈的磨损会造成滚刀刀圈半径R以及刀刃宽度T的变化,引起刀具承受的三向力载荷的变化。基于CSM[1]刀具三向力模型,考虑刀具磨损量的影响,得到刀具在实际中承受的三向力:
| $\left\{ {\begin{array}{*{20}{c}} {RT = ({R_0} - H)({T_0} + 2H.\frac{\phi }{2})}\\ {{F_V} = C\frac{{\phi RT}}{{1 + \psi }}{{\left[ {\frac{{S{\sigma _c}^2{\sigma _t}}}{{\phi \sqrt {RT} }}} \right]}^{\frac{1}{3}}}cos(\frac{\phi }{2})}\\ {{F_R} = C\frac{{\phi RT}}{{1 + \psi }}{{\left[ {\frac{{S{\sigma _c}^2{\sigma _t}}}{{\phi \sqrt {RT} }}} \right]}^{\frac{1}{3}}}sin(\frac{\phi }{2})}\\ {Fs = \frac{{{\sigma _t}Rh\left( {2R - h} \right)\phi }}{{2{\rho _i}}}} \end{array}} \right.$ | (13) |
式中:R0为新刀圈的半径,T0为新刀圈的刃宽,H为刀具磨损量,α为刀刃角。
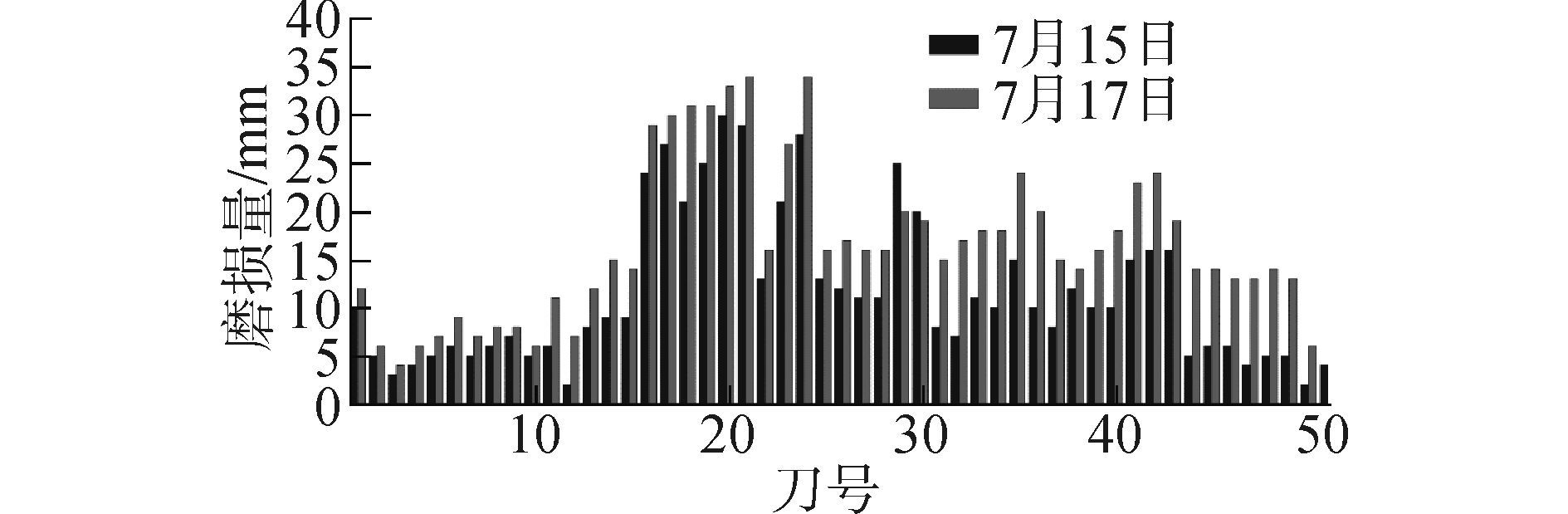
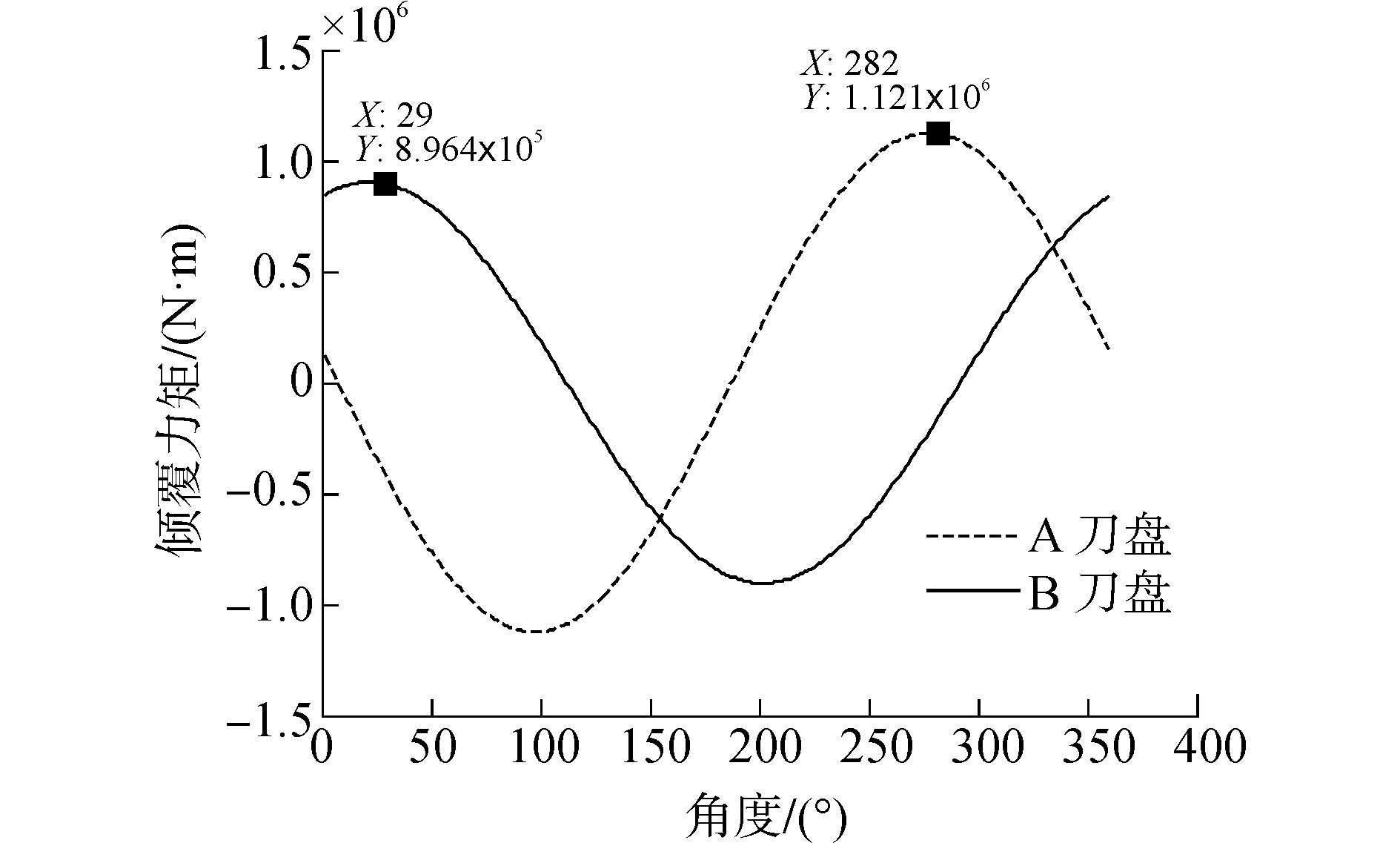
在刀盘掘进过程中刀圈受到磨损,磨损后刀具半径减小,刃宽变大,引起刀具三向力的改变,从而导致刀盘外载的变化。工程中不同位置刀具的磨损量不同,刀具磨损量具有较大的随机性。基于工程中某两天刀具实际磨损量统计情况,如图 8所示,考虑实际刀具磨损的影响,计算得到两个刀盘倾覆力矩MX随刀盘旋转的变化趋势,如图 9所示。
|
| 图8 B刀盘工程中刀具实际磨损量 Figure 8 Actual cutters wear loss of B cutterhead in engineering |
|
| 图9 刀具磨损工况倾覆力矩MX分布 Figure 9 Variation of overturning moment under cutters weared |
从图 9中可见,在刀具磨损的影响下,两刀盘倾覆力矩的变化趋势与理想工况下基本相同,倾覆力矩数值偏大于理想工况下刀盘倾覆力矩。其中,A刀盘倾覆力矩MX最大达到1 121 kN·m,比理想工况下要大7%,出现在刀盘旋转105°~285°附近;B刀盘倾覆力矩MX最大为896.4 kN·m,比理想工况下要大9.8%,出现在刀盘旋转28°~208°附近。
考虑刀盘自重引起的倾覆力矩,总倾覆力矩为
| ${M_A} = {M_G}^B + M_{X.A}^{\max } = 2833.4kN.m$ |
对两刀盘结构进行有限元静力学分析,采用四面体十节点单元SOLID187对其进行网格划分。在TBM刀盘的法兰盘底面施加全约束,并在刀盘的每把刀具上施加的垂直力与滚动力。按照刀具的额定载荷加载外载,其中 19寸滚刀施加315 kN的垂直力,17寸中心刀施加250 kN的垂直力,并将刀盘额定扭矩转化为每把滚刀的平均滚动力施加在每把刀具上。通过静力学分析得到刀盘的应力变形分布情况,以下为响应的仿真结果分析。
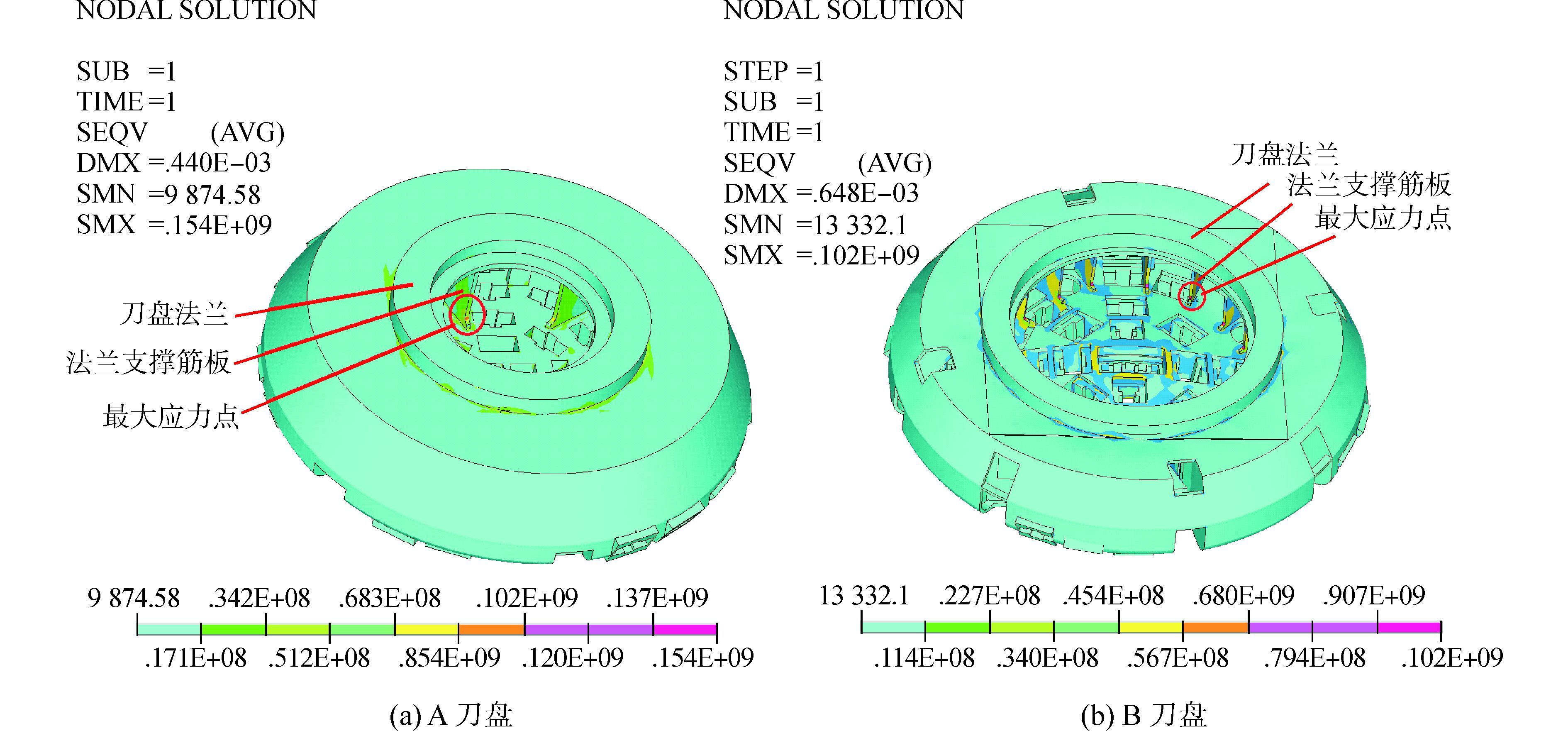
3.1 刀盘应力结果对比如图 10所示,A与B两刀盘上应力较大的区域出现在刀盘面板中心区域以及刀盘背板与法兰支撑筋板连接处。刀盘面板中心区域刀具安装密集,受载大且相对集中,法兰支撑筋板是刀盘内较为薄弱的部分,这两处区域容易出现应力较大现象。A刀盘最大应力达到154 MPa,B刀盘最大应力为102 MPa,A刀盘最大应力为B刀盘的1.5倍,这与A刀盘内法兰支撑筋板的布置数量直接相关。A刀盘只布置了6块支撑筋板,数量偏少,这是导致其应力偏大的重要原因。
|
| 图10 A和B刀盘应力分布 Figure 10 Stress distribution of A and B cutterhead |
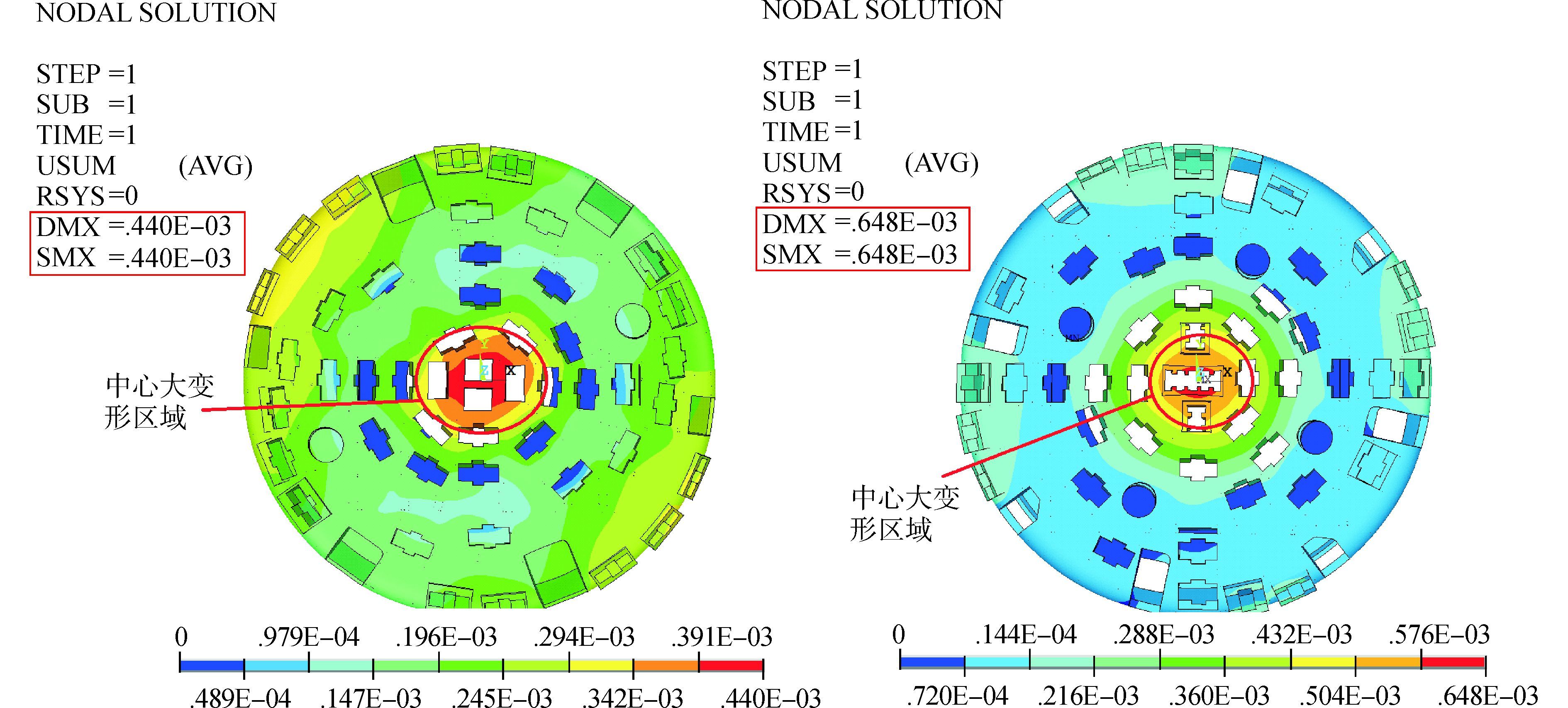
如图 11所示,两刀盘变形分布情况相似,变形的最大位置处均出现在刀盘面板中心处,变形分布呈伞状从刀盘中心刀边缘处沿半径方向是逐渐减小,这是因为刀盘中心处刀具布置集中,受力较大,并且刀盘背面中心没有支撑筋支撑,刚度较小。A刀盘面板中心处最大变形量为0.44 mm,在左上方和右下方刀盘边缘处出现较大变形;B刀盘面板中心处最大变形量为0.676 mm,分别在上下左右四处刀盘边缘刀具密集区域出现较大变形。
|
| 图11 A和B刀盘变形分布 Figure 11 Stress distribution of A and B cutterhead |
刀盘中心处变形量主要受中心块内无法兰支撑筋区域的直径影响,该区域直径越大,刀盘中心越容易变形;A刀盘主轴承外径为4.2 m,B刀盘主轴承外径为5.2 m,直接决定A刀盘法兰直径小于B刀盘,导致A刀盘中心块内无支撑筋支撑区域的直径比B小,所以A刀盘中心处最大变形量小于B刀盘。
4 结论1) 刀盘的径向载荷远小于最大倾覆力矩,可见倾覆力矩对刀盘性能的影响远大于径向载荷。
2) 将刀盘上的刀具分为中心刀、正面滚刀和边缘滚刀三部分计算刀具受载产生的倾覆力矩,其中正面滚刀受载产生的倾覆力矩最大,其次是边缘滚刀,中心滚刀受载产生的倾覆力矩最小。
3) 米字型布置刀盘B刀具分布对称性优于双螺旋线布置刀盘A,在相同工况下,A刀盘的倾覆力矩和径向载荷大于B刀盘;理想工况下,A刀盘刀具布置产生的最大倾覆力矩是B刀盘的1.3倍。
4) 在上软下硬的特殊地质工况下,刀盘的倾覆力矩较大,可达到5 000 kN·m以上。考虑刀具磨损的影响,A刀盘总倾覆力矩最大达到2 800 kN·m以上,比理想工况下要大7%。
5) 两刀盘最大应力出现在刀盘背板和支撑筋板连接处,A刀盘最大应力为154 MPa,B刀盘最大应力为102 MPa,A刀盘最大应力为B刀盘的1.5倍;A刀盘面板中心处最大变形量为0.44 mm,B刀盘面板中心处最大变形量为0.676 mm。
在实际掘进中,刀具破岩承受的三向力为不断变化的瞬时动态载荷,其变化规律复杂,导致刀盘倾覆力矩及径向载荷也是瞬时变化的动态载荷。以上计算得到的是刀盘外载平均值的情况,下一步,将针对刀盘瞬时动态力学性能展开研究,更具有工程实际意义。
| [1] | GERTSCH R, GERTSCH L, ROSTAMI J. Disc cutting tests in Colorado Red Granite:implications for TBM performance prediction[J]. International journal of rock mechanics and mining sciences, 2007, 44(2): 238–246. |
| [2] | ACAROGLU O, OZDEMIRB L, ASBURY B. A fuzzy logic model to predict specific energy requirement for TBM performance prediction[J]. Tunnelling and underground space technology, 2008, 23(5): 600–608. |
| [3] | CHANG S H, CHOI S W, BAE G J, et al. Performance prediction of TBM disc cutting on granitic rock by the linear cutting test[J]. Tunnelling and underground space technology, 2006, 21(3/4): 271. |
| [4] | ZHAO J, GONG Q M, EISENSTEN Z. Tunnelling through a frequently changing and mixed ground:a case history in singapore[J]. Tunnelling and underground space technology, 2007, 22(4): 388–400. |
| [5] |
霍军周, 杨静, 孙伟, 等. TBM刀盘支撑筋结构设计及静动态特性分析[J].
哈尔滨工程大学学报, 2014, 35(7): 883–888.
HUO Junzhou, YANG Jing, SUN Wei, et al. Structure design and static/dynamic analysis of TBM cutterhead supporting ribs[J]. Journal of Harbin Engineering University, 2014, 35(7): 883–888. |
| [6] |
张照煌, 乔永立. 全断面岩石掘进机盘形滚刀布置规律研究[J].
工程力学, 2011, 28(5): 172–177.
ZHANG Zhaohuang, QIAO Yongli. Research on the layout of TBM disc cutter[J]. Engineering mechanics, 2011, 28(5): 172–177. |
| [7] |
霍军周, 史彦军, 滕弘飞, 等. 全断面岩石掘进机刀具布置设计方法[J].
中国机械工程, 2008, 19(15): 1832–1836.
HUO Junzhou, SHI Yanjun, TENG Hongfei, et al. Cutter layout design of full-face rock tunnel boring machine(TBM)[J]. China mechanical engineering, 2008, 19(15): 1832–1836. |
| [8] | HUO Junzhou, SUN Wei, CHEN Jing, et al. Disc cutters plane layout design of the full-face rock tunnel boring machine (TBM) based on different layout patterns[J]. Computers & industrial engineering, 2011, 61(4): 1209–1225. |
| [9] |
苏鹏程, 王宛山, 霍军周, 等. TBM的滚刀布置优化设计研究[J].
东北大学学报:自然科学版, 2010, 31(6): 877–881.
SU Pengcheng, WANG Wanshan, HUO Junzhou, et al. Optimal layout design of cutters on tunnel boring machine[J]. Journal of Northeastern University:natural science, 2010, 31(6): 877–881. |
| [10] | 耿麒, 魏正英, 孟昊, 等. TBM的平面刀盘与两级刀盘的力学性能对比分析[J]. 西安交通大学学报, 2015, 49(3): 121–128. |
| [11] | XIA Yimin, OUYANG Tao, ZHANG Xinming, et al. Mechanical model of breaking rock and force characteristic of disc cutter[J]. Journal of central south university, 2012, 19(7): 1846–1852. |



