2. 黑龙江工程学院 机电工程学院, 黑龙江 哈尔滨 150030;
3. 北京航空航天大学 材料科学与工程学院, 北京 100191
2. Mechanical and Electronic Engineering Department, Heilongjiang Institute of Technology, Harbin 150030, China;
3. Materials Science & Engineering School, BeiHang University, Beijing 100191, China
随着复合材料层合板结构在飞机、导弹、舰艇等结构中的广泛应用,层合板结构的连接设计也变得越来越重要。机械连接形式以其装配简单、承载能力强、连接可靠等诸多优点而成为复合材料层合板结构连接设计过程中主要采用的连接形式。
为获得可靠且具有高效承载能力的螺栓连接层合板结构,结构力学性能的影响因素分析是必不可少的重要环节。在以往的研究中,累积损伤的分析方法[1-4]为连接结构的性能分析提供了有力的工具。近期,针对纤维增强树脂基复合材料的特点(由纤维、基体组分材料复合而成),宏-细观多尺度的分析方法为层合板螺栓连接结构的设计与分析提供了新的研究手段。该方法能够从细观材料组分及性能出发来预报整体宏观结构的力学性能及损伤响应,更加科学合理地揭示复杂应力状态下结构损伤模式的破坏机理,为层合板螺栓连接结构的设计与优化提供指导作用。
本文利用ABAQUS软件及其提供的用户自定义子程序USDFLD,将考虑复合材料细观组分材料性能的改进的通用单胞模型(GMC模型)和组分材料的失效准则嵌入到层合板螺栓连接宏观结构的数值模型中,建立层合板螺栓连接结构的宏-细观多尺度相结合的数值分析方法,实现了从细观组分材料的层次研究层合板的铺层形式、几何尺寸、螺栓预紧力以及螺栓与试件孔之间的配合关系、夹具诸多方面对层合板螺栓连接结构挤压性能测试结果的影响,从而指导层合板螺栓连接结构的设计。
1 试验 1.1 试验材料单钉双剪层合板螺栓连接结构性能测试试验过程中所用材料为:碳纤维T700/双马来酰亚胺(BMI)树脂(由中国航空工业第一集团公司北京航空材料研究院提供),材料力学性能参数见表 1。
| 组分材料 | 性能指标 | 数值 |
| 纤维半径rf/μm | 3.5 | |
| 纵向拉伸模量EfL/GPa | 230 | |
| 横向拉伸模量EfT/GPa | 15 | |
| T700 | 纵横剪切模量GfLT/GPa | 15 |
| 横向剪切模量GfTT/GPa | 7 | |
| 纵横(主)泊松比νfLT | 0.20 | |
| 横向(次)泊松比νfTT | 0.07 | |
| 密度ρf/(kg·m-3) | 1760 | |
| 拉伸模量Em/GPa | 3.3 | |
| 剪切模量Gm/GPa | 1.48 | |
| 泊松比νm | 0.35 | |
| BMI树脂 | 拉伸强度Xmt/MPa | 76 |
| 压缩强度Xmc/MPa | 150 | |
| 剪切强度Sm/MPa | 70 | |
| 密度ρ/(kg·m-3) | 1260 |
依据单钉双剪层合板螺栓连接结构的测试标准(美标ASTM D 5961-A),进行试件的制作。首先,采用热压罐成型工艺进行层合板的制作,试件的铺层形式充分遵照测试标准的要求:即[45°/0°/-45°/90°]4S;其次,将层合板试件按照标准进行切割、研磨、钻孔,经检测开孔处无分层的试件为合格的待装配试件,如图 1(a);最后,将试件与测试夹具组装成单钉双剪形式的层合板螺栓连接结构试件(螺栓预紧力3N·m),如图 1(b)。

|
| 图1 层合板螺栓连接结构测试试件 Figure 1 Testing specimen of the bolted joint composite laminate structure |
首先,将测试试件装夹在测试试验机的上下夹头上(此过程应保持试件与夹具的相对位置不变,以免影响已施加的预紧力)。其次,在试件上安装50 mm 的引伸计以便获得试验过程中试件孔挤压部位的变形量,(引伸计安装时要能够采集跨孔的应变数据且不能与夹具干涉),如图 2所示。

|
| 图2 试件的安装与测试 Figure 2 Installation and testing of specimens |
安装完毕后,为了消除孔间隙等负面因素的影响,先预加2 kN载荷,卸载后再次加载直至复合材料层合板连接结构的性能出现大幅度的下降后,停止试验,测试结果如图 3所示。由测试结果可以看出:试验曲线的重复性较好,结构的初始挤压强度约为600 MPa,极限挤压强度为869 MPa。
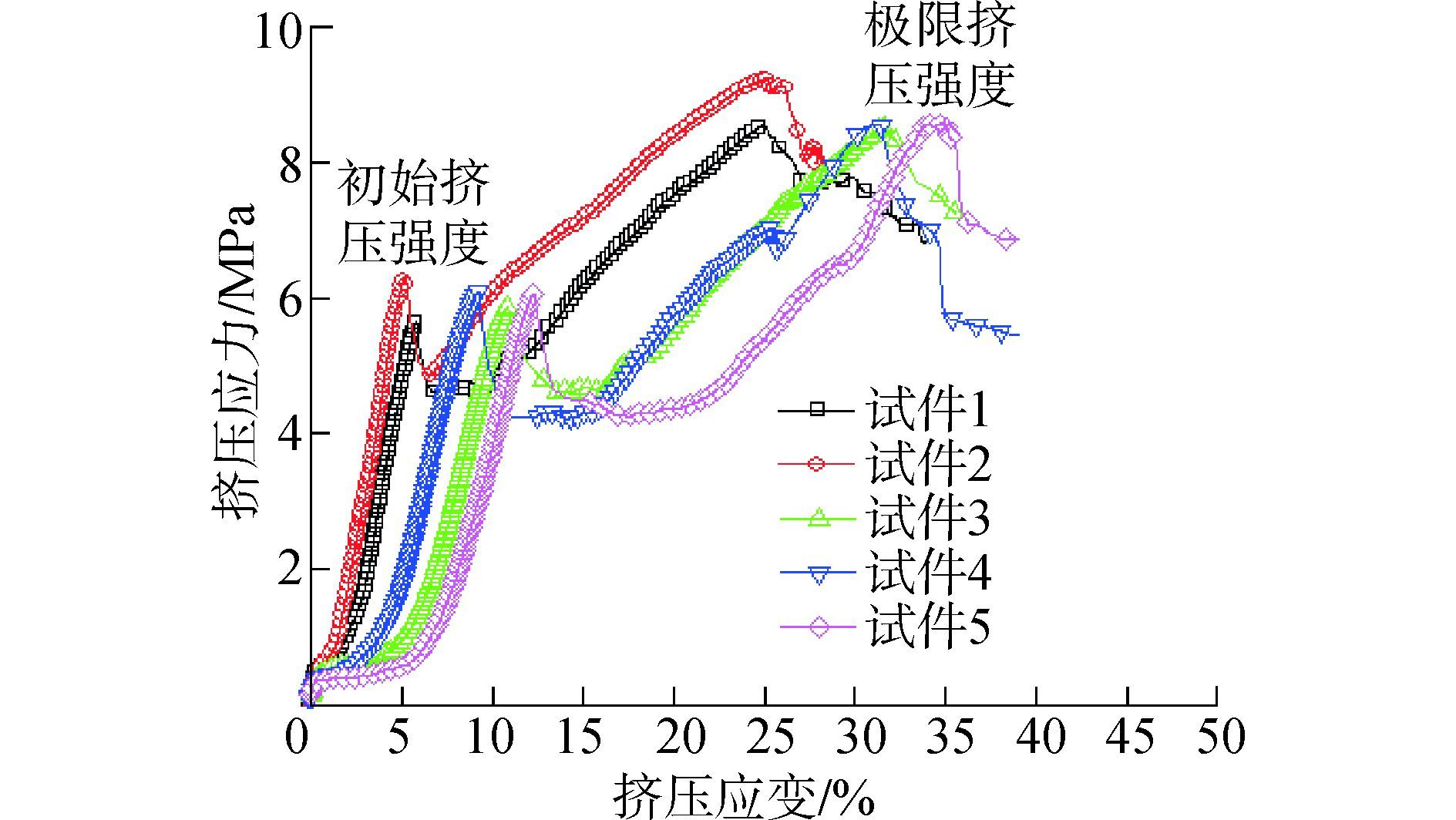
|
| 图3 层合板螺栓连接结构挤压强度的测试结果 Figure 3 Testing results of bearing strength of the bolted joint composite laminate structure |
传统的GMC模型由Paley和Aboudi[5]提出,主要用于周期性分布纤维复合材料的力学响应预报,该模型计算效率非常低,影响其在多尺度力学方面的应用。本文采用Pindera提出的改进GMC模型[6],该模型基于树脂基复合材料纤维周期性分布假设,选取代表性单胞来研究其整体性能,如图 4所示。
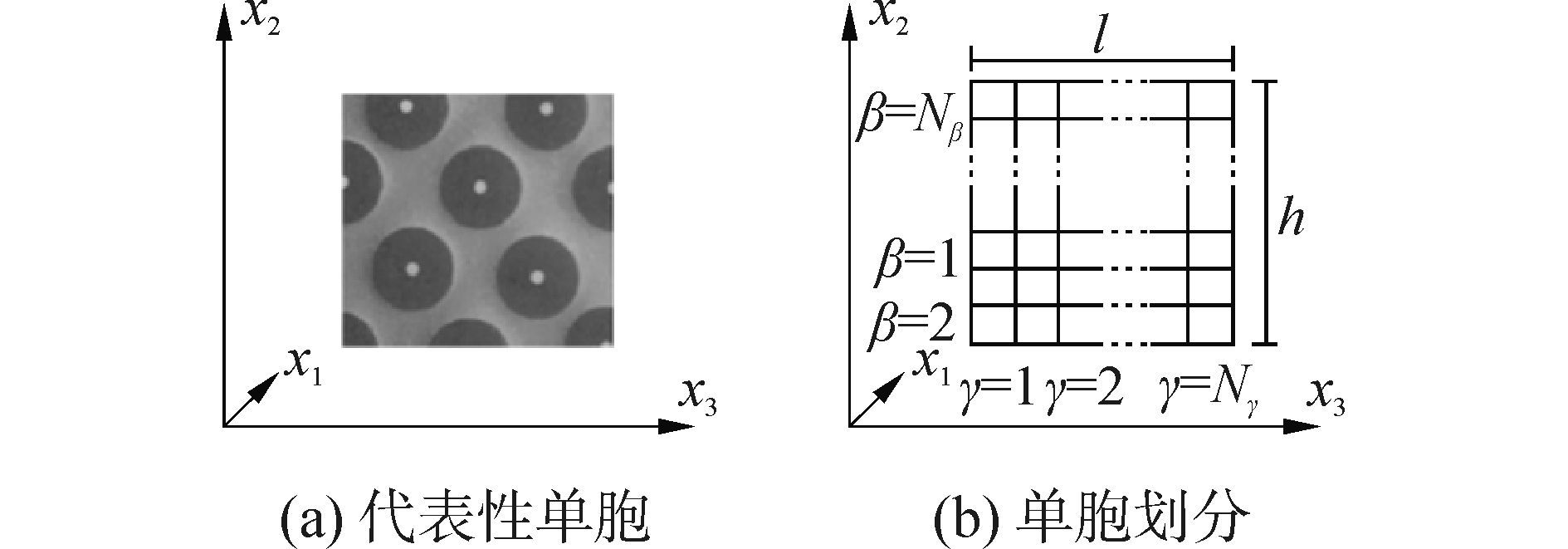
|
| 图4 单向纤维增强复合材料中代表性单胞及其划分 Figure 4 Representative unit cell and its division for the unidirectional fiber reinforced composite |
在局部坐标内,将单胞划分成Nβ×Nγ个子胞, 每个子胞可单独赋予材料属性,并基于单胞内一阶线性位移假设、体积平均假设、子胞界面位移、应力连续假设,建立单胞宏观平均应力与细观子胞应力的关系:
| $\bar \sigma = \frac{1}{{hl}}\sum\limits_{\beta = 1}^{{N_\beta }} {\sum\limits_{\gamma = 1}^{{N_\gamma }} {{h_\beta }} } {l_\gamma }{\bar \sigma ^{(\beta \gamma )}}$ | (1) |
从而进行多相复合材料的细观力学分析。
2.2 宏-细观多尺度数值模型利用有限元软件ABAQUS提供的用户自定义子程序(USDFLD)[7]的接口将改进的GMC模型和组分材料的失效准则嵌入到螺栓连接层合板结构有限元分析模型并遵循一定的材料性能衰减规律,即可实现考虑细观组分材料损伤/失效的宏-细观多尺度渐进损伤分析和强度预报。
2.2.1 细观组分的失效准则充分借鉴Tsai-Hill[8]、Tsai、Wu[9]和Hoffman[10]等宏观失效判据。对于细观组分材料采用如下失效判据(失效判据中的应力及强度分别对应各自组分的应力值和强度),其表达式如下:
基体拉伸(压缩)失效:
| ${e_m} = \left\{ {\begin{array}{*{20}{c}} {{{({\sigma _2}/{Y_t})}^2} + {{({\tau _{12}}/S)}^2},{\sigma _2} \ge 0}\\ {{{({\sigma _2}/{Y_c})}^2} + {{({\tau _{12}}/S)}^2},{\sigma _2} < 0} \end{array}} \right.$ | (2) |
纤维拉伸失效:
| ${e_f} = {({\sigma _f}/{X_t})^2},{\rm{ }}{\sigma _1} \ge 0$ | (3) |
当复合材料各组分材料的细观应力场满足上面任何一个失效判据时,就认为发生了相应的损伤失效,此时需要进行相应的刚度衰减。通常采用的刚度衰减方式主要有两种[11]。本文采用了部分刚度衰减的方式,即当某一层发生损伤的时候,这一层会在某些方向上失去承载能力,而在其他方向上仍具有承载力。相应的刚度衰减与失效状态的对应关系[12-13]见表 2。
| 完好状态 | 基体失效 | 纤维失效 | 界面失效 |
| E11 | E11 | 0.01E11 | 0.4E11 |
| E22 | 0.3E22 | E22 | 0.1E22 |
| γ12 | γ12=0 | γ12=0 | γ12 |
| G12 | 0.3G12 | 0.01G12 | 0.1G12 |
| G13 | G13 | 0.01G13 | 0.1G13 |
| G23 | 0.3G23 | G23 | 0.1G23 |
| FV1 | FV1=1 | FV1=0 | FV1=0 |
| FV2 | FV2=0 | FV2=1 | FV2=0 |
| FV3 | FV3=0 | FV3=0 | FV3=1 |
| 注:FV1,FV2 ,FV3为abaqus中用户自定义子程序USDFLD中与损伤模式对应的变量。 | |||
基于通用有限元软件ABAQUS及其子程序(USDFLD),结合改进的GMC模型建立宏-细观相结合的多尺度数值分析模型的流程如图 5所示。
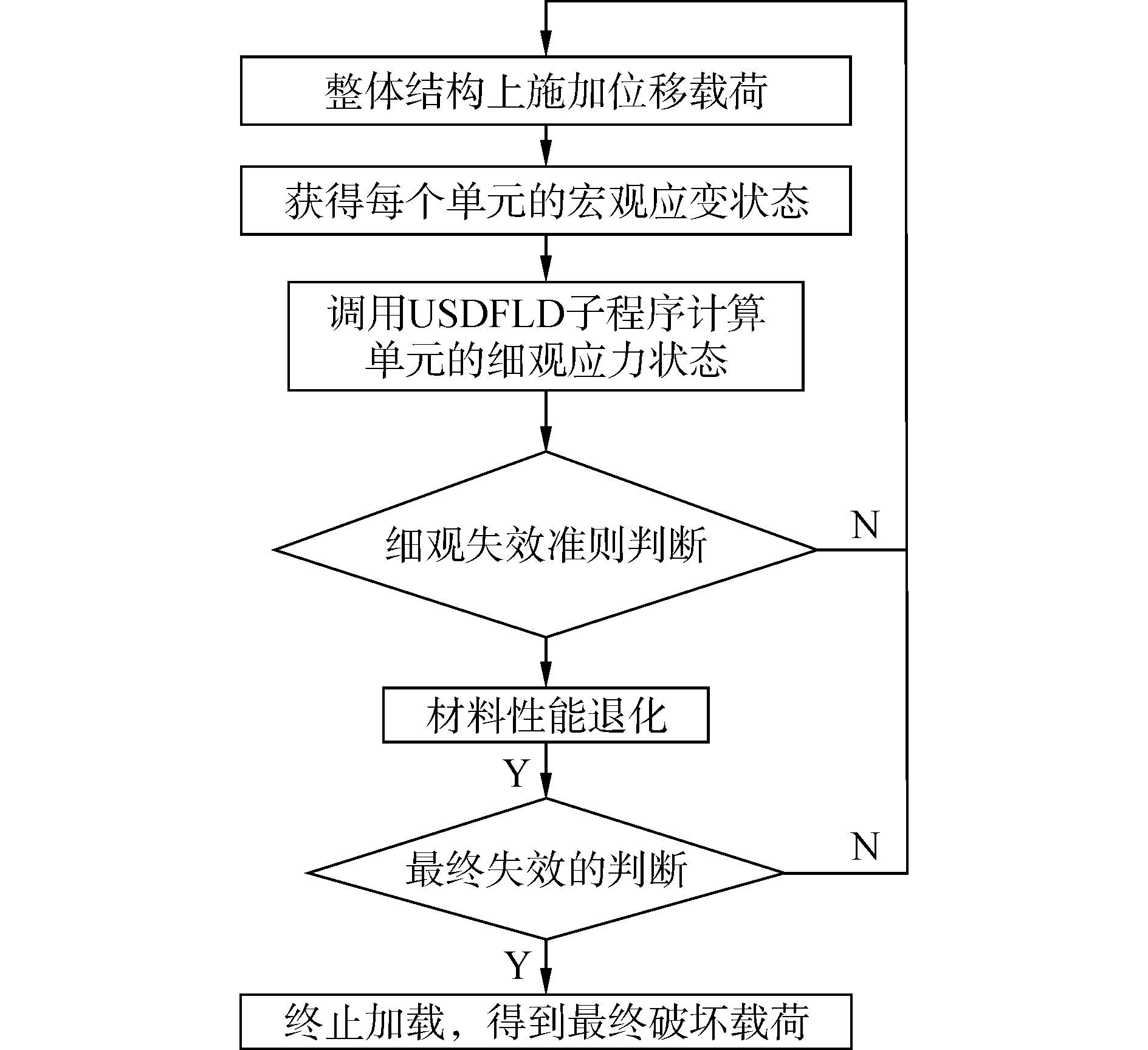
|
| 图5 结合GMC的宏-细观多尺度数值分析流程图 Figure 5 Flow chart of macro-micro multi-scale numerical analysis combined with GMC mode |
基于ABAQUS软件建立单钉双剪层合板螺栓连接结构的数值分析模型。螺栓及夹具选择非协调模式的八结点线性六面体单元(C3D8I),层合板试件选择连续壳单元(SC8R);螺栓与夹具孔之间定义为绑定约束关系,螺栓与层合板试件孔之间、螺栓与夹具的侧面以及夹具与层合板试件的侧面定义为接触约束;为平稳建立各部件间的相互作用关系,避免各部件产生位移,设置多个分析步(6个分析步),并施加相应的载荷,数值分析模型如图 6所示。
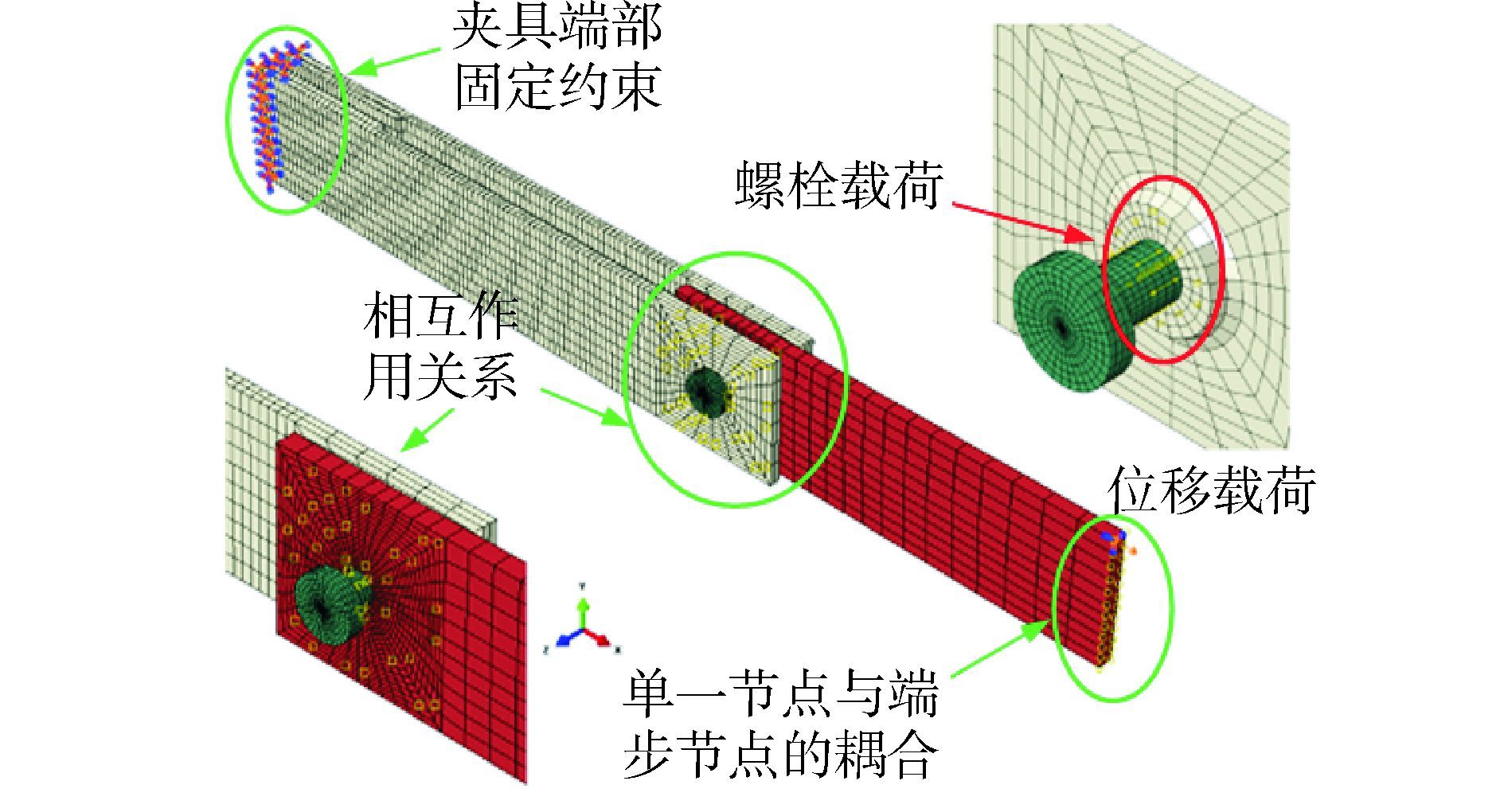
|
| 图6 单钉双剪层合板螺栓连接结构的数值分析模型 Figure 6 The numerical model of bolted joint composite laminate structure>laminate structure |
基于2.2节所建立的宏-细观多尺度数值分析模型模拟得到的层合板螺栓连接结构的应力-应变曲线与试验结果的对比如图 7所示。由图 7可知:利用该模型得到的单钉双剪层合板螺栓连接结构在拉伸载荷作用下的刚度、初始挤压强度、以及极限挤压强度均与试验结果基本吻合。因此,可以利用该模型对单钉双剪层合板螺栓连接结构力学性能的影响因素进行分析。

|
| 图7 数值分析结果与试验结果的对比 Figure 7 Camparation between numerical results and experimental results |
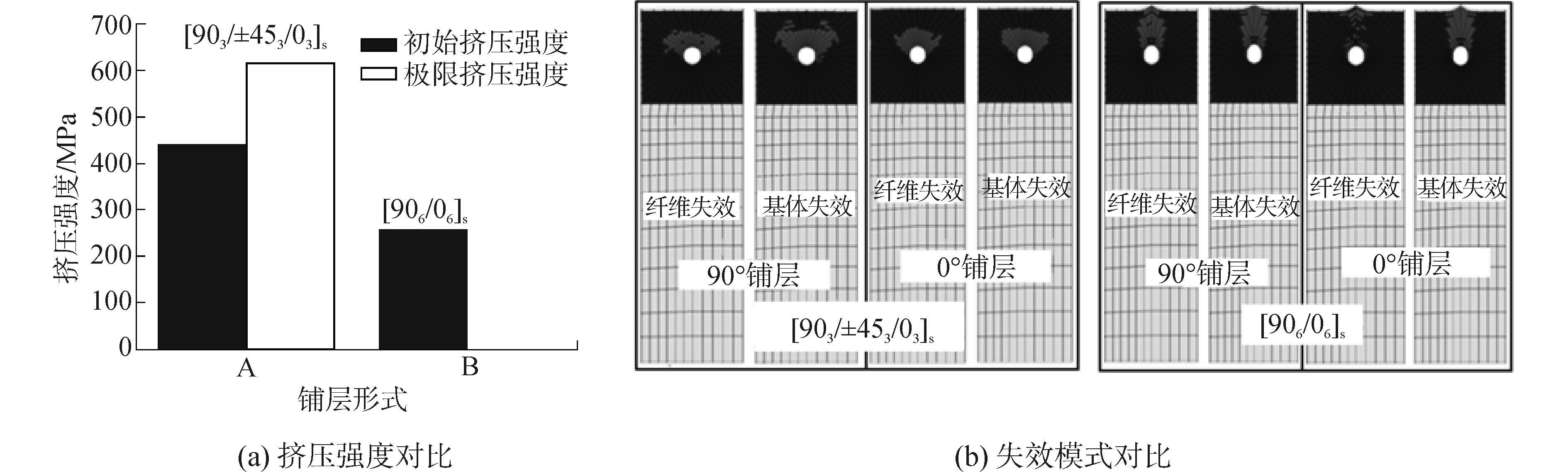
对比分析准各向同性([903/±453/03]S),和正交各项异性([906/06]S)两种不同铺层形式的层合板螺栓连接结构的挤压性能,结果如图 8所示。
|
| 图8 不同铺层形式的层合板螺栓连接结构的挤压强度与失效模式对比 Figure 8 Comparation of bearing strength and failure model between different layup bolted joint composite laminate structure |
由图 8(a)可以看出:正交各向异性的层合板螺栓连接结构只具有初始挤压强度一个峰值。因此,当正交各向异性的层合板螺栓连接结构达到其初始挤压强度后,该结构的承载能力显著下降,不再具有承担载荷的能力。此时,结构表现出明显的脆性性能;正交各向异性的层合板螺栓连接结构的初始挤压强度远小于相同材料体系的准各向同性的层合板螺栓连接结构的初始挤压强度。图 8(b)可知,准各向同性的层合板螺栓连接结构在双剪切载荷的作用下出现螺栓孔周围的挤压失效模式;而正交各向异性的层合板螺栓连接结构在双剪切载荷的作用下表现出明显的剪出失效模式,即一块材料沿纤维方向平行移动,该失效模式将会带来灾难性的破坏,实际使用中应尽量避免。从0°铺层可以明显看出,该损伤模式下螺栓孔前面区域的纤维很少被压坏、而出现了大量基体的失效。因此,该失效模式主要是基体的破坏。
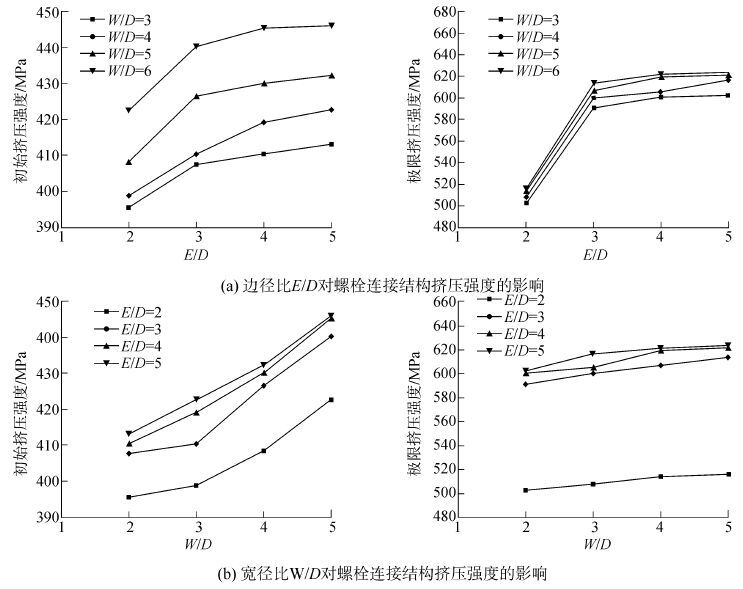
3.2 层合板几何尺寸的影响层合板螺栓连接结构中,试件的主要的几何尺寸包括层合板的长度L,宽度W,开孔直径D以及的孔的位置尺寸,即孔边距E(详见ASTM5961-A标准)。基于2.2节所建立的宏-细观多尺度数值分析模型分析几何尺寸W/D为3~6,E/D为2~5,铺层形式为 [903/±453/03]S层合板螺栓连接结构的挤压性能(初始挤压强度和极限挤压强度),如图 9所示。
|
| 图9 层合板的几何尺寸对螺栓连接结构挤压强度的影响 Figure 9 The effect of laminate geometry size on the bearing strength of bolted joint composite laminate structure |
由图 9可以看出:当层合板的E/D由2到3时,不同W/D的连接结构的初始和极限挤压强度均出现突然上升的趋势;但是,当E/D大于3时,不同W/D的连接结构的初始和极限挤压强度均处于平稳的趋势。说明:当层合板螺栓连接结构的E/D大于3时,E/D的变化对结构的承载能力的影响较小,尤其是对结构的极限承载能力,几何没有影响。
3.3 螺栓预紧力与配合关系的影响螺栓预紧力(预紧力的大小分别为2.4、3、3.6、4.2、4.8kN·m),螺栓与层合板试件孔之间的配合关系(间隙配合1%、2%、4%,过盈配合-0.5%)对层合板螺栓连接结构挤压性能的影响如图 10所示。

|
| 图10 预紧力与配合关系对层合板螺栓连接结构挤压强度的影响 Figure 10 The effect of pretension and fitting on the bearing strength of bolted joint composite laminate structure |
图 10可以看出:当预紧力大于4.2 N·m时,层合板螺栓连接结构的极限挤压强度逐渐趋于一稳定值,即结构的极限挤压强度不再随着螺栓预紧力的增加而增大。相反,由经验可知,过大的螺栓预紧力会导致层合板与夹具的接触表面出现损伤和破坏,反而会降低该结构的承载能力;干涉配合时结构的初始挤压强度和极限挤压强度高于其他的配合情况。由此可见,复合材料层合板螺栓连接结构在实际的工程应用中,可以适应增加干涉配合。
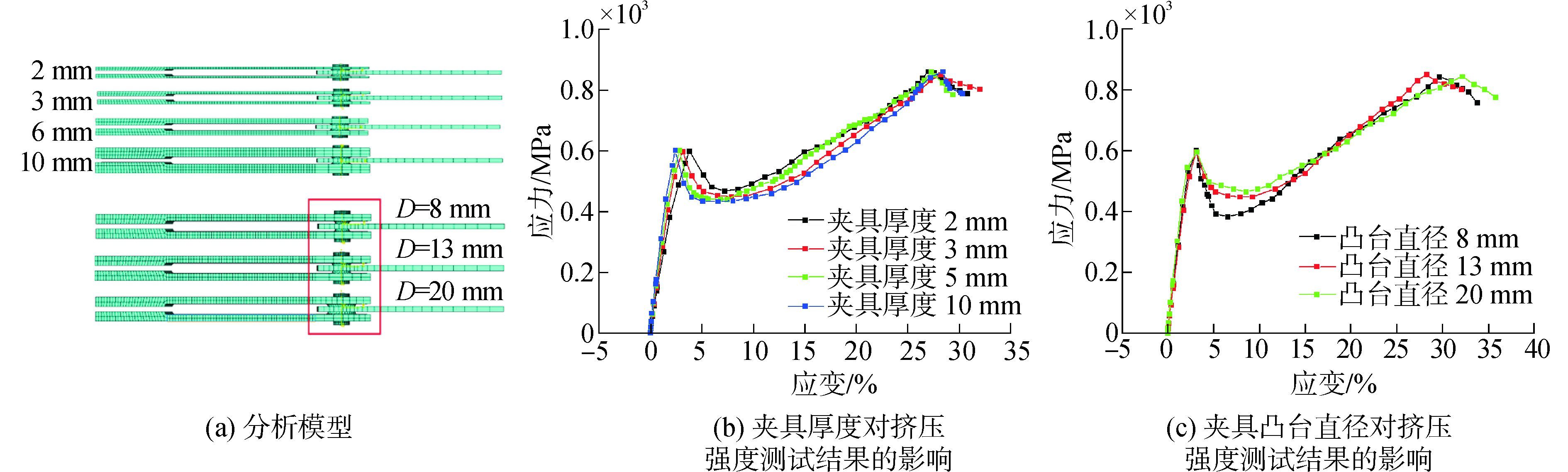
3.4 测试夹具的影响夹具体的主要几何尺寸包括夹具体的厚度以及夹具体与层合板试件接触处凸台的直径,夹具影响的分析模型及其分析结果如图 11所示。
由图 11(b)、(c)可知,随着夹具厚度的增加,结构的刚度会有较小的增加,尤其是当夹具厚度由2 mm增加至3 mm时,结构刚度增加较为明显。由此可见,在层合板螺栓连接结构测试过程中夹具的厚度不能小于3 mm;夹具厚度对结构的初始挤压强度以及极限挤压强度几乎没有影响;夹具体与层合板试件相接触的凸台部分的直径大小也会影响测试结果,当凸台直径较小时(8 mm,层合板开孔直径为6 mm),层合板结构达到初始挤压强度后,结构承载能力的下降幅度较大,这将导致结构的偏移挤压强度降低。因此,在进行层合板螺栓连接结构的测试时,夹具的凸台直径至少为层合板开孔直径的2倍左右。
|
| 图11 夹具对层合板螺栓连接结构挤压强度测试结果的影响 Figure 11 The effect of testing fixture on the bearing strength test result of the bolted joint composite laminate structure |
1) 准各向同性的层合板螺栓连接结构的失效模式为挤压失效,具有较高的挤压强度;正交各向异性层合板螺栓连接结构的失效模式为剪出失效,结构的承载能力低,实际使用中应尽量避免。
2) 当层合板的E/D大于3时,不同W/D的层合板螺栓连接结构的初始挤压强度和极限挤压强度趋近稳定值;相同E/D的层合板连接结构,其初始挤压强度和极限挤压强度随着W/D的增大而增大,尤其是结构的初始挤压强度,其增大的幅度较为明显。
3) 预紧力大于4.2 N·m时,结构的承载能力达到一稳定状态,过大的预紧力将降低结构的承载能力;适当的干涉配合能提高结构的承载能力,0~2%的间隙配合结构的承载能力趋于稳定,过大的间隙配合4%,将导致结构的承载能力下降。
4) 测试夹具的厚度及凸台直径均会影响其测试结果,夹具的厚度应不小于3 mm,凸台的直径应为层合板开孔直径的2倍左右。
| [1] |
王丹勇, 温卫东, 崔海涛. 复合材料单钉接头三维逐渐损伤破坏分析[J].
复合材料学报, 2005, 22(3): 168–174.
WANG Danyong, WEN Weidong, CHUI Haitao. Three-dimensional progressive damage analysis of single fastener joints in composite laminates[J]. Acta materiae compositae sinica, 2005, 22(3): 168–174. |
| [2] | SEN F, PAKDIL M, SAYMAN O, et al. Experimental failure analysis of mechanically fastened joints with clearance in composite laminates under preload[J]. Materials & design, 2008, 29(6): 1159–1169. |
| [3] | KHASHABA U A, SALLAM H E M, AL-SHORBAGY A E, et al. Effect of washer size and tightening torque on the performance of bolted joints in composite structures[J]. Composite structures, 2006, 73(3): 310–317. |
| [4] | OLMEDO Á, SANTIUSTE C. On the prediction of bolted single-lap composite joints[J]. Composite structures, 2012, 94(6): 2110–2117. |
| [5] | PALEY M, ABOUDI J. Micromechanical analysis of composites by the generalized cells model[J]. Mechanics of materials, 1992, 14(2): 127–139. |
| [6] | PINDERA M J, BEDNARCYK B A. An efficient implementation of the generalized method of cells for unidirectional, multi-phased composites with complex microstructures[J]. Composites part B, 1999, 30(1): 87–105. |
| [7] | Hibbit, Karlson, Sorensen, Inc. Section 1.1.34:User subroutine to define a material's mechanical behavior;1.1.43:User subroutine to redefine field variables at a material point[M]. ABAQUS User Subroutines Reference Manual. Ver. 6. 8. 7. |
| [8] | HILL R. A theory of the yielding and plastic flow of anisotropic metals[J]. Proceedings of the royal society of London. series A, 1948, 193(1033): 281–297. |
| [9] | TSAI S W, WU E M. A general theory of strength for anisotropic materials[J]. Journal of composite materials, 1971, 5(1): 58–80. |
| [10] | HOFFMAN O. The brittle strength of orthotropic materials[J]. Journal of composite materials, 1967, 1(2): 200–206. |
| [11] | (美)STEPHEN W T. 复合材料设计[M]. 沈阳: 航空工业部第601研究所, 1988: 155 -156. |
| [12] |
李伟占. 复合材料层合板损伤失效模拟分析[D]. 哈尔滨:哈尔滨工程大学, 2012:3.
LI Weizhan. Progressive damage analysis of composite laminates[D]. Harbin:Harbin Engineering University, 2012:3. |
| [13] | BABA B O. Behavior of pin-loaded laminated composites[J]. Experimental mechanics, 2006, 46(5): 589–600. |



