2. State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100084, China
近年来,鱼眼相机由于其超大的视场范围,在全景视觉、机器人导航、虚拟现实及视觉监控等领域中得到广泛应用。然而大视场同时也带来严重的图像畸变,影响人眼直观的视觉感受以及图像信息的利用。为了对图像畸变进行校正,需要进行鱼眼相机标定[1]。标定选用的成像模型方面,大多根据径向畸变和切向畸变建模,也有多项式逼近模型、抛物面投影模型、球面投影模型等等[2-5]。标定方法方面,主要分为传统标定法、主动视觉法和自标定法。其中传统标定法标定过程相对复杂,但精度最高[6-10]。鱼眼相机标定对精度要求较高,因而采用传统标定法。
用传统标定法对鱼眼相机进行标定时,由于鱼眼相机的大视场,单幅图像中标定板难以覆盖整幅图像从而导致标定误差增大。为弥补这一缺陷,一般采用多图标定法,将平面标定板放置于相机前不同的位置采集多张图像,以获得分布范围较大的标定原始数据。该方法需多次摆放棋盘并采集图像,对于某些需要快速安装并完成标定的场合并不适用,比如在生产线上批量装配车载相机时。针对这一问题,本文提出一种立体标定法,利用三块平面黑白棋盘搭建立体标定板,采集一幅图像即可实现快速标定。
1 鱼眼相机标定原理 1.1 成像模型相机标定首先要建立成像模型。本文选用Scaramuzza提出的折反射模型[5]作为鱼眼相机成像模型。
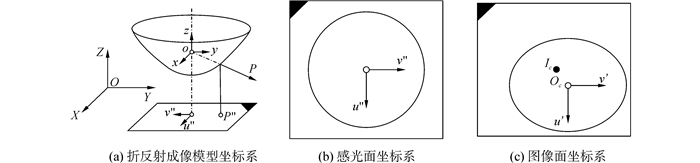
折反射模型坐标系设定如图 1。其中,(X, Y, Z)为世界坐标,(x, y, z)为相机坐标,(u", v")为感光面坐标,(u′, v′)为输出图像坐标。由世界坐标系至相机坐标系的映射模型为外部模型,与相机的安装位置有关,涉及参数称为外参;由相机坐标系至图像坐标系的映射模型为内部模型,与相机的内部构造有关,涉及参数称为内参。
|
| 图1 成像模型坐标系 Figure 1 Coordinate systems for imaging |
世界坐标系中的一点P经相机成像落于感光面的P", 由相机坐标系原点O至P点的向量记为p, 折反射模型对于如何由P"逆投影至P做以下假设:
| $\mathit{\boldsymbol{p=}}\left[ \begin{matrix} x \\ y \\ z \\ \end{matrix} \right]=\lambda \left[ \begin{matrix} {{u}''} \\ {{v}''} \\ f\left( \rho \right) \\ \end{matrix} \right]$ | (1) |
式中:λ为尺度变换因子,f(ρ)为包含相机畸变参数的非线性投影函数,用泰勒级数展开多项式表示为
| $f\left( \rho \right)={{a}_{0}}+{{a}_{1}}\rho +{{a}_{2}}{{\rho }^{2}}+{{a}_{n}}{{\rho }^{n}}$ | (2) |
其中,
成像面坐标到图像坐标的映射需经过仿射变换和中心偏移,关系式为
| $\left[ \begin{matrix} {{u}'} \\ {{v}'} \\ \end{matrix} \right]=\left[ \begin{matrix} c&d \\ e&1 \\ \end{matrix} \right]\left[ \begin{matrix} {{u}''} \\ {{v}''} \\ \end{matrix} \right]+\left[ \begin{matrix} {{u}_{c}} \\ {{v}_{c}} \\ \end{matrix} \right]$ | (3) |
式中:c、d、e为仿射变换系数,uc、vc为图像中心偏移量。
以上参数为相机内参。
相机坐标(x, y, z)与世界坐标(X, Y, Z)间存在旋转和平移,其映射关系为
| $\left[ \begin{matrix} x \\ y \\ z \\ \end{matrix} \right]=\left[ \begin{matrix} \mathit{\boldsymbol{R}}&\mathit{\boldsymbol{T}} \\ \end{matrix} \right]\left[ \begin{matrix} x \\ y \\ z \\ 1 \\ \end{matrix} \right]$ | (4) |
其中,旋转矩阵:
| $\mathit{\boldsymbol{R}}=\left[ \begin{matrix} {{\mathit{\boldsymbol{r}}}_{1}}&{{\mathit{\boldsymbol{r}}}_{2}}&{{\mathit{\boldsymbol{r}}}_{3}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{r}_{11}}&{{r}_{12}}&{{r}_{13}} \\ {{r}_{21}}&{{r}_{22}}&{{r}_{23}} \\ {{r}_{31}}&{{r}_{32}}&{{r}_{33}} \\ \end{matrix} \right]$ |
平移向量:
| $\mathit{\boldsymbol{T}}={{\left[ \begin{matrix} {{t}_{1}}&{{t}_{2}}&{{t}_{3}} \\ \end{matrix} \right]}^{\rm{T}}}$ |
二者构成相机外参。
1.2 模型参数求取要进行模型参数求取,首先需获取多个样点的世界坐标(X, Y, Z)和图像坐标(u′, v′)。对标定板拍摄图像,其上样点世界坐标已知,通过图像检测可获得样点图像坐标。
文献[4]中详细介绍了平面多图标定法的模型参数求解方法。参考文献中的方法,首先忽略仿射变换及图像中心偏移量,以(u, v)表示图像坐标,同时也可表示感光面坐标。以下标j代表样点序号。将式(1)两边叉乘并展开后得到如下公式:
| $\begin{align} &\ \ \ \ \ \ {{v}_{j}}\left( {{r}_{31}}{{X}_{j}}+{{r}_{32}}{{Y}_{j}}+{{r}_{33}}{{Z}_{j}}+{{t}_{3}} \right)- \\ &f\left( {{\rho }_{j}} \right)\left( {{r}_{21}}{{X}_{j}}+{{r}_{22}}{{Y}_{j}}+{{r}_{23}}{{Z}_{j}}+{{t}_{2}} \right)=0 \\ \end{align}$ | (5) |
| $\begin{align} &f\left( {{\rho }_{j}} \right)\left( {{r}_{11}}{{X}_{j}}+{{r}_{12}}{{Y}_{j}}+{{r}_{13}}{{Z}_{j}}+{{t}_{1}} \right)- \\ &\ \ \ \ \ {{u}_{j}}\left( {{r}_{31}}{{X}_{j}}+{{r}_{32}}{{Y}_{j}}+{{r}_{33}}{{Z}_{j}}+{{t}_{3}} \right)=0 \\ \end{align}$ | (6) |
| $\begin{align} &\ \ {{u}_{j}}\left( {{r}_{21}}{{X}_{j}}+{{r}_{22}}{{Y}_{j}}+{{r}_{23}}{{Z}_{j}}+{{t}_{2}} \right)- \\ &{{v}_{j}}\left( {{r}_{11}}{{X}_{j}}+{{r}_{12}}{{Y}_{j}}+{{r}_{13}}{{Z}_{j}}+{{t}_{1}} \right)=0 \\ \end{align}$ | (7) |
其中式(7)为线性方程,以此为突破口进行参数求解。由于旋转矩阵R内部存在约束关系,不能直接简单地对式(7)求解,需改进求解算法。
首先从标定板的三个平面中选取样点较多的一个平面,利用该平面内的样点坐标求外参初值。因为无论选定哪个平面,都只涉及r1、r2、r3中的某两个向量,不存在内部约束,可简单求解。然后令所有样点的三维坐标都参与计算,对外参进行优化。
以下按选定X-O-Y面为例进行说明。在该平面上,所有点的坐标Z=0,式(7)简化为
| ${{u}_{j}}\left( {{r}_{21}}{{X}_{j}}+{{r}_{22}}{{Y}_{j}}+{{t}_{2}} \right)-{{v}_{j}}\left( {{r}_{11}}{{X}_{j}}+{{r}_{12}}{{Y}_{j}}+{{t}_{1}} \right)=0$ | (8) |
该式中包含r11、r12、r21、r22、t1、t2六个参数,可构建超定线性方程组并求解[11]。然后根据旋转矩阵R内部存在的约束关系,即r1、r2、r3两两相互正交,且|| r1||=|| r2||=1,求得除t3外的其他外参。
然后用所有样点数据根据式(7)对外参进行最小二乘迭代优化[11-13]。迭代步长为
| ${{\delta }_{k}}={{\left( {{\mathit{\boldsymbol{J}}}_{k}}^{\rm{T}}{{\mathit{\boldsymbol{J}}}_{k}} \right)}^{-1}}{{\mathit{\boldsymbol{J}}}_{k}}^{\rm{T}}{{\varepsilon }_{k}}$ | (9) |
式中:ε表示上一次的估计误差,J表示Jacob矩阵,下标k代表第k次迭代。以函数g表示式(7)左部,Jacob矩阵如式(10)所示,式中n代表样点数量:
| $\mathit{\boldsymbol{J}}=\left[ \begin{matrix} \frac{\partial {{g}_{1}}}{\partial {{r}_{11}}}&\frac{\partial {{g}_{1}}}{\partial {{r}_{12}}}&\frac{\partial {{g}_{1}}}{\partial {{r}_{21}}}&\frac{\partial {{g}_{1}}}{\partial {{r}_{22}}}&\frac{\partial {{g}_{1}}}{\partial {{t}_{1}}}&\frac{\partial {{g}_{1}}}{\partial {{t}_{2}}} \\ \frac{\partial {{g}_{2}}}{\partial {{r}_{11}}}&\frac{\partial {{g}_{2}}}{\partial {{r}_{12}}}&\frac{\partial {{g}_{2}}}{\partial {{r}_{21}}}&\frac{\partial {{g}_{2}}}{\partial {{r}_{22}}}&\frac{\partial {{g}_{2}}}{\partial {{t}_{1}}}&\frac{\partial {{g}_{2}}}{\partial {{t}_{2}}} \\ \vdots &\vdots &\vdots &\vdots &\vdots &\vdots \\ \frac{\partial {{g}_{n}}}{\partial {{r}_{11}}}&\frac{\partial {{g}_{n}}}{\partial {{r}_{12}}}&\frac{\partial {{g}_{n}}}{\partial {{r}_{21}}}&\frac{\partial {{g}_{n}}}{\partial {{r}_{22}}}&\frac{\partial {{g}_{n}}}{\partial {{t}_{1}}}&\frac{\partial {{g}_{n}}}{\partial {{t}_{2}}} \\ \end{matrix} \right]$ | (10) |
每次迭代过程中,r11、r12、r21、r22、t1、t2由式(9)计算迭代步长后更新,而r13、r23则由更新后的r11、r12、r21、r22计算得到。
外参优化完成后,利用式(5)、(6),采用最小二乘法[12]求解畸变参数a0,a1,…,an以及t3。
最后,采用Levenberg-Marquardt迭代优化算法[14-15]对所有参数进行优化。其中,c、d、e初值为1、0、0,uc、vc初值分别为图像高宽的一半。至此,所有参数求解完成。
2 鱼眼相机快速标定方法 2.1 标定板设计立体标定板由两两互相垂直的三块黑白棋盘模板构成,如图 2所示。此标定板有如下优点:棋盘格成像后角点(即黑白方格的顶点,作为参数求取所需的样点)邻域内灰度梯度较大,易检测;立体标定板可包围相机,使棋盘角点遍布整幅图像;平面交界处绘有红色边界线,方便角点检测前进行所属平面划分,确定三维世界坐标。

|
| 图2 立体标定板 Figure 2 Stereoscopic calibration board |
1)图像采集
将标定板置于待标定相机前,调整标定板位置及角度,使图像中遍布棋盘角点,采集标定图像一张,如图 3。

|
| 图3 立体标定图像 Figure 3 Stereoscopic calibration image |
2)图像分割与角点检测
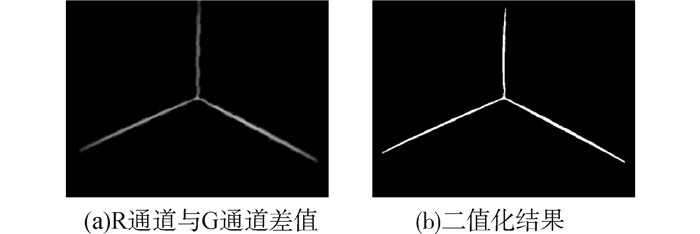
标定图像中没有复杂的干扰物,只有黑白方格与红色曲线,因而RGB三通道中,边界线处像素点的R通道灰度值明显高于G、B通道,其他区域三通道灰度值接近。求R通道与G或B通道的灰度差,采用自适应阈值进行二值化处理,可将边界线检测出来[16],结果如图 4。
|
| 图4 边界线检测 Figure 4 Boundary detection |
对三条边界线分别进行二次多项式拟合,依据边界线将原始图像分割为三个区域,形成三幅子图像,如图 5。

|
| 图5 图像分割 Figure 5 Image segmentation |
对三幅子图像分别进行角点检测并排序[3, 6]。由于角点在子图像中的坐标与其在原始图像的坐标相同,因而可以得到原始图像中所有角点的图像坐标,如图 6所示。

|
| 图6 角点检测结果 Figure 6 Corner detection result |
3)坐标映射建立
各区域的角点都有一维世界坐标为0,对应图 5中三幅子图像分别为Y=0,X=0,Z=0。根据棋盘方格边长以及与世界坐标原点间隔的方格数,可得到所有角点的世界坐标。从而建立起二维图像坐标与三维世界坐标的一一映射,用于模型参数的求解。
4)参数求解
依据标定原理,求解鱼眼相机参数。
以上标定过程在Visual Studio 2010平台下,用C/C++语言结合OpenCV编写标定程序,输入标定图像,得到鱼眼相机参数。
3 实验验证图 3的标定结果如下
| $\begin{align} &\ \ \ \ \ \ \ \ \ \ {{a}_{0}}=-1.5362\times {{10}^{2}},{{a}_{1}}=0, \\ &{{a}_{2}}=1.5294\times {{10}^{-3}},{{a}_{3}}=-5.1205\times {{10}^{-6}} \\ &\ \ \ \ \ \ \ {{a}_{4}}=1.8467\times {{10}^{-8}},c=0.9992, \\ &d=-1.3012\times {{10}^{-5}},e=2.7501\times {{10}^{-3}} \\ &\ \ \ \ \ \ \ \ {{u}_{c}}=243.5637,{{v}_{c}}=323.4531 \\ \end{align}$ |
| $\begin{align} &\ \ \ \ \ \mathit{\boldsymbol{R=}}\left[ \begin{matrix} 0.3657&0.3410&-0.8660 \\ -0.7142&0.6994&-0.0262 \\ 0.5968&0.6281&0.4780 \\ \end{matrix} \right] \\ &{{\mathit{\boldsymbol{T}}}^{\rm{T}}}=\left[ \begin{matrix} 30.5170&-3.8548&-125.0822 \\ \end{matrix} \right] \\ \end{align}$ |
上述相机参数中,只有平移向量T可以简单测得,旋转矩阵R由于旋转角较难测量而无法得到真实值,内参由于是抽象模型参数也无法获取真实值。因而难以通过所得参数本身来评价标定精度。
本文设计了四组对比实验对标定结果进行评价。
3.1 实验设计 3.1.1 标定实验设计设计四组标定实验如下:
A、B两组采用立体标定法,标定板可在保证棋盘角点遍布整幅图像的前提下随意摆放;C、D两组采用平面多图标定法,各自用平面棋盘拍摄八幅图像进行标定,其中C组严格控制棋盘摆放位置,使棋盘绕相机光轴等角度旋转一周,D组棋盘摆放较为随意, 如图 7所示。

|
| 图7 四组对比标定实验 Figure 7 Four calibration experiments for contrast |
由于四组标定所获图像的场景各不相同,要进行结果对比,需设计一个统一的验证实验。在杂物较少的水平地面上摆放一张棋盘,棋盘长约1 m,宽约0.6 m,相机距地面高度1.2 m。采集鱼眼图像作为测试图像,如图 8。

|
| 图8 测试图像 Figure 8 Test image |
结合标定实验所得四组相机内参,对测试图像标定外参。此过程只需通过求解超定线性方程组即可得到外参[15]。由此获得同一场景的四组相机内外参数,用于对比分析。
3.2 实验结果及分析 3.2.1 鱼眼图像畸变校正首先利用四组参数对测试图像进行畸变校正,从视觉效果上进行主观评价。为了便于分析校正效果,在校正基础上进行俯视投影。结果如图 9所示。

|
| 图9 鱼眼图像校正效果 Figure 9 Fisheye image correction results |
在校正效果图中,A、B、C组的整体校正效果较好,将棋盘及地面的方格较好的还原;D组还原效果稍差,图像左下角和右下角可看出弯曲变形未完全校正。
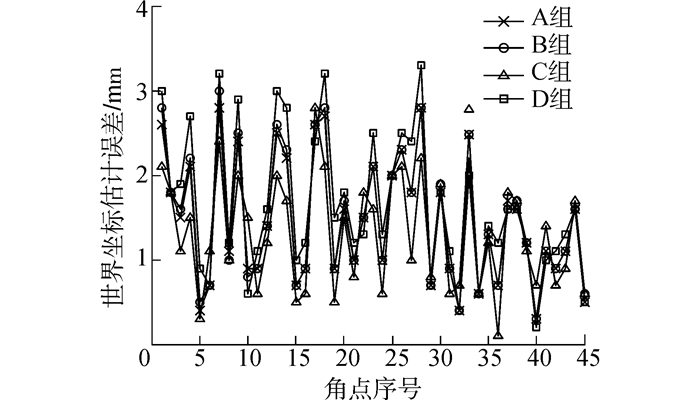
3.2.2 世界坐标估计利用标定所得相机参数,用角点的图像坐标逆投影得到其世界坐标的估计值,计算估计坐标与真实坐标的距离作为估计误差,如图 10。世界坐标估计误差分析见表 1。
|
| 图10 世界坐标估计误差 Figure 10 World coordinates estimation errors |
| 实验组 | 估计误差 均值/mm |
估计误差 标准差/mm |
| A | 1.46 | 0.73 |
| B | 1.49 | 0.76 |
| C | 1.32 | 0.67 |
| D | 1.65 | 0.84 |
由以上数据可看出四组实验中世界坐标的估计误差相近。粗略计算世界坐标估计值的相对误差,棋盘中心与相机距离取1 300 mm,估计误差取3 mm,则相对误差为0.23%,可认为误差较小,说明四组标定都有较高的标定精度。
其中,C组标定精度最高,A组与B组精度极为接近,D组精度相对略低。分析原因,A组与B组采用立体标定板,虽然标定板位置随意摆放,但都保证了棋盘角点遍布整幅图像,数据分布较好,因而求得的参数精度较高;C组标定板摆放位置经过精心设计以保证角点分布较均匀且遍布图像,D组为随意放置,角点分布散乱,无法保证获取的角点数据的分布情况,因而出现标定精度上的差异。
在标定过程的复杂程度上,A、B组采用的立体标定法,只需采集一幅图像,且因其标定板的立体设计,使得摆放棋盘时很容易将角点覆盖整幅图像,极易操作;C、D组采用的平面多图标定法,需多次采集图像,若要实现高精度标定,需要兼顾每幅图像中的棋盘位置,且若无辅助设备则人工操作较为繁琐。
4 结束语本文提出了一种利用立体标定板对鱼眼相机进行快速标定的方法,根据鱼眼相机成像特点设计专用的立体标定板,并提出适用于立体标定的参数求解方法。经实验验证,与传统的平面标定法相比,该方法具有较高的标定精度和鲁棒性,同时简化了标定流程,操作简易,耗时较短。对于车载鱼眼相机安装等需要进行批量标定的场合,该方法具有实际应用意义。
无论是本文所述方法还是传统标定法,由于鱼眼图像边缘区域畸变较大,与图像中心区域相比样点较密集且棋盘方格变形较大,样点检测精度降低,对标定参数的精度存在一定影响。本文认为可以尝试样点非均匀分布的标定板,改善边缘样点检测精度以提高相机参数标定精度。
| [1] | 张广军. 视觉测量[M]. 北京: 科学出版社, 2008: 102 . |
| [2] |
迟瑞娟, 赵木祯, 王建强, 等. 一种基于折反射相机的客车全景环视系统[J].
哈尔滨工程大学学报, 2013, 34(2): 190–196.
CHI Ruijuan, ZHAO Muzhen, WANG Jianqiang, et al. A top-view system for buses based on catadioptric fisheye camera[J]. Journal of Harbin engineering university, 2013, 34(2): 190–196. |
| [3] |
张春燕, 邹伟. 一种鱼眼镜头标定板的设计、检测与排序方法[J].
计算机工程与应用, 2015, 51(15): 188–192.
ZHAGN Chunyan, ZOU Wei. Design, detection and ranking method for a kind of fisheye camera's calibration board[J]. Computer engineering and applications, 2015, 51(15): 188–192. |
| [4] | ZHANG Zhengyou. A flexible new technique for camera calibration[J]. IEEE transactions on pattern analysis and machine intelligence, 2000, 22(11): 1330–1334. DOI:10.1109/34.888718 |
| [5] | SCARAMUZZA D, MARTINELLI A, SIEGWART R. A toolbox for easily calibrating omnidirectional cameras[C]//Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. Beijing, China: IEEE, 2006: 5695-5701. |
| [6] |
舒娜.摄像机标定方法的研究[D].南京:南京理工大学, 2014: 2-4, 14-20.
SHU Na. Research on camera calibration methods[D]. Nanjing: Nanjing University of Science and Technology, 2014: 2-4, 14-20. http://cdmd.cnki.com.cn/Article/CDMD-10288-1014176311.htm |
| [7] |
严春燕. 全景摄像机标定方法综述[J].
电脑知识与技术, 2014(12): 8291–8292.
YAN Chunyan. Overview of panoramic camera calibration method[J]. Computer knowledge and technology, 2014(12): 8291–8292. |
| [8] | KIM J S, KWEON I S. Camera calibration system using planar concentric circles and method thereof: US, US 7155030 B2[P]. 2006. |
| [9] | 马颂德, 张正友. 计算机视觉-计算理论与算法基础[M]. 北京: 科学出版社, 1998 . |
| [10] |
孟晓桥, 胡占义. 摄像机自标定方法的研究与进展[J].
自动化学报, 2003, 29(l): 110–124.
MENG Xiaoqiao, HU Zhanyi. Recent progress in camera self-calibration[J]. Acta automatica sinica, 2003, 29(l): 110–124. |
| [11] |
李排昌. 矩阵与解线性方程组[J].
中国人民公安大学学报:自然科学版, 2011(3): 106–108.
LI Paichang. Matrix and linear equations solution[J]. Journal of Chinese people's public security university: natural science edition, 2011(3): 106–108. |
| [12] |
杨曙光. 超定方程组残量极小化的定向扰动最小二乘法[J].
武汉大学学报:自然科学版, 1990(3): 17–25.
YANG Shuguang. Directional perturbation least-squares method of minimizing the residual of an overdetermined system of linear equations[J]. Journal of Wuhan university: natural science edition, 1990(3): 17–25. |
| [13] |
崔明根, 章森, 胡乃丽. 求解超定线性方程组的直接修正法[J].
哈尔滨工业大学学报, 1990(2): 20–27.
CUI Minggen, ZHANG Sen, HU Naili. A direct correction algorithm for solving overdetermined linear equations[J]. Journal of Harbin institute of technology, 1990(2): 20–27. |
| [14] | DUC-HUNG L, CONG-KHA P, TRANG N T T, et al. Parameter extraction and optimization using Levenberg-Marquardt algorithm[C]//Proceedings of the 2012 Fourth International Conference on Communications and Electronics (ICCE). Hue, Vietnam: IEEE, 2012: 434-437. |
| [15] |
张鸿燕, 耿征. Levenberg-Marquardt算法的一种新的解释[J].
计算机工程与应用, 2009, 45(19): 5–8.
ZHANG Hongyan, GENG Zheng. Novel interpretation for Levenberg-Marquardt algorithm[J]. Computer engineering and applications, 2009, 45(19): 5–8. |
| [16] | GONZALEZ R C, WOODS R E.数字图像处理[M]. 3版.阮秋琦, 阮宇智, 译.北京:电子工业出版社, 2011: 445-475. |



