2. CNOOC Research Institute, Beijing 100028, China
由于溶蚀、构造运动、水力压裂等因素,地下岩石,特别是碳酸盐岩中广泛存在不同尺度的裂缝。而裂缝是油气运移的主要通道,也是重要的储集空间[1]。裂缝性碳酸盐岩的非均质性强,构造内幕及断裂系统复杂,导致地震勘探过程中频谱分析精度低,使得常规预测与模拟方法不能很好的适用于碳酸盐岩储层[2]。VTI介质是指具有垂直对称轴的横向各向同性介质。不同地质年代形成的地层绝大多数是成层分布的,在纵向上由于沉积物的历史不同而具有不同的岩性,因此从宏观角度看,地层可近似为具有法向对称轴的横向各向同性介质[3]。随着非常规油气资源勘探开发的不断深入,地下孔、缝及周期性薄互层引起的各向异性严重干扰了弹性波场的分析[4]。研究岩石的弹性波传播特性,对于储层流体预测、裂缝识别、岩石内部结构预测等具有重要意义。因此,对于介质各向异性及弹性波传播机理与规律的研究近年来逐渐得到学者的重视[5]。国内外众多学者建立基于相似性原理构建地震岩石物理模型[6],分析了孔隙特性(形状、流体饱和、裂缝密度)对碳酸盐岩中弹性波传播的影响[7-9],并采用有效介质模型与实验结果进行比较,分析了孔隙结构的影响。然而,真实岩心孔隙结构的定量化分析比较复杂、成本高,人造物理模型又难以实现复杂孔隙结构的定量控制,因此数值模拟成为研究复杂孔隙结构介质弹性波特性的重要辅助方法。数值模拟不仅实现单一变量控制,而且可以方便的进行大量裂缝结构模拟,极大的减少了研究时间和成本。陈乔等[10]对裂缝介质的声波衰减开展了微观数值模拟研究。Wang等[11]采用数值模拟方法对不同孔隙结构的弹性波性质进行了研究。针对单独VTI介质或裂缝介质中弹性波传播特性影响已有大量研究,但是对于两者结合的分析还有待进一步深入和综合。
基于以上分析,本文拟以波动理论和相似性原理为基础,从尺度上类比理想条件下地震勘探的情景,采用有限元方法模拟弹性波在含裂缝VTI介质中的传播,分析VTI介质中不同裂缝结构对弹性波传播的影响规律,为碳酸盐岩裂缝性油气藏高效安全地开发提供理论支撑。
1 弹性波数值模拟原理 1.1 相似性原理岩石中的裂缝尺寸分布广泛。一般实际地震勘探中的频率在几赫兹至几百赫兹之间[12],其中常规地震勘探方法可分辨的裂缝特征尺寸为30~200 m[13],因此为了使数值模拟得到的弹性波传播和散射特性与实际地层中的地震勘探特性成比例,设计数值模拟中几何模型的尺寸与实际地质构造的尺寸也要成相应的比例关系——几何相似原理[14]。如果在模型介质中波传播速度与实际勘探中地震波的传播速度相同,即
| ${{{\lambda _{\bmod el}}} \over {{l_{\bmod el}}}} = {\lambda \over l}$ | (1) |
| ${\lambda _{\bmod el}} = {{f\lambda } \over f}$ | (2) |
式中:f、λ为地震勘探中实际介质中波的频率和波长,fmodel、λmodel为模型介质中波的频率和波长,l、lmodel分别为实际介质和模型介质中裂缝特征尺寸。模型中选用裂缝主轴作为裂缝特征尺寸。依据几何相似原理,通过建立不同裂缝特征尺寸的物理模型,模拟实际地震勘探中裂缝对声波的影响,相应的尺寸比例如表 1所示。
| 参数 | 物理模型 | 地震勘探参数 | 比例 |
| 波速/(m·s-1) | 3 000~5 000 | 3 000~5 000 | 1∶1 |
| 频率/Hz | fp为500 | fpmodel为10~200 | 5∶1 |
| 波长/m | 6~10 | 15~500 | 1∶5 |
| 裂缝特征尺寸/m | 30* | 30~200 | 1∶5 |
| λ/l** | ≈0.5 | ≈0.5 | 1∶1 |
| 注:*通过式(2)计算,对比常规地震中可分辨裂缝尺度得到的模型参数;λ/l**指波长与裂缝特征尺寸比值。 | |||
对于理想的简谐波,波速就是其相位传播的速度,即相速度。但在大多数介质(色散介质)中波传播过程中会发生频散现象,造成不同频率的波的速度互不相同[15]。对于地下岩石,随着弹性波传播距离的增加,由于介质内部的非均质性,弹性波发生反射、散射的次数增多,组合波波形发生变化。这时合成波的包络传播速度为群速度,代表了波能量和信息传播的速度。在实际测试和信号处理中,如果发射信号的时间延迟为0,根据接收信号首波起跳点和峰值点确定传播时间而计算的速度分别对应相速度Cp和群速度Cg。计算公式为
| ${C_p} = {h \over {{t_1}}}$ | (3) |
| ${C_g} = {h \over {{t_2} - {1 \over {4f}}}}$ | (4) |
式中:h为波传播距离,t1为接收端首波起跳时间,t2为接收端首波峰值时间,f为脉冲源频率。
品质因子Q是描述岩石非弹性特征的重要参数,在岩石受迫振动时,可以表征岩石内摩擦的大小。品质因子的倒数表征弹性波衰减[16],即耗损因子Q-1:
| ${Q^{ - 1}} = {{20\lg \left[ {{{A\left( x \right)} \over {{A_0}}}} \right]{C_g}} \over {\pi fh}}$ | (5) |
式中:A0为无裂缝参考模型首波振幅,A(x)为不同裂缝模型首波振幅。
2 含裂缝VTI介质弹性波场模拟方法 2.1 几何模型构建模型由固体基质和裂缝构成,基质设定为均匀各项同性线弹性材料,裂缝(裂缝纵横比α=1/300)内饱和不可压缩流体。为了模拟碳酸盐岩地层的真实情况,几何模型分两层(如图 1所示),下层为碳酸盐岩层(70 m×30 m),主要组成矿物为方解石,上层为泥岩层(70 m×30 m),主要组成矿物为黏土。采用微小的圆形线脉冲压力源,四周界面采用可抑制反射的平面波辐射界面。透射波接收端为模型的下边界,反射波接收端模拟实际检波器与地表的相对位置,接近于模型的上边界,利用线平均处理方法消除计算过程中的误差波,如图 1所示。

|
| 图1 数值模型构建示意图 Figure 1 The structure chart of numerical model |
裂缝内流体的控制方程为
| ${1 \over {\rho {f^{{c^2}}}}}{{{\partial ^2}{p_t}} \over {\partial {t^2}}} + \nabla \cdot \left[ { - {1 \over {\rho f}}\left( {\nabla {p_t} - q} \right)} \right] = {Q_m}$ | (6) |
| ${p_t} = p + {p_b}$ | (7) |
式中: q 为偶极子源,N/m3;Qm为单极子源,1/s2;ρf为裂缝中流体密度,kg/m3;pt为总压力,Pa;pb为模型背景压力,Pa;p为波动压力,Pa。
在小应力条件下,岩石可近似认为线弹性材料,因此基质采用各项同性的线弹性材料[17],指定体积模量和剪切模量,遵循Duhamel-Hooke定律,其控制方程如下
| $\rho {{{\partial ^2}u} \over {\partial {t^2}}} - \nabla \cdot \sigma = {F_V}$ | (8) |
| $\sigma = {s_0} + C\left( {K,G} \right):\left( {\varepsilon - {\varepsilon _0}} \right)$ | (9) |
| $\varepsilon = {1 \over 2}\left[ {{{\left( {\nabla u} \right)}^T} + \nabla u} \right]$ | (10) |
式中: u (x,y)为二维空间的位移矢量, σ 为应力张量, F v为激发源应力矢量,C(K,G)为包含体积模量和剪切模量的四阶弹性张量,“∶”表示双点张量积(收缩积),s0和 ε 0为初始应力和应变, ε 为总应变张量。
模型中假设流体和基质边界处应力和加速度是连续的:
| $ - n \cdot \left[ {{1 \over {\rho f}}\left( {\nabla {p_t} - q} \right)} \right] = - n \cdot {{{\partial ^2}u} \over {\partial {t^2}}}$ | (11) |
| $\sigma \cdot n = {p_t} \cdot n$ | (12) |
式中: n 为边界处单位法向量。
圆形线脉冲源采用边界载荷压力激励方式模拟纵波震源:
| ${p_0} = \left\{ \matrix{ {A_0}\sin \left( {2\pi {f_{\bmod el}}t} \right)\sin \left( {{1 \over 3}\pi {f_{\bmod el}}t} \right),t \le {3 \over {{f_{\bmod el}}}} \hfill \cr 0,t > {3 \over {{f_{\bmod el}}}} \hfill \cr} \right.$ | (13) |
| $\sigma \cdot n = - {p_0}n$ | (14) |
式中:A0为脉冲源振幅,为1×107 Pa;fmodel=500 Hz。
定义模型初始条件:
| $\left\{ \matrix{ p\left( {x,y} \right)\left| {_{t = 0}} \right. = 0 \hfill \cr {{\partial p\left( {x,y} \right)} \over {\partial t}}\left| {_{t = 0}} \right. = 0 \hfill \cr} \right.$ | (15) |
为了消除计算过程中边界对内部波场的影响。采用Givoli和Neta提出的平面波辐射边界[18],通常可使入射波反射系数降为零,这样可以最大限度的减少声波反射的影响:
| $ - n \cdot \left( { - {1 \over \rho }\left( {\nabla {p_t}} \right)} \right) + {1 \over \rho }\left( {{1 \over c}{{\partial p} \over {\partial t}}} \right) = {Q_i}$ | (16) |
采用有限元方法对式(6)~(16)确定的定解问题进行求解,利用广义最小残量方法求解上述线性方程组,迭代方法选用可加速收敛的超松弛迭代法。该求解方法有效减少了占用内存。网格划分在保证每个波长含有10~12个自由度的基础上对裂缝部分进行局部加密,总网格数为105~107。以10-5为时间步长,迭代3 000步,计算得到各点声压p(x,y)随时间变化的离散数据作为接收信号。
通常在碳酸盐岩储层的上、下存在泥岩或页岩层。本模型里碳酸盐岩层基本矿物设定为方解石,泥岩层矿物基本设定为黏土,其弹性参数见《岩石物理手册》[19],裂缝中充填水,模型中假设碳酸盐岩层组成为80%方解石+10%黏土+10%水,泥岩层组成为90%黏土+10%水。采用Voigt-Reuss-Hill平均计算背景介质的弹性模量,采用Wood公式计算密度,在此基础上,计算对应的弹性波速度。数学模型材料基本参数见表 2。
| 地层模型 | 密度/(g·cm-3) | 纵波速度/(m·s-1) | 剪切模量/GPa | 体积模量/GPa |
| 碳酸盐岩层 | 2.523 | 5 855 | 12.419 | 27.049 |
| 泥岩层 | 2.395 | 3 590 | 4.021 | 9.333 |
| 裂隙 | 1 | 1 613 | — | — |
为了验证模型的可靠性,在脉冲源位置、模型尺寸等都不变的情况下,建立无裂缝模型,获得由模型计算出的透射波和界面反射波的时差,同时利用时间平均模型计算出理论时差,二者相比较(如表 3所示),验证模型的精确性与可靠性。
| 接收点 | 理论计算时间/10-3s | 模型读取时间/10-3s | 相对误差/% |
| (32,0) | 13.48 | 13.53 | 0.371 |
| (32,55) | 15.34 | 15.37 | 0.175 |
| (29,55) | 15.41 | 15.45 | 0.252 |
| (26,55) | 15.52 | 15.56 | 0.231 |
| (23,55) | 15.68 | 15.74 | 0.378 |
| (20,55) | 15.88 | 15.91 | 0.190 |
| (17,55) | 16.12 | 16.16 | 0.249 |
| (14,55) | 16.40 | 16.40 | 0.006 |
由表可知,两者误差均不超过0.5%。因此,可以推断利用该数学模型得到的数据是可靠的。
2.4 实验方案设计为了研究VTI介质中裂缝性质(裂缝密度、裂缝角度)对透射波和裂缝反射波波速、振幅衰减的影响,根据控制变量法原理,采用相同的数学模型,分别改变裂缝数量和裂缝角度(波传播方向与裂缝面法向夹角),建立两个系列几何模型,定性分析裂缝对弹性波传播的影响。数值模拟实验设计如表 4所示。系列A分析裂缝参数对弹性波传播(透射波、裂缝反射波)的影响,系列B分析两条裂缝间距对透射波的影响。
| 模型系列 | 裂缝个数 | 裂缝角度 | 缝间距/波长 |
| A | 1,2,3,4 | 0,15,30 45,60 | 1 |
| B | 2 | 0,30,45 | 0.05~1 |
模型系列A在上下层中以中轴线为中心均匀的加入数量1~4个及分布角度0~60°的椭圆形裂缝,读取接收端线平均声压与时间函数,从而可计算出透射波波速及衰减。图 2为三个30°裂缝在不同时刻的波场切片示意图。

|
| 图2 不同时刻波场示意图 Figure 2 Schematic of wave field at different times |
图 3显示了随着裂缝数量的增加,透射波波速降低,且相速度大于群速度。同时裂缝角度增大,群速度降低,相速度则基本不变。说明在裂缝纵横比很小的情况下,裂缝角度对声波穿透介质的影响较小,主要是对能量产生了一个延迟作用,使得波向前传播的过程中,产生频散现象,频率逐渐降低致使波长增大,因此群速度降低。

|
| 图3 裂缝参数(角度、数量)对弹性波波速的影响 Figure 3 Effects of crack (angle and number) on velocity |
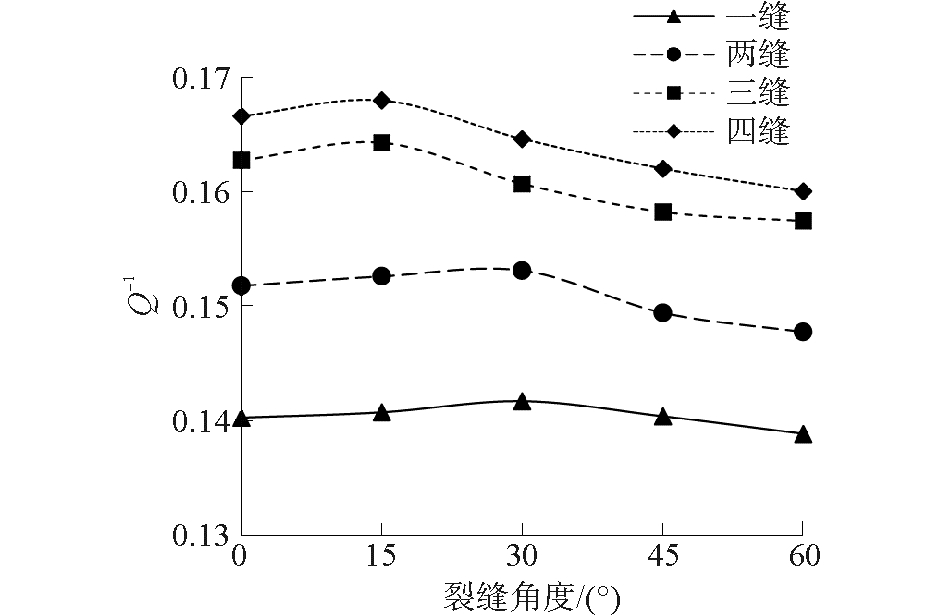
由于本模型中,波长与裂缝尺寸的比值约为0.5(λ/l<1),属于射线理论应用范围内[20]。图 4显示了随着裂缝数量的增加,裂缝耗损因子增加,散射影响加强。主要是随着裂缝界面的增多,在界面处由于反射使能量损失增大。裂缝角度对衰减影响较小,当裂缝角度处于低角度(0~30°)时衰减较为强烈。且随着裂缝数量的增多,裂缝角度对衰减的影响增大。说明在当前尺度下,裂缝处于低角度时,裂缝中稀疏介质吸收及裂缝界面反射产生的衰减影响 效果大,而当裂缝角度逐渐增大时,由于裂缝周围产生波的绕射衰减对透射波的影响效果增大。
|
| 图4 裂缝参数(角度、数量)对弹性波衰减的影响 Figure 4 Effect of crack (angle and number) on attenuation |
理论上波具有线性叠加性,且叠加时不会对各自的能量产生影响,所以可以将无裂缝和有裂缝两种情况下的接收信号直接相减,分离裂缝反射部分。以泥岩层单一30°裂缝模型为例,得到如图 5所示波形同时利用几何方法计算出裂缝反射波和界面反射波首波达到时间,验证了利用相减分离反射波方法的正确性。

|
| 图5 裂缝反射波相减分离原理 Figure 5 Subtraction separation principle of the crack reflected wave |
裂缝反射波的衰减是两部分组成的:1)传播过程中介质吸收产生的衰减和波阵面增大导致的扩散衰减;2)裂缝界面处反射和散射产生的衰减。为了获得单纯由于裂缝存在而导致的衰减,应用有裂缝时的衰减量减去传播相同路程时由于吸收和扩散的衰减量。定义裂缝自身导致的衰减百分比(%):
| $\beta = {{\left( {{A_1} - {A_2}} \right) - \left( {{A_0} - {A_1}} \right)} \over {{A_0}}} \times 100 = {{{A_1} - {A_2}} \over {{A_0}}} \times 100$ | (17) |
式中:A0为脉冲源声幅值,A1为传播相同距离时直达波声幅值,A2为裂缝反射波声幅值。
为了得到基质中传播相同距离时的直达波声幅值A1,建立相同参数的单泥岩层模型,采用相同的脉冲震源作为激励,根据7个接收点位置利用反射定律计算出裂缝反射波传播距离和入射波与裂缝界面的夹角θ,计算出7个反射波接收点处等效无裂缝直达波声幅值A1,进而根据式(17)计算裂缝自身产生的衰减百分比β。图 6显示了同一裂缝角度下,在裂缝界面随着入射角的增加,裂缝自身产生的衰减线性降低;且裂缝角度越大,衰减降低地越快。说明裂缝自身产生的衰减不仅与入射角有关,也与模型中裂缝角度有关。并且在入射角小于25°时,裂缝自身衰减百分比对裂缝角度具有很好的区分能力。与地震勘探类比,这里入射角不同,代表着不同的检波器位置和偏移距,这意味着裂缝自身衰减百分比是采用不同偏移距数据预测裂缝角度的一个有利属性。

|
| 图6 同一裂缝角度下衰减百分比β与入射角θ的关系 Figure 6 The relationship between β and θ at same crack angle |
模型系列B的裂缝数目和裂缝角度保持不变(如表 4所示),通过改变两条裂缝(0°、30°、45°)之间的距离(d),研究裂缝间距d与波长λ之比ε(ε=d/λ)与透射波波速和衰减的关系。裂缝间距对透射波的影响如图 7所示。

|
| 图7 ε对纵波参数的影响 Figure 7 Effects of ε on compressional wave |
从图 7(a)可以看出,裂缝间距对透射波波速影响较小,当裂缝间距小于一个波长(ε<1.0)时,裂缝间距变化对相速度和群速度的影响均小于10%,且当裂缝间距大于半个波长(ε>0.5)后,波速趋于稳定,这表明裂缝间距与频散现象之间响应关系较弱,弹性波速度对相邻裂缝间距的分辨率较差。从图 7(b)可以看到,当ε<0.5时,间距对透射波的衰减影响较大,且随着裂缝角度从0°增大到45°,受裂缝间距的影响范围增大,衰减最小处从ε=0.2增大到ε=0.4。当ε>0.5后,影响基本消失,衰减达到一个定值。这表明对于邻近裂缝(ε<0.5),弹性波损耗因子是区分其间距的有效属性。
4 结论针对VTI介质和裂缝介质共同对弹性波影响的问题,以波动理论和相似性原理为基础,从尺度上类比理想条件下地震勘探的情景,建立了含裂缝VTI介质中弹性波传播的有限元数值模拟方法,分析了不同裂缝结构下的弹性波响应特征,结果表明:
1) 透射波的相速度大于群速度,随着裂缝数量的增加,透射波速度降低、衰减增大;裂缝角度对群速度的影响大于相速度,低角度裂缝对弹性波衰减影响较大。
2) 以无裂缝条件下弹性波信号为参照,采用裂缝自身衰减百分比定量描述单纯由裂缝存在而引起的弹性波衰减。在入射角小于25°时,裂缝自身衰减百分比对裂缝角度具有很好的区分能力,是采用不同偏移距数据预测裂缝角度的一个有利属性。
3) 对于裂缝发育储层,裂缝间距小于波长时,弹性波速度对相邻裂缝间距的分辨率较差;而对于邻近裂缝(d/λ<0.2),弹性波损耗因子是区分其间距的有效属性。该结果为基于弹性波数据的裂缝识别奠定基础。
本次研究仅仅是对数值模拟方法对VTI介质和裂缝介质双重影响的初步探究。未来的工作将着力于进一步增加裂缝数量,建立三维模型计算方法。
| [1] |
徐雄飞, 王嘉伟, 杨波, 等. 塔里木盆地轮南地区侏罗系砂岩储层成岩作用研究[J].
岩性油气藏, 2011, 23(5): 21–27.
XU Xiongfei, WANG Jiawei, YANG Bo, et al. Study on diagenesis of Jurassic sandstone reservoirs in Lunnan area, Tarim Basin[J]. Lithologic reservoirs, 2011, 23(5): 21–27. |
| [2] | WANG Haiyang, SUN S Z, YANG Haijun, et al. The influence of pore structure on P- & S-wave velocities in complex carbonate reservoirs with secondary storage space[J]. Petroleum science, 2011, 8(4): 394–405. |
| [3] | ZHOU H, ZHANG G, BLOOR R. An anisotropic acoustic wave equation for VTI media[C]//Proceedings of the 68th EAGE Conference &Exhibition. Vienna, Austria, 2006. |
| [4] |
谢桂生, 包吉山. 横向各向同性介质中弹性波模拟及波场特征研究[J].
石油地球物理勘探, 1996, 31(6): 806–814.
XIE Guisheng, BAO Jishan. Elastic wave simulation and the wave field character study in azimuthal isotropic medium[J]. Oil geophysical prospecting, 1996, 31(6): 806–814. |
| [5] |
何现启, 朱自强, 鲁光银, 等. VTI介质中弹性波的波动特征研究[J].
地球物理学进展, 2009, 24(4): 1291–1298.
HE Xianqi, ZHU Ziqiang, LU Guangyin, et al. The study of volatility characteristics in VTI media[J]. Progress in geophysics, 2009, 24(4): 1291–1298. |
| [6] |
李天阳, 王子振, 王瑞和, 等. 含裂缝VTI介质的弹性波传播特性研究[J].
地球物理学进展, 2015, 30(6): 2498–2504.
LI Tianyang, WANG Zizhen, WANG Ruihe, et al. Elastic wave propagation characteristics in the VTI media containing cracks[J]. Progress in geophysics, 2015, 30(6): 2498–2504. |
| [7] |
尹志恒, 狄帮让, 魏建新, 等. 裂缝参数对纵波能量衰减影响的物理模型研究[J].
石油地球物理勘探, 2012, 47(5): 728–734.
YIN Zhiheng, DI Bangrang, WEI Jianxin, et al. P-wave attenuation by fracture parameter on physical models[J]. Oil geophysical prospecting, 2012, 47(5): 728–734. |
| [8] | RATHORE J S, FJAER E, HOLT R M, et al. P-and S-wave anisotropy of a synthetic sandstone with controlled crack geometry[J]. Geophysical prospecting, 1995, 43(6): 711–728. |
| [9] | TILLOTSON P, SOTHCOTT J, BEAT A I, et al. Experimental verification of the fracture density and shear-wave splitting relationship using synthetic silica cemented sandstones with a controlled fracture geometry[J]. Geophysical prospecting, 2012, 60(3): 516–525. |
| [10] |
陈乔, 刘向君, 梁利喜, 等. 裂缝模型声波衰减系数的数值模拟[J].
地球物理学报, 2012, 55(6): 2044–2052.
CHEN Qiao, LIU Xiangjun, LIANG Lixi, et al. Numerical simulation of the fractured model acoustic attenuation coefficient[J]. Chinese journal of geophysics, 2012, 55(6): 2044–2052. |
| [11] | WANG Zizhen, WANG Ruihe, WEGER R J, et al. Pore-scale modeling of elastic wave propagation in carbonate rocks[J]. Geophysics, 2015, 80(1): D51–D63. |
| [12] |
任科英. 实验室岩心声学速度测试中的频散现象[J].
石油地球物理勘探, 2011, 46(5): 779–782.
REN Keying. Velocity dispersion of ultrasonic core measurement in laboratory[J]. Oil geophysical prospecting, 2011, 46(5): 779–782. |
| [13] |
杨林. 地震频谱分解技术应用中有关问题的讨论[J].
石油物探, 2008, 47(4): 405–409.
YANG Lin. Discussion on the problems in using the technology of seismic spectral decomposition[J]. Geophysical prospecting for petroleum, 2008, 47(4): 405–409. |
| [14] |
牟永光.
三维复杂介质地震物理模拟[M]. 北京: 石油工业出版社, 2003: 15 -25.
MU Yongguang. Seismic physical modeling for 3-D complex media[M]. Beijing: Beijing:Petroleum Industry Press, 2003: 15 -25. |
| [15] |
潘帅, 万雨挺, 陈洪山. 超声波在液体中相速与群速的测量[J].
物理实验, 2011, 31(4): 39–41.
PAN Shuai, WAN Yuting, CHEN Hongshan. Phase velocity and group velocity of ultrasonic wave in liquid[J]. Physics experimentation, 2011, 31(4): 39–41. |
| [16] | 陈颙, 黄庭芳, 刘恩儒. 岩石物理学[M]. 合肥: 中国科学技术大学出版社, 2009: 66 -68. |
| [17] | FJAER E, HOLT R M, HORSRUD P, et al. Petroleum related rock mechanics[M].2nd ed. Amsterdam: Elsevier, 2008 . |
| [18] | GIVOLI D, NETA B. High-order non-reflecting boundary scheme for time-dependent waves[J]. Journal of computational physics, 2003, 186(1): 24–46. |
| [19] | MAVKO G, MUKERJI T, DVORKIN J. The rock physics handbook:tools for seismic analysis of porous media[M]. Cambridge: Cambridge University Press, 2009: 260 -263. |
| [20] | LIU Yinbin, SCHMITT D R. The transition between the scale domains of ray and effective medium theory and anisotropy:numerical models[J]. Pure and applied geophysics, 2006, 163(7): 1327–1349. |



