2. Offshore Oil Engineering Company Limited, Tianjin 300451, China
海底管道作为油气运输的主要方式,是油气开发中的重要组成部分,海底管道的铺设施工技术也随之成为了必须解决的关键环节[1]。国内外海底管道铺设施工方法主要有拖管法、“S”型铺设法、“J”型铺设法和卷管铺设法[2-5]。卷管铺设法是一种较为新型的铺设方式,可使用于较深海域,且效率高、成本低、风险小,在长距离、小管径的海底管道铺设中有明显优势,近年来逐渐成为了研究的热点。
在卷管铺设施工之前,需要在陆地上将管道卷至卷筒,此时,管道发生了巨大的塑性变形,需要在入水之前对其进行校直处理,消除残余曲率。目前,世界上能进行卷管铺设和具有相关装备设计制造能力的公司都集中在欧美国家,而且都进行了技术封锁,能获取的相关研究资料较少,校直过程相关技术和理论都无法深入了解;国内对卷管铺设法的研究才刚刚起步,还处于研究国外装备技术的阶段[6-7]。国外Das Talukder等[8-9]较早对轴类零件校直过程的变形机理进行了分析。国内对校直的研究主要集中在钢材的轧制行业,钢材在热处理过程中,由于受到了外力、热应力和组织应力的影响,不可避免的会导致钢材的弯曲变形。崔甫[10]最先对校直进行研究,建立了轴类零件校直的数学模型。李俊等[11-12]从校直过程中载荷-挠度关系出发,建立了一套载荷-挠度模型的计算方法,但在实际操作过程中,压力校直很难操作,不易于实际施工需要。此外,人们基于大量实验数据,建立起了基于经验的经验校直公式[13];但经验公式的获取非常艰难,并且对不同的工件需要建立不同的公式,通用性不强。本文针对卷管铺设的实际需求,确立了管道校直方案;基于弹塑性理论,建立起管道校直的理论模型,获得了校直行程计算公式;并通过仿真对理论模型进行了验证。
1 校直方案管道铺设过程中,校直需要满足3个要求:1) 不破坏管道及表面涂层;2) 能实现连续、快速校直;3) 校直过程易实现,操作方便。通过分析研究,确立了如图 1校直方案,校直器由三副履带和校准器组成。校直器工作时,履带1和校准器作为支点,履带3作为中间压点,履带1和履带2加紧管道,防止管端翘起对张紧器产生不利影响。校直器采用履带结构形式,增加了管道接触面积,保护了管道表面涂层。校直时,压点在最大挠度处对管道施加反向行程,管道在外部载荷的作用下,将越过管道的反向屈服点;当卸载后,管道将会发生弹性回弹,当回弹量等于反向弯曲量时,管道则被校直。校准器除了作为校直器支点外,还有另一功能,即将离开滚筒有不同曲率的管道调整为同一曲率,实现对管道的连续快速校直。

|
| 图1 退卷校直过程 Figure 1 Straightening process of reel-off |
为便于分析,对校直过程进行了简化,如图 2所示。δ0是管道在经过校准器曲率调整并发生弹性回弹后的残余挠度,δw为管道在校直过程中的反弯下压量,δΣ为校直过程的全部下压量,它们的数学关系为δΣ=δ0+δw。

|
| 图2 校直原理 Figure 2 Straightening principle |
管道校直的力学行为属于塑性力学问题,为简化研究过程,建立适用于管道校直的理论公式,对管道做出了以下假设[14]:
1) 材料在变形过程中符合伯努利平面假设;
2) 除垂直于截面的应力外,不考虑其他应力条件对屈服条件的影响;
3) 中性轴保持不变;
4) 忽略剪力的影响;
5) 忽略包辛格效应。
材料应力应变关系比较复杂,本文将材料力学性能进行了线性化处理。
2.1 弯矩根据材料力学的相关知识可知,管道弯曲与其所受弯矩息息相关。为得到校直弯矩,建立了管道截面的应力应变模型,如图 3所示,其中,R1和R2为管道的内径和外径,H为整个截面的厚度,Ht为弹性区厚度,c为弹性区最外层与中性层的距离,且c=Ht/2;σs和εt为弹性极限应力和应变;σ和ε为弹性区内任意一点的应力和应变;σ′和ε′为塑性区内任意一点的应力和应变;σh和εh为最外层的应力和应变。可以得到管道的弹性极限弯矩:
| $ {M_t} = \int_A {z\sigma dA} = \frac{{\pi {\sigma _s}R_2^3}}{4}\left( {1 - {\alpha ^4}} \right) $ | (1) |
式中α=R1/R2。

|
| 图3 管道受力模型 Figure 3 Mechanical model of pipe |
管道校直时弯矩的求解有两种情况:如图 3(b),距中性层距离0 < c≤R1;另外一种如图 3(c),距中性层距离R1 < c≤R2。曲率为κ时,距中性层c=εt/κt处的纤维达到初始屈服,κt为弹性极限曲率,则弹区比:
| $ \xi = \frac{c}{{{R^2}}} = \frac{{{\kappa _t}}}{\kappa } $ | (2) |
在卷管铺设中,管道校直受力属于图 3(b)中的模型。在不同材料模型的情况下,求出了管道承受的弯矩。当材料模型为线性强化模型时,线性强化系数:
| $ \lambda = {E_p}/E $ | (3) |
式中:Ep为切线模量,E为弹性模量。
材料模型为理想弹塑性模型时,管道塑性弯矩:
| $ \begin{array}{l} M = {\sigma _s}\left( {5R_2^2 - 2{c^2}} \right){\left( {R_2^2 - {c^2}} \right)^{\frac{1}{2}}}/6 - \\ {\sigma _s}\left( {5R_1^2 - 2{c^2}} \right){\left( {R_1^2 - {c^2}} \right)^{\frac{1}{2}}}/6 + \\ {\sigma _s}R_2^4\left[ {\arcsin \left( {c/{R^2}} \right) - {\alpha ^4}\arcsin \left( {c/{R_1}} \right)} \right]/\left( {2c} \right) \end{array} $ | (4) |
塑弯比m=M/Mt,结合式(1)和(2)可以求得
| $ \begin{array}{l} m = \frac{2}{{\pi \left( {1 - {\alpha ^4}} \right)}}\left[ {\frac{1}{3}\left( {5 - 2{\xi ^2}} \right){{\left( {1 - {\xi ^2}} \right)}^{\frac{1}{2}}} - } \right.\\ \frac{1}{3}\left( {5{\alpha ^2} - 2{\xi ^2}} \right){\left( {{\alpha ^2} - {\xi ^2}} \right)^{\frac{1}{2}}} + \\ \left. {\frac{1}{\xi }\left( {arcsin\xi - {\alpha ^4}\arcsin \frac{\xi }{\alpha }} \right)} \right] \end{array} $ | (5) |
当材料模型选取线性强化模型时,可以分别求得管道的塑性弯矩和塑弯比:
| $\begin{array}{l} M\frac{{{\sigma _s}\left( {1 - \lambda } \right)}}{6}\left[ {\left( {5R_2^2 - 2{c^2}} \right){{\left( {R_2^2 - {c^2}} \right)}^{\frac{1}{2}}} - } \right.\\ \left. {\left( {5{\alpha ^2}R_2^2 - 2{c^2}} \right){{\left( {{\alpha ^2}R_2^2 - {c^2}} \right)}^{\frac{1}{2}}}} \right] + \\ \frac{{{\sigma _s}\left( {1 - \lambda } \right)R_2^4}}{{2c}}\left( {\arcsin \frac{c}{{{R_2}}} - {\alpha ^4}\arcsin \frac{c}{{{R_1}}}} \right) + \\ \frac{{\pi \lambda {\sigma _s}R_2^4}}{{4c}}\left( {1 - {\alpha ^4}} \right) \end{array} $$ | (6) |
| $ \begin{array}{l} m = \frac{1}{\xi } + \frac{2}{{\pi \left( {1 - {\alpha ^4}} \right)}}\left[ {\frac{1}{3}\left( {1 - \lambda } \right)\left( {5 - 2{\xi ^2}} \right)} \right.\\ {\left( {1 - {\xi ^2}} \right)^{\frac{1}{2}}} - \frac{1}{3}\left( {1 - \lambda } \right)\left( {5{\alpha ^2} - 2{\xi ^2}} \right)\\ {\left( {{\alpha ^2} - {\xi ^2}} \right)^{\frac{1}{2}}}\left( {1 - \lambda } \right)\left. {\frac{1}{\xi }\left( {arcsin\xi - {\alpha ^4}\arcsin \frac{\xi }{\alpha }} \right)} \right] \end{array} $ | (7) |
假设管道在弯曲过程中中性层的长度不变,因此中性层的长度可以直接反映出管道弯曲过程中曲率的变化。取管道中性层的单位长度为$ \mathop {oa}\limits^{\frown} $,该弧所对应的弧心角也就是该段的曲率。
假定管道在校直之前的曲率为C0,校直曲率为Cw,校直载荷去除后的弹复曲率为Cf,卸载后的残余曲率为Cc,校直过程中的总弯曲曲率为CΣ,于是有以下关系式:
| $ \left\{ \begin{array}{l} 弹复曲率{C_f} = {C_w} - {C_c}\\ 总弯曲率{C_\sum } = {C_0} + {C_w} \end{array} \right. $ | (8) |
校直时,弹复曲率Cc=0,即Cf=Cw。为了计算方便,将所有曲率都无量纲化,即都除以弹性极限曲率。于是
| $ \left\{ \begin{array}{l} 相对弹复曲率{{\bar C}_f} = {C_f}/{C_t}\\ 相对校直曲率{{\bar C}_w} = {C_w}/{C_t}\\ 相对总弯曲率{{\bar C}_\sum } = {C_\sum }/{C_t} \end{array} \right. $ | (9) |
式中弹性极限曲率为Ct=κt=Mt/EI。

|
| 图4 校直曲率关系 Figure 4 Relationship of straightening curvatures |
总弯曲率CΣ=f(ξ),弹区比ξ=εt/εΣ=Ht/H=1/CΣ,又可以写成弹性弯矩的函数ξ=f(M),于是Cf/Ct=M/Mt=m。因此塑弯比m是相对总弯曲率CΣ的函数,m也相应的是Cw+C0的函数。根据前面的数学关系可知Cw=Cf=m,故可以写出Cw-m=0,把它再写成Cw和C0的函数关系式,即校直曲率方程:
| $ \psi \left( {{{\bar C}_w},{{\bar C}_0}} \right) = 0 $ | (10) |
在校直之前,需要校准器对管道曲率进行调整。校准器曲率为Ca,管道弹性极限曲率为Ct,管道曲率在经过校准器调整后变为C0,即校直前管道的残余曲率,它们之间的数学关系如下:
| $ {C_0} = {C_a} - {C_t} $ | (11) |
对式(11)进行无量纲化处理,可得
| $ {{\bar C}_0} = {{\bar C}_a} - 1 $ | (12) |
线性强化模型和理想弹塑性模型的相对校直曲率分别为
| $ \begin{array}{l} {{\bar C}_w} = \lambda {{\bar C}_\sum } + \frac{2}{{\pi \left( {1 - {\alpha ^4}} \right)}}\left[ {\frac{1}{3}\left( {1 - \lambda } \right)\left( {5 - \frac{2}{{\bar C_\sum ^2}}} \right)} \right.\\ {\left( {1 - \frac{1}{{\bar C_\sum ^2}}} \right)^{\frac{1}{2}}} - \frac{1}{3}\left( {1 - \lambda } \right)\left( {5{\alpha ^2} - \frac{2}{{\bar C_\sum ^2}}} \right)\\ {\left( {{\alpha ^2} - \frac{1}{{\bar C_\sum ^2}}} \right)^{\frac{1}{2}}} + \left( {1 - \lambda } \right)\left( {{{\bar C}_\sum }} \right)\\ \left. {\left( {arcsin\frac{1}{{{{\bar C}_\sum }}} - {\alpha ^4}\arcsin \frac{{\tilde 1}}{{\alpha {{\bar C}_\sum }}}} \right)} \right] \end{array} $ | (13) |
| $ \begin{array}{l} {{\bar C}_w} = \frac{2}{{\pi \left( {1 - {\alpha ^4}} \right)}}\left[ {\frac{1}{3}\left( {5 - \frac{2}{{\bar C_\sum ^2}}} \right)} \right.{\left( {1 - \frac{1}{{\bar C_\sum ^2}}} \right)^{\frac{1}{2}}} - \\ \frac{1}{3}\left( {5{\alpha ^2} - \frac{2}{{\bar C_\sum ^2}}} \right){\left( {{\alpha ^2} - \frac{1}{{\bar C_\sum ^2}}} \right)^{\frac{1}{2}}} + \\ {{\bar C}_\sum }\left. {\left( {arcsin\frac{1}{{{{\bar C}_\sum }}} - {\alpha ^4}\arcsin \frac{{\tilde 1}}{{\alpha {{\bar C}_\sum }}}} \right)} \right] \end{array} $ | (14) |
式中CΣ=Cw+Ca-1。
2.3 校直行程通过前面的理论计算,得到了管道校直曲率,但在实际校直过程中,通过曲率来实现校直,非常不方便,费时费力,可行性不强,而通过对下压量的精确控制,可以实现管道的校直。
由于求出的校直曲率Cw与弹复曲率Cf是相等的,故属于弹性变形。因此校直时的反弯下压量也属于弹性挠度,根据材料力学的挠度计算公式可以求出校直反弯下压量:
| $ {\delta _w} = \frac{{{l^2}M}}{{12EI}} = \frac{{{l^2}}}{{12}}{C_w} = \frac{{{l^2}}}{{12}}{C_t}{{\bar C}_w} $ | (15) |
式中l为支点距离。
因此,可以得到中间压点履带的校直行程:
| $ {\delta _\sum } = {\delta _0} + \frac{{{l^2}}}{{12}}{C_w} = {\delta _0} + \frac{{{l^2}}}{{12}}{C_t}{{\bar C}_w} $ | (16) |
校直曲率Cw是校直过程中一个重要参数,直接决定了校直行程的大小,影响到校直效果的好坏,因此对材料参数、几何参数对管道校直曲率的影响程度进行了讨论。讨论中,选取材料为X60,屈服强度σs=414 MPa,杨氏模量E=207 GPa。
材料应力-应变关系直接决定了海底管道的弯曲力学性能。卷管铺设中,管道截面塑性变形所占比例很大,不同的材料模型是否对管道校直曲率有所影响。由图 5可知,两种材料模型下的校直曲率几乎完全一样,为减小计算量,可忽略切线模量Ep,采用理想弹塑性材料模型。

|
| 图5 材料本构模型对管径与校直曲率关系的影响 Figure 5 Influence of material constitutive model on relation of diameter and Cw |
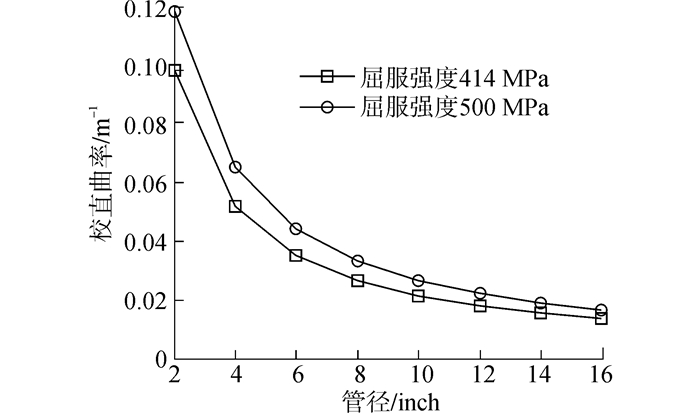
屈服强度是材料的一个重要参数,随着屈服强度的增加,管道承受弯矩的能力也在逐步加强。从图 6可以看出,材料屈服强度增加时,对小管径管道的校直曲率影响更大;而随着管径的增加,这种影响越来越小。
|
| 图6 屈服强度对管径与校直曲率关系的影响 Figure 6 Influence of yield stress on relation of diameter and Cw |
径厚比(D/t)作为海底油气管最为重要的几个参数之一,对管道的力学性能有着重大的影响。由图 7可知,径厚比对校直曲率有一定的影响,但是随着管径的增加,这种影响越来越小。海底管道对残余曲率要求较高,为了校直的精度,因此需要考虑径厚比对管道校直曲率的影响。

|
| 图7 径厚比对管径与校直曲率关系的影响 Figure 7 Influence of D/t on relation of diameter and Cw |
通过以上比较不难发现,管道材料的应力应变模型对校直曲率几乎没有影响,因此,为减小校直过程的计算量,可以采用理想弹塑性模型;而管径、材料屈服强度和径厚比,对管道校直曲率影响比较大。
4 算例算例中,选择外径为4inch和8inch管道。校准器直径D=18 m。为减小计算量,仿真过程中,取支点距离为管径的6倍。管道1~4号管径为4 inch,其中1、2号材料为X60,3、4号为X65;5~8号管径为8inch,其中5、6号材料为X60,7、8号为X65。X65屈服强度σs=448 MPa,杨氏模量E=207 GPa。
有限元分析采用ANSYS软件,采用Brick 8 Node 185实体单元,材料模型选取理想弹塑性等向强化模型。由于对称的关系,取其四分之一模型,以减少计算量。其加载过程分为4步:
1) 施加弯曲载荷,使管道弯曲曲率与校准器调整曲率相同,模拟实际过程中的校准过程;
2) 卸载,模拟实际过程中的弹性回复;
3) 位移加载,模拟实际过程中的校直过程;
4) 卸载,弹性回复。
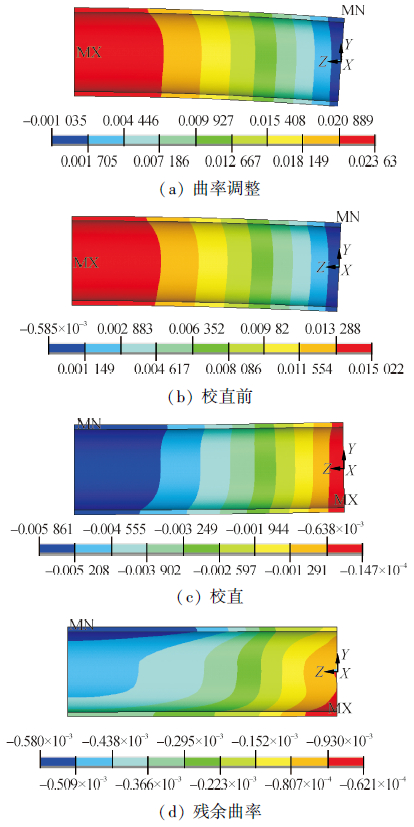
图 8中的变形云图分别反映了管道所经历的4个过程。通过仿真实验,得到了所有管道的校直行程,并与理论计算进行了比较,具体详见表 1。从表中可以看出:1) 理论模型计算和仿真得到的校直行程比较吻合,尤其当管径较大时,误差更小,理论结果和仿真结果之间的误差在6%以内,证明该理论模型对卷管铺设施工的校直过程具有指导意义;2) 仿真结果相对于理论值偏大,因为理论模型是基于弹塑性力学的相关假设建立起来的,只考虑了管道的轴向受力,而在仿真中,管道是三维受力,使得管道在相同校直行程时,变形曲率小于校直曲率,因此需要更大的校直行程才能将管道校直。
|
| 图8 有限元仿真 Figure 8 FEM simulation |
| 编号 | 理论值 | 校直行程 | ||
| 校直曲率 | 校直行程 | ANSYS/mm | 误差/% | |
| 1 | 0.051 9 | 4.94 | 5.19 | 4.82 |
| 2 | 0.051 4 | 4.92 | 5.15 | 4.46 |
| 3 | 0.055 9 | 4.96 | 5.26 | 5.70 |
| 4 | 0.055 4 | 4.95 | 5.22 | 5.17 |
| 5 | 0.026 5 | 20.28 | 20.81 | 2.55 |
| 6 | 0.026 2 | 20.25 | 20.83 | 2.78 |
| 7 | 0.028 5 | 20.23 | 20.78 | 2.65 |
| 8 | 0.028 3 | 20.21 | 20.77 | 2.70 |
针对卷管铺设实际需要,确立了校直方案;基于弹塑性理论,建立起管道校直的理论模型,获得了校直行程计算公式;并通过仿真对理论模型进行了验证。得到以下结论:
1) 切线模量Ep对校直曲率的影响很小,为减小计算量,可忽略Ep而采用理想弹塑性材料模型;
2) 校直理论模型计算的校直行程与仿真结果相比误差较小,在6%以内,证明了本文提出校直理论模型的正确性,可为卷管铺设中管道校直提供理论参考;
3) 理论模型计算的校直行程相对于仿真结果偏小。
| [1] | LI Zhigang, WANG Cong, HE Ning, et al. An overview of deepwater pipeline laying technology[J]. China ocean engineering, 2008, 22(3): 521–532. |
| [2] | BECK R, LIAPIS S. Transient motions of floating bodies at zero forward speed[J]. Journal of ship research, 1987, 31(3): 34–48. |
| [3] |
郭艳林, 梁政. 海底管道铺设施工设计分析[J].
石油学报, 1999, 20(4): 83–87.
GUO Yanlin, LIANG Zheng. Design and analysis of laying for submarine pipeline[J]. Acta petrolei sinica, 1999, 20(4): 83–87. |
| [4] |
党学博, 龚顺风, 金伟良, 等. 海底管道铺设技术研究进展[J].
中国海洋平台, 2010, 25(5): 5–10.
Xuebo, GONG Shunfeng, JIN Weiliang, et al. Research progress on submarine pipeline laying technology[J]. China offshore platform, 2010, 25(5): 5–10. |
| [5] |
黄维平, 曹静, 张恩勇. 国外深水铺管方法与铺管船研究现状及发展趋势[J].
海洋工程, 2011, 29(1): 135–142.
HUANG Weiping, CAO Jing, ZHANG Enyong. State of the art and developing trend of deepwater pipelaying and pipelaying vessel abroad[J]. The ocean engineering, 2011, 29(1): 135–142. |
| [6] | 叶玮. 海底管道新型铺管方法-卷管法的施工技术研究[D]. 杭州: 浙江大学, 2006: 6-9. YE Wei. Study on new pipe-laying technique-Reel lay method[D]. Hangzhou: Zhejiang University, 2006: 6-9. |
| [7] |
党学博, 龚顺风, 金伟良, 等. 深水海底管道极限承载能力分析[J].
浙江大学学报: 工学版, 2010, 44(4): 778–782.
DANG Xuebo, GONG Shunfeng, JIN Weiliang, et al. Analysis on ultimate bearing capacity of deepwater submarine pipe[J]. Journal of Zhejiang university: engineering science, 2010, 44(4): 778–782. |
| [8] | DAS TALUKDER N K, SINGH A N. Mechanics of bar straightening, Part 1: general analysis of straightening process[J]. Journal of engineering for industry, 1991, 113(2): 224–227. |
| [9] | DAS TALUKDER N K, SINGH A N. Mechanics of bar straightening, Part 2: straightening in cross-roll straighteners[J]. Journal of engineering for industry, 1991, 113(2): 228–232. |
| [10] | 崔甫. 矫直理论与参数计算[M].2版. 北京: 机械工业出版社, 1994: 78 -88. |
| [11] |
李俊, 邹慧君, 熊国良, 等. 压力校直过程的理论模型研究及其实验验证[J].
机械强度, 2005, 27(5): 636–639.
LI Jun, ZOU Huijun, XIONG Guoliang, et al. Research on theoretical model of press straightening and its experiment[J]. Journal of mechanical strength, 2005, 27(5): 636–639. |
| [12] | 李骏. 基于校直过程模型的校直工艺理论及实验研究[D]. 上海: 上海交通大学, 2005: 14-20. LI Jun. Study on theory and experiment of press straightening technology based on straightening process model[D]. Shanghai: Shanghai Jiao Tong University, 2005: 14-20. |
| [13] |
高展, 刘春旭, 朱世忠, 等. 钢管压力矫直行程计算公式的理论研究[J].
宝钢技术, 2009(1): 52–55.
GAO Zhan, LIU Chunxu, ZHU Shizhong, et al. Theoretical research on formula of press straightening stroke of steel tubes[J]. Baosteel technology, 2009(1): 52–55. |
| [14] |
弓海霞, 闫通海, 王进礼. 钻具校直的理论研究[J].
哈尔滨工程大学学报, 2002, 23(3): 116–119.
GONG Haixia, YAN Tonghai, WANG Jinli. Straightening of drill pipe[J]. Journal of Harbin engineering university, 2002, 23(3): 116–119. |



