2. Rugao Maritime Safety Administration, Rugao 226500, China
现代船舶、海洋平台及其他大型海洋结构物大多使用钢结构,裂纹的出现对钢结构的极限强度有极大的削弱作用,传统的规范设计法没有考虑渐进裂纹损伤的影响,因此并不能在设计阶段给出结构寿命周期内的真实强度。船舶结构在逐渐增加的外载作用下,受压的结构逐步屈曲变形,船体并不是瞬间整体失效,在结构整体崩溃之前未屈曲的结构可以继续承载失效构件转嫁来的载荷[1],直至船体达到其极限承载能力而崩溃破坏。目前,各大船级社开始注重船舶结构极限强度在设计中的应用,并考虑损伤结构的极限承载能力。对于工作环境较为恶劣的船舶与海洋工程结构来说,极限承载能力的研究为结构设计提供参考,如DNV船级社已经针对FPSO极限强度校核方面提出了要求[2],船舶共同规范(CSR)规定船舶设计过程必须考虑服务、极限、疲劳、破损四种极限状态,由此可见船舶与海洋工程结构设计正逐渐跨入基于极限强度的(ultimate strength design)阶段。极限强度设计的目标就是准确把握结构的极限承载力,在满足安全性的前提下提高结构材料的利用率[3]。加筋板作为船舶及海洋结构的基本组成单元,研究其在裂纹损伤影响下的极限强度就显得十分必要。
许多国内外专家已使用非线性有限元分析法对板/加筋板的极限强度进行了研究。初始缺陷将会影响板格以及加筋板的非线性屈曲模式,且多种复杂载荷的作用将会降低结构的极限强度[4-5],文献[6]综合上述因素,开展具有初始变形缺陷的加筋板在轴向载荷和侧向压力同时作用下的极限强度分析,并通过与规范结果比较验证了非线性有限元方法的正确性。同时初始缺陷也会影响结构的后屈曲模式,开展了船体结构经历极限强度后非线性承载阶段的结构承载能力的计算[7]。目前已有关于裂纹损伤下板或是加筋板的极限强度的研究成果,如长裂纹损伤下钢板的轴向压缩载荷下的剩余极限强度[8],边缘、中心裂纹损伤下的加筋板的破坏特性及模式的研究,并探讨了裂纹方向的影响[9]。
本文运用非线性有限元法进行具有初始变形缺陷的含裂纹加筋板模型的剩余极限强度研究,并与试验结果进行比较,探讨了不同裂纹长度、倾角和位置的加筋板剩余极限承载能力,获得了裂纹加筋板模型在无初始缺陷影响和具有初始位移缺陷影响的屈曲模式,以及后屈曲过程的应力分布特性。该项研究对分析含裂纹损伤的船舶整体结构剩余极限强度具有重要的工程指导意义。
1 计算模型裂纹深度在较厚钢结构中一般不超过钢板厚度。但由于材料的不断发展,高强度钢材在现代船舶中大量采用,因此考虑节能、高效,其构件厚度一般较小,而使穿透裂纹在现代船舶结构中较为常见。本文仿真模型为六组穿透裂纹加筋板轴向压缩试验的结构模型,模型边界受力形式及边界条件均为试验中的受力和约束条件,试验总体布置图如图 1所示。加筋板的失效模式与其板格的柔度、加强筋的柔度以及初始缺陷有关,主要有:板格屈服、屈曲、加筋侧倾、梁柱型屈曲等。本文仅仅讨论不同裂纹对于相同尺寸加筋板失效的影响,不涉及加筋板所有失效模式的讨论。

|
| 图1 试验总体布置图 Figure 1 The layout of the test |
其边界条件为简支,设计的工装如图 1所示,约束了板格的板宽度和长度的位移以及加筋沿板宽方向的位移,放松其高度方向的转角。板格两侧不加约束,不会影响应力-应变曲线的变化趋势[10]。
六组加筋板模型几何参数一致,加筋板主板和加筋钢材型号均为Q235,弹性模量E为200 GPa,屈服应力σy为235 MPa,泊松比γ为0.3。加筋主板的长度a=1 500 mm,宽度b=400 mm,厚度t=8 mm,加强筋的高度hw=65 mm,加强筋的厚度tw=6 mm。
Paik在完整矩形板在轴向压缩载荷作用下的极限强度研究时认为其与板的柔度参数β有关[5];同样在加筋板极限强度研究中,也考虑了板的柔度β和加筋柔度λ的影响:
| $\beta =b/t\sqrt{{{\sigma }_{y}}/E}$ | (1) |
| $\lambda =a/\left( \pi r\sqrt{{{\sigma }_{yp}}/E} \right)$ | (2) |
| $r=\sqrt{I/A}$ | (3) |
式中: σyp为加筋板材料弹性极限应力,I为加筋板横剖面转动惯量,A为加筋板横剖面面积。本文中的模型,β为1.714,λ为1.248。
本文共分析了三种不同形式的裂纹加筋板模型,即垂直于加筋的中心穿透裂纹加筋板,相对加筋有一定倾角的中心穿透裂纹加筋板和垂直于加筋的边缘穿透裂纹加筋板。主要用来分析在加筋板长宽比、加筋主板柔度和加筋柔度一致的情况下,不同裂纹长度、位置及角度对加筋板屈曲崩溃模式的影响,裂纹尺寸及位置参数表 1所示。
| 模型 | 裂纹长度cp/mm | cp/b | cp/a | 裂纹类型 |
| 模型1 | 80 | 0.2 | — | 中心穿透 |
| 模型2 | 80 | 0.2 | — | 中心穿透 |
| 模型3 | 120 | 0.3 | — | 中心穿透 |
| 模型4 | 160 | — | 0.107 | 中心穿透 |
| 模型5 | 80 | 0.2 | — | 边缘穿透 |
| 模型6 | 120 | 0.3 | — | 边缘穿透 |
目前,使用计算机资源结合有限元软件分析结构的极限强度取得了一定的进展。该方法的主要思想是通过逐步增加较小的载荷增量进行结构的非线性有限元分析,直到结构达到崩溃,获得每一载荷步下的结构状态,以此来分析结构的极限过程。该方法因具有耗费低、结果分析精度较高的优点而广泛被研究者使用。另外,非线性有限元方法可以模拟具有初始缺陷、复杂边界条件和在载荷作用下的任何结构的变形过程以及屈曲模态,确定结构的极限承载力。
2.1 有限元模型有限元网格精度不仅是保证有限元分析结果收敛的前提,而且与非线性数值分析计算花费时间有很大的关系,网格划分的不同、单元类型的差异、边界条件的设置会对有限元分析结果有一定的影响,四节点四边形壳单元在屈曲计算中具有较好的精度和收敛性。本文有限元分析模型采用4节点shell181单元。根据试验模型参数(见表 1)建立的有限元分析模型如图 2所示。模型划分采用四边形网格,为了得到较为精确的分析结果,对裂纹处网格进行细化处理,其最小尺寸为裂纹的间距,这样可以保证单元的收敛性。其余部分单元网格尺寸的收敛性已在文献[6]中进行了验证。

|
| 图2 含裂纹加筋板有限元模型 Figure 2 FE models of cracked stiffened panels |
现代钢质焊接构件或多或少存在初始缺陷,初始缺陷的产生主要是由于将加强筋焊接到主壳板的过程中结构受热及冷却不均匀造成的。结构初始缺陷一般包括初始变形、残余应力以及初始结构损伤三种形式。焊接初始变形增大了结构的偏心效应,已有研究表明加筋板结构初始变形对其极限强度大小和屈曲模式有着不可忽视的影响[5]。
采用ANSYS自带APDL语言编写程序来模拟加筋板初始形状。加筋板的初始变形分为局部凹凸、加筋横向挠度以及主壳板的纵向弯曲变形。采用三维扫描仪获得主要板格的初始变形,其测点数为11×4。根据试验测量数据模拟加筋板主壳板的初始变形缺陷,初始变形值如图 3所示。

|
| 图3 加筋主板初始缺陷 Figure 3 Initial deformation of main plate of stiffened panels |
实船加筋板结构边界通常受到强构件如纵桁和横梁的支撑,其边界支撑介于简单支撑和固定支持之间。实际的研究中模型边界条件通常认为是简单支撑。在如图 2所示坐标系下,x轴为船长方向,y轴为船宽方向,z轴为型深方向。加筋板设置为沿y轴方向的短边约束、z方向上的线位移和x、z方向的角位移,同试验工况。
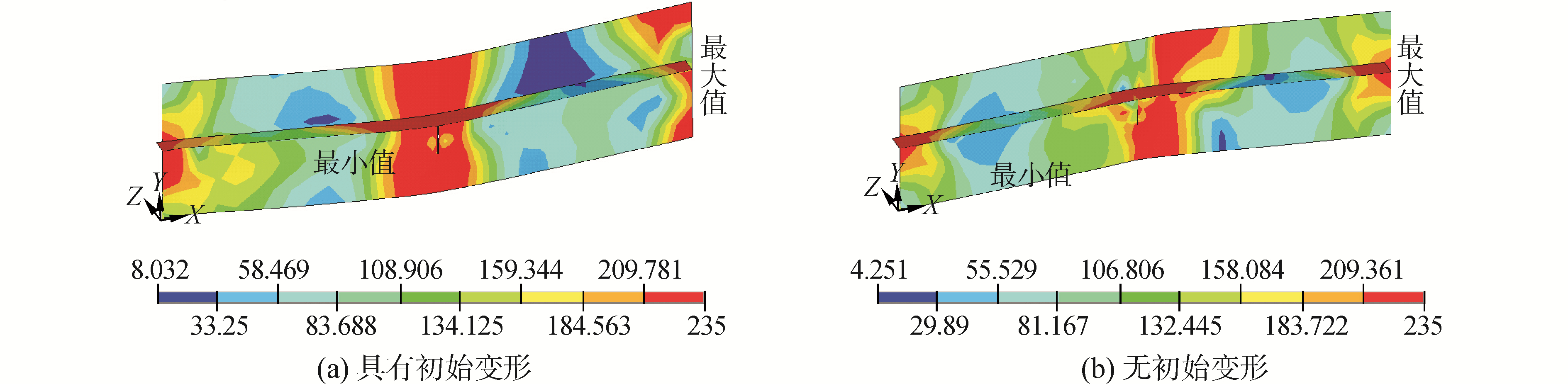
3 有限元与试验结果比较分析图 4、5分别为相对裂纹长度cp/b为0.2和0.3的80 mm和120 mm的中心穿透裂纹加筋板变形和应力分布情况。由于加筋板中部裂纹的存在,破坏了结构完整性,无初始变形的中心穿透裂纹加筋板模型中部应力分布并不对称;具有初始变形的模型在靠近裂纹中部两侧应力小于裂纹尖端其他部位的应力,相对裂纹长度为0.3时该现象更加明显。
|
| 图4 80 mm的中心穿透裂纹加筋板变形和应力分布 Figure 4 Deformed shapes and von mises stress distributions of stiffened panel with 80 mm center crack |

|
| 图5 120 mm中心穿透裂纹加筋板变形和应力分布 Figure 5 Deformed shapes and von mises stress distributions of stiffened panel with 120 mm center crack |
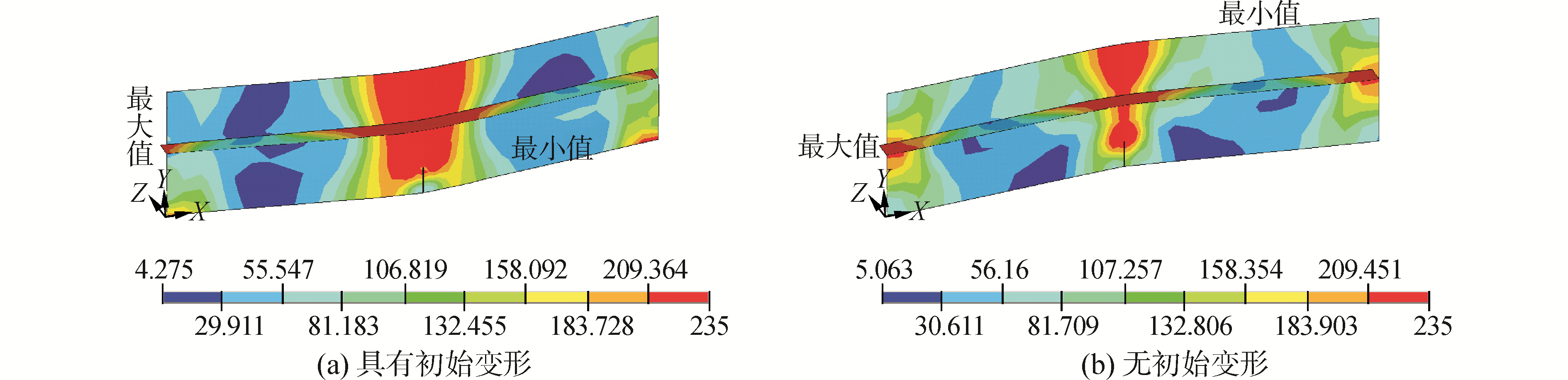
图 6、7分别为相对裂纹长度cp/b为0.2和0.3的80 mm和120 mm边缘穿透裂纹的变形和应力分布图。相比于图 4~5中心穿透裂纹加筋板,无初始变形边缘穿透裂纹加筋板应力大致沿短轴方向中线对称分布,裂纹尖端出现应力集中现象,在无裂纹一侧主壳板中部结构达到材料屈服极限,但靠近加筋部位主壳板屈服范围较小,可见加筋的存在有效承担了外载荷,提高了整体结构的承载能力。有裂纹一侧加筋主壳板从裂纹尖端到加筋范围内的主壳板材料达到屈服极限,沿裂纹长度方向范围内的主壳板应力未达到屈服极限,也即由于边缘裂纹的存在,加筋板中部结构完整性的破坏使其中部承受外载主要依靠连续的部分。
|
| 图6 80 mm的边缘穿透裂纹加筋板变形和应力分布 Figure 6 Deformed shapes and von mises stress distributions of stiffened panel with 80 mm edge crack |
|
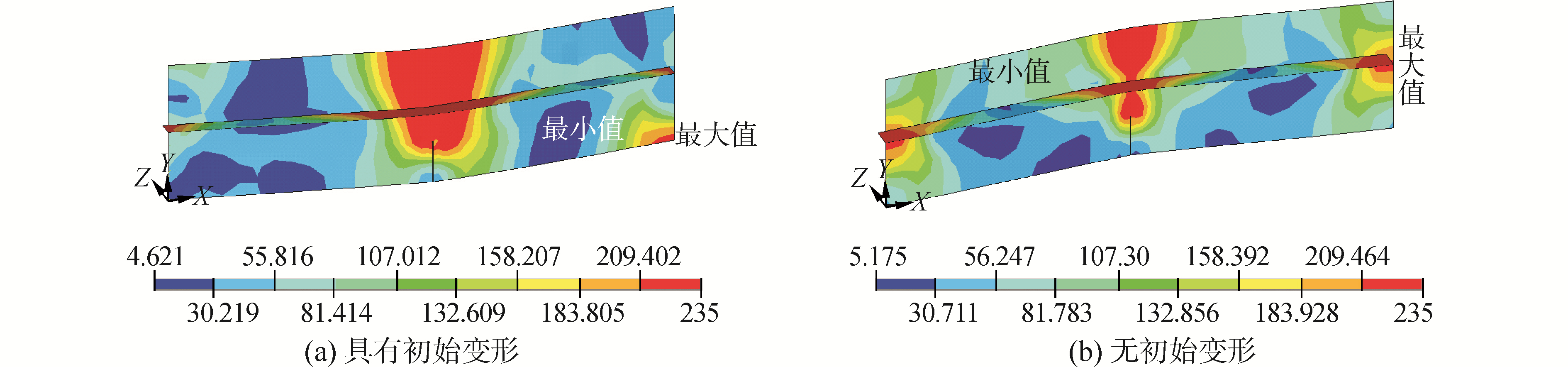
| 图7 120 mm的边缘穿透裂纹加筋板模型变形和应力分布 Figure 7 Deformed shapes and von mises stress distributions of stiffened panel with 120 mm edge crack |
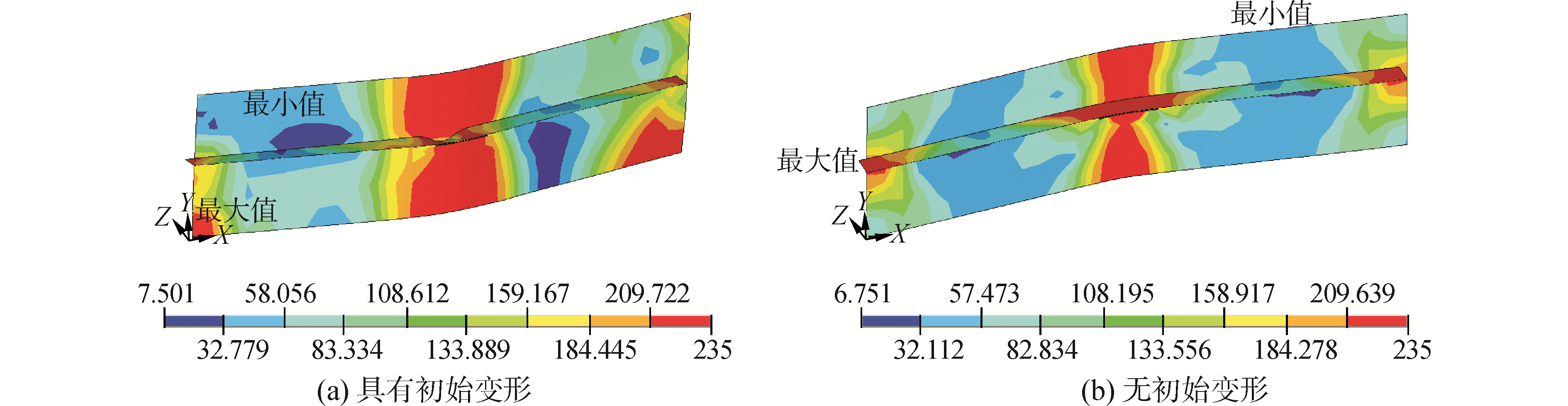
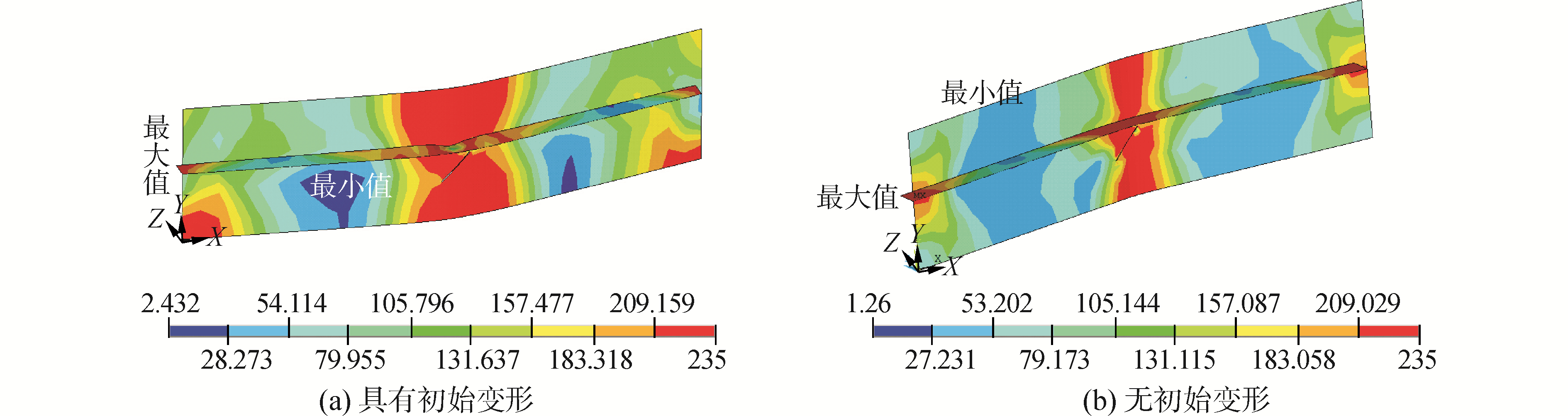
图 8、9分别为裂纹倾角为90°和45°的加筋板在轴向压力作用下的变形及应力分布图,很明显可以看出由于裂纹存在的影响,含裂纹一侧加筋主壳板其应力分布有别于不含裂纹一侧主壳板应力分布,裂纹尖端附近的并未出现应力集中现象,相反沿裂纹长度方向附近应力大于裂纹尖端应力。
|
| 图8 倾斜90°的中心穿透裂纹加筋板模型变形和应力分布 Figure 8 Deformed shapes and von mises stress distributions of center cracked stiffened panel with the angel 90° between crack and longitudinal side |
|
| 图9 倾斜45°的中心穿透裂纹加筋板模型变形和应力分布 Figure 9 Deformed shapes and von mises stress distributions of center cracked stiffened panel with with the angel 45° between crack and longitudinal side |
图 10为倾斜45°角裂纹的加筋板试验模型屈曲变形图,与具有初始缺陷的有限元模型分析屈曲变形(图 9(a))吻合,与图 9(b)比较可以发现初始缺陷的存在对加筋板屈曲失效模式的影响较大,表明有限元方法可较好地模拟具有初始缺陷的加筋板屈曲变形过程。

|
| 图10 倾斜45°的中心穿透裂纹加筋板试验屈曲破坏 Figure 10 Buckling mode of center cracked stiffened panel with angle 45° between crack and longitudinal side |
从图 4~9可以看出无初始变形和具有初始变形加筋板模型屈曲变形朝向截然相反,可见初始变形缺陷的存在增大了结构的偏心效应,进而影响结构发生破坏时的变形方向。
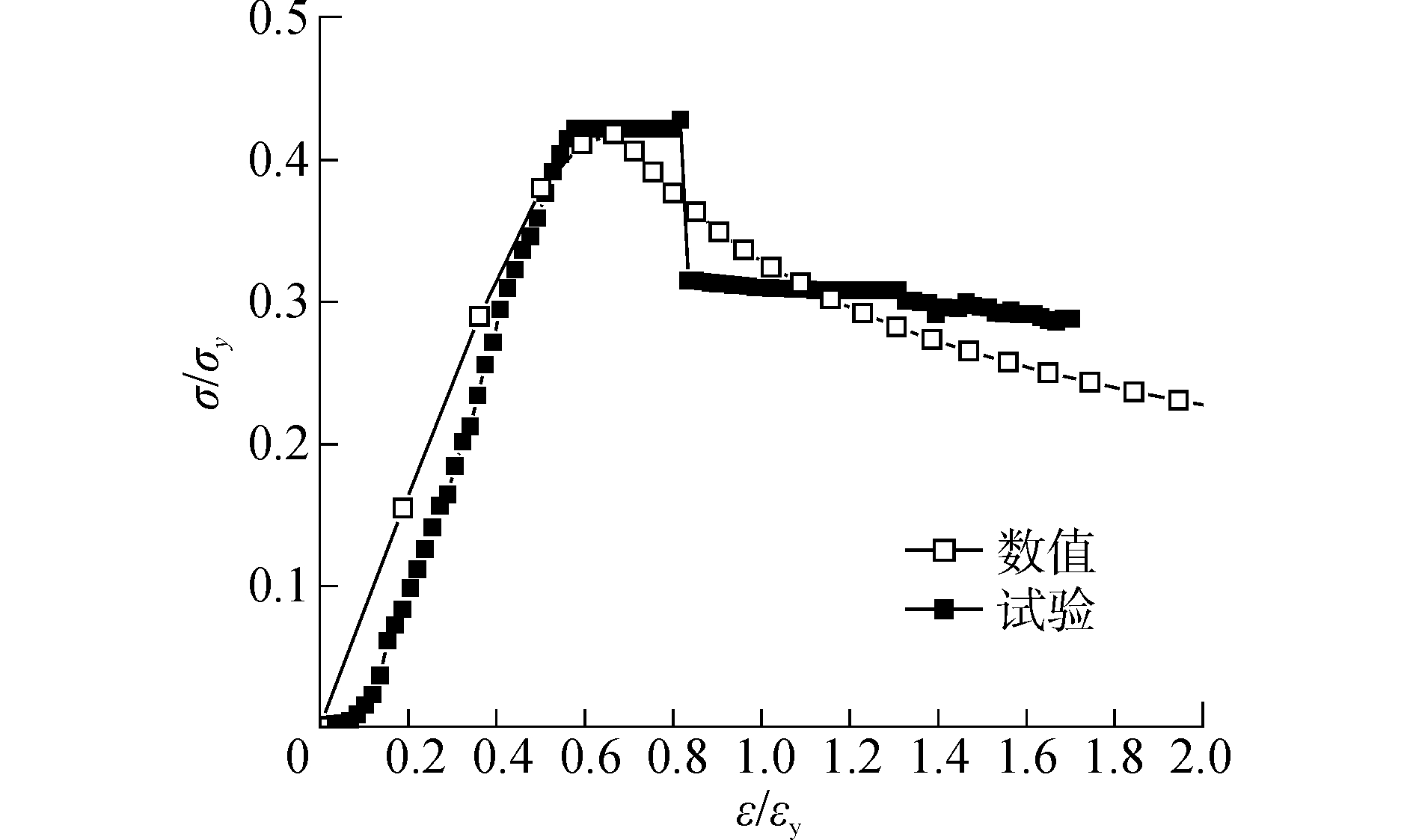
图 11 给出了裂纹损伤模型(模型1)的试验与有限元的结果对比,从图中的应力应变关系可看出,两者吻合的较好,表明数值方法可以很好的模拟裂纹损伤结构的屈曲过程,并能较准确地预报极限强度值。
|
| 图11 模型1的试验与仿真对比 Figure 11 Comprison of the results of model 1 by experiment and numerical method |
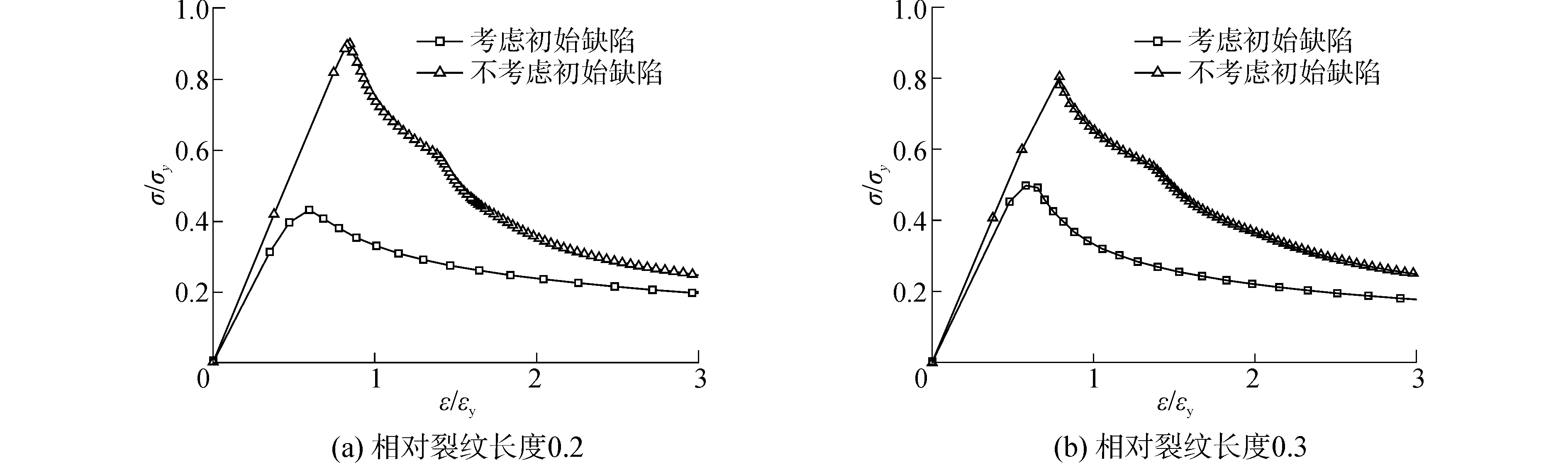
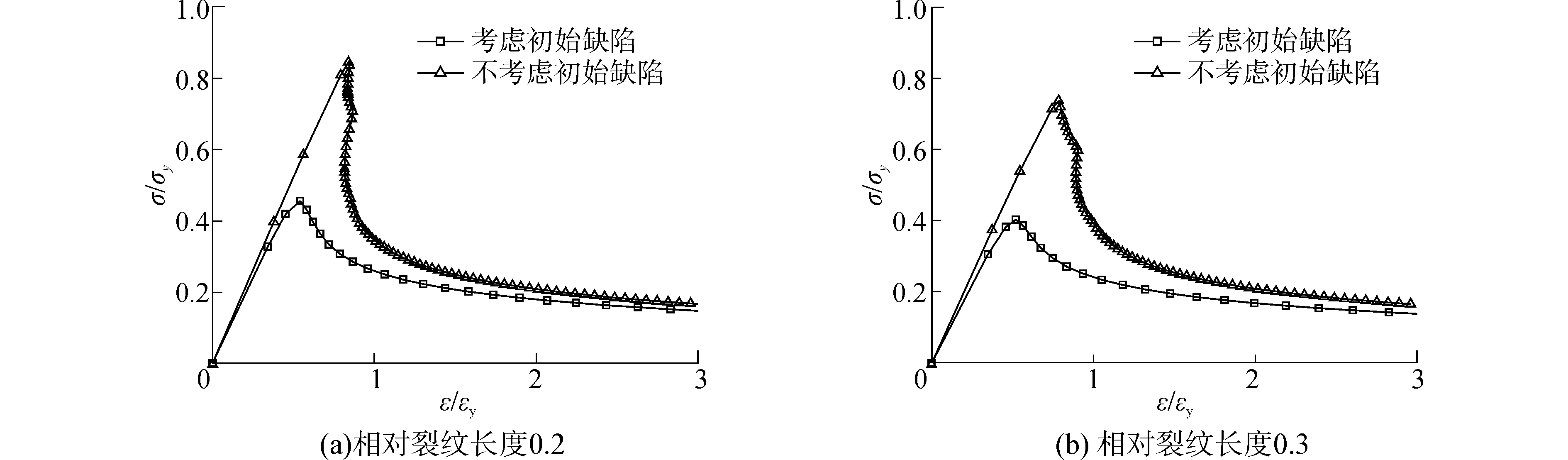
图 12、13分别为中心/边缘穿透裂纹加筋板无量纲应力-应变曲线。从图中可看出,无初始变形的中心裂纹加筋板相对裂纹长度cp/b为0.2、0.3时σ/σy最大值分别为0.899和0.804,边缘穿透裂纹加筋板相对裂纹长度cp/b为0.2、0.3时σ/σy值最大分别为0.844和0.737,也即无论边缘穿透裂纹还是中心穿透裂纹,相对裂纹长度cp/b为0.3时加筋板剩余极限强度小于cp/b为0.2时加筋板的剩余极限强度。当相对裂纹长度相同时,具有边缘穿透裂纹的加筋板剩余极限强度小于中心穿透裂纹加筋板,也即边缘穿透裂纹对结构强度的削弱作用较大。计及初始缺陷对裂纹加筋板的影响时中心穿透裂纹加筋板σ/σy最大值分别为0.430和0.498,边缘穿透裂纹加筋板σ/σy最大值分别为0.520和0.258,与无初始缺陷模型相比,剩余极限承载力大幅下降,由此可见初始缺陷对裂纹加筋板结构极限强度的影响不可忽略。
|
| 图12 80 mm和120 mm中心穿透裂纹加筋板无量纲应力-应变曲线 Figure 12 Stress-strain curves of stiffened plate suffer 80 mm and 120 mm center through-thickness crack |
|
| 图13 80 mm和120 mm边缘穿透裂纹加筋板无量纲应力-应变曲线 Figure 13 Stress-strain curves of stiffened plate suffer edge through-thickness crack 80 mm and 120 mm |
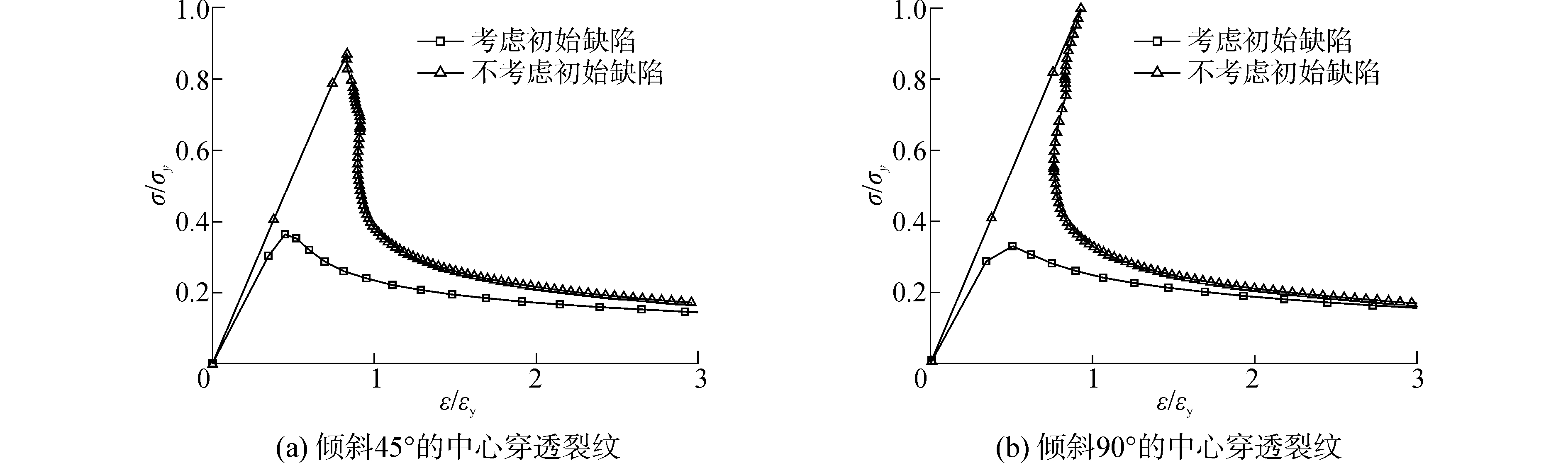
图 14(a)为裂纹倾角45°的加筋板无量纲应力-应变曲线,σ/σy最大值为0.869,计及初始变形缺陷时σ/σy最大值为0.407。图 14(b)为裂纹倾角90°的加筋板无量纲应力-应变曲线,σ/σy最大值为0.998,计及初始变形缺陷时σ/σy最大值为0.427。从图中可看出,在无初始缺陷影响时,纵向裂纹加筋板的极限应力接近材料的屈服应力,可以认为当裂纹分布沿受力方向时,垂直于受力方向的加筋板横剖面面积损失很小,其对极限承载能力的影响较小。
|
| 图14 倾斜45°和90°中心穿透裂纹加筋板无量纲应力-应变曲线 Figure 14 Stress-strain curves of angel 45° and 90° center cracked stiffened model |
一般受压加筋板无量纲平均应力-应变曲线可以近似分为两个阶段:1)在达到极限强度以前载荷随变形呈线性变化的稳定区;2)达到极限承载后,变形继续增加,单元承载能力开始下降的卸载区。从图 12~14可看出,无初始变形缺陷的加筋板在达到极限承载力后的曲线变化较陡,具有初始变形缺陷的加筋板应力-应变曲线在达到极限承载力后曲线变化较为平缓。从图 13可以看出无初始缺陷边缘穿透裂纹加筋板模型在达到极限载荷后继续承载的过程,卸载区曲线变化大致可以分为两段,前一段曲线表明模型随着变形的不断增大,应力逐渐减小,后一段表明模型在变形量不变的情况下,应力继续减小直到某一数值,也即该段加载过程加筋板未发生变形,截面承载能力持续减小到某一平衡点后,应力值随着结构继续变形而逐渐减小。
极限承载力的试验值与有限元分析结果比较如表 2所示。从表中数据可以看出使用非线性有限元方法计算中心穿透裂纹的极限承载能力值与试验结果有较好的吻合度。具有一定裂纹倾角的加筋板模型和边缘裂纹加筋板数值模拟结果在不同程度上与试验结果有一定的误差。造成这一现象的原因主要是:1)试验模型长轴两端模拟处于简单支撑,具体如图 1所示,有限元模拟短边采用简单支撑边界条件,长边固定转角和沿厚度方向的位移,相比之下数值模拟的边界对模型的支撑作用更强。2)在有限元分析时,只考虑了主板上的初始变形,还应计及加强筋的初始变形以及残余应力的影响,这是造成偏差的另一个原因。
| 六种模型 | 试验结果/kN | FEA结果/kN | 误差/% |
| 模型1 | 368.00 | 342.09 | 7.0 |
| 模型2 | 435.00 | 419.89 | 3.5 |
| 模型3 | 376.26 | 343.53 | 8.7 |
| 模型4 | 399.90 | 359.51 | 10.1 |
| 模型5 | 482.50 | 439.08 | 9.0 |
| 模型6 | 246.30 | 217.73 | 11.6 |
本文采用试验和非线性有限元法对具有初始缺陷的含裂纹加筋板在轴向压缩载荷作用下的极限强度进行分析。为了研究裂纹参数对加筋板极限强度的影响规律,分别对六个几何尺寸相同的加筋板模型在不同裂纹长度、位置及倾角的影响下受轴向压缩载荷时的屈曲变形过程进行数值仿真,得到了裂纹加筋板模型的应力分布及屈曲模态,并与试验结果进行比较,得出以下结论:
1) 与实验结果相比,数值模拟方法可以很好地模拟具有初始缺陷的裂纹损伤加筋板的屈曲过程,较为准确地预报其极限强度。
2) 加筋板的屈曲变形破坏是一个渐进过程,结构无裂纹缺陷的部位主要承载施加在模型上的外载荷,相比于完整加筋板,裂纹的存在改变了结构的应力分布,削弱了结构的极限承载能力。在不考虑初始变形的情况下,无论中心穿透裂纹还是边缘穿透裂纹,加筋板的剩余极限强度随着裂纹长度的增加而减小。
3) 初始变形缺陷的存在明显改变了结构的屈曲模式,不仅结构的屈曲变形更加明显,而且大大削弱了加筋板的极限强度。
4) 压缩载荷作用下裂纹损伤加筋板的崩溃过程中,由于初始缺陷等因素的影响,裂纹并未闭合而不可忽略其影响。研究表明,裂纹的存在对于结构的压缩极限强度有一定的影响,但与拉伸载荷下结构极限强度相比较,其折减规律更为复杂。
| [1] |
隋智享. 船舶与海洋工程结构极限强度分析[D]. 大连:大连理工大学, 2004.
SUI Zhixiang. Study of ultimate strength of ship and ocean engineering[D]. Dalian:Dalian University of Technology, 2004. |
| [2] |
王璞. 极限强度在FPSO总纵强度规范校核中的应用[J].
上海造船, 2006(3): 12–15.
WANG Pu. Application of ultimate strength assessment in global strength rule check for FPSO[J]. Shipbuilding of Shanghai, 2006(3): 12–15. |
| [3] |
谢仲安. 舱段极限强度试验模型设计研究[D]. 上海:上海交通大学, 2010.
XIE Zhong'an. Study on design of ultimate strength testing cabin model[D]. Shanghai:Shanghai Jiaotong University, 2010. |
| [4] |
张涛, 刘土光, 赵耀, 等. 初始缺陷加筋板的屈曲与后屈曲分析[J].
船舶力学, 2003, 7(1): 79–83.
ZHANG Tao, LIU Tuguang, ZHAO Yao, et al. Buckling and postbuckling of imperfect stiffened plates[J]. Journal of ship mechanics, 2003, 7(1): 79–83. |
| [5] |
崔虎威, 杨平. 复合受力作用下的板格和加筋板的极限强度计算与研究[J].
武汉理工大学学报:交通科学与工程版, 2012, 36(3): 496–500.
CUI Huwei, YANG Ping. Calculation and research on ultimate strength of panels and stiffened-plates under combined loads[J]. Journal of Wuhan university of technology:transportation science & engineering, 2012, 36(3): 496–500. |
| [6] |
张婧, 施兴华, 顾学康. 具有初始缺陷的船体加筋板结构在复杂受力状态下的极限强度研究[J].
中国造船, 2013, 54(1): 60–70.
ZHANG Jing, SHI Xinghua, GU Xuekang. Ultimate strength study of stiffened plate under complex loading with initial imperfections[J]. Shipbuilding of China, 2013, 54(1): 60–70. |
| [7] |
丁超, 赵耀. 船舶总纵极限强度后剩余承载能力有限元仿真方法研究[J].
中国造船, 2014, 55(1): 54–65.
DING Chao, ZHAO Yao. Simulation of ship residual carrying capacity after longitudinal ultimate strength[J]. Shipbuilding of China, 2014, 55(1): 54–65. |
| [8] | PAIK J K. Residual ultimate strength of steel plates with longitudinal cracks under axial compression-Nonlinear finite element method investigations[J]. Ocean engineering, 2009, 36(3/4): 266–276. |
| [9] |
张琴, 肖桃云, 刘敬喜. 均匀受压含裂纹损伤加筋板的极限承载能力分析[J].
中国舰船研究, 2011, 6(5): 16–22.
ZHANG Qin, XIAO Taoyun, LIU Jingxi. Ultimate strength analysis of cracked stiffened plates under uniaxial compression loads[J]. Chinese journal of ship research, 2011, 6(5): 16–22. |
| [10] | CHEN Qishi, ZIMMERMAN T, DEGEER D, et al. Strength and stability testing of stiffened plate components[R]. Ship Structural Committee Report SSC-399, 1997. |



