2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
随着海洋资源开发受到世界各国的高度重视,高速水声通信、远程探测声呐等水声技术得到快速发展,其中宽带信号在声学设备中被广泛采用。宽带换能器和宽带发射系统成为声呐系统设计的重要组成部分,如何扩展工作频带且保证波形失真度成为关键技术。另外一些采用电池供电的声呐设备如水声浮标、便携式通信声呐,由于能源有限要求发射系统具有较高的发射效率,因此实际的声呐设备要求发射系统不仅具有宽的工作频带还要具有较高的功率因数和理想的发射波形[1-3]。
为提高声呐发射系统的效率,必须实现换能器与声呐功放的良好匹配。对于压电陶瓷换能器而言,其阻抗特性会随着频率的变化而变化,且很难用解析函数来表示,因此想要在较宽频带范围内达到良好的宽带匹配效果是很困难的。目前水声换能器宽带匹配电路常采用单点谐振方式达到可用带宽或采用多谐振法在换能器的工作频段内构造几个谐振峰以完成匹配电路设计,但实际的匹配效果远没有达到预期。在无线电领域,天线宽带匹配理论与方法得到了很好的发展,结合计算机辅助设计(CAD)技术,包括实频数据法,Smith圆图法及遗传算法等一系列宽带匹配方法在天线宽带匹配以及微波放大器方面得到广泛的应用并取得了较好的效果[4-6],采用CAD技术对水声换能器的匹配电路进行设计的研究则相对较少。 预均衡技术通常应用于通信系统中,是指发射机利用有关信道的先验信息预先对将要发射的信号进行处理,以克服信道多途扩展等因素导致的码间干扰,从而简化接收机结构[7]。近年来,已有学者将均衡技术应用于换能器发射信号的补偿中。文献[8]在功率放大器前加入与换能器频响互补的均衡电路,减少高速数字传输系统的码间干扰;文献[9]研究了数字均衡器的特点,并将其引入到宽带接收系统中用于补偿匹配换能器;文献[10]采用分段快速傅里叶正反变换和频率能量补偿技术实现回声转发信号的发射声源级补偿,以上文献取得了较好的效果,但均从频域的角度对信号进行均衡处理,并未对系统的工作效率进行论述。
本文从声呐系统的整体角度进行考虑,联合实频数据和预均衡技术对宽带声呐系统进行设计,使发射系统在整个工作频带内达到较高的工作效率和较低的波形失真度。本文首先给出发射系统的设计思想,其次对换能器的宽带匹配电路进行设计,并对预均衡器设计方法进行仿真,最终在消声水池对发射系统的匹配效率和发射波形进行测试。
1 发射系统匹配均衡设计 1.1 基本思想一般声呐发射接收系统的组成如图 1所示,发射系统由功率放大器、匹配网络和换能器组成。在发射系统设计过程中,多通过设计合理的匹配电路以改善系统工作效率、带宽及波形失真度,但实际的设计效果一般难以达到预期,计算过程较为复杂。

|
| 图1 一般声呐收发系统组成框图 Figure 1 Block diagram for general sonar transceiver system |
率并扩展带宽,简化传统匹配设计过程中繁琐的计算过程。匹配后的系统发射波形相比匹配前虽有明显改善,但相比理想波形依然存在较大的失真。因此在匹配电路设计完成后,再采用预均衡技术对发射系统的冲激响应函数进行准确估计,并构造与冲激响应互逆的预均衡器,实现对发射信号波形的补偿,降低发射波形失真度。通过采用实频数据技术和预均衡技术的联合设计技术可以有效保证声呐发射系统的工作效率、带宽及波形失真度。 宽带匹配的基本原理已有很多学者进行过论述[1-3],在此不再赘述,下面给出预均衡技术的基本思想。为方便定性的研究现做如下假设:1)水声信道为理想信道;2)功率放大器、水听器和测量放大器在信号带宽内幅频响应平坦,相位响应线性;3)匹配网络和换能器均为线性系统,两者整体的冲激响应函数为h[n]。 换能器的发射信号y[n]为理想激励信号x[n]与匹配网络和换能器的冲击响应函数h[n]的线性卷积:
| $y\left[ n \right]=x\left[ n \right]\otimes h\left[ n \right]$ | (1) |
为了消除匹配网络和换能器对理想激励信号造成的影响,必须对两者的整体冲激响应函数进行准确估计,构造与之相对应的逆系统。利用均衡算法对h[n]进行估计,根据估计的系统冲激响应函数
| $w[n]={{\hat{h}}^{*}}[-n]$ | (2) |
预均衡原理如图 2所示,理想激励信号首先经过预均衡器进行预处理,然后依次通过功放、宽带匹配网络,最后经过换能器将信号辐射到水中,此时发射的信号yeq[n]为均衡后的信号。均衡后的发射信号与理想激励信号的差异主要取决于匹配网络和换能器的冲激响应函数估计的准确性:
| ${{y}_{eq}}\left[ n \right]=x\left[ n \right]\otimes w\left[ n \right]\otimes h\left[ n \right]\approx x\left[ n \right]$ | (3) |

|
| 图2 预均衡原理图 Figure 2 Schematic diagram of pre-equalization |
以下小节将结合具体的通信声呐的发射系统的实际需求,对其发射系统进行设计。
1.2 宽带匹配电路设计 1.2.1 实频数据技术实频数据技术作为一种计算机辅助设计技术在天线宽带匹配网络设计方面取得了广泛的应用,其核心思想是将待设计的阻抗匹配网络利用其策动点函数来表示,而系统的功率传输增益可以由该函数和实际的负载阻抗数据以简单的函数形式表达;然后对该函数进行优化,得到系统的最优功率传输增益,并给出优化后的策动点函数,由最终的策动点函数综合出工程中易于实现的匹配网络。实频数据技术无需负载阻抗的等效电路模型以及解析表达式,也无需选定匹配网络的拓扑结构,整个计算过程全部由计算机完成,因此非常适合于实际工程应用。实频数据技术主要包括:原始实频法、直接实频法和简易实频法。本文采用直接实频数据法对换能器的宽带匹配电路进行设计。
对于一般的双匹配问题如图 3所示,EG为理想电压源,输出阻抗为ZG,E为无损二端口匹配网络,Zq1为由信号源向负载端看去的匹配网络阻抗,Zq为匹配网络的策动点阻抗函数,负载阻抗为ZL。ρl为复数归一化反射系数,SG为信号源端的单位归一化反射系数,Sin为匹配网络输入端的单位归一化反射系数。
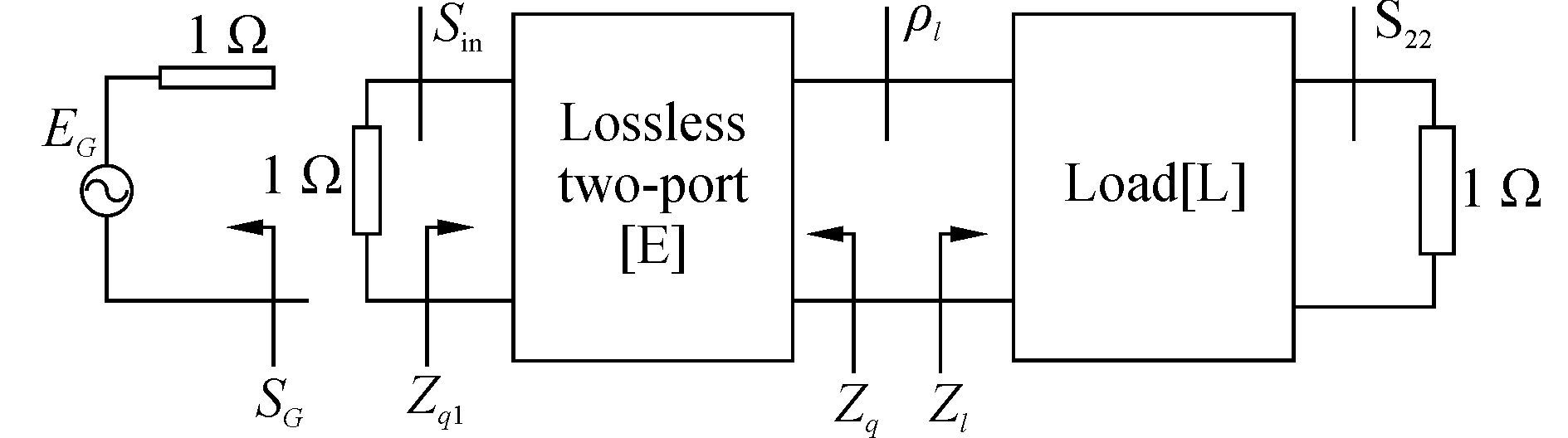
|
| 图3 双匹配连接示意图 Figure 3 Diagram for double matching connection |
根据图 3给出的双匹配连接示意图,系统功率传输增益(transducer power gain,TPG)表达式为
| $T\left( \omega \right)=\frac{\left( 1-{{\left| {{S}_{G}} \right|}^{2}} \right)\left( 1-{{\left| {{S}_{in}} \right|}^{2}} \right)}{{{\left| 1-{{S}_{G}}Sin \right|}^{2}}}$ | (4) |
由Yarman的理论证明可知[11],Sin表达式为
| ${{S}_{in}}=\frac{{{h}_{q}}\left( -s \right)}{{{h}_{q}}\left( s \right)}\cdot \frac{{{Z}_{l}}\left( s \right)-{{Z}_{q}}\left( -s \right)}{{{Z}_{l}}\left( s \right)+{{Z}_{q}}\left( s \right)}\text{ }$ | (5) |
式中:hq(s)满足hq(s)·hq(-s)=EV{Zq(s)}的关系式,hq(s)与策动点阻抗函数的实部RB(s2)之间满足如下关系式:
| ${{R}_{q}}\left( {{s}^{2}} \right)={{E}_{V}}\{{{Z}_{q}}\left( s \right)\}=\frac{{{n}_{q}}\left( s \right){{n}_{q}}\left( -s \right)}{{{b}_{q}}\left( s \right){{b}_{q}}\left( -s \right)}={{h}_{q}}\left( s \right){{h}_{q}}\left( -s \right)$ | (6) |
| ${{h}_{q}}\left( s \right)=\frac{{{n}_{q}}\left( -s \right)}{b\left( s \right)}$ | (7) |
式中:nq(-s)为Rq(s2)的分子多项式右半平面和jω轴上的根构成的胡维兹多项式;b(s)为Rq(s2)的分母多项式左半平面的根构成的胡维兹多项式。
故系统的功率传输增益表达式唯一地由一个以电阻为终端的匹配网络的策动点阻抗函数Zq(s)所决定,假设Zq(s)为最小函数,即满足Zq(s)=Rq(s)+jXq(s)=Rq(s)+j·Hilbert{Rq(s)}。
因此宽带匹配的唯一未知问题为Rq(s)表达式。为得到工程中便于实现的匹配电路,采用的有理函数表达式:
| $\begin{matrix} {{R}_{q}}\left( {{\omega }^{2}} \right)=\frac{{{A}_{0}}{{\omega }^{2\cdot ndc}}\prod\limits_{i=1}^{nz}{{{\left( {{\omega }^{2}}_{i}-{{\omega }^{2}} \right)}^{2}}}}{{{B}_{1}}{{\omega }^{2n}}+{{B}_{2}}{{\omega }^{2(n-1)}}+\ldots +{{B}_{n}}{{\omega }^{2}}+1}= \\ \frac{A\left( {{\omega }^{2}} \right)}{B\left( {{\omega }^{2}} \right)}\ge 0,\forall \omega \\ \end{matrix}$ | (8) |
式中:
| $B\left( {{\omega }^{2}} \right)=\frac{1}{2}\left[ {{c}^{2}}\left( \omega \right)+{{c}^{2}}\left( -\omega \right) \right]>0$ | (9) |
| $c\left( \omega \right)={{c}_{1}}{{\omega }^{n}}+{{c}_{2}}{{\omega }^{(n-1)}}+\ldots +{{c}_{n}}\omega +1$ | (10) |
这样,在设定目标功率传输增益T0以及阻抗函数实部Rq的相关系数(cj,j=1,2,…,n}和A0后,可以得出误差函数ε表达式:
| $\varepsilon =\frac{\left( 1-\left| {{S}_{G}}^{2} \right| \right)(1-{{\left| {{S}_{in}} \right|}^{2}})}{{{\left| 1-{{S}_{G}}{{S}_{in}} \right|}^{2}}}-{{T}_{0}}$ | (11) |
采用非线性最小二乘算法优化误差函数,完成增益优化后即可得到匹配网络的策动点阻抗函数Zq(s),最后将有理函数进行综合,得到以电阻为终端的无损宽带匹配网络。
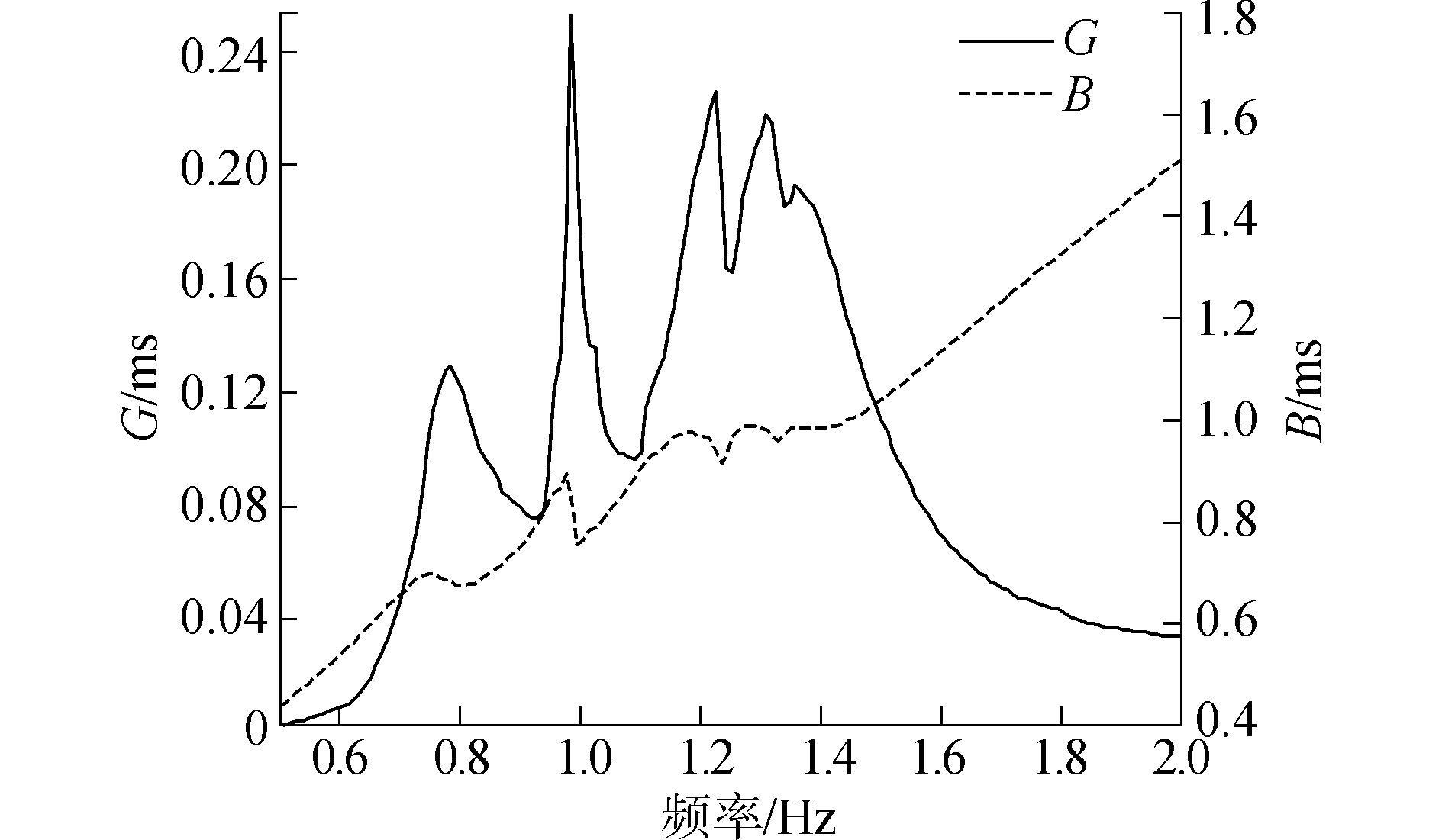
1.2.2 匹配电路设计现在利用直接实频数据法对某通信系统中的耐压圆管换能器的匹配电路进行设计。该换能器使用的工作频率范围9~14kHz,换能器并联等效模型下的导呐特性曲线如图 4所示。区别于传统的单谐振换能器,该换能器存在多个振动模态,在工作带宽内阻抗变化剧烈且呈现多峰状态。工作带宽内并联等效电阻起伏由最小3.95kΩ到最大13.13kΩ,电抗起伏由最小1.02kΩ到最大1.32kΩ。声呐系统中采用的功放为JYH500A型线性功率放大器,输出阻抗为50Ω。
|
| 图4 换能器的导呐特性曲线 Figure 4 The admittance curve of the transducer |
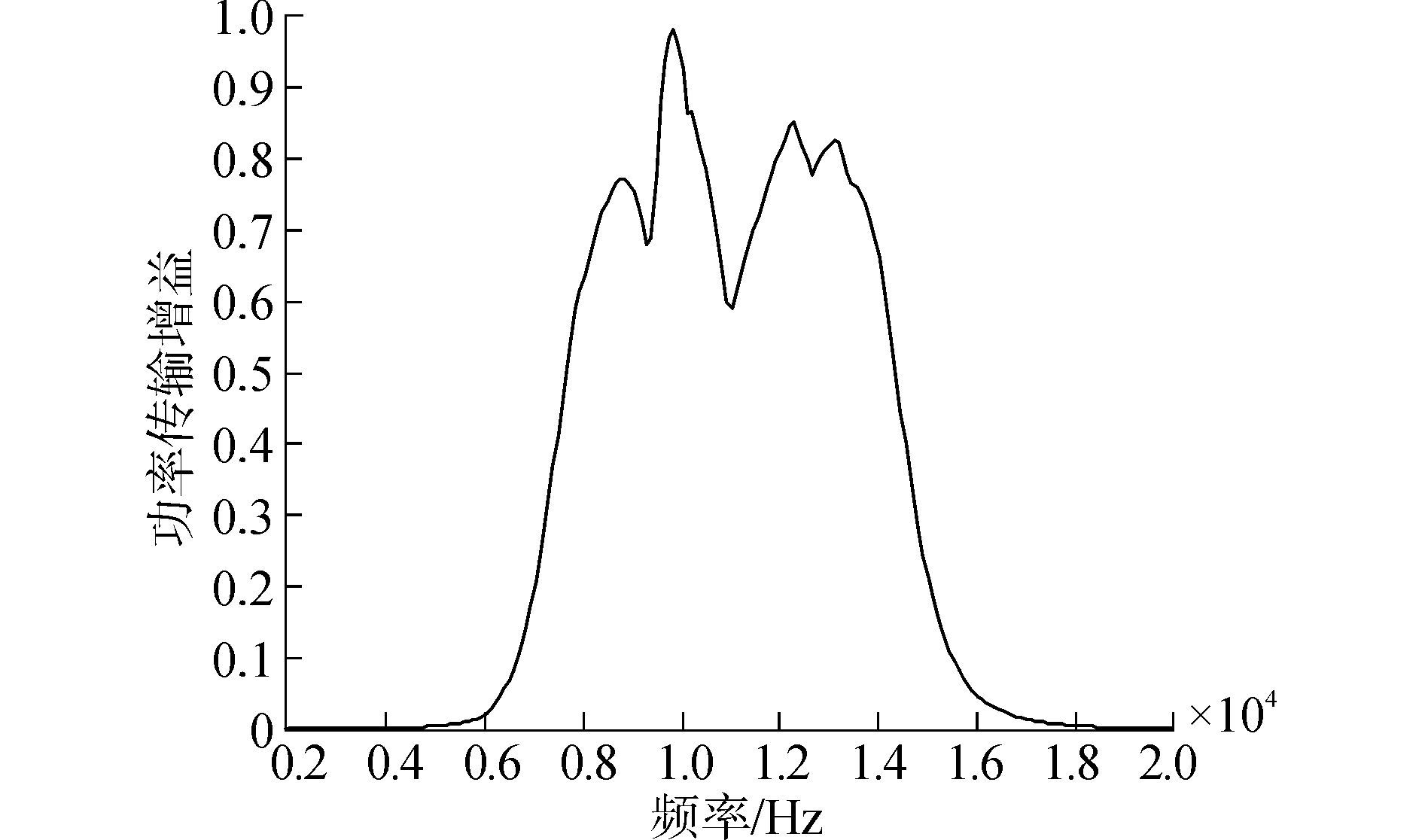
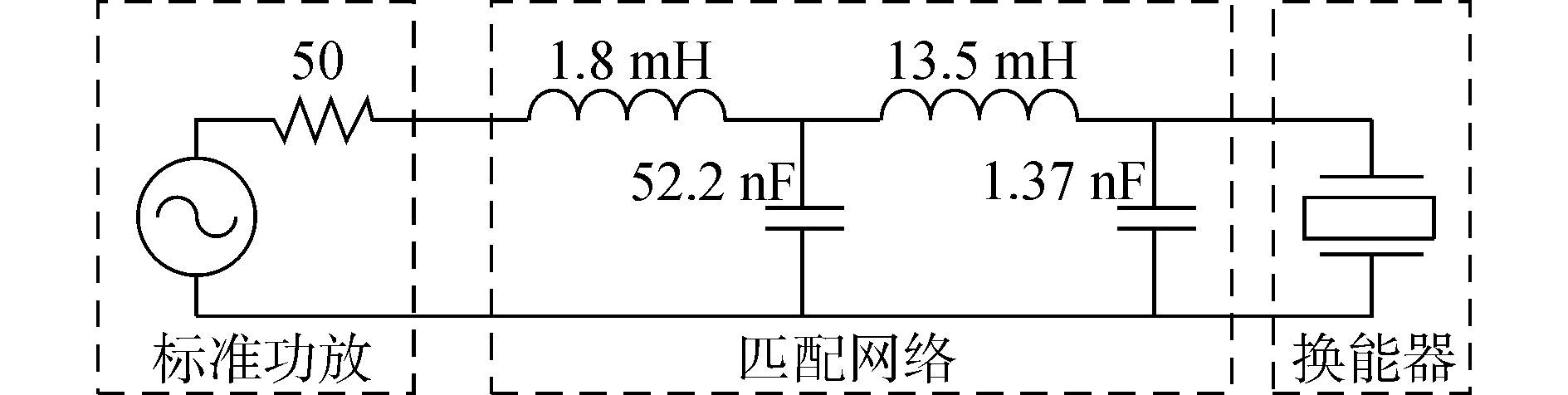
根据直接实频数据法的理论,编写实频数据程序。设置程序初始参数:目标传输增益:T0=0.75;匹配元件数量:4;匹配带宽:9~14kHz;匹配电路的端接电阻50Ω。导入换能器的阻抗数据,给定cj初始值并计算Rq,利用Gewertz法得到匹配网络的阻抗Zq,计算功率传输增益并得到误差函数,利用非线性最小二乘算法对增益进行优化,使得功率传输增益在要求的带宽内高并且平整。优化得到的功率传输增益曲线如图 5所示,仿真结果表明带宽内的功率传输增益基本在0.75附近变化,基本符合预定指标。但功率传输增益存在较大起伏,特别在11kHz频率点附近的传输增益较低,主要是由于换能器在带宽内的电阻起伏较大所导致。最终综合出的宽带匹配电路原理图如图 6所示。
|
| 图5 优化后的TPG曲线 Figure 5 The TPG curve after optimization |
|
| 图6 综合出的匹配电路图 Figure 6 Schematic of broadband matching circuit |
为使设计出的预均衡器可以准确地对系统发射信号进行补偿,就必须对发射系统的冲激响应函数进行精准估计。在通信系统的信道估计方法中,广泛采用的算法有最小平方(Least squares,LS)算法、最小均方误差(minimum mean square error,MMSE)算法。近年来,利用压缩感知(compressed sensing,CS)技术对稀疏信道冲激响应进行估计,得到广泛的研究并取得了较好的估计效果[12]。本文将发射系统视为一种广义信道,选用带宽为工作频带的线性调频信号作为训练序列,结合压缩感知算法对发射系统的冲激响应函数进行估计,以此设计预均衡器的冲激响应函数,实现发射信号的均衡。
1.3.1 基于OMP的系统冲击响应估计方法在压缩感知中,采样过程是由稀疏度为k的原信号x∈RN和测量矩阵Φ∈RM×N相乘,得到测量向量y∈RM:
| $y=\Phi x$ | (12) |
式中Φ=[φ1φ2 … φN]。
在冲激响应函数估计中,系统发射线性调频信号作为训练序列,具体信号形式如式(13)所示。其中f1为起始频率,T为脉冲宽度,N为信号采样点数,Δf为信号带宽。假设换能器发射的信号为y,根据训练序列构造测量矩阵Φ,发射系统的冲激响应为h,观测的噪声向量为n,则发射系统的输入输出关系:
| $\begin{matrix} x\left[ n \right]=cos(2\pi {{f}_{1}}\frac{T}{N}n+\pi \frac{\Delta f}{N}{{\left( \frac{T}{N}n \right)}^{2}}) \\ n=0,1,\ldots ,N-1\text{ } \\ \end{matrix}$ | (13) |
| $y=\Phi h\text{ }+n$ | (14) |
为有效地重构系统冲激响应h,需找到合理的重构算法。在压缩感知的重构算法中,基于贪婪迭代思想的正交匹配追踪(orthogonal matching pursuit,OMP)算法得到了广泛的应用,OMP算法的基本思想是在每一次迭代过程中从字典中找到和信号最匹配的原子来构建原始信号,然后求出信号残差,并在剩余的原子中继续选择和信号残差最匹配的原子,经过多次迭代后,通过观测向量和选择出的原子即可重构稀疏信号[13-14],以下为OMP算法的迭代流程。
1) 初始化残差r0=y,索引集
2) 寻找测量矩阵Φ中与残差最匹配的原子:
| ${{\lambda }_{i}}=arg\underset{j=1,\ldots ,N}{\mathop{max}}\,|<{{r}_{i-1}},{{\varphi }_{j}}>|$ |
3) 增加支撑集
4) 利用索引集中现有的原子逼近原始信号:
| ${{\hat{h}}_{\Lambda i}}=arg\underset{{{h}_{\Lambda i}}}{\mathop{min}}\,\left\| y-{{{\tilde{\psi }}}_{i}}{{h}_{\Lambda i}} \right\|$ |
5) 更新残差信号:
| ${{r}_{i}}=y-{{\tilde{\Psi }}_{_{i}}}{{\hat{h}}_{\Lambda i}}$ |
6) 若i<k,迭代索引加1,返回到第2)步。若i=k,得到最后的近似信号
根据以上所述的OMP重构算法可以实现对发射系统冲激响应函数的估计,再根据式(2)完成预均衡器传递函数的设计并设计出最终的预均衡器。
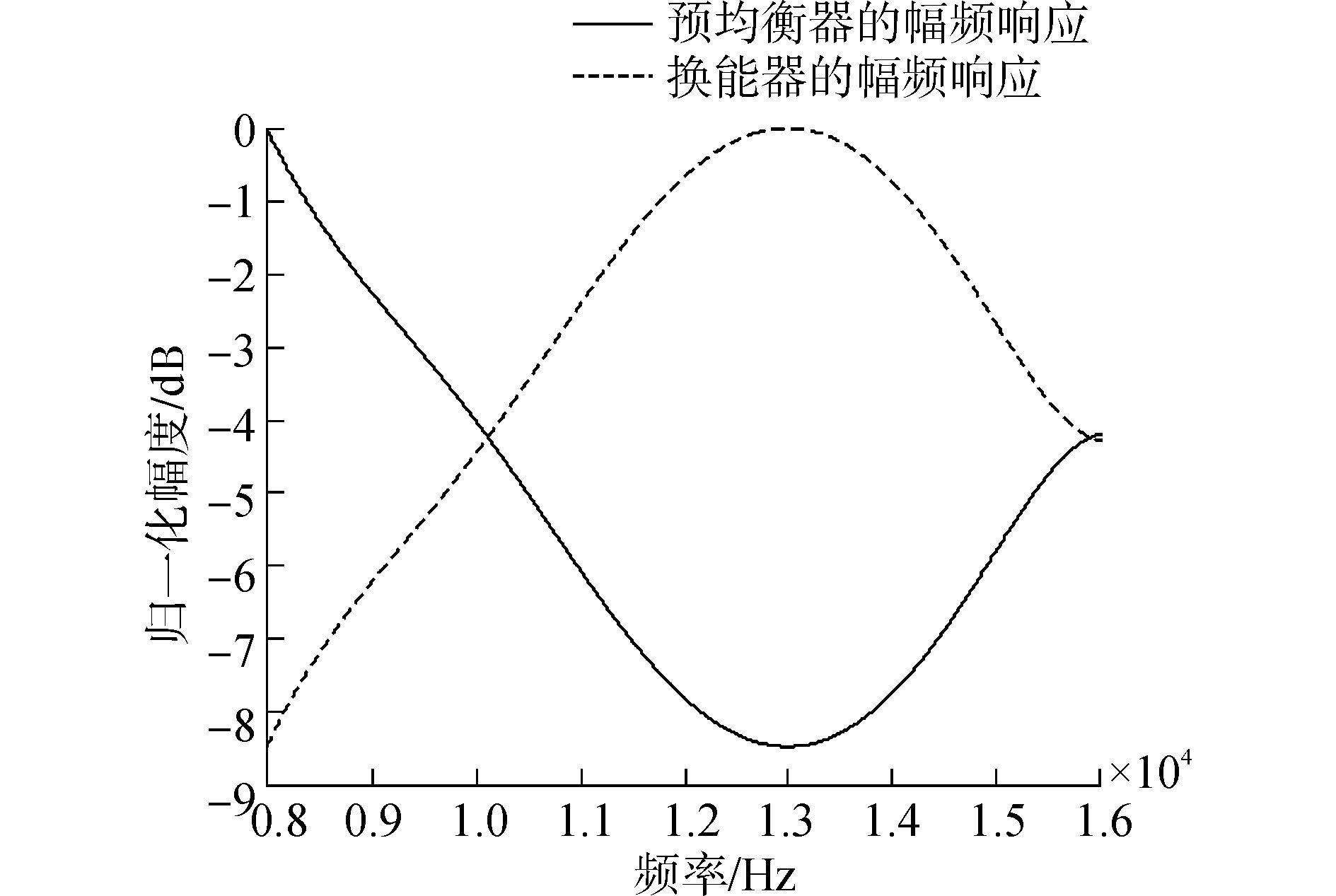
1.3.2 仿真分析为验证预均衡器对发射波形的均衡效果,构造带宽为9~14kHz的发射系统冲激响应函数,其频响曲线如图 7中虚线所示,带内的幅度起伏约为6dB。
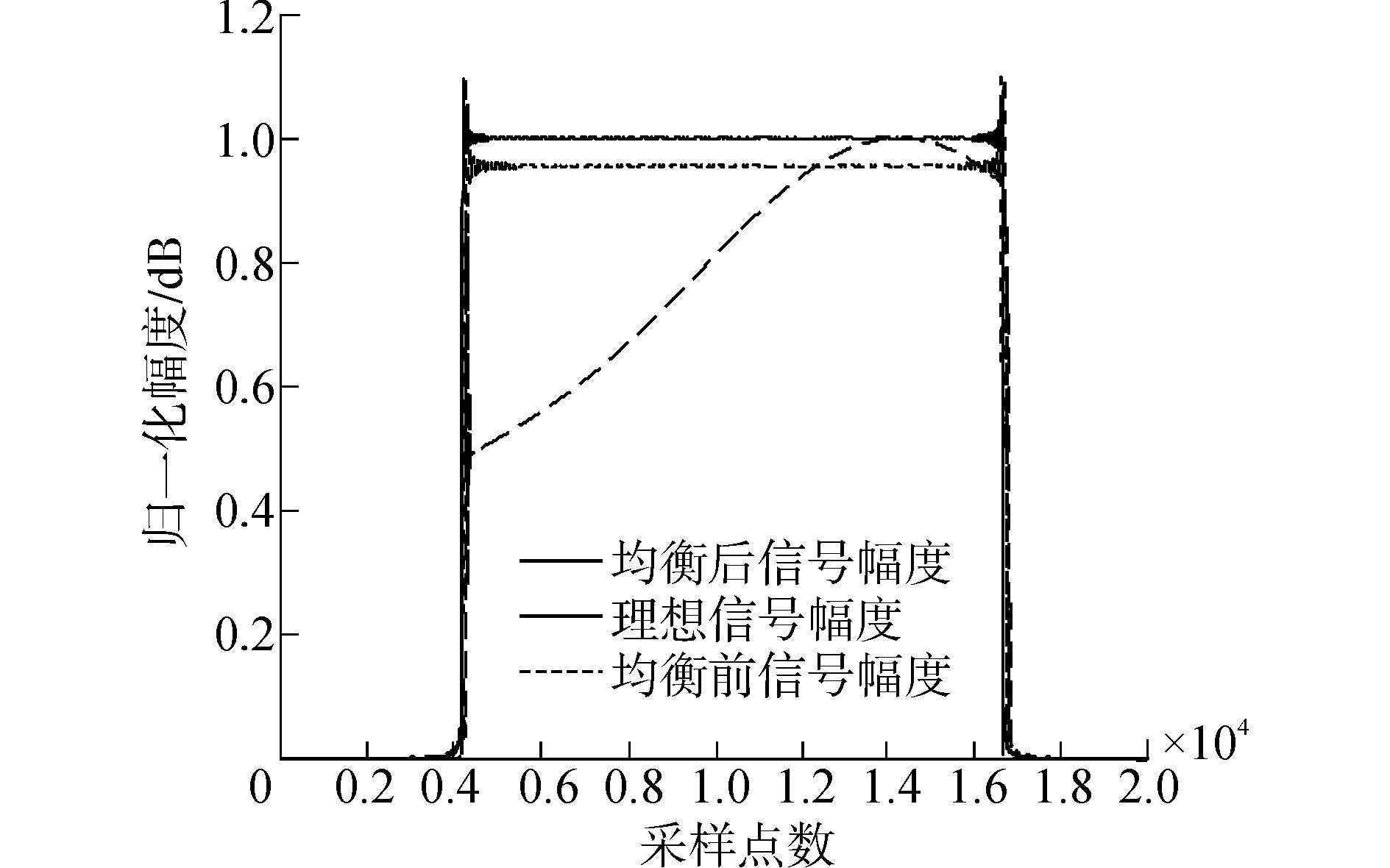
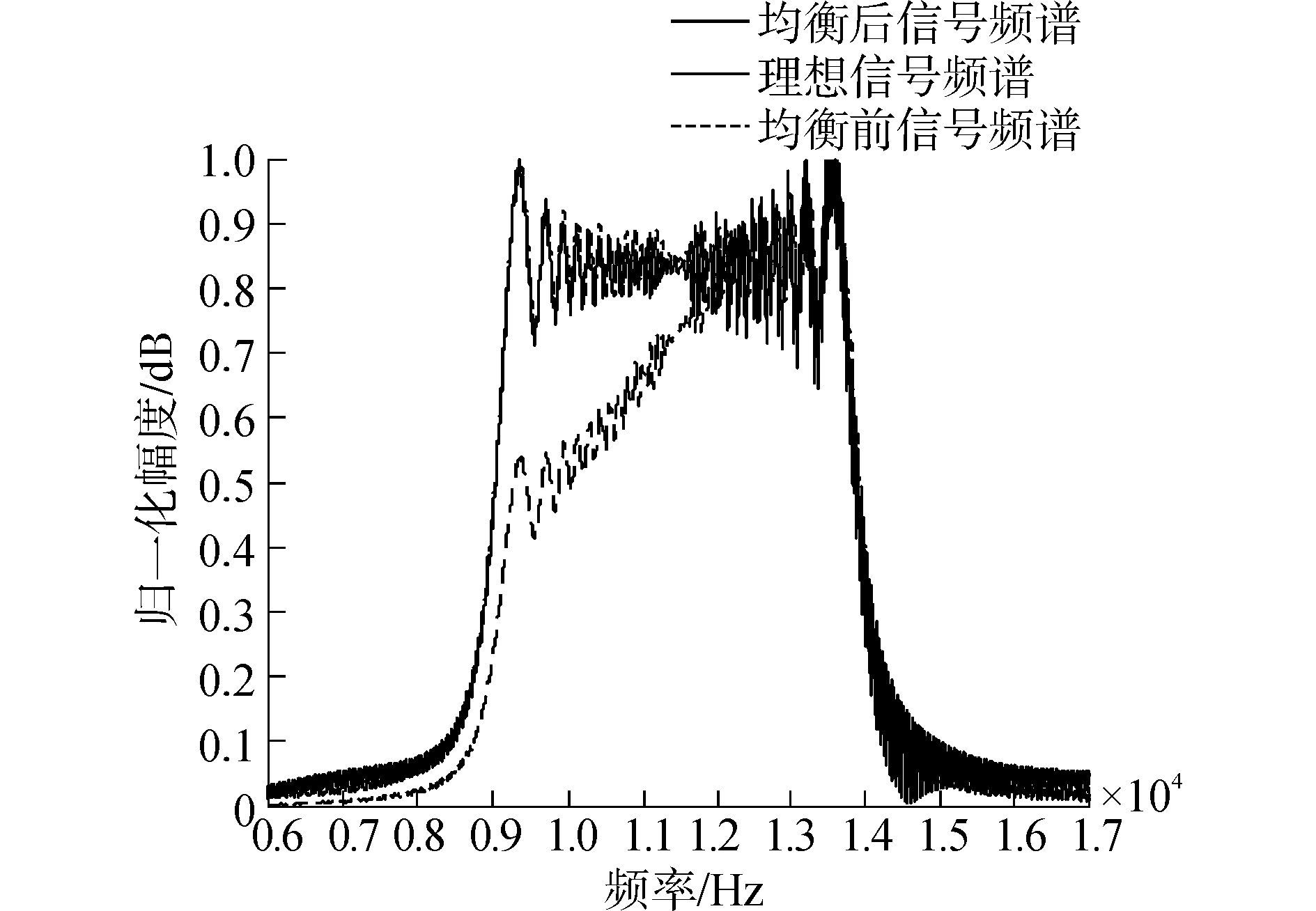
根据压缩感知理论,系统发射9~14kHz的线性调频信号。设计出的预均衡器频响如图 7中实线所示,预均衡器频响与发射系统频响互补,使得均衡后的发射信号与理想信号基本一致。图 8为理想信号幅度和预均衡前后信号幅度的对比曲线,预均衡器将信号的幅度起伏由6dB降低到0.35dB。图 9为理想信号频谱和预均衡前后信号频谱的对比曲线,均衡后信号的低频能量得到提升,整体的信号频谱接近于理想信号。计算均衡前后信号的信号失真比(the ratio of the signal-to-distortion,SDR)以定量给出匹配均衡前后的效果,SDR定义如式为[15]
| $SDR=\frac{{{P}_{S}}}{{{P}_{E}}}=\frac{{{P}_{S}}}{{{P}_{S}}-{{P}_{D}}}$ | (15) |
式中:PS为根据Parseval定理计算的理想信号频域能量,PD为失真信号的频域能量,PE为理想信号与失真信号的频域能量差。
|
| 图7 优化后的TPG曲线 Figure 7 The TPG curve after optimization |
|
| 图8 综合出的匹配电路图 Figure 8 Schematic of broadband matching circuit |
|
| 图9 理想信号频谱与预均衡后信号频谱 Figure 9 The ideal signal spectrum and the signal spectrum before and after pre-equalization |
根据信号失真比的定义计算得到预均衡前信号的SDR为3.53,预均衡后信号的SDR为6.63,均衡后信号SDR较匹配均衡前提高约1.88倍。
仿真结果表明:基于OMP算法的压缩感知技术可以有效地对仿真的发射系统冲激响应进行估计,设计出的预均衡器可以有效地减少信号幅度失真度,达到信号均衡的目的。
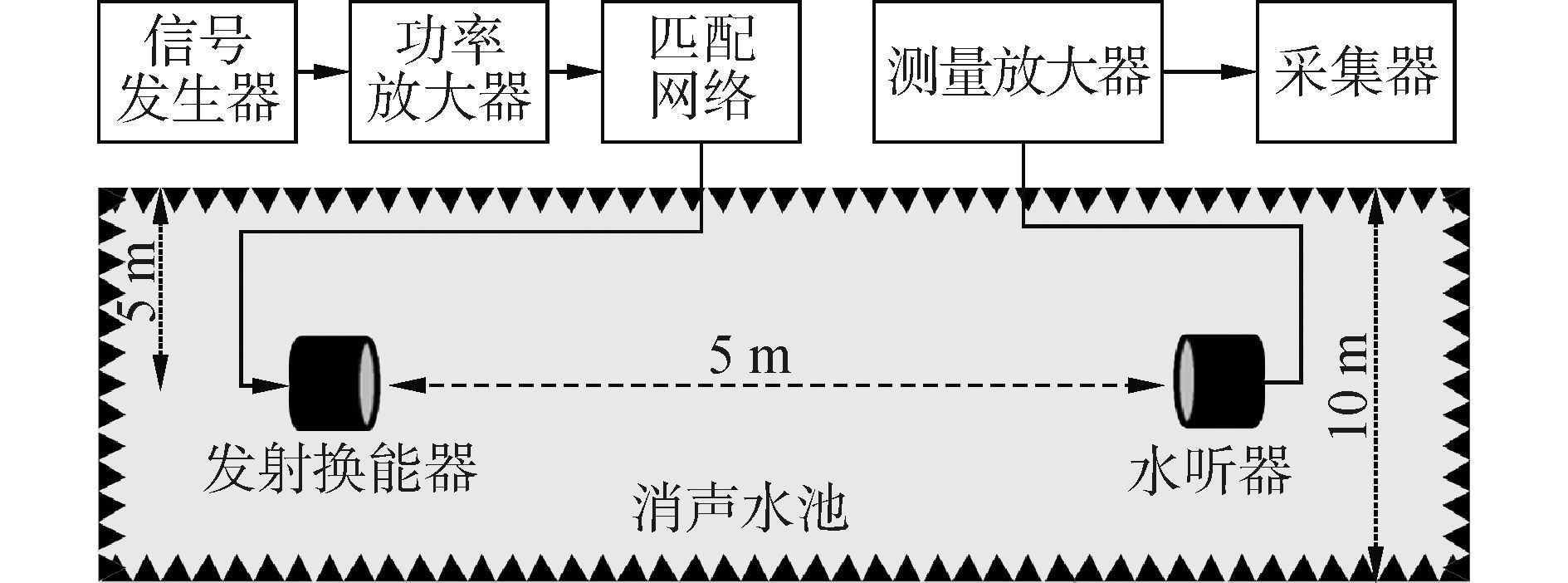
2 水池实验结果及分析在消声水池构建如图 10所示的发射接收系统,测试联合设计技术的实际效果。利用信号源Angilent33522产生信号,采用标准功放JYH500A进行信号的功率放大,发射换能器使用1.2.2 节中的耐压圆管换能器,入水深度5m,距离其水平5m处放置Reson公司标准水听器TC4040进行信号接收,测量放大器为美国PFI的28000信号调理系统,采集器使用美国NI公司的6733型数据采集器。
|
| 图10 水池实验原理框图 Figure 10 Schematic diagram of pool experiment |
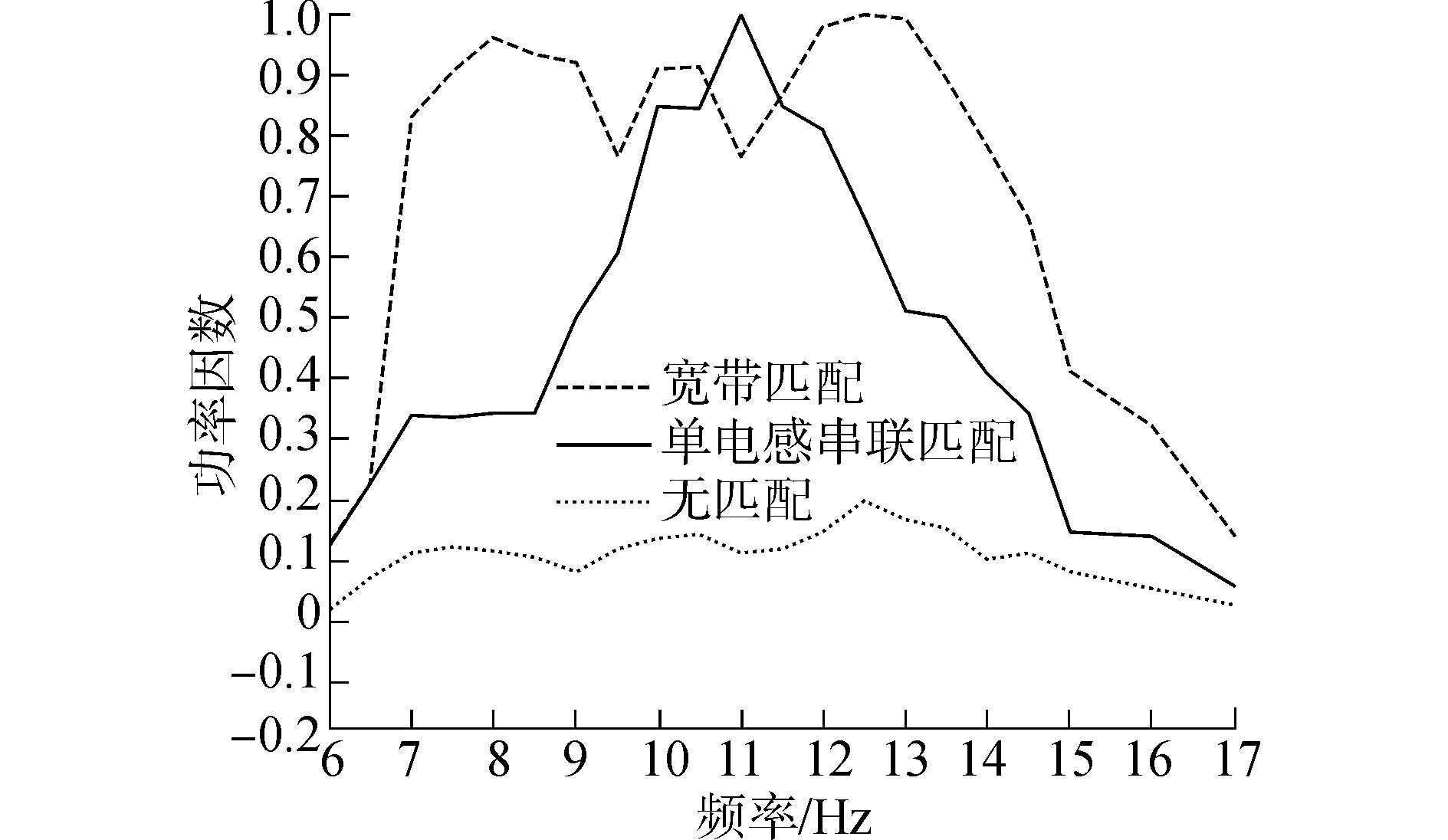
为了考察宽带匹配电路的匹配效果,构造了工程中常用的单电感串联匹配电路与之进行对比,谐振频率为11kHz。图 11给出了不同匹配状态下的功放的输出功率因数曲线。对于无匹配电路的系统,由于换能器整体呈现容性,在工作频带内功率因数在0.1~0.2,功放处于失配状态;单点匹配的功率因数在0.4~1;宽带匹配的功率因数在0.68~1。单电感匹配电路仅在谐振点附近10~12kHz有较好的工作效率,而宽带匹配电路则在7~14kHz频段内均有较好的工作效率,因此宽带匹配电路更好地改善了发射系统的工作效率。
|
| 图11 不同匹配方式下功放的输出功率因数 Figure 11 The output power factors of the power amplifier with different matching modes |
系统发射9~14kHz线性调频信号,图 12(a)和图 12(b)分别给出了换能器匹配前后的信号幅度曲线和频谱曲线,相比于理想的线性调频信号频谱,经过换能器的发射信号在频率9~11kHz处明显失真。匹配后的信号频谱表明,宽带匹配电路对失真的频率有一定补偿作用,但对于9.5、11kHz附近频率的补偿效果不明显,主要是由于换能器在频率9.5、11kHz附近的并联电阻相对较大,导致匹配效果不佳。 根据匹配后的换能器发射波形,采用压缩感知技术对系统的冲激响应函数进行估计,构造预均衡器对信号进行均衡。图 12(c)给出了系统匹配均衡前后发射波形的幅度,实线为匹配均衡前的信号幅度,虚线为匹配均衡后的信号幅度。根据对比可知,预均衡器有效地对系统在频率9.5、11kHz处的能量进行补偿,减少了发射信号的幅度失真,幅度起伏由匹配均衡前的12dB降低为3.3dB。图 12(d)给出匹配均衡前后信号频谱。根据信号失真比的定义计算得到的匹配前、匹配后以及匹配均衡后的信号SDR分别为:2.70、4.14、6.76。由数据可知:匹配后信号SDR为匹配前信号SDR的1.53倍,而匹配均衡后信号SDR为匹配前信号SDR的2.5倍,反映了匹配均衡技术对降低系统发射信号失真度的有效性。

|
| 图12 匹配均衡前后对比效果 Figure 12 The contrast effects before and after broadband matching and equalization |
水池测试结果表明:采用联合技术的发射系统具有较好的工作效率和较低的波形失真度,验证了该联合技术的有效性。
3 结论本文提出了一种设计宽带发射系统的联合技术,首先利用实频数据技术设计宽带匹配电路,提高工作效率并扩展工作频带,然后采用预均衡技术降低匹配后发射波形的失真度。文中分别讨论了实频数据技术和预均衡技术的基本原理,并针对工程中使用多谐振模态换能器,仿真分析了实频数据和预均衡器的效果,最后进行了水池试验。结果表明:联合技术在保证系统工作效率和匹配带宽的同时有效降低发射信号的失真度。该技术为宽带高效声呐发射系统的设计提供了参考方案,具有一定的工程实用价值。但在研究中发现,实频数据程序在计算过程存在不收敛的情况,此时需要对设定的匹配参数进行调整;同时该方法的计算量相比简化实频数据法以及参量法较大,在后续的工作中可以对计算量相对小的算法展开研究。
| [1] |
陈友淦, 许肖梅, 雷开卓, 等. 宽带水声发射系统换能器分段匹配方法研究[J].
兵工学报, 2010, 31(3): 296–303.
CHEN Yougan, XU Xiaomei, LEI Kaizhuo, et al. Piecewise matching method of transducer for broadband underwater acoustic transmitter system[J]. Acta armamentarii, 2010, 31(3): 296–303. |
| [2] |
徐亚军. 数字功放与宽带匹配技术研究[D]. 哈尔滨:哈尔滨工程大学, 2006:1-6.
XU Yajun. Research on digital power amplifier and broadband matching[D]. Harbin:Harbin Engineering University, 2006:1-6. |
| [3] | RAMESH R, EBENEZER D D. Equivalent circuit for broadband underwater transducers[J]. IEEE transactions on ultrasonics, ferroelectrics and frequency control, 2008, 55(9): 2079–2083. |
| [4] |
陈爱新, 张艳君, 姜铁华, 等. 电小天线宽带匹配网络的优化设计[J].
北京航空航天大学学报, 2009, 35(11): 1311–1314.
CHEN Aixin, ZHAND Yanjun, JIANG Tiehua, et al. Optimal design of broadband matching network for electrically small antennas[J]. Journal of Beijing university of aeronautics and astronautics, 2009, 35(11): 1311–1314. |
| [5] | HUANG Haiying, PARAMO D. Broadband electrical impedance matching for piezoelectric ultrasound transducers[J]. IEEE transactions on ultrasonics, ferroelectrics and frequency control, 2011, 58(12): 2699–2706. |
| [6] | AN Jianfei, SONG Kezhu, ZHANG Shuangxi, et al. Design of a broadband electrical impedance matching network for piezoelectric ultrasound transducers based on a genetic algorithm[J]. Sensors, 2014, 14(4): 6828–6843. |
| [7] |
龙航. 无线协同中继通信的预编码技术研究[D]. 北京:北京邮电大学, 2010:5-6.
LONG Hang. Research on precoding techniques in wireless cooperative/relay communication systems[D]. Beijing:Beijing University of Posts and Telecommunications, 2010:5-6. |
| [8] |
胡智兵, 王清池, 许鹭芬, 等. 水声信道高速率数据传输中换能器频谱特性的均衡[J].
厦门大学学报:自然科学版, 1999, 38(4): 524–527.
HU Zhibing, WANG Qingchi, XU Lufen, et al. Equalization of transducers spectral characteristic in high-speed data transmission within underwater acoustic channel[J]. Journal of Xiamen university:natural science, 1999, 38(4): 524–527. |
| [9] |
周伟江, 景永刚, 陈梦英. 数字均衡技术在水声宽带系统中的应用[J].
声学技术, 2012, 31(2): 219–222.
ZHOU Weijiang, JING Yonggang, CHEN Mengying. Application of digital equalizer technology in underwater broadband system[J]. Technical acoustics, 2012, 31(2): 219–222. |
| [10] |
曹清刚, 吴亮, 王晋. 水下回波模拟器频率补偿技术[J].
舰船科学技术, 2012, 34(7): 96–103.
CAO Qinggang, WU Liang, WANG Jin. Equalize technique of underwater echo simulator research and achieve[J]. Ship science and technology, 2012, 34(7): 96–103. |
| [11] | YARMAN B S. Design of ultra wideband power transfer networks[M]. London: John Wiley & Sons, Ltd, 2010: 571 -576. |
| [12] |
尹艳玲, 乔钢, 刘凇佐, 等. 基于基追踪去噪的水声正交频分复用稀疏信道估计[J].
物理学报, 2015, 64(6): 064301.
YIN Yanling, QIAO Gang, LIU Songzuo, et al. Sparse channel estimation of underwater acoustic orthogonal frequency division multiplexing based on basis pursuit denoising[J]. Acta physica sinica, 2015, 64(6): 064301. |
| [13] |
王妮娜. 基于压缩感知理论的无线多径信道估计方法研究[D]. 北京:北京邮电大学, 2012:84-90.
WANG Ni'na. Research on wireless multipath channel estimation method based on compressive sensing[D]. Beijing:Beijing University of Posts and Telecommunications, 2012:84-90. |
| [14] |
熊承义, 董攀峰. 基于FPGA的正交匹配追踪算法的硬件实现[J].
中南民族大学学报:自然科学版, 2013, 32(2): 73–76.
XIONG Chengyi, DONG Panfeng. Hardware implementation of OMP algorithm based on FPGA[J]. Journal of south-central university for nationalities:natural science edition, 2013, 32(2): 73–76. |
| [15] | PROAKIS J G, MANOLAKIS D K. Digital signal processing-principles, algorithms, and applications[M].3rd ed. New Jersey: Prentice Hall, 1996: 815 -821. |



