冲击机械中经常采用两圆柱形实心杆件的撞击来产生冲击力。目前冲击杆件主要采用一维弹性杆的波动力学理论进行设计。在一维弹性杆的波动力学理论中,第一个基本假设就是忽略杆中质点径向惯性作用,沿截面只有均匀分布的轴向应力[1]。文献[2-6]的实验研究表明,距离撞击端2倍杆直径区域内的轴向应力分布是不均匀的,故一维弹性杆的波动力学理论不再适用。文献[7]通过采用考虑径向惯性效应的数值仿真发现在实心杆的撞击端邻近区域的轴线上将发生应力集中,提出轴线上的应力集中点是弹性解析解的奇异点,其理论应力为无限大。文献[8]在对钎杆断裂的研究中发现,断裂的位置都偏向于撞击端,其中有些断裂就是由内部的裂纹源引起的。由文献[9-10]可知,冲击机械在工作过程中,冲击杆轴线上的应力集中将大大降低冲击杆的强度,促进疲劳裂纹的产生。所以在进行冲击杆的设计时有必要考虑径向惯性作用在撞击端附近引起的应力集中。
很多文献对撞击杆端部附近区域中质点的径向惯性作用进行了研究。文献[3]对实心杆表面和杆轴心上的轴向应变进行了实验研究。除了在表面粘贴应变片,还在距离撞击端不同距离的位置上嵌入应变片,实验发现杆轴心上的应变始终比杆表面的应变大。但在试验中采用的是圆头冲击杆,故不能充分说明应变的不同是由径向惯性效应引起的。文献[5]采用文献[3]的方法,在实心铝圆杆的端部嵌入应变片来测量圆杆内部的弹性应变。实验测量了两个3/4英寸直径的6061-T6铝杆撞击的弹性应变波。实验中是采用平头冲击杆,测量结果与数值解的一致性非常好。文献[7]发展了一种有限差分算法来对应力波在线弹性固体中传播的偏微分控制方程组进行数值积分,并用该数值算法研究了端部承受拉伸冲击的半无限圆杆,发现了von Schmidt波在被冲击圆杆端部轴线上的聚焦现象。文献[9-11]通过优化冲击杆的形状来调整分离式霍普金森压杆入射脉冲的形状。文献[12]对关于两杆撞击过程中,在线弹性响应范围内,邻近杆撞击端部区域的应力分布情况的理论和实验研究进行了综述。文献[13-14]对冲击端部具有不同形状及不同撞击面积的冲击杆与同一实心圆杆的撞击进行了数值研究和实验研究[13-14],其数值结果和实验结果证明冲击杆的端部形状将决定被撞圆杆在冲击端的敏感区域的长度[13]。根据理论研究的解析解敏感区域的长度大概不会超过2.2倍的直径[14]。
为了获得考虑径向惯性效应时,两实心圆杆和两空心圆杆在撞击过程中撞击端部附近的轴向应力分布情况。本文在文献[9]中的数值算法基础上,通过修改初始条件和边界条件对两实心圆杆及两空心圆杆的撞击进行了数值分析,并根据文献[3, 5]的试验原理,测量了实心杆轴心和空心杆内表面的轴向应力。
1 冲击动力学方程和数值方法 1.1 冲击动力学方程对于一个等截面、质量分布均匀、各向同性材料的半无限圆杆,考虑其在不发生扭转变形,只发生弹性轴对称变形的情况下,以圆杆的轴作为z轴,将r轴置于圆杆的端面上建立一个拉格朗日柱坐标系。此柱坐标系下的半无限圆杆弹性动力学方程为
| $\left\{ \begin{gathered} \frac{{\partial {\sigma _z}}}{{\partial t}} = \rho c_l^2\frac{{\partial {v_z}}}{{\partial z}} + \eta \frac{{\partial {v_r}}}{{\partial r}} + \eta \frac{{{v_r}}}{r} \hfill \\ \frac{{\partial {\sigma _r}}}{{\partial t}} = \eta \frac{{\partial {v_z}}}{{\partial z}} + \rho c_l^2\frac{{\partial {v_r}}}{{\partial r}} + \eta \frac{{{v_r}}}{r} \hfill \\ \frac{{\partial {\sigma _\varphi }}}{{\partial t}} = \eta \frac{{\partial {v_z}}}{{\partial z}} + \eta \frac{{\partial {v_z}}}{{\partial z}} + \rho c_l^2\frac{{{v_r}}}{r} \hfill \\ \frac{{\partial {\sigma _{rz}}}}{{\partial t}} = \rho c_s^2\frac{{\partial {v_r}}}{{\partial z}} + \rho c_s^2\frac{{\partial {v_z}}}{{\partial r}} \hfill \\ \frac{{\partial {v_z}}}{{\partial t}} = \frac{1}{\rho }\frac{{\partial {\sigma _z}}}{{\partial z}} + \frac{1}{\rho }\frac{{\partial {\sigma _{rz}}}}{{\partial r}} + \frac{1}{\rho }\frac{{{\sigma _{rz}}}}{r} \hfill \\ \frac{{\partial {v_r}}}{{\partial t}} = \frac{1}{\rho }\frac{{\partial {\sigma _{rz}}}}{{\partial z}} + \frac{1}{\rho }\frac{{\partial {\sigma _r}}}{{\partial r}} + \frac{1}{\rho }\frac{{{\sigma _r} - {\sigma _\varphi }}}{r} \hfill \\ \end{gathered} \right.$ | (1) |
式中:σz、σr、σφ、σrz为质点的应力分量,vz和vr为质点在轴向和径向的速度,cl为材料的纵波波速,cs为材料的剪切波速,系数η=(ρcl2-ρcs2)。令U=[σz σr σφ σrz vz vr]T,则方程组(1)的矩阵形式为
| $\frac{{\partial U}}{{\partial t}} = {A_1}\frac{{\partial U}}{{\partial z}} + {A_2}\frac{{\partial U}}{{\partial r}} + {A_3}U$ | (2) |
式中:A1、A2、A3为系数矩阵。
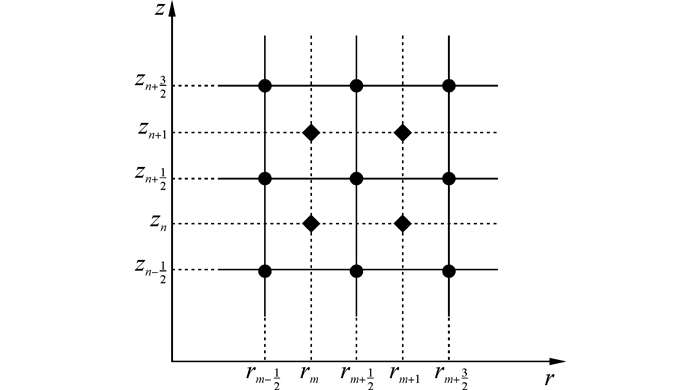
1.2 数值方法建立两半无限等截面弹性圆杆共轴碰撞的数值模型,设两杆接触但还未发生形变的时刻为t=0,并在此时刻对圆杆建立二维拉格朗日柱坐标系。当圆杆为实心杆时,将z轴置于杆的中心轴线上;当圆杆为空心杆时,将z轴置于杆的内壁上。设被撞杆的自由端为z=0,将r轴垂直于z轴置于圆杆的端面上建立一个拉格朗日柱坐标系。取步长△z=△r,将该平面均匀划分为正方形网格,如图 1所示。图中实心圆点表示网格节点,实心菱形表示单元。将实心杆半径R或空心杆壁厚S划分为M份,则有△z=△r=R/M或△z=△r=S/M。为了取得稳定的差分格式及尽可能准确地模拟两弹性杆的撞击波形,取柯朗数${N_c} = \frac{{{c_l}\Delta t}}{{\Delta z}} = 1$,则可以确定差分格式的时间步长△t。由需要的总仿真时间确定被撞杆轴向划分的份数N1及撞击杆轴向划分的份数N2。
|
| 图1 拉格朗日计算网格 Figure 1 Lagrangian computational grid |
采用Lax-Wendroff有限差分格式对控制方程组(1)中的空间导数进行离散,可以得到一个两步差分格式:
| $\begin{align} & U_{m+\frac{1}{2},n+\frac{1}{2}}^{t+\frac{1}{2}}=\frac{1}{4}\left( U_{m,n}^{t}+U_{m+1,n}^{t}+U_{m,n+1}^{t}+U_{m+1,n+1}^{t} \right)+ \\ & \frac{\mu }{4}{{A}_{1}}\left( U_{m+1,n+1}^{t}-U_{m,n}^{t}+U_{m+1,n}^{t}-U_{m,n+1}^{t} \right)+ \\ & \frac{\mu }{4}{{A}_{2}}\left( U_{m+1,n+1}^{t}-U_{m,n}^{t}-U_{m+1,n}^{t}+U_{m,n+1}^{t} \right)+ \\ & \frac{\Delta t}{8}{{A}_{3}}\left( U_{m+1,n+1}^{t}+U_{m,n}^{t}+U_{m+1,n}^{t}+U_{m,n+1}^{t} \right) \\ \end{align}$ | (3) |
| $\begin{align} & U_{m,n}^{t+1}=U_{m,n}^{t}+ \\ & \frac{\mu }{2}{{A}_{1}}\left( U_{m+\frac{1}{2},n+\frac{1}{2}}^{t+\frac{1}{2}}+U_{m+\frac{1}{2},n-\frac{1}{2}}^{t+\frac{1}{2}}-U_{m-\frac{1}{2},n+\frac{1}{2}}^{t+\frac{1}{2}}-U_{m-\frac{1}{2},n-\frac{1}{2}}^{t+\frac{1}{2}} \right)+ \\ & \frac{\mu }{2}{{A}_{2}}\left( U_{m+\frac{1}{2},n+\frac{1}{2}}^{t+\frac{1}{2}}-U_{m+\frac{1}{2},n-\frac{1}{2}}^{t+\frac{1}{2}}+U_{m-\frac{1}{2},n+\frac{1}{2}}^{t+\frac{1}{2}}-U_{m-\frac{1}{2},n-\frac{1}{2}}^{t+\frac{1}{2}} \right)+ \\ & \frac{\Delta t}{4}{{A}_{3}}\left( U_{m+\frac{1}{2},n+\frac{1}{2}}^{t+\frac{1}{2}}+U_{m+\frac{1}{2},n-\frac{1}{2}}^{t+\frac{1}{2}}+U_{m-\frac{1}{2},n+\frac{1}{2}}^{t+\frac{1}{2}}+U_{m-\frac{1}{2},n-\frac{1}{2}}^{t+\frac{1}{2}} \right) \\ \end{align}$ | (4) |
式中:μ=△t/△z=△t/△r。首先在单元上施加初始条件,然后通过式(3)及施加在边界节点上的边界条件计算t+1/2时刻节点的状态,然后通过式(4)更新t+1时刻的单元状态。
两杆撞击的初始条件为
| $ \begin{gathered} U_{m,n}^0 = {\left[ {\sigma _{1z}^0\sigma _{1r}^0\sigma _{1\varphi }^0\sigma _{1rz}^0\sigma _{1z}^0\sigma _{1r}^0} \right]^{\text{T}}} \hfill \\ 1 \leqslant m \leqslant M,1 \leqslant n \leqslant {N_1} \hfill \\ U_{m,n}^0 = {\left[ {\sigma _{2z}^0\sigma _{2r}^0\sigma _{2\varphi }^0\sigma _{2rz}^0\sigma _{2z}^0\sigma _{2r}^0} \right]^{\text{T}}} \hfill \\ 1 \leqslant m \leqslant M,{N_1}{\text{ < }}n \leqslant {N_1} + {N_2} \hfill \\ \end{gathered} $ |
实心杆和空心杆在内边界r=r$\frac{1}{2}$上的边界条件不同,而在外边界r=rM+$\frac{1}{2}$=r0上的边界条件完全相同,其中ro是杆的外径。实心杆在r=r$\frac{1}{2}$=0的内边界条件为vr=0,σrz=0。内径为ri的空心杆在r=r$\frac{1}{2}$=ri的内边界条件为σr=Pi,σrz=Ti,Pi为空心杆内壁上受到的压应力,Ti为空心杆内壁上受到的切应力。杆的外边界条件为σr=Po,σrz=To,Po为杆外壁上受到的压应力,To为杆外壁上受到的切应力。
两杆撞击端面的边界条件的处理。由于是两半无限杆的撞击不需要考虑两杆的分离,所以将z=zN1+$\frac{1}{2}$作为两撞击杆公共节点,作为两杆的撞击端面。撞击端面上的σz、σr和σφ可以由式(3)给出的关系求出,撞击端面上的σrz为两撞击端面之间的摩擦力,可用摩擦系数k与轴向应力σz表示为σrz=kσz,当两个端面之间润滑情况较好时k=0。
2 数值分析采用6061-T6铝作为两实心杆和两空心杆弹性撞击模型的材料,材料密度为2 780 kg·m-3、纵波波速5 089 m·s-1、横波波速3 151 m·s-1。撞击杆的撞击速度均为1 m·s-1。实心杆和空心杆的初始条件均为
| $ \begin{gathered} U_{m,n}^0 = {\left[ {000000} \right]^{\text{T}}} \hfill \\ 1 \leqslant m \leqslant M,1 \leqslant n \leqslant {N_1} \hfill \\ U_{m,n}^0 = {\left[ {000010} \right]^{\text{T}}} \hfill \\ 1 \leqslant m \leqslant M,{N_1}{\text{ < }}n \leqslant {N_1} + {N_2} \hfill \\ \end{gathered} $ |
两实心杆的直径均为2 cm,为了与实心杆的横截面积相同,两空心杆的尺寸都是外径2.5 cm内径1.5 cm的圆管。不考虑两杆撞击界面上的摩擦,设置摩擦系数k=0;设杆外壁上受到的压应力Po=0,杆外壁上受到的切应力To=0;设空心杆内壁上受到的压应力Pi=0,空心杆内壁上受到的切应力Ti=0。
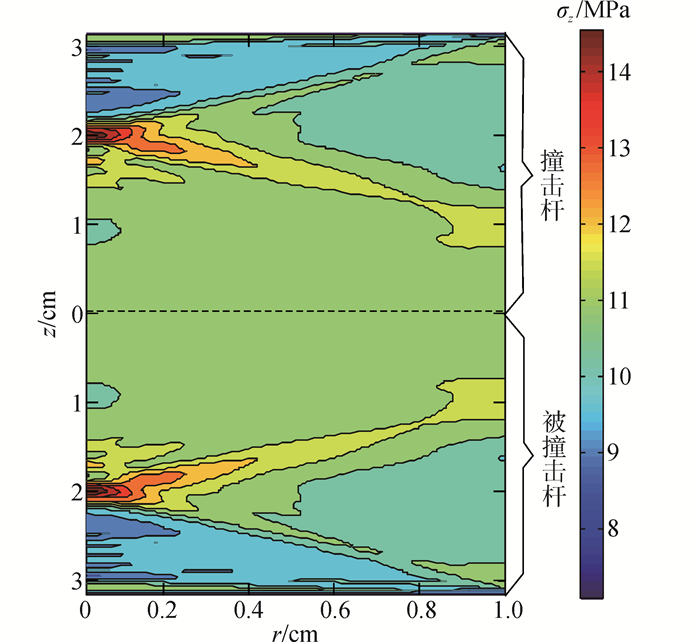
2.1 两实心杆撞击的数值分析从仿真结果中提取两实心杆撞击过程中,杆中出现最大应力时杆中应力的分布情况,计算结果如图 2所示。
|
| 图2 实心杆轴向应力分布 Figure 2 Axial stress distribution in the solid bar |
图 2中虚线表示两杆的碰撞端面。可以看出图中撞击杆和被撞击杆的轴向应力分布基本相同。撞击杆和被撞杆的轴向应力值都在距离碰撞端面2 cm左右的轴心区域内急剧升高。这是由于在碰撞的瞬间,在整个碰撞端面上形成平面压缩波的同时产生了一个平面膨胀波,而随着膨胀波的传播以及膨胀波在杆表面的卸载,将在杆的表面形成von Schmidt波,并向杆内传播。当von Schmitdt波传播到杆轴时,由于轴线上的质点不能发生径向位移,所以von Schmidt波将在轴线上聚焦产生应力集中。
为进一步研究von Schmidt波的聚焦现象,在保持杆的直径不变的情况下,逐渐减小计算网格的边长增大网格的密度进行数值计算。从不同网格边长的计算结果中提取两杆撞击过程中,杆中出现最大轴向应力的时刻、位置及轴向应力值,如表 1。
| 网格边长/mm | 时刻/μs | 位置/mm | 应力/MPa |
| 1 | 3.53 | (0,23) | 10.79 |
| 0.5 | 3.14 | (0,23.5) | 12.07 |
| 0.333 | 2.94 | (0,23.7) | 12.92 |
| 0.25 | 2.89 | (0,24.3) | 13.63 |
| 0.2 | 2.82 | (0,24.8) | 14.25 |
| 0.167 | 2.78 | (0,21.2) | 14.81 |
表 1给出的位置是相对于杆的轴线及两杆的撞击端面的位置,括号中第一个值是与杆轴线的距离,第二个值是与撞击端面的距离。表 1中给出的时刻是以压缩波的波前到达该位置的时刻为零时刻。可以看出,轴向应力最大值出现的相对位置及相对时间几乎不随计算网格变化而变化。根据一维初等理论两撞击杆的轴向应力为7.07 MPa,而从表 1中可知在考虑径向惯性效应的情况下,当网格尺寸为1 mm仅为杆半径的十分之一时,杆中应力集中处的轴向应力最大值是一维初等理论轴向应力值的1.53倍。随着计算网格尺寸的缩小,轴线上出现的轴向应力增大。上述现象说明实心杆轴线上的轴向应力的数值仿真结果仍未达到其极限。
从以上两实心杆弹性撞击的仿真结果可以看出,尽管撞击速度仅为1 m·s-1,但在两弹性杆轴线附近的应力集中区域也是十分明显的。据此可知,若是两弹塑性材料的实心杆以更大的速度撞击时,将在距离邻近撞击端的轴线附近区域产生严重的应力集中,而该区域在撞击过程中也将发生塑性变形,并且随着撞击次数的增加极易发生破坏。
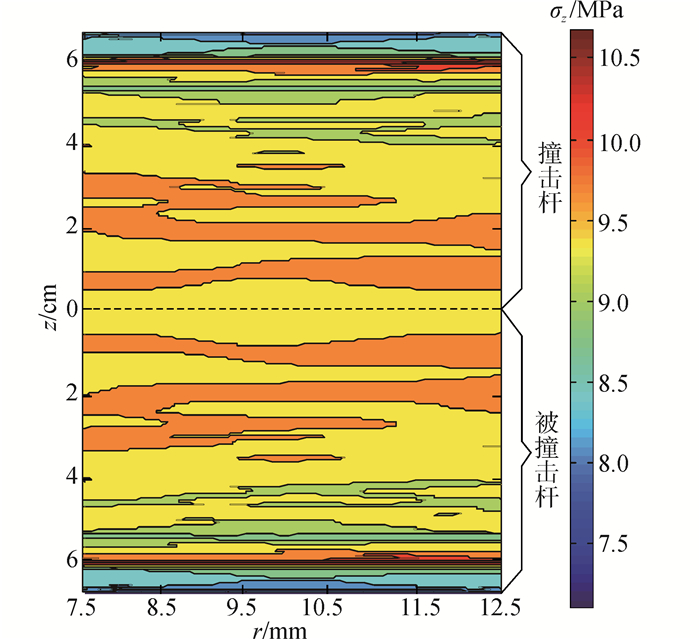
2.2 两空心杆撞击的数值分析横截面积相同的实心杆和空心杆的一维初等理论杆模型是完全相同的,而在二维杆模型中实心杆和空心杆在处理内边界条件上有明显的不同,在本文1.2节中已经给出。结合2.1节及下面两空心杆撞击的二维数值仿真结果可以明显的看出由内边界条件不同带来的影响。同样从仿真结果中提取出两空心杆撞击过程中,杆中出现最大轴向应力时,空心杆中应力的分布情况。计算结果如图 3所示。
|
| 图3 空心杆轴向应力分布 Figure 3 Axial stress distribution in the hollow bar |
图 3中虚线仍表示两空心杆的撞击面。从图中可以看出,在两实心杆撞击过程中出现的应力集中现象,在两空心杆撞击过程中没再出现。在空心杆的纵截面轴向应力云图中,压缩波的波阵面呈明显的带状分布,而且在空心杆从撞击端到应力最大值所在的横截面之间的区域应力分布相对于实心杆中此区域的应力分布均匀很多。
当减小计算网格的边长时,从不同网格边长的计算结果中提取两杆撞击过程中,杆中出现最大轴向应力的时刻、位置及轴向应力值,如表 2所示。
| 网格边长/mm | 时刻/ μs | 位置/mm | 应力/MPa |
| 0.5 | 1.76 | (12.5,57) | 8.91 |
| 0.25 | 1.62 | (12.5,59.8) | 9.80 |
| 0.167 | 1.54 | (12.5,60.5) | 10.23 |
| 0.125 | 1.49 | (12.5,61.5) | 10.50 |
| 0.1 | 1.47 | (12.5,62.1) | 10.67 |
| 0.083 | 1.46 | (12.5,62.7) | 10.78 |
表 2中给出的位置是相对于杆的轴线及两杆的撞击端面的位置,括号中第一个值是与杆轴线的距离,第二个值是与撞击端面的距离。表 2中给出的时刻是以压缩波的波前到达该位置的时刻为零时刻。可以看出同两实心杆撞击一样,两空心杆撞击过程中轴向应力最大值出现的相对位置及相对时刻几乎不随计算网格边长的变化而变化,相对位置稳定在距离杆撞击端12倍空心杆壁厚左右的外壁上。横截面积相同的实心杆和空心杆的一维初等理论模型是相同的,所以这两个空心杆撞击的一维轴向应力解仍为7.07 MPa。从表 2可知考虑径向效应的两空心杆在撞击过程中的最大轴向应力大概为一维轴向应力解的1.5倍。
根据以上两空心杆撞击的数值计算结果可以发现,当两空心杆撞击时,杆中不会出现应力集中区域。撞击端至压缩波波前的区域中的应力分布比较均匀。撞击过程中的轴向应力最大值是有界的。
3 实验验证为了验证数值分析的结果,根据文献[5, 7]的实验原理。考虑到实心杆和空心杆都是轴对称形状,通过在半圆杆剖截面轴线上布置应变片来近似测量撞击过程中实心杆轴线处的轴向应力。通过在半圆管的内壁中线上布置应变片来近似测量空心杆内壁上的轴向应力。并在与之相对的表面位置上粘贴应变片,用来测得半圆杆及半圆管外表面上的轴向应变。用相同尺寸的圆管与圆杆,在距离碰撞端相同距离的外表面上粘贴应变片测量轴向应变作为对照试验。采用同样尺寸的圆杆与圆管作为冲击杆。为了降低撞击端面上的摩擦,在撞击杆与被撞击杆的端面上都涂有润滑油。
为了方便实验,仅在被撞击杆上粘贴应变片。实验采用的被撞击杆如图 4所示。撞击杆与被撞击杆都是采用6061-T6铝的铝杆和铝管,几何尺寸都与数值仿真中采用的几何尺寸一样。根据数值仿真的结果,在直径为20 mm的实心半圆杆的轴线上距离撞击端20 mm处及对应的半圆杆外表面上都贴有应变片。作为对比的同尺寸的圆杆也在距离碰撞端20 mm处的外表面上贴有应变片。外径为25 mm、内径为15 mm的半圆管在距离撞击端60 mm处的内表面中线上及对应的外表面上都贴有应变片。作为对比的同尺寸的圆管也在距离碰撞端60 mm处的外表面上贴有应变片。实验中使用的应变片型号为BX120-1AA,敏感栅长1 mm。

|
| 图4 被撞击杆 Figure 4 Impacted rod |
下面各应力历程图中的时间都是相对时间,零时刻是指压缩波的波前到达测量位置时的时刻。
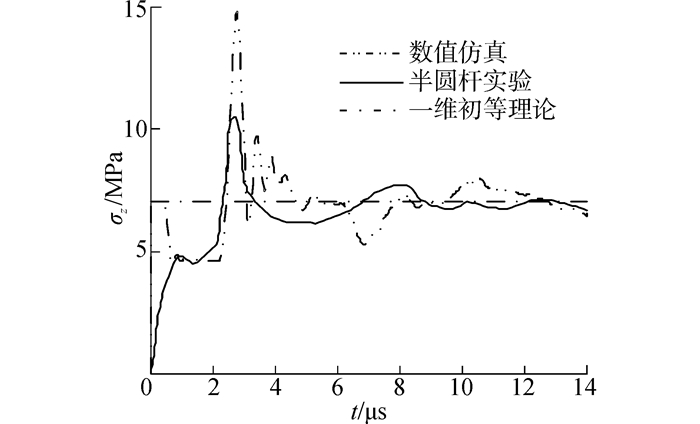
图 5和图 6中的数值仿真结果都是网格边长为0.167 mm的仿真结果。从图 5和图 6中可以看出,数值计算得到的应力历程与实验测得的应力历程是相似的。由图 5可知,与仿真结果一样,实验过程中在杆的轴线上确实存在应力升高的现象。由图 6可以看出,在距离碰撞端相同位置处,半圆杆外表面与圆杆外表面上的应力历程基本相符,说明半圆杆实验并不会对杆表面上的应力产生显著影响,因此可知在半圆杆轴线上测得的应力历程与圆杆轴线上的应力历程近似相符。
|
| 图5 距离撞击端20 mm处实心杆轴线上的轴向应力时间历程的实验和仿真结果 Figure 5 Experimental and numerical result at distance of 20 mm from impact on the solid rod center line |
|
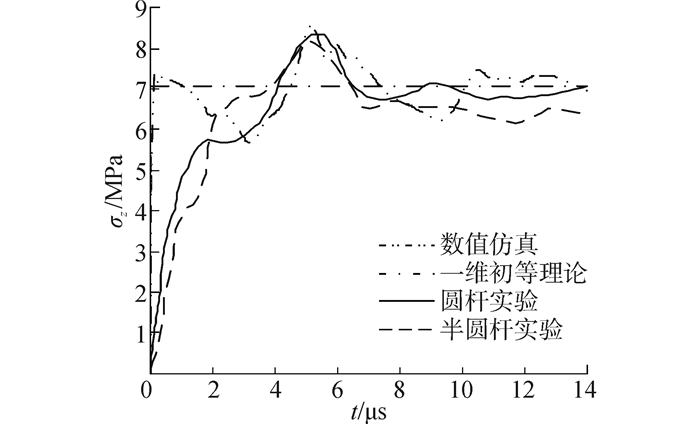
| 图6 距离撞击端20 mm处实心杆外表面上的轴向应力时间历程的实验和仿真结果 Figure 6 Experimental and numerical result at distance of 20 mm from impact on the solid rod surface |
对比图 5和图 6可以看出,当压缩波的波前到达测量位置后的2~6 μs这段时间内,各时刻杆轴线与杆表面上的轴向应力相差较大。可以说明这段时间内杆中的轴向应力分布极不均匀,结合图 5中测量到的应力峰值,据此可知这段时间内圆杆此处的轴线附近区域将发生应力集中。由数值结果及试验结果可知,一维初等理论不适用于两实心冲击杆的撞击端附近区域。
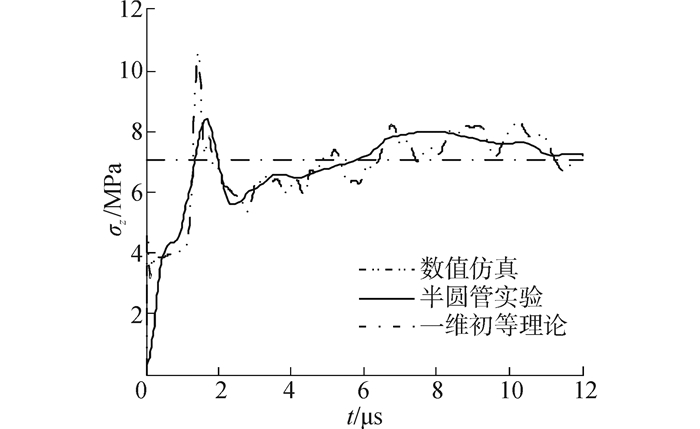
图 7和图 8中的数值仿真结果都是网格边长为0.083 mm的仿真结果。从图 7和图 8中可以看出,数值计算得到的应力历程与实验测得的应力历程基本相符。由图 8可以看出,在距离碰撞端相同位置处,半圆管外表面与圆管外表面上的轴向应力历程非常相似,说明采用半圆管进行实验并不会明显影响管外表面上的轴向应力,因此可知在半圆管内表面中线上测得的应力历程与圆管内表面上的应力历程近似相符。对比图 7和图 8可以看出,半圆管内表面和半圆管外表面上应力变化基本一致,几乎同时达到应力最大值,据此可知碰撞过程中圆管壁中的应力分布是比较均匀的,不会发生应力集中现象。
|
| 图7 距离撞击端60 mm处管内壁中线上的轴向应力 时间历程的实验和仿真结果 Figure 7 Experimental and numerical result at distance of 60 mm from impact on the tube’s internal surface center line |

|
| 图8 距离撞击端60 mm处管外壁中线上的轴向应力 时间历程的实验和仿真结果 Figure 8 Experimental and numerical result at distance of 60 mm from impact on the tube’s external surface center line |
利用二维Lax-Wendroff有限差分格式对两半无限圆杆和两半无限圆管的碰撞进行了数值模拟,并采用半圆杆和半圆管进行了碰撞实验并近似测量了内部的轴向应变。经对比仿真结果与实验数据有较好的一致性。
1) 数值仿真表明,对于两实心杆撞击,将在靠近撞击端1倍直径左右的区域发生明显的应力集中现象,当计算网格为0.167 mm时,应力集中区域的最大轴向应力为14.81 MPa,是一维初等理论轴向应力的2.1倍,并且数值结果还有继续升高的趋势。实验测得的半圆杆轴线上的应力历程及半圆杆外表面上的应力历程同样表明此区域确实发生了应力集中。
2) 从对两圆管撞击的数值仿真及半圆管的实验可知,圆管内表面和外表面上的轴向应力历程几乎相同。管壁内的轴向应力分布比较均匀。
3) 半圆杆轴线上测得的轴向应力历程可以近似圆杆轴线上的轴向应力历程。半圆管内表面中线上测得的轴向应力历程可以近似圆管内壁上的轴向应力历程。
综上,等横截面积的实心杆和空心杆在弹性撞击过程中,空心杆的轴向应力分布均匀,受力情况要优于实心杆。故在冲击机械中采用空心杆作为冲击杆件将能改善冲击杆的受力情况,提高设备的使用寿命。
| [1] |
王礼立.
应力波基础[M].2版. 北京: 国防工业出版社, 2005: 7 -9.
WANG Lili. Foundation of stress waves[M].2nd ed. Beijing: National Defence Industry Press, 2005: 7 -9. |
| [2] | DAVIES R M. Stress waves in solids[J]. British journal of applied physics, 1956, 7(6): 203–209. |
| [3] | BAKER W E, DOVE R C. Measurement of internal strains in a bar subjected to longitudinal impact[J]. Experimental mechanics, 1962, 2(10): 307–311. |
| [4] | BERTHOLF L D, KARNES C H. Axisymmetric elastic-plastic wave propagation in 6061-T6 Aluminum bars of finite length[J]. Journal of applied mechanics, 1969, 36(3): 533–541. |
| [5] | HABBERSTAD J L, HOGE K G, FOSTER J E. An experimental and numerical study of elastic strain waves on the center line of a 6061-T6 Aluminum bar[J]. Journal of applied mechanics, 1972, 39(2): 367–371. |
| [6] | HE L, MA G W, KARP B, et al. Investigation of dynamic saint-venant's principle in a cylindrical waveguide-experimental and numerical results[J]. Experimental mechanics, 2015, 55(3): 623–634. |
| [7] | LIN Xiao, BALLMANN J. A numerical scheme for axisymmetric elastic waves in solids[J]. Wave motion, 1995, 21(2): 115–126. |
| [8] |
黄吕权, 夏琴香, 唐耀辉. 锤杆的疲劳强度研究[J].
机械强度, 1992, 14(1): 33–39.
HUANG Lvquan, XIA Qinxiang, TANG Yaohui. Study on the fatigue strength of hammer rod[J]. Journal of mechanical strength, 1992, 14(1): 33–39. |
| [9] |
李夕兵, 古德生, 赖海辉. 冲击载荷下岩石动态应力-应变全图测试中的合理加载波形[J].
爆炸与冲击, 1993, 13(2): 125–130.
LI Xibing, GU Desheng, LAI Haihui. On the reasonable loading stress waveforms determined by dynamic stress-strain curves of rocks by SHPB[J]. Explosion and shock waves, 1993, 13(2): 125–130. |
| [10] |
李夕兵, 刘德顺, 古德生. 消除岩石动态实验曲线振荡的有效途径[J].
中南工业大学学报, 1995, 26(4): 457–460.
LI Xibing, LIU Deshun, GU Desheng. Effective method of elimilating the oscillation of rock dynamic stress-strain-strain rate curves[J]. Journal of central south university, 1995, 26(4): 457–460. |
| [11] |
邹广平, 王新征, 陈剑杰, 等. 空心锥撞击杆对分离式霍普金森压杆入射脉冲弥散的抑制效果分析[J].
兵工学报, 2012, 33(11): 1346–1351.
Guangping, WANG Xinzheng, CHEN Jianjie, et al. Restrain effect of hollow cone striker bar on incident pulse dispersion of split Hopkinson pressure bar[J]. Acta armamentarii, 2012, 33(11): 1346–1351. |
| [12] | KARP B, DURBAN D. Saint-Venant's principle in dynamics of structures[J]. Applied mechanics reviews, 2011, 64(2): 020801. |
| [13] | KARP B, DOROGOY A, WANG Zonggang. Non-uniform impact excitation of a cylindrical bar[J]. Journal of sound and vibration, 2009, 323(3/4/5): 757–771. |
| [14] | HE L, MA G W, KARP B, et al. Investigation of dynamic Saint-Venant's principle in a cylindrical waveguide-Analytical results[J]. International journal of impact engineering, 2014, 73: 135–144. |



