水下液压系统是液压技术在海洋工程领域的应用,由于海洋的特殊环境,使得水下液压系统设计须解决外部海水压力对系统的影响。早期水下液压系统是将动力源、控制单元和执行器分别安装在压力容器中防止海水压力对系统的影响[1],20世纪60年代,美国开始研制载人潜水器,水下液压技术迅速发展,这时期出现的压力补偿技术,可以消除海水压力对水下液压系统影响,使得水下液压系统设计可采用和陆上设计类似的方法,因此压力补偿技术是深海潜水器从第一代发展到第二代的标志[2]。
压力补偿技术依靠压力补偿器实现,目前得到应用的压力补偿器有皮囊式、波纹管式和橡胶膜片式[3],国外还有使用压缩空气瓶进行压力补偿的[4]。 这几种压力补偿器补偿压力跟随海水压力随动变化,且补偿器中未使用动力源,因此被称为被动式压力补偿器。
文献[5]设计了一种主动式压力补偿器,即使用一个微小油泵给执行器回油路始终施加一个略高于海水压力的补偿压力,使用这种压力补偿的水下液压系统,动力源和控制阀件均安装在潜水器内部常压环境,执行器件安装在潜水器外部海水环境,但其液压系统设计方法和陆上相比有较大不同,因此这种主动式压力补偿器被较少应用。
被动式压力补偿器中,皮囊、波纹管式和压缩空气瓶式适用对体积不发生变化的容腔进行补偿,被称为静态补偿,只有橡胶膜片式压力补偿器适用于对体积变化容腔进行补偿,水下液压系统属于体积变化容腔,因此须使用橡胶膜片式压力补偿器。
橡胶膜片又分为平膜片、波形膜片和滚动膜片[6],平膜片补偿量小;波形膜片补偿量大,但轴向形变与形变力成严重非线性[8];滚动膜片密封好、行程大、变形阻力小[10],因此滚动膜片式压力补偿器在目前的深海设备上得到广泛应用,我国“蛟龙”号载人潜水器的液压系统就使用了滚动膜片式压力补偿器。
滚动膜片压力补偿器适用于补偿体积变化容腔,因此其常和油箱设计为一体,补偿器既充作液压系统油箱,又可对整个液压系统进行压力补偿。目前滚动膜片压力补偿器设计依靠经验,对设计方法的研究较少且未成系统,现有研究仅限于对补偿容积的研究,文献[3]对补偿器工作容积进行了分析,但未考虑执行器和管路中油液被海水压缩后所需的补偿容积。为解决滚动膜片式压力补偿器定量、精确和可靠设计要求,本文对滚动膜片式压力补偿器进行了深入研究,建立了一套系统化设计方法。
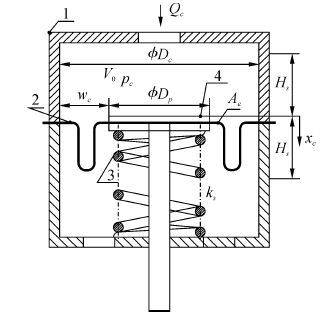
1 补偿压力稳态特性滚动膜片式压力补偿器工作原理类似于充气油箱,不同的是其内部初始压力由弹簧预压缩提供,在潜水器上浮或下潜过程中,由Δp=EΔV/V可知,海水压力挤压滚动膜片使得ΔV/V发生变化,补偿器内部压力随海水深度自动变化,且由于弹簧预压力的存在而始终略高于海水压力。使用压力补偿器的液压系统,其系统压力建立在海水压力基础上,系统可按照陆上设计方法进行设计而不必考虑外界海水压力[9]。采用压力补偿器的液压系统油箱须做成封闭式,并且补偿器容腔和油箱容腔相通。滚动膜片式压力补偿器原理如图 1所示。
弹簧的初始压缩量为x0,此时活塞所处的位置称为中位面,活塞具有中位面上下各为Hs的行程。补偿器垂直安装时,在工作点(x0,ps0),稳态时活塞受力平衡
| ${{p}_{c}}{{A}_{e}}+{{m}_{c}}g={{p}_{s0}}{{A}_{e}}+{{k}_{s}}({{x}_{0}}+{{x}_{c}})+k({{x}_{c}}){{x}_{c}}$ | (1) |
式中:pc为补偿(油箱)压力,Ae为滚动膜片等效面积,mc为活塞组件和滚动膜片总质量,ps0为某工作深度海水压力,ks为弹簧刚度,x0为弹簧预压缩量,xc为活塞稳态时位移,k(xc)为滚动膜片刚度。
式(1)变换为
| ${{p}_{c}}{{A}_{e}}+{{m}_{c}}g={{p}_{s0}}{{A}_{e}}+{{k}_{s}}{{x}_{0}}+{{k}_{x}}{{x}_{c}}$ | (2) |
式中:kx=ks+k(xc)。
稳态时补偿压力pc为
| ${{p}_{c}}={{p}_{s0}}+\frac{{{k}_{s}}{{x}_{0}}-{{m}_{c}}g+{{k}_{x}}{{x}_{c}}}{{{A}_{e}}}$ | (3) |
从式(3)可看出,稳态时补偿压力略高于海水压力,且跟随海水压力自动变化。在工作点(x0,ps0)点,滚动膜片内外压差pd是一个常量和一个变量之和:
| ${{p}_{d}}={{p}_{c}}-{{p}_{s0}}=\frac{{{k}_{s}}{{x}_{0}}-{{m}_{c}}g}{{{A}_{e}}}+\frac{{{k}_{x}}{{x}_{c}}}{{{A}_{e}}}$ | (4) |
式中:ksx0-mcg/Ae是常量,不受干扰量影响,kxxc/Ae是变量,受干扰量影响,补偿压力的波动即来源于此,后面将会详细分析。对于补偿器非垂直安装的工况,式(4)中的mcg取为在垂直方向的分量。
|
| 图1 滚动膜片式压力补偿器原理 Figure 1 Rolling diaphragm pressure compensator structure |
由式(4)知,在工作点(x0,ps0),补偿压力pc受kxxc影响会发生波动。
由于kx=ks+k(xc),ks为常值,k(xc)是补偿器膜片刚度,表示膜片轴向形变和形变阻力之间的关系,此值对补偿压力影响较大,对于滚动膜片,k(xc)近似为0,此时kx≈ks,这也是动态补偿领域采用滚动膜片的原因。
xc是补偿器活塞轴向位移,在工作点(x0,ps0),活塞发生位移xc的原因除了海水压缩滚动膜片形程的微小压缩位移,最主要是液压系统使用了非对称执行器(这对载人深潜器是非常普遍的工况)。非对称执行器工作会给补偿器注入阶跃流量qc,使得活塞发生较大位移,此位移会对补偿压力pc产生影响,并最终在稳态时产生一个稳态变量pcss。下面分析qc对pc的影响。
压力补偿器和油箱一体,其所组成容腔的初始体积为V0:
| ${{V}_{0}}={{V}_{cr}}+{{V}_{b}}$ | (5) |
Vcr是后面式(30)所确定的补偿容积,Vb是按照陆上液压系统设计方法所确定的油箱容积。非对称执行器动作时,会对油箱输入一个阶跃流量qc,设活塞位移为xc时V0变为V′0,流量连续性方程为
| ${{q}_{c}}={{A}_{e}}\frac{d{{x}_{c}}}{dt}+\frac{V_{0}^{\prime }}{E}\frac{d{{p}_{c}}}{dt}$ | (6) |
| $V_{0}^{\prime }={{V}_{0}}+{{A}_{e}}{{x}_{c}}$ | (7) |
由于Aexc相较于V0小的多,且远小于E,因此式(6)可写为
| ${{q}_{c}}={{A}_{e}}\frac{d{{x}_{c}}}{dt}+\frac{{{V}_{0}}}{E}\frac{d{{p}_{c}}}{dt}$ | (8) |
活塞组件和滚动膜片力平衡
| ${{p}_{c}}{{A}_{e}}-{{p}_{s0}}{{A}_{e}}-{{k}_{s}}{{x}_{0}}-{{k}_{x}}{{x}_{c}}={{m}_{c}}\frac{{{d}^{2}}{{x}_{c}}}{d{{t}^{2}}}+B\frac{d{{x}_{c}}}{dt}$ | (9) |
式(8)、(9)是补偿器动态方程,拉氏变换得
| ${{Q}_{c}}={{A}_{e}}s{{X}_{c}}+\frac{{{V}_{0}}}{E}s{{P}_{c}}$ | (10) |
| $({{P}_{c}}-{{p}_{s0}}){{A}_{e}}-{{k}_{s}}{{x}_{0}}-{{k}_{x}}{{X}_{c}}={{m}_{c}}{{s}^{2}}{{X}_{c}}+Bs{{X}_{c}}$ | (11) |
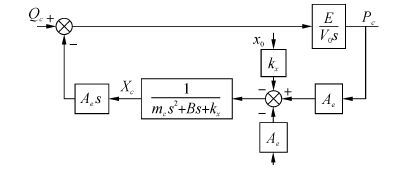
整理(10)、(11)两式可得传递函数框图如图 2所示。
|
| 图2 压力补偿器传递函数框图 Figure 2 Block diagram of system transfer function |
输入量是流量Qc,输出量是补偿压力Pc,海水压力ps0和弹簧预压缩量x0是常量,系统闭环传递函数为
| $\Phi \left( s \right)=\frac{{{P}_{c}}\left( s \right)}{{{Q}_{c}}\left( s \right)}=\frac{E({{s}^{2}}+\frac{B}{{{m}_{c}}}s+\frac{{{k}_{x}}}{{{m}_{c}}})}{{{V}_{0}}s({{s}^{2}}+\frac{B}{{{m}_{c}}}s+\frac{{{k}_{x}}+{{k}_{h}}}{{{m}_{c}}})}$ | (12) |
式中:
| $K={{k}_{h}}+{{k}_{x}}$ | (13) |
从式(13)看出,压力补偿器的等效刚度等于圆柱容腔液压弹簧刚度和弹簧刚度之和,两弹簧并联,这与实际情况相符。
qc为阶跃量,拉氏变换得
| ${{Q}_{c}}\left( s \right)=\frac{{{q}_{c}}}{s}$ | (14) |
因此补偿压力为
| ${{P}_{c}}\left( s \right)=\Phi \left( s \right){{Q}_{c}}\left( s \right)=\frac{C({{m}_{c}}{{s}^{2}}+Bs+{{k}_{x}})}{{{s}^{2}}({{m}_{c}}{{s}^{2}}+Bs+{{k}_{x}}+{{k}_{h}})}$ | (15) |
式中C=Eqc/V0。
使用符号运算工具将上式分解为基本环节:
| $\begin{align} & C(\frac{\frac{{{k}_{x}}}{K}}{{{s}^{2}}}+\frac{{{k}_{h}}}{{{K}^{2}}}(\frac{B}{s}+\frac{{{m}_{c}}Bs+{{B}^{2}}-{{m}_{c}}K}{{{m}_{c}}{{s}^{2}}+Bs+K}))= \\ & C(\frac{\frac{{{k}_{x}}}{K}}{{{s}^{2}}}+\frac{B{{k}_{h}}}{{{K}^{2}}}(\frac{1}{s}+\frac{s+\frac{B}{2{{m}_{c}}}}{{{(s+\frac{B}{2{{m}_{c}}})}^{2}}+{{\omega }_{d}}^{2}}+ \\ & \frac{{{B}^{2}}-2K{{m}_{c}}}{B\sqrt{4{{m}_{c}}K-{{B}^{2}}}}\frac{{{\omega }_{d}}}{{{(s+\frac{B}{2{{m}_{c}}})}^{2}}+{{\omega }_{d}}^{2}})) \\ \end{align}$ | (16) |
式中
根据潜水器使用工况,在时域研究输入流量qc对补偿压力pc的影响,式(16)拉氏反变换得
| $\begin{align} & {{p}_{c}}\left( t \right)=C(\frac{{{k}_{x}}}{K}t+\frac{B{{k}_{h}}}{{{K}^{2}}}(1+exp(-\frac{B}{2{{m}_{c}}}t)(cos({{\omega }_{d}}t)+ \\ & \frac{{{B}^{2}}-2K{{m}_{c}}}{B\sqrt{4{{m}_{c}}K-{{B}^{2}}}}sin({{\omega }_{d}}t))))= \\ & C(\frac{{{k}_{x}}}{K}t+\frac{B{{k}_{h}}}{{{K}^{2}}}(1+exp(-\frac{B}{2{{m}_{c}}}t)Asin({{\omega }_{d}}t+\varphi )))~ \\ & \varphi =arctan\frac{B\sqrt{4{{m}_{c}}K-{{B}^{2}}}}{{{B}^{2}}-2K{{m}_{c}}} \\ & A=\frac{2K{{m}_{c}}}{B\sqrt{4{{m}_{c}}K-{{B}^{2}}}} \\ \end{align}$ | (17) |
式(17)即为滚动膜片式压力补偿器在工作点(x0,ps0)处补偿压力波动方程。
2.2 补偿器结构参数对压力波动影响从式(17)可以看出,补偿压力变化量分为三部分。补偿压力波动产生的油液压缩量很小,所以有qc≈Aedxc/dt,同时V0kx$\ll $EAe2,首项可写为
| $C\frac{{{k}_{x}}}{K}t=\frac{E{{q}_{c}}{{k}_{x}}}{{{V}_{0}}{{k}_{x}}+EA_{e}^{2}}\approx \frac{{{q}_{c}}}{A_{e}^{2}}{{k}_{x}}t\approx \frac{{{k}_{x}}{{x}_{c}}}{{{A}_{e}}}$ | (18) |
从式(18)可以看出首项压力变化量主要是流量qc流入后造成的弹簧压缩所产生。
在补偿器容腔空气排净情况下,有kh≈K,次项可写为
| $C\frac{B{{k}_{h}}}{{{K}^{2}}}=\frac{B{{q}_{c}}}{A_{e}^{2}}\approx \frac{B}{{{A}_{e}}}\frac{d{{x}_{c}}}{dt}$ | (19) |
从式(19)可以看出次项压力变化量是由阻尼力产生,且只在动态过程中出现。
最后一项是活塞-滚动膜片组件的阻尼正弦振动,因阻尼很小,有B2$\ll $K,ωd≈ωn,正弦振动幅值可写为
| $\frac{CB{{k}_{h}}A}{{{K}^{2}}}=\frac{E{{q}_{c}}}{{{V}_{0}}{{\omega }_{d}}}\approx \frac{{{q}_{c}}}{{{A}_{e}}\sqrt{E{{m}_{c}}/{{V}_{0}}}}$ | (20) |
正弦振动频率ωd是液压弹簧和活塞组件构成的弹簧-质量系统有阻尼自然频率,正弦振动相角为φ,由
补偿压力波动峰值为
| $\begin{align} & {{p}_{cmax}}=\frac{{{q}_{c}}}{A_{e}^{2}}{{k}_{x}}t+\frac{B{{q}_{c}}}{{{A}_{e}}^{2}}+\frac{{{q}_{c}}}{{{A}_{e}}\sqrt{E{{m}_{c}}/{{V}_{0}}}}= \\ & \frac{{{q}_{c}}}{{{A}_{e}}}(\frac{{{k}_{x}}}{{{A}_{e}}}t+\frac{B}{{{A}_{e}}}+\sqrt{\frac{{{V}_{0}}}{E{{m}_{c}}}}) \\ \end{align}$ | (21) |
稳态时补偿压力变化量为
| ${{p}_{css}}=\frac{{{q}_{c}}{{k}_{x}}t}{A_{e}^{2}}$ | (22) |
从式(21)入手对补偿压力峰值的影响因素进行分析:
1) qc和Qct由系统负载工况决定,为确定值;
2)kx对压力影响较大,因此补偿器弹簧应设计为软弹簧,并要求补偿器膜片有小的变形阻力;
3) 阻尼B产生自油液与补偿器内壁作相对运动时的粘性阻尼,以及滚动膜片和补偿器内壁之间充满牛顿液体的平行平板运动的粘性阻尼,以及滚动膜片褶皱间的库伦摩擦阻尼;
4)V0由补偿体积和油箱体积确定,是某一确定值;
5) mc是活塞组件和膜片总质量,此值减小可提高系统阻尼比,增大可减小补偿压力波动峰值,但考虑E远大于mc,mc对峰值的影响不大,相反其对阻尼比影响较大,因此mc应尽量小,以减轻补偿器重量并提高阻尼比,同时mc减小也可减小补偿器非垂直安装时活塞质量对补偿压力稳态值的影响,并能提高滚动膜片的使用寿命;
6) Ae对补偿压力波动峰值影响显著,因此需将补偿器壳体内径设计的尽可能大。
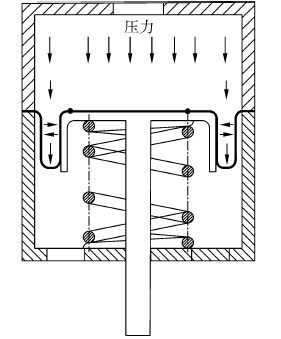
3 补偿器基本结构参数确定文献[3]给出了补偿器容积Vcr的估算公式,补偿容积的确定需要考虑温度、压力以及维护水平等诸多因素,无法进行定量描述,而仿真得到的结果是在7000m深度下,油液压缩率达到4.2%左右,因此Vcr可取文献[3]和仿真结果中较大值,而实际上“蛟龙”号应用了大量静态补偿,其补偿效果纯依赖于补偿容积的合适取值,而“蛟龙”号的历次下潜也证明了这种方法的可行性。在补偿容积Vcr确定情况下,补偿器设计最主要是确定基本结构参数:补偿器壳体内径Dc。前面通过分析得到Dc越大,补偿压力峰值越小,但Dc过大会降低膜片承压能力,并显著降低其寿命。图 3是滚动膜片式压力补偿器滚动膜片的受力分布。
滚动膜片的卷积宽度为
| ${{w}_{c}}=\frac{{{D}_{c}}-{{D}_{p}}}{2}$ | (23) |
式中:Dc为补偿器壳体内径,Dp为活塞直径。
由图 3可看出,大部分压力由活塞顶部支撑,小部分由膜片的狭窄卷积处支撑,卷积宽度过大,膜片承受内外压差能力下降,卷积宽度过小,滚动时膜片褶皱处互相摩擦影膜片寿命,活塞直径和补偿器壳体内径之间需满足如下关系[10]:
| $\frac{{{D}_{p}}+2\delta }{{{D}_{c}}-2\delta }=\varepsilon $ | (24) |
式中:ε取0.8~0.9,δ为滚动膜片厚度。
由式(23)、(24)得卷积宽度为
| ${{w}_{c}}=\frac{1-\varepsilon }{2}{{D}_{c}}+(\varepsilon +1)\delta $ | (25) |
滚动膜片的拉伸强度和膜片厚度关系:
| ${{\sigma }_{\tau }}={{K}_{\tau }}\delta $ | (26) |
式中:στ为滚动膜片的抗张力强度,Kτ为滚动膜片的抗张力系数。滚动膜片的爆裂压力,即所能承受的膜片最大内外压差为
| ${{p}_{b}}=\frac{2{{\sigma }_{\tau }}}{{{w}_{c}}}=\frac{2{{K}_{\tau }}\delta }{{{w}_{c}}}$ | (27) |
滚动膜片式压力补偿器实际是一个拥有可变体积和可活动侧壁的压力容器,因此基于较高安全系数,滚动膜片的安全工作压力为
| $~\left[ {{p}_{b}} \right]=\frac{{{p}_{b}}}{n}=\frac{2{{K}_{\tau }}\delta }{n{{w}_{c}}}$ | (28) |
式中:n为安全系数,一般取4。在进行补偿器设计时,补偿膜片内外压差峰值须小于安全工作压力,由式(4)、(28)得
| ${{p}_{dmax}}={{p}_{c}}-{{p}_{s0}}=\frac{{{k}_{s}}{{x}_{0}}-{{m}_{c}}g}{{{A}_{e}}}+{{p}_{cmax}}\le \left[ {{p}_{b}} \right]$ | (29) |
滚动膜片等效面积Ae=πDc2/4,由式(37)可得Dc需满足:
| $a{{D}_{c}}^{4}+b{{D}_{c}}^{3}+c{{D}_{c}}^{2}+d{{D}_{c}}+e\ge 0$ | (30) |
式中:a=Kτδ/n,
式(30)可根据费拉里求根公式确定Dc的取值域U。
对式(29)进行分析发现,滚动膜片内外压差峰值pdmax与Dc2成反比,而膜片安全工作压力pb与Dc成反比,因此补偿器壳体内径Dc越大,膜片强度的安全裕量越大,同时压力波动峰值pdmax也越小。因此可知由式(38)得到的Dc的取值域U只有下边界,即U=[m,+∞)。补偿器内径Dc在U内任取一值,均可满足滚动膜片强度要求。
补偿器壳体内径并不是可以无限大取值,其值必须满足深海潜水器设计者总体布置要求,假定某深海潜器总体设计要求补偿器内径不得大于Dz,考虑加工实际,内径Dc需取整数值,则补偿器实际内径取为
| ${{D}_{c}}={{D}_{z}},{{D}_{z}}\in U$ | (31) |
如果Dz∉U,则需调整ks、x0,或者更换滚动膜片型号,使得Dz∈U。
预充压力为活塞位于中位面时的补偿器内部压力。补偿器壳体内径Dc还受到弹簧限制,由式(4)可知,滚动膜片式压力补偿器的预充压力为
| ${{p}_{before}}=\frac{4\left( {{k}_{s}}{{x}_{0}}-{{m}_{c}}g \right)}{\pi {{D}_{c}}^{2}}$ | (32) |
预充压力pbefore一般取0.1×10-6~0.8×10-6 MPa,Dc太大,弹簧刚度ks或预压缩量x0需要做的很大,这将为潜水器的总体布置人员提出较大挑战。
|
| 图3 滚动膜片所受压力分布 Figure 3 Pressure distribution |
上述所建立的补偿器设计方法在一些深海设备上获得应用,图 4为其压力补偿器所使用的滚动膜片。

|
| 图4 滚动膜片 Figure 4 Rolling diaphragm |
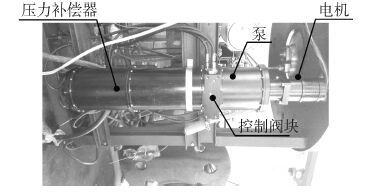
图 5为泵站基本结构,设计压力18 MPa,流量1 L/min,最大工作水深8 000 m。图 6为被其驱动的液压设备在90 MPa压力筒内作试验前的准备,试验压力78 MPa。
|
| 图5 压力筒内78MPa压力实验 Figure 5 Experiment in 90 MPa pressure cylinder |

|
| 图6 压力筒内78 MPa 压力实验 Figure 6 Experiment in 90 MPa pressure cylinder |
1) 建立了补偿压力数学模型,通过分析得出非对称执行器动作是造成补偿压力波动的主要因素;
2) 对非对称执行器动作造成补偿压力波动这一过程进行了数学建模,得到了稳态工作点处补偿压力波动峰值和滚动膜片内外压差峰值,并指出补偿器内径是影响压力波动峰值和内外压差峰值的主要结构参数,其应取大值;
3) 结合滚动膜片强度理论,依据滚动膜片内外压差峰值须小于滚动膜片安全工作压力这一设计准则,推导出补偿器内径的边界约束,得到了内径的取值域,并结合实际设计要求和工艺,得到了补偿器内径的取值方法;
4) 基于补偿器内径这一关键结构参数,设计了一些应用于深海设备的补偿器,并经过了大量压力筒试验,实际使用情况证明了该设计方法的可行性。
| [1] | ESTABROOK N, WHEELER H, UHLER D, et al. Development of deep-ocean work system[C]//Proceedings of the Oceans 75 Conference. San Diego, CA: IEEE, 1975, 7: 573-577. |
| [2] | GREENERT W. Navy's deep ocean technology project evolution and progress[C]//Proceedings of the IEEE 1971 Conference on Engineering in the Ocean Environment. San Diego, CA, USA: IEEE, 1971, 3: 50-53. |
| [3] |
孟庆鑫, 王茁, 魏洪兴, 等. 深水液压动力源压力补偿器研究[J].
船舶工程, 2000(2): 60–61.
MENG Qingxin, WANG huo, WEI Hongxing, et al. Development of pressure compensator for deep water hydraulic power station[J]. Ship engineering, 2000(2): 60–61. |
| [4] | LEE A E. Pressure equalizer: US, 2026548A[P]. 1953-05-19. |
| [5] |
李延民. 潜器外置设备液压系统的压力补偿研究[D]. 杭州: 浙江大学, 2005.
LI Yanmin. Research on the pressure compensation for external hydraulic systems of submersible vehicles[D]. Hangzhou: hejiang University, 2005. http://cdmd.cnki.com.cn/article/cdmd-10335-2006175700.htm |
| [6] | 吕百龄, 刘登祥. 实用橡胶手册[M]. 北京: 化学工业出版社, 2001 . |
| [7] | AXINTE I. Finite element analysis of the deformation of a rubber diaphragm[D]. Blacksburg, Virginia: Virginia Polytechnic Institute and State University, 2001. |
| [8] | 宁士夏. 滚动膜片的特性及其应用[J]. 特种橡胶制品, 1994, 15(3): 33–35. |
| [9] |
顾临怡, 罗高生, 周峰, 等. 深海水下液压技术的发展与展望[J].
液压与气动, 2013(12): 1–7.
GU Linyi, LUO Gaosheng, HOU Feng, et al. Development and future of deep-sea underwater hydraulic technique[J]. Chinese hydraulics & pneumatics, 2013(12): 1–7. |
| [10] | AMEDURI B, BOUTEVIN B, OSTOV G. Fluoroelastomers: synthesis, properties and applications[J]. Progress in polymer science, 2001, 26(1): 105–187. DOI:10.1016/S0079-6700(00)00044-7 |



