波浪破碎是海洋中常见的现象,是许多海洋工程和海岸工程问题的重要影响因素。深水波浪(主要是风浪)发生破碎,会产生白浪,破碎波若遇到建筑物会产生很大的冲击力[1]。然而由于实际海洋中的波浪破碎无论是在时间上,还是在空间中,存在着不连续的情况,这往往导致进行大洋中深水波浪破碎的连续观测是非常困难的。而在实验室中,可以控制波浪破碎产生的初始情况,同时详细的测量也是可行的。因此进行实验室的实验研究对于理解波浪破碎特点是一种重要的手段。Rapp等[2]提出了在实验室中利用聚焦波理论产生深水破碎波浪的方法,指出了频宽对聚焦波浪传播过程中破碎引起的能量和动量损失不显著。Kway等[3]利用聚焦波浪的方法产生了破碎波,对比了不同输入谱型时,分析了波浪传播过程中的波面变化及能谱变化,指出波浪破碎强度与一阶频谱高频部分的斜率有很强的相关性。Drazen [4]详细分析了势能变化受频宽的影响,得出了与Rapp等[2]相反的结论,指出频宽对势能的损失有比较明显的影响。黄金刚[5]利用实验的方法对频谱形式、频率宽度和中心频率对聚焦波浪传播过程中的波面特性、波谱演化的影响进行了详细分析,指出在中心频率相同时,频宽越大波幅越大,波前都越陡。王岩[4]通过实验进行了聚焦波浪的影响因素分析,指出中心频率越小产生的最大聚焦波幅越大,CWS谱型时产生的波前陡和整体波陡大于CWA谱型时。孙一艳[6]应用JONSWAP谱生成不同谱峰频率、不同频率范围和不同波幅的聚焦波浪,研究了波浪的聚焦过程、波面特性及振幅谱等的变化情况,并对聚焦波浪的非线性特性进行了详细的研究。
尽管国内外对聚焦波浪以及波浪破碎的非线性特性进行了大量的研究,但主要是集中在浅水或中等水深,一些学者[2-3, 7]提到的深水波浪也只是组成波的部分满足深水波浪,其次对于波浪破碎后波浪特征参数如群速、周期变化的研究很少。本文将在实验室中生成完全的深水聚焦波浪,并分析中心频率fc,频率范围Δf/fc以及频谱类型对波浪破碎过程中的波面特征及波参数的影响。
1 实验方法和设置 1.1 聚焦波的生成实验室采用能量聚焦的方法产生深水波浪破碎现象,该方法是由Longuet-Higgins (1974)[8]提出的,随后Rapp等[2]和其他一些学者[3, 7, 9]对该方法进行了发展和完善。所谓聚焦波浪即在水槽中生成一个含有不同频率波的波群,通过调整每个波浪成份的相位,使在预定位置处产生聚焦,从而形成破碎。其产生的机理是由于长波传播的快,短波传播的慢造成的。对于二维情况,根据线性叠加原理,波浪产生的自由水面可以表示为
| $\eta x,t=\sum\limits_{n=1}^{N}{{{a}_{n}}}cos\left( {{k}_{n}}x-{{\omega }_{n}}t+{{\varphi }_{n}} \right)$ | (1) |
式中:N为组成波的个数,an为第n个变量的振幅,kn为波数,ωn=2πfn为角频率,φn为初始相位。波数与频率满足色散关系:
| ${{\omega }_{n}}=g{{k}_{n}}tanh\left( {{k}_{n}}h \right)$ | (2) |
式中:g为重力加速度,h为水深。
设定在位置(xb,tb)发生聚焦,即各组成波的波峰在tb时刻在xb处叠加,令相位满足:
| $cos\left( {{k}_{n}}{{x}_{b}}-{{\omega }_{n}}{{t}_{b}}+{{\varphi }_{n}} \right)=1$ | (3) |
则各组成波的初始相位可写为
| ${{\varphi }_{n}}={{k}_{n}}{{x}_{b}}-{{\omega }_{n}}{{t}_{b}}+2\pi m\left( m=0,\pm 1,\pm 2,\ldots \right)$ | (4) |
将式(4)代入式(1),并取m=0,可得任意波面的自由水面表达式为
| $\eta \left( x,t \right)=\sum\limits_{n=1}^{N}{{{a}_{n}}}cos\left[ {{k}_{n}}\left( x-{{x}_{b}} \right)-{{\omega }_{n}}\left( t-{{t}_{b}} \right) \right]$ | (5) |
由此可知,对于给定的聚焦位置(xb,tb),影响聚焦波面的参数主要取决于各组成波的振幅值an。
在式(5)中,各组成波的振幅an取决于波浪的频谱分布形式,聚焦波波幅A由输入的频谱参数决定,假设把A定义为聚焦点处的波浪振幅,则有
| $A=\sum\limits_{n=1}^{N}{{{a}_{n}}}$ | (6) |
振幅谱一般可以采用多种形式,一是等振幅分布(CWA),即每个组成波的振幅相同,为常数,可得
| ${{a}_{n}}=\frac{A}{N}$ | (7) |
另一种称为等波陡分布(CWS),即每个组成波的波陡相同,即s=knan为常数,则有
| ${{a}_{n}}=A/\left( {{k}_{n}}\sum\limits_{n=1}^{N}{1}/{{k}_{n}} \right)$ | (8) |
此外谱型还可以采用PM谱[1],即
| $S\left( \omega \right)=0.78{{\omega }^{-5}}exp\left[ -1.25{{\left( {{\omega }_{m}}/\omega \right)}^{4}} \right]$ | (9) |
式中ωm为谱峰频率。由于实际在大波峰区域内,极限波的平均波形同海浪谱的自相关函数的形状基本一致,对于波浪中的最大波,其振幅可由瑞利分布给出,则生成聚焦波组成波的振幅可表示为
| ${{a}_{n}}=A\sqrt{2S\left( \omega \right)\Delta \omega }/\sum\limits_{n=1}^{N}{\sqrt{2S\left( \omega \right)\Delta \omega }}$ | (10) |
另外我们假设离散频率fn均匀分布在频率区间[f1,f2]内,可以定义频率区间的宽度和中心频率分别为
| $\Delta f={{f}_{2}}-{{f}_{1}}$ | (11) |
| ${{f}_{c}}=\frac{1}{2}\left( {{f}_{1}}+{{f}_{2}} \right)$ | (12) |
实验是在大连理工大学海岸和近海工程国家重点实验室的波流水槽内进行的,水槽长69 m,宽4 m,深2.5 m,最大工作水深2.0 m,本次实验水深h=1.5 m。配有引进美国MTS公司的不规则波造波机,微机控制与数据采集系统及2台0.8 m3/s轴流泵的双向造流系统。每次实验需要有8-10 min的时间间隔,以保证水槽水面恢复平静。在水槽的末端布置吸波装置,减小波浪反射的影响。
1.2.2 浪高仪布置波面的测量是通过沿水槽波浪传播方向布置的22个电阻式浪高仪测量的,浪高仪的具体位置如图 1中所示。浪高仪在正式实验前,都进行了严格的率定,以确保测量的精度。浪高仪采集频率为100 Hz,即采集间隔为0.01 s。实验中,采集时长为163.84 s。
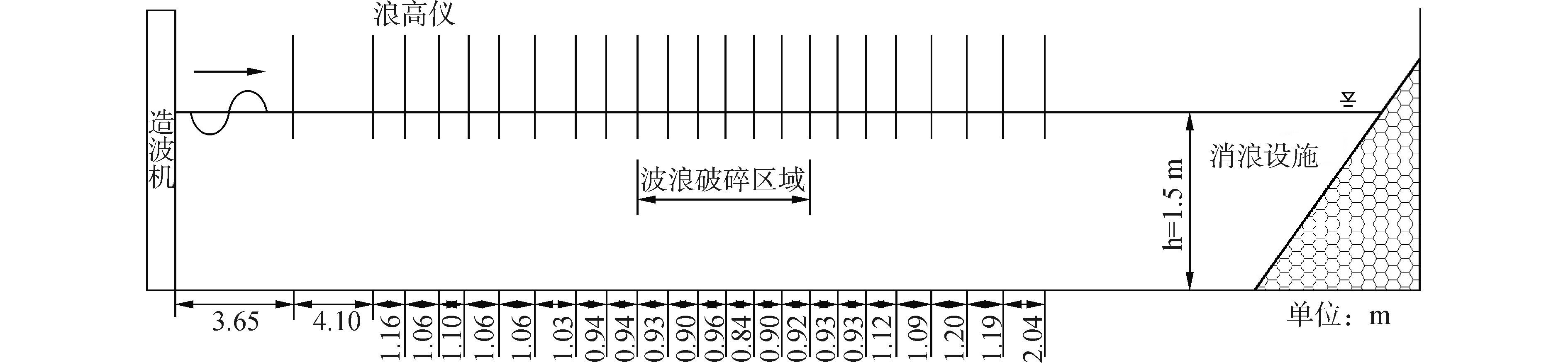
|
| 图1 实验布置简图 Figure 1 Experimental layout schematic |
深水聚焦波浪生成过程中,由1.1节聚焦波浪的生成原理可知,生成的波面特性可以表示为以下的参数的函数:
| $\eta =f\left[ A,N,{{f}_{c}},\Delta f,{{x}_{b}},{{t}_{b}},h \right]$ |
由式(13)知,当聚焦波的水深h,聚焦位置xb、聚焦时间tb以及波长波个数N给定时,影响聚焦波浪特性的主要参数有聚焦振幅A,中心频率fc,频率范围Δf,而聚焦振幅A的计算与谱型有很大的关联。本文将设置9种工况实验来分析,中心频率fc,频率范围Δf以及频谱类型对波浪破碎过程中的波面特征及波参数的影响。不同工况的各参数见表 1。工况1、2、3用来分析中心频的影响,工况4、5、6用来分析频宽的影响,工况7、8、9用来分析谱型的影响。每组工况进行三次重复试验,取三次实验的平均值作为实验结果进行分析。
| 工况 | fc | Sinput | Δf/fc | 谱型 |
| 1 | 0.943 | 0.35 | 0.46 | CWS |
| 2 | 1.019 | 0.35 | 0.46 | CWS |
| 3 | 1.093 | 0.35 | 0.46 | CWS |
| 4 | 1.019 | 0.38 | 0.288 | CWS |
| 5 | 1.019 | 0.38 | 0.359 | CWS |
| 6 | 1.019 | 0.38 | 0.455 | CWS |
| 7 | 1.019 | 0.38 | 0.46 | CWS |
| 8 | 1.019 | 0.38 | 0.46 | CWA |
| 9 | 1.019 | 0.38 | 0.46 | PM |
由于我们研究的是聚焦波(即波群)在深水中的传播及破碎特性,这里提到的特征波参数主要是指与波群有关的参数,如最大波面陡度、特征群速,特征波频,特征周期等。对波特征参数的分析,有助于我们了解波浪破碎过程中的破碎特征。
2.1.1 最大波面陡度聚焦波浪传播过程中,随着向聚焦位置接近,组成波逐渐叠加,波面的陡度将会逐渐变大。为此我们定义最大波面陡度:
| ${{S}_{max}}={{k}_{s}}{{\eta }_{max}}$ |
式中:ks为谱权重波数,ηmax为水槽不同位置处浪高仪获得的最大波高值。
2.1.2 特征群速准确的描述聚焦波的特征群速对于利用波面过程线计算沿程能量损失是必要的[10]。用中心频率对应的群速来描述聚焦波的传播是比较常用的,但是对于本文中的实验情况,如等波陡(CWS)情况,以及波浪传播过程由于波谱的演化,存在着低频部分能量较高频部分能量大,若用中心频对应的群速来描述会显得不够准确,因此Drazen 等[10]提出了更好的描述聚焦波传播特性的群速,即“谱权重群速”(Cgs),来作为描述波群传播的特征群速:
| ${{C}_{gs}}=\frac{\sum \left( {{C}_{gn}}a_{n}^{2} \right){{\left( \Delta f \right)}_{n}}}{\sum \left( a_{n}^{2} \right){{\left( \Delta f \right)}_{n}}}$ |
式中:an和Cgn分别表示第n个组成波的振幅和线性波速,(Δf)n表示的是各组成波的频率差,此处取常值。Drazen 等[10]指出通常学者选择的中心频率群速(Cgc)在表征波群速度时较小,Tian 等[11]也通过对比Cgs和Cgc,认为Cgs能更好的表征聚焦波传播速度,因此此处采用Cgs作为特征群速。
2.1.3 特征波频此外Tian 等[11]指出采用“谱权重波频”基于线性波浪理论和有限水深色散关系时得出的群速与“谱权重群速Cgs”更接近,同时考虑与谱权重群速Cgs保持统一,因此选择“谱权重波频”作为特征波频,定义为
| ${{f}_{s}}=\frac{\sum \left( {{f}_{n}}a_{n}^{2} \right)\left( \Delta {{f}_{n}} \right)}{\sum \left( a_{n}^{2} \right){{\left( \Delta f \right)}_{n}}}$ |
式中:fn表示第n个组成波的频率。同时根据fs按照线性色散关系得出相应的特征波数ks。
2.1.4 整体波陡Rapp等[2]首次提出了利用整体波陡(Sc=kca,kc为中心频率,a为聚焦点处波幅)来表征波浪破碎的强度。随后一些学者得出了按Skn=∑knan定义整体波陡,并得出了与Rapp等[2]相似的结论。此处采用与Tian 等[11]相同的定义方法,即
| $S={{k}_{s}}\sum {{a}_{n}}$ |
式中:an是根据浪高仪波面数据通过快速傅里叶变化得到的振幅谱值。距离造波板最近的第一个浪高仪得出的整体波陡定义为入射整体波陡,定义为Sinput。
2.1.5 谱平均周期由谱矩计算波浪周期有多种公式,相当于按波面上跨零点法定义的平均周期[1],计算公式为
| $\begin{align} & {{T}_{02}}=\sqrt{\frac{{{m}_{0}}}{{{m}_{2}}}},{{m}_{0}}=\int_{0}^{\infty }{E\left( f \right)}df \\ & {{m}_{2}}=\int_{0}^{\infty }{{{f}^{2}}}E\left( f \right)df \\ \end{align}$ |
在计算波特征参数时,式中的an、fn、(Δf)n根据浪高仪波面数据进行谱分析得出的振幅谱进行选取。由3.2节波谱分析可知,本文中聚焦波浪的能量主要集中在[0.6 Hz,1.5 Hz]频率范围内,为充分考虑各组成波的影响,本文在计算波特征参数时频率截取范围取[0.3 Hz,4.0 Hz]。
2.2 波能谱分析波浪在沿水槽传播、聚焦以及发生破碎的过程中,波面发生了很大的变化,这表明波浪的能量在频域上亦有很大的变化。通过对水槽沿程不同位置处波浪能量在频域分布的变化分析,可以了解波浪破碎过程中耗散谱的情况,也就是能量耗散在频域上的分布情况。为此,对水槽沿程不同位置处的波面数据,采用快速傅里叶变化(FFT)方法进行谱分析。实验中,对浪高仪记录的波面数据以最大波高为中心,左右对称截取20.46 s的波面数据,进行谱分析,这样既能包含所有主要的波成分,又能避免由于分析时间过长而掺入反射波的影响。
3 实验结果讨论 3.1 中心频的影响图 2是CWS谱时不同中心频下最大波面高度(图 2(a))与最大波面陡度(图 2(b))沿水槽变化情况,可以看出,随着波浪向破碎区域传播,由于波浪叠加,最大波面高度和最大波面陡度都逐渐变大。在相同波浪破碎强度时(Sinput一致),中心频越小越能产生较大的波面高度,而最大波面陡度在不同中心频时比较一致,在CWA和PM谱时存在相似的规律。

|
| 图2 CWS谱时不同中心频下最大波面高度和最大波面陡度沿水槽分布 Figure 2 The change of maximum wave height and maximum wave surface steepness for different center frequencies along the flume when it is CWS spectrum |
图 3是CWS谱型下中心频分别为fc=0.943 Hz(图 3(a))、1.019 Hz(图 3(b))、1.093 Hz(图 3(c))时水槽不同位置处的波能谱图;虚线为初始位置处(x=3.65 m)的谱,x=11.07 m、x=15.16 m为破碎前位置,x=18.89 m、x=20.63m为破碎带位置,x=24.53 m、x=30.05 m为破碎后位置。可知,相同波浪破碎强度时,中心频越小,谱能密度峰值越大,且谱包络总能量也越大。

|
| 图3 CWS谱下不同中心频时波谱沿水槽变化图 Figure 3 The change of wave spectrum for different center frequency along the flume when it is CWS spectrum |
在波浪传播过程中,由于非线性和波浪破碎作用,波能在高频产生显著的耗散,且存在着波能由高频向低频转移,波谱峰值增加现象。由于Δf/fc相同,中心频越小,频宽绝对值越小,能量在相应的高频处耗散越明显,低频增加的也更加显著。不同中心频时,随着聚焦波浪的传播和破碎,频宽都逐渐变窄。
图 4是CWS谱型下不同中心频时,特征波参数沿水槽变化情况,相同破碎强度时,中心频越大,相应的Cgs和T02越小。波浪破碎导致特征波参数在破碎区域上下游产生了变化,使得Cgs和T02下游比上游增加,fs下游比上游减少。相同破碎强度时,中心频fc=0.943 Hz时,破碎区域下游的fs平均减小了约5.3%,Cgs和T02分别平均增大了约5.6%;中心频fc=1.019 Hz时,破碎区域下游的fs平均减小了约5.6%,Cgs和T02分别平均增大了约5.8%和5.9%;中心频fc=1.093 Hz时,破碎区域下游的fs平均减小了约5.3%,Cgs和T02分别平均增大了约5.2%和5.8%。可以看出,不同中心频下波浪破碎导致的特征波参数的改变率比较一致,没有显著的差异。

|
| 图4 CWS谱下不同中心频时Cgs、T02和fs沿水槽变化 Figure 4 The change of Cgs、T02 and fs for different frequencies when it is CWS spectrum |
图 5是CWS谱时不同频宽下最大波面高度(图 5(a))与最大波面陡度(图 5(b))沿水槽变化情况,可以看出,相同破碎强度时,不同频宽时在水槽不同位置产生的最大波面高度在破碎前比较接近,而破碎发生后,频宽越大,会有较大的波面高度存在。而最大波面陡度在破碎前频宽比较宽时相对略大,破碎后比较接近。

|
| 图5 CWS谱时不同频宽下最大波面高度和最大波面陡度沿水槽分布 Figure 5 The change of maximum wave height and maximum wave surface steepness for different frequency bandwidth along the flume when it is CWS spectrum |
图 6是CWS谱下频宽Δf/fc=0.288(图 6(a))、Δf/fc=0.359(图 6(b))、Δf/fc=0.455(图 6c)时水槽不同位置处的波能谱图;虚线为初始位置处(x=3.65 m)的谱,x=11.07 m、x=15.16 m是破碎前位置,x=18.89 m、x=20.63 m为破碎带位置,x=24.53 m、x=30.05 m为破碎后位置。在相同波浪破碎强度下,由于频宽的增加,使得波能在频宽区间上分布更加平缓,波谱峰值也相应的减小。聚焦波传播过程中,由于非线性和波浪破碎作用,波能在高频产生显著的耗散,且存在着波能由高频向低频转移,即低频处能量增加,波谱峰值增加。频宽越大,破碎后会产生越明显的频宽变窄现象。通过对波谱包络总能量沿水槽变化的分析可知,频宽对破碎导致的能量损失不产生明显的影响。
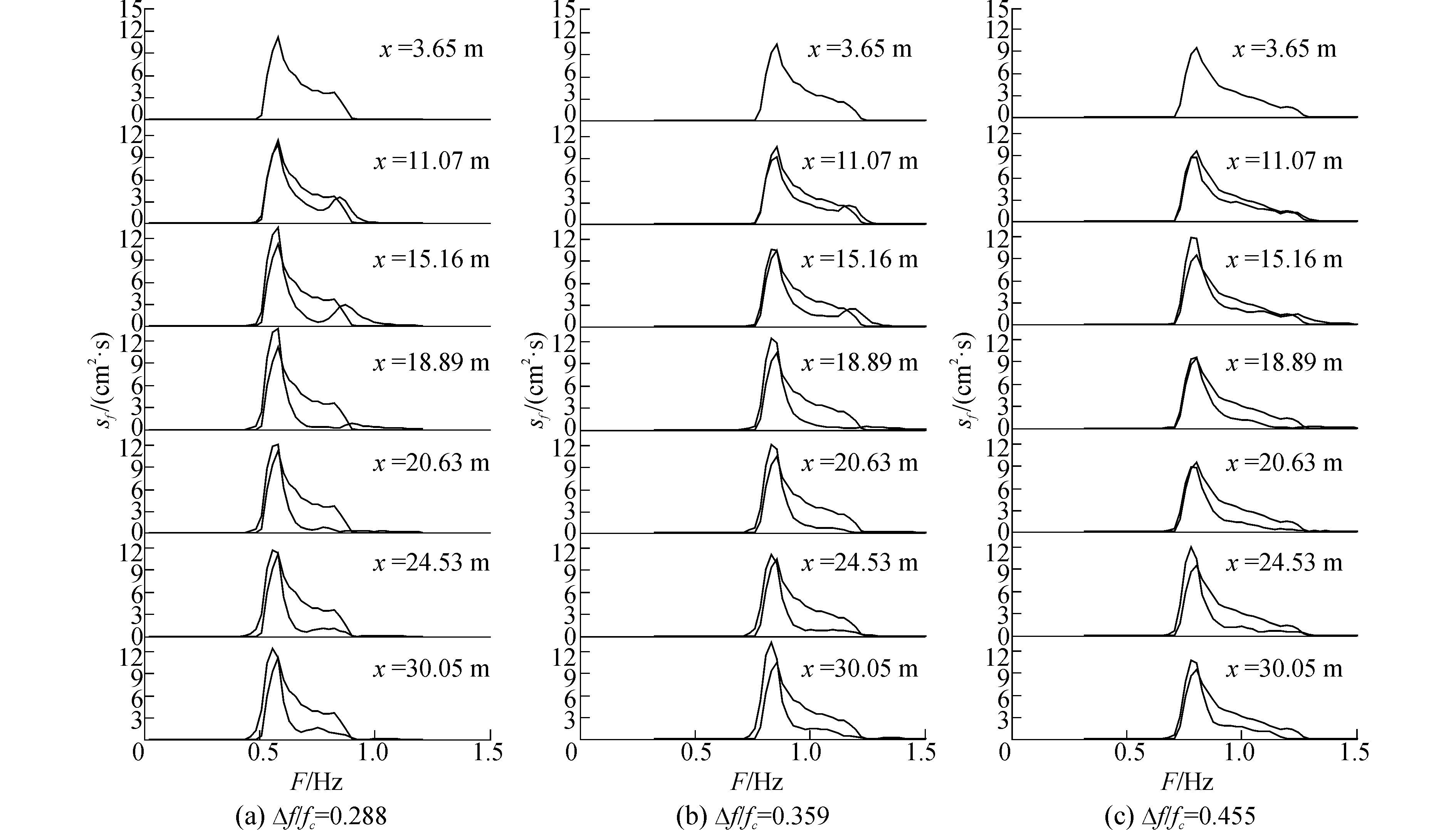
|
| 图6 CWS谱下不同频宽时波谱沿水槽变化图 Figure 6 The change of wave spectrum for different frequency bandwidth along the flume when it is CWS spectrum |
图 7为CWS谱型下不同频宽时,特征波参数沿水槽变化情况,相同破碎强度时,频宽越宽,相应的Cgs和T02越大,而fs越小。波浪破碎导致破碎区域下游Cgs和T02增加,而fs减小。相同破碎强度时,频宽Δf/fc=0.288时,破碎区域下游的fs平均减小了约6.1%,Cgs和T02分别平均增大了约6.1%和6.7%;频宽Δf/fc=0.359时,破碎区域下游的fs平均减小了约6.4%,Cgs和T02分别平均增大了约6.6%和6.9%;频宽Δf/fc=0.455时,破碎区域下游的fs平均减小了约6.4%,Cgs和T02分别平均增大了约6.4%和7.1%。由此可以看出,波浪破碎导致的特征波参数的改变率在不同频宽时比较接近,受频宽变化的影响不明显。

|
| 图7 不同频宽时Cgs、T02和fs沿水槽变化 Figure 7 The change of Cgs、T02 and fs for different frequency bandwidth when it is CWS spectrum |
图 8是不同谱型时,最大波面高度与最大波面陡度沿水槽分布情况。可以看出,相同破碎强度时,破碎前后,PM谱产生更大的最大波面高度,CWS谱次之,CWA谱最小。相应的最大波面陡度,在破碎前仍是PM谱产生更大的最大波面陡度,CWS谱次之,CWA谱最小,但之间的差别较最大波面高度明显减小;破碎后,三种谱下的最大波面陡度较接近。
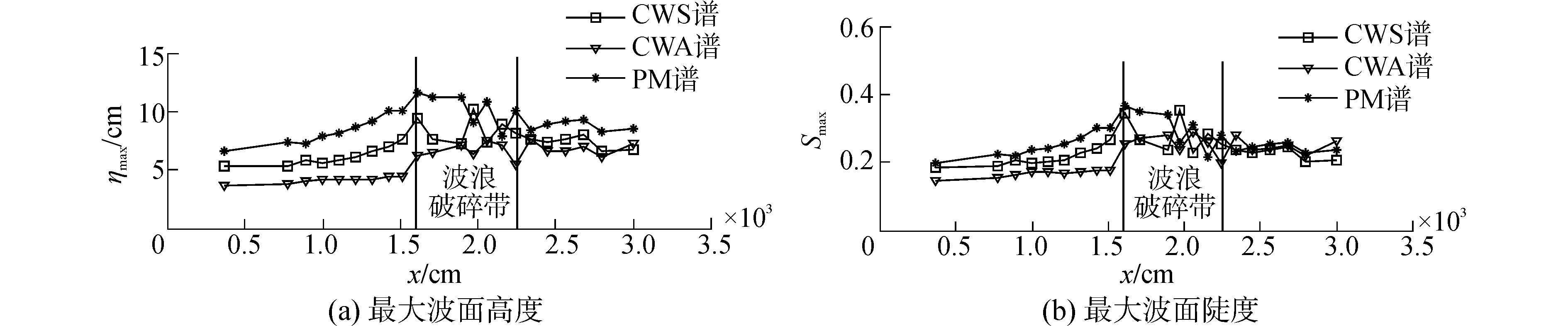
|
| 图8 不同谱型时最大波面高度和最大波面陡沿水槽分布 Figure 8 The change of maximum wave height and maximum wave surface steepness for different spectrum types along the flume |
图 9是CWS谱型(图 9(a))、CWA谱型(图 9(b))和PM谱型(图 9c)时水槽不同位置处的波能谱图;虚线为初始位置处(x=3.65 m)的谱,x=11.07 m、x=15.16 m是破碎前位置,x=18.89 m、x=20.63 m为破碎带位置,x=24.53 m、x=30.05 m为破碎后位置。由初始波能谱可以知道,相同波浪破碎强度时,PM谱时具有的波能谱峰值最大,超过了25 cm2·s,CWS谱时次之,谱密度峰值可达到9 cm2·s,CWA谱时最小,约为3.5 cm2·s;而相应的虽然中心频和频宽相同,PM谱时能量更加集中在峰频附件,CWS谱时次之,CWA谱时沿频宽分布最均匀,这是由造波时输入的谱型决定的。聚焦波传播及破碎过程中,CWA谱时,谱型变化最为剧烈,高频部分能量损失最为明显,能量向低频转移情况也最为显著;PM谱型时,在波浪传播与破碎过程中,谱型形态保持的最为稳定;由远离破碎位置(x=30.05 m)处的谱型形态来看,三种不同初始能量分布谱型形态下,随着波浪的传播和破碎的产生,三种都趋于向比较稳定的PM谱型形态演化,以达到稳定。此外,破碎会导致CWS和CWA谱型时的低频部分能量增加,即波能谱峰值增大,而PM谱时相反,低频部分能量有所减小。三种谱型下,都存在着峰频向低频移动现象。三种谱型下,随着波浪的传播,谱宽都逐渐收窄,此时的波浪才更加稳定。
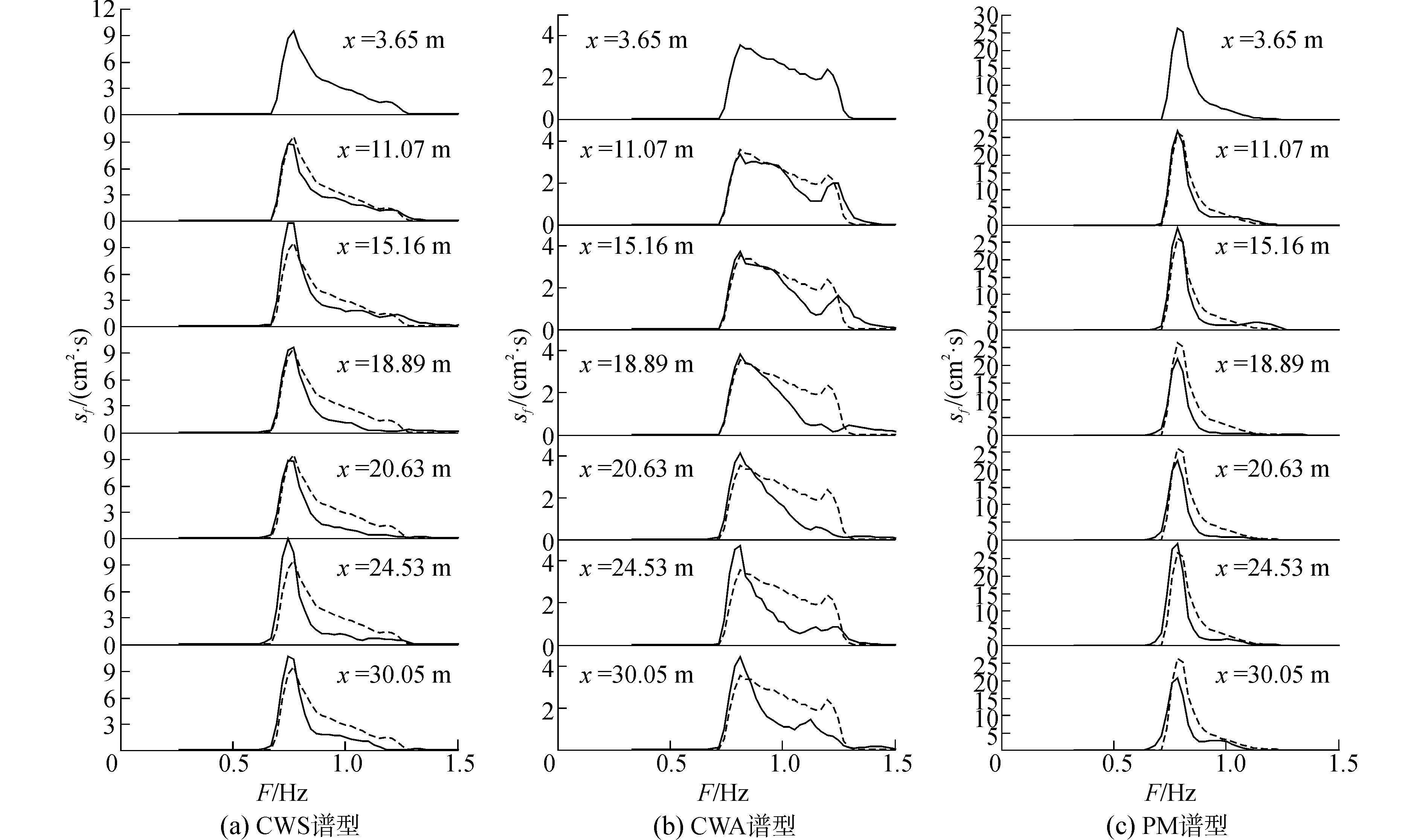
|
| 图9 不同谱型时波谱沿水槽变化图 Figure 9 The change of wave spectrum for different spectrum types along the flume |
图 10为不同谱型下,特征波参数沿水槽变化情况。相同破碎强度时,PM谱型下,产生的Cgs和T02最大,而fs最小,CWS谱型时次之,CWA谱型时产生的Cgs和T02最小,而fs最大。相同破碎强度时,PM谱型时,破碎区域下游的fs平均减小了约3.8%,Cgs和T02分别平均增大了约3.7%和4.3%;CWA谱型时,破碎区域下游的fs平均减小了约5.6%,Cgs和T02分别平均增大了约6.4%和5.5%;CWS谱型时,破碎区域下游的fs平均减小了约6.8%,Cgs和T02分别平均增大了约6.9%和7.5%。可以看出,破碎强度相同时,PM谱型下波浪破碎导致的波特征参数变化率最小,CWA谱型下次之,CWS谱型下的影响最为显著。这主要是由于不同谱型下,能量的耗散程度和引起的能量转移和谱型变化有直接的关系(见图 9)。

|
| 图10 不同谱型时Cgs、T02和fs沿水槽变化 Figure 10 The change of Cgs ,T02 and fs for different spectrum types |
本文基于聚焦波浪理论生成了深水聚焦波,并产生了波浪破碎,研究了中心频率fc,频率范围Δf/fc以及频谱类型对波浪破碎过程中的波面特征及波参数的影响。
在破碎波浪产生的过程中,随着波浪的聚焦,波面陡度逐渐增大,波浪的稳定性降低,当波浪的波面陡度足够大时,破碎会随之产生,这表明波面的最大陡度可以作为表征波浪传播过程中稳定性的特征参数。通过分析中心频、频宽和谱型对波浪传播过程中的最大波面高度和最大波面陡度的影响,可以看出,相同的波浪破碎强度时,在波浪传播过程中,中心频对波浪的稳定性影响很小,频宽略有影响,而谱型对波面最大陡度的影响比较明显,尤其在破碎前,这种影响更加显著。
相同波浪破碎强度时,中心频越小,频宽越窄,谱型为PM谱时,谱能密度峰值越大,且谱包络总能量也越大;中心频越小,频宽越窄,谱型为CWA谱时,高频耗散的越明显,低频增加的也更加显著。对比来看,谱型为PM谱,频宽越窄,波谱越稳定。
对比了不同因素对波特征参数变化率的影响。中心频和频宽的变化,对波浪特征参数的变化率不产生明显的影响,而谱型的影响相对较大。PM谱型下波浪破碎导致的波特征参数变化率最小,CWA谱型下次之,CWS谱型下的影响最为显著。这主要是由于不同谱型下,能量的耗散程度和引起的能量转移和谱型变化有直接的关系。
有关深水波浪破碎过程中能量损失和耗散的量化,以及破碎导致的波浪参数变化的影响因素量化将在下一步研究中展开。
| [1] | 俞聿修. 随机波浪及其工程应用[M]. 大连: 大连理工大学出版社, 1999 . |
| [2] | RAPP R J, MELVILLE W K. Laboratory measurements of deep-water breaking waves[J]. Philosophical transactions of the royal society of London. Series A:, mathematical, physical and physical sciences, 1990, 331(1662): 735–800. |
| [3] | KWAY J H L, LOH Y S, CHAN E S. Laboratory study of deep-water breaking waves[J]. Ocean engineering, 1998, 25(8): 657–676. |
| [4] |
王岩. 聚焦波浪特性研究及其对直墙的作用[D]. 大连:大连理工大学, 2007.
WANG Yan. The characteristic research and effect to vertical wall of focusing wave[D]. Dalian:Dalian University of Technology, 2007. |
| [5] |
黄金刚. 二维聚焦极限波浪的模拟研究[D]. 大连:大连理工大学, 2004.
HUANG Jingang. Simulation studies of 2-D focusing extreme wave[D]. Dalian:Dalian University of Technology, 2004. |
| [6] |
孙一艳. 二维聚焦波浪及其与直立圆柱作用的研究[D]. 大连:大连理工大学, 2010.
SUN Yiyan. Studies of 2-D focusing wave and interactions with a vertical cylinder[D]. Dalian:Dalian University of Technology, 2010. |
| [7] | DRAZEN D. Laboratory studies of nonlinear and breaking surface waves[D]. San Diego:University of California, 2006. |
| [8] | LONGUET-HIGGINS M S. Breaking waves in deep or shallow water[C]//Proceedings of the 10th Conference on Naval Hydrodynamics. Cambridge:MIT, 1974:597-605. |
| [9] | LOEWEN M R, MELVILLE W K. Microwave backscatter and acoustic radiation from breaking waves[J]. Journal of fluid mechanics, 1991, 224: 601–623. |
| [10] | DRAZEN D A, MELVILLE W K, LENAIN L. Inertial scaling of dissipation in unsteady breaking waves[J]. Journal of fluid mechanics, 2008, 611: 307–332. |
| [11] | TIAN Zhigang G, PERLIN M, CHOI W. Energy dissipation in two-dimensional unsteady plunging breakers and an eddy viscosity model[J]. Journal of fluid mechanics, 2010, 655: 217–257. |


