2. Wuhan Institute of Shipbuilding Technology, Wuhan 430050, China
在锥-柱结合部位引入环壳,以其双曲率的几何形状,可以使得锥柱结合处应力分布平缓。这是锥-环-柱结合壳相对于普通锥-柱结合壳的明显优势[1]。经过系列模型试验及理论分析[2-7],证明了加肋锥-环-柱结合壳(以下简称锥-环-柱结合壳)是一种优越的连接结构形式。目前部分学者对圆柱壳结构的初始几何缺陷形态及其对力学性能的影响进行了系列研究[8-12],介绍了耐压结构初始几何缺陷的形成及对其力学性能的影响。张二等[13-14]研究了初始几何缺陷对含加肋凸型锥-环-柱结合壳连接分段应力和稳定性的影响,提出了对其影响较大的典型初始几何缺陷形态。
本文研究局部初始几何缺陷对含凸锥-环-柱结合壳连接分段极限承载能力的影响。根据已有锥-环-柱模型形状测量报告以及现行规范[15]对初始几何缺陷的要求,针对锥-环-柱结合壳加工工艺,探讨了环壳附近局部初始几何缺陷形状特征,并在此基础上设计了初始几何缺陷不同组合形式的计算方案。采用计算机仿真技术,分析各种初始几何缺陷形态对含凸锥-环-柱结合壳连接分段极限承载能力的影响规律;选取典型初始几何缺陷组合,分析初始几何缺陷幅值变化对极限载荷影响的同时,探讨连接分段极限载荷几何修正系数的计算方法。最后根据分析结果,对含凸型锥-环-柱结合壳连接分段加工制造过程中的偏差控制提出建议。
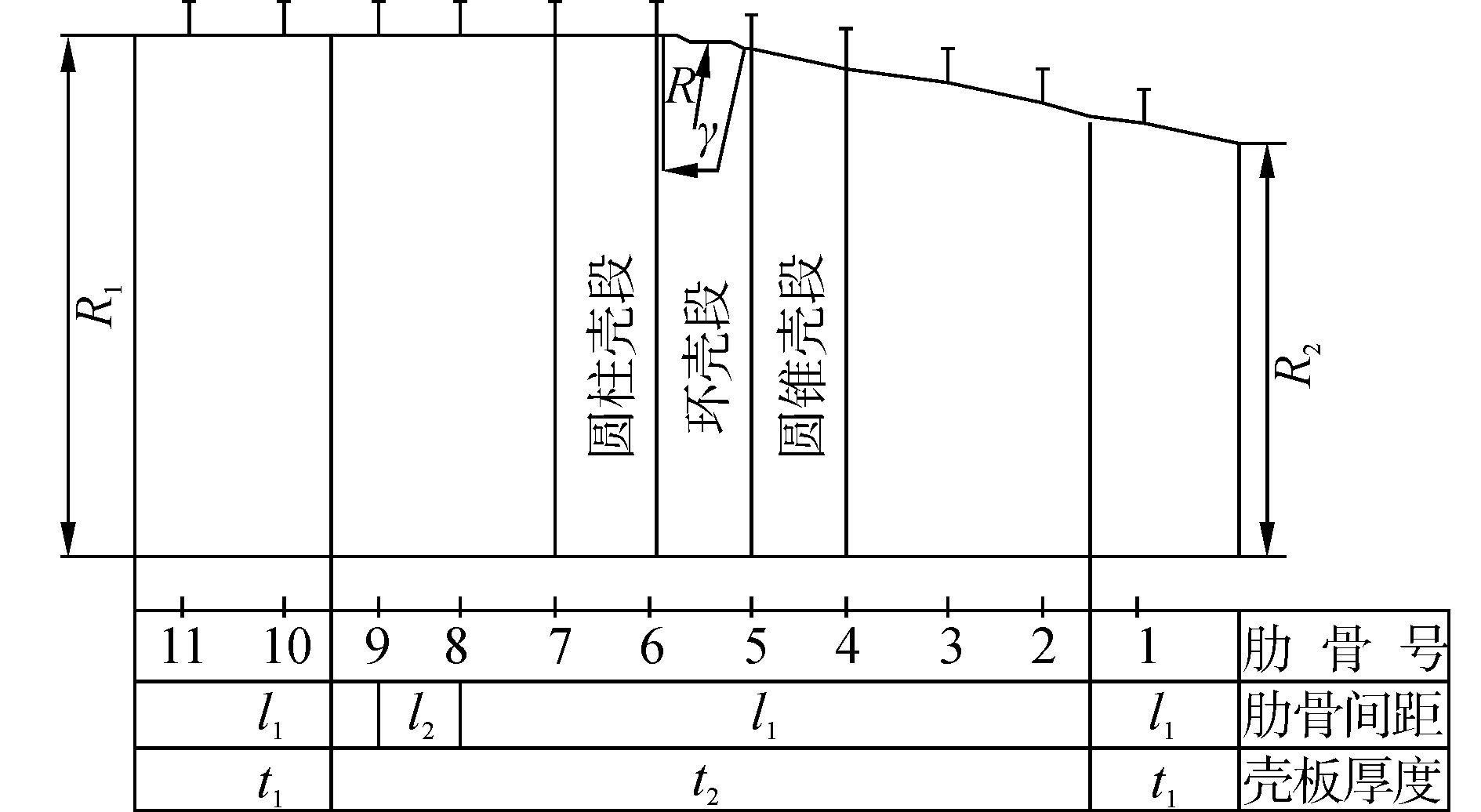
1 计算模型的建立 1.1 模型材料及尺寸模型采用理想弹塑性材料,弹性模量E=2.1×105MPa,泊松比μ=0.3,σs=785 MPa。模型尺寸如图 1所示,其中,R/R1=0.69,R2/R1=0.8,l1/R1=0.17,l2/R1=0.14,t1/R1=0.014,t2/R1=0.009。肋骨采用同一型号,I=608170mm4。壳体与肋骨均采用ANSYS中的shell181单元。
|
| 图1 含凸型锥-环-柱结合壳连接分段示意图 Figure 1 cabin with convex cone-toriod-cylinder combined shell |

|
| 图2 有限元模型 Figure 2 finite element model |
模型施加静水压力P,圆柱壳一侧边界固支,圆锥壳一侧边界滑动固支,仅放松轴向,并受集中载荷F的作用。其中F=P×πR22/n,n为圆锥壳一侧边界节点数。
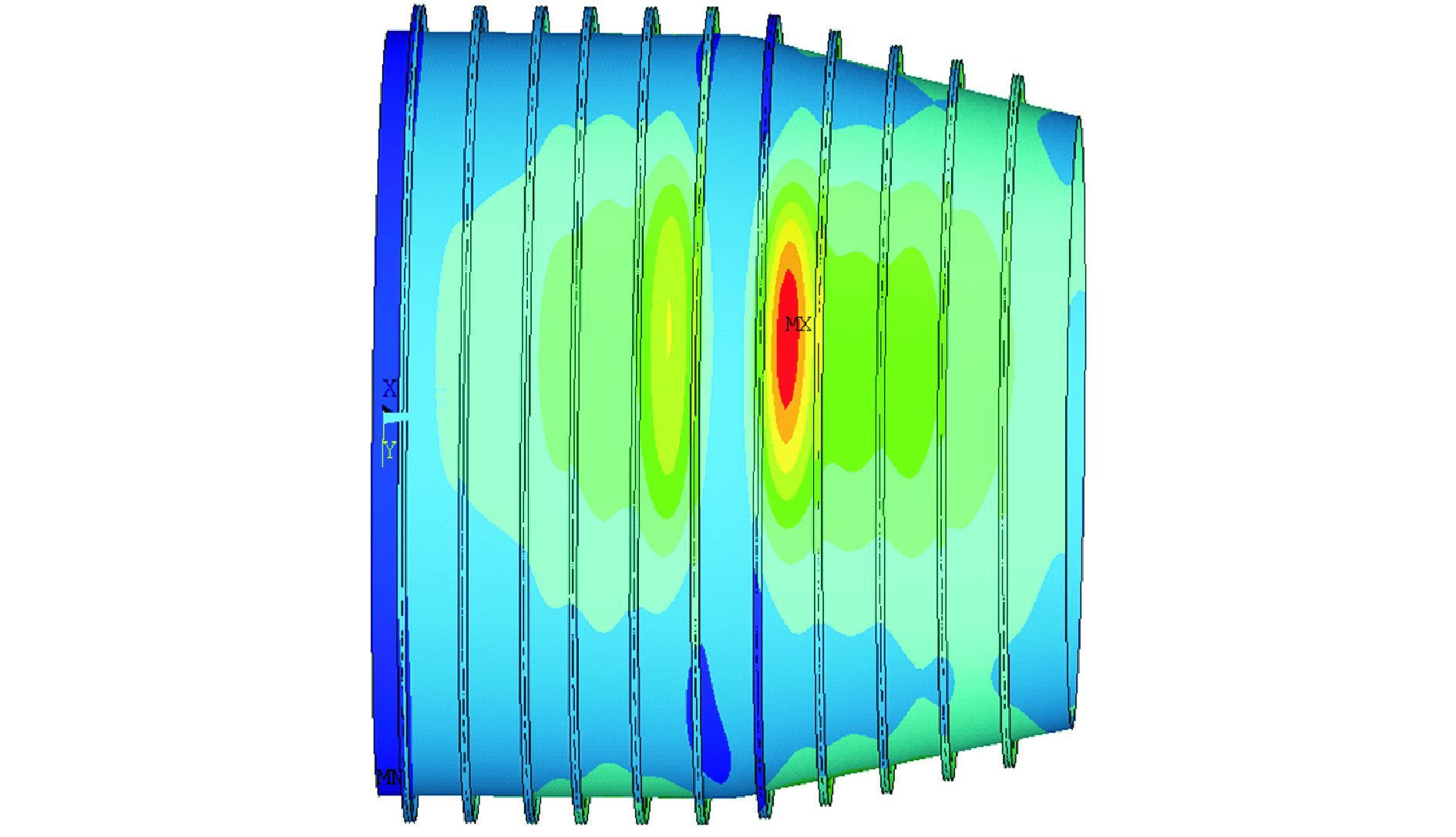
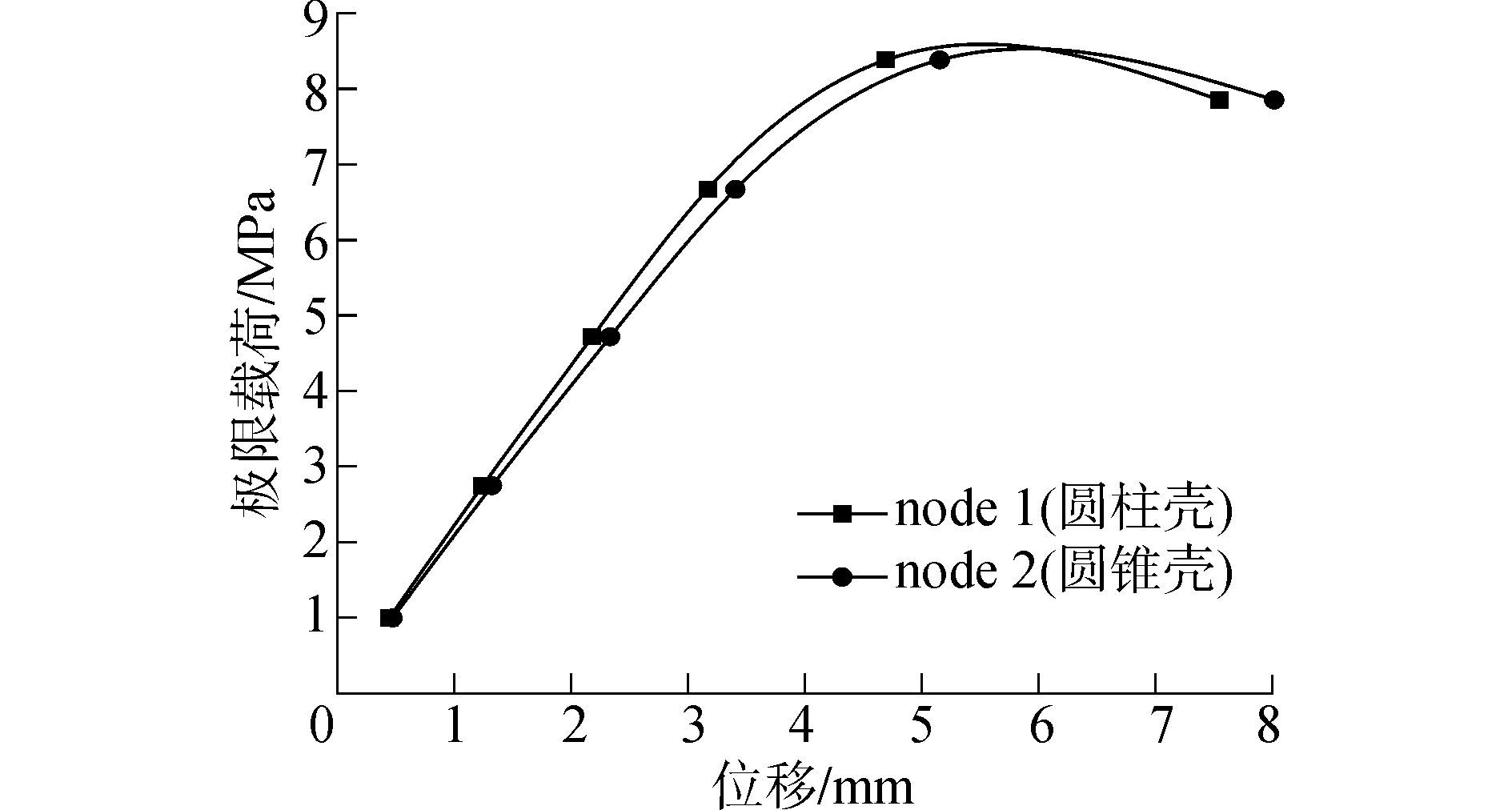
2 理想连接分段极限承载分析当含凸型锥-环-柱结合壳的连接分段无初始几何缺陷时,采用弧长法,设置合理的弧长半径以控制载荷增量的变化,激活大应变效应以考虑刚度矩阵的变化,分析此时连接分段的极限承载能力。图 3所示为极限载荷下连接分段的位移云图,图 4所示为典型节点位移—载荷曲线。其中,典型节点为连接分段在极限载荷作用下,圆柱壳段壳板、圆锥壳段壳板中位移最大的点。
|
| 图13 位移云图 Figure 13 displacement fringe |
|
| 图4 位移—载荷曲线 Figure 4 displacement-loading curve |
从图 3可看出,在极限载荷作用下,连接分段的破坏模式为壳板屈服破坏,破坏区域集中在圆柱壳段与圆锥壳段。这主要是因为环壳段的存在使得圆柱壳段、圆锥壳段弯矩加大,加速两处的变形。图 4所示为选取的圆柱壳段壳板与圆锥壳段壳板上位移最大的两个节点所作的位移—载荷曲线,曲线峰值点所对应的极限载荷约为8.4MPa。在同一载荷作用下,圆锥壳上的节点node2所发生的位移要大于圆柱壳上的节点node1所发生的位移,表明在逐渐增加的外载荷作用下,圆锥壳段壳板刚度相对较低,更易发生破坏变形。
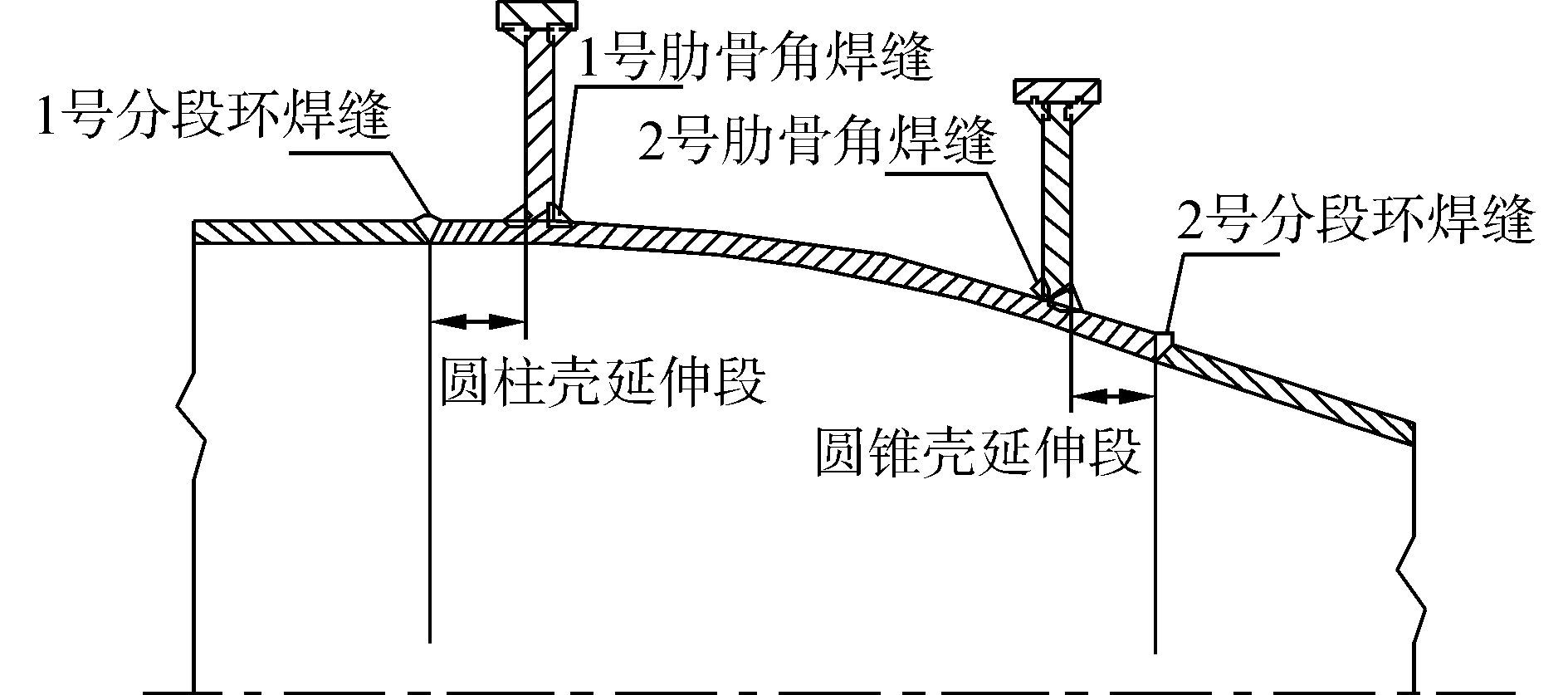
3 含初始几何缺陷连接分段极限承载分析 3.1 初始几何缺陷形态分析锥-环-柱结合壳加工过程为,环壳块及其延伸段采用数控机床切削加工,精度较高,与环肋圆柱壳辊焊加工相比较,前者可视为无初始几何缺陷;在环壳块壳两端分别焊接1、2号肋骨形成环壳段,再与艇体圆柱壳段、圆锥壳段对接,形成含锥-环-柱结合壳的连接分段结构。由焊接所形成的1、2号肋骨角焊缝主要引起肋骨初始几何缺陷,1、2号分段环焊缝则引起壳板初始几何缺陷。根据现行规范的规定,肋骨初始几何缺陷分析垂直度偏差、波纹度偏差以及径向偏差(即初挠度);壳板初始几何缺陷主要为壳板凹凸度。
图 5为锥-环-柱结合壳焊缝示意图。
|
| 图5 加肋锥-环-柱结合壳焊缝示意图 Figure 5 welding line of ring-stiffened cone-toric-cylinder combined shell |
通过工厂调研,根据大量环肋薄壳结构的制造经验可知,垂直度偏差与波纹度偏差值一般较小,且易于修正;肋骨初挠度偏差不易于修正。针对以往加工锥-环-柱缩比模型形状测量记录中初始几何缺陷测量数据统计结果,垂直度偏差值、波纹度偏差值一般控制在最大规范允许值(0.03h,h为肋骨高度)的50%以内,且易于修正;肋骨径向初挠度偏差虽满足规范要求(≤0.0025R,R为壳板半径),但不易于修正。因此,本文主要分析肋骨初挠度对连接分段极限承载能力的影响。
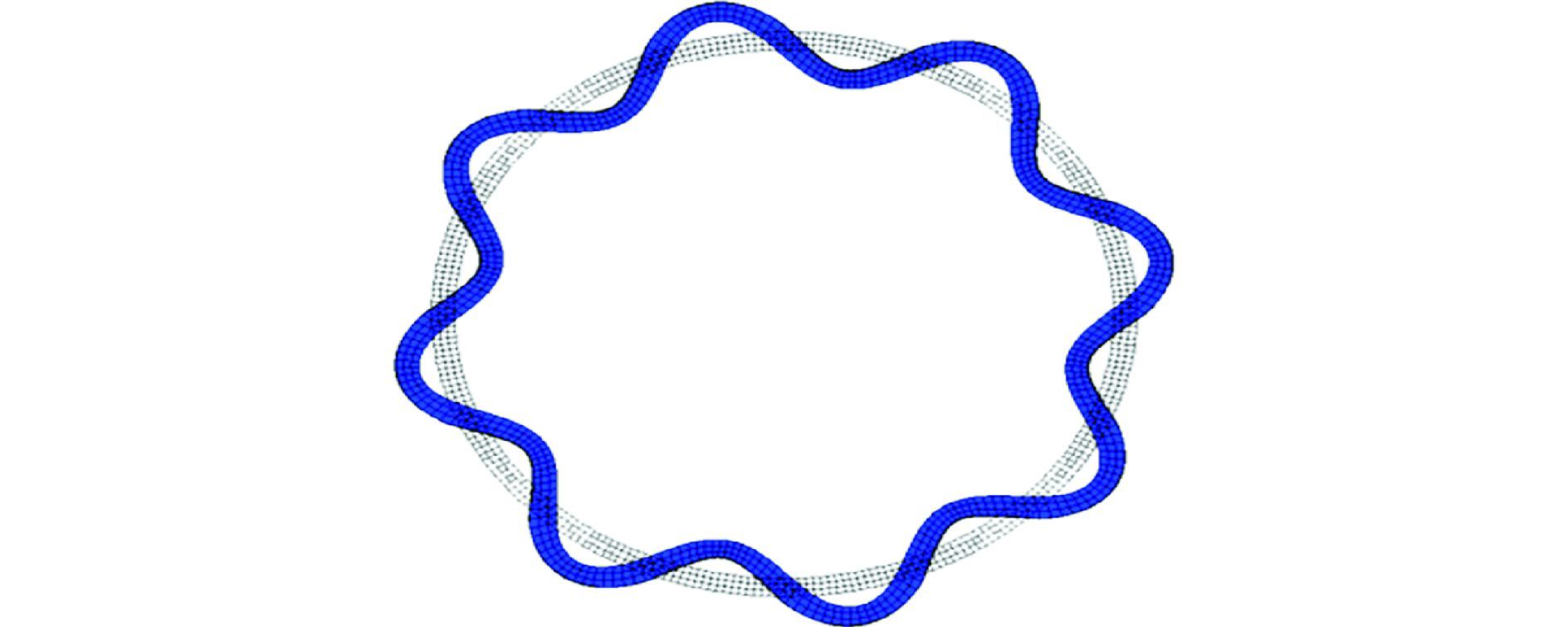
根据环肋薄壳结构的建造经验,分析环向布置的多个初始几何缺陷测点所得数据,肋骨初挠度的形态基本为4、6、8、16个半波或其组合形式等。图 6为肋骨初挠度为16个半波时的示意图。
|
| 图6 16个半波图 Figure 6 frame with 16 half waves |
|
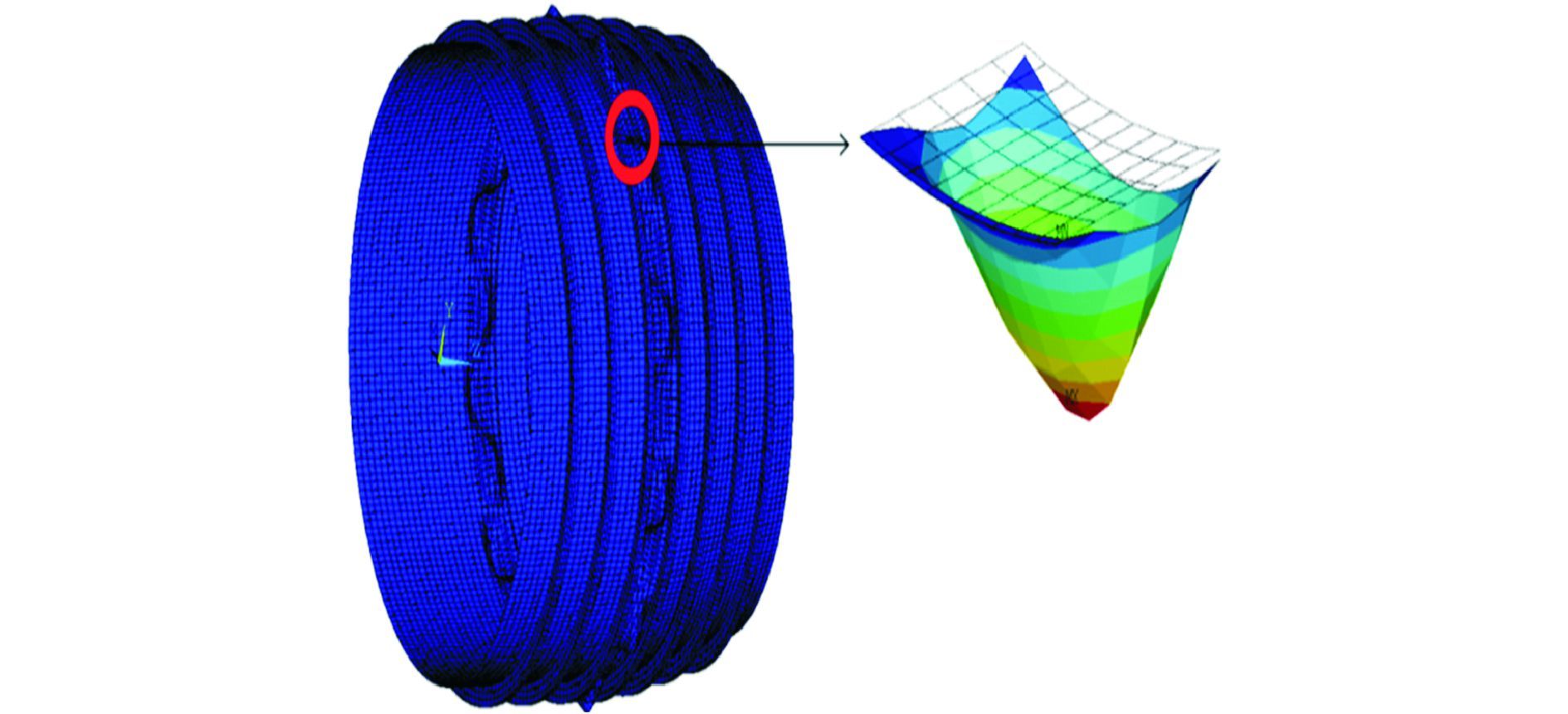
| 图7 壳板局部凹凸度偏差示意图 Figure 7 shell with concave-convex deflection |
壳板初始几何缺陷主要表现为壳板局部凹凸度。本文主要考虑由1、2号分段环焊缝引起的壳板凹凸度,主要分布于圆柱壳段壳板或圆锥壳段壳板,相邻肋骨无变形。取圆柱壳段、圆锥壳段屈曲失稳时的壳板变形作为壳板初始几何缺陷,如图 7所示为壳板局部凹凸度示意图,其中局部放大区域中的网格表示变形前壳板。
3.2 连接分段极限承载能力分析 3.2.1 仅肋骨含初始几何缺陷表好像不对现分别考虑单根肋骨具有初挠度以及1、2号肋骨同时具有初挠度,分析不同形态的肋骨初挠度组合对连接分段极限承载能力的影响。此时肋骨初挠度最大值为0.0025R(R为肋骨半径)。表 1所示为连接分段极限承载能力随肋骨初挠度形态组合变化情况。
| 1号肋骨初挠度半波数 | 2号肋骨初挠度半波数 | ||||
| 0 | 4 | 6 | 8 | 16 | |
| 0 | 8.45 | 7.9 | 7.3 | 7.7 | 7.8 |
| 4 | 8.0 | 7.7 | 7.4 | 7.5 | 7.6 |
| 6 | 7.7 | 7.6 | 7.1 | 7.3 | 7.3 |
| 8 | 7.75 | 7.7 | 7.3 | 7.4 | 7.4 |
| 16 | 7.75 | 7.7 | 7.5 | 7.5 | 7.8 |
从表 1中可以看出,当仅1(2)号肋骨初挠度为6个半波时,肋骨初挠度对连接分段极限承载能力的不利影响最大。其中2号肋骨初挠度对连接分段极限承载能力的不利影响大于1号肋骨初挠度,这是因为肋骨初挠度引起了相邻壳板的变形,降低了壳板刚度,而圆锥壳段壳板刚度相对圆柱壳段壳板刚度较弱,更易变形破坏(见图 3)。
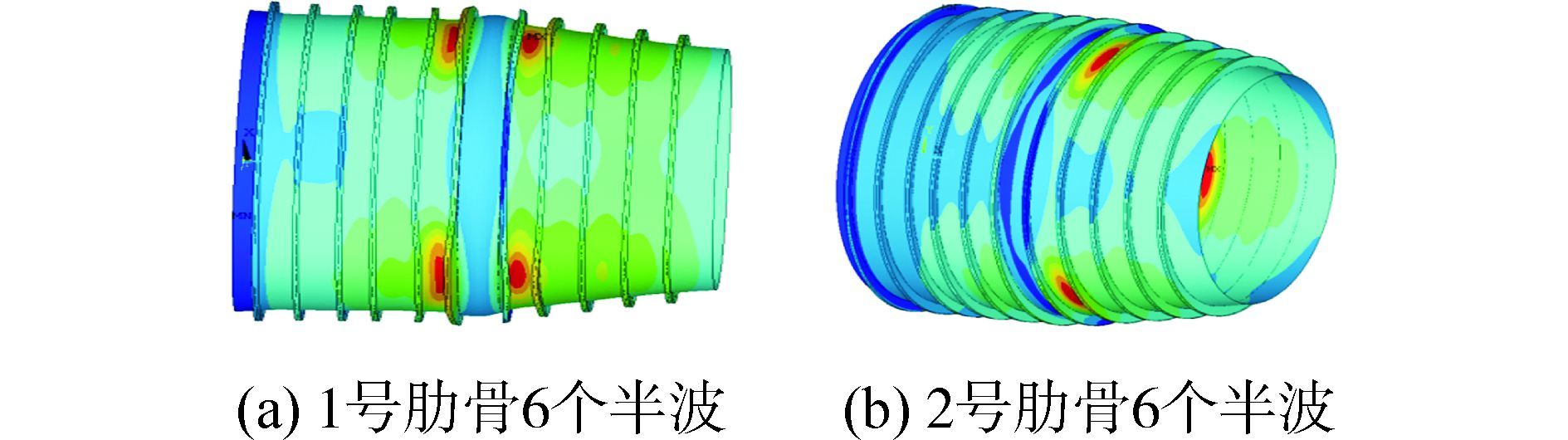
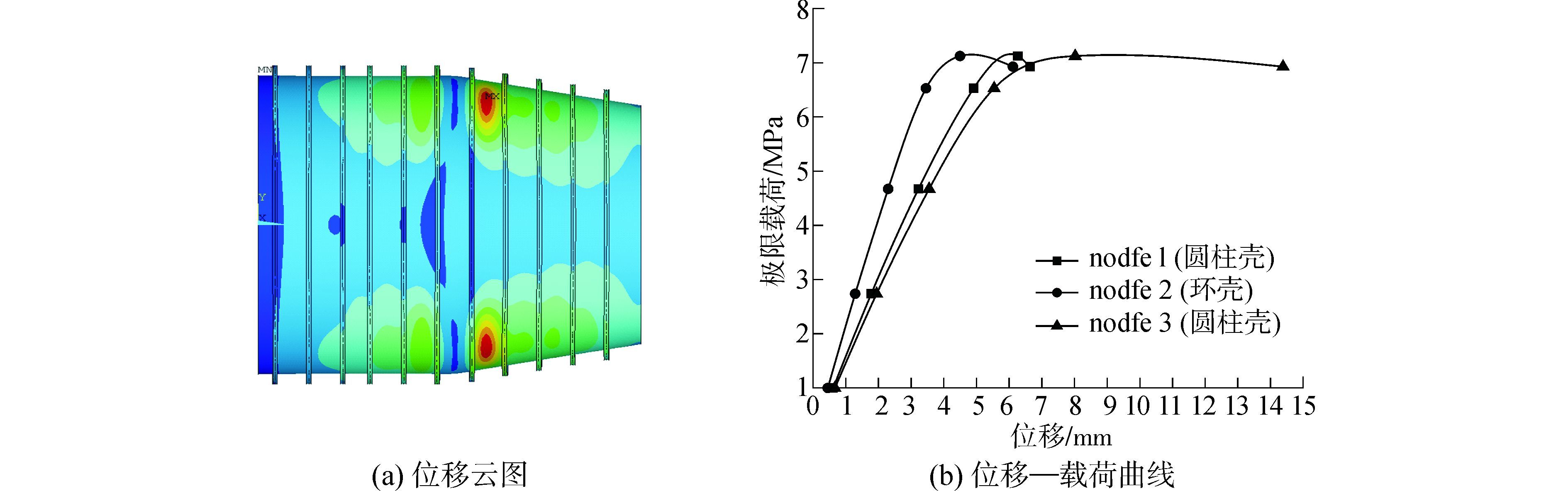
图 8所示为仅单根肋骨具有6个半波的初挠度时,连接分段在极限载荷下的位移云图。图 9所示为1、2号肋骨初挠度均为6个半波时,连接分段在极限载荷下的位移云图、典型节点的载荷—位移曲线。其中,典型节点分别为极限载荷作用下,圆柱壳段壳板、环壳段壳板以及圆锥壳段壳板中位移最大的节点。
|
| 图8 极限载荷下连接分段位移云图(单根肋骨6个半波) Figure 8 abin’s displacement fringe under limit load (only one frame with 6 half waves) |
|
| 图9 极限载荷下连接分段变形分析(1、2号肋骨6个半波) Figure 9 cabin’s displacement fringe under limit load (No.1 frame and No.2 frame with 6 half waves both) |
从图 8中可以看出,肋骨初挠度的存在不仅降低了连接分段的极限承载能力,同时改变了连接分段在极限载荷下的破坏模式:当仅1号肋骨具有6个半波时,连接分段破坏模式为圆柱壳段、圆锥壳段壳板局部失稳破坏;当仅2号肋骨具有6个半波时,连接分段破坏模式为圆锥壳段壳板局部失稳破坏。破坏区域所处位置与初挠度向内凹陷的3个波谷的周向位置相同,这是因为向内凹陷的初挠度促进了壳板在外载荷下的径向移动,不利于连接分段的承载。
当1、2号肋骨同时具有6个半波的初挠度时,连接分段在极限载荷下的破坏模式表现为圆锥壳段壳板的局部失稳,如图 9-a所示。其所处区域的周向位置同肋骨初挠度向内凹陷的3个波谷的周向位置相同。分析图 9-b,相同载荷下圆锥壳段典型节点位移大于其它两处典型节点位移,尤其是当静水压力达到极限载荷后,圆锥壳段节点出现较大的位移而破坏,表明圆锥壳段壳板更易发生破坏变形,验证了圆锥壳段壳板刚度相对较差。
肋骨初挠度的存在,不仅降低了连接分段的极限承载能力,同时将连接分段破坏模式由圆锥壳、圆柱壳段壳板的屈服破坏变为圆锥壳段等的壳板局部失稳破坏,降低了连接分段承载能力。因此在锥-环-柱结合壳加工建造过程中,需尽量避免出现1、2号肋骨6个半波的肋骨初挠度。
3.2.2 仅壳板含初始几何缺陷忽略跨越多档肋距的壳板凹凸度,主要考虑集中在圆柱壳段、圆锥壳段1、2号环焊缝处的局部壳板凹凸度。分别选取圆柱(锥)壳段壳板前100阶各阶屈曲失稳模态对应的壳板变形作为壳板初始几何缺陷,此时壳板凹凸度最大值为0.2t(t为壳板厚度)。
表 2所示为圆柱(锥)壳段壳板前100阶屈曲失稳变形对应的壳板凹凸度中,对连接分段极限承载能力影响最大的壳板变形对应的模态阶数及极限载荷。
| 位置 | 失稳模态阶数 | 极限载荷 |
| 圆柱壳段壳板 | 45 | 7.3 |
| 圆锥壳段壳板 | 45 | 7.2 |
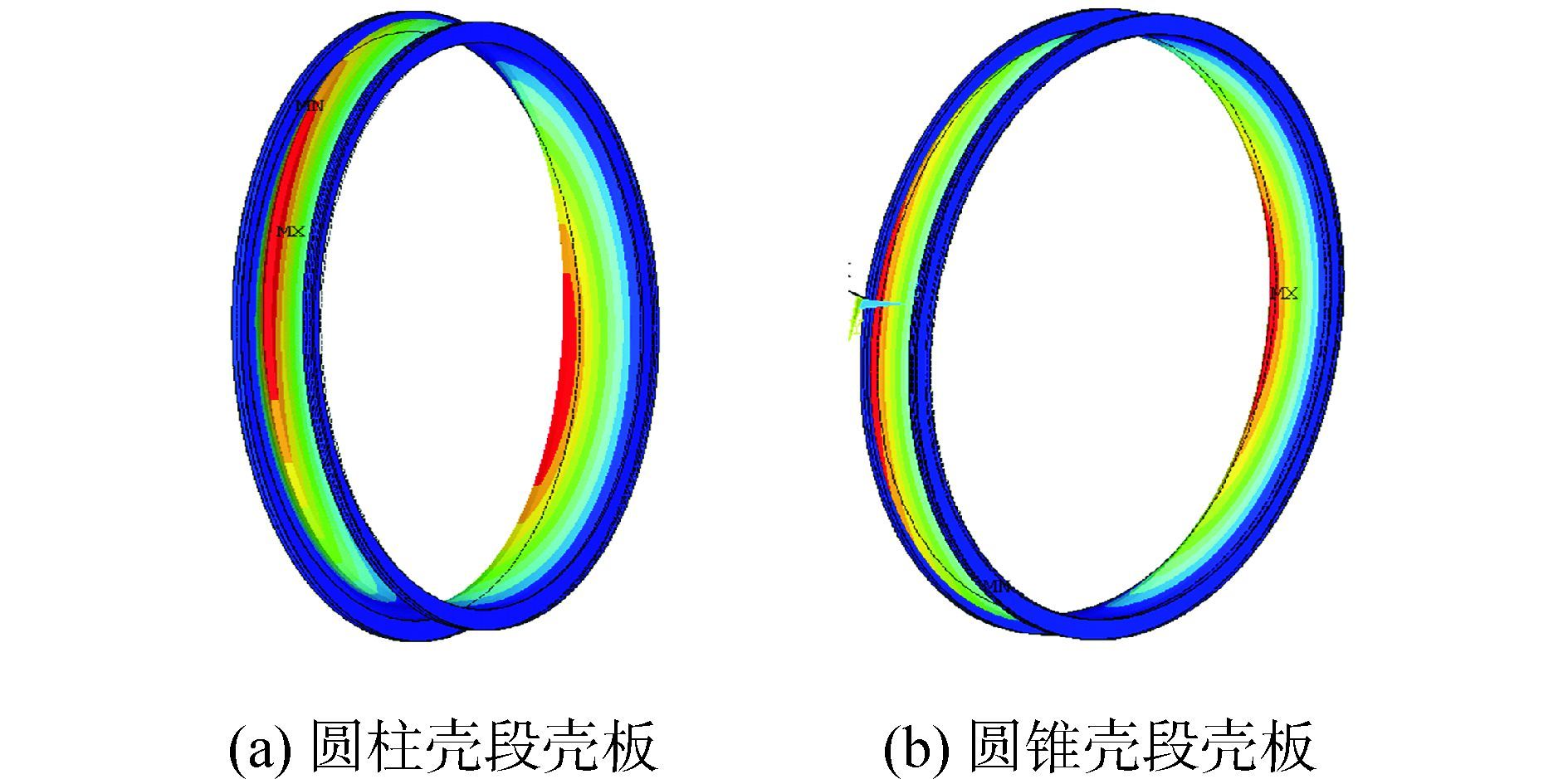
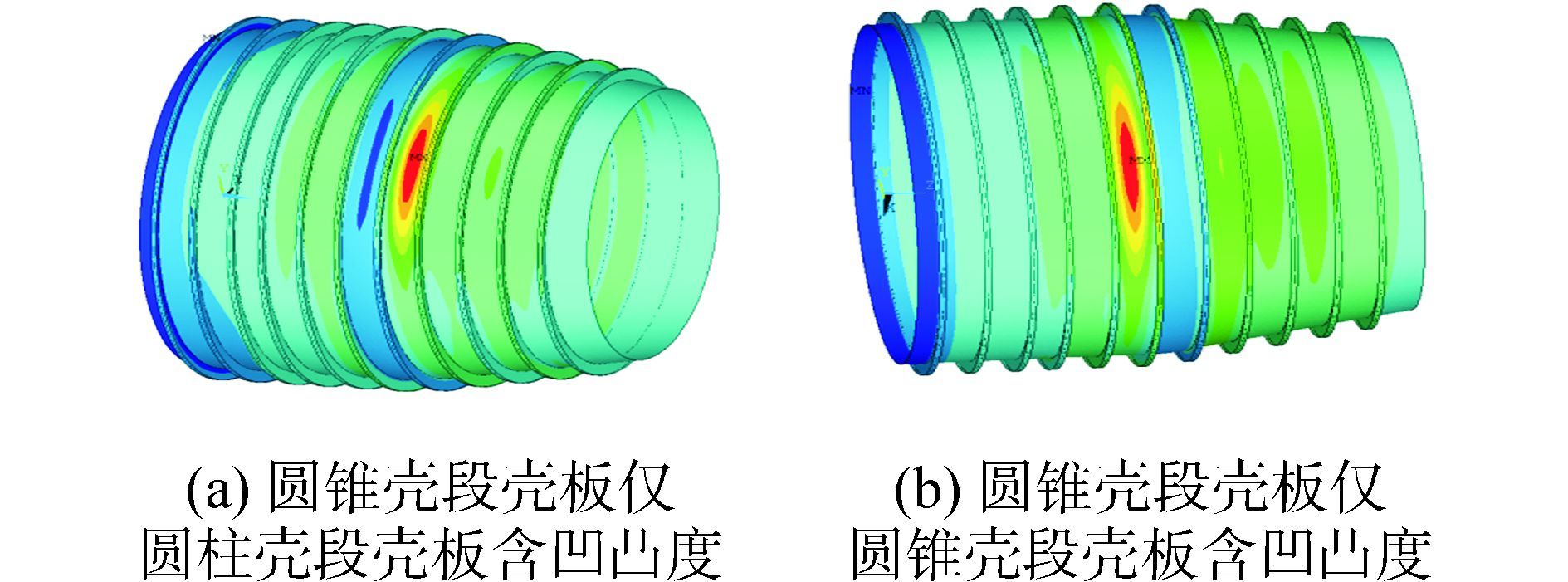
图 10所示为圆柱(锥)壳段壳板45阶失稳模态对应的壳板变形云图。图 11所示为连接分段在极限载荷作用下位移云图。
|
| 图10 壳板45阶失稳变形示意图 Figure 10 buckling shell’s deformationsame with 45th mode |
|
| 图11 极限载荷下连接分段位移云图 Figure 11 cabin’s deformation under limit load |
取圆柱(锥)壳段壳板凹凸度在周向呈2个半波,亦即此时壳板在周向呈椭圆状(见图 10),此时圆锥壳段壳板凹凸度对连接分段极限承载能力的不利影响大于圆柱壳段壳板凹凸度,因为圆锥壳段壳板刚度相对圆柱壳段壳板刚度较弱。在极限载荷下连接分段的破坏表现为壳板局部失稳破坏(见图 11-a),破坏区域所处周向位置同壳板凹凸度向内凹陷区域的周向位置相同。
壳板凹凸度的存在不仅降低了连接分段的极限承载压力,同时改变了连接分段的破坏模式,使其由理想连接分段对应的圆锥壳段、圆柱壳段壳板的屈服破坏,变为圆锥壳段、圆柱壳段的壳板局部失稳破坏,不利于连接分段承载。在锥-环-柱结合壳的加工建造过程中,需尽量避免出现圆锥(柱)壳45阶失稳模态变形对应的壳板凹凸度。
3.2.3 典型初始几何缺陷幅值变化对连接分段极限承载影响分析由上节分析可知,1、2号肋骨具有6个半波对连接分段极限承载能力的不利影响相对较大;圆柱(锥)壳段45阶失稳模态变形对应的壳板凹凸度对连接分段极限承载能力的不利影响最大。
选取上述典型形态的初始几何缺陷为对象,分析其初始几何缺陷值变化对连接分段极限承载能力的影响。在分析过程中,采取肋骨初挠度与壳板凹凸度幅值等梯度变化原则,即同时施加等倍数的初始几何缺陷允许幅值。其中,Wc=0.00275R,fc=0.15t。
| $\left\{ \begin{align} & W=\Delta \left[ {{W}_{c}} \right] \\ & f=\Delta \left[ {{f}_{c}} \right] \\ \end{align} \right.$ | (1) |
式中,Δ为施加的初始几何缺陷允许值的倍数,Wc为肋骨初挠度最大允许值,fc为壳板凹凸度最大允许值。
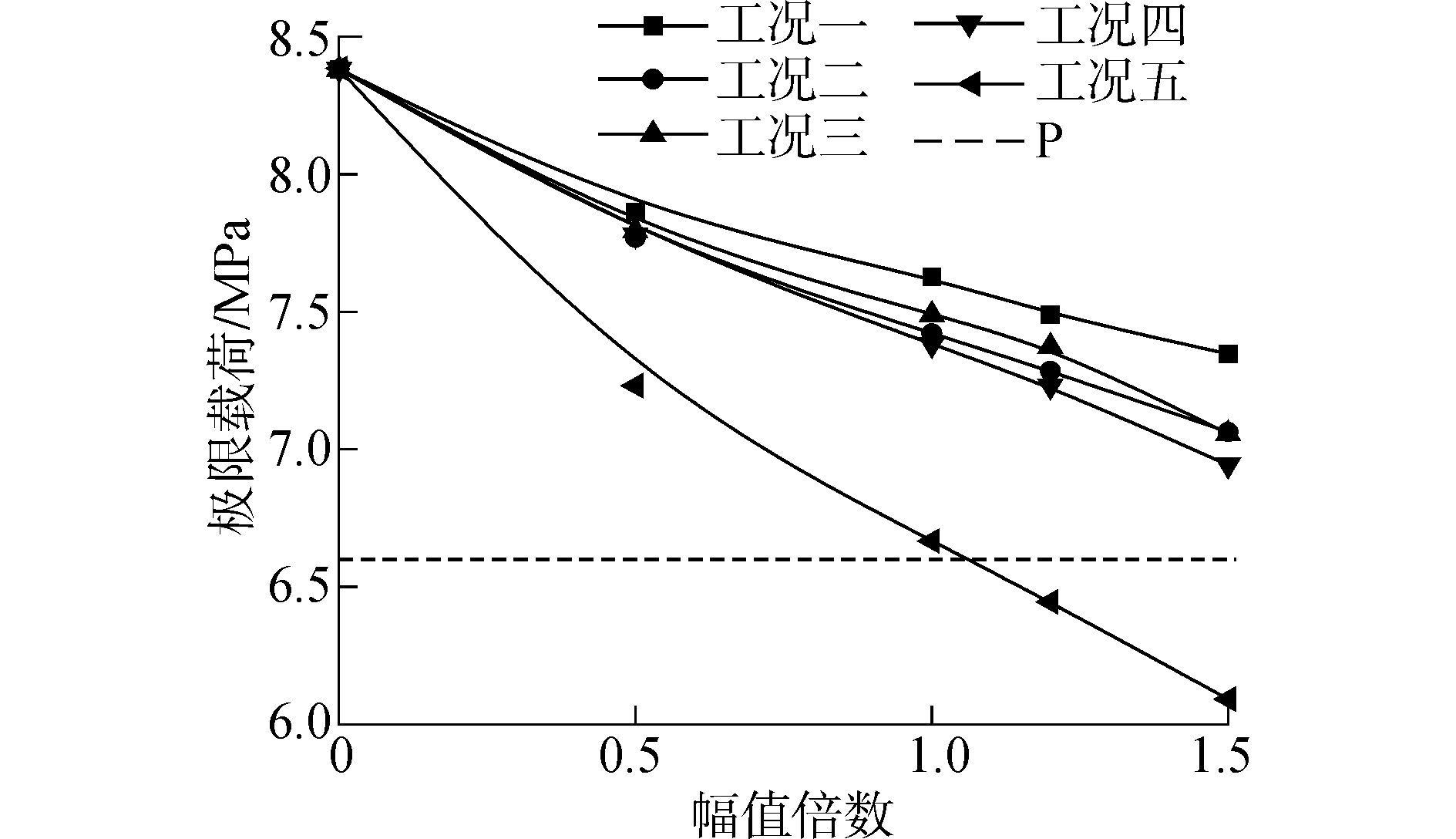
|
| 图12 极限载荷随初始几何缺陷幅值变化情况 Figure 12 limit load varies with imperfection’s amplitude changing |

|
| 图3 工况五极限载荷下位移云图(△=1) Figure 3 cabin’s deformation under case 5’s limit load (△=1) |
从图 12可以看出,当初始几何缺陷的幅值倍数相同时,圆锥壳段初始几何缺陷对连接分段极限承载能力的不利影响大于圆柱壳段初始几何缺陷,壳板凹凸度带来的不利影响大于肋骨初挠度。这是因为与圆柱壳段壳板刚度相比,圆锥壳段壳板刚度相对较弱,而壳板凹凸度直接影响了壳板刚度。从图 13可以看出,当肋骨、壳板初始几何缺陷同时存在时,连接分段的破坏模式表现为圆锥壳段壳板局部失稳破坏。破坏所处区域的周向位置同肋骨初挠度向内凹陷的半波以及壳板凹凸度向内凹陷的半波的周向位置相同。
当肋骨、壳板初始几何缺陷未超出允许幅值Wc、fc时,连接分段极限载荷均不低于6.7MPa,均大于大潜深状态下的计算载荷,表明此时初始几何缺陷对连接分段极限承载能力的影响是可以接受的。
当肋骨、壳板初始几何缺陷幅值为允许的最大幅值Wc、fc时,取几何修正系数Cg如下:
| ${{c}_{g}}=min\left( \frac{{{P}_{ui}}}{{{P}_{0}}} \right)$ | (2) |
式中,Pui为工况i对应的连接分段的极限载荷,P0为理想连接分段的极限载荷。
当肋骨、壳板初始几何缺陷同时存在时,Cg达到最小值0.795。则在设计与本文模型相类似的连接分段时,其极限载荷Pu应满足如下要求:
| ${{c}_{g}}{{P}_{u}}\ge P$ | (3) |
式中,P为计算载荷,Cg为几何修正系数(Cg=0.795,偏于安全)。
初始几何缺陷的存在不仅降低了连接分段的极限承载能力,同时改变了连接分段的破坏模式,使其由理想连接分段的圆锥壳、圆柱壳段壳板屈服破坏变为圆锥壳段壳板局部失稳破坏,降低连接分段的极限承载能力。在锥-环-柱结合壳的加工建造过程中,尽量避免出现文中出现的典型初始几何缺陷形态。
4 结论本文根据大量环肋薄壳结构的建造经验,分析多组锥-环-柱结合壳的建造工艺及形状测量报告,设计了系列典型初始几何缺陷形态,采用有限元法分析诸上初始几何缺陷形态及幅值变化对含凸锥-环-柱结合壳连接分段极限承载能力的影响,并得到以下结论:
1) 初始几何缺陷的存在会引起含加肋凸型锥-环-柱结合壳连接分段破坏形式的改变。当初始结合缺陷形态同图 11中工况五相同时,初始几何缺陷对连接分段极限承载能力的不利影响最大,在加工建造过程中需尽量避免出现类似的形状偏差。
2) 在设计与本文类似的连接分段时,极限载荷几何修正系数Cg的选取可参考本文结论,偏于安全。Cg与初始几何缺陷形态及幅值的关系,有待进一步研究
| [1] |
黄加强, 郭日修. 加肋锥-环-柱组合壳强度及稳定性模型实验研究[J].
中国造船, 1988(4): 57–65.
HUANG Jiaqiang, GUO Rixiu. Model experimental research on stresses and stability of ring-stiffened cone-toroid-cylinder combined shell[J]. Shipbuilding of China, 1988(4): 57–65. |
| [2] |
白雪飞, 陈昕, 丁锦超, 等. 凹型加肋锥-环-柱结合壳强度的模型试验研究[J].
船舶力学, 2006, 10(2): 65–72.
BAI Xuefei, CHEN Xin, DING Jinchao, et al. Experimental research of the strength of ring-stiffened concave cone-toroid-cylinder combined shell[J]. Journal of ship mechanics, 2006, 10(2): 65–72. |
| [3] |
郭日修, 吕岩松, 黄加强, 等. 加肋锥-环-柱结合壳试验研究[J].
船舶力学, 2008, 12(2): 252–257.
GUO Rixiu, LYU Yansong, HUANG Jiaqiang, et al. Experimental research on the ring-stiffened cone-toroid-cylinder combination shell[J]. qJournal of ship mechanics, 2008, 12(2): 252–257. |
| [4] |
郭日修, 吕岩松. 凹型加肋锥-环-柱结合壳局部加强方式的研究[J].
哈尔滨工程大学学报, 2010, 31(2): 170–176.
GUO Rixiu, LYU Yansong. Research on local strengthening modes for ring-stiffened concave cone-toroid-cylinder combination shell[J]. Journal of Harbin engineering university, 2010, 31(2): 170–176. |
| [5] |
吕岩松, 郭日修. 含凸、凹型加肋锥-环-柱结合壳的连接结构试验研究[J].
哈尔滨工程大学学报, 2011, 32(9): 1140–1143.
LYU Yansong, GUO Rixiu. Experimental research on ring-stiffened convex and concave cone-toroid-cylinder combination shell[J]. Journal of Harbin engineering university, 2011, 32(9): 1140–1143. |
| [6] |
吕岩松. 加肋锥-环-柱结合壳应力峰值的计算方法[J].
舰船科学技术, 2014, 36(4): 63–65.
LYU Yansong. Calculation of peak stress of ring-stiffened cone-toroid-cylinder combined shell[J]. Ship science and technology, 2014, 36(4): 63–65. |
| [7] |
肖文勇, 黄旎. 不同结构参数的锥环柱结构强度性能分析[J].
船海工程, 2015, 44(1): 19–22.
XIAO Wenyong, HUANG Ni. A structural parametric analysis on the strength of the cone-toroid-cylinder combined shell[J]. Ship & ocean engineering, 2015, 44(1): 19–22. |
| [8] | ATHIANNAN K, PALANINATHAN R. Experimental investigations on buckling of cylindrical shells under axial compression and transverse shear[J]. Sadhana, 2004, 29(1): 93–115. |
| [9] | PALANINATHAN R, ATHIANNAN K, THOMAS G. Investigations on stability of cylindrical shells under axial compression[C]//Proceedings of Transactions, SMiRt 16. Washington DC, 2001:1-8. |
| [10] | SINGER J. The status of experimental buckling investigations of shells[M]//RAMM E. Buckling of Shells. Berlin:Springer-Verlag, 1982:501-533. |
| [11] | ARBOCZ J. The imperfection data bank, a mean to obtain realistic buckling loads[M]//RAMM E. Buckling of Shells. Berlin:Springer-Verlag, 1982:535-567. |
| [12] | ZHU Enchun, KHAKINA P N, ZHOU Huazhang. Buckling load of thin spherical shells and single-layer reticulated spherical shells[J]. Information engineering letters, 2012, 2(3): 35–42. |
| [13] |
张二, 吴梵, 吕岩松. 局部初始几何缺陷对凸型锥-环-柱结合壳应力影响的分析[J].
中国造船, 2015, 56(2): 11–21.
ZHANG Er, WU Fan, LYU Yansong. Effect of local original geometrical imperfection on stress of ring-stiffened convex shell integrated with cone-toroid and cylinder[J]. Shipbuilding of China, 2015, 56(2): 11–21. |
| [14] |
张二, 吴梵, 吕岩松, 等. 含局部初始几何缺陷的凸型锥-环-柱结合壳舱段稳定性仿真分析[J].
海军工程大学学报, 2015, 27(4): 70–74.
ZHANG Er, WU Fan, LYU Yansong, et al. Simulation analysis of stability of cabin of convex cone-toroid-cylinder combined shell with local initial imperfection[J]. Journal of naval university of engineering, 2015, 27(4): 70–74. |
| [15] | GJB/Z 21A-2001. 潜艇结构设计计算方法[S]. 北京:国防工业技术委员会, 2001. |



