2. 浙江大学 智能系统与控制研究所 工业控制技术国家重点实验室, 浙江 杭州 310027;
3. 中国科学院 工程热物理研究所, 北京 100190;
4. 中航工业航宇救生装备有限公司, 湖北 襄阳 441003
2. State Key Laboratory of Industrial Control Technology, Institute of Cyber-Systems and Control, Zhejiang University, Hangzhou 310027, China;
3. Institute of Engineering Thermophysics, Chinese Academy of Sciences, Beijing 100190, China;
4. AVIC Aerospace Lifesaving Equipment Co. Ltd, Xiangyang 441003, China
可控翼伞在空投领域中是一个非常诱人的先进设备,是一种具有可控性和滑翔性的降落伞,能够在空中转弯,相较于传统空投技术在准确性和安全性方面有一定改进。精确空投和“定点无损”着陆这两个目标的实现,在各个领域有着广泛的需求和应用[1]。空降作战被视为重要的军力优势,精确空投能更准确、更安全的将人员、物资投送到战场,并且可以使价格高昂的运输机远离敌方火力的威胁; 在发生自然灾害时,如山体滑坡、地震等,利用精确空投系统能够在第一时间将救援物资投送到受灾地区[2];在宇航探索中,利用翼伞系统能够对航天飞机、火箭以及人造卫星等进行回收,不仅有效减少了宇宙垃圾,还可以对各类资源(实验数据、操作系统等) 回收再利用,能够节约大量人力、物力和财力[3]。
在过去60年中,翼伞系统有了长足的进步[4],翼伞系统归航轨迹方面的研究可粗略分为:径向、锥形归航之类的简单归航方法,最优控制归航法[5],分段归航法[6-7]。1998 年,Betts总结了多种轨迹优化问题数值方法[8];2002 年,Ross等介绍了很多种方法在轨迹优化问题中的应用前景[9]。求解最优控制轨迹的数值算法有很多,如文献[10-12];对于地形追踪/规避方面:1988 年,Asseo 利用最速下降法求解飞行器地形跟踪与规避的轨迹优化问题[13];2007 年,Sharma 等介绍了一种军用飞行器地形跟踪与规避的最优控制方法[14];2007 年,Williams 拓展了飞行器贴地轨迹的即时最优控制策略[15];2011 年,Iman 等利用直接转录方法(direct transcription method) 模拟求解F-16 战斗机的贴地轨迹最优控制问题[16];2012 年,Fan 等给出了多种影响范围不同的威胁规避的最优控制方法[17]。针对翼伞系统最优控制归航问题,2005 年,熊菁提取了翼伞多种自由度模型的质点模型,利用共轭梯度法进行了求解[18]; 2011 年,焦亮等提出基于混沌粒子群优化算法的翼伞系统轨迹规划智能算法[19-20];2013 年,高海涛等利用基于 Gauss 伪谱法的归航轨迹容错设计方法求解不同工作状态下轨迹规划的最优控制问题[21];2014 年,白瑞光等将伪谱法应用于多个无人机的协同轨迹规划[22]。然而,对于无动力源的翼伞系统的威胁规避问题至今还没有深入的研究。
本文从实现精确投递,“定点无损”着陆,规避山峰地形,躲避防空火力打击的需求条件出发,采用了一种新型的优化算法对翼伞系统的最优控制问题进行求解,对控制量进行优化。并且与粒子群算法(particle swarm optimization,PSO) 进行了比照。仿真结果表明,在需求约束条件下,该方法控制效果良好,计算速度快,为进一步发展翼伞精确空投以及回收系统提供了可行的理论和技术解决方案。
1 数学模型的建立 1.1 翼伞系统数学模型翼伞系统的结构图如图 1所示。翼伞的物理模型涉及到其自身的动力学方程、姿态,以及空气阻力、升力等多个因素,是一个高度复杂的非线性系统。由于翼伞的动力学特性不是本文的研究重点,为了简化问题的规模,这里把翼伞看作质点,翼伞无动力源,仅能够通过微型电机改变伞面到负载的操纵绳长度,采用基于三自由度的翼伞系统模型[18]。三自由度质点模型基于如下假设[23]:

|
| 图1 翼伞系统结构图 Figure 1 Structure of parafoil system |
1) 翼伞展面对称,在归航操纵控制中具有固定的形状;
2) 负载物与翼伞刚性连接,构成一个整体;
3) 稳定下降阶段,将翼伞系统整体看做一个质点。翼伞系统在重力和气动力共同作用下达到了平衡状态,此时翼伞系统的垂直下落速度vz和水平飞行速度vs均保持不变;
4) 翼伞系统对控制的输入响应没有延迟;
5) 将大地作为平面,且水平风场己知(可以是固定风,也可以是变化的风) 。
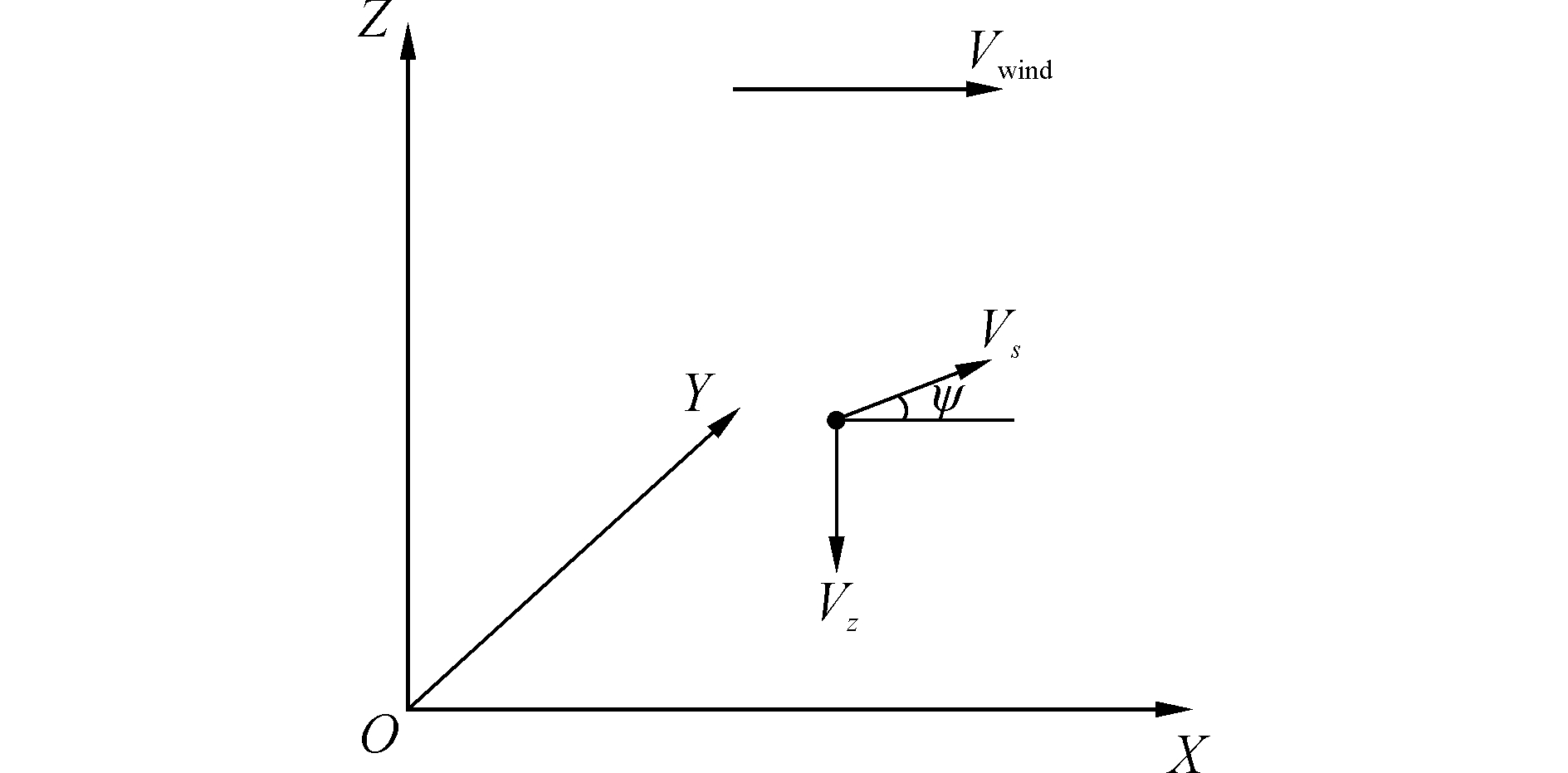
分析翼伞系统整体工作过程可以发现,其中的主要动作分为:拉直、充气、转换吊挂、归航和着陆。雀降操纵发生的高度可以通过翼伞系统确定,不包含于翼伞归航轨迹的设计中。那么,现在需要研究的过程是从翼伞完全展开后系统的初步稳定点直到雀降操纵发生实施点。这里取大地坐标系,以水平风向为为X轴方向,Z轴垂直于地面向上,Y轴由右手系来确定,如图 2所示,则翼伞系统运动方程可以简化为
| $\left\{ \begin{matrix} \dot{x}={{v}_{s}}\cos \psi +{{v}_{wind}} \\ \dot{y}={{v}_{s}}\sin \psi \\ \dot{\psi }=u \\ \dot{z}={{v}_{z}} \\ \end{matrix} \right.$ | (1) |
|
| 图2 大地坐标系 Figure 2 Geodetic coordinate system |
式中:x、y、z为翼伞在大地坐标系中坐标,vs为翼伞的水平飞行速度,vz为翼伞的垂直下降速度; vwind为水平方向风速,ψ为翼伞的转弯角度,u为控制量(通过微型电机改变伞面到负载的操纵绳长度,非动力项) 。各个状态量的初始条件为
| $\left\{ \begin{matrix} x\left( {{t}_{0}} \right)={{x}_{0}},y\left( {{t}_{0}} \right)={{y}_{0}} \\ z\left( {{t}_{0}} \right)={{z}_{0}},\psi \left( {{t}_{0}} \right)={{\psi }_{0}} \\ \end{matrix} \right.$ | (2) |
翼伞的归航环境可以大致分为:地形环境,即空投范围内的地形、地貌等;敌情环境,即空投范围内敌方对运输机以及整个空投系统的发现与破坏能力;气象环境,即在翼伞归航过程中空投范围内的大气气压、风场特性、天气状况等因素;电磁环境,即翼伞系统在归航过程中对于信号的接收环境。本文中研究的威胁因素主要是指地形环境和敌情环境。
1.2.1 地形威胁建模翼伞系统在归航过程中,大致会遇到两种地形: 一类是相对平缓的区域,对翼伞系统影响较小; 另一类是独立山峰,对翼伞系统威胁较大,翼伞在归航过程中需要尽可能回避此种地形。本文着重研究威胁较大的独立山峰地形,地形的威胁建模如下
| $T\left( x,y \right)={{T}_{0}}\left( x,y \right)+\sum\limits_{i=1}^{M}{{{T}_{i}}\exp \left[ -{{\left( \frac{x-{{x}_{0i}}}{{{x}_{si}}} \right)}^{2}}-\left( \frac{y-{{y}_{0i}}}{{{y}_{si}}} \right) \right]}$ |
式中:T0(x,y)为基准地形高度,Ti为第i个山峰的相对高度,(x0i,y0i) 是第i个山峰的坐标,(xsi,ysi)为第i个山峰沿着x轴和y轴方向与坡度有关的量。本文使用的独立山峰如图 3所示,这里山峰的最高海拔为3 000 m,中心地面坐标(2 000,1 500) 。

|
| 图3 山峰三维地形图 Figure 3 Three-dimensional topographic map for mountain peak |
翼伞系统需要面对的敌情威胁主要来源于防空火力打击,中低空小口径、高发射率高射炮具有很大威胁。此类高射炮对翼伞系统的破坏率表示为
| ${{P}_{f}}={{P}_{1}}{{\left[ 1-{{\left( 1-\frac{R}{\delta }\sqrt{\frac{N}{2}} \right)}^{M}} \right]}^{2}}$ |
式中:Pf表示翼伞系统被破坏的概率,Pl表示敌方高射炮正常工作的概率,R表示敌方高射炮有效半径,N表示高射炮的数量,δ表示高射炮的射击偏差,M表示单一高射炮发射弹药数量。本文仿真中直接把敌情威胁等效成一个具有一定作用半径和威胁概率的虚拟独立山峰威胁。
2 翼伞系统威胁规避最优控制问题翼伞系统在归航过程中,需要满足以下条件:
1) 翼伞的着陆位置要尽可能接近目标投放点;
2) 翼伞迎风着陆,从而减小着陆时的水平速度,避免着陆对负载造成损伤;
3) 由于电机能够提供的能量有限,对翼伞操纵绳的耗能需要尽可能小;
4) 翼伞归航路径不能与障碍物相接触,也不能进入敌方火力打击范围。
因此,翼伞系统归航轨迹的最优控制问题可以描述为:设计最优控制量 u 使得下式的目标函数达到最小值:
| $J=\int_{{{t}_{0}}}^{{{t}_{f}}}{{{u}^{2}}dt}$ | (3) |
控制量 u 同时需满足动态方程(1) 、初始条件(2) ,以及如下的约束条件:
1) 终端约束:终端时间tf=z0/vz,为使终端到达目标点,需满足:
| $x\left( {{t}_{f}} \right)={{x}_{f}},y\left( {{t}_{f}} \right)=z\left( {{t}_{f}} \right)=0$ | (4) |
2) 根据逆风着陆的要求,终端时翼伞转弯的角度需满足:
| $\psi \left( {{t}_{f}} \right)=\left( 2n+1 \right)\pi $ | (5) |
3) 控制约束:
| $\left| u \right|\le {{u}_{\max }}$ | (6) |
其中,允许的最大控制量umax对应最小转弯半径。
4) 路径约束:
| $z\left( t \right)\ge h\left( x\left( t \right),y\left( t \right) \right)$ | (7) |
式中:z(t)=z0-vzt,h(x,y) 为(x,y) 坐标处的等效威胁的高度。
由于具有终端状态约束和路径约束,为了方便计算求解,可采用精确罚函数的方法[24-25]将有约束的最优控制问题转化为无约束的最优控制问题。
对于一般不等式类型的约束条件:
| $g\left( x,t \right)\le 0.t\in \left[ 0,T \right]$ |
可以等价表示为如下约束条件:
| $\int_{0}^{T}{\max \left\{ g\left( x,t \right),0 \right\}dt=0}$ |
采用如下近似函数积分来代替上面的约束条件:
| $\int_{0}^{T}{\varphi \left\{ g\left( x,t \right) \right\}dt<\varepsilon }$ |
其中ε> 0 为参数,函数:
| $\varphi \left( \eta \right)=\left\{ \begin{matrix} 0,\eta <-e \\ x,\eta >\varepsilon \\ \frac{{{\left( \eta +\varepsilon \right)}^{2}}}{4\varepsilon },其他 \\ \end{matrix} \right.$ |
的逼近效果见图 4,其中实线为函数φ(η) ,虚线为函数max{η,0}。

|
| 图4 函数φ(η) 的逼近效果图 Figure 4 Approximation effect for function φ(η) |
将终端约束条件式(4) 、(5) 通过添加权值的方式加到目标函数式(3) 中。增加两个新的状态变量y4和y5,对应地分别将控制约束条件式(6) 和路径约束条件式(7) 添加到目标函数式(3) 中。改造后的翼伞系统轨迹优化的最优控制问题可描述为
问题1:设计方程:
| $\left\{ \begin{matrix} {{{\dot{y}}}_{1}}=a\cos {{y}_{3}}+{{v}_{wind}}, \\ {{{\dot{y}}}_{2}}=a\sin {{y}_{3}}, \\ {{{\dot{y}}}_{3}}=u, \\ {{{\dot{y}}}_{4}}=b{{u}^{2}}, \\ {{{\dot{y}}}_{5}}=\varphi \left( h\left( {{y}_{1}},{{y}_{2}} \right)+{{v}_{z}}t-{{z}_{0}} \right) \\ \end{matrix} \right.$ | (8) |
的最优控制量 u 使得如下目标函数达到最小值:
| $\begin{align} & J={{q}_{1}}\left[ {{\left( {{y}_{1}}\left( T \right)-{{y}_{1f}} \right)}^{2}}+{{\left( {{y}_{2}}\left( T \right)-{{y}_{2f}} \right)}^{2}} \right]+ \\ & {{q}_{2}}\left( \cos \left( {{y}_{3}}\left( T \right) \right)+1 \right)+{{q}_{3}}{{y}_{4}}\left( T \right)+{{q}_{4}}{{y}_{5}}\left( T \right) \\ \end{align}$ | (9) |
y1f = xf ,y2f = yf ,q1、q2、q3、q4均为大于 0 的权值,T 为预计着陆时间,整个系统需同时满足动态方程式(8) 、初始条件式(2) 和控制约束式(6) 。
3 最优控制问题求解 3.1 控制变量参数化这里
| $Y\left( t \right)={{\left( {{y}_{1}}\left( t \right),{{y}_{2}}\left( t \right),{{y}_{3}}\left( t \right),{{y}_{4}}\left( t \right),{{y}_{5}}\left( t \right) \right)}^{T}}$ |
可以将问题1变换为如下标准形式:
| $\underset{u}{\mathop{\min }}\,w\left( Y\left( T \right) \right)$ | (10) |
| $\begin{align} & \dot{Y}\left( t \right)=f\left( Y\left( t \right),u\left( t \right) \right),t\in \left[ 0,T \right] \\ & Y\left( 0 \right)={{Y}_{0}} \\ & a\le u\left( t \right)\le b,t\in \left[ 0,T \right] \\ \end{align}$ | (11) |
其中
| $\begin{align} & w\left( Y\left( T \right) \right)={{q}_{1}}\left[ {{\left( {{y}_{1}}\left( T \right)-{{y}_{1f}} \right)}^{2}}+{{\left( {{y}_{2}}\left( T \right)-{{y}_{2f}} \right)}^{2}} \right] \\ & +{{q}_{2}}\left( \cos \left( {{y}_{3}}\left( T \right)+1 \right)+{{q}_{3}}{{y}_{4}}\left( T \right)+{{q}_{4}}{{y}_{5}}\left( T \right) \right) \\ \end{align}$ |
状态方程
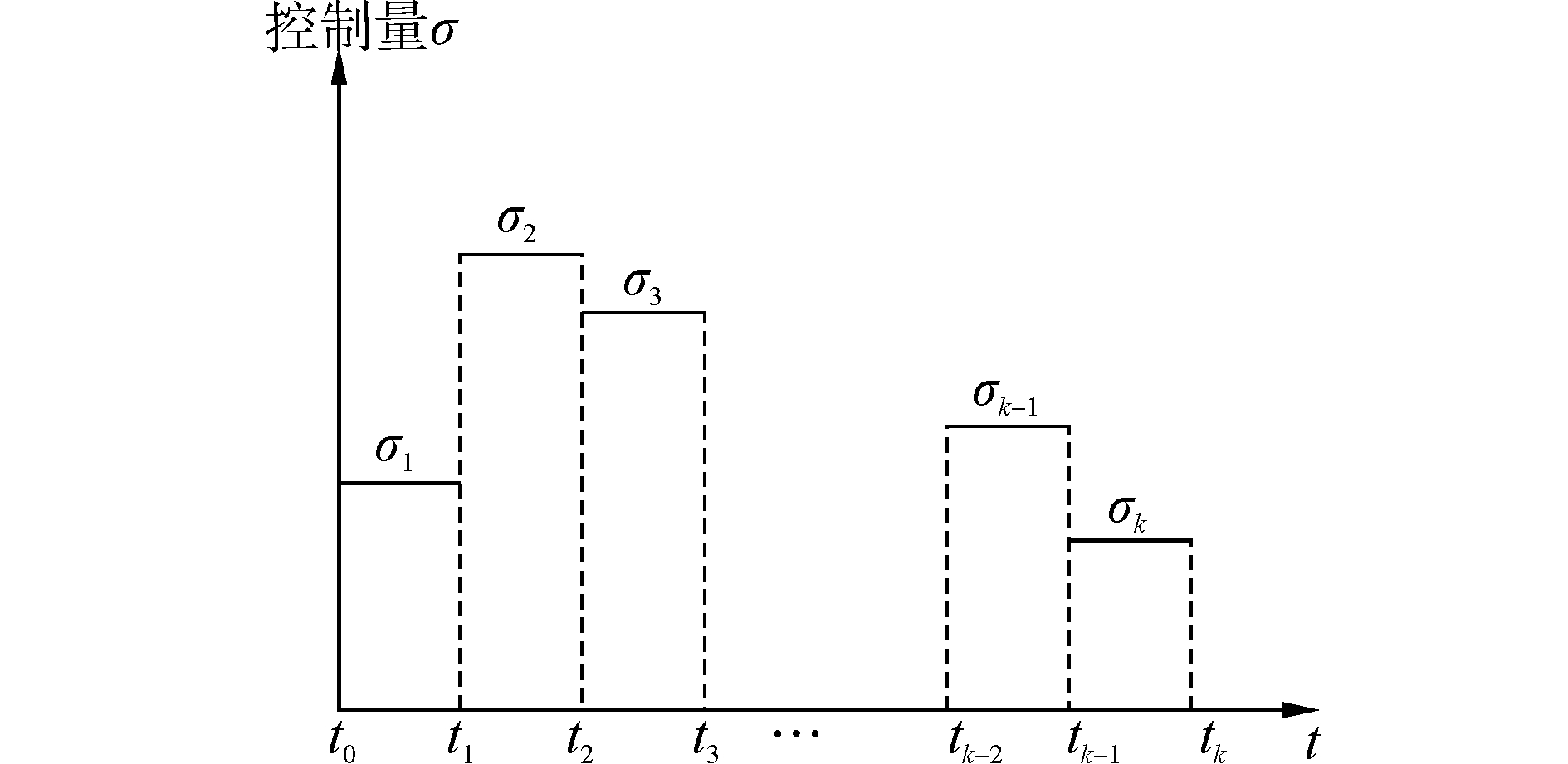
|
| 图5 分段常值控制 Figure 5 Piecewise constant control |
其中,tk是在时间区间 T 上顺次的时间切换点,且满足:
| $0={{t}_{0}}\le {{t}_{1}}\le \cdots {{t}_{p-1}}\le {{t}_{p}}=T$ |
定义
| $\begin{align} & {{U}^{P}}=\left\{ \sigma =\left( {{\sigma }^{1}},{{\sigma }^{2}},\cdots {{\sigma }^{P}} \right)\in {{R}^{P}} \right\} \\ & \left\| {{\sigma }^{k}} \right\|\le {{U}_{\max }},k=1,2,\cdots ,p \\ \end{align}$ |
控制变量u 的值在每个时间段上用一个常数来近似:
| $u\left( t \right)={{\sigma }^{k}},t\in \left[ {{t}_{k-1}},{{t}_{k}} \right]$ |
那么控制函数在整个时间段上可以用如下分片常值形式表示出来:
| $u\left( t \right)\approx {{u}_{p}}\left( t \right)=\sum\limits_{k=1}^{p}{{{\sigma }^{k}}{{\chi }_{\left[ {{t}_{k-1}},{{t}_{k}} \right]}}\left( t \right),t\in \left[ {{t}_{k-1}},{{t}_{k}} \right)}$ | (12) |
χ[tk-1,tk) 为如下特征函数:
| ${{\chi }_{\left[ {{t}_{k-1}},{{t}_{k}} \right]}}=\left\{ \begin{align} & 1,t\in \left[ {{t}_{k-1}},{{t}_{k}} \right) \\ & 0,其他 \\ \end{align} \right.$ |
将离散后的控制量(12) 代入式(11) ,可以得到新的目标函数:
| $\begin{align} & G\left( \sigma \right)=w\left( Y\left( T\left| \sigma \right. \right) \right)={{q}_{1}}{{\left[ {{y}_{1}}\left( T\left| \sigma \right. \right)-{{y}_{1f}}+{{y}_{1}}\left( T\left| \sigma \right. \right)-{{y}_{1f}} \right]}^{2}} \\ & +\left( {{q}_{2}}\left( \cos \left( {{y}_{3}} \right)T\left| \sigma \right. \right) \right)+1+{{q}_{3}}{{y}_{4}}\left( T\left| \sigma \right. \right)+{{q}_{4}}{{y}_{5}}\left( T\left| \sigma \right. \right) \\ \end{align}$ | (13) |
通过控制变量参数化后,问题 2 变成了一个标准的参数优化选择问题,实际上,这类问题可以采用序列二次最优化方法(sequential quadratic programming,SQP) 进行求解。为了实现 SQP 方法,需要利用到目标函数(13) 关于控制量参数的梯度信息。
3.2 梯度公式目标函数(13) 对控制量σk的梯度为
| $\frac{\partial G\left( \sigma \right)}{\partial {{\sigma }^{k}}}=\frac{\partial w\left( x\left( T\left| \sigma \right. \right) \right)}{\partial x}\Gamma \left( T\left| \sigma \right. \right)+\frac{\partial w\left( x\left( T\left| \sigma \right. \right) \right)}{\partial x}$ |
其中,
推导:由式(11) 可得,状态变量x(t|σ) 的解的形式为
| $x\left( t\left| \sigma \right. \right)={{x}^{0}}\left( \sigma \right)+\int_{0}^{t}{f\left( s,x\left( s\left| \sigma \right. \right),\sigma \right)}ds$ |
令
| $\matrix{ {{\delta _{kl}} = \{ \matrix{ {1,k = 1} \hfill \cr {0,其他} \hfill \cr } } \hfill \cr {{\delta _{kl}} = \{ \matrix{ {1,k \le 1} \hfill \cr {0,其他} \hfill \cr } } \hfill \cr } $ |
式中:l 表示所等分的时间区间的个数。
对于 l = 1,2,…,p,当 k < l 时,状态变量 x(t|σ) 对控制变量σk的偏导数为
| $\begin{align} & \frac{\partial x\left( t\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}}=\frac{\partial x\left( {{t}_{l-1}}\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}} \\ & +\int_{{{t}_{l-1}}}^{t}{\frac{\partial f\left( s,x\left( s\left| \sigma \right. \right),{{\sigma }^{l}} \right)}{\partial x}\frac{\partial x\left( s\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}}ds} \\ & t\in \left[ {{t}_{l-1}},{{t}_{l}} \right) \\ \end{align}$ | (14) |
当 k = l 时,状态变量x(t|σ) 对控制变量σk的偏导数为
| $\begin{align} & \frac{\partial x\left( t\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}}=\frac{\partial x\left( {{t}_{l-1}}\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}} \\ & +\int_{{{t}_{l-1}}}^{t}{\frac{\partial f\left( s,x\left( s\left| \sigma \right. \right),{{\sigma }^{l}} \right)}{\partial x}\frac{\partial x\left( s\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}}ds}+ \\ & \int_{{{t}_{l-1}}}^{t}{\frac{\partial f\left( s,x\left( s\left| \sigma \right. \right),{{\sigma }^{l}} \right)}{\partial x}\frac{\partial x\left( s\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}}ds},t\in \left[ {{t}_{l-1}},{{t}_{l}} \right) \\ \end{align}$ | (15) |
当 k > l 时,显然有
| $\frac{\partial x\left( t\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}}=0,t\in \left[ {{t}_{l-1}},{{t}_{l}} \right)$ | (16) |
综合式(14) ~(16) 得
| $\begin{align} & \frac{\partial x\left( t\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}}={{{\hat{\delta }}}_{kl}}\frac{\partial x\left( {{t}_{l-1}}\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}} \\ & +\int_{{{t}_{l-1}}}^{t}{{{{\hat{\delta }}}_{kl}}\frac{\partial f\left( s,x\left( s\left| \sigma \right. \right),{{\sigma }^{l}} \right)}{\partial x}\frac{\partial x\left( s\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}}ds}+ \\ & \int_{{{t}_{l-1}}}^{t}{{{{\hat{\delta }}}_{kl}}\frac{\partial f\left( s,x\left( s\left| \sigma \right. \right),{{\sigma }^{l}} \right)}{\partial x}\frac{\partial x\left( s\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}}ds},t\in \left[ {{t}_{l-1}},{{t}_{l}} \right) \\ \end{align}$ | (17) |
式(17) 对时间 t 进行求偏导得
| $\begin{align} & \frac{d}{dt}\left\{ \frac{\partial x\left( t\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}} \right\}={{{\hat{\delta }}}_{kl}}\frac{\partial f\left( s,x\left( s\left| \sigma \right. \right),{{\sigma }^{l}} \right)}{\partial x}\frac{\partial x\left( s\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}}+ \\ & {{\delta }_{kl}}\frac{\partial f\left( s,x\left( s\left| \sigma \right. \right),{{\sigma }^{l}} \right)}{\partial x},t\in \left[ {{t}_{l-1}},{{t}_{l}} \right) \\ \end{align}$ |
由此可以得到
| $\left\{ \begin{matrix} \Gamma \left( t \right){{{\dot{\delta }}}_{kl}}\frac{\partial f\left( s,x\left( s\left| \sigma \right. \right),{{\sigma }^{l}} \right)}{\partial x}\Gamma \left( t \right)+ \\ {{\delta }_{kl}}\frac{\partial f\left( s,x\left( s\left| \sigma \right. \right),{{\sigma }^{l}} \right)}{\partial x} \\ \Gamma \left( 0 \right)=\frac{\partial {{x}^{0}}\left( {{\sigma }^{k}} \right)}{\partial {{\sigma }^{k}}} \\ \end{matrix} \right.$ | (18) |
根据式(18) 可以求解Γ(t|σ) ,即
| $\frac{\partial x\left( t\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}}=\frac{\partial w\left( x\left( T\left| \sigma \right. \right) \right)}{\partial x}\frac{\partial x\left( t\left| \sigma \right. \right)}{\partial {{\sigma }^{k}}}+\frac{\partial w\left( x\left( T\left| \sigma \right. \right) \right)}{\partial x}\Gamma \left( T\left| \sigma \right. \right)+\frac{\partial w\left( x\left( T\left| \sigma \right. \right) \right)}{\partial x}$ |
1) 在可行域中,任意选取初始控制参数σ0∈Up;
2) 令m=0;
3) 利用梯度公式计算目标函数对于控制参数在σm处的梯度;
4) 最优性检验,若最优,则迭代结束;若不是最优,到步骤5;
5) 利用拟牛顿法(不需要二阶梯度信息) 计算σm 处的搜索方向;
6) 应用线搜索确定最优步长;
7) 得到新的控制参数σm+1;
8) 令m=m+1,回到步骤3。
4 仿真结果及分析系统初始值选取原则:
1) 必须使得威胁模型对翼伞归航轨迹有制约作用,即选取翼伞投放坐标与目标着陆点坐标之间存在威胁;
2) 问题有解,若投放坐标相距威胁太近,翼伞系统将无法规避威胁。
根据上述模型以及初始值选取的两个原则,在保证转弯时系统倾斜角小于20°的前提下,设翼伞系统基本运动参数为vs = 18 m/s,vz = 6 m/s,umax = vs /R min =0.18(R为转弯半径) 。初始高度为z0 =3 000 m,则对应的ηmax=90,目标着陆地点(500,1 000,0) 在威胁的后方。根据这些参数,利用控制变量参数化的方法,做如下仿真实验。
由于对威胁的规避是必须满足的,那么威胁项的权重系数应该占有很高的值,首先取权值为 q1 = 100,q2 = 1,q3 = 1,q4 = 5 000,这里弱化了雀降要求和控制能量要求,得到仿真结果如图 6(a) ,从结果可以看出,着陆点离目标地点的差距并不理想;然后将雀降权重增加,改权值为 q1 = 100,q2 = 100,q3 = 1,q4 = 5 000,得到仿真结果如图 6(b) ,结果着陆点离目标地点也有一定的差距,同时与前一仿真结果对比可以发现雀降要求对于最终着陆点的影响并不是很大;为了让着陆点更精确,增加q1的值,取各项权值为 q1 = 500,q2 = 100,q3 = 1,q4 = 5 000,得到最终仿真结果如图 6(c) ,从结果可以看出,翼伞几乎精确到达了目标地点,并且完美地避开了威胁区域;最后考虑控制能量部分,增加权值q3 的值,取各项权值为 q1 = 500,q2 = 100,q3 = 10,q4 = 5 000,得到最终仿真结果如图 6(d) ,从结果可以看到,牺牲了微小的着陆精度降低了控制的能量,可以在满足着陆精度的要求同时减小控制变化量。

|
| 图6 不同权值下的翼伞最优轨迹 Figure 6 Parafoil optimal trajectory for different weight |
作为方法对照,本文将优化问题1利用标准粒子群(PSO) 算法进行优化求解。同样的,将控制变量u 进行分段常值近似处理,取分段数为10,即在粒子群算法中粒子的维数为10,目标函数中权值取第四组参数q1 = 500,q2 = 100,q3 = 10,q4 = 5 000,初始点为(3 000,3 000,-60°,0,0) ,设粒子数为20,惯性因子w = 0.7 ,学习因子c1= c2 = 2,最大迭代步数为1 000。将优化结果与上述精确罚函数优化算法进行结果比较,如表 1 所示。
| 算法 | 目标初值 | 目标终值 | 耗时/s |
| 粒子群算法 | 1.429×1010 | 5 890.5 | 2 373.21 |
| 精确罚函数算法 | 1.754×1010 | 1 042.6 | 258.63 |
对比表中数据可以发现,相较于粒子群算法,精确罚函数优化算法有更好的优化效果,并且计算耗时更短。如果使用粒子群算法想要达到更好的优化效果,则需增加粒子数量,但随之产生的结果是计算耗时会更长。因此,精确罚函数优化算法在计算翼伞系统避障最优归航轨迹这一问题上具有一定的优势。
5 结论1) 考虑到翼伞系统在归航过程中会遇到一系列的威胁,建立了带威胁的三自由度翼伞系统归航控制数学模型。
2) 利用控制参数化方法将翼伞系统归航威胁规避最优控制问题转化为带约束条件的轨迹规划问题,采用精确罚函数方法将具有路径约束与控制约束轨迹规划问题转化为无约束问题,然后求解出问题的梯度信息并利用 SQP 算法求解。
3) 利用仿真实验验证了本文算法的可行性:在建立的三自由度翼伞模型上,控制效果好,所需控制能耗低,距离偏差与方向偏差均满足翼伞投递精度要求。对于工程实践具有很高的参考价值。
4) 与常用智能算法 PSO 计算结果相比较,本文算法在高效性与可靠性方面具有一定优势。
今后的工作可进一步完善仿真模型(例如使用翼伞六自由度模型、九自由度模型等) ,提高系统的准确性,同时也可以考虑实际复杂地貌的建模分析(例如使用实际卫星拍摄的地貌参数) ,并利用激光探测定位系统(light detection and ranging,LIDAR) 进行实时风向测量并对空投范围内气流做出预测,为翼伞系统提供更精确的环境数据。还可以将翼伞系统与旋翼机[27]相结合,利用翼伞精准归航的功能,增强无人机试验的安全性。
| [1] |
韩雅慧, 杨春信, 肖华军, 等. 翼伞精确空投系统关键技术和发展趋势[J].
兵工自动化, 2012, 31(7): 1–7.
HAN Yahui, YANG Chunxin, XIAO Huajun, et al. Review on key technology and development of parafoil precise airdrop systems[J]. Ordnance industry automation, 2012, 31(7): 1–7. |
| [2] |
谢亚荣. 空投任务下翼伞建模与飞行控制研究[D]. 南京: 南京航空航天大学, 2011. XIE Yarong. Research on modeling and flight control of parafoil under the airdrop mission[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2011. |
| [3] |
殷俊. GPS引导定点空投系统的自动归航[D]. 北京: 北京航空航天大学, 2001. YIN Jun. The anatysis of GPS automatics homing system[D]. Beijing:Beihang University, 2001. |
| [4] |
史献林, 余莉. 翼伞空中回收系统的研究及其进展[J].
航天返回与遥感, 2008, 29(1): 1–5.
SHI Xianlin, YU Li. The study and development of the parafoil mid-air retrieval system[J]. Spacecraft recovery & remote sensing, 2008, 29(1): 1–5. |
| [5] |
熊菁, 秦子增, 文红武. 翼伞系统归航的最优控制[J].
航天控制, 2004, 22(6): 32–36.
XIONG Jing, QIN Zizeng, WEN Hongwu. Optimal control of parafoil system homing[J]. Aerospace control, 2004, 22(6): 32–36. |
| [6] |
熊菁, 秦子增, 程文科, 等. 翼伞系统分段归航轨迹的优化设计[J].
航天返回与遥感, 2004, 25(3): 11–16.
XIONG Jing, QIN Zizeng, CHENG Wenke, et al. Optimal design in multiphase trajectory of parafoil system[J]. Spacecraft recovery & remote sensing, 2004, 25(3): 11–16. |
| [7] |
张兴会, 朱二琳. 基于能量约束的翼伞系统分段归航设计与仿真[J].
航天控制, 2011, 29(5): 43–47.
ZHANG Xinghui, ZHU Erlin. Design and simulation in the multiphase homing of parafoil system based on energy confinement[J]. Aerospace control, 2011, 29(5): 43–47. |
| [8] | BETTS J T. Survey of numerical methods for trajectory optimization[J]. Journal of guidance, control, and dynamics, 1998, 21(2): 193–207. |
| [9] | ROSS I M, FAHROO F. A perspective on methods for trajectory optimization[C]//Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Monterey, CA, 2002. |
| [10] |
李树荣, 张强. 计算机数控系统光滑时间最优轨迹规划[J].
控制理论与应用, 2012, 29(2): 192–198.
LI Shurong, ZHANG Qiang. Smooth and time-optimal trajectory planning for computer numerical control systems[J]. Control theory & applications, 2012, 29(2): 192–198. |
| [11] |
赵娟平, 高宪文, 符秀辉, 等. 移动机器人路径规划的改进蚁群优化算法[J].
控制理论与应用, 2011, 28(4): 457–461.
ZHAO Juanping, GAO Xianwen, FU Xiuhui, et al. Improved ant colony algorithm of path planning for mobile robot[J]. Control theory & applications, 2011, 28(4): 457–461. |
| [12] |
巩敦卫, 耿娜, 张勇. 密集障碍物环境下基于凸包和微粒群优化的机器人路径规划[J].
控制理论与应用, 2012, 29(5): 609–616.
GONG Dunwei, GENG Na, ZHANG Yong. Robot path planning in environments with dense obstacles based on convex hull and particle swarm optimization[J]. Control theory & applications, 2012, 29(5): 609–616. |
| [13] | ASSEO S J. Terrain following/terrain avoidance path optimization using the method of steepest descent[C]//Proceedings of the IEEE 1988 National on Aerospace and Electronics Conference, 1988. NAECON 1988. Dayton, OH:IEEE, 1988. |
| [14] | SHARMA T, WILLIAMS P, BIL C, et al. Optimal three dimensional aircraft terrain following and collision avoidance[J]. ANZIAM journal, 2005, 47: 695–711. |
| [15] | WILLIAMS P. Three-dimensional aircraft terrain-following via real-time optimal control[J]. Journal of guidance, control, and dynamics, 2007, 30(4): 1201–1206. |
| [16] | KHADEMI I, MALEKI B, MOOD A N. Optimal three dimensional terrain following/terrain avoidance for aircraft using direct transcription method[C]//Proceedings of the 201119th Mediterranean Conference on Control & Automation (MED). Corfu:IEEE, 2011:254-258. |
| [17] | FAN X, YAN H, ZHANG G P. A UAV path planning method based on threat sources[C]//Proceedings of the Advances in Biomedical Engineering-2012 International Conference on Environmental Engineering and Technology. Wuhan, 2012:317-325. |
| [18] |
熊菁. 翼伞系统动力学与归航方案研究[D]. 长沙: 国防科学技术大学, 2005: 31-49. XIONG Jing. Research on the dynamics and homing project of parafoil system[D]. Changsha:National University of Defense Technology, 2005:31-49. |
| [19] |
焦亮. 基于翼伞空投机器人系统的自主归航研究[D]. 天津: 南开大学, 2011: 30-43. JIAO Liang. Research on autonomous homing based on parafoil and air-dropped robot system[D]. Tianjin:Nankai University, 2011:30-43. |
| [20] |
焦亮, 孙青林, 亢晓峰. 基于混沌粒子群优化算法的翼伞系统轨迹规划[J].
复杂系统与复杂性科学, 2012, 9(1): 47–54.
JIAO Liang, SUN Qinglin, KANG Xiaofeng. Route planning for parafoil system based on chaotic particle swarm optimization[J]. Complex systems and complexity science, 2012, 9(1): 47–54. |
| [21] |
高海涛, 张利民, 孙青林, 等. 基于伪谱法的翼伞系统归航轨迹容错设计[J].
控制理论与应用, 2013, 30(6): 702–708.
GAO Haitao, ZHANG Limin, SUN Qinglin, et al. Fault-tolerance design of homing trajectory for parafoil system based on pseudo-spectral method[J]. Control theory & applications, 2013, 30(6): 702–708. |
| [22] |
白瑞光, 孙鑫, 陈秋双, 等. 基于Gauss伪谱法的多UAV协同航迹规划[J].
宇航学报, 2014, 35(9): 1022–1029.
BAI Ruiguang, SUN Xin, CHEN Qiushuang, et al. Multiple UAV cooperative trajectory planning based on Gauss pseudospectral method[J]. Journal of astronautics, 2014, 35(9): 1022–1029. |
| [23] |
梁海燕, 任志刚, 许超, 等. 翼伞系统最优归航轨迹设计的敏感度分析方法[J].
控制理论与应用, 2015, 32(8): 1003–1011.
LIANG Haiyan, REN Zhigang, XU Chao, et al. Optimal homing trajectory design for parafoil systems using sensitivity analysis approach[J]. Control theory & applications, 2015, 32(8): 1003–1011. |
| [24] | JIANG Canghua, LIN Qun, YU Changjin, et al. An exact penalty method for free terminal time optimal control problem with continuous inequality constraints[J]. Journal of optimization theory and applications, 2012, 154(1): 30–53. |
| [25] | LOXTON R C, TEO K L, REHBOCK V, et al. Optimal control problems with a continuous inequality constraint on the state and the control[J]. Automatica, 2009, 45(10): 2250–2257. |
| [26] | LIN Qun, LOXTON R, TEO K L. The control parameterization method for nonlinear optimal control:a survey[J]. Journal of industrial & management optimization, 2014, 10(1): 275–309. |
| [27] |
张广玉, 张洪涛, 李隆球, 等. 四旋翼微型飞行器设计[J].
哈尔滨理工大学学报, 2012, 17(3): 110–114.
ZHANG Guangyu, ZHANG Hongtao, LI Longqiu, et al. Design of quad-rotor micro air vehicle[J]. Journal of Harbin university of science and technology, 2012, 17(3): 110–114. |



