2. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China
近几十年来,索结构广泛的应用于输电线、斜拉桥等大跨越空间结构。索结构具有很强的非线性特性,索结构受力分析需要考虑扰度和大变形的影响。在索结构的研究方面,陈太聪等[1]总结和分析了不同工况下索结构中拉索的受力特点,将拉索行为归纳为已知原长和已知索力两种典型受力情况。利用悬链线拉索解析解的线性展开,引入适当的约束条件,建立两种新型的拉索单元,提出索结构非线性静力分析的一般迭代算法,利用等效线自重考虑弹性变形对拉索静力状态的影响。魏建东等[2]基于有限元分析的基本原理,创建了一种新的滑移索单元,分析索结构中索段在鞍座上的滑动问题。唐建民等[3]根据张拉结构的特点,提出了一种五节点等参数单元有限元模型,采用四节点多项式作为位移差值函数及单元初始形状函数,基于修正的Lagrangian坐标描述法,建立了非线性有限元基本方程和切线刚度矩阵,利用Newton-Raphson法进行了实例计算。黄涛等[4]提出了具有扭转自由度的五节点索单元非线性有限元法,考虑了索结构沿轴向的转动自由度,这种方法不仅适用于一般的悬索结构的分析,也适用于需要考虑扭转的特殊悬索结构的分析。
现有的索结构数值分析技术主要采用下面两种方法:1)基于多项式插值函数的有限元方法,2)基于弹性悬链线解析表达式的分析方法。在第1种方法中,采用插值函数来描述索结构的非线性,这种方法常用来模拟两节点和多节点单元及具有转动自由度的曲线单元,但是该方法只适合模拟具有较大预应力的索结构。对于长度较小,承受拉力较高的索,采用等效弹性模量来计算是足够准确的,但对于弧垂比较大的索,该方法的适用性较差[5]。对大弧垂索结构,一般采用一系列的直线单元来模拟几何弯曲的索结构,多节点索单元是基于高阶多项式的插值函数[6-8]来构造,因此计算结果的精度较两节点索单元有一定的提高,但多节点单元会破坏索结构曲线斜率的连续性。除此之外,多节点单元需要使用大量的单元来建立几何弯曲的索结构模型,对于多索结构体系,这种方法的计算成本巨大。第二种方法是由Jayaraman 等[9]提出的采用弹性悬链线的精确表达式来描述索结构的真实力学行为,经过Wang[10]、 Andreu[11]、 Yang[12]、Such[13]、Andreu[14]等进行改进。用悬链线单元对曲线索结构进行建模,与多项式插值函数有限元方法相比有很多优点,如计算需要的自由度数少,可以完全考虑索结构的非线性效应。
基于弹性悬链线解析理论,本文开发了一种空间两节点悬链线索单元,用来对索结构承受的静态和动态荷载进行非线性分析。考虑索结构的预应力效应,推导并给出索单元的切线刚度矩阵和内部力向量。采用构造的索单元对弧垂较小的索网结构和弧垂较大的输电线索结构进行计算分析,并对计算结果进行了验证。
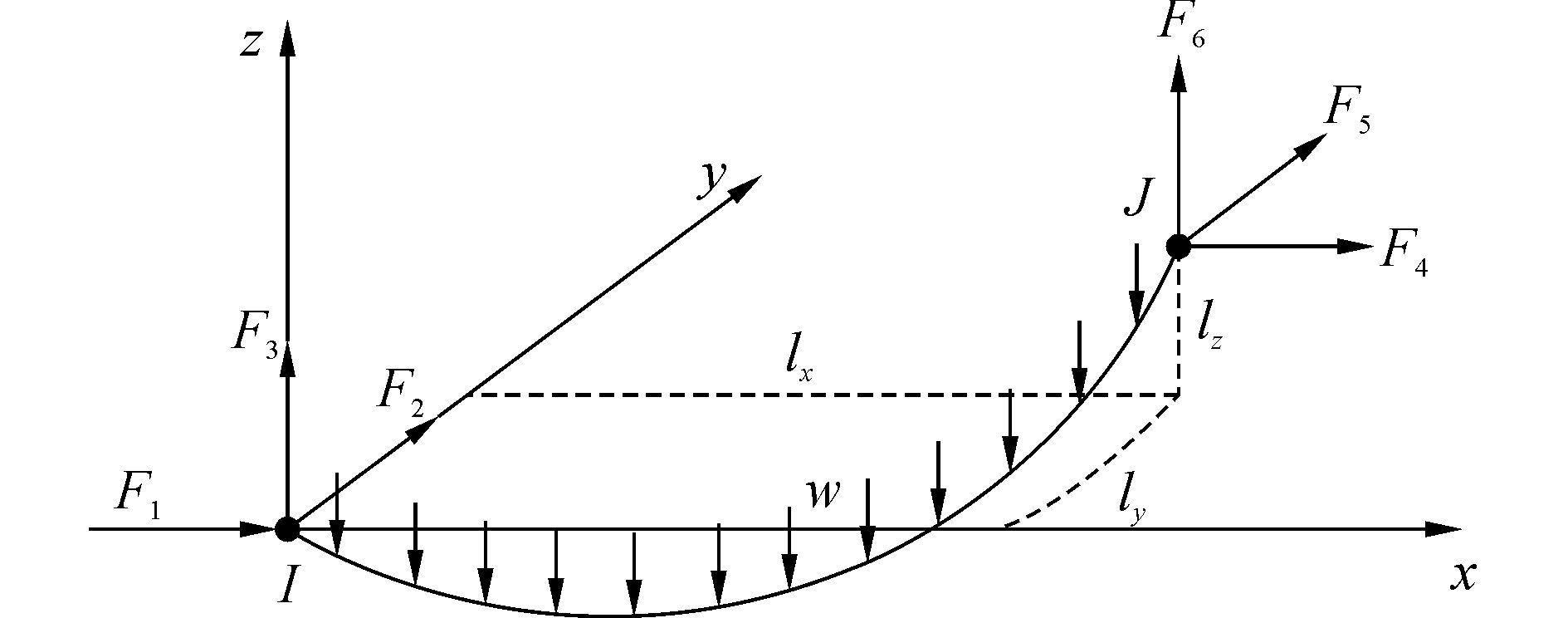
1 悬链线索单元为了能够模拟索结构的真实形态,根据弹性悬链线单元的解析表达式,本文推导出来一种新的悬链线索单元。假设索结构是完全柔性的,自重沿索长度均匀分布,索的横截面积保持不变。图 1显示了索结构两悬挂点I、 J的笛卡尔坐标分别为(0,0,0)和(lx,ly,lz),s和p为变形前后索上任意一点的曲线坐标。索在平衡时的方程可以表示为
| $T\left( \frac{dx}{dp} \right)=-{{F}_{1}},T\left( \frac{dy}{dp} \right)=-{{F}_{2}},T\left( \frac{dz}{dp} \right)=-{{F}_{3}}+ws$ | (1) |
式中:F1、F2和F3分别是索结构在x、y和z轴的张力分量,w是索结构的自重,索结构的张力在拉格朗日坐标下的表达式为
| $T\left( s \right)=\sqrt{F_{1}^{2}+F_{2}^{2}+{{\left( {{F}_{3}}-ws \right)}^{2}}}$ | (2) |
索的张力T与应变ε的关系符合胡克定律:
| $T=EA\varepsilon =EA\left( \frac{dp-ds}{ds} \right)=EA\left( \frac{dp}{ds}-1 \right)\text{ }$ | (3) |
式中:E是索的弹性模量,A是索的横截面积。曲线坐标s与笛卡尔坐标之间的关系可以表示为
| $\left\{ \begin{align} & x\left( s \right)=\int \frac{dx}{ds}ds=\int \frac{dx}{dp}\frac{dp}{ds}ds \\ & y\left( s \right)=\int \frac{dy}{ds}ds=\int \frac{dy}{dp}\frac{dp}{ds}ds \\ & z\left( s \right)=\int \frac{dz}{ds}ds=\int \frac{dz}{dp}\frac{dp}{ds}ds \\ \end{align} \right.$ | (4) |
|
| 图1 三维悬链线索单元 Figure 1 Three-dimensional catenary cable element |
在索两端点处的边界条件为
| $\left\{ \begin{align} & x\left( 0 \right)=y\left( 0 \right)=z\left( 0 \right)=0 \\ & x\left( {{L}_{0}} \right)={{l}_{x}},y\left( {{L}_{0}} \right)={{l}_{y}},z\left( {{L}_{0}} \right)={{l}_{z}} \\ \end{align} \right.$ | (5) |
将方程(1)~(3)代入方程(4),引入边界条件(5),索的长度在x、y和z 3个方向的分量为
| $\begin{align} & {{l}_{x}}=-\frac{{{F}_{1}}{{L}_{0}}}{EA}-\frac{{{F}_{1}}}{w}\left\{ ln \right.\left[ \sqrt{F_{1}^{2}+F_{2}^{2}+{{\left( w{{L}_{0}}-{{F}_{3}} \right)}^{2}}} \right.+w{{L}_{0}}-\left. {{F}_{3}} \right] \\ & -ln\left. \left( \sqrt{F_{1}^{2}+F_{2}^{2}+F_{3}^{2}}-{{F}_{3}} \right) \right\} \\ & {{l}_{y}}=-\frac{{{F}_{2}}{{L}_{0}}}{EA}-\frac{{{F}_{2}}}{w}\left\{ ln \right.\left[ \sqrt{F_{1}^{2}+F_{2}^{2}+{{\left( w{{L}_{0}}-{{F}_{3}} \right)}^{2}}} \right.+w{{L}_{0}}-\left. {{F}_{3}} \right] \\ & -ln\left. \left( \sqrt{F_{1}^{2}+F_{2}^{2}+F_{3}^{2}}-{{F}_{3}} \right) \right\} \\ & {{l}_{Z}}=-\frac{{{F}_{3}}{{L}_{0}}}{EA}+\frac{w{{L}_{0}}^{2}}{2EA}-\frac{1}{w}\left[ \sqrt{F_{1}^{2}+F_{2}^{2}+{{\left( w{{L}_{0}}-{{F}_{3}} \right)}^{2}}} \right.-\left. \sqrt{F_{1}^{2}+F_{2}^{2}+F_{3}^{2}} \right] \\ \end{align}$ | (6) |
式中:L0是索的原长,根据端部节点力(F1,F2,F3),lx、ly和lz可以表示成如下形式:
| $\left\{ \begin{align} & {{l}_{x}}=f\left( {{F}_{1}},{{F}_{2}},{{F}_{3}} \right) \\ & {{l}_{y}}=g\left( {{F}_{1}},{{F}_{2}},{{F}_{3}} \right) \\ & \backslash {{l}_{z}}=h\left( {{F}_{1}},{{F}_{2}},{{F}_{3}} \right) \\ \end{align} \right.$ | (7) |
切线刚度矩阵和相应单元的内力向量可以通过求解方程(6)来推导,对方程(6)的两边同时进行微分,可以得到下面的方程:
| $\left\{ \begin{align} & d{{l}_{x}}={{\frac{\partial f}{\partial F}}_{1}}d{{F}_{1}}+\frac{\partial f}{\partial {{F}_{2}}}d{{F}_{2}}+\frac{\partial f}{\partial {{F}_{3}}}d{{F}_{3}} \\ & d{{l}_{y}}={{\frac{\partial g}{\partial F}}_{1}}d{{F}_{1}}+{{\frac{\partial g}{\partial F}}_{2}}d{{F}_{2}}+{{\frac{\partial g}{\partial F}}_{3}}d{{F}_{3}} \\ & d{{l}_{z}}=\frac{\partial h}{\partial {{F}_{1}}}d{{F}_{1}}+\frac{\partial h}{\partial {{F}_{2}}}d{{F}_{2}}+\frac{\partial h}{\partial {{F}_{3}}}d{{F}_{3}} \\ \end{align} \right.$ | (8) |
或表示成矩阵的形式:
| $\left[ \begin{matrix} d{{l}_{x}} \\ d{{l}_{y}} \\ d{{l}_{z}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{f}_{11}} & {{f}_{12}} & {{f}_{13}} \\ {{f}_{21}} & {{f}_{22}} & {{f}_{23}} \\ {{f}_{31}} & {{f}_{32}} & {{f}_{33}} \\ \end{matrix} \right]\left[ \begin{matrix} d{{F}_{1}} \\ d{{F}_{2}} \\ d{{F}_{3}} \\ \end{matrix} \right]=F\left[ \begin{matrix} d{{F}_{1}} \\ d{{F}_{2}} \\ d{{F}_{3}} \\ \end{matrix} \right]$ | (9) |
F是柔度矩阵,具体可以表示为
| $\left\{ \begin{align} & {{f}_{11}}=-\left( \frac{{{L}_{0}}}{EA}+\frac{1}{w}log\frac{{{T}_{j}}+{{F}_{6}}}{{{T}_{i}}-{{F}_{3}}} \right)+ \\ & \frac{F_{1}^{2}}{w}\left[ \frac{1}{{{T}_{i}}\left( {{T}_{i}}-{{T}_{3}} \right)}-\frac{1}{{{T}_{j}}\left( {{T}_{j}}+{{F}_{6}} \right)} \right] \\ & {{f}_{12}}={{f}_{21}}=\frac{{{F}_{1}}{{F}_{2}}}{w}\left[ \frac{1}{{{T}_{i}}\left( {{T}_{i}}-{{F}_{3}} \right)}-\frac{1}{{{T}_{j}}\left( {{T}_{j}}+{{F}_{6}} \right)} \right] \\ & {{f}_{13}}={{f}_{31}}=\frac{{{F}_{1}}}{w}\left[ \frac{1}{{{T}_{j}}}-\frac{1}{{{T}_{i}}} \right] \\ & {{f}_{22}}=-\left( \frac{{{L}_{0}}}{EA}+\frac{1}{w}log\frac{{{T}_{j}}+{{F}_{6}}}{{{T}_{i}}-{{F}_{3}}} \right)+ \\ & \frac{F_{2}^{2}}{w}\left[ \frac{1}{{{T}_{i}}\left( {{T}_{i}}-{{F}_{3}} \right)}-\frac{1}{{{T}_{j}}\left( {{T}_{j}}+{{T}_{6}} \right)} \right] \\ & {{f}_{23}}={{f}_{32}}=\frac{{{F}_{2}}}{w}\left[ \frac{1}{{{T}_{j}}}-\frac{1}{{{T}_{i}}} \right] \\ & {{f}_{33}}=-\frac{{{L}_{0}}}{EA}-\frac{1}{w}\left[ \frac{{{F}_{6}}}{{{T}_{j}}}+\frac{{{F}_{3}}}{{{T}_{i}}} \right] \\ \end{align} \right.$ | (10) |
式中:Ti和Tj分别是节点I、J的张力,可以定义为
| $\left\{ \begin{align} & {{T}_{i}}=F_{1}^{2}+F_{2}^{2}+F_{3}^{2} \\ & {{T}_{j}}=F_{4}^{2}+F_{5}^{2}+F_{6}^{2} \\ \end{align} \right.$ | (11) |
节点J的节点力(F4,F5,F6)可以通过平衡方程获得
| $\left\{ \begin{align} & {{F}_{4}}=-{{F}_{1}} \\ & {{F}_{5}}=-{{F}_{2}} \\ & {{F}_{6}}=-{{F}_{3}}+w{{L}_{0}} \\ \end{align} \right.$ | (12) |
刚度矩阵通过对求柔度矩阵F的逆矩阵而得到
| $K={{F}^{-1}}={{\left[ \begin{matrix} {{f}_{11}} & {{f}_{12}} & {{f}_{13}} \\ {{f}_{21}} & {{f}_{22}} & {{f}_{23}} \\ {{f}_{31}} & {{f}_{32}} & {{f}_{33}} \\ \end{matrix} \right]}^{-1}}$ | (13) |
索单元的切线刚度矩阵和内力向量可以表示成六自由度的形式:
| ${{K}_{T}}=\left[ \begin{matrix} -K & K \\ K & -K \\ \end{matrix} \right]$ | (14) |
| ${{F}_{int}}={{\left[ {{F}_{1}}{{F}_{2}}{{F}_{3}}{{F}_{4}}{{F}_{5}}{{F}_{6}} \right]}^{T}}$ | (15) |
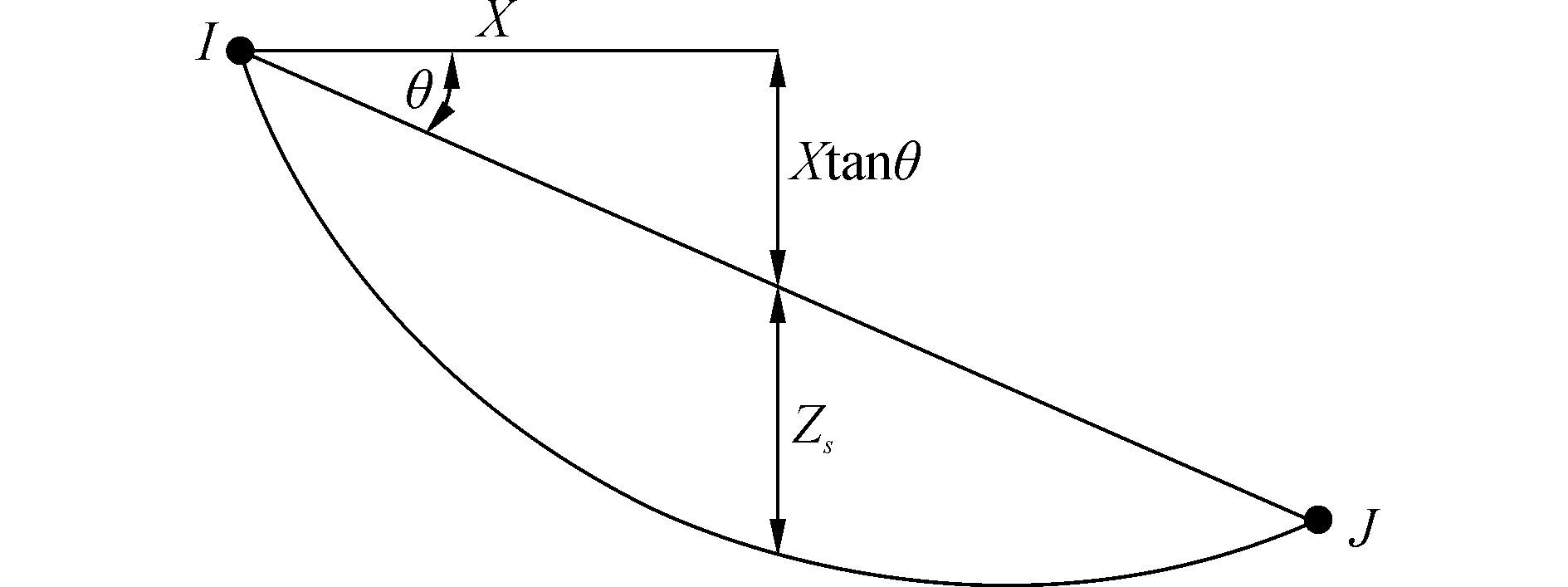
如果索单元的切线刚度矩阵和内力向量已经确定,索长和索的弧垂如图 2可以获得[9, 14]:
| $S=\sqrt{{{l}_{z}}^{2}+\left( l_{x}^{2}+l_{y}^{2} \right)\frac{sin{{h}^{2}}\lambda }{{{\lambda }^{2}}}}$ | (16) |
| ${{z}_{s}}=\lambda L\left[ 3+\left( 1-2\bar{x} \right)\lambda sin\theta \right]\bar{x}\left( 1-\bar{x} \right)/3$ | (17) |
式中:
| $\left\{ \begin{align} & \lambda =\frac{w}{2}\sqrt{\left( l_{x}^{2}+l_{y}^{2} \right)/\left( F_{1}^{2}+F_{2}^{2} \right)} \\ & L=\sqrt{{{l}_{x}}^{2}+{{l}_{y}}^{2}+{{l}_{z}}^{2}} \\ & x-=x/\sqrt{{{l}_{x}}^{2}+{{l}_{y}}^{2}} \\ \end{align} \right.$ | (18) |
|
| 图2 斜拉索的弧垂Zs Figure 2 The sag of stay cable Zs |
采用弹塑性铰模型来表示索单元的非弹性行为,假设索单元的塑性分布是集中在索的两端,而整个索单元仍然保持弹性。如果索的轴向力大于屈服力Py=Aσy,索单元的弹性模量等于零,轴向力等于屈服力Py [15]。
2 刚度矩阵及求解方法应用迭代算法来计算索单元的切线刚度矩阵和内力向量。这个程序的计算需要端点力的初值(F1,F2,F3),根据已知的悬链线方程,端点力的初值可以通过以下的方式获得[9]
| $\left\{ \begin{align} & {{F}_{1}}=-\frac{w{{l}_{x}}}{2{{\lambda }_{0}}} \\ & {{F}_{2}}=-\frac{w{{l}_{y}}}{2{{\lambda }_{0}}} \\ & {{F}_{3}}=\frac{w}{2}\left( -{{l}_{z}}\frac{cosh{{\lambda }_{0}}}{sinh{{\lambda }_{0}}}+{{L}_{0}} \right) \\ \end{align} \right.$ | (19) |
式中:
| $\left\{ \begin{matrix} {{\lambda }_{0}}={{10}^{6}},\left( l_{x}^{2}+l_{y}^{2} \right)=0 \\ 0.2,L_{0}^{2}\le l_{x}^{2}+l_{y}^{2}+{{l}_{z}}^{2} \\ 3\frac{{{L}_{0}}^{2}-{{l}_{z}}^{2}}{{{l}_{x}}^{2}+{{l}_{y}}^{2}}-1,{{L}_{0}}^{2}>{{l}_{x}}^{2}+{{l}_{y}}^{2}+{{l}_{z}}^{2} \\ \end{matrix} \right.$ | (20) |
计算切线刚度矩阵和内力矢量的迭代程序如下:
1) 输入w、E、A、L0,节点I(xi,yi,zi)和节点J(xj,yj,zj)。
2) 计算lx0=xj-xi,ly0=yj-yi,lz0=zj-zi。
3) 应用式(19)对端点力F1,F2,F3进行初始化。
4) 使用式(6)更新(lx,ly,lz)。
5) 计算闭合差向量
| $dL={{\left[ \left( {{l}_{x0}}-{{l}_{x}} \right) \left( {{l}_{y0}}-{{l}_{y}} \right) \left( {{l}_{z0}}-{{l}_{z}} \right) \right]}^{T}}$ |
6) 如果dL小于预设的允许值,应用式(14)计算KT,用式(15)计算Fint,如果dL大于预设的允许值,程序继续进行下一步。
7) 计算端点力的修正向量dF=F-1dL。
8) 更新端点力Fi+1=Fi+dF,然后回到4)。
如果给定索单元的张力初值为T0,索原长未知,可以采用一个类似的迭代程序来计算无应力索的原长,具体迭代程序如下:
1) 输入w,E,A,节点I(xi,yi,zi)和节点J(xi,yi,zi)。
2) 计算lx0=xj-xi,ly0=yj-yi,lz0=zj-zi。
3) 对索原长L0和端点力(F1,F2,F3)进行初始化:
| $\left\{ \begin{align} & {{L}_{0}}={{l}_{x0}}^{2}+{{l}_{y0}}^{2}+{{l}_{z0}}^{2} \\ & {{F}_{1}}=-\frac{{{l}_{x0}}}{{{L}_{0}}}{{T}_{0}} \\ & {{F}_{2}}=-\frac{{{l}_{y0}}}{{{L}_{0}}}{{T}_{0}} \\ & {{F}_{3}}=-\frac{{{l}_{z0}}}{{{L}_{0}}}{{T}_{0}} \\ \end{align} \right.$ | (21) |
4) 使用式(6)更新(lx,ly,lz)。
5) 计算闭合差向量dL=lx0-lxly0-lylz0-lzT
6) 如果
7) 将式(6)分别对F2,F3和L0进行微分,得到矩阵D。
| $D=\left[ \begin{matrix} \frac{\partial f}{\partial {{F}_{2}}} & \frac{\partial f}{\partial {{F}_{3}}} & \frac{\partial f}{\partial {{L}_{0}}} \\ \frac{\partial g}{\partial {{F}_{2}}} & \frac{\partial g}{\partial {{F}_{3}}} & \frac{\partial g}{\partial {{L}_{0}}} \\ \frac{\partial h}{\partial {{F}_{2}}} & \frac{\partial h}{\partial {{F}_{3}}} & \frac{\partial h}{\partial {{L}_{0}}} \\ \end{matrix} \right]$ | (22) |
8) 计算[dF2dF3dL0]T=D-1dL
9) 更新F2=F2+dF2,F3=F3+dF3,L0=L0+dL0,然后回到4)。
对于非线性静力分析,每一个荷载增量的残余力使用牛顿迭代法进行离散,对于非线性时程分析,采用增量迭代法,以Newmark直接积分法和牛顿迭代法为基础,来求解非线性运动方程。结构的增量运动方程可以写成如下的形式:
| $M\Delta \ddot{u}+C\Delta \dot{u}+K\Delta u=\Delta F$ | (23) |
式中:Δü、Δ
| $C={{\alpha }_{M}}M+{{\alpha }_{K}}K$ | (24) |
式中:αM和αK分别是质量和刚度比例阻尼系数,采用将Newmark法中常平均加速度法(γ=1/2,β=1/4),增量加速度和速度在每一时间步的第一次迭代可以写成:
| $\Delta \ddot{u}=\frac{4}{\Delta {{t}^{2}}}\Delta u-\frac{4}{\Delta t}{{\dot{u}}_{n}}-2{{\ddot{u}}_{n}}$ | (25) |
| $\Delta \dot{u}=\frac{2}{\Delta t}\Delta u-2{{\dot{u}}_{n}}$ | (26) |
式中:n为迭代次数,将方程(25)和(26)代入到方程(23)中,增量位移可表示为
| $\hat{K}\Delta u=\Delta \hat{F}$ | (27) |
式中:
| $\hat{K}=\frac{4}{\Delta {{t}^{2}}}M+\frac{2}{\Delta t}C+K$ | (28) |
| $\Delta {{\hat{F}}^{=}}\Delta F+\left\{ \frac{4}{\Delta t}M+2C \right\}{{\dot{u}}_{n}}+2M{{\ddot{u}}_{n}}$ | (29) |
在每一时间步的第一次迭代,基于增量位移向量Δu,对时间t+Δt时的总位移,速度和加速度进行更新。
| ${{u}_{n+1}}={{u}_{n}}+\Delta u$ | (30) |
| ${{\dot{u}}_{n+1}}=-{{\dot{u}}_{n}}+\frac{2}{\Delta t}\Delta u$ | (31) |
| ${{\ddot{u}}_{n+1}}=-{{\ddot{u}}_{n}}-\frac{4}{\Delta t}{{\dot{u}}_{n}}+\frac{4}{\Delta {{t}^{2}}}\Delta u$ | (32) |
对于每个时间步的第二次以及后续的迭代,可以求解结构体系在残余力ΔR作用下的解。
| $\hat{K}\Delta U=\Delta R$ | (33) |
根据总外力F、惯性力、阻尼力和更新的内力Fint计算残余力ΔR为
| $\Delta R={{F}_{n+1}}-M{{\ddot{u}}_{n+1}}-C{{\dot{u}}_{n+1}}-{{F}_{int}}$ | (34) |
一旦计算满足收敛准则,结构响应在下一步被更新为
| $\Delta {{u}^{k+1}}=\Delta {{u}^{k}}+\Delta U\text{ }$ | (35) |
| ${{u}_{n+1}}={{u}_{n}}+\Delta {{u}^{k+1}}$ | (36) |
| ${{\dot{u}}_{n+1}}=-\dot{u}+\frac{2}{\Delta t}\Delta {{u}^{k+1}}$ | (37) |
| ${{\ddot{u}}_{n+1}}=-{{\ddot{u}}_{n}}-\frac{4}{\Delta t}{{\dot{u}}_{n}}+\frac{4}{\Delta {{t}^{2}}}\Delta {{u}^{k+1}}$ | (38) |
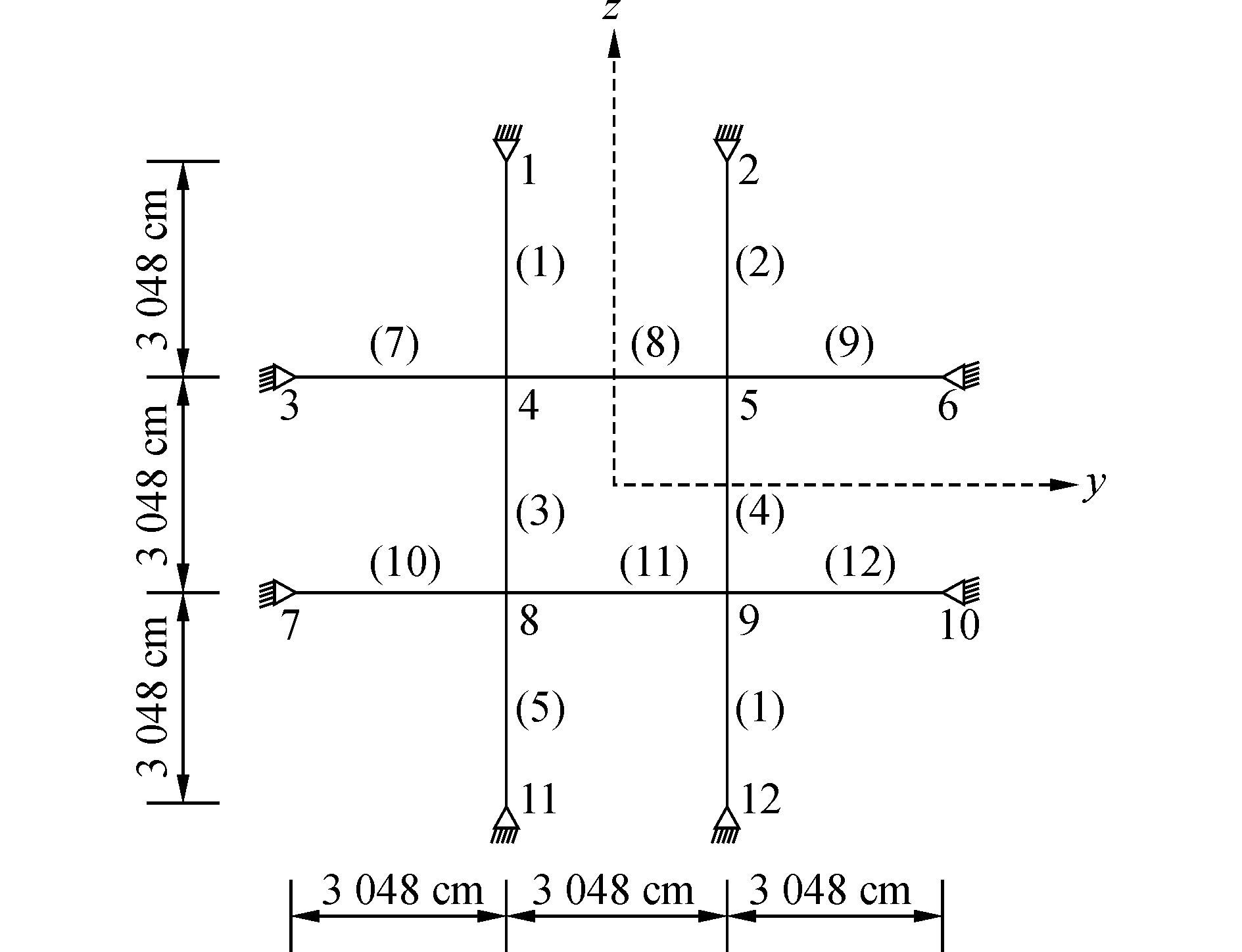
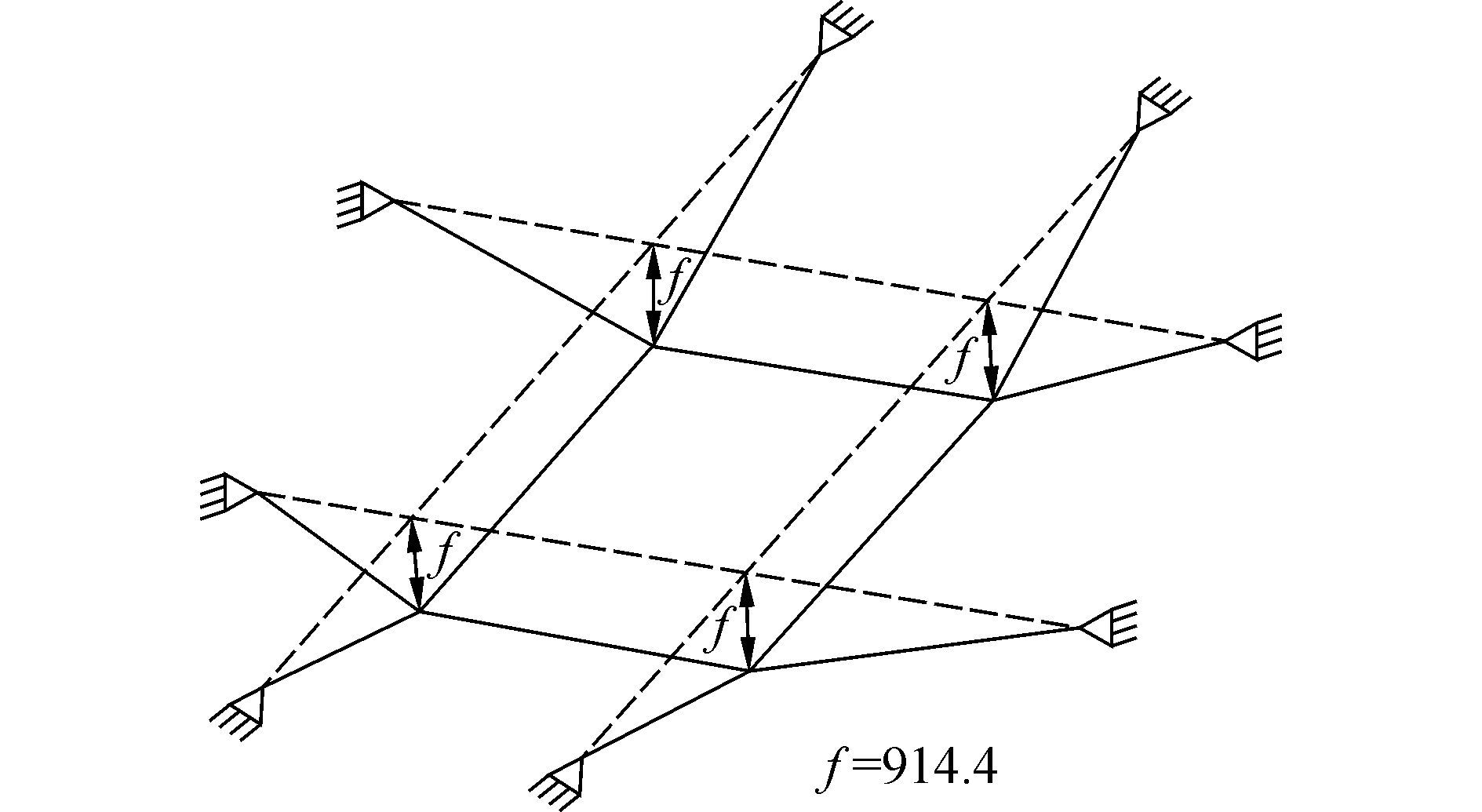
此算例来自文献[4]。该问题不考虑转动自由度,只需将外力矩设为零即可。图 3为索网的离散图,图 4为索网的初始几何形状。每根索的截面面积为1.48 cm2,弹性模量为82.68 GPa,标号为3、4、8和11的水平位置的四根索的预应力为37.61 MPa,其余倾斜的索的预应力为36.69 MPa。采用12个两节点非线性空间索单元划分此索网,竖直集中载荷同时作用在4、5、8和9 4个连接点上,大小为都为55.12 MPa,计算时取相对误差限为0.01,为简洁起见,表 1只给出了典型连接点4的位移分量,同时给出了文献[4]采用五节点索单元的计算结果。
|
| 图3 索网离散图 Figure 3 The discrete figure of cable-nets |
|
| 图4 索网初始几何形状 Figure 4 The initial geometry of cable⁃nets |
从表 1可以看出,采用空间两节点悬链线索单元与采用五节点索单元计算的结果非常接近,说明应用空间两节点悬链线索单元来模拟索网结构的方法和程序是正确可靠的。
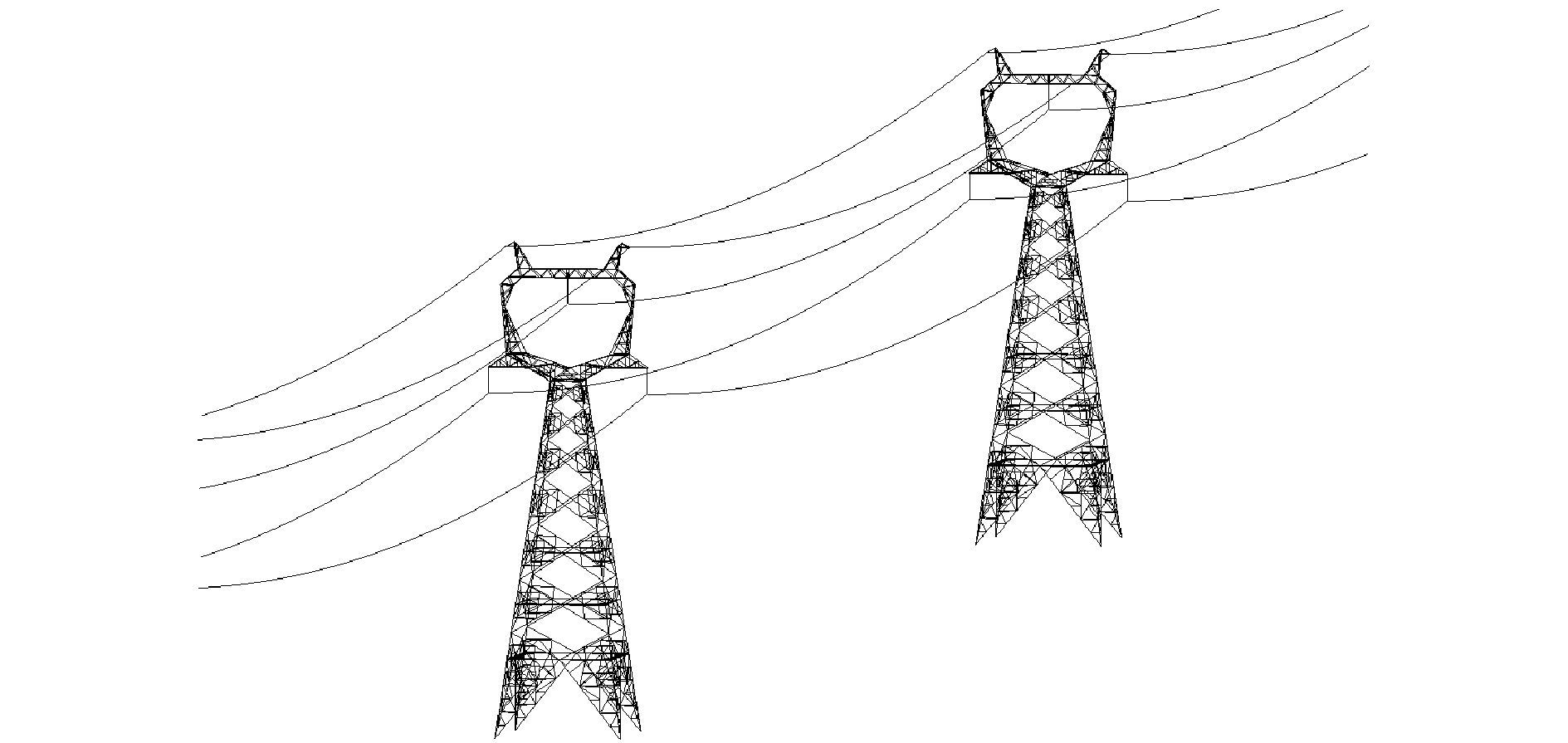
3.2 输电线动力响应分析算例 3.2.1 算例1索结构在风荷载作用下表现出很强非线性特性[3, 16],采用本文提出的两节点非线性空间索单元计算索结构的非线性时程反应。为验证该方法的正确性,同时应用ANSYS有限元分析软件进行计算,选取在实际工程中使用的500 kV猫头塔,该输电塔总高为56.2 m,呼称高为42 m,跨距为300 m。利用空间梁单元模拟塔的杆件,将导线看成理想的柔性索,用杆单元来模拟导线,建立输电塔-线耦合的空间有限元模型,塔底和线端处理成固结。塔的材料阻尼比取0.03,如图 5所示。导线选用4×LGJ-400/35型钢芯铝绞线,将四分裂导线简化为一根导线建模,根据GB/T 1179-2008《圆线同心绞架空导线》[17]查得技术参数如表 2所示。
|
| 图5 输电塔-线耦合的空间有限元模型 Figure 5 The coupled transmission tower-line system |
| 导线 根数 | 横截 面积/mm2 | 计算抗拉 断力/N | 单位长度质量/ (kg·km-1) | 直径/mm |
| 单根 | 425.24 | 103 900 | 1 349 | 23.27 |
| 四根 | 1 700.96 | 415 600 | 5 396 | 46.55 |
本文采用AR法[18]同时模拟了78点的空间脉动风速,但由于输电塔属于高耸结构,所以纵向脉动风速谱选用沿高度变化的Kaimal谱,自然风场对结构离散化节点的脉动作用在空间上存在位置相干性,当输电线路位于陡坡地段或杆塔不等高时,导线落差梯度较大,或由于导线跨距较大,导线垂度效应明显时,各离散点的平均风速和风速谱均不相同,应同时考虑了横向与竖向的空间相关性。
| $\frac{f{{S}_{V}}\left( z,f \right)}{{{V}_{*}}^{2}}=\frac{200{{f}_{*}}}{{{\left( 1+50f \right)}_{*}}^{5/3}}$ | (39) |
式中:SV 是功率谱密度,f 是频率,V* 是剪切速度,f* 为无量纲的Monin坐标。不同高度处的风速作用的相位是不同,一般先作用于结构的较高处,然后到达较低的结构,作用时差为f,可以用互功率谱密度函数来表达这些信息,互谱函数一般为复数形式:
| ${{S}_{xy}}\left( f \right)=\sqrt{{{S}_{xx}}\left( f \right)\cdot {{S}_{yy}}\left( f \right)}\cdot ch\left( f \right)\cdot {{e}^{ij\left( f \right)}}$ | (40) |
式中:Sxxn与Syyn分别为第1点和第2点的自功率谱密度。
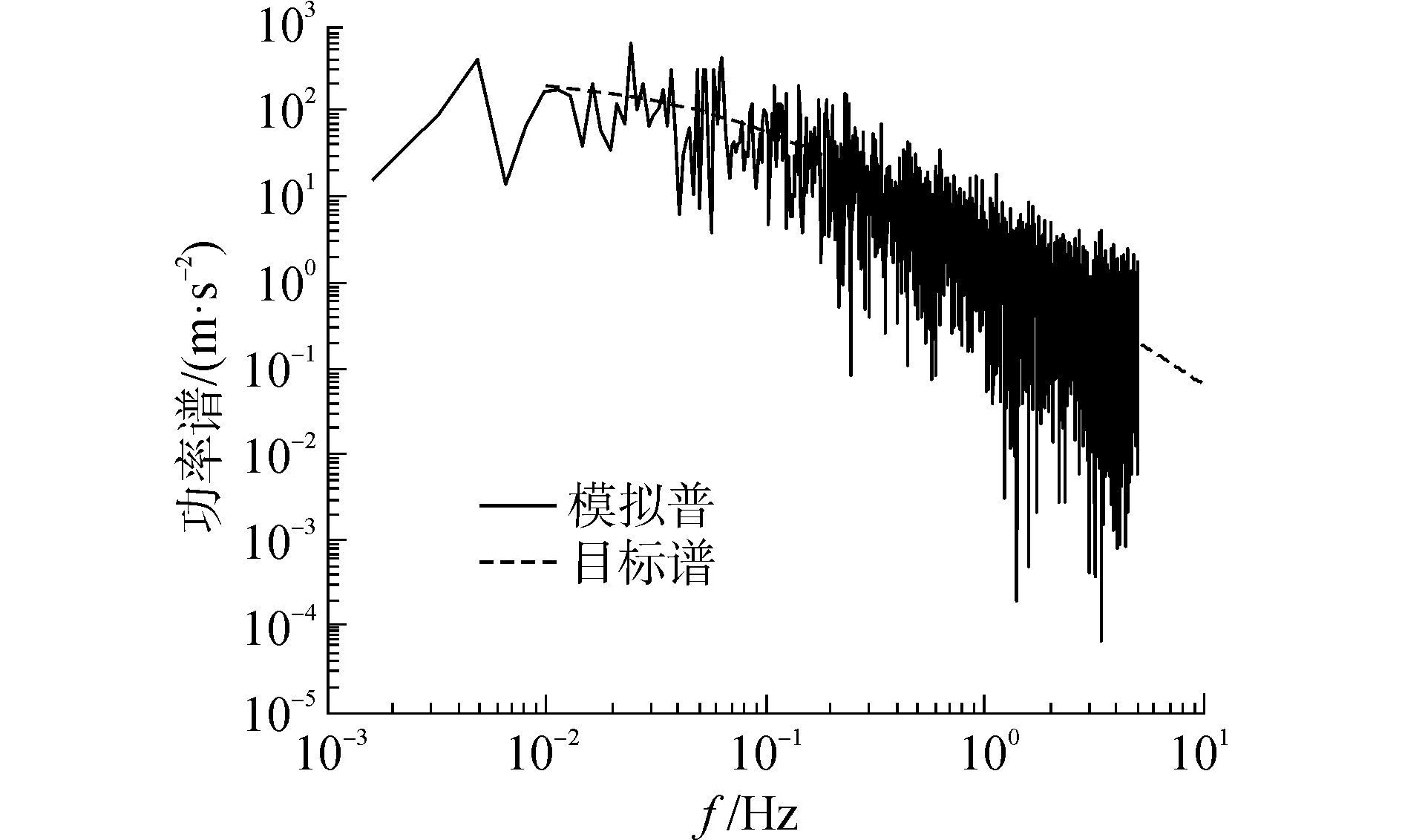
假设模型所处位置标准高度(10 m) 处的平均风速为V10 = 10 m/s,地面粗糙度系数k=0.005;脉动风速时间间隔为0.05 s,共模拟了600 s的风速数据,风速时程曲线如图 6所示,图 7为脉动风速功率谱密度,可以看出模拟谱与目标谱吻合较好,可以用于本文中的时程分析。

|
| 图6 风速时程 Figure 6 Wind velocity time-history |
|
| 图7 脉动风速功率谱密度 Figure 7 The power spectral density of wind velocity |
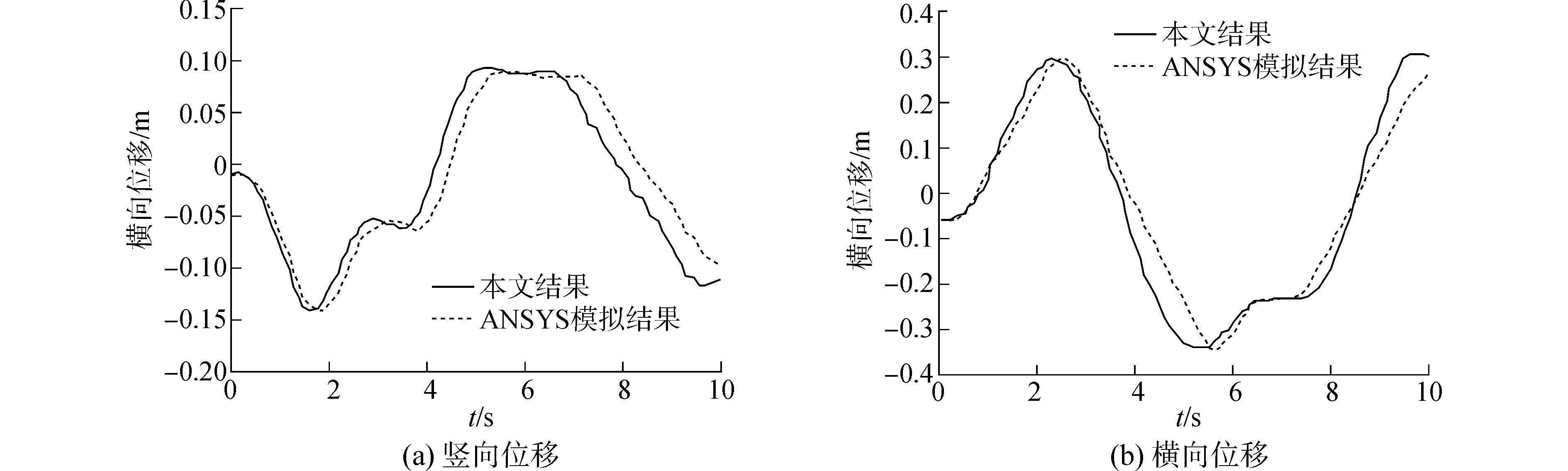
经过分析,得出了子导线1中点的位移时程曲线,如图 8,图中实线给出了由本文方法得到的子导线1中点位移时程曲线。虚线为有限元分析软件ANSYS的计算结果,从两条曲线的分布情况可以看出,本文方法和ANSYS计算得到的子导线1中点处的竖向位移、横向位移结果基本一致,但是在计算时间上,采用ANSYS计算在4 248 s时达到收敛,采用本文方法的计算达到收敛时间为700 s,因此,应该空间两节点索单元进行计算,在满足计算的正确性和精度的同时,可以节省计算时间,降低计算代价。
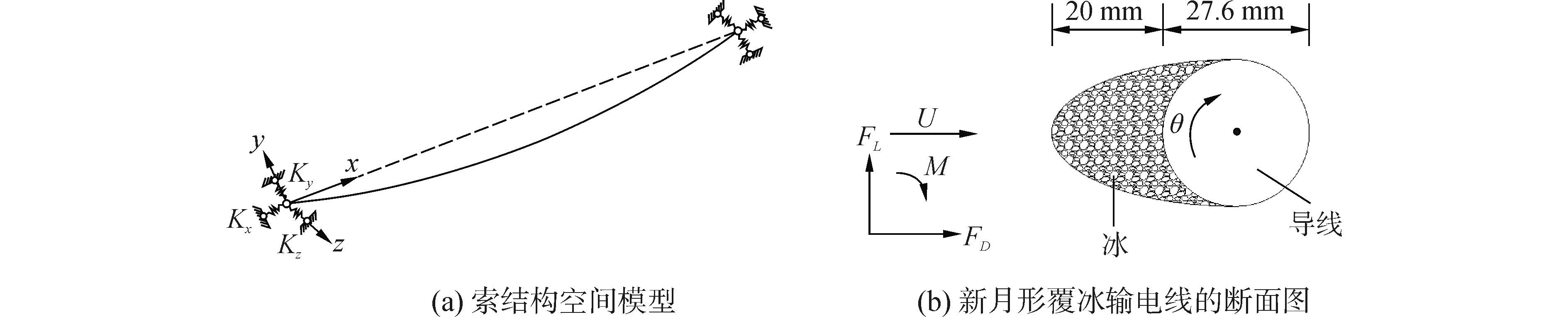
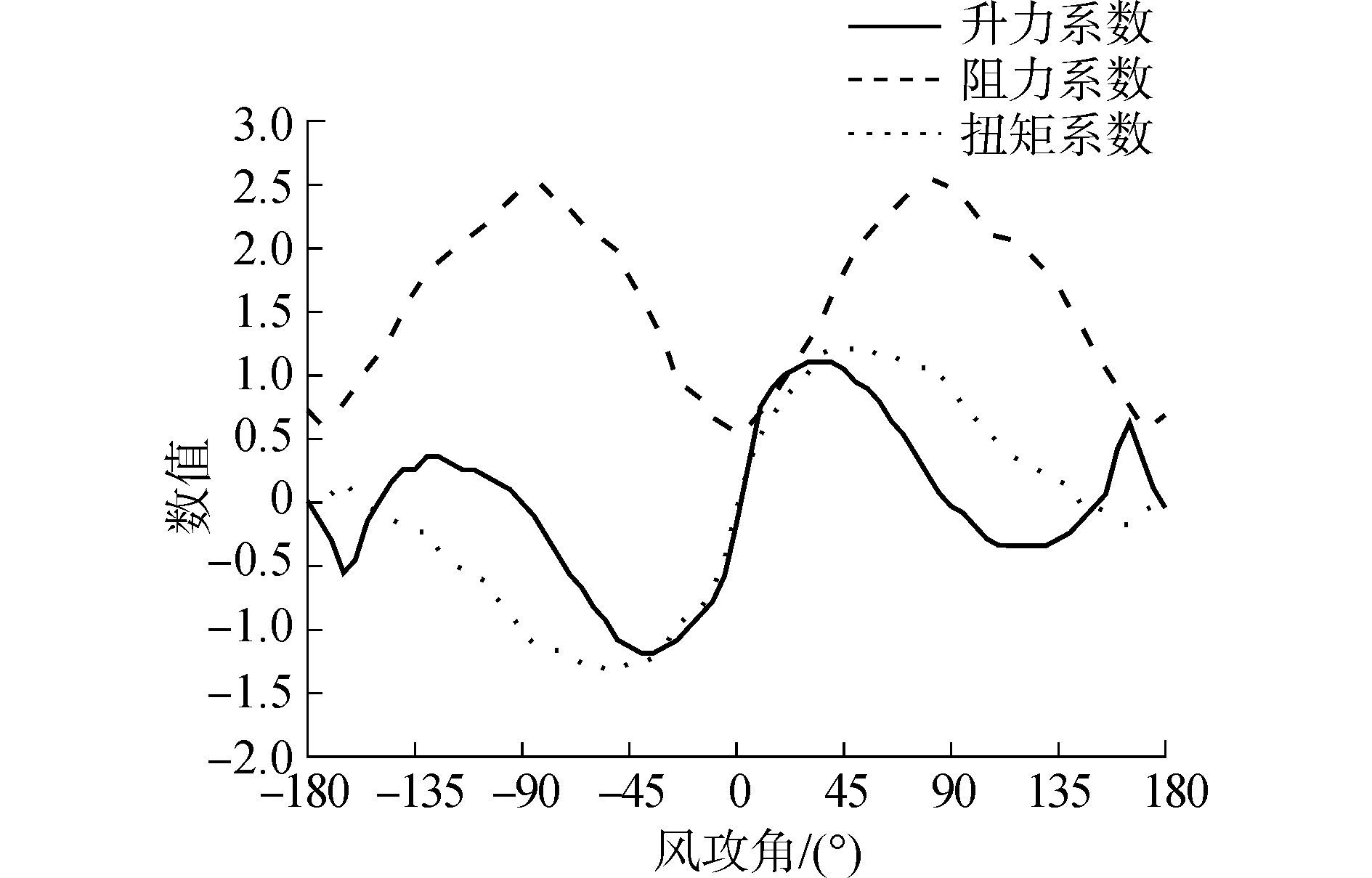
3.2.2 算例2文献[19]中采用三节点曲线梁法分析单跨输电线路,导线为单导线,输电线路主要是由输电塔、输电线、绝缘子、间隔棒以及其他连接金具构成,对于一个输电线路的截断模型,输电塔、绝缘子串和相邻跨的刚度可以用简化的弹簧模型来表示,如图 9(a)所示。Kx、Ky、Kz分别表示输电线两端输电塔、绝缘子以及相邻子跨在x、y、z方向上的简化边界条件。导线选用LGJ-400/50型钢芯铝绞线,档距为250 m,弧垂为1.3 m,跨中单元的张力为106.8 kN,通过悬链线理论对导线进行找形分析。由于覆冰的作用,导线覆冰形状为新月形,如图 9(b)是覆冰输电导线的断面图,导线直径为27.6 mm,覆冰厚度为20 mm。导线的轴向刚度为EA=31.1×106 N,扭转刚度为GJ=159 Nm2/rad,抗弯刚度为1 965 Nm2,导线的弹性模量为69 000 N/mm2,覆冰导线参数见表 3,新月形覆冰导线的气动力系数曲线由风洞试验测得,分别测试了10 m/s风速下,风攻角在-180°~180°范围内的升力系数、阻力系数和扭矩系数,如图 10。
|
| 图8 风荷载作用下子导线1中点位移变化曲线 Figure 8 The displacement at midpoint of subconductor 1 under wind loads |
|
| 图9 索结构空间模型和覆冰导线断面图 Figure 9 The model of cable structure and the cross-section diagram of the iced conductor |
|
| 图10 新月形覆冰导线的升力、阻力和扭矩系数曲线 Figure 10 The lift,drag and moment coefficients of the iced conductor with crescent section |
| 参数 | 数值 | |
| 覆冰厚度/mm | 20 | |
| 裸导线横截面积/mm2 | 598.28 | |
| 覆冰面积/mm2 | 343.04 | |
| 裸导线单位长度质量/(kg·m-1) | 1.51 | |
| 覆冰导线单位长度质量/(kg·m-1) | 0.308 | |
| 覆冰导线的偏心距/mm | 19.17 |
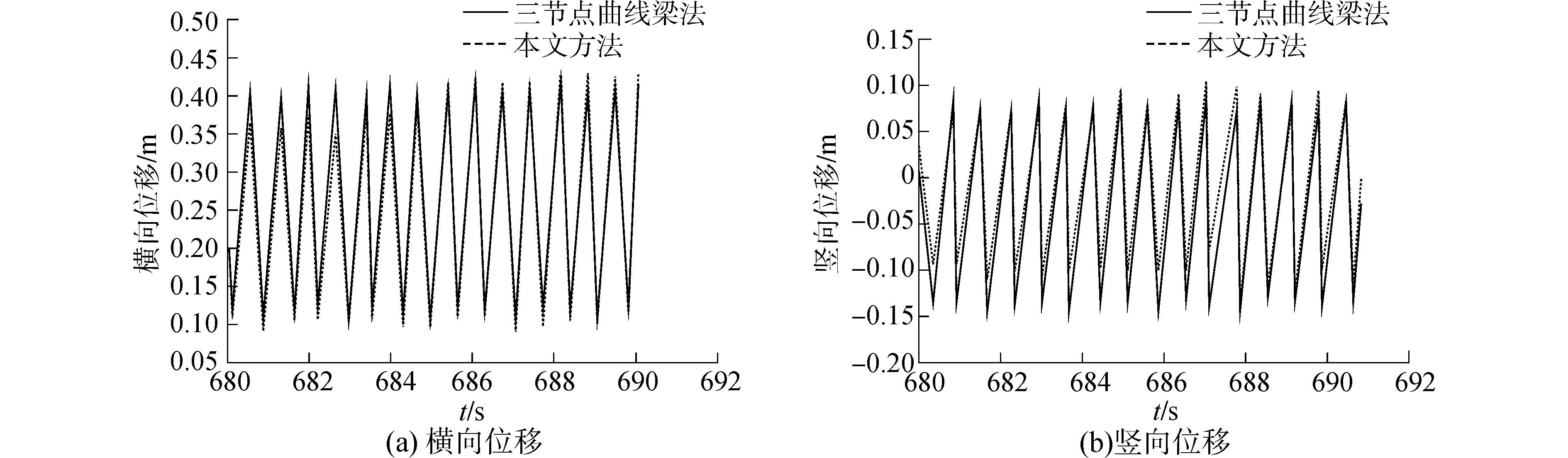
在10 m/s风速,风攻角为-10°情况下,选取时间步长为0.001 s,总的仿真时间为700 s,经过计算,得出导线动力响应位移时程,截取680~690 s的子导线1中点的位移时程曲线如图 11所示。
|
| 图11 跨中节点的位移时程曲线 Figure 11 The time-history curve of displacement at mid-span node |
图 11中实线给出了文献[19]中采用三节点曲线梁法来模拟的索单元得到的子导线1中点横向位移、竖向位移时程曲线。虚线为借助本文方法得出的结果,从两条曲线的分布情况可以看出,用本文方法和三节点曲线梁法计算得到的跨中节点处的横向位移、竖向位移的结果达到非常好的吻合,较好的验证本文方法及程序的正确性,充分考虑了导线的非线性效应,计算中需要的自由度数更少,有利于节省计算时间。
4 结论针对现有索结构模型在模拟非线性方面的不足,本文基于弹性悬链线解析理论开发了一种空间两节点悬链线索单元。经过计算,得出的结论主要有以下几点:
1) 采用构造的空间两节点悬链线索单元编制计算机程序对弧垂较小的索网结构和弧垂较大的输电线索结构进行计算分析。可以精确有效的计算悬索结构受到的静态和动态荷载,并给出了相应的切线刚度矩阵和内力矢量,索网中的每个索单元可以通过一个单元来建模,通过与现有研究结果比较发现,本文提出的两节点悬链线索单元可以很好地预测悬索结构的线性和非线性行为。数值算例分析验证了本文方法的有效性和计算程序的准确性。
2) 采用两节点索单元进行索结构计算无需太多的结构单元及自由度数即可得到精度较高的计算结果,对节省计算时间降低计算代价有利。编制的计算机程序具有良好的通用性,不仅适用于输电线路这类弧垂较大的索结构的分析,也可以用于大跨度的悬索和索网结构的分析。
| [1] |
陈太聪, 苏成, 马海涛. 索结构静力分析的新型拉索单元研究[J].
工程力学, 2014, 31(2): 46–52.
Taicong, SU Cheng, MA Haitao. Study on the development of new-type cable elements for static analysis of cable structures[J]. Engineering mechanics, 2014, 31(2): 46–52. |
| [2] |
魏建东. 索结构分析的滑移索单元法[J].
工程力学, 2004, 21(6): 172–176.
Jiandong. Sliding cable element for the analysis of cable structures[J]. Engineering mechanics, 2004, 21(6): 172–176. |
| [3] |
唐建民, 董明, 钱若军. 张拉结构非线性分析的五节点等参单元[J].
计算力学学报, 1997, 14(1): 108–113.
Jianmin, DONG Ming, QIAN Ruojun. A finite element method with five-node isoparametric element for nonlinear analysis of tension structures[J]. Chinese journal of computational mechanics, 1997, 14(1): 108–113. |
| [4] |
黄涛, 周金枝, 朱若燕. 具有扭转自由度的五节点索单元非线性有限元法[J].
武汉理工大学学报:交通科学与工程版, 2010, 34(6): 1150–1153.
T ao, ZHOU Jinzhi, ZHU Ruoyan. A finite element method with five-node cable element with a axial rotational freedom[J]. Journal of Wuhan university of technology:transportation science & engineering, 2010, 34(6): 1150–1153. |
| [5] | LIEW J Y R, PUNNIYAKOTTY N M, SHANMUGAM N E. Limit-state analysis and design of cable-tensioned structures[J]. International journal of space structures, 2001, 16(2): 95–110. |
| [6] | GRECO L, IMPOLLONIA N, CUOMO M. A procedure for the static analysis of cable structures following elastic catenary theory[J]. International Journal of Solids and Structures, 2014, 51(7/8): 1521–1533. |
| [7] | ABAD M S A, SHOOSHTARI A, ESMAEILI V, et al. Nonlinear analysis of cable structures under general loadings[J]. Finite elements in analysis and design, 2013, 73: 11–19. |
| [8] | CHEN Z H, WU Y J, YIN Y, et al. Formulation and application of multi-node sliding cable element for the analysis of Suspen-Dome structures[J]. Finite elements in analysis and design, 2010, 46(9): 743–750. |
| [9] | JAYARAMAN H B, KNUDSON W C. A curved element for the analysis of cable structures[J]. Computers & structures, 1981, 14(3/4): 325–333. |
| [10] | WANG Chunjiang, WANG Renpeng, DONG Shilin, et al. A new catenary cable element[J]. International journal of space structures, 2003, 18(4): 269–275. |
| [11] | ANDREU A, GIL L, ROCA P. A new deformable catenary element for the analysis of cable net structures[J]. Computers & structures, 2006, 84(29/30): 1882–1890. |
| [12] | YANG Y B, TSAY J Y. Geometric nonlinear analysis of cable structures with a two-node cable element by generalized displacement control method[J]. International journal of structural stability and dynamics, 2007, 7(4): 571–588. |
| [13] | SUCH M, JIMENEZ-OCTAVIO J R, CARNICERO A, et al. An approach based on the catenary equation to deal with static analysis of three dimensional cable structures[J]. Engineering structures, 2009, 31(9): 2162–2170. |
| [14] | THAI H T, KIM S E. Nonlinear static and dynamic analysis of cable structures[J]. Finite elements in analysis and design, 2011, 47(3): 237–246. |
| [15] |
刘克同, 汤爱平, 刘玥君, 等. 基于MRT-LBM大涡模拟的桥梁气动参数数值仿真[J].
四川大学学报:工程科学版, 2013, 45(6): 87–95.
Ketong, TANG Aiping, LIU Yuejun, et al. Numerical simulation for aerodynamic parameters of bridge decks using MRT-LBM-LES[J]. Journal of Sichuan university:engineering science edition, 2013, 45(6): 87–95. |
| [16] | 全国电线电缆标准化委员会. GB/T 1179-2008圆线同心绞架空导线[S]. 北京:中国标准出版社, 2009:15-17. |
| [17] | OWEN J S, ECCLES B J, CHOO B S, et al. The application of auto-regressive time series modelling for the time-frequency analysis of civil engineering structures[J]. Engineering structures, 2001, 23(5): 521–536. |
| [18] | YAN Zhitao, LI Zhengliang, SAVORY E, et al. Galloping of a single iced conductor based on curved-beam theory[J]. Journal of wind engineering and industrial aerodynamics, 2013, 123: 77–87. |



