2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China
游走运动作为水下自重构机器人的主要运动方式,其运动性能的优劣直接决定了水下自重构机器人的应用范围。评价游走运动性能优劣的一项重要指标是运动的稳定性。
目前,有关游动的研究主要集中在机械鱼[1-4]、水下蛇形机器人[5-7]、两栖机器人[8-14](例如,两栖蛇形机器人、蝾螈机器人、七鳃鳗机器人、两栖龟等)。文献[1-4]对机械鱼的控制、游动性能、推进效率进行了研究;文献[5-7]研究了水下蛇形机器人的动力学建模、控制问题;文献[8-11]对ACM-R5和AmphBot系列机器人进行了研究,给出了关节设计方法以及步态生成方法;文献[12-13]通过对蝾螈的生物学研究,提出了基于CPG的运动控制系统;文献[14]解决了七鳃鳗的运动控制问题。现有的研究成果主要是针对游动构形的某一具体构形进行研究[15-19],研究的内容包括设计、建模、控制等,针对游动稳定性的研究几乎没有。
水下自重构机器人的游动构形是多种多样的(主要包括水下蛇形、水下四肢游动等,随着模块的不断完善,还会出现其他构形),不同构形之间可以通过自重构策略相互转换,并且每一种具体构形在游动过程中身体形状是随时间变化的,因此,对整个游动构形进行研究是非常困难的。考虑到水下自重构机器人是由相同模块通过不同的连接方式重构而成,在研究游动稳定性的问题时,可以分别对每个模块的稳定性进行研究,最后换算成整个游动构形的稳定性。水下自重构机器人的组成模块本身并不配备推进装置,并且游动过程中只受到重力、水动力和控制力矩的作用,因此,只能通过重力与浮力形成的力偶矩来抵抗外界环境干扰下的横滚或纵倾。重力与浮力形成的力偶矩,称之为恢复力矩。恢复力矩的方向与横滚和纵倾的方向相反,即恢复力矩总是在抑制横滚和纵倾的增长趋势。恢复力矩的数值越大,说明稳定性越好。游动构形单个组成模块的恢复力矩可以采用AUV计算恢复力矩的方式获得。由于各个模块的恢复力矩是以自身的载体坐标系为参考系获得的,在将所有模块的恢复力矩叠加时,需要选择一个参考模块,将所有模块的恢复力矩转换到该参考模块的载体坐标系下进行叠加。参考模块的选择应以具体的游动构形为依据,例如,水下蛇形游动构形可以选择中间模块为参考模块,而水下四肢游动构形应选择身体的组成模块为参考模块。
1 游动构形的稳定性分析 1.1 单个模块的恢复力矩计算方法水下自重构机器人的基本组成模块sk的载体坐标系如图 1所示,zk可通过右手法则确定。模块sk的重力和浮力总是垂向的。重力可以分成模块本体的重力G0sk和载荷的变化量ΔGisk,前者作用于重心(xgsk,ygsk,zgsk),后者作用于载荷的重心(xgisk,ygisk,zgisk)。浮力也可分为两部分:模块sk本体的浮力B0sk,它作用于浮心(xcsk,ycsk,zcsk);浮力的变化量ΔBjsk,它作用于载荷引起的浮力的浮心(xcjsk,ycjsk,zcjsk)。上述坐标为重心和浮心相对于载体坐标系Okxkykzk原点的矢径在载体坐标系下的表示形式。所以总的重力和浮力为
| $\left\{ \begin{matrix} {{G}^{{{s}_{k}}}}=G_{0}^{{{s}_{k}}}+\sum\limits_{i=1}^{m}{\Delta G_{i}^{{{s}_{k}}}} \\ {{B}^{{{s}_{k}}}}=B_{0}^{{{s}_{k}}}+\sum\limits_{j=1}^{l}{\Delta B_{i}^{{{s}_{k}}}} \\ \end{matrix} \right.$ | (1) |

|
| 图1 模块及其载体坐标系 Figure 1 Module and its body coordinate system |
本体和载荷的等效重心为
| $\left\{ \begin{matrix} \bar{x}_{g}^{{{s}_{k}}}=\frac{x_{g}^{{{s}_{k}}}G_{0}^{{{s}_{k}}}+\sum\limits_{i=1}^{m}{x_{gi}^{{{s}_{k}}}\Delta G_{i}^{{{s}_{k}}}}}{{{G}^{{{s}_{k}}}}} \\ \bar{y}_{g}^{{{s}_{k}}}=\frac{y_{g}^{{{s}_{k}}}G_{0}^{{{s}_{k}}}+\sum\limits_{i=1}^{m}{y_{gi}^{{{s}_{k}}}\Delta G_{i}^{{{s}_{k}}}}}{{{G}^{{{s}_{k}}}}} \\ \bar{z}_{g}^{{{s}_{k}}}=\frac{z_{g}^{{{s}_{k}}}G_{0}^{{{s}_{k}}}+\sum\limits_{i=1}^{m}{z_{gi}^{{{s}_{k}}}\Delta G_{i}^{{{s}_{k}}}}}{{{G}^{{{s}_{k}}}}} \\ \end{matrix} \right.$ | (2) |
本体和载荷的等效浮心为
| $\left\{ \begin{matrix} \bar{x}_{c}^{{{s}_{k}}}=\frac{x_{c}^{{{s}_{k}}}B_{0}^{{{s}_{k}}}+\sum\limits_{j=1}^{l}{x_{cj}^{{{s}_{k}}}\Delta B_{j}^{{{s}_{k}}}}}{{{B}^{{{s}_{k}}}}} \\ \bar{y}_{c}^{{{s}_{k}}}=\frac{y_{c}^{{{s}_{k}}}B_{0}^{{{s}_{k}}}+\sum\limits_{j=1}^{l}{y_{cj}^{{{s}_{k}}}\Delta B_{j}^{{{s}_{k}}}}}{{{B}^{{{s}_{k}}}}} \\ \bar{z}_{c}^{{{s}_{k}}}=\frac{z_{c}^{{{s}_{k}}}B_{0}^{{{s}_{k}}}+\sum\limits_{j=1}^{l}{z_{cj}^{{{s}_{k}}}\Delta B_{j}^{{{s}_{k}}}}}{{{B}^{{{s}_{k}}}}} \\ \end{matrix} \right.$ | (3) |
重力和浮力对于模块sk载体坐标系Okxkykzk原点的力矩为
| ${{M}^{{{s}_{k}}}}=r_{g}^{{{s}_{k}}}\times {{G}^{{{s}_{k}}}}+r_{c}^{{{s}_{k}}}\times {{B}^{{{s}_{k}}}}$ | (4) |
式中:rgsk、rcsk表示等效重心和等效浮心相对于模块sk载体坐标系原点的矢径。将式(4) 展开得
| $\begin{align} & {{G}^{{{s}_{k}}}}\left| \begin{matrix} i & j & k \\ \bar{x}_{g}^{{{s}_{k}}} & \bar{y}_{g}^{{{s}_{k}}} & \bar{z}_{g}^{{{s}_{k}}} \\ -{{\sin }^{o}}{{\vartheta }^{{{s}_{k}}}} & {{\cos }^{o}}{{\vartheta }^{{{s}_{k}}}}{{\sin }^{o}}{{\varphi }^{{{s}_{k}}}} & {{\cos }^{o}}{{\vartheta }^{{{s}_{k}}}}{{\cos }^{o}}{{\varphi }^{{{s}_{k}}}} \\ \end{matrix} \right|- \\ & {{B}^{{{s}_{k}}}}\left| \begin{matrix} i & j & k \\ \bar{x}_{c}^{{{s}_{k}}} & \bar{y}_{c}^{{{s}_{k}}} & \bar{z}_{c}^{{{s}_{k}}} \\ -{{\sin }^{o}}{{\vartheta }^{{{s}_{k}}}} & {{\cos }^{o}}{{\vartheta }^{{{s}_{k}}}}{{\sin }^{o}}{{\varphi }^{{{s}_{k}}}} & {{\cos }^{o}}{{\vartheta }^{{{s}_{k}}}}{{\cos }^{o}}{{\varphi }^{{{s}_{k}}}} \\ \end{matrix} \right| \\ \end{align}$ |
式中:i、j、k表示相应于三个坐标轴xk、yk、zk的单位矢量;
| $\left\{ {\begin{array}{*{20}{l}} \begin{gathered} M_{{x_k}}^{{s_k}} = \left( {{G^{{s_k}}}\bar y_g^{{s_k}} - {B^{{s_k}}}\bar y_c^{{s_k}}} \right){\cos ^o}{\vartheta ^{{s_k}}}{\cos ^o}{\varphi ^{{s_k}}} - \hfill \\ \left( {{G^{{s_k}}}\bar z_g^{{s_k}} - {B^{{s_k}}}\bar z_c^{{s_k}}} \right){\cos ^o}{\vartheta ^{{s_k}}}{\sin ^o}{\varphi ^{{s_k}}} \hfill \\ \end{gathered} \\ \begin{gathered} M_{{y_k}}^{{s_k}} = - \left( {{G^{{s_k}}}\bar z_g^{{s_k}} - {B^{{s_k}}}\bar z_c^{{s_k}}} \right){\sin ^o}{\vartheta ^{{s_k}}} - \hfill \\ \left( {{G^{{s_k}}}\bar x_g^{{s_k}} - {B^{{s_k}}}\bar x_c^{{s_k}}} \right){\cos ^o}{\vartheta ^{{s_k}}}{\cos ^o}{\varphi ^{{s_k}}} \hfill \\ \end{gathered} \\ \begin{gathered} M_{{z_k}}^{{s_k}} = \left( {{G^{{s_k}}}\bar x_g^{{s_k}} - {B^{{s_k}}}\bar x_c^{{s_k}}} \right){\cos ^o}{\vartheta ^{{s_k}}}{\sin ^o}{\varphi ^{{s_k}}} - \hfill \\ \left( {{G^{{s_k}}}\bar y_g^{{s_k}} - {B^{{s_k}}}\bar y_c^{{s_k}}} \right){\sin ^o}{\vartheta ^{{s_k}}} \hfill \\ \end{gathered} \end{array}} \right.$ | (5) |
游动构形要求每个模块的浮力的大小等于重力,即Gsk=Bsk,且在增减载荷和调节浮力时,要求
| $\left\{ \begin{array}{*{35}{l}} M_{{{x}_{k}}}^{{{s}_{k}}}=-{{G}^{{{s}_{k}}}}h{{\cos }^{o}}{{\vartheta }^{{{s}_{k}}}}{{\sin }^{o}}{{\varphi }^{{{s}_{k}}}} \\ M_{{{y}_{k}}}^{{{s}_{k}}}=-{{G}^{{{s}_{k}}}}h{{\sin }^{o}}{{\vartheta }^{{{s}_{k}}}} \\ M_{{{z}_{k}}}^{{{s}_{k}}}=0 \\ \end{array} \right.$ | (6) |
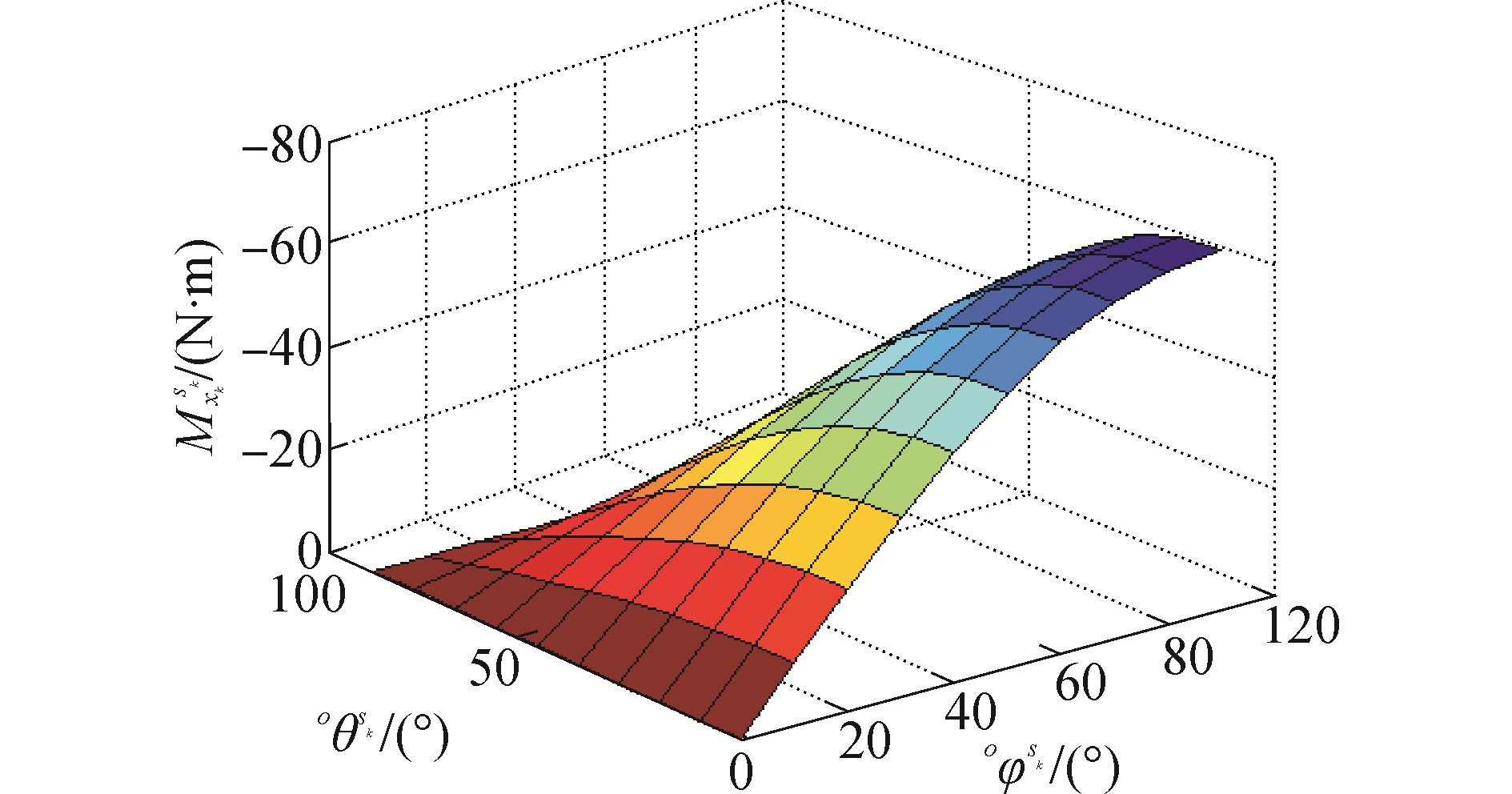
由式(6) 可知,Myksk按照正弦规律变化。“-”表示恢复力矩与
|
|
图2
Mxksk与 |
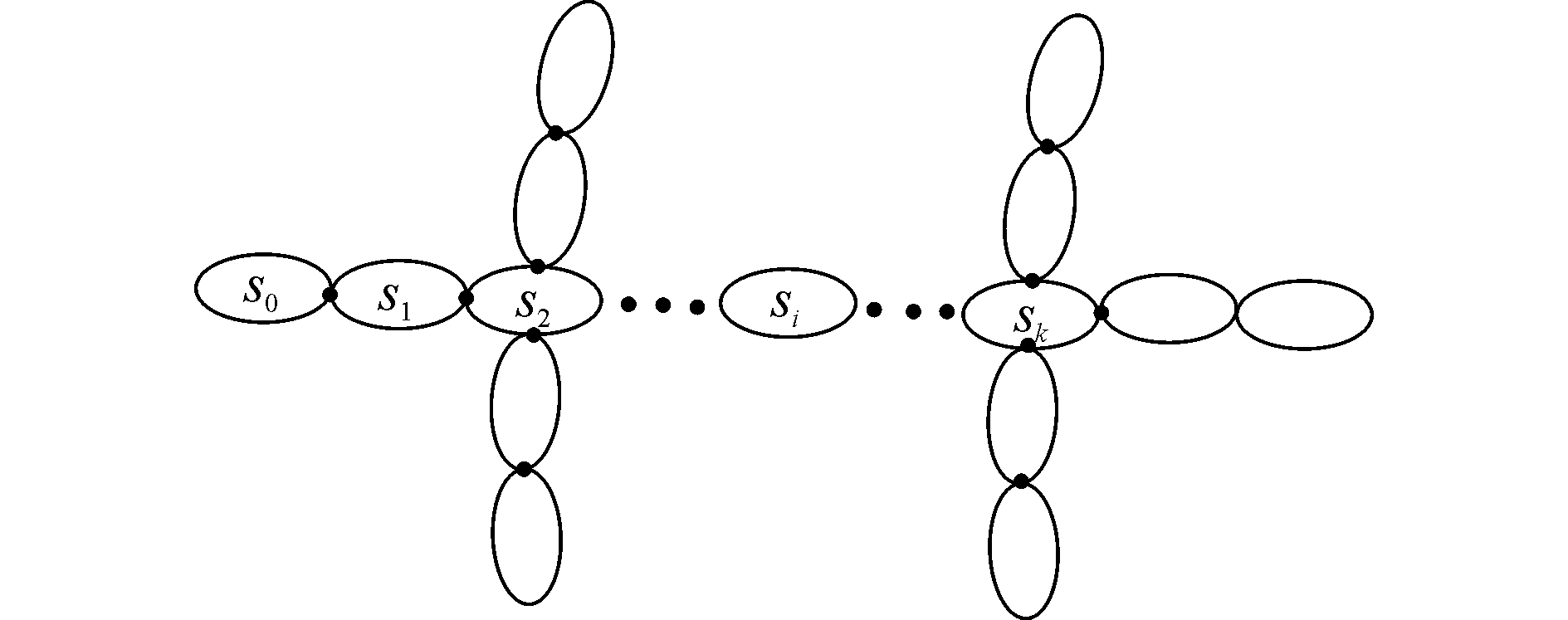
水下自重构机器人的游动构形由n个模块组成,如图 3所示。单个组成模块的恢复力矩可按照1.1节中的方法来计算。整个游动构形的恢复力矩可以通过将所有模块的恢复力矩相加来获得。由于每个模块的恢复力矩都是在自身载体坐标系下计算得到的,因此,在叠加的过程中,应首先选取一个参考坐标系,将所有模块的恢复力矩转换到该参考坐标系下,然后叠加。选取模块si为参考模块,所有模块的恢复力矩统一转换到模块si的载体坐标系下,进行叠加。
|
| 图3 水下自重构机器人的游动构形 Figure 3 Swimming configuration of underwater self-configurable robot |
采用通路矩阵[20]表示游动构形。通路矩阵的每一行表示一条通路,通路中元素1对应的模块为该通路中存在的模块,列数即为模块的编号,编号从0开始,以此类推。通路中相邻模块间有连接关系。模块si与模块sk的欧拉角可以表示为
| $\left\{ \begin{matrix} ^{o}{{\theta }^{{{s}_{i}}}}{{=}^{o}}{{\theta }^{{{s}_{0}}}}+\sum\limits_{{{s}_{0}}\to {{s}_{i}}}{\alpha _{jl}^{{{s}_{j}}}{{\theta }^{{{s}_{l}}}}} \\ ^{o}{{\theta }^{{{s}_{k}}}}{{=}^{o}}{{\theta }^{{{s}_{0}}}}+\sum\limits_{{{s}_{0}}\to sk}{\alpha _{jl}^{{{s}_{j}}}{{\theta }^{{{s}_{l}}}}} \\ \end{matrix} \right.$ | (7) |
式中:j和l取模块s0到模块si的通路中的模块编号(0≤j,<i,j<l≤i),sjθsl表示模块sl相对于模块sj的转动角度;如果模块sl和模块sj位于模块s0到模块si的通路中,且模块sl和模块sj相邻,则αjl=1;否则,αjl=0。
模块sk相对于模块si的欧拉角为
| $^{{{s}_{i}}}{{\theta }^{{{s}_{k}}}}{{=}^{o}}{{\theta }^{{{s}_{k}}}}{{-}^{o}}{{\theta }^{{{s}_{i}}}}$ | (8) |
模块sk的恢复力矩在模块si的载体坐标系下的表示形式为
| $^{{{s}_{i}}}{{M}^{{{s}_{k}}}}=T_{{{s}_{k}}}^{{{s}_{i}}}{{M}^{{{s}_{k}}}}$ | (9) |
式中:Tsksi表示模块sk的载体坐标系向模块si的载体坐标系的转换矩阵。
游动构形的恢复力矩可以表示为
| $M=\sum\limits_{k=0}^{n-1}{^{{{s}_{i}}}{{M}^{{{s}_{k}}}}}$ | (10) |
参考模块应根据具体的构形来选择。例如,水下蛇形构形可以选择中间的模块作为参考模块,而水下四肢游动构形可以选择组成身体的模块作为参考模块。
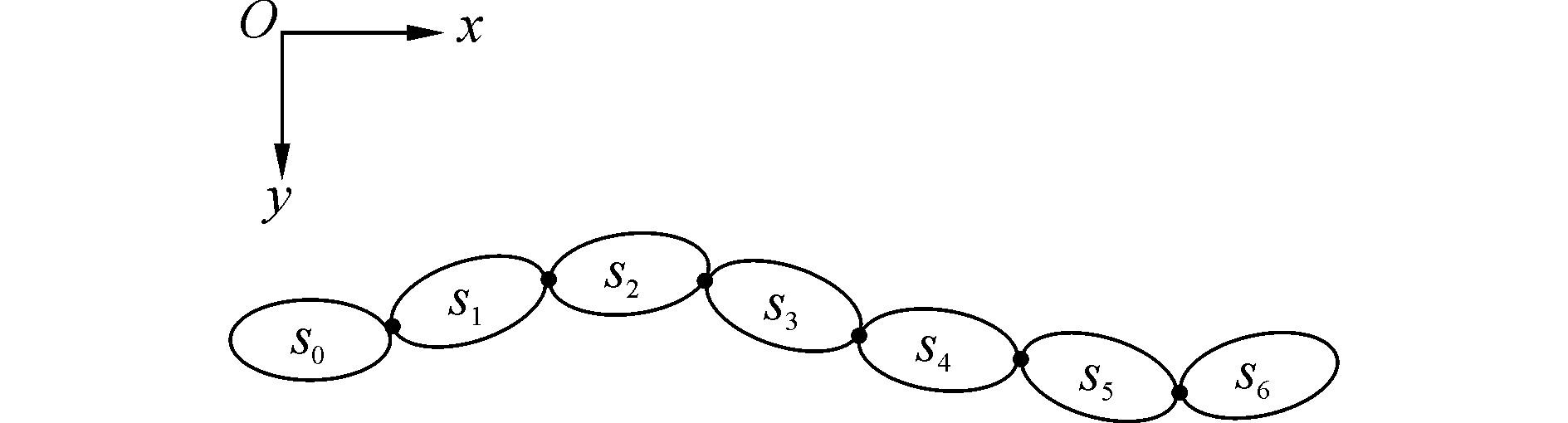
2 游动构形稳定性的仿真验证本文设计完成的水下自重构机器人的游动构形包括水下蛇形游动构形和水下四肢游动构形。以7个模块组成的水下蛇形游动为例(如图 4所示),选择模块3为参考模块,分析它的恢复力矩。
|
| 图4 水下蛇形游动构形 Figure 4 Swimming configuration of underwater snakelike configuration |
水下蛇形游动构形的恢复力矩可以表示为
| $M=\sum\limits_{k=0}^{6}{^{{{s}_{3}}}{{M}^{{{s}_{k}}}}}=\sum\limits_{k=0}^{6}{T_{{{s}_{k}}}^{{{s}_{3}}}{{M}^{{{s}_{k}}}}}$ | (11) |
由于相邻模块间只有一个自由度,因此,模块sk相对于模块s3的欧拉角为
| $^{{{s}_{3}}}{{\theta }^{{{s}_{k}}}}{{=}^{o}}{{\theta }^{{{s}_{k}}}}{{-}^{o}}{{\theta }^{{{s}_{3}}}}={{\left[ \begin{matrix} 0 & 0 & ^{{{s}_{3}}}{{\varphi }^{{{s}_{k}}}} \\ \end{matrix} \right]}^{T}}$ | (12) |
Tsks3可以表示为
| $T_{{{s}_{k}}}^{{{s}_{3}}}=\left[ \begin{matrix} \cos \left( ^{{{s}_{3}}}{{\psi }^{{{s}_{k}}}} \right) & -\sin \left( ^{{{s}_{3}}}{{\psi }^{{{s}_{k}}}} \right) & 0 \\ \sin \left( ^{{{s}_{3}}}{{\psi }^{{{s}_{k}}}} \right) & \cos \left( ^{{{s}_{3}}}{{\psi }^{{{s}_{k}}}} \right) & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right]$ | (13) |
根据蛇形机器人的运动特点,关节角应满足以下条件:
| $\begin{matrix} ^{{{s}_{k-1}}}{{\psi }^{{{s}_{k}}}}A\sin \left( \omega t+\left( k-1 \right)\varphi \right) & \left( k=1,2,\cdots ,6 \right) \\ \end{matrix}$ | (14) |
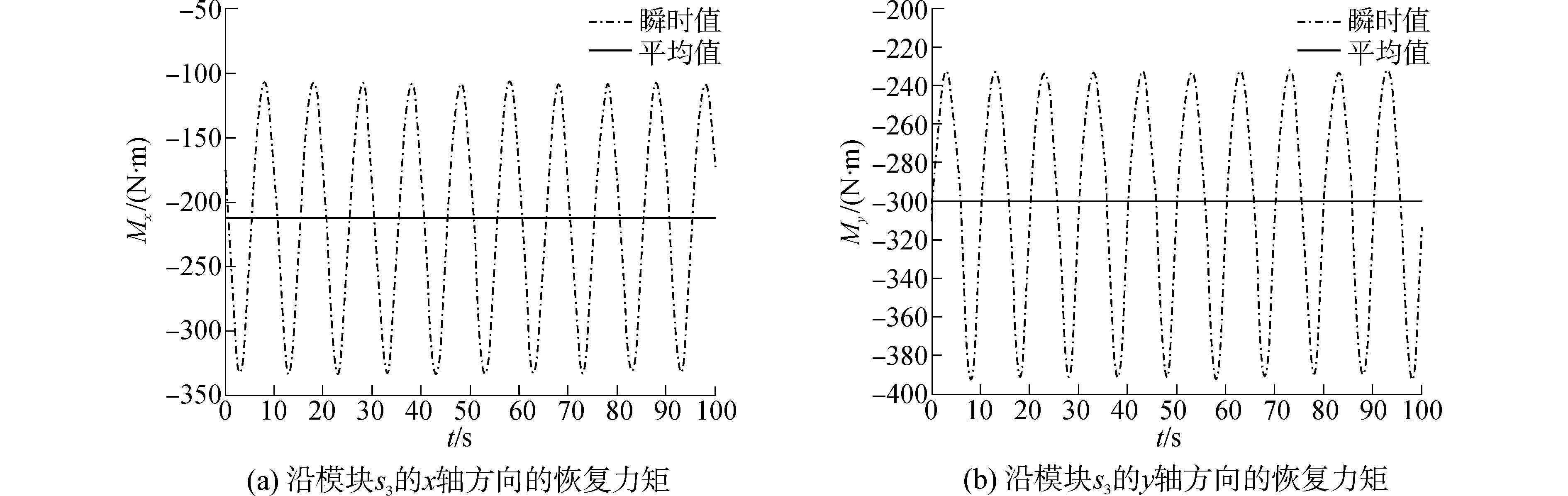
给定以下参数:Gsk=700 N,h=0.1 m,Oφsk=45°,
|
| 图5 恢复力矩随时间的变化曲线 Figure 5 The curves of restoring moment changing with time |
水下蛇形机器人可以通过调整关节角的幅值和相位差来改变身体的弯曲程度和运动路径,以适应外界环境的变化。因此,关节角的幅值和相位差在水下蛇形机器人的游动过程中起着非常重要的作用。用恢复力矩的平均值代替瞬时值,研究关节角的幅值和相位差与恢复力矩的关系。由图 6可知,相位差对恢复力矩的影响非常小,可以忽略;幅值对恢复力矩有显著的影响,幅值越大,恢复力矩的数值越小(不考虑方向)。图中恢复力矩为负,这说明恢复力矩与横滚和纵倾的方向相反(本文设置的横滚角和纵倾角为正)。

|
| 图6 恢复力矩与A、φ的关系 Figure 6 The relation between restoring moment and A, φ |
虽然针对游动的研究已取得了一些成果,但这些研究成果仅适用于固定构形机器人,且研究内容主要为设计制造、建模与控制。针对构形可变的模块化机器人的稳定性的研究几乎没有。
本文从运动学的角度出发,对水下自重构机器人游动构形的稳定性进行了研究。针对游动构形的特点,提出首先计算单个模块的恢复力矩,然后选择参考模块,并将所有模块的恢复力矩转换到参考模块的载体坐标系下进行叠加,作为游动的稳定性判据;通过仿真研究了恢复力矩与横滚角、纵倾角的关系,并以水下蛇形游动构形为例,研究了关节角的变化对恢复力矩的影响。研究结果表明:该方法可以准确、高效地判定水下自重构机器人游动构形的稳定性。
在今后的工作中,将从动力学的角度对水下自重构机器人游动构形的稳定性进行研究,进一步完善游动构形稳定性的判据。
| [1] |
孙飞虎, 喻俊志, 徐德. 具有嵌入式视觉的仿生机器鱼头部的平稳性控制[J].
机器人, 2015, 37(2): 188–195.
SUN Feihu, YU Junzhi, XU De. Stability control for the head of a biomimetic robotic fish with embedded vision[J]. Robot, 2015, 37(2): 188–195. |
| [2] |
王耀威, 纪志坚, 翟海川. 仿生机器鱼运动控制方法综述[J].
智能系统学报, 2014, 9(3): 276–284.
WANG Yaowei, JI Zhijian, ZHAI Haichuan. A survey on motion control of the biomimetic robotic fish[J]. CAAI transaction on intelligent systems, 2014, 9(3): 276–284. |
| [3] |
孙琴, 武海健, 夏庆锋. 机器鱼游动性能改善方法[J].
兵工自动化, 2014, 33(12): 67–71.
SUN Qin, WU Haijian, XIA Qingfeng. Robot fish swimming performance improve method[J]. Ordnance industry automation, 2014, 33(12): 67–71. |
| [4] |
沈奇, 韩晨皓, 王田苗, 等. 基于IPMC仿生机器鱼推进效率实验研究[J].
北京航空航天大学学报, 2014, 40(12): 1730–1735.
SHEN Qi, HAN Chenhao, WANG Tianmiao, et al. Experimental investigation of biomimetic robotic fish actuated by IPMC[J]. Journal of Beijing university of aeronautics and astronautics, 2014, 40(12): 1730–1735. |
| [5] | YANG Ke, WANG Xuyang, GE Tong, et al. Dynamic model of underwater snake-like robot using Kane'S method[J]. Journal of Shanghai jiaotong university:Science, 2014, 19(2): 146–154. |
| [6] | YANG Ke, WANG Xuyang, GE Tong, et al. Modeling and control of head of the underwater snake-like robot swimming[J]. Journal of Harbin institute of technology, 2014, 21(1): 77–83. |
| [7] | YANG Ke, WANG Xuyang, GE Tong, et al. Simulation platform for the underwater snake-like robot swimming based on Kane'S dynamic model and central pattern generator[J]. Journal of Shanghai Jiaotong university:Science, 2014, 19(3): 294–301. |
| [8] | YAMADA H, CHIGISAKI S, MORI M, et al. Development of amphibious snake-like robot ACM-R5[C]//Proceedings of 36th International Symposium on Robotics. Tokyo, Japan, 2005:433-440. |
| [9] | CRESPI A, IJSPEERT A J. Online optimization of swimming and crawling in an amphibious snake robot[J]. IEEE transactions on robotics, 2008, 24(1): 75–87. |
| [10] | CRESPI A, BADERTSCHER A, GUIGNARD A, et al. AmphiBot I:an amphibious snake-like robot[J]. Robotics and autonomous systems, 2005, 50(4): 163–175. |
| [11] | CRESPI A, IJSPEERT A J. AmphiBot Ⅱ:an amphibious snake robot that crawls and swims using a central pattern generator[C]//Proceedings of the 9th International Conference on Climbing and Walking Robots. Piscataway, 2006:19-27. |
| [12] | IJSPEERT A J, CRESPI A, CABELGUEN J M. Simulation and robotics studies of salamander locomotion[J]. Neuroinformatics, 2005, 3(3): 171–196. |
| [13] | IJSPEERT A J, CRESPI A, RYCZKO D, et al. From swimming to walking with a salamander robot driven by a spinal cord model[J]. Science, 2007, 315(5817): 1416–1420. |
| [14] | IJSPEERT A J, CRESPI A. Online trajectory generation in an amphibious snake robot using a lamprey-like central pattern generator model[C]//Proceedings of the 2007 IEEE International Conference on Robotics and Automation. Roma, 2007:262-268. |
| [15] |
王扬威, 王振龙, 李健. 仿生机器鱼研究进展及发展趋势[J].
机械设计与研究, 2011, 27(2): 22–32.
WANG Yangwei, WANG Zhenlong, LI Jian. Research development and tendency of biomimetic robot fish[J]. Machine design and research, 2011, 27(2): 22–32. |
| [16] |
张毅, 杨锐敏, 王洲, 等. 机器鱼的研究动态综述[J].
重庆邮电大学:自然科学版, 2007, 19(5): 598–601.
ZHANG Yi, YANG Ruimin, WANG Zhou, et al. An overview on dynamic research of robotic fish[J]. Journal of Chongqing university of posts and telecommunications:natural science edition, 2007, 19(5): 598–601. |
| [17] |
喻俊志, 陈尔奎, 王硕, 等. 仿生机器鱼研究的进展与分析[J].
控制理论与应用, 2003, 20(4): 485–491.
YU Junzhi, CHEN Erkui, WANG Shuo, et al. Research evolution and analysis of biomimetic robot fish[J]. Control theory & application, 2003, 20(4): 485–491. |
| [18] | LILJEBÄCK P, PETTERSON K Y, STAVDAHL Ø, et al. A review on modelling, implementation, and control of snake robots[J]. Robotics and autonomous systems, 2012, 60(1): 29–40. |
| [19] |
杨海清, 喻俊志, 谭民, 等. 两栖仿生机器人研究综述[J].
机器人, 2007, 29(6): 601–608.
YANG Haiqing, YU Junzhi, TAN Min, et al. Amphibious biomimetic robots:a review[J]. Robot, 2007, 29(6): 601–608. |
| [20] | MUTHYUNJAYA T S. Kinematic structure of mechanisms revisited[J]. Mechanism and machine theory, 2003, 38(4): 279–320. |



