在喷淋冷却、降膜蒸发、喷墨打印等诸多领域都存在液滴撞击固体表面的现象,事实上,当液滴撞击固体表面后,往往在其表面覆盖形成一层薄液膜,液滴撞击固体表面的过程实质上是液滴撞击液膜的过程。液滴撞击液膜后会发生与液膜融合、反弹、形成飞溅水花等变化,在不同的条件下表现出不同变形形态与动力学特征,其中包含复杂的流动机理。当多个液滴同时撞击液膜时,每个液滴与液膜撞击后的演化形态又相互影响,使整个流动过程更为复杂化。
双液滴撞击液膜过程是多液滴撞击液膜过程的最为简化的特例,对该过程进行研究,既可以探索多液滴与液膜相互耦合作用的动力学机理,又能够在现有的计算条件下实现。故本文拟对双液滴同时撞击液膜的动力学变形过程展开模拟。现有不少文献从实验测试和数值模拟两个角度对单液滴撞击液膜的流动现象进行了研究,如沈胜强等[1]对液滴撞击液膜的射流与水花形成进行了机理分析和研究。Hu Hai-Bao等[2]对液滴撞击有规律的微槽道表面进行了实验研究,得出了在不同韦伯数下液滴撞击过程及最大铺展直径的变化。Vander Wal等[3]研究了液滴撞击后的飞溅现象,给出了飞溅的定义,即有小液滴从水花边缘分离的现象,归纳了发生飞溅时的临界参数。然而鲜有公开发表的关于双液滴撞击液膜的研究,可查到的文献仅有Fujimoto[4-5]实验观测了两个液滴相继撞击固体表面的流动过程。T.Minamikawa等[6]对双液滴连续撞击热表面进行了数值模拟并与试验进行了对比,数值模拟结果与试验较吻合。Sivakumar[7]实验观测了在喷雾过程中液滴冲击物体表面液膜的情况,并将结果与单液滴的冲击结果进行了比较,讨论了多液滴的相互干扰作用。Nikolopoulos[8]用轴对称模型模拟了空间内两个相同尺寸的液滴以相同的速度相向撞击的过程,研究表明,根据Weber数的大小不同,碰撞后会发生反弹、合并和破碎几种情况。胡雷等[9]采用格子Boltzmann方法数值模拟了两液滴同时撞击液膜的流动,分析了撞击速度、液滴间距对过程的影响。
本文拟采用CLSVOF(coupled level set and volume of fluid)[10]方法对双液滴同时撞击平面液膜进行数值模拟,该方法既能够利用VOF方法良好的守恒性,又能够利用Level Set方法对界面曲率和法向量进行精确计算,从而捕捉两相流界面,模拟结果显示出双液滴同时撞击液膜后的变形特点,分析了两液滴水平间距、液膜厚度、撞击速度等因素对撞击后液膜形态的影响。
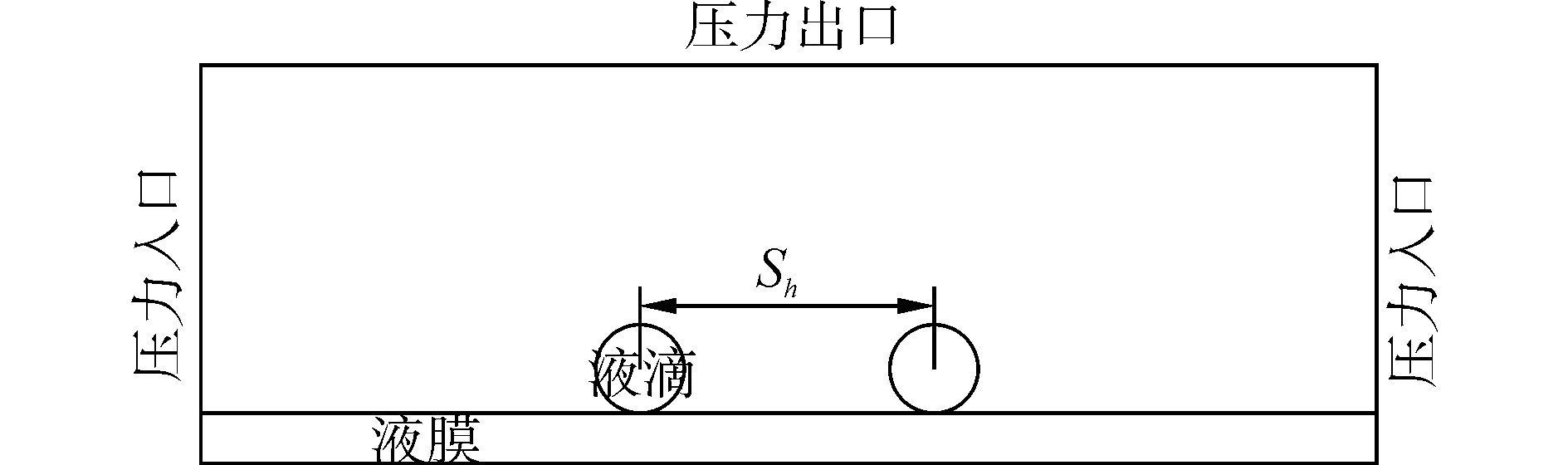
1 物理数学模型本文研究对象为水平间隔的两个液滴同时撞击物体表面液膜的变形情况,撞击过程是非稳态的,流动为层流。双液滴同时撞击液膜初始时刻模型如图 1所示,中心水平距离为Sh的两液滴,以相同速度同时撞击平面液膜,将液滴底部与液膜开始接触,即圆形截面的液滴与液膜相切的时间设为初始时刻,即t=0,液滴与液膜相切时的速度计为V。设液膜厚度为h,初始速度为0。组成液滴和液膜的液体均为水,其粘性系数和各点的表面张力系数均为常数,计算中考虑重力的作用。
|
| 图1 初始时刻模型 Figure 1 Physical model at the beginning of the impact |
在CLSVOF方法中,界面的重构采用Youngs[11]提出的分段线性几何重构思想,与体积分数法[12]的不同之处在于对界面法向量n的获取由符号距离函数φ的计算得出:
| $n=\frac{\nabla \varphi }{\left| \nabla \varphi \right|}$ | (1) |
两相界面曲率κ可由式(2)得出:
| $k=\nabla \centerdot \frac{\nabla \varphi }{\left| \nabla \varphi \right|}$ | (2) |
引入Heaviside函数来光顺界面处的密度和粘度,Heaviside函数定义:
| $H\left( \varphi \right)=\left\{ \begin{matrix} 0 & \varphi <-a \\ \frac{1}{2}\left[ 1+\frac{\varphi }{a}-\frac{1}{\pi }sin\left( \frac{\pi \varphi }{a} \right) \right] & \left| \varphi \right|\le a \\ 1 & \varphi >a \\ \end{matrix} \right.$ | (3) |
式中:a=1.5w,w为最小网格尺寸。光滑后的密度和粘度分别为
| $\rho \left( \varphi \right)={{\rho }_{g}}+\left( {{\rho }_{l}}-{{\rho }_{g}} \right)H\left( \varphi \right)$ | (4) |
| $\mu \left( \varphi \right)={{\mu }_{g}}+\left( {{\mu }_{l}}-{{\mu }_{g}} \right)H\left( \varphi \right)\text{ }$ | (5) |
式中:ρ、μ分别表示密度和动力粘度,下标g、l分别表示气相和液相。
对表面张力的处理采用连续表面张力(CSF)模型[13]:
| ${{F}_{s}}=\sigma \kappa \delta (\varphi )\nabla \varphi $ | (6) |
| $\delta (\varphi )=\frac{dH\left( \varphi \right)}{d\varphi }$ | (7) |
式中σ为表面张力系数。
流动及能量控制方程如式(8)~(10)所示:
| $\nabla U=0$ | (8) |
| $\begin{align} & \frac{\rho \left( \varphi \right)\partial U}{\partial t}+\rho \left( \varphi \right)\nabla \cdot \left( UU \right)=-\nabla P+\nabla \cdot \mu \left( \varphi \right) \\ & \left[ \nabla U+{{\left( \nabla U \right)}^{T}} \right]-\delta \kappa \delta \left( \varphi \right)\nabla \varphi +\rho \left( \varphi \right)g\text{ } \\ \end{align}$ | (9) |
| $\frac{\rho \left( \varphi \right)\partial U}{\partial t}+\rho \left( \varphi \right)\nabla \cdot \left( UT \right)=\nabla \cdot \left( \frac{\lambda }{{{c}_{p}}}\nabla T \right)+S$ | (10) |
式中:p、g、λ、cp、S和T分别表示压力、重力加速度、导热系数、比热容、源相和温度。
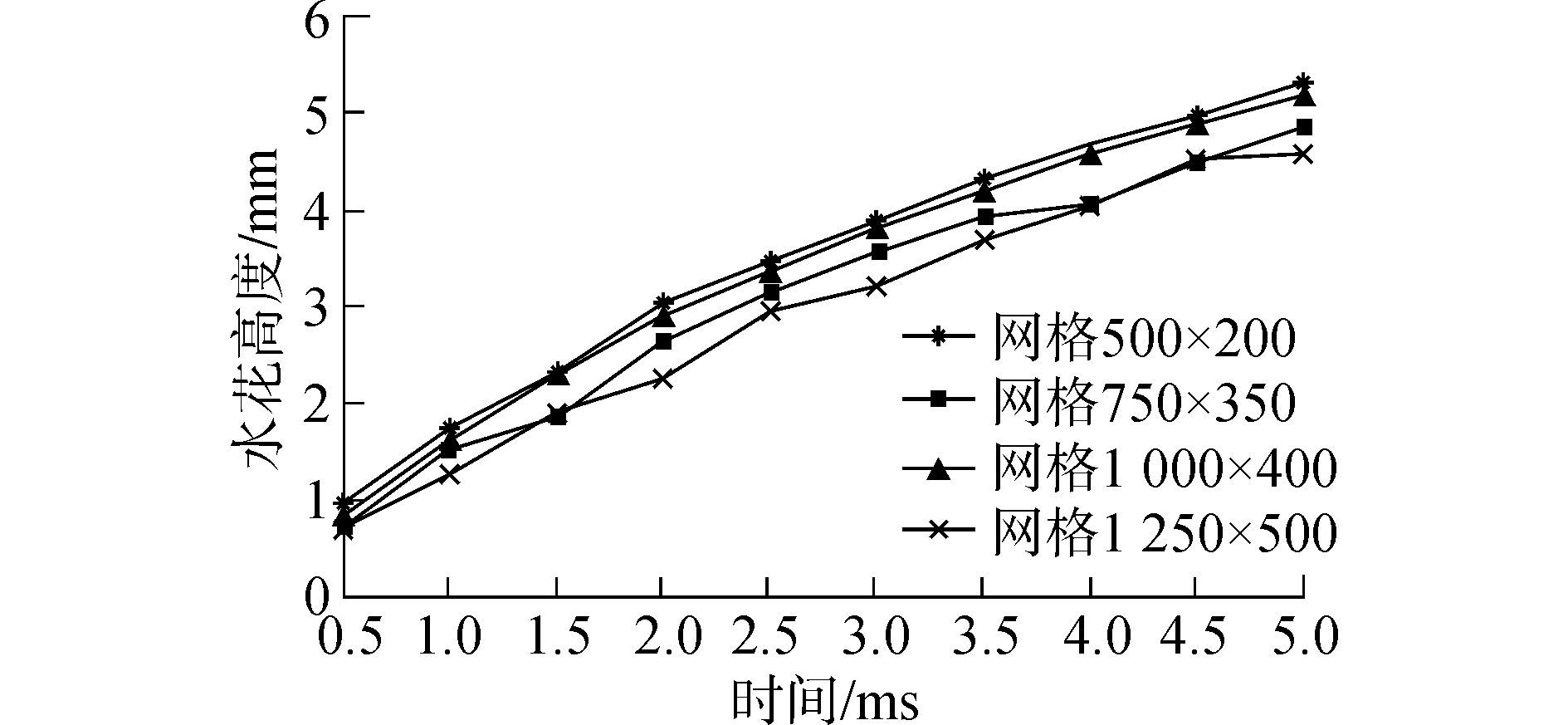
计算区域为50 mm×20 mm,计算中采用均匀四边形网格。图 2为在不同网格密度下,直径为2 mm双液滴在液滴水平间距Sh=4 mm时以v=2 m/s的速度同时撞击厚度h=1.2 mm的液膜后水花高度的演变图。
|
| 图2 网格无关性验证 Figure 2 Verifying the grid dependence |
可见,当网格密度低于1 000×400时,随着网格密度的增大,水花高度改变明显,且中间还存在一定的波动,当网格密度大于1 000×400时,网格密度变化对水花高度的变化影响很小,故本文采用1 000×400的网格密度。对流项离散采用QUICK格式,压力-速度耦合的求解采用PISO算法,对Level Set方程的求解采用QUICK算法。
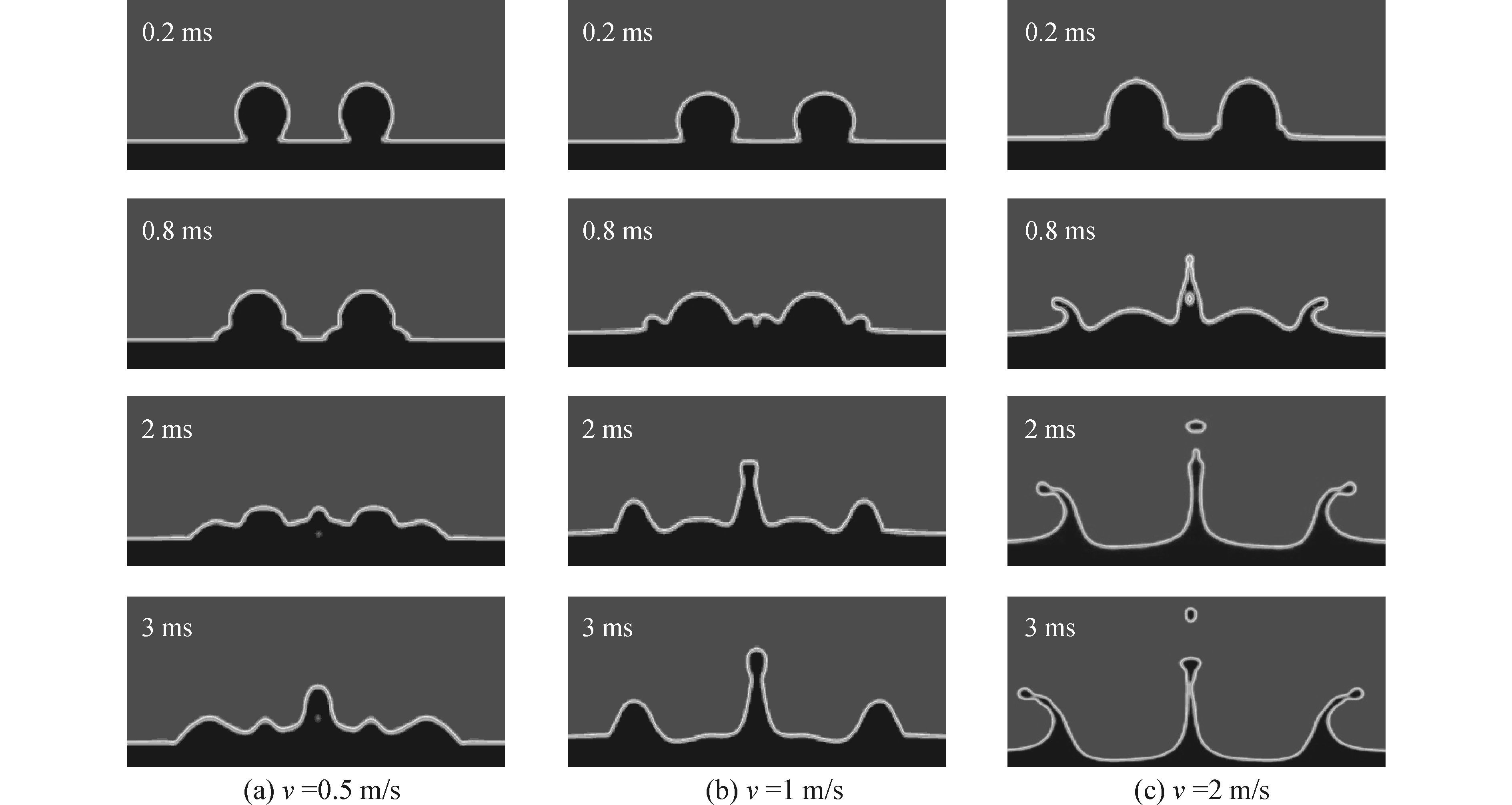
2 模拟结果与讨论图 3为直径2 mm的双液滴在液滴水平间距为Sh=4 mm时分别以v为0.5、1.0和2.0 m/s的速度同时撞击厚度为1.2 mm液膜后流动形态演变图。由图 3(a)可见,当双液滴撞击速度较小时,撞击后形成的水花区域和高度都很小,两液滴撞击后各自溅起的水花均向其两侧扩展,并在两个液滴撞击点的中间处相遇,两水花碰撞后形成一沿相交线的片状射流,其高度高于周围水花高度,以此片状射流为中心,周围形成多个波峰存在的水花(3 ms),但水花高度较小,即碰撞仅引起撞击点两侧的表面轻微波动,在3 ms时相交处的片状射流高度大概是周围水花高度的2.42倍。由图 3(b)撞击速度为1 m/s时的演变可以看出,随着撞击速度的增大,双液滴同时撞击液膜后产生的水花直径、水花高度都变大,两个液滴形成的水花在两液滴中间位置相遇的时间比0.5 ms时早,且相交处的片状射流高度增大,片状射流周围的水花高度比0.5 m/s时的大,但由于较大的撞击速度能够促使液滴与液膜较快地融合,故3 ms时仅在周围形成一组具有明显波峰的水花,片状射流高度大约是周围水花高度的2.63倍。由图 3(c)可以看出,当撞击速度增大到2 m/s时,双液滴同时撞击液膜后以两液滴的撞击点为中心均形成了两个皇冠状水花,并且在水花顶端迅速破碎,产生许多小液滴,两个冠状水花在两液滴的中间位置相撞后沿水花相交线亦形成片状射流,且该射流形成的时间明显早于撞击速度较小时的情况,如图 3所示,2 m/s时在0.8 ms就发现明显射流,而1 m/s时出现明显射流的时间为2、0.5 m/s时在3 ms时刻射流高度都远低于另外两个碰撞速度下的射流高度。图 3(c)中沿两水花相交线形成的片状射流高度是周围水花的1.68倍左右,最后片状射流的顶部亦破碎生成许多小液滴。
|
| 图3 撞击速度不同的双液滴撞击液膜后流动形态变化图 Figure 3 The variation of flow pattern after double droplets simultaneously impact liquid film at different impact speed |
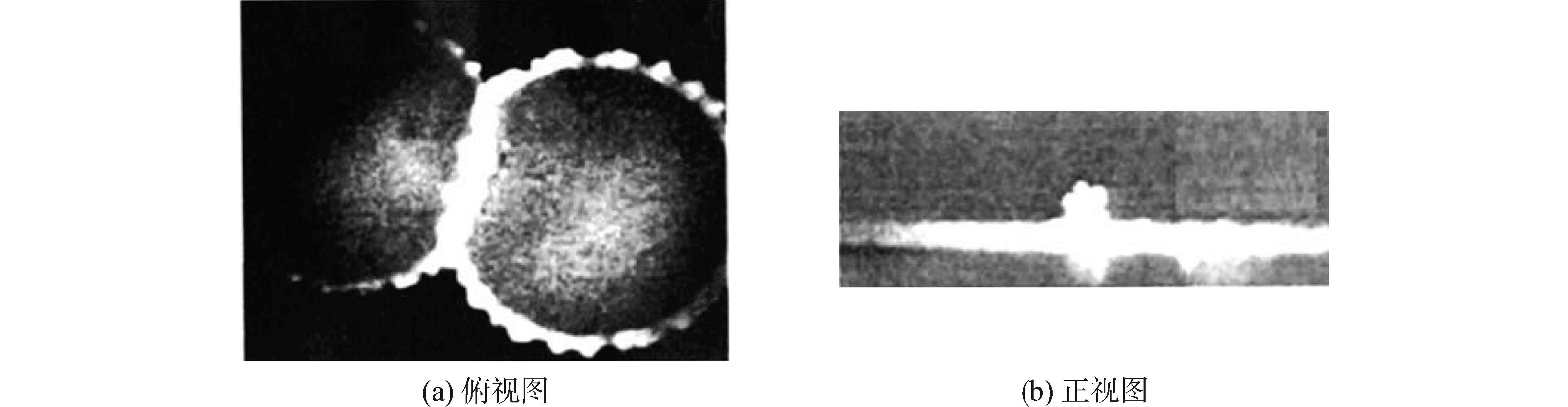
图 4为Roismann等[14]实验拍摄图片,观测的是两液滴撞击带有薄层液膜的固体表面后的变化,实验中设计将两个液滴同时撞击到固壁。对比该实验结果图 4(b)正视图与本文的模拟结果图 3(a),可以看出,本文的模拟结果能够反应出液滴撞击液膜后的主要变形特征,即中心的射流,故模拟与实验结果具有比较好的一致性。
|
| 图4 液滴撞击液膜的实验照片 Figure 4 Experimental photos of droplet impact liquid film |
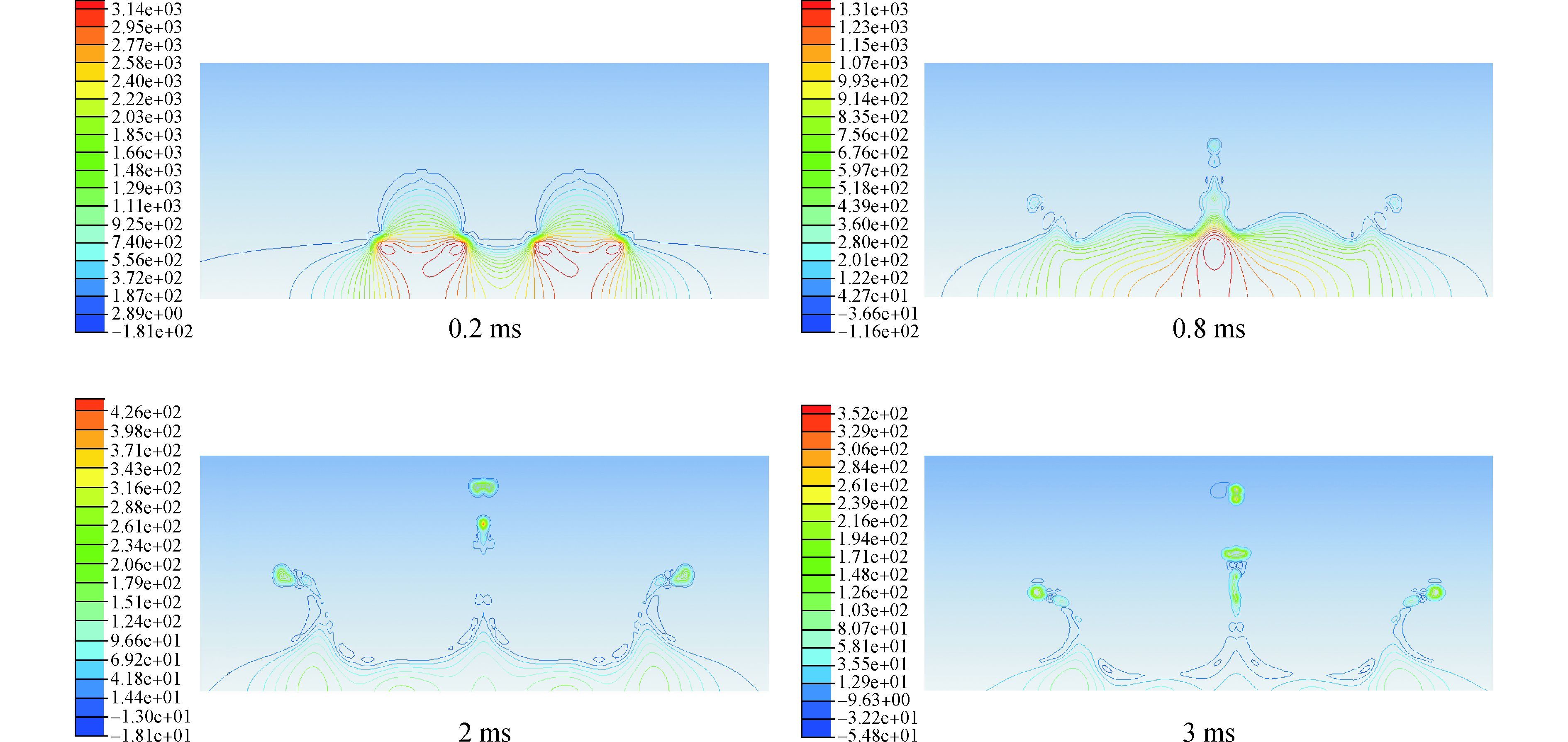
图 5是双液滴以2 m/s的速度撞击液膜后的压力分布状况。可以看出,当双液滴同时撞击液膜后,在双液滴与液膜的“颈部”位置形成四个压力滞止点,滞止区内压力较高,而滞止点的压力相对于大气压非常高,与自由表面产生很大的压力梯度,正是在这种压力梯度的驱动下,“颈部”位置出现向外和向上方向的射流。随着撞击过程的继续,两个液滴都沿径向向外运动,两边的压力梯度逐渐减小,而在中间区域,两液滴在向外运动时相遇,彼此之间相互撞击,在撞击处产生压力滞止点(0.8 ms),此处压力较高,同非中间区域相比,中间区域与自由表面处的压力差最大,所以在两液滴相交处,在此压差作用下产生向上的射流,液体持续碰撞,周围的液体不断进入射流区域,射流高度越来越高,液体的动能逐渐转变为射流水花的势能。
|
| 图5 双液滴同时与液膜撞击后的压力分布 Figure 5 Pressure distribution after droplets simultaneously impact liquid film |
而在两液滴与液膜撞击的接触点区域,即非“颈部”位置,由于液体内部与自由表面的压差较小,没有射流生成,这部分液体补充进入射流区域,故该区域的液层越来越薄。
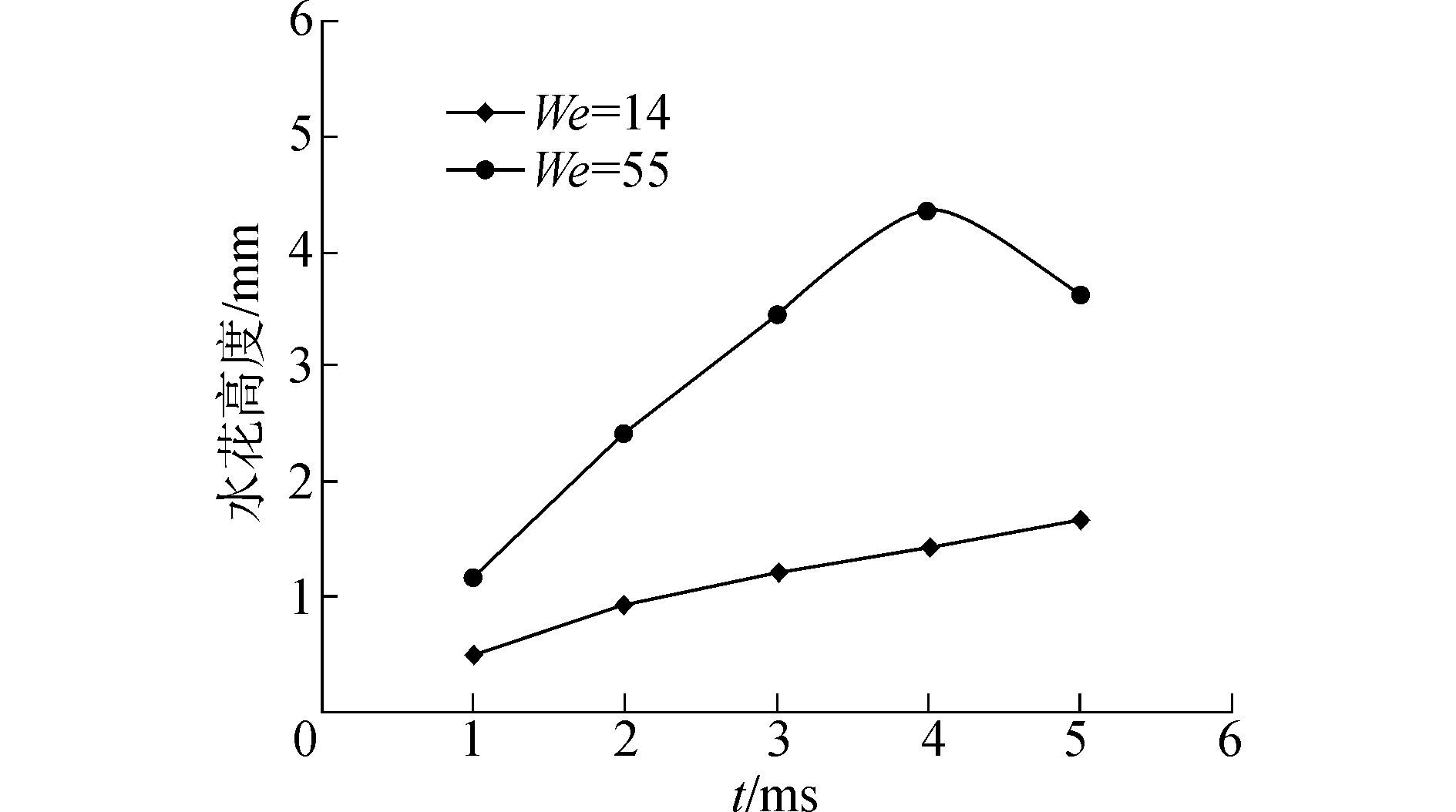
无量纲的韦伯数和雷诺数分别定义为We=ρDV2/σ,Re=ρDv/u。图 6、7分别为Re=2 211时不同We下水花高度、射流高度随时间的变化。
|
| 图6 We数对水花高度的影响(Re=2 211) Figure 6 The influence of We on spray height (Re=2211) |
由图 6可以发现,水花高度随着We的增加而增大,出现回落的时间也随We数的增大而提前,即We数较大的,在4 ms水花开始回落,而We数较小的,水花一直在增大,在计算时间内还没开始回落,且在水花高度上升阶段,We大时的水花高度上升速度高于We小时的。
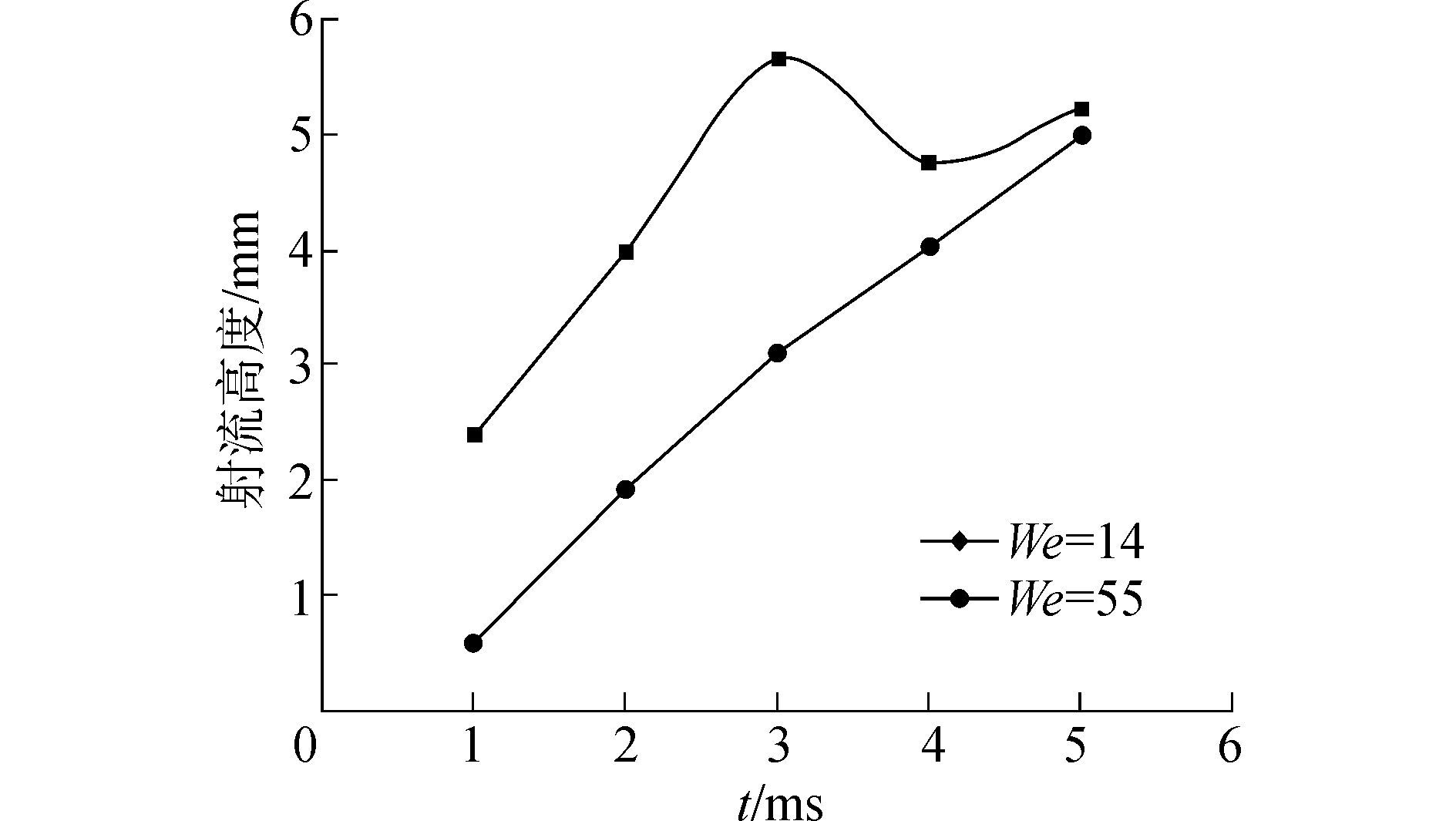
由图 7可见,中心射流回落的时间也随We数的增大而提前,即We=55时3 ms开始出现射流回落,而We=14时在计算时间没出现中心射流回落。当We增大时,与表面张力相比,在液膜内最终形成的向上运动的流体所具有的惯性相应增大,则克服表面张力的能力增强,导致中心射流顶部液膜破碎,故射流高度下降,随着撞击过程的持续进行,不断有液体进入射流区域,故射流高度又在下降后上升。
|
| 图7 We数对射流高度的影响(Re=2 211) Figure 7 The influence of We on jet height (Re=2 211) |
可以看出,在双液滴同时撞击液膜后,在We较小的情况下,水花高度随时间逐渐增加,水花高度值较小;中心射流高度随时间也逐渐增加,中心射流高度较大;在We较大时,水花高度随时间先增加,到达最大高度后而逐渐降低;中心射流高度在前3 ms内逐渐增大,达到最大高度后开始减小,4 ms后又逐渐增大,这种脉动变化是由中心射流空间液膜的破碎造成。
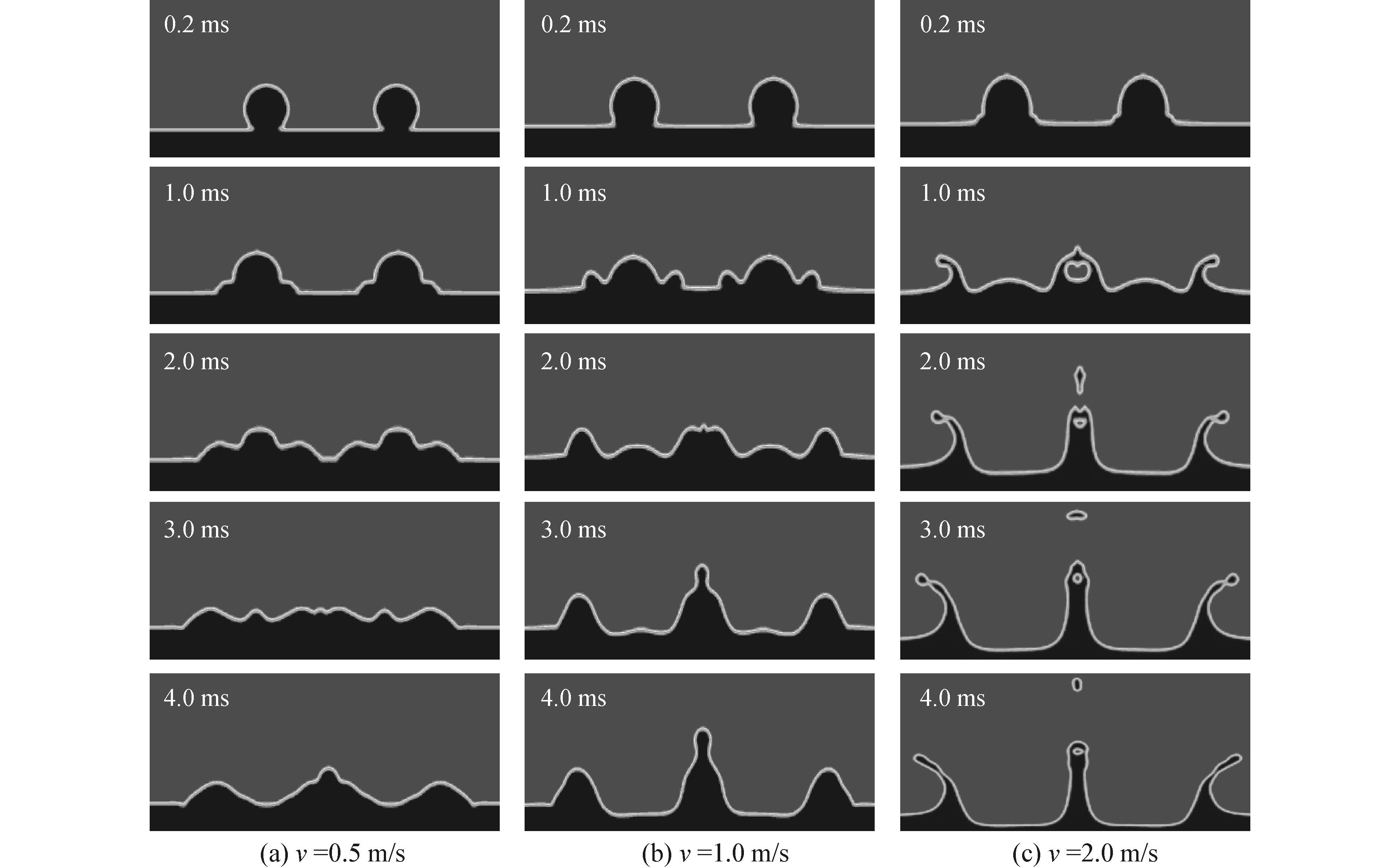
图 8为直径为2 mm双液滴在液滴水平间距为6 mm时分别以0.5、1.0和2.0的速度同时撞击1.2 mm厚度液膜后水花形态演变图。
|
| 图8 撞击速度不同的双液滴撞击液膜后水花形态演变图(Sh=3D) Figure 8 The change of the spray after double droplets simultaneously impact liquid film at different impact speed (Sh=3D) |
对比图 8和图 3可以看出,与双液滴水平间距较小时相比,水平间距较大时,两个液滴同时撞击液膜后产生的水花相遇所需的时间更长,且在撞击速度较大时,两液滴水平距离较大的撞击变形明显不同于距离较小时的,即在两液滴中间位置飞溅的冠状水花相遇合并后,水花底部与顶部之间存在“空心”,如图 8(c)。图 8(a)中在撞击速度较小0.5 m/s时,2 ms时两液滴撞击液膜产生的水花才刚刚相遇,而图 3(a)中2 ms时已经由于水花相撞形成了中心射流,图 8(a)所形成的水花高度较小,中间射流高度与周围水花高度相当。图 8(b)中当撞击速度逐渐增大到1.0 m/s时,产生水花的时间早于图 8(a),产生的水花在空中相遇相撞,相互合并并向上发展,如图 8(b) 3.0 ms时所示,射流高度是周围水花高度的1.76倍。撞击速度增大到2.0 m/s时,双液滴同时撞击液膜后迅速产生飞溅,飞溅起来的水花不仅在空中较早地相撞,而且底部水花也相撞,如图 8(c)1.0 ms所示,撞击后速度发生变化,产生垂直撞击面的向上的速度,使得液体继续向上运动,而且空中相遇的水花由于撞击同样产生向上的速度,致使一部分液体脱离表面张力的作用,产生二次液滴,继续向上运动,相交处射流高度与周围水花高度相当。
图 9为We=55时在不同的双液滴水平间距下水花高度随时间的发展趋势。图 9显示,前3 ms时间内双液滴水平间距对两侧水花高度几乎不产生影响,这是由于撞击刚开始时双液滴撞击液膜后在两液滴两侧引起的水花飞溅与单个液滴撞击液膜引起的水花飞溅状况相似,主要不同之处在于两液滴相撞时在中间位置相互作用力引起中间射流,而在这个时间内还未对两侧的水花高度产生明显影响。在3~4 ms,Sh值越大水花高度反而越小,4 ms之后,Sh值越小水花高度越小,这是因为Sh值越小,两液滴的相互作用力较早的互相影响,使得两液滴撞击液膜后产生水花、发生飞溅的时间越早,所以Sh=4 mm时水花高度较早地达到最大值,而Sh=6 mm时的水花高度还在继续向上发展。
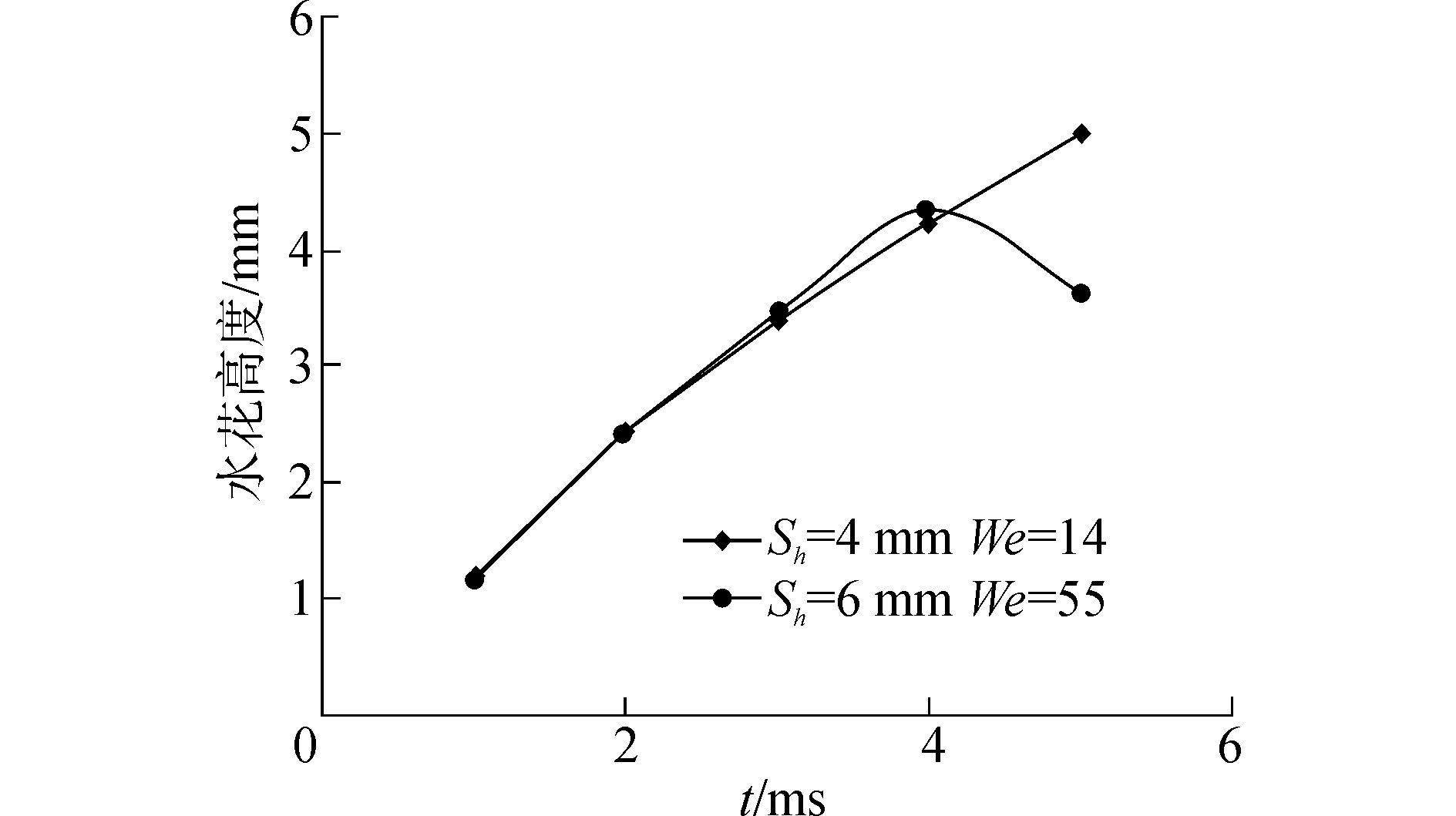
|
| 图9 双液滴水平间距对水花高度的影响 Figure 9 The influence of horizontal spacing of double droplet on spray height |
图 10显示了We=55时在不同的双液滴水平间距下射流高度随时间的发展趋势。可以看出,在3.5 ms之前,Sh越大射流高度越小;3.5 ms之后,Sh越大射流高度越大,这是由于水平间距Sh较小时,双液滴撞击液膜后产生的水花在空中相遇较早,相遇时速度方向相差不大,相遇后很快相互融合一起继续向上发展,所以刚开始射流高度较大,而运动一段时间后由于顶部二次液滴的产生、脱离使得后来射流高度较小;而水平间距Sh较大时,两液滴撞击液膜后各自水花都充分发展后才相遇,如图 8(c)1.0 ms所示,两水花顶部的运动方向几乎相反,碰撞使得一部分液体摆脱粘性力和表面张力的作用,脱离主流液体自己向上运动,水花的动能逐渐转变为液体的势能,向上射流的速度减小所以射流高度刚开始较小,而由于液体的继续向外扩展,液体不断进入射流区域使得后来射流高度增大。
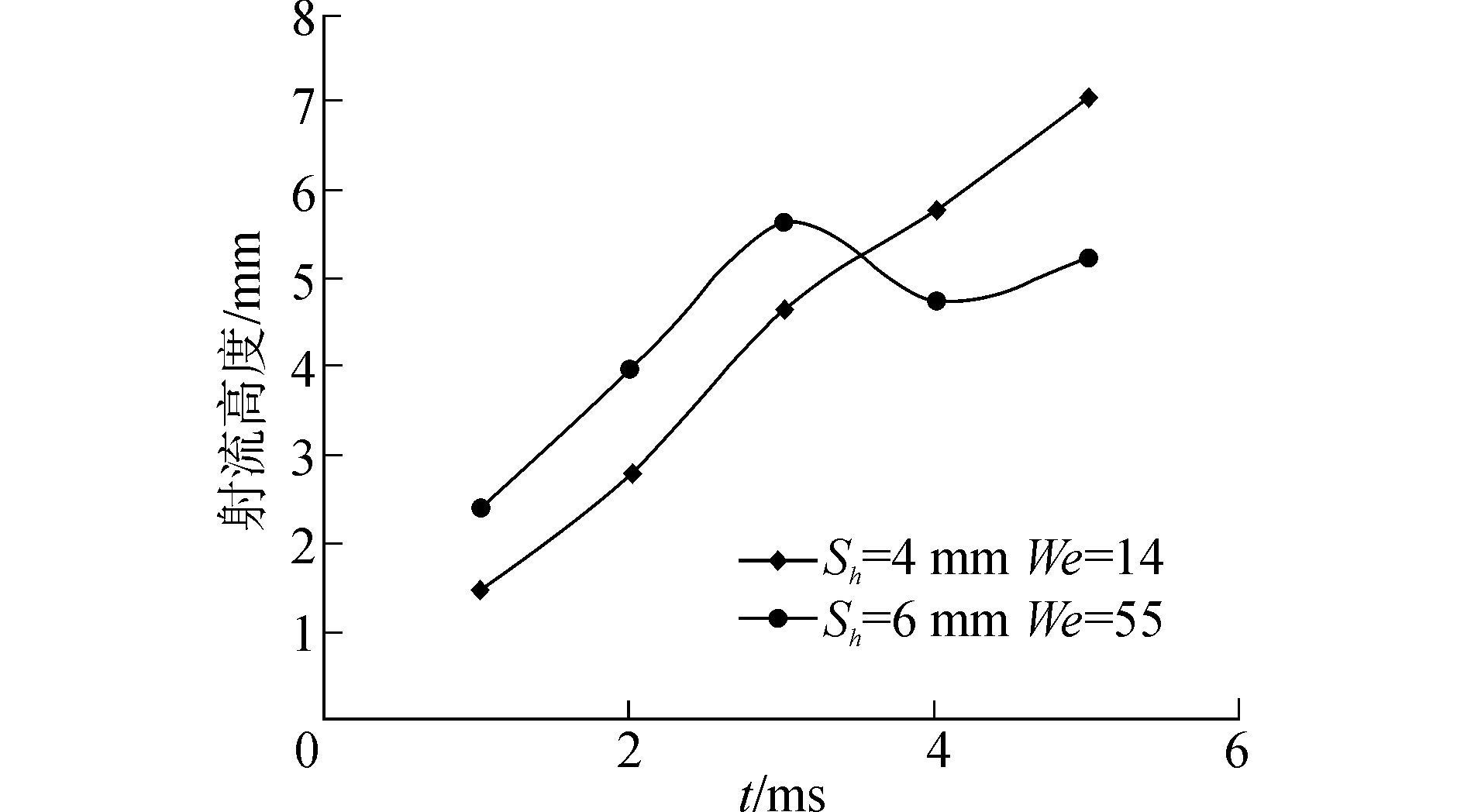
|
| 图10 双液滴水平间距对射流高度的影响 Figure 10 The influence of horizontal spacing of double droplet on jet height |
1) 双液滴以不同速度撞击液膜后的动力学变形不同。碰撞速度较小时,在撞击点两侧仅形成表面波动、中间位置形成中心液膜射流;碰撞速度增大时,在撞击点两侧形成的波动幅度增强、中间位置形成中心液膜射流高度大于碰撞速度较小时的;碰撞速度继续增大时,在撞击点两侧形成皇冠状水花、中间位置形成中心液膜射流能够产生二次液滴。
2) 两液滴撞击液膜后撞击点两侧的水花高度和中心射流高度均随We数的增大而增大,且水花高度和射流高度开始回落的时间也随We数的增大而提前;We数决定了中心射流顶端是否有飞溅产生,We较小时不能产生二次液滴飞溅,随着We数的增大,中心射流顶端将产生二次液滴。
3) 液滴间距变化能够引起撞击后液体变形的不同。液滴间距较大时,两个液滴同时撞击液膜后产生的水花相遇所需的时间更长,且在撞击速度较大时,在两液滴中间位置飞溅的冠状水花底部与顶部均相遇合并,且两水花顶部的速度方向相反,水花底部与顶部之间存在“空心”,在液滴间距较小时不存在这一变形。
4) 在所研究的参数范围内,液滴间距对撞击后初始时(3 ms之前)撞击点两侧的开始水花高度没有明显影响,在3~4 ms,液滴间距Sh值越大水花高度反而越小,4 ms之后,Sh值越小水花高度越小。而对射流高度,在3.5 ms之前,Sh越大射流高度越小;3.5 ms之后,Sh越大射流高度越大。
| [1] |
梁刚涛, 郭亚丽, 沈胜强. 液滴撞击液膜的射流与水花形成机理分析[J].
物理学报, 2013, 62(2): 024705.
Gangtao, GUO Yali, SHEN Shengqiang. Analysis of liquid sheet and jet flow mechanism after droplet impinging onto liquid film[J]. Acta physica sinica, 2013, 62(2): 024705. |
| [2] | HU Haibao, HUANG Suhe, CHEN Libin. Droplet impact on regular micro-grooved surfaces[J]. Chinese physics B, 2013, 22(8): 084702. |
| [3] | VANDER WAL R L, BERGER G M, MOZES S D. Droplets splashing upon films of the same fluid of various depths[J]. Experiments in fluids, 2006, 40(1): 33–52. |
| [4] | FUJIMOTO H, OGINO T, TAKUDA H, et al. Collision of a droplet with a hemispherical static droplet on a solid[J]. International journal of multiphase flow, 2001, 27(7): 1227–1245. |
| [5] | FUJIMOTO H, ITO S, TAKEZAKI I. Experimental study of successive collision of two water droplets with a solid[J]. Experiments in fluids, 2002, 33(3): 500–502. |
| [6] | MINAMIKAWA T, FUJIMOTO H, HAMA T, et al. Numerical simulation of two droplets impinging successively on a hot solid in the film boiling regime[J]. ISIJ international, 2008, 48(5): 611–615. |
| [7] | SIVAKUMAR D, TROPEA C. Splashing impact of a spray onto a liquid film[J]. Physics of fluids, 2002, 14(12): 85–88. |
| [8] | NIKOLOPOULOS N, NIKAS K S, BERGELES G. A numerical investigation of central binary collision of droplets[J]. Computers & fluids, 2009, 38(6): 1191–1202. |
| [9] |
胡雷, 郭家宏, 王小永. 格子Boltzmann方法模拟双液滴同时冲击固体表面液膜[J].
水动力学研究与进展, 2011, 26(1): 11–18.
L ei, GUO Jiahong, WANG Xiaoyong. Numerical simulation of two droplets impact on the liquid film at the same time using lattice Boltzmann method[J]. Chinese journal of hydrodynamics, 2011, 26(1): 11–18. |
| [10] | FEDORCHENKO A I, WANG Anbang. On some common features of drop impact on liquid surfaces[J]. Physics of fluids, 2004, 16(5): 1349–1365. |
| [11] | MORTON K M, BAINES M J. Numerical methods for fluid dynamics[M]. New York: Academic Press, 1982: 273 . |
| [12] |
沈胜强, 崔艳艳, 郭亚丽. 液滴撞击等温斜面的数值模拟[J].
热科学与技术, 2009, 8(3): 194–197.
Shengqiang, CUI Yanyan, GUO Yali. Numerical simulation of droplet striking on inclined isothermal surface[J]. qJournal of thermal science and technology, 2009, 8(3): 194–197. |
| [13] | YARIN A L, WEISS D A. Impact of drops on solid surfaces:self-similar capillary waves, and splashing as a new type of kinematic discontinuity[J]. Journal of fluid mechanics, 1995, 283: 141–173. |
| [14] | ROISMAN I V, PRUNET-FOCH B, TROPEA C, et al. Multiple drop impact onto a dry solid substrate[J]. Journal of colloid and interface science, 2002, 256(2): 396–410. |



