伴随着石油和煤炭等化石燃料的过度消耗,像海洋能、风能、太阳能等清洁再生能源的开发利用越来越受到世界各国的重视[1]。潮流能作为海洋能的重要形式,与风能和太阳能相比,具有能量密度大、对环境污染小、变化有规律、可预测性好等优点[2,3]。目前,对潮流能的开发,多为利用旋转叶片的水轮机进行潮流能量捕获,然而这种潮流能捕获方式存在占地面积大、噪声大、对周围海洋生物产生影响等问题[4]。海洋中的生物,如金枪鱼、鲨鱼等,利用尾鳍的摆动从周围的流体中获得能量实现游动,具有能量获取效率高、噪声低、水动力特性好等特点[5]。受此启发,本文开展了一种利用被动式摆动水翼实现潮流能量捕获技术研究,与利用旋转叶片的水轮机潮流能量捕获方式相比,具有对海洋环境及海洋生物影响小、翼片结构简单、捕能效率高、可在河流等浅水中应用等优点[6]。
对于利用摆动水翼进行潮流能量获取,美国蒙特利海军研究生院开展了单翼片摆动水翼潮流能量捕获实验,表明最大输出功率与摆动频率和俯仰幅度的适当组合有关系,对双翼片水翼进行了流体数值仿真分析,预计效率达到40%,但实验结果和仿真结果差距较大[7]。英国工程商业公司通过液压系统改变摆动水翼有效攻角,研制了150kW半主动式摆动水翼潮流能量捕获实验样机,并进行了河流实验,最高捕能效率达到11.5%[8],Kinsey等进行了2D和3D仿真分析对比,分析了不同折算频率对摆动水翼捕能的影响[9]。近年来,国内也开展了利用摆动水翼进行潮流能量获取的仿真分析与实验研究,于海等利用两端的弹性碰头改变摆动水翼攻角,对水平方向运动的摆动水翼进行了循环水槽环境下的潮流能量获取实验研究,开辟了国内摆动水翼潮流能量获取研究的先河[10],王勇通过液压驱动改变摆动水翼攻角的方式,对竖直方向运动的摆动水翼进行了能量获取能力仿真分析[11],Xie Yonghui等研究了摆动水翼的能量获取能力与效率、折算频率和水翼俯仰角度之间的关系[12]。
为了实现摆动水翼能量提取过程,设定摆动水翼升沉和俯仰两个自由度按照正弦规律变化,通过曲柄摇杆机构改变水翼攻角,以实现摆动水翼的周期循环运动,在分析水翼运动过程中的功率、功率系数、折算频率等各参数之间关系的基础上,设计了被动式摆动水翼潮流能量获取装置,在循环水槽环境下进行了摆动水翼潮流能量获取实验验证,得出摆动水翼潮流能量获取功率和来流速度、折算频率等参数之间的关系。
1 摆动水翼水动力分析按照潮流能量获取方式,摆动水翼分为被动式、半主动式和主动式3种[13]。被动式摆动水翼利用水流的动能实现升沉和俯仰运动的自动周期循环,水翼俯仰角度与升沉位移按照设定规律耦合运动,半主动式摆动水翼利用水流的动能实现升沉运动,通过主动实时控制水翼俯仰角度以提高潮流能量获取效率,对于主动式摆动水翼,由于对摆动水翼升沉速度和俯仰角度的实时控制,不但能够优化潮流能量获取效率,而且能够抑制摆动水翼潮流能量获取过程中存在的周期波动问题。与被动式摆动水翼潮流能量获取相比,半主动式摆动水翼潮流能量获取方式机械结构较为简单,但需要增加一套水翼俯仰角度检测、驱动及控制部件,主动式摆动水翼潮流能量获取方式需要实时检测水翼升沉速度和俯仰角速度,利用硬件驱动系统实时校正,控制最为复杂。本文为了验证摆动水翼的潮流能量获取能力,采用被动式摆动水翼潮流能量获取方式。
1.1 被动式摆动水翼运动规律分析忽略被动式摆动水翼在运动过程中的变形和横向移动,视水翼在流场中的运动为刚体运动,被动式摆动水翼的运动规律如图 1所示。将摆动水翼在流场中的运动分解为升沉运动和俯仰运动的二自由度运动,升沉运动指的是水翼在竖直方向上运动h(t),俯仰运动指的是水翼的摆角运动θ(t)。为简化机构设计,将摆动水翼的运动设计为两种同频率正弦运动的耦合,其运动规律为:
| $ \left\{ \begin{matrix} h\left( t \right)={{H}_{0}}\sin \left( 2\pi ft+\varphi \right) \\ \theta \left( t \right)={{\theta }_{0}}\sin \left( 2\pi ft \right) \\ \end{matrix} \right. $ | (1) |

|
| 图 1 摆动水翼的运动模型 Fig. 1 Kinetic model of oscillating hydrofoil |
由摆动水翼的耦合运动规律可知,摆动水翼的瞬时升沉速度νy(t)和瞬时俯仰角速度ω(t)为:
| $ \left\{ \begin{matrix} {{v}_{y}}\left( t \right)=2\pi f{{H}_{0}}\cos \left( 2\pi ft+\varphi \right) \\ \omega \left( t \right)=2\pi f{{\theta }_{0}}\cos \left( 2\pi ft \right) \\ \end{matrix} \right. $ | (2) |
基于摆动水翼的耦合运动规律和来流速度,摆动水翼的有效攻角α(t)定义为:
| $ \alpha \left( t \right)=\theta \left( t \right)-\arctan \left( \frac{{{v}_{y}}\left( t \right)}{{{U}_{\infty }}} \right) $ | (3) |
利用来流速度和水翼摆动频率,定义无量纲参数折算频率f*为:
| $ {{f}^{*}}=fc/{{U}_{\infty }}\ $ | (4) |
设计采用 NACA0015型对称水翼,均匀流场环境下的来流可获取流体运动能量为:
| $ {{P}_{\alpha }}=0.5\rho {{U}_{\infty }}^{3}bd\ $ | (5) |
被动式摆动水翼运动时的瞬时能量获取功率定义为:
| $ P\left( t \right)={{P}_{y}}\left( t \right)+{{P}_{\theta }}\left( t \right)={{F}_{y}}\left( t \right){{v}_{y}}\left( t \right)+M\left( t \right)\omega \left( t \right) $ | (6) |

|
| 图 2 摆动水翼的受力 Fig. 2 Forces on oscillating hydrofoil |
一个运动周期内,摆动水翼能量获取的平均功率表达为:
| $ \bar{P}=\frac{1}{T}\int_{t}^{t+T}{P\left( t \right)\text{d}t} $ | (7) |
定义摆动水翼升力系数CL,力矩系数CM和功率系数CP分别为:
| $ \begin{matrix} {{C}_{L}}\left( t \right)=\frac{{{F}_{y}}\left( t \right)}{0.5\rho {{U}_{\infty }}^{2}bc}\ \ \ \ \ \ {{C}_{M}}\left( t \right)=\frac{M\left( t \right)}{0.5\rho {{U}_{\infty }}^{2}b{{c}^{2}}} \\ {{C}_{P}}\left( t \right)=\frac{P\left( t \right)}{0.5\rho {{U}_{\infty }}^{3}bc}\ =\frac{1}{{{U}_{\infty }}}\left( {{C}_{L}}\frac{\text{d}h\left( t \right)}{\text{d}t}+{{C}_{M}}\frac{\text{d}\theta \left( t \right)}{\text{d}t}c \right) \\ \end{matrix}\ $ | (8) |
| $ {{{\bar{C}}}_{P}}=\frac{1}{T}\int_{t}^{t+T}{{{C}_{P}}\left( t \right)\text{d}t}\ $ | (9) |
摆动水翼的能量获取效率表达为:
| $ \eta =\frac{{\bar{P}}}{{{{\bar{P}}}_{\alpha }}}={{{\bar{C}}}_{P}}\frac{c}{d} $ | (10) |
因此,通过摆动水翼潮流能量获取功率系数CP(t)和能量获取效率η可以描述摆动水翼的能量获取能力。
1.3 摆动水翼数值模拟分析采用网格划分软件GAMBIT对水翼周围流域进行网格划分,基于区域运动代替单独的翼片运动思想,结合动网格和滑移网格模型,滑移网格交界面将流域划分为内部运动区域和外部静止区域两部分,两部分通过滑移交界面实现数据传递,运动区域和翼片一起实现升沉和俯仰两自由度的同步运动,具体网格划分和边界条件如图 3所示。

|
| 图 3 网格划分 Fig. 3 details of meshing |
利用计算流体力学分析软件Fluent对被动式摆动水翼在流场中运动进行水动力仿真,通过FLUENT提供的二次开发接口自定义函数User-Defined-Function来定义水翼的运动规律。设定水翼弦长c为0.22m,展长b为0.65m,升沉运动幅值H0为水翼弦长c,俯仰运动的幅值θ0为π/3,相位差φ为π/2,摆动频率f为0.7,通过公式(4),可知折算频率f*为0.096,设定无限远处来流速度U∞为1.6m/s,设定俯仰轴线位于距翼型前缘点三分之一处,当迭代到第五个周期后输出曲线趋于稳定,取迭代第六个周期曲线进行分析,得到摆动水翼一个运动周期内能量获取的升力系数和升沉速度,力矩系数和俯仰角速度,功率系数曲线分别如图 4,图 5和图 6所示。

|
| 图 4 升力系数和升沉速度 Fig. 4 Lift coefficient and heaving velocity |

|
| 图 5 力矩系数和俯仰角速度 Fig. 5 Moment coefficient and heaving velocity |
|
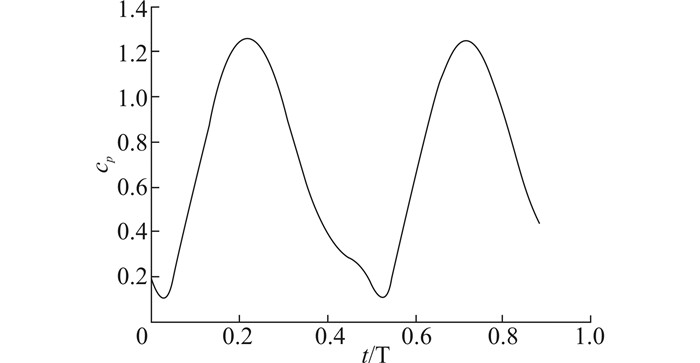
| 图 6 摆动水翼的功率系数 Fig. 6 Power coefficient of oscillating hydrofoil |
从图 4可看出,摆动水翼的升力系数和升沉速度在周期内变化趋势一致,保持在同一方向变化,根据公式(8)可知,摆动水翼的升沉运动能够实现能量获取,从图 5可知,由于力矩系数较小且和俯仰角速度变化趋势不一致,表明摆动水翼俯仰运动只是用来改变水翼攻角,对能量的获取起到了很小的作用,仿真曲线对比表明摆动水翼的能量获取主要来自升沉运动的作用。
根据图 6,能量获取的功率系数在一个周期内随时间近似正弦波动,当摆动水翼处于升沉运动的上、下极限位置时,水翼处于水平方向,流体对摆动水翼不产生升力,所以此时摆动水翼表现出了最小的能量获取,当摆动水翼处于T/4和3T/4时,摆动水翼位于升沉速度最大的位置,此时摆动水翼实现了最大的能量获取,通过式(9)、(10)计算可知,最大的瞬时能量获取功率系数达到1.25和效率达到0.52,平均能量获取功率系数${{{\bar{C}}}_{P}}$达到0.6697,能量获取效率η达到0.279,仿真结果表明被动式摆动水翼在一个运动周期内能够实现潮流能量的获取。
2 被动式摆动水翼实验装置设计本文设计的摆动式水翼潮流能量获取实验装置主要由能量转换机构、增速发电系统两部分组成,其中,能量转换机构又包括摆动水翼升沉运动机构和摆动水翼俯仰角度控制机构两部分。实验装置三维模型如图 7所示。

|
| 图 7 摆动水翼能量获取装置 Fig. 7 Capture energy device based on oscillating hydrofoil |
摆动水翼升沉运动机构主要包括NACA0015型摆动水翼翼片,反向曲柄摇杆机构以及连接部分,用于把流场中流体的动能转化为水翼升沉运动的机械能,通过反向曲柄摇杆机构把水翼的升沉运动机械能转化为输出轴的旋转机械能。摆动水翼俯仰角度控制机构包括正向曲柄摇杆机构、同步带传动机构,正向曲柄摇杆机构把输出轴的单向旋转运动转化为水翼俯仰角度控制轴的双向角度摆动,水翼俯仰角度控制轴通过两套同步带传动机构驱动摆动水翼俯仰轴,实时控制水翼俯仰角度。增速发电系统与输出轴相连,包括扭矩传感器、增速箱、飞轮以及发电机,扭矩传感器用于测量输出轴转速和转矩,由于输出轴转速较低,利用增速箱把转速提高到发电机的额定输入转速范围,通过飞轮既可以克服曲柄摇杆机构存在的死点问题,又可以有效抑制输出轴旋转过程中存在的转矩和速度波动。
当水平方向的水流流过摆动水翼时,除摆动上下两个极限位置外,摆动水翼对称面与水平方向来流具有一定的角度,流场对水翼翼面产生竖直方向的升力,在升力的作用下,水翼上下运动,通过反向曲柄摇杆机构驱动输出轴,从而完成将流场的流体动能转化为旋转机械能,实现流场能量获取,输出轴通过正向曲柄摇杆机构和同步带传动机构实现摆动水翼俯仰角度的实时控制,因此在流场流体的作用下,摆动水翼实现了的升沉运动和俯仰运动,通过合理配置飞轮,实现了摆动水翼能量获取的周期循环过程。
被动式摆动水翼潮流能量获取实验装置具有以下特点:
1)通过简单机械机构实现了摆动水翼升沉运动和俯仰运动的运动耦合,耦合运动规律固定;
2)无需主动控制摆动水翼二自由度运动及运动信息检测,降低了系统硬件结构的复杂性;
3)实验装置为搭接式结构,改进方便,为今后进行多翼片能量获取、半主动式摆动水翼能量提取等研究奠定了基础。
3 被动式摆动水翼能量获取实验结果及分析 3.1 特定流速下摆动水翼能量获取实验和结果分析在哈尔滨工程大学循环水槽环境下开展了被动式摆动水翼能量获取实验研究,水槽实验段宽度为1.70m,水深为1.50m,最大水流速度为2.0m/s。分别进行了0.7m/s、0.8m/s、1.0m/s、1.2m/s、1.4m/s、1.6m/s、1.8m/s以及2.0m/s来流速度下的能量获取实验,针对同一来流速度,完成了不同模拟负载下的输出转矩和输出转速检测。实验装置如图 8所示,被动式摆动水翼实验装置置于循环水槽中,以滑动变阻器作为发电机的可调负载,通过改变滑动变阻器的阻值来测试给定流速下的摆动水翼能量获取能力。设定摆动水翼升沉运动的最上端为初始位置,当有最小来流速度为0.7m/s时,输出轴施加一定启动力矩,实验装置即可实现自动周期循环运动。

|
| 图 8 循环水槽能量获取实验 Fig. 8 Energy capturing experiment in circulating water channel |
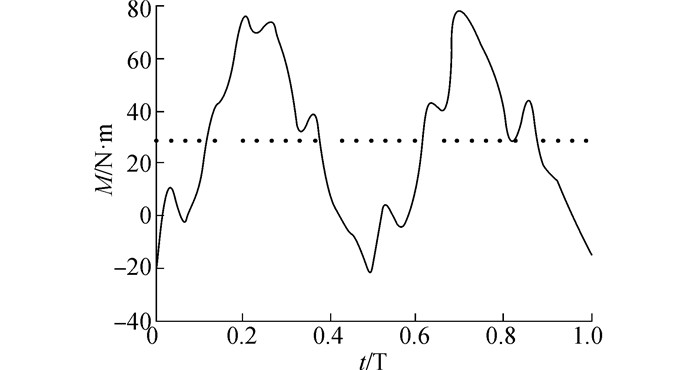
对1.6m/s来流速度下的摆动水翼能量获取情况进行实验结果分析,通过扭矩传感器测量输出轴的转矩和转速,当来流速度为1.6m/s,折算频率f*为0.096时,摆动水翼输出轴的瞬时测量转矩曲线如图 9所示,瞬时测量转速曲线如图 10所示。从图 9可以看出,在一个循环周期内,平均转矩$ {\bar{M}} $为28N·m,在T/4和3T/4时,摆动水翼能量获取装置达到最大输出转矩为79N·m。
|
| 图 9 瞬时输出转矩 Fig. 9 The instantaneous torque output |

|
| 图 10 瞬时输出转速 Fig. 10 The instantaneous angular velocity output |
由于摆动水翼升沉运动的上、下极限位置为水平方向,流体对摆动水翼不产生升力,此时利用飞轮惯性改变摆动水翼攻角,在0,T/2和T时刻附近的一小段时间内摆动水翼能量获取装置出现了负的转矩输出。从图 10可以看出,在一个运动周期内,输出轴旋转速度在42r/min附近波动,最大波动峰值达到11.4%,对摆动水翼能量获取性能产生一定影响,可以通过优化飞轮配置或增加发电机电子驱动器的方式进行改进。
根据输出轴的转矩和转速信息,计算得到摆动水翼输出功率变化情况,如图 11所示。利用公式(7),计算得到一个循环周期内平均能量获取功率$ {\bar{P}} $为125 W,利用公式(10),计算得到能量获取效率η为0.18。实验结果表明,尽管输出轴一个周期内的能量获取功率曲线存在小幅度波动,但从能量获取功率和能量获取效率角度分析,表明利用被动式摆动水翼实现潮流能量的获取方案是可行的。

|
| 图 11 实验输出功率 Fig. 11 Power output of the experiment |
在实验中,由于输出轴采用分段加工后相连接,导致输出轴刚度及同轴度较差,同步带传动存在松动,曲柄摇杆机构传动精度较差和流速的不稳定导致瞬时输出转矩、瞬时转速和瞬时功率曲线均有波动。该问题可以通过进一步优化机械结构,增加其他波动抑制装置进行解决。
来流速度为1.6m/s时,针对不同模拟负载下的摆动水翼能量获取效率进行了实验和仿真分析对比研究。实验通过改变滑动变阻器的阻值来调节发电机的负载,负载的变化决定了摆动水翼摆动频率的变化,进而影响了摆动水翼折算频率发生变化,折算频率从0.04到0.14变化时,摆动水翼能量获取效率和仿真效率随折算频率的变化关系曲线如图 12所示,从实验曲线可以看出,当折算频率f*为0.096时,摆动水翼能量获取效率最高,能量获取效率η达到0.18。当f*<0.096时,摆动水翼能量获取效率随着折算频率的增大而增大。当f*大于0.1时,由于负载逐渐减小,水翼摆动频率逐渐增大,由于机械摩擦、装置转动惯量而造成的机械动能损失逐渐增大等,导致能量获取效率随折算频率的增大而减小。

|
| 图 12 效率和折算频率 Fig. 12 Efficiency and reduced frequency |
对比图 12中的实验仿真效率曲线,可以看出仿真效率和实验效率变化趋势一致,当摆动频率f达到0.7,折算频率f*达到0.096时,仿真和实验结果同时达到最大能量输出效率,但仿真最大能量输出效率达到0.28,而实验最大能量输出效率达到0.18,这主要由于实验过程中机械摩擦、飞轮转动惯性消耗等造成了能量损失,导致实验得到的能量获取效率比仿真结果小。
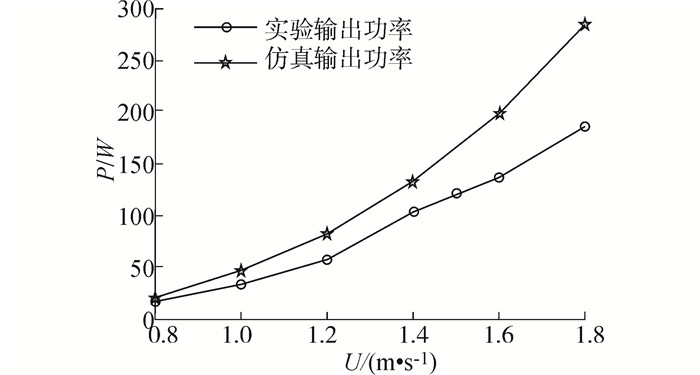
3.2 不同流速下实验和实验结果分析通过不同来流速度下的实验功率数据整理,得到在来流速度0.8、1.0、1.2、1.4、1.6和1.8m/s下,水翼实现最佳能量获取时对应的摆动频率值分别为0.3,0.4,0.5,,0.6,,0.7和0.8,可见随着来流速度的增大,水翼最佳能量输出频率值一直在增大。针对最佳能量输出功率进行分析,得到实验最佳能量输出功率和仿真输出功率随来流速度的对比变化关系如图 13所示。
|
| 图 13 不同流速下的输出功率 Fig. 13 Power output under different water velocity |
通过图 13看出,摆动水翼在不同来流速度情况下都表现出了很好的能量获取效果。随着来流速度的逐渐增大,能量获取功率增大,当来流速度在1.2m/s 和1.6m/s 之间时,能量获取功率与来流速度近似成线性关系,当水速达到1.8m/s 时,实验装置最高平均功率输出为180W。
通过实验曲线和仿真曲线的对比可以看出,实验输出功率和仿真输出功率变化趋势一致,随着来流速度的增大,捕获的能量增大。当来流速度0.8m/s 时,仿真输出功率为21W,实验输出功率达到18W,实验和仿真结果吻合较好,但随着来流速度的逐步增大,仿真输出和实验输出的偏差也越来越大,当来流速度达到1.8m/s 时,仿真功率输出为281W,而实验功率输出为180W,这主要是由于流速的增大,造成机械部件间传动的摩擦增大,流体表面的粘性阻力也增大,造成传动损耗的能量增多。
4 结束语1) 基于水中生物尾鳍的仿生推进原理,提出一种潮流能量获取方式,研制了被动式摆动水翼能量获取实验装置。
2)在循环水槽环境下进行了能量获取能力的实验研究,验证了利用被动式摆动水翼进行潮流能量获取的可行性,并和仿真分析进行了对比,发现实验结果和仿真结果变化趋势一致。
3)与旋转式水轮机相比,摆动水翼翼型简单,便于加工,特别适合在低速流速下和浅水区域中使用,弥补了旋转水轮机存在的许多不足,在潮流能源开发利用中具有较大的发展空间。
| [1] | LIU Hongwei, MA Shun, LI Wei, et al. A review on the development of tidal current energy in China[J]. Renewable and sustainable energy reviews, 2011, 15(2): 1141-1146. |
| [2] |
张亮, 李新仲, 耿敬, 等. 潮流能研究现状2013[J]. 新能源进展, 2013, 1(1): 53-68. ZHANG Liang, LI Xinzhong, GENG Jing, et al. Tidal current energy update 2013[J]. Advances in new and renewable energy, 2013, 1(1): 53-68. |
| [3] |
张亮, 王树齐, 马勇, 等. 潮流能水平轴叶轮纵摇运动水动力分析[J]. 哈尔滨工程大学学报, 2015, 36(3): 307-311. ZHANG Liang, WANG Shuqi, MA Yong, et al. The pitch hydrodynamic analysis of tidal current energy horizontal axis impeller[J].Journal of Harbin Engineering University, 2015, 36(3): 307-311. |
| [4] | XIAO Qing, LIAO Wei, YANG Shuchi, et al. How motion trajectory affects energy extraction performance of a biomimic energy generator with an oscillating foil?[J]. Renewable energy, 2012, 37(1): 61-75. |
| [5] | TRIANTAFYLLOU M S, TECHET A H, HOVER F S. Review of experimental work in biomimetic foils[J]. IEEE journal of oceanic engineering, 2004, 29(3): 585-594. |
| [6] | ZHU Qiang. Energy harvesting by a purely passive flapping foil from shear flows[J]. Journal of fluids and structures, 2012, 34: 157-169. |
| [7] | LINDSEY K. A feasibility study of oscillating-wing power generators[D]. Monterey: Naval Postgraduate School, 2002: 1-63. |
| [8] | BEDARD R. EPRI Final Report[EB/OL].[2005-11-09]. http://oceanenergy.epri.com/attachments/streamenergy/reports/004TISECDeviceReportFinal111005.pdf. |
| [9] | KINSEY T, DUMAS G. Computational fluid dynamics analysis of a hydrokinetic turbine based on oscillating hydrofoils[J]. Journal of fluids engineering, 2012, 134(2): 021104. |
| [10] |
于海. 流水摆式发动机装置研究[D]. 哈尔滨: 哈尔滨工程大学, 2006: 33-72. YU Hai. The research of stingry current engine equipment[D].Harbin: Harbin Engineering University, 2006: 33-72. |
| [11] |
逯建伟. 振荡水翼捕获潮流能系统的水动力和能量捕获性能研究[D]. 济南: 山东大学, 2014: 58-86. LU Jianwei. Study on hydrodynamic and energy extraction performance of a tidal energy extraction system based on an oscillating hydrofoil[D].Jinan: Shandong University, 2014: 58-86. |
| [12] | XIE Yonghui, LU Kun, ZHANG Di. Investigation on energy extraction performance of an oscillating foil with modified flapping motion[J]. Renewable Energy, 2014, 63: 550-557. |
| [13] | YOUNG J, LAI J C S, PLATZER M F. A review of progress and challenges in flapping foil power generation[J]. Progress in aerospace sciences, 2014, 67: 2-28. |



