2. Dalian Ocean University, Dalian 116023, China
波浪经过结构物后,透射波浪的能量和波面变化情况是设计关心的主要问题之一。通常的研究都假定海水密度均一,但实际海洋环境中,海水密度在垂向上存在显著的层化现象。这一特性导致在海洋内部也会产生波动,因此对结构的反射、透射问题都存在显著的影响[1]。把流体看作密度均匀的两层,在两层交接面上密度存在突变,此时波浪会以两种不同的模态传播,一种是表面波模态,另一种是内波模态[2]。尤云祥[3]和Dhillon等[4]分别研究了垂直薄板在有限深和无限深两层流体中的反射及透射特性。Behera等[5]分析了矩形多孔结构在有限深两层流体中与斜向入射波浪的相互作用问题。本文针对水面固定箱型结构,从反射系数和透射系数的角度出发,通过自由表面和内界面上波面的变化情况研究两种模态波浪的变化特性。
采用势流理论求解两层流中结构的水动力特性时,Kashiwagi等[6]基于边界元方法,利用满足自由水面条件和内界面条件的格林函数,计算了二维情况下作用于物体上的激振力以及运动响应特性,并与物理模型试验结果进行了对比。Nguyen等[7]推导出三维情况下有限水深的两层流体中满足自由水面条件和内界面条件的格林函数。计算结果表明,在一定频率范围内分层效应对结构物水动力特性有显著影响,并且当入射波浪以内波模态入射时会在特定频率范围内引起方箱较大的转动。勾莹等[8]采用简单格林函数建立了时域方法求解积分方程,对漂浮圆柱、方箱等的水动力特性进行了研究。石强[9]基于分离变量法,建立了大直径圆柱体和方箱在两层流体中绕射势与辐射势的解析计算方法。Zhang等[11]运用特征函数匹配的方法,研究了两层流中月池结构垂向振荡的附加质量和辐射阻尼,以及在共振频率时自由水面和内界面上的波动情况。
本文采用数值方法和解析方法相结合的研究手段,将流域分为内域和外域两部分,内域采用利用简单格林函数的边界元法求解,外域速度势及导数利用解析展开式表示。这一模型既能求解任意物体的水动力特性,又避免了求解复杂的满足自由水面条件的格林函数;同时外域采用解析方法也使无穷远处的散射条件得到了很好的满足。通过计算方箱的激振力并与解析方法结果对比,验证了模型的正确性。根据单层流中波能流守恒原理推导出了两层流中的波能流守恒关系,利用这一关系对模型的精确性进行了进一步的验证。最后给出了两层流体中各模态的反射系数及透射系数的定义,研究了某一模态入射波浪与物体作用后,自由水面及内界面上的波面变化情况。
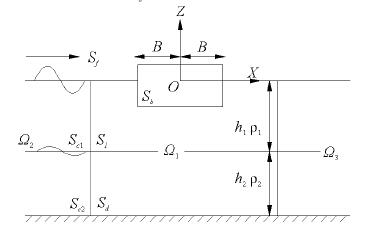
1 数学模型考虑二维情况下的两层理想流体,定义直角坐标系OXZ,坐标轴OZ垂直向上,OX与静水面重合。上层流体的密度和深度分别为ρ1和h1,下层流体的密度和深度分别为ρ2和h2,两层流体的密度比为γ=ρ1/ρ2,总水深为h=h1+h2。在物体周围取辐射边界Sc1和Sc2,将流域分为3部分:内域Ω1、左外域Ω2和右外域Ω3。内域中自由水面、物面、内界面及水底分别表示为Sf、Sb、SI、和Sd,如图 1所示。
|
| 图1 计算域定义 Figure 1 Definition sketch of computation domain |
两层流模型中存在两个模态的入射波浪,设入射波的方向与x轴正向相同,波数为k0(m)的入射波,速度势可表示为[7, 8, 10]
| $ \begin{array}{l} \varphi _i^{\left( {l,m} \right)}\left( {x,z} \right) = - \frac{{{\rm{i}}{{\rm{a}}_m}{{\rm{k}}_0}^{\left( m \right)}g}}{\omega }{Z^{\left( l \right)}}\left( {k_0^{\left( m \right)},z} \right) \cdot \\ \exp (ik_0^{\left( m \right)}x)(l = 1,2;m = 1,2) \end{array} $ | (1) |
m=2时,为内波模态入射
a2(k0(2))=a0(2)(k0(2))
式中:a0(1)(k0(m))和a0(2)(k0(m))分别表示波数为k(m)0的水波在自由水面和内界面上的波幅,它们之间满足如下关系式:
| $ \frac{{{a_0}^{(2)}\left( {{k_0}^{\left( m \right)}} \right)}}{{{a_0}^{\left( 1 \right)}\left( {{k_0}^{\left( m \right)}} \right)}} = {\rm{ch}}{k_0}^{\left( m \right)}{h_1}(1 - \frac{{g{k_0}^{(m)}}}{{{\omega ^2}}}th{k_0}^{\left( m \right)}{h_1}) $ | (2) |
垂向特征函数:
| $ \begin{array}{l} {Z^{\left( 1 \right)}}\left( {{k_0}^{\left( m \right)},z} \right) = \frac{{\frac{{{\omega ^2}}}{{g{k_0}^{\left( m \right)}}}{\rm{sh}}{k_0}^{\left( m \right)}z + {\rm{ch}}{k_0}^{\left( m \right)}z}}{{{\rm{h}}{k_0}^{\left( m \right)}{h_1}\left( {1 - \frac{{{\omega ^2}}}{{g{k_0}^{\left( m \right)}}}{\rm{h}}{k_0}^{\left( m \right)}{h_1}} \right)}}\\ {Z^{\left( 2 \right)}}\left( {{k_0}^{\left( m \right)},z} \right) = \frac{{{\omega ^2}}}{{g{k_0}^{\left( m \right)}{\rm{sh}}{k_0}^{\left( m \right)}{h_2}}}{\rm{ch}}{k_0}^{\left( m \right)}\left( {z + h} \right) \end{array} $ |
当入射波作用到结构物上后,会产生反射波和透射波,其速度势用φd表示,并且满足以下定解条件。拉普拉斯方程:
| $ {\nabla ^2}{\varphi _d} = 0 $ | (3) |
自由水面、内界面(垂向速度连续、压力连续)和水底边界条件:
| $ \frac{{\partial {\varphi _d}^{\left( {1,m} \right)}}}{{\partial z}} = K{\varphi _d}^{\left( {1,m} \right)}\;\;\;\;\left( {z = 0} \right) $ | (4) |
| $ \frac{{\partial {\varphi _d}^{\left( {1,m} \right)}}}{{\partial z}} = \frac{{\partial {\varphi _d}^{\left( {2,m} \right)}}}{{\partial z}}\;\;\;\;\left( {z = - {h_1}} \right) $ | (5) |
| $ \gamma \left( {\frac{{\partial {\varphi _d}^{\left( {1,m} \right)}}}{{\partial z}} - K{\varphi _d}^{\left( {1,m} \right)}} \right) = \frac{{\partial {\varphi _d}^{\left( {2,m} \right)}}}{{\partial z}} - K{\varphi _d}^{\left( {2,m} \right)}\left( {z = - {h_1}} \right) $ | (6) |
| $ \frac{{\partial {\varphi _d}^{\left( {2,m} \right)}}}{{\partial z}} = 0\left( {z = - h} \right) $ | (7) |
物面条件:
| $ \frac{{\partial {\varphi _d}^{\left( {l,m} \right)}}}{{\partial n}} = - \frac{{\partial {\varphi _i}}}{{\partial n}}\left( {on\;{S_b}} \right) $ | (8) |
另外还有向外传播的远场条件,其中,K=ω2/g。
1.2.1 外域速度势外域反射和透射速度势用下面级数展开的方式表达[10],对于左外域:
| $ \begin{array}{l} {\varphi _{d2}}^{\left( {l,m} \right)}(x,z) = - \frac{{{\rm{i}}{a_m}\left( {k_0^{\left( m \right)}} \right)g}}{\omega } \cdot \\ \left\{ {{A_{01}}^{\left( m \right)}{\rm{exp[- i}}{k_0}^{\left( 1 \right)}\left( {x + B} \right){\rm{]}}{{\rm{Z}}^{\left( l \right)}}\left( {{k_0}^{\left( 1 \right)},z} \right) + } \right.\\ {A_{02}}^{\left( m \right)}{\rm{exp[- i}}{k_0}^{\left( 2 \right)}\left( {x + B} \right){\rm{]}}{{\rm{Z}}^{\left( l \right)}}\left( {{k_0}^{\left( 2 \right)},z} \right) + \\ \sum\limits_{n = 1}^{ + \infty } {{A_{n1}}^{\left( m \right)}{\rm{exp[}}{k_n}^{\left( 1 \right)}\left( {x + B} \right){\rm{]}}{{\rm{Z}}^{\left( l \right)}}\left( {{k_n}^{\left( 1 \right)},z} \right)} + \\ \left. {\sum\limits_{n = 1}^{ + \infty } {{A_{n2}}^{\left( m \right)}{\rm{exp[}}{k_n}^{\left( 2 \right)}\left( {x + B} \right){\rm{]}}{{\rm{Z}}^{\left( l \right)}}\left( {{k_n}^{\left( 2 \right)},z} \right)} } \right\} \end{array} $ | (9) |
对于右外域:
| $ \begin{array}{l} {\varphi _{d3}}^{\left( {l,m} \right)}(x,z) = - \frac{{{\rm{i}}{a_m}\left( {k_0^{\left( m \right)}} \right)g}}{\omega } \cdot \\ \left\{ {{B_{01}}^{\left( m \right)}{\rm{exp[- i}}{k_0}^{\left( 1 \right)}\left( {x + B} \right){\rm{]}}{{\rm{Z}}^{\left( l \right)}}\left( {{k_0}^{\left( 1 \right)},z} \right) + } \right.\\ {B_{02}}^{\left( m \right)}{\rm{exp[- i}}{k_0}^{\left( 2 \right)}\left( {x + B} \right){\rm{]}}{{\rm{Z}}^{\left( l \right)}}\left( {{k_0}^{\left( 2 \right)},z} \right) + \\ \sum\limits_{n = 1}^{ + \infty } {A{B_{n1}}^{\left( m \right)}{\rm{exp[}}{k_n}^{\left( 1 \right)}\left( {x + B} \right){\rm{]}}{{\rm{Z}}^{\left( l \right)}}\left( {{k_n}^{\left( 1 \right)},z} \right)} + \\ \left. {\sum\limits_{n = 1}^{ + \infty } {{B_{n2}}^{\left( m \right)}{\rm{exp[}}{k_n}^{\left( 2 \right)}\left( {x + B} \right){\rm{]}}{{\rm{Z}}^{\left( l \right)}}\left( {{k_n}^{\left( 2 \right)},z} \right)} } \right\} \end{array} $ | (10) |
上述两式中的前两项分别为表面波模态和内波模态的传播项,后两项分别为表面波模态和内波模态的非传播项。考虑到非传播项的衰减性,本文展开式中n都取到有限项N,此时未知系数的个数为2(N+N+2)即4(N+1)。辐射边界及外域速度势的求解转化为求解级数展开式中的有限项系数,这些系数反映了外域中势函数的组成及其变化规律。
1.2.2 内域积分方程在内域上下两层流体区域内分别运用格林第二定理,可将问题转化为边界积分方程求解。对于上层流体有积分方程:
| $ \begin{align} & \alpha {{\varphi }_{d}}^{\left( 1,m \right)}+\iint\limits_{{{s}_{f}}}{{{G}^{(1)}}}\frac{\partial {{\varphi }_{d}}^{\left( 1,m \right)}}{\partial n}\text{d}S-\iint\limits_{{{s}_{f}}}{{{\varphi }_{d}}^{\left( 1 \right)}}\frac{\partial {{G}^{\left( 1,m \right)}}}{\partial n}\text{d}S+ \\ & \iint\limits_{{{s}_{l}}}{{{G}^{^{(1)}}}}\frac{\partial {{\varphi }_{d}}^{\left( 1,m \right)}}{\partial n}\text{d}S-\iint\limits_{{{s}_{l}}}{{{\varphi }_{d}}^{\left( 1 \right)}}\frac{\partial {{G}^{\left( 1,m \right)}}}{\partial n}\text{d}S+ \\ & \iint\limits_{{{s}_{cl}}}{{{G}^{(1)}}}\frac{\partial {{\varphi }_{d}}^{\left( 1,m \right)}}{\partial n}\text{d}S-\iint\limits_{{{s}_{cl}}}{{{\varphi }_{d}}^{\left( 1,m \right)}}\frac{\partial {{G}^{(1)}}}{\partial n}\text{d}S- \\ & \iint\limits_{{{s}_{b}}}{{{\varphi }_{d}}^{\left( 1,m \right)}}\frac{\partial {{G}^{(1)}}}{\partial n}\text{d}S=-\iint\limits_{{{s}_{b}}}{{{G}^{(1)}}}\frac{\partial {{\varphi }_{d}}^{\left( 1,m \right)}}{\partial n}\text{d}S \\ \end{align} $ | (11) |
对于下层流体有积分方程:
| $ \begin{align} & \alpha {{\varphi }_{d}}^{\left( 2,m \right)}+\iint\limits_{{{s}_{l}}}{{{G}^{^{(2)}}}}\frac{\partial {{\varphi }_{d}}^{\left( 2,m \right)}}{\partial n}\text{d}S-\iint\limits_{{{s}_{l}}}{{{\varphi }_{d}}^{\left( 2,m \right)}}\frac{\partial {{G}^{^{(2)}}}}{\partial n}\text{d}S+ \\ & \iint\limits_{{{s}_{c2}}}{{{G}^{^{(2)}}}}\frac{\partial {{\varphi }_{d}}^{\left( 2,m \right)}}{\partial n}\text{d}S-\iint\limits_{{{s}_{c2}}}{{{\varphi }_{d}}^{\left( 2,m \right)}}\frac{\partial {{G}^{^{(2)}}}}{\partial n}\text{d}S=0 \\ \end{align} $ | (12) |
式中α为固角系数,法线方向均以指出积分区域为正。上层流体取Rankine源为格林函数,下层流体取Rankine源和它关于海底的镜像作为格林函数,分别表示如下:
| $ {G^{\left( 1 \right)}} = \frac{1}{{2\pi }}\ln r;{G^{\left( 2 \right)}} = \frac{1}{{2\pi }}\left( {\ln r + \ln {r_1}} \right) $ |
在自由水面、物面和内界面积分时,未知量为速度势,而在辐射面积分时,通过辐射面上内、外域速度势及其导数的连续性,将未知量转化为外域速度势展开式中的系数A和B。最后通过在自由水面、物面、内界面及辐射面划分网格,对积分方程(11)、(12)分别进行离散可得两组线性方程组:
| $ \left( {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}&{{a_{14}}}&{{a_{15}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}&{{a_{24}}}&{{a_{25}}}\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}}&{{a_{34}}}&{{a_{35}}}\\ {{a_{41}}}&{{a_{42}}}&{{a_{43}}}&{{a_{44}}}&{{a_{45}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\{ {\varphi _d}^{\left( {1,n} \right)}\} {S_f}}\\ {\{ {\varphi _d}^{\left( {1,n} \right)}\} {S_b}}\\ {\{ {\varphi _d}^{\left( {1,n} \right)}\} {S_l}}\\ {{{\left\{ {\frac{{\partial {\varphi _d}^{\left( {1,n} \right)}}}{{\partial n}}} \right\}}_{{s_1}}}}\\ {\{ C\} } \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{b_1}}\\ {{b_2}}\\ {{b_3}}\\ {{b_4}} \end{array}} \right) $ | (13) |
| $ \left( {\begin{array}{*{20}{c}} {{e_{11}}}&{{e_{12}}}&{{e_{13}}}\\ {{e_{21}}}&{{e_{22}}}&{{e_{23}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{\left\{ {{\varphi _d}^{(2,n)}} \right\}}_S}_{_I}}\\ {{{\left\{ {\frac{{\partial {\varphi _d}^{\left( {2,n} \right)}}}{{\partial n}}} \right\}}_{{S_I}}}}\\ {\left\{ C \right\}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right) $ | (14) |
式中:{C}由外域速度势展开式中的系数A和B组成,与积分方程离散时辐射面上所取源点个数相等。通过上下层流体间内界面上速度和压力的连续性条件(5)和(6),联立方程组(13)和(14),可得最终求解方程组:
| $ \left( {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}&{{a_{14}}}&{{a_{15}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}&{{a_{24}}}&{{a_{25}}}\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}}&{{a_{34}}}&{{a_{35}}}\\ {{a_{41}}}&{{a_{42}}}&{{a_{43}}}&{{a_{44}}}&{{a_{45}}}\\ 0&\gamma &{{e_{11}}}&{\frac{{\gamma - 1}}{K}{e_{11}} + {e_{12}}}&{{e_{13}}}\\ 0&\gamma &{{e_{21}}}&{\frac{{\gamma - 1}}{K}{e_{21}} + {e_{22}}}&{{e_{23}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{\left\{ {{\varphi _d}^{\left( {1,n} \right)}} \right\}}_{{S_f}}}}\\ {{{\left\{ {{\varphi _d}^{\left( {1,n} \right)}} \right\}}_{{S_b}}}}\\ {{{\left\{ {{\varphi _d}^{\left( {1,n} \right)}} \right\}}_{{S_I}}}}\\ {{{\left\{ {\frac{{\partial {\varphi _d}^{\left( {1,n} \right)}}}{{\partial n}}} \right\}}_{{S_I}}}}\\ {\left\{ C \right\}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{b_1}}\\ {{b_2}}\\ {{b_3}}\\ {{b_4}}\\ 0\\ 0 \end{array}} \right) $ | (15) |
为验证所建立模型及求解过程的正确性,以水面固定箱型结构为例,计算了其波浪激振力以及波能流的守恒关系。上层流体水深h1=1.4 m、密度ρ1= 1 000 kg/m3,下层流体水深h2=0.6 m、密度ρ2=1 020 kg/m3,总水深h=2.0 m,方箱半宽B=0.5h=1.0 m,吃水T=0.5h=1.0 m。
2.1 网格划分及收敛性验证不同节点数的计算结果如图 2所示。

|
| 图2 不同节点数下收敛性分析 Figure 2 Convergence test for various node numbers |
图中纵坐标表示表面波模态波浪从左侧入射时,自由水面和内界面固定点x=8.5 m处波面升高随频率的变化情况。经比较可知,节点数为1 062时数值结果已经收敛。此时自由水面节点数为202,物面节点数为239,内界面节点数为343,上下辐射面分别为178和100。
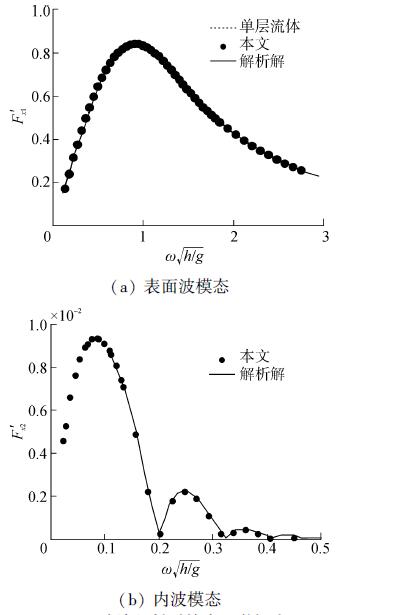
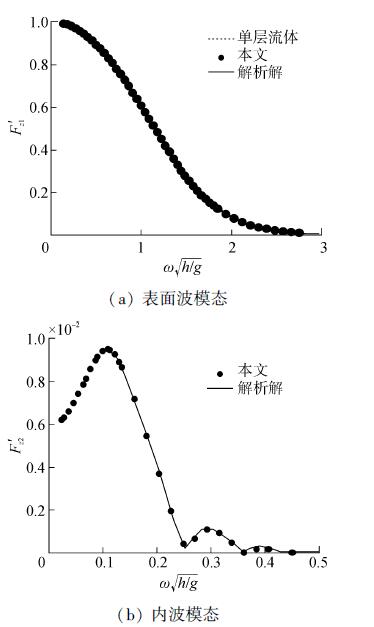
2.2 波浪激振力图 3~5分别给出了方箱在表面波模态和内波模态波浪入射时的无因次化激振力,其中水平波浪力和垂向波浪力均以ρ1ga0(m)h无因次化,绕y轴力矩以ρ1ga0(m)Bh无因次化。由数值计算结果与解析解[10]的对比可以看出,本文的计算结果与解析解吻合很好,验证了本文求解模型的正确性。
|
| 图3 波浪入射时的水平激振力 Figure 3 Horizontal exciting force under incident |
|
| 图4 波浪入射时的垂向激振力 Figure 4 Vertical exciting force under incident |

|
| 图5 波浪入射时的绕y轴力矩 Figure 5 Exciting force moment under incident |
由图可知,当入射波浪为表面波模态时,水平波浪力、垂向波浪力和绕y轴力矩都与单层流体中作用力基本重合,说明此时激振力基本不受分层效应的影响。当入射波浪为内波模态时,3个方向的作用力在低频处都有多个极值和零点,并且远小于表面波模态入射的激振力,随着频率的不断增大,激振力最后都减小为0。
2.3 能量守恒关系根据波能流守恒定理可得:
| $ \overline {\int\limits_{ - h}^0 {{\Phi _{2t}}{\Phi _{2x}}{\rm{d}}z} } = \overline {\int\limits_{ - h}^0 {{\Phi _{3t}}\Phi {3_{2x}}{\rm{d}}z} } $ | (16) |
式中:Φ2、Φ3分别为左外域和右外域中加入时间因子的速度势,将速度势表达式代入式(16)并化简可得到如下能量守恒关系式:
| $ \begin{array}{l} P = {P_m}^1{\left| {{A_{01}}^{\left( m \right)}} \right|^2} + {P_m}^2{\left| {{A_{02}}^{\left( m \right)}} \right|^2} + \\ {P_m}^1{\left| {{B_{01}}^{\left( m \right)}} \right|^2} + {P_m}^2\left| {{B_{02}}^{\left( m \right)}} \right| = 1\left( {m = 1或2} \right) \end{array} $ | (17) |
式中:m=1代表入射波浪模态为表面波模态,m=2代表入射波浪模态为内波模态。并有如下定义式:
| $ {P_m}^k = \frac{{{k_0}^{\left( k \right)}}}{{{k_0}^{\left( m \right)}}}\frac{{{{\int\limits_{ - h}^0 {{\rho _l}\left[{{Z^{\left( l \right)}}\left( {{k_0}^{\left( k \right)},z} \right)} \right]} }^2}{\rm{d}}z}}{{\int\limits_{ - h}^0 {{\rho _l}{{\left[{{Z^{\left( 2 \right)}}\left( {{k_0}^{\left( k \right)},z} \right)} \right]}^2}{\rm{d}}z} }} $ | (18) |
图 6两曲线分别为入射波为表面波模态和内波模态时,模型所计算出的能量P随无因次化频率的变化关系,可以看出所建立模型能很好地满足能量守恒关系式(16),进一步证明了模型的精确性。

|
| 图6 波能流守恒关系数值结果 Figure 6 Numerical results of wave energy flow conservation relation |
参考单层流体中反射、透射系数的定义[12],定义两层流体中反射系数Kr(l,m)和透射系数Kt(l,m):
| $ {k_r}^{\left( {l,m} \right)} = {\eta _r}/{\eta _i} $ | (19) |
| $ {k_t}^{\left( {l,m} \right)} = {\eta _t}/{\eta _i} $ | (20) |
式中:l=1,2分别代表自由水面和内界面,m=1,2分别代表反射(透射)波浪为表面波模态和内波模态;ηr、ηt和ηi分别为反射波、透射波和入射波波高。入射波为表面波模态时,ηi取自由表面入射波波高;入射波为内波模态时,ηi取内界面入射波波高。
虽然自由水面和内界面上都存在两种模态的波浪,但是由于自由水面上以表面波模态波浪成分为主,内界面上以内波模态波浪成分为主,因此在后续分析中,只给出自由水面上表面波模态波浪的反透射系数和内界面上内波模态波浪的反透射系数。其余系数可通过关系式(2)确定。
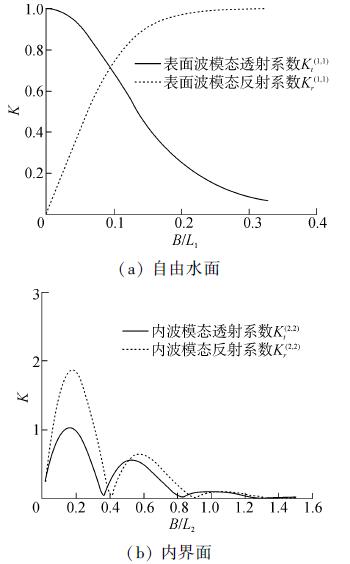
图 7(a)给出了表面波模态波浪入射时,自由水面上表面波模态的反射和透射系数,其中L1为表面波模态波长。可以看出,随波长的减小自由水面上表面波模态反射系数趋近于1,透射系数趋近于0,趋势与单层流体一致。图 7(b)给出了表面波模态波浪入射时,内界面上内波模态波浪的反射和透射系数,其中L2为内波模态波长。
|
| 图7 入射波为表面波模态时自由水面及内界面上的反射和透射系数 Figure 7 Reflection and transmission coefficients on free-surface and interface under incident surface-wave mode |
由图 7可知,表面波模态的入射波浪与结构物作用后将在内界面上产生较大幅度的波动,最高可接近自由表面入射波浪波幅的2倍左右。这是因为两层流体间密度差很小,其恢复力很小,相当于将分层介质置于微重力场,流体受到很小的扰动就会偏离其平衡位置而产生“轩然大波”,但其对于能量的贡献较小。从图中还可以看出随着入射波浪频率的变化,反射、透射系数有多个零点,即在某些频率处,内界面上没有内波模态的反射波或透射波。此外,自由水面上表面波模态的反射系数和透射系数变化趋势(图 7(a)),当结构位于上层流体时,内界面上内波模态的反射系数和透射系数的变化趋势则相同。
图 8(a)给出了内波模态波浪入射时,自由水面上表面波模态的反射和透射系数。由图可知,当内波模态波浪入射时,入射波与结构物作用后,自由水面仅有非常微小的波动,所引起的波面升高基本可以忽略。图 8(b)给出了内波模态波浪入射时,内界面上内波模态波浪的反射和透射系数。由图可知,由于本文所研究的结构物只位于上层流体,因此内界面上内波模态透射系数很大,接近于1,反射系数则很小,高频时趋于0。

|
| 图8 入射波为内波模态时自由水面及内界面上的反射和透射系数 Figure 8 Reflection and transmission coefficients on free-surface and interface under incident internal-wave mode |
根据图 7、8的结果可知,表面波模态入射时自由水面上表面波模态反透射特性与单层流体趋于一致;内波模态入射时自由水面上表面波模态反透射系数都很小接近于0,内界面上内波模态透射系数很大接近于1,反射系数则很小。因此下文仅研究表面波模态入射时,密度比、水深比及方箱宽度等参数的变化对内界面上内波模态反透射系数的影响规律。
图 9为改变上下层密度比、入射波浪为表面波模态时,内界面上内波模态的反射和透射系数。由图可以看出,随着下层流体密度的增大,内界面反射和透射系数的最大值都减小,这是因为随着密度差的增大,恢复力相应增大,内界面处抗扰动能力增强。同时,从结果中可以看出反射和透射系数零点的位置并不随密度比的改变而改变,只与B/L2有关。反射系数零点出现在B/L2约为0.42、0.90和1.35的位置,透射系数零点出现在B/L2约为0.37、0.84和1.30的位置。

|
| 图9 入射波为表面波模态时不同密度比下内界面反射和透射系数 Figure 9 Reflection and transmission coefficients on interface with different density ration, under incident sur- face-wave mode |
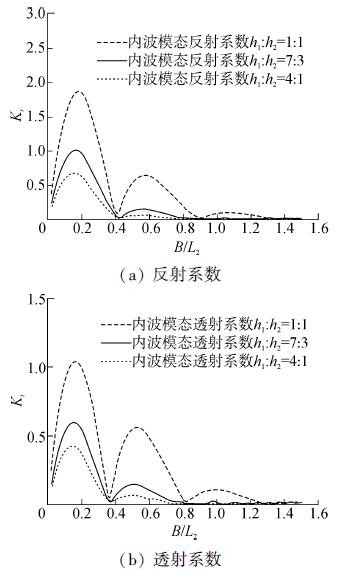
图 10为改变上下层水深比、入射波浪为表面波模态时,内界面内波模态的反透射系数。由图可知,结构物离内界面越近,则波浪入射后内界面的扰动越大,即反射和透射系数越大。内界面的位置同样不影响反射和透射系数零点的位置。
|
| 图10 入射波为表面波模态时不同水深比下内界面反射 和透射系数 Figure 10 Reflection and transmission coefficients on interface with different water depth ration, under incident surface-wave mode |
图 11为改变方箱宽度、入射波为表面波模态时,内界面内波模态的反射和透射系数。由图可知随结构物宽度的增加,内界面内波模态的反射和透射系数在低频时变化不大,高频时明显增大。但反射系数和透射系数的零点位置都几乎不发生变化。

|
| 图11 入射波为表面波模态时不同方箱宽度下内界面反射 和透射系数 Figure 11 Reflection and transmission coefficients on interface with different box width, under incident surface- wave mode |
本文基于海洋密度层化的两层流体简化模型,基于线性势流理论研究了两层流体中箱型结构对波浪的反射和透射特性,得到结论如下:
1) 无论入射波为何种模态,随着入射频率的变化,在某些频率处内界面上的扰动为零,零点的位置只与B/L2的值相关,而与上下层密度比、水深比及箱体宽度没有明显关系。并且表面波模态波浪入射时,内界面上内波模态波浪的反射和透射系数的变化趋势基本相同;
2) 内波模态入射波浪与结构物作用后,自由水面将产生非常微小的扰动;表面波模态入射波浪与结构物作用后,在内界面上则会产生大幅扰动,在高频区域扰动趋于零。
| [1] | 方欣华, 杜涛. 海洋内波基础和中国海内波[M]. 青岛: 中国海洋大学出版社, 2005: 1 -19. |
| [2] | LAMB H. Hydrodynamics[M].6th ed. Cambridge: Cambridge University Press, 1993: 1 -30. |
| [3] |
尤云祥, 缪国平, 程建生, 等. 两层流体中水波在垂直薄板上的反射与透射[J].
力学学报, 2005, 37(5): 529–541.
Yunxiang, MIAO Guoping, CHENG Jiansheng, et al. Reflection and transmission of water waves past a vertical thin barrier in a two-layer fluid[J]. Chinese journal of theoretical and applied mechanics, 2005, 37(5): 529–541. |
| [4] | DHILLON H, BANERJEA S, MANDAL B N. Wave scattering by a thin vertical barrier in a two-layer fluid[J]. International journal of engineering science, 2014, 78: 73–88. |
| [5] | BEHERA H, SAHOO T. Gravity wave interaction with porous structures in two-layer fluid[J]. Journal of engineering mathematics, 2014, 87(1): 73–97. |
| [6] | KASHIWAGI M, TEN I, YASUNAGA M. Hydrodynamics of a body floating in a two-layer fluid of finite depth. Part 2. diffraction problem and wave-induced motions[J]. Journal of marine science and technology, 2006, 11(3): 150-164. |
| [7] | NGUYEN T C, YEUNG R W. Unsteady three-dimensional sources for a two-layer fluid of finite depth and their applications[J]. Journal of engineering mathematics, 2011, 70(1/2/3): 67–91. |
| [8] | GOU Ying, CHEN Xinjia, TENG Bin. A time-domain boundary element method for wave diffraction in a two-layer fluid[J]. Journal of applied mathematics, 2012: 686824. |
| [9] | 石强. 分层流体中浮式结构物水动力特性研究[D]. 上海: 上海交通大学, 2008: 55-89. |
| [10] |
石强, 尤云祥, 缪国平. 两层流体中矩形箱浮体的附加质量和阻尼系数[J].
海洋工程, 2007, 25(2): 33–42.
SHI Qiang, YOU Yunxiang, MIAO Guoping. Added mass and damping of a floating rectangular box in a two-layer fluid[J]. The ocean engineering, 2007, 25(2): 33–42. |
| [11] | ZHANG Xinshu, BANDYK P. On two-dimensional moonpool resonance for twin bodies in a two-layer fluid[J]. Applied ocean research, 2013, 40: 1–13. |
| [12] | 李玉成, 滕斌. 波浪对海上建筑物的作用[M]. 北京: 海洋出版社, 2002: 12 -74. |



