2. Nanjing Institute of Agricultural Mechanization Ministry of Agriculture, Nanjing 210094, China;
3. Nanjing Sanai industrial co., LTD, Nanjing 211100, China
电子皮带秤是一种散状物料连续累计称量设备,是大宗散状物料贸易运输过程中进行称重计量的最佳方式,广泛应用于各种工业原、燃料集散地。如今,市场对电子皮带秤的精度要求越来越高。皮带秤为了提高精度提出了各种改进手段,如改善皮带秤机械结构、采用软件误差补偿等。随着技术发展,越来越多的皮带秤研究者发现,采用多个单托辊承载器组成多托辊组合承载将大大提高称重精度,而阵列式皮带秤就是一种采用多托辊组合单点悬浮承载、多称重传感器分布的高精度电子皮带秤[1]。影响皮带秤精度的原因有很多,其中最主要因素是称重力误差[2]。皮带秤称重力误差研究颇多,美国Thayer衡器公司的F.Hyer博士使用卡氏定理导出较为粗略的误差公式[2-3];Colijn从简支梁出发导出了较为精确的误差公式,但仅限于单托辊皮带秤;Knut在采用叠加原理对误差模型进行推导,并用试验对误差比例系数进行调节以减少实际过程中水平力影响,但未推广到多托辊皮带秤[3]。也有些研究尝试利用有限单元法进行误差研究,但至今未见显著成效[4-5]。
然而,有效的皮带秤精确补偿,除了建立精确的力学模型外,还需依靠可靠的软件误差补偿技术。软件误差补偿技术是提高皮带秤称重精度及其对环境适应能力的重要途径。以现有力学模型为基础,采用高效的测量方法对误差贡献最大的几个因素进行检测、获取大量数据,再基于大量数据采用合适的建模方法建立皮带秤称重与各关键因素之间的统计数学模型。对于难以检测到的变量可通过软测量方法获得。诸多研究已将人工神经网络、支持向量机等监督学习方法应用到称重误差补偿中:严洁等将BP神经网络应用到混凝土搅拌站的称重系统中,对其称重传感器的输入输出进行非线性补偿[6];林海军等提出一种多传感器信息融合的汽车衡误差补偿,其实质就是利用径向基函数神经网络(RBF)对其称重传感器输入以及一些影响称重误差因素进行非线性补偿,减少汽车衡线性度、偏载等误差[7];庄育锋等将BP神经网络引入到微量药品动态称重系统中,同时采用L-M算法进行网络训练以提高模型补偿性能及收敛速度。但是,上述称重误差补偿模型的输入和输出都是瞬时对应的、模型不需对输入进行时间累积的运算。而皮带秤的瞬时称重量是未知的,只有累计称重量是已知的,因此皮带秤的称重误差补偿模型的输入依赖于持续一定时间的输入过程,需要将输入在时域上有所扩展,而输出不变[8]。
针对上述问题,本文首先对电子皮带秤的称重力误差模型机理研究,结合梁理论、从能量角度出发,引入弹性理论的变分原理推导出单托辊皮带秤称重力误差,再在此基础上,得到阵列式皮带秤称重力误差模型——内力理论;然后对过程神经网络进行改进、集成过程神经网络和极限学习机提出一种过程极限学习机,并结合阵列式皮带秤“内力理论”提出一种基于过程极限学习机的阵列式皮带秤误差补偿模型;最后以试验对本文研究结果进行验证。
1 阵列式皮带秤的“内力理论”电子皮带秤是用于只有一个称重托辊的单托辊皮带秤,影响电子皮带秤称重力误差的因素有很多,最主要的是“皮带效应”。“皮带效应”是指由输送带张力、称重托辊非准直度、输送带刚度、输送带自重等引起的称重力测量误差[2, 9],因此本研究需要建立称重力误差与输送带张力、称重托辊非准直度、输送带刚度、称重载荷等参数之间的数学模型。在研究皮带秤称重误差时,由于皮带秤截面惯性矩变化较小,故大多数研究都是基于梁理论进行的[3, 10-11]。本文首先在梁理论的基础上,采用最小位能原理和变分原理对单托辊皮带秤误差模型进行推导,然后将之推广到阵列式皮带秤中得到阵列式皮带秤的误差补偿模型——“内力理论”。
1.1 单托辊皮带秤误差模型的简化单托辊皮带秤是最简单、最普遍的电子皮带秤,其梁理论模型如图 1。

|
| 图1 皮带秤梁理论模型 Figure 1 Beam theory model of belt weigher |
本文所有研究均以皮带秤正常稳定运行为准,正常稳定运行时,输送带无跑偏,故由于运动产生的横向载荷很小、可忽略。在此基础上,根据文献[2-3, 11],作出以下合理假设:
1) 皮带秤为一根截面惯性矩不变、无限长、并由无数等距离的支点所支撑的梁;
2) 托辊直径是可以忽略不计的;
3) 皮带秤上的载荷是均匀的;
4) 皮带秤的落料点离称重托辊足够远。
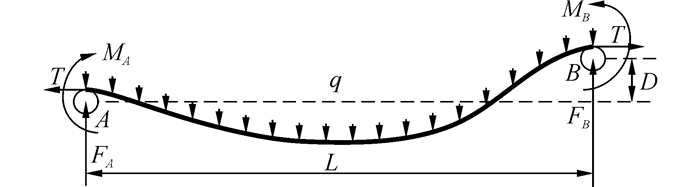
基于以上假设,单托辊皮带秤的误差分析可简化为只对AB段进行。如图 2,单托辊皮带秤的称重力误差即为B点实际所受载荷QB与未出现托辊非准直度时(D=0)B点的理想载荷QB0之间的差值。
|
| 图2 AB称重段载荷 Figure 2 Load diagram of AB segment in belt weigher |
如图 3,以A点为原点建立笛卡尔坐标系,研究从能量的角度对AB段进行力学分析,以求出A、B点受力载荷。

|
| 图3 AB段挠度曲线 Figure 3 Deflection curve of AB segment |
由平衡条件得AB段的弯矩M(x)及应变能V为:
| $ M\left( x \right) = EI\omega ''\left( x \right) = - \frac{1}{2}q{x^2} + {F_A}x + T\omega \left( x \right) + {M_A} $ | (1) |
式中:E为输送带的弹性模量;I为输送带的截面惯性矩。
| $ V = \int\limits_0^L {\frac{1}{2}\frac{{{M^2}\left( x \right)}}{{EI}}} dx $ | (2) |
外力对AB段做的功W:
| $ W = \int\limits_0^L { - q\omega \left( x \right)dx + \left( { - T} \right) \bullet \lambda {\kern 1pt} } $ | (3) |
其中,λ为梁长度的变化且$\lambda = \int\limits_0^L {\left( {ds - dx} \right)} \approx \frac{1}{2}\int\limits_0^L {\left( {\omega '} \right){\kern 1pt} dx{\kern 1pt} } $,综合二者可得出AB段的总位能Π为:
| $ \begin{array}{l} \prod = V - W = \\ \int\limits_0^L {\frac{1}{2}\frac{{{M^2}\left( x \right)}}{{EI}}} dx - \int\limits_0^L { - q \bullet \omega \left( x \right)dx + \left( { - T} \right) \bullet \lambda {\kern 1pt} } = \\ \int\limits_0^L {\left[ {\frac{1}{2}EI{{\left( {\omega ''} \right)}^2} + \frac{1}{2}T \bullet {{\left( {\omega '} \right)}^2} + q \bullet \omega \left( x \right)} \right]} {\kern 1pt} {\kern 1pt} dx \end{array} $ | (4) |
由最小位能原理可得:
| $ \begin{array}{l} \delta \prod = \\ \delta \left\{ {\int\limits_0^L {\left[ {\frac{1}{2}EI{{\left( {\omega ''} \right)}^2} + \frac{1}{2}T \bullet {{\left( {\omega '} \right)}^2} + q \bullet \omega \left( x \right)} \right]} {\kern 1pt} {\kern 1pt} dx} \right\} = 0 \end{array} $ | (5) |
另外,梁的边界条件为已知,即
| $ \omega \left( 0 \right) = 0,\omega \left( L \right) = D,\omega '\left( 0 \right) = 0,\omega '\left( L \right) = 0 $ | (6) |
根据固定边界问题的变分原理可由式(5)、(6)得函数ω(x)应满足的欧拉-泊松微分方程:
| $ \omega '''' - \frac{T}{{EI}}\omega '' = - \frac{q}{{EI}} $ | (7) |
其通解为
| $ \left\{ \begin{array}{l} \omega \left( x \right) = {C_1} + {C_2}x + {C_3}{e^{\sqrt {\frac{T}{{EI}}x} }} + {C_4}{e^{ - \sqrt {\frac{T}{{EI}}x} }} + \frac{{q{x^2}}}{{2T}}\\ \omega '\left( x \right) = {C_2} + \sqrt {\frac{T}{{EI}}} {C_3}{e^{\sqrt {\frac{T}{{EI}}x} }} - \sqrt {\frac{T}{{EI}}} {C_4}{e^{ - \sqrt {\frac{T}{{EI}}x} }} + \frac{{qx}}{T}\\ \omega ''\left( x \right) = \frac{T}{{EI}}{C_3}{e^{\sqrt {\frac{T}{{EI}}x} }} + \frac{T}{{EI}}{C_4}{e^{ - \sqrt {\frac{T}{{EI}}x} }} + \frac{q}{T} \end{array} \right. $ | (8) |
将式(6)代入式(8)中解得
| $ {C_2} = - \frac{{qL}}{{2T}} + \frac{{\sqrt {\frac{T}{{EI}}} D}}{{\sqrt {\frac{T}{{EI}}} L + 2\left( {\frac{{2 - {e^{\sqrt {\frac{T}{{EI}}L} }} - {e^{ - \sqrt {\frac{T}{{EI}}L} }}}}{{{e^{\sqrt {\frac{T}{{EI}}L} }} - {e^{ - \sqrt {\frac{T}{{EI}}L} }}}}} \right)}} $ | (9) |
又因为式(1)对于∀x∈[0,L]恒成立,将式(8)、(9)代入式(1)中得
| $ \begin{array}{l} {F_A} + T{C_2} = 0 \Rightarrow {F_A} = \frac{1}{2}qL - \frac{{TD}}{{L - \frac{{2\sqrt {EI} }}{{\sqrt T }}\tanh \left( {\frac{1}{2}\sqrt {\frac{T}{{EI}}L} } \right)}}\\ \Rightarrow {F_B} = \frac{1}{2}qL + \frac{{TD}}{{L - \frac{{2\sqrt {EI} }}{{\sqrt T }}\tanh \left( {\frac{1}{2}\sqrt {\frac{T}{{EI}}L} } \right)}} \end{array} $ | (10) |
由于AB段与BC段对称关系,称重托辊B的载荷QB为
| $ {Q_B} = qL + \frac{{2TD}}{{L - \frac{{2\sqrt {EI} }}{{\sqrt T }}\tanh \left( {\frac{1}{2}\sqrt {\frac{T}{{EI}}L} } \right)}} $ | (11) |
最后得到称重力误差△Q为
| $ \begin{array}{l} \Delta Q = \frac{{2TD}}{{L - \frac{{2\sqrt {EI} }}{{\sqrt T }}\tanh \left( {\frac{1}{2}\sqrt {\frac{T}{{EI}}L} } \right)}} = \\ 2TD \bullet k\left( {T,L,\left( {EI} \right)} \right) \end{array} $ | (12) |
由式(12)可以得到称重力误差是关于皮带秤托辊非准直度D、输送带张力T、输送带刚度EI以及托辊间距L的一个多元非线性函数,只有当输送带张力T固定时,称重力误差△Q与托辊的非准直度D成正比关系(从推导过程还可看出,当皮带秤具有较小倾角时,该模型依旧成立)。
1.3 阵列式皮带秤的“内力理论”如图 4,阵列式皮带秤是由若干个对垂直方向力敏感的单点悬浮称重单元组成,每个称重单元由两个称重托辊和一个单点悬浮称重传感器组成,两个称重托辊刚性连接到同一个单点悬浮称重传感器,每个称重单元等价于两个单托辊称重单元的叠加。因此,在得到单托辊皮带秤称重力误差后,可将其结论扩展到阵列式皮带秤中去。称重段每两个托辊组成一个单点悬浮称重单元,共有N有单点悬浮称重单元,N个称重单元都安装在输送带运动方向上张力变化很小的一段[12],因此可视托辊组内输送带张力一致。

|
| 图4 阵列式皮带秤梁理论模型 Figure 4 Beam theory model of array belt weigher |
定义第i个称重单元左边托辊受力Fi-、非准直度为Di;右边受力Fi+、非准直度为Di,得
| $ \left\{ \begin{array}{l} F_1^ - = 2T{D_1} \bullet k\left( {T,L,\left( {EI} \right)} \right) + qL\\ F_i^ - = 2T\left( {{D_i} - {D_{i - 1}}} \right) \bullet k\left( {T,L,\left( {EI} \right)} \right) + qL,\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2 \le i \le N\\ F_i^ + = 2T\left( {{D_i} - {D_{i + 1}}} \right) \bullet k\left( {T,L,\left( {EI} \right)} \right) + qL,\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2 \le i \le N - 1\\ F_N^ + = 2T{D_N} \bullet k\left( {T,L,\left( {EI} \right)} \right) + qL \end{array} \right. $ | (13) |
| $ \begin{array}{l} \sum\limits_{i = 1}^N {\Delta {Q_i}} = \left( {F_1^ - + F_1^ + } \right) + \cdots + \left( {F_N^ - + F_N^ + } \right) - 2NqL = \\ 2T\left( {{D_1} + {D_N}} \right) \bullet k\left( {T,L,\left( {EI} \right)} \right) = \\ \frac{{2T\left( {{D_1} + {D_N}} \right)}}{{L - \frac{{2\sqrt {EI} }}{{\sqrt T }}\tanh \left( {\frac{1}{2}\sqrt {\frac{T}{{ET}}L} } \right)}} \end{array} $ | (14) |
从上式可以得出,若将阵列式皮带秤N个称重单元结果累加,可消除“皮带效应”对中间内部所有称重单元称重力误差的影响,本文称之为阵列式皮带秤的“内力理论”。该理论表明:阵列式皮带秤工作时可忽略中间内部称重托辊组的输送带张力和非准直度对测量精度影响,只需对阵列式皮带秤两端称重托辊组进行输送带张力和非准直度的误差补偿即可消除“皮带效应”、大大提高皮带秤的称重精度。因此,若采用“内力理论”进行称重误差补偿,不但可以降低阵列式皮带秤称重托辊同心度(传统≤0.2 mm)和秤架刚度的要求、节约设备制造和安装成本,而且还可大大降低补偿模型输入数据的特征维度,从而减少需要检测的参数、降低模型复杂度、提高模型的误差补偿性能。
2 基于过程极限学习机的阵列式皮带秤累计称重误差补偿皮带秤每个称重单元的称重原理使用的是累加法,即在运行时,每当输送带移动一段路程d就测量称重单元上载荷值Q一次。一段时间后,输送带运行了nd行程,则这段时间内累计流量$\tilde Q = \sum\limits_{k = 1}^n {{Q_k}} $(Qk为第k段行程的称重单元载荷,亦称之为实时脉冲载荷)。因此最理想的误差补偿方法是建立一误差补偿模型Qk′=Q(xk)(xk为模型输入向量,包括各个称重单元实时数据以及各个误差影响因素的实时检测值),对Qk进行实时补偿计算,然后得到补偿后的累计流量$\tilde Q' = \sum\limits_{i = 1}^n {Q\left( {{x_k}} \right)} $。现有的误差补偿大都是采用类似式(14)的理论数学公式建立线性或非线性回归模型。然而,由于皮带秤工作现场环境非常复杂,传统基于理论公式线性或非线性回归分析的误差补偿很难考虑一些隐含设备参数或环境参数对皮带秤精度的动态影响。此外,由于试验条件限制,试验过程中只能得到累计称重量的真实准确值,传统的监督学习方法很难获得误差补偿模型Qk′=Q(xk),正如引言中所说的,误差补偿模型的输出依赖于持续一定时间的输入过程。所以,为了消除一些隐含参数对称重精度的影响、避免直接获得补偿模型Qk′=Qxk,在上述得到式(12)、(14)的基础上提出基于过程极限学习机的皮带秤误差实时补偿模型。
2.1 过程神经网络过程神经网络(process neural network,PNN)与传统神经网络最大的区别是时间积分(或聚合)。传统神经网络的输入和输出都是静态的量或都是动态与时间相关的量,而PNN的输入是与时间相关的量,而输出是静态的量。具体地,在网络结构上,PNN与传统神经网络不同之处在于PNN采用过程神经元替代传统的神经元。
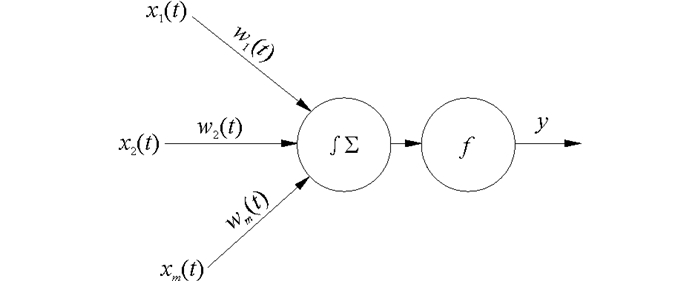
过程神经元由加权、聚合和激励三部分组成[8],单个过程神经元如图 5。
|
| 图5 过程神经元 Figure 5 Process neural |
输出与输入之间的数学关系为:$y = f\left( {\int_0^T {\left( {\sum\limits_{i = 1}^m {{x_i}\left( t \right){w_i}\left( t \right)} } \right)dt - \theta } } \right)$。与传统神经网络相似,PNN也可以分前向型和反馈型网络。本文研究基于前向型PNN的误差补偿模型。
2.2 过程神经网络极限学习机(extreme learning machine)是一种神经网络的训练算法,其预测网络模型为三层前向型反馈神经网络,包括输入层、隐含层和输出层[13]。对任意给定的${\tilde N}$个不同的样本(xi,ti),i=1,...,${\tilde N}$,其中,xi=[xi1,xi2,...,xip]T∈Rp,ti=[ti1,ti2,...,tiq]T∈Rq,其带有NH个隐含层单元的单层前向型反馈神经网络模型的输入和输出之间理想关系可表示为[19]
| $ \sum\limits_{i = 1}^{{N_H}} {{\beta _i}f\left( {w_i^T \bullet {x_j} + {b_i}} \right)} = {y_j},j = 1,2, \cdots ,\tilde N $ | (15) |
其中,wi=[wi1,wi2,...,wip]T为从输入层到隐含层第i个单元的权值向量,βi=[βi1,βi2,...,βiq]T为从隐含层第i个单元到输出层的权值向量,bi为隐含层第i个单元的阈值,f(·)为隐含层激励函数且无限可微。模型的训练目标是对于给定的输入样本能够以零误差逼近预测目标$\sum\limits_{i = 1} {\left\| {{y_i} - {t_i}} \right\| = 0} $,即寻找一组W=[w1,...,wNH]、β、b=[b1,...,bNH]以使得
| $ H\beta = T $ | (16) |
其中,$\begin{array}{l} H\left( {{w_1}, \cdots ,{w_{{N_H}}},{b_1}, \cdots ,{b_{{N_H}}},{x_1}, \cdots ,{x_{\tilde N}}} \right) = \\ {\left[ {\begin{array}{*{20}{c}} {f\left( {w_1^T \bullet {x_1} + {b_1}} \right)}& \cdots &{f\left( {w_{{N_H}}^T \bullet {x_1} + {b_{{N_H}}}} \right)}\\ \vdots & \cdots & \vdots \\ {f\left( {w_1^T \bullet {x_{\tilde N}} + {b_1}} \right)}& \cdots &{f\left( {w_{{N_H}}^T \bullet {x_{\tilde N}} + {b_{{N_H}}}} \right)} \end{array}} \right]_{\tilde N \times {N_H}}},\\ \beta = \left[ {\beta _1^T \cdots \beta _{{N_H}}^T} \right]_{{N_H} \times q}^T,T = \left[ {t_1^T \cdots t_N^T} \right]_{\tilde N \times q}^T. \end{array}$。
ELM的训练思想是,在W、b随机给定的情况下,将模型训练过程从非线性优化问题转化为求解线性方程组问题。故其训练过程可总结为如下几个步骤:
1) 随机初始化输入层到隐含层的权值和阈值W、b;
2) 对任意给定的${\tilde N}$个不同的样本(xi,ti),i=1,...,${\tilde N}$,选择合适的隐含层激励函数f(·),然后求解隐含层输出矩阵H[15-16];
3) 求解出隐含层输出矩阵H的Moor-Penrose广义逆H+,并求解出隐含层到输出层的权值$\hat \beta = {H^ + }T$,完成ELM神经网络训练。
此外,由矩阵分析理论可知,$\hat \beta = {H^ + }T$是式(16)唯一的极小范数解,即$\left\| {\hat \beta } \right\| = \mathop {\min }\limits_{H\beta = T} \left\| \beta \right\|$,故而采用ELM训练的神经网络模型不仅能达到最小训练误差,而且VC维相对较低、有很好的泛化性能[17]。
2.3 基于过程神经网络误差补偿模型的建立采用神经网络建立误差补偿模型前,首先依据式(12)、(14)的结论,选择相关的物理量并对其进行实时检测,所检测到的数据作为模型的样本输入,然后以物料总重量为模型输出。依托南京三埃工控股份有限公司QPS-皮带秤全性能试验中心,皮带秤的每次误差补偿试验都能得到各个传感器采样周期为△t的实时脉冲载荷数据Qk、各个环境参数的实时采集数据以及试验中物料的累计实际称重量${{\tilde Q}_0}$(${{\tilde Q}_0} = \sum\limits_{k = 1}^n {{Q_{0,k}},{Q_{0,k}}} $为每个脉冲载荷的实际真实值)。但由于试验条件限制,无法获知每个脉冲载荷的实际真实值Q0,k,且每次试验时间长度和试验物料总重量Q0都不一定一样。因此,研究只能在输出为Q0的样本数据基础上,建立误差补偿模型。
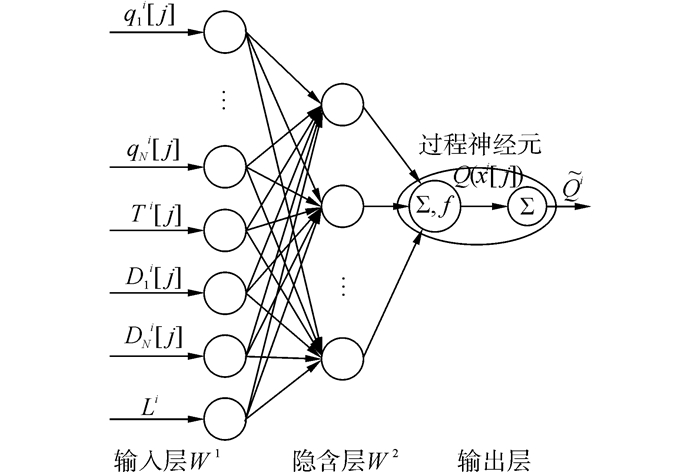
令第i次试验数据集${D^i} = \left\{ {{X^i},\tilde Q_0^i} \right\}$,其中Xi={xi[1],xi[2],...,xi[ki]},ki∈N,i=1,2,...,n为第i次试验的输入向量序列,该序列为Ti=(ki-1)·△t时间内多个传感器测量所得到的时间序列。xi[j]=q1i[j],q2i[j],...,qNi[j],Ti[j],D1i[j],DNi[j],Li,[j]=1,2,...,ki为第i次试验中第[j]-1·△t时刻N个称重单元称重数据、称重区域输送带张力、第一个与最后一个托辊的非准直度以及皮带秤相邻托辊间的间隔长度所组成的输入向量;${\tilde Q_0^i}$为第i次试验的理想输出。很显然,输入为与时间相关的量、输出为静态的量,而传统神经网络是难以基于这样的样本建立模型,因此本文引入PNN进行误差补偿。考虑到称重误差补偿实时性的问题,本文对传统PNN进行改进、提出如下改进型PNN如图 6。
|
| 图6 基于过程神经网络的误差补偿模型 Figure 6 Error compensation model based on process neural network |
该模型结构简单,适合实时误差补偿,与传统三层前向型PNN不同在于:
1) 网络中,所有权值W1、W2均为静态值,非与时间相关的量;
2) 网络中所采用的过程神经元与传统过程神经元计算次序相反,所采用的过程神经元先进行非线性映射再进行聚合运算(累加运算)。
3) 网络中,输入层和隐含层都采用传统神经元,只有输出层采用过程神经元。
第i次试验的输入Xi={xi[1],...,xi[ki]},ki∈N,其输出${{\tilde Q}^i}$表示为:
| $ \begin{array}{l} {{\tilde Q}^i} = I_{{k_i}}^T \bullet Q\left( {{X^i}} \right) = \\ \sum\limits_{j = 1}^{{k_i}} {g\left( {{W^2}F\left( {{W^1}{x^i}\left[ j \right] + {b^1}} \right) + {b^2}} \right)} \end{array} $ | (17) |
式中:b1、b2分别为隐含层和输入层神经元的阈值,f(·)为隐含层神经元的映射函数,采用Sigmoid函数;g(·)为输出层神经元的映射函数,采用线性函数;Q(xi[j])为脉冲载荷的补偿输出。由式(17)得n次试验的样本输入与模型输出关系为
| $ \left[ \begin{array}{c} \sum\limits_{j = 1}^{{k_1}} {g\left( {{W^2}F\left( {{W^1}{x^1}\left[ j \right] + {b^1}} \right) + {b^2}} \right)} \\ \vdots \\ \sum\limits_{j = 1}^{{k_n}} {g\left( {{W^2}F\left( {{W^1}{x^{{k_n}}}\left[ j \right] + {b^1}} \right) + {b^2}} \right)} \end{array} \right] $ | (18) |
同时还可得到模型的经验误差ED为
| $ {E_D} = e_D^H{e_D} = {\left[ \begin{array}{c} {{\tilde Q}^1} - \tilde Q_0^1\\ \vdots \\ {{\tilde Q}^n} - \tilde Q_0^n \end{array} \right]^H}\left[ \begin{array}{c} {{\tilde Q}^1} - \tilde Q_0^1\\ \vdots \\ {{\tilde Q}^n} - \tilde Q_0^n \end{array} \right] $ | (19) |
模型的训练目标是寻求最优的网络权值和阈值使得经验误差ED最小,即minED(W1,W2,b1,b2)。
2.4 基于过程极限学习机的误差补偿模型针对PNN的训练,许多文献都提出训练算法,但大都数是基于BP算法[18-19]。然采用BP算法或改进型BP训练PNN的过程过于复杂、收敛慢且泛化性能一般[20],故而本文将ELM引入到PNN中,提出过程极限学习机(process extreme learning machine)。该模型采用ELM算法进行网络训练,输出层神经元的映射函数g(·)采用线性函数(可以证明当输出层单元的激励函数是线性时,聚合和映射运算的次序先后是等价的),输出层阈值b2为0,式(18)可化简为
| $ \begin{array}{*{20}{l}} \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{{\tilde Q}^1}}\\ \vdots \\ {{{\tilde Q}^n}} \end{array}} \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\sum\limits_{j = 1}^{{k_1}} {{W^2}F\left( {{W^1}{x^1}\left[ j \right] + {b^1}} \right)} }\\ \vdots \\ {\sum\limits_{j = 1}^{{k_n}} {{W^2}F\left( {{W^1}{x^{{k_n}}}\left[ j \right] + {b^1}} \right)} } \end{array}} \right]{\rm{ = }}\\ \left[ {\begin{array}{*{20}{c}} {\sum\limits_{j = 1}^{{k_1}} {\sum\limits_{i = 1}^{{N_H}} {{\beta _i}f\left( {w_i^T{x^1}\left[ j \right] + b_i^1} \right)} } }\\ \vdots \\ {\sum\limits_{j = 1}^{{k_n}} {\sum\limits_{i = 1}^{{N_H}} {{\beta _i}f\left( {w_i^T{x^n}\left[ j \right] + b_i^1} \right)} } } \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^{{N_H}} {\sum\limits_{j = 1}^{{k_1}} {{\beta _i}f\left( {w_i^T{x^1}\left[ j \right] + b_i^1} \right)} } }\\ \vdots \\ {\sum\limits_{i = 1}^{{N_H}} {\sum\limits_{j = 1}^{{k_n}} {{\beta _i}f\left( {w_i^T{x^1}\left[ j \right] + b_i^1} \right)} } } \end{array}} \right] = \end{array}\\ {\left[ {\begin{array}{*{20}{c}} {\sum\limits_{j = 1}^{{k_1}} {f\left( {w_1^T{x^1}\left[ j \right] + b_1^1} \right)} }& \cdots &{\sum\limits_{j = 1}^{{k_1}} {f\left( {w_{{N_H}}^T{x^1}\left[ j \right] + b_{{N_H}}^1} \right)} }\\ \vdots & \vdots & \vdots \\ {\sum\limits_{j = 1}^{{k_n}} {f\left( {w_1^T{x^{{k_n}}}\left[ j \right] + b_1^1} \right)} }& \cdots &{\sum\limits_{j = 1}^{{k_n}} {f\left( {w_{{N_H}}^T{x^{{k_n}}}\left[ j \right] + b_{{N_H}}^1} \right)} } \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\beta _1}}\\ \vdots \\ {{\beta _{{N_H}}}} \end{array}} \right]} \end{array} $ |
因此,对于n组训练样本数据${D^i} = \left\{ {{X^i},\tilde Q_0^i} \right\},i = 1,2 \ldots ,n$,模型的训练问题可由minED(W1,W2,b1,b2)转化为随机给定W1和b1后求解线性方程组:
| $ \begin{array}{l} H\beta = {{\tilde Q}_0}H = \\ {\left[ {\begin{array}{*{20}{c}} {\sum\limits_{j = 1}^{{k_1}} {f\left( {w_1^T{x^1}\left[ j \right] + b_1^1} \right)} }& \cdots &{\sum\limits_{j = 1}^{{k_1}} {f\left( {w_{{N_H}}^T{x^1}\left[ j \right] + b_{{N_H}}^1} \right)} }\\ \vdots & \vdots & \vdots \\ {\sum\limits_{j = 1}^{{k_n}} {f\left( {w_1^T{x^{{k_n}}}\left[ j \right] + b_1^1} \right)} }& \cdots &{\sum\limits_{j = 1}^{{k_n}} {f\left( {w_{{N_H}}^T{x^{{k_n}}}\left[ j \right] + b_{{N_H}}^1} \right)} } \end{array}} \right]_{n \times {N_H}}}\\ \beta = \left[ {{\beta _1}, \cdots {\beta _{{N_H}}}} \right]_{{N_H} \times 1}^T,{{\tilde Q}_0} = \left[ {\tilde Q_0^1, \cdots ,\tilde Q_0^n} \right]_{n \times 1}^T \end{array} $ | (20) |
训练网络时,依照§3.2中所描述的步骤进行训练:随机给定W1和b1后,求出
| $ \hat \beta = {H^ + }{{\tilde Q}_0} $ | (21) |
由式(20)可知,H中所有参数都是已知,因此很容易求解出。具体PELM的算法实现全部采用MATLAB编程实现,隐含层输出矩阵的M-P逆H+采用MATLAB中的函数pinv()实现,其原理是采用奇异值分解法求解M-P逆。
基于PELM的误差补偿模型训练好后,若皮带秤任意k·△t时间段的称重序列数据为X={x[1],x[2],...,x[k]},k∈N,x[j]={q1[j],...,qN[j],T[j],D1[j],DN[j],L},j=1,2,...,k则k·△t时间段内补偿后的皮带秤上累计称重量为:
| $ \tilde Q' = \left[ \begin{array}{c} \sum\limits_{j = 1}^{{k_1}} {f\left( {w_1^T{x^1}\left[ j \right] + b_1^1} \right)} \\ \vdots \\ \sum\limits_{j = 1}^{{k_n}} {f\left( {w_{{N_H}}^T{x^{{k_n}}}\left[ j \right] + b_{{N_H}}^1} \right)} \end{array} \right] \bullet \hat \beta $ | (22) |
为了说明“内力理论”及基于PELM误差补偿模型的有效性,本研究使用上述式(14)、(20)~(22)的结论,对阵列式皮带秤的称重系统进行误差补偿。皮带秤实际运行时,为了提供足够的摩擦传动、防治传动滚筒打滑,输送带会被施以一定的预紧张力。而输送带各段的张力一般只会以预紧张力值为基准进行上下波动、输送带张力值变化相对较小。只有改变预紧张力后,输送带各段的张力值变化才会有相对明显的变化。因此,本研究中的试验验证分为两步,依次为预紧张力固定不变和预紧张力有改变的误差补偿情况。本文以南京三埃工控股份有限公司QPS-皮带秤全性能试验中心的4#阵列式皮带秤为故障诊断试验对象,该试验系统可循环走料。4#阵列式皮带秤采用的是单点悬浮称重传感器、采样率10 Hz,该秤落料点需离最近的称重单元距离为10L。根据V.K.Donis的理论[11],落料点需要离称重托辊足够远的距离才不会对称重精度产生明显影响。4#秤具体参数如表 1。
| 输送带宽度B/mm | 托辊间距L/mm | 输送带厚度t/mm | 输送带弹性模量E/(N·m-2) | 托辊槽角α/(°) |
| 1 200 | 1 200 | 12 | 2.65×108 | 30 |
本研究在4#阵列式皮带秤上分别模拟200、500、800 t/h3个不同流量下误差补偿试验,以验证本文所提出模型有效性。此外,每次试验的实际累计称重值由精度为±0.02%FS的料斗称给出,现场所有数据皆通过RS485总线传输,采用周立功RSM485CHT转换器接收,上位机采用串口通信实时采集。测试硬件环境是:Core i3-2.35G的CPU,内存6 G,硬盘500 G。
3.1 两端输送带张力及托辊非准直度检测两端称重托辊非准直度采用德国LEAZE公司的LOD2-85W20型激光位移传感器进行实时检测,该传感器分辨率10 um,检测区域65-105 mm,采样频率最高可达2 kHz。以NXP公司的LPC2138FBD64微控制器为采集处理芯片对两端激光位移传感器检测数据进行采集、降噪处理,保证降噪后的采样频率为1 Hz且时序一致。
两端输送带张力检测采用软测量思想:首先采用激光位移传感器实时检测托辊组两端最大输送带垂度;然后,在流量已知的情况下,以最大垂度对输送带张力进行间接估计[21]。皮带秤稳定流量运行时,两段输送带张力变化相对很小,因此可将输送带张力采样频率可以适当降低:采用激光位移传感器对输送带最大垂度实时检测、采样频率1 Hz,两端检测数据时序一致;然后采用滑动平均滤波对最大垂度检测数据降噪,再以降噪后的垂度值计算输送带张力值;最后将得到的输送带张力值作为PELM输入的一维,如图 6所示。
3.2 固定预紧张力试验在固定预紧张力试验中,首先不使用误差补偿、直接对不同流量下的皮带秤进行试验。试验的称重、预紧张力、等效流量、现场温度由现场仪表直接读取,具体如表 2。
等效流量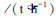 |
预紧张力/N | 现场温度/℃ | 标定数值/t | 料斗秤/kg | 相对误差/% |
| 217.75 | 5 929 | 20.45 | 6 917 | 6 889 | 0.406 |
| 216.95 | 5 937 | 20.5 | 6 181 | 6 152 | 0.471 |
| 524.26 | 5 924 | 20.66 | 16 190 | 16 147 | 0.266 |
| 500.33 | 5 957 | 21.15 | 15 443 | 15 406 | 0.240 |
| 796.03 | 5 928 | 21.38 | 24 122 | 24 024 | 0.408 |
然后,采用本文中的误差补偿模型,并以上述5组试验的数据对误差补偿模型进行训练。每组数据特征维度的都是12,5组数据的容量分别为2 899、2 340、2 201、2 015、1 799。PELM的隐含层单元个数为20,隐含层激励函数选用f[x]=1/[1+e(-x)],平均训练时间为0.022 419 1 s。再采用训练好后的基于PELM误差补偿模型对不同流量下的皮带秤进行累计称重误差补偿试验,补偿试验数据如表 3。
等效流量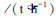 |
预紧张力/N | 现场温度/℃ | 标定数值/t | 料斗秤/kg | 相对误差/% |
| 217.35 | 5 914 | 21.96 | 6 468 | 6 456 | 0.186 |
| 218.50 | 5 951 | 23.15 | 9 062 | 9 056 | 0.066 |
| 487.76 | 5 930 | 23.35 | 13 276 | 13 272 | 0.030 |
| 510.07 | 5 944 | 23.39 | 15 464 | 15 449 | 0.097 |
| 789.05 | 5 918 | 23.73 | 22 768 | 22 732 | 0.158 |
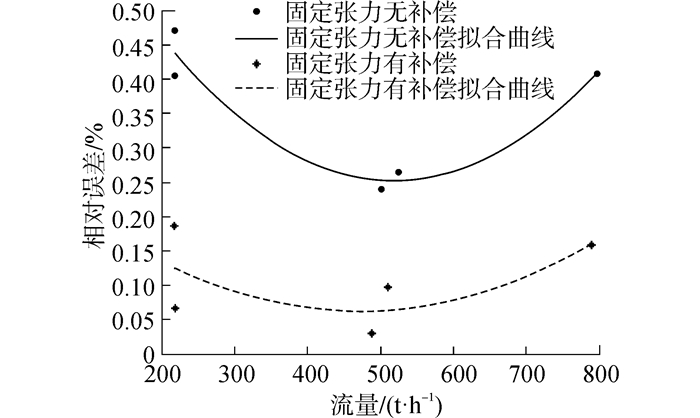
表 2、表 3两次试验都是在流量为200、500、800 t/h左右完成的,两次试验温度无明显变化,其最后拟合得到的累计称重误差随流量的关系对比如图 7。
|
| 图7 固定预紧张力时的称重误差对比图 Figure 7 Weighing error comparison of fixed preload tension |
从对比图可明显得出,尽管称重误差会有所波动,但在采用本文的PELM误差补偿方法后,称重误差还是有了明显的改善,不同流量的称重相对误差均在0.2%内,且流量为500 t/h时误差较小。
3.3 预紧张力变化试验固定预紧张力试验只验证了式(14)中输送带张力变化相对较小时托辊非准直度对称重精度的影响,因此还需采用PELM误差模型对输送带张力因素进行误差补偿试验。由于设备的限制,暂时难以使得输送带张力实时明显变化,只能静态的改变预紧张力。首先将张力6 000 N左右调整到8 400 N左右,调整后的称重试验结果如下。
表 4中对比了第一次改变预紧张力后无补偿的累计称重相对误差和采用3.2节中训练好的PELM模型补偿后的累计称重相对误差。对比结果显示,采用了PELM补偿模型的称重相对误差虽然有所改善,但仍没有达到预想的0.2%。这是因为该样本为表 2试验的数据,该训练样本中的输送带张力变化相对较小、几乎不变,故而当输送带张力变化较大时,PELM的泛化性能有所下降。因此,为了提高PELM的泛化性能、验证式(14)的正确性,还需将表 4试验数据加入到训练样本中,对PELM重新训练,最后采用重新训练好后的PELM进行再次改变预紧张力后的称重试验。
等效流量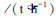 |
预紧张力/N | 温度/℃ | 标定数值/t | 料斗秤/kg | 无补偿误差/% | PELM补偿后误差/% |
| 212.63 | 8 373 | 19.65 | 11 949 | 11 897 | 0.437 | 0.276 |
| 508.50 | 8 394 | 19.69 | 17 136 | 17 065 | 0.416 | 0.266 |
| 937.43 | 8 349 | 19.94 | 22 937 | 22 838 | 0.433 | 0.271 |
表 5中预紧张力再次静态地从8 400 N左右增加到10 330~10 370 N,同样也比较了无补偿的累计称重相对误差和采用PELM模型补偿后的累计称重相对误差。两次试验都是在流量为200、500、950 t/h左右完成的。从表 4、5中可看出,当预紧张力发生变化后,本文提出的称重误差理论及基于PELM误差补偿模型实际应用效果仍然十分良好,可将称重相对误差保证在0.2%以内。
等效流量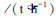 |
预紧张力/N | 温度/℃ | 标定数值/t | 料斗秤/kg | 无补偿误差/% | PELM补偿后误差/% |
| 508.81 | 10 331 | 20.3 | 16 815 | 16 794 | 0.405 | 0.125 |
| 934.39 | 10 369 | 20.5 | 22 798 | 22 768 | 0.422 | 0.132 |
4次试验的结果表明,采用式(14)、(20)~(22)的结论对阵列式皮带秤进行误差补偿、再重新校准零点后,可实现±0.1%的称重精度。
4 结论1) 从梁理论出发,推导出了阵列式皮带秤的“内力理论”,该理论表明:阵列式皮带秤称重精度主要与两端称重托辊组的输送带张力和非准直度有关,内部称重单元的影响可忽略。
2) 将传统PNN进行了改进、引入ELM训练算法,提出了一种过程极限学习机。结合阵列式皮带秤“内力理论”提出了一种基于PELM的阵列式皮带秤误差补偿模型,该模型通过“内力理论”降低了补偿输入数据特征维度。
3) 对运行在不同流量、不同预紧张力下的阵列式皮带秤进行了称重误差补偿试验,验证了基于“内力理论”及PELM的阵列式皮带秤误差补偿模型的实用性:模型训练时收敛速度快、预测时泛化性能好,提高累计称重精度到±0.1%,对于大宗散状物料贸易具有重大意义。
| [1] | 方原柏. 电子皮带秤[M]. 北京: 冶金工业出版社, 2008 . |
| [2] | ALEKSANDROVIc S, JOVIc M. Analysis of belt weigher accuracy limiting factors[J]. International journal of coal preparation and utilization, 2011, 31(5): 223–241. |
| [3] | FRISTEDT K. A contribution to the analysis of conveyor belt weighing errors[M]//WIERINGA H. Mechanical Problems in Measuring Force and Mass. Netherlands: Springer, 1986: 65-73. |
| [4] | PARVINI M, HARANDI J N, KAVOUSIAN A, et al. Structural analysis of conveyor belts. II. Finite element approach[J]. Journal of applied polymer science, 1992, 46(5): 775–781. |
| [5] | 陈堃, 干洪, 丁盼, 等. 电子皮带秤测量系统的静力学分析[J]. 起重运输机械, 2013(1): 47–49. |
| [6] | 严洁, 赵研, 张俊利. 基于BP神经网络的称重传感器静态非线性误差补偿研究[J]. 传感技术学报, 2008, 21(6): 1025–1028. |
| [7] | 林海军, 滕召胜, 迟海, 等. 基于多传感器信息融合的汽车衡误差补偿[J]. 仪器仪表学报, 2009, 30(6): 1245–1250. |
| [8] | 何新贵, 梁久祯, 许少华. 过程神经网络的训练及其应用[J]. 中国工程科学, 2001, 3(4): 31–35. |
| [9] | 袁延强. 皮带秤误差理论与耐久性讨论[C]//第十一届称重技术研讨会论文集. 南京: 2012: 184-192. |
| [10] | GAO Hongbin, PANG Weiyi. A high-accuracy dynamic weighing system based on single-idler conveyor belt[C]//Proceedings of International Conference on Machine Learning and Cybernetics. Baoding, 2009: 2483-2487. |
| [11] | DONIS V K, RACHKOVSKII A E, SIN V M. How the conveyor belt length affects belt weigher accuracy[J]. Measurement techniques, 2004, 47(2): 163–167. |
| [12] | ALEKSANDROVIc S, JOVIc M. Testing and calibration of continuously operating belt weighers[J]. Przeglad elektrotechniczny, 2011, 87(7): 276–279. |
| [13] | HUANG Guangbin, ZHU Qinyu, SIEW C K. Extreme learning machine: theory and applications[J]. Neurocomputing, 2006, 70(1/2/3): 489–501. |
| [14] | 王之琼, 刘红艳, 肖静, 等. 基于ELM的室性早搏检测算法[J]. 计算机研究与发展, 2013, 50(S1): 196–204. |
| [15] | HUANG Guangbin. Learning capability and storage capacity of two-hidden-layer feedforward networks[J]. IEEE transactions on neural networks, 2003, 14(2): 274–281. |
| [16] | HUANG Guangbin. An insight into extreme learning machines: random neurons, random features and kernels[J]. Cognitive computation, 2014, 6(3): 376–390. |
| [17] | HUANG Gao, HUANG Guangbin, SONG Shiji, et al. Trends in extreme learning machines: a review[J]. Neural Networks, 2015, 61: 32–48. |
| [18] | 葛利, 印桂生. 竞争型径向基过程神经网络时序分类器[J]. 哈尔滨工程大学学报, 2012, 33(6): 741–744. |
| [19] | 许少华, 宋美玲, 许辰, 等. 一种基于混合误差梯度下降算法的过程神经网络训练[J]. 东北石油大学学报, 2014, 38(4): 92–96. |
| [20] | 李盼池, 施光尧. 基于数值积分的离散过程神经网络算法及应用[J]. 系统工程理论与实践, 2013, 33(12): 3216–3222. |
| [21] | 梅松. 散状物料输送带垂度检测与张力分析系统设计开发[D]. 南京: 南京理工大学, 2013. |



