液体燃料的喷雾燃烧是内燃机中普遍采用的燃烧方式,但是受内燃机几何结构的限制,在很多情况下,喷雾油滴会产生碰壁现象,形成附壁油膜[1]。附壁油膜比自由液滴的蒸发慢很多,不利于燃料蒸发和油气均匀混合,是产生较高碳氢化合物(HC)和颗粒物(PM)排放的重要原因[2]。因此必须对附壁油膜蒸发问题进行深入研究,以改善蒸发和燃烧,减少污染物排放。
附壁油膜的形成和蒸发有其自身的特殊性[3-4]。首先,高压喷射油滴所产生的油膜厚度很小[5],通常不超过50 μm;其次,整个附壁油膜的蒸发过程处于一个高速瞬态的湍动流场以及高温高压的瞬态环境之中[6]。这些因素决定了对附壁油膜的研究具有很大的困难性。现有的实验研究[7-8]多是在诸多简化的条件下进行的,受限于实验设备和测量精度,具有很大的局限性;现有的数值模拟研究[9-10],大都是基于常温常压的条件下建立的模型,其适用性还需进一步验证。
本文应用比拟法建立了计算油膜蒸发速率的模型,并在此基础上建立了预测一维非稳态附壁油膜加热蒸发过程的简化数学模型。应用此模型可以计算不同时刻油膜的厚度和蒸发率,以及附壁油膜温度的空间分布。在此基础上讨论了初始油膜厚度、环境温度、环境压力和对流换热系数对油膜蒸发的影响。该模型可以用于商业软件CFD(KIVA或FLUENT)中,以提高附壁油膜在多维模拟研究中计算的准确性。
1 数学模型本文建立的附壁油膜加热蒸发模型基于以下几点假设[11-12]:
1)由于附壁油膜很薄,它的运动速度相比气缸中空气的流速很小,因此认为油膜在水平方向上是静止的,在垂直方向不考虑表面的波动情况以及液滴与油膜的碰撞和二次雾化现象;
2)认为附壁油膜与气缸壁直接接触,忽略其他传热机理;
3)在附壁油膜蒸发阶段气缸中的气体还未燃烧,气缸内温度不是很高,忽略辐射换热对液膜蒸发的影响。
在这些假设成立的基础上,该一维非稳态附壁油膜加热蒸发的物理模型如图 1所示,其中δ和δb分别是油膜厚度和气缸壁面厚度,qh,qe,qw分别是油膜与环境气体对流换热所吸收的热量,自身蒸发所释放的热量以及与壁面接触所传递的热量。
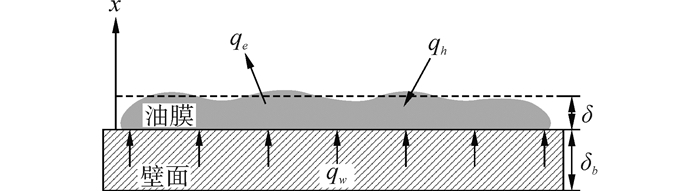
|
| 图1 附壁油膜加热蒸发物理模型 Figure 1 The physical mode of the wall film heating evaporation |
一维非稳态导热微分方程为
| $\frac{\partial T}{\partial t}={{a}_{1}}\frac{{{\partial }^{2}}T}{\partial {{x}^{2}}}$ | (1) |
式中:T、t分别是温度和时间;x是距汽缸壁的距离;al=λl、(ρl、cl)是油膜的热扩散系数,其中λl、ρl和cl分别是液体的导热系数,密度和比热。假设油膜的初始温度是定值T0,则初始条件可以表示为
| $T\left( x,0 \right)={{T}_{0}}$ | (2) |
认为与气体接触的油膜表面既受到高温空气对流换热的加热作用,同时由于蒸发而被冷却,因此在油膜表面x= δ处的边界条件可以表示为
| $h\left( {{T}_{g}}-{{T}_{s}} \right)={{\rho }_{ls}}L\dot{\delta }+{{\lambda }_{l}}\frac{\partial T}{\partial x}\left| _{x=\delta } \right.$ | (3) |
式中:h为对流换热系数,Tg为空气温度,Ts和ρls是油膜表面温度和密度,L为燃油的汽化潜热。$\dot{\delta }$为液膜厚度的变化率;x = 0处的边界条件设置为第二类边界条件:
| $\frac{\partial T}{\partial x}\left| _{x=0} \right.=-\frac{q}{{{\lambda }_{b}}}$ | (4) |
式中:q为汽缸壁与油膜间的热流密度,给定为q=λb(Tw-Tb)/δb,λb和δb分别为气缸套的导热系数和厚度,Tw为气缸套外侧水的温度,Tb为油膜下表面的温度,认为它与气缸套内侧温度相同。
方程(1)~(4)即为该一维非稳态导热微分方程及其定解条件,引入参数有效温度Teff=Tg-ρlsL$\dot{\delta }$/h和过余温度θ=T(x,t)-Teff,可将方程(1)~(4)转换为
| $\frac{\partial \theta }{\partial t}={{a}_{1}}\frac{{{\partial }^{2}}\theta }{\partial {{x}^{2}}}$ | (5) |
| $\theta \left( x,0 \right)={{T}_{0}}-{{T}_{\text{eff}}}$ | (6) |
| $\frac{\partial \theta }{\partial x}\left| _{x=\delta } \right.+\frac{h}{{{\lambda }_{1}}}\theta =0$ | (7) |
| $\frac{\partial \theta }{\partial x}\left| _{x=0} \right.=-\frac{q}{{{\lambda }_{b}}}$ | (8) |
若要求解该方程组,必须将方程(8)齐次化,因此令
| $F\left( x,y \right)=\theta \left( x,y \right)+\frac{q}{{{\lambda }_{b}}}\left( x-\frac{{{\lambda }_{s}}}{h}-\delta \right)$ | (9) |
显然F(x,t)满足原微分方程和边界条件。则将F(x,t)代入方程(5)~(8)可得
| $\frac{\partial F}{\partial t}={{a}_{1}}\frac{{{\partial }^{2}}F}{\partial {{x}^{2}}}$ | (10) |
| $F\left( x,0 \right)={{T}_{0}}-{{T}_{\text{eff}}}+\frac{q}{{{\lambda }_{b}}}\left( x-\frac{{{\lambda }_{s}}}{h}-\delta \right)$ | (11) |
| $\frac{\partial F}{\partial x}{{|}_{x=\delta }}+\frac{h}{{{\lambda }_{1}}}F=0$ | (12) |
| $\frac{\partial F}{\partial x}{{|}_{x=0}}=0$ | (13) |
令f(x) = F (x,0),采用分离变量法[13]对该方程组进行求解,则可得F(x,t)的解析解为
| $\begin{align} & F\left( x,t \right)=\sum\limits_{m=1}^{\infty }{\cos \left( \frac{{{\beta }_{m}}x}{\delta } \right)}\times \\ & \exp \left( -\beta _{m}^{2}\frac{at}{{{\delta }^{2}}} \right)\frac{1}{N\left( {{\beta }_{m}} \right)}\int_{0}^{\delta }{f\left( x \right)}\cos \left( \frac{{{\beta }_{m}}x}{\delta } \right)\text{d}x \\ \end{align}$ | (14) |
式中:N(βm)=δ(βm+sin βm+cosβm)/(2βm),βm(m = 1,2,3,…)是超越方程βtanβ=Bi的正根,其中毕渥数Bi=hδ/λl。于是一维非稳态附壁油膜的温度分布可表示为
| $T\left( x,t \right)={{T}_{\text{eff}}}+F\left( x,t \right)-\frac{q}{{{\lambda }_{b}}}\left( x-\frac{{{\lambda }_{s}}}{h}-\delta \right)$ | (15) |
目前对于传质速率的研究成果绝大多数都是通过传质与传热的类比所得到的。在低质量速率传递的情况下,用舍伍德数(Sh)和施密特数(Sc)分别代替传热中的努塞尔数(Nu)和普朗特数(Pr),可以得到传质过程的经验关联式。如流体外掠平壁的努塞尔数的半经验公式[14]为:
| $Nu=\frac{hl}{{{\lambda }_{g}}}=0.03{{\Pr }^{0.6}}{{\operatorname{Re}}^{0.8}}$ | (16) |
通过传热与传质的类比则有
| $\text{Sh=}\frac{{{g}^{*}}l}{{{\gamma }_{g}}}=0.03\text{S}{{\text{c}}^{0.6}}{{\operatorname{Re}}^{0.8}}$ | (17) |
式中:l、λg和γg分别是特征长度、气体导热系数和燃油蒸汽在空气中的扩散速率;g*是低传质速率时的传质系数。两式相比可得
| ${{g}^{*}}=h\frac{{{\gamma }_{g}}}{{{\lambda }_{g}}}{{\left( \frac{\text{Sc}}{\Pr } \right)}^{0.6}}$ | (18) |
将刘易斯数Le=Sc/Pr=λg/(γgcpg)代入式(18)可得
| ${{g}^{*}}=L{{e}^{-0.4}}\frac{h}{{{c}_{pg}}}$ | (19) |
高质量传递时的传质系数可以表示为
| $g={{g}^{*}}\frac{\ln \left( 1+{{B}_{M}} \right)}{{{B}_{M}}}$ | (20) |
其中斯伯丁数:
| ${{B}_{M}}={{Y}_{\text{fs}}}/\left( 1-{{Y}_{\text{fs}}} \right)$ | (21) |
油膜表面的质量分数:
| ${{Y}_{\text{fs}}}={{\left[ 1+\left( \frac{P}{{{P}_{\text{fs}}}}-1 \right)\frac{{{M}_{a}}}{{{M}_{f}}} \right]}^{-1}}$ | (22) |
式中:pfs是油膜表面的饱和蒸汽压力。对流传质速率$\dot{m}=g{{B}_{M}}$,并且在一般情况下可以认为气体的Le约等于1。于是附壁油膜的蒸发速率可以表示为
| $\dot{m}=\frac{h}{{{c}_{\text{pg}}}}\ln \left( 1+{{B}_{M}} \right)$ | (23) |
与此同时可以得到油膜厚度的减小速率:
| $\dot{\delta }=\frac{h}{{{\rho }_{1s}}{{c}_{\text{pg}}}}\ln \left( 1+{{B}_{M}} \right)$ | (24) |
通过迭代计算后得到新的油膜厚度为
| ${{\delta }_{\text{new}}}={{\delta }_{\text{old}}}-\dot{\delta }\Delta t$ | (25) |
式中:△t为时间步长。
2 计算参数的选取在本文中选用了具有较高饱和温度的正十二烷[15](C12H26)作为研究对象,其摩尔质量 Mf = 170 kg/kmol,临界温度Tcr = 659 K,临界压力Pcr = 1.82 MPa。考虑到温度对燃料热力学性质的影响较大,燃料的其他热力学参数给定为
| ${{\lambda }_{1}}=0.02667\frac{T}{300}-0.02087\left( \text{W/}\left( \text{m }\!\!\times\!\!\text{ K} \right) \right)$ | (26) |
| ${{c}_{l}}=2.18+0.0041\left( T-300 \right)\left( \text{kJ/}\left( \text{kg }\!\!\times\!\!\text{ K} \right) \right)$ | (27) |
| ${{P}_{fs}}=\exp \left[ 8.1948-7.8099\frac{300}{{{T}_{s}}}-9.0098{{\left( \frac{300}{{{T}_{s}}} \right)}^{2}} \right]\text{bar}$ | (28) |
| ${{\rho }_{1}}\text{=}744.11-0.771\left( T-300 \right)\left( \text{kg }\!\!\times\!\!\text{ }{{\text{m}}^{3}} \right)$ | (29) |
| $L=37.44{{\left( {{T}_{cr}}-{{T}_{s}} \right)}^{0.38}}\left( \text{kJ/kg} \right)$ | (30) |
计算中的其他相关参数给定为:空气的定压比热cpg = 1 141 kJ/(kg·K),空气摩尔质量Ma = 28.97 kg/kmol,气缸壁厚度δw = 10 mm,汽缸壁导热系数λw= 50 W/(m·K),气缸壁外冷却水的温度Tw= 360 K,时间步长Δt = 0.01 ms。
在整个计算过程中,当油膜的厚度小于0.1 μm时即认为油膜已经完全蒸发。油膜表面温度接近临界温度时,燃油物性变化剧烈,为保证计算的准确性,当Ts > 650 K时认为计算结束。
3 计算结果与分析图 2为不同位置附壁油膜随时间变化的温度分布图。计算条件为δ0 = 20 μm,T0 = 400 K,Tg= 900 K,P = 5 MPa,h = 2 500 W/(m2·K),图 3为相同条件下附壁油膜蒸发率和油膜厚度随时间的变化规律。从图 2和图 3可以看出,在环境温度较高时,附壁油膜的加热蒸发可以分为3个阶段。初始阶段表面温度上升的很快,此时油膜与环境的对流换热主要用来加热油膜,而下表面由于壁面冷却热流的存在,温度会降低。随着温度的升高,油膜表面的蒸发增强,加热和蒸发同时进行,表面温度进入稳定升高阶段,同时对流换热吸收的热量逐渐传递到油膜内部,使得油膜温度从表面向内部依次逐渐升高。当表面温度接近临界温度时,由于燃油的汽化潜热几乎为零,所以油膜表面温度再次迅速升高,直至其达到临界温度。由图可以看出,在该初始条件下,经过大约6 ms,油膜表面温度达到临界温度,此时附壁油膜的厚度减少到10 μm左右。
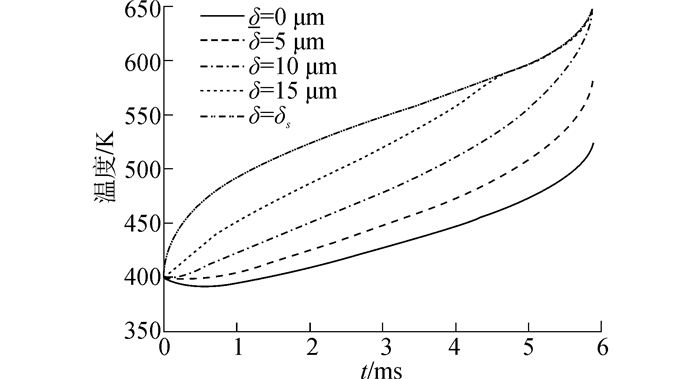
|
| 图2 附壁油膜温度分布图 Figure 2 Wall film temperature distribution versus time |
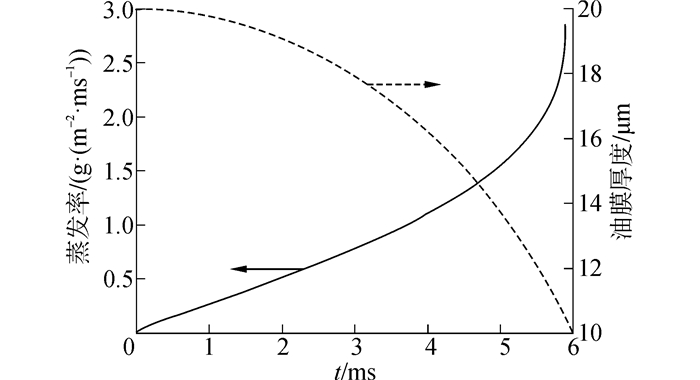
|
| 图3 附壁油膜蒸发率和油膜厚度随时间变化 Figure 3 Temporal evolution of wall film evaporation rate and thickness |
在研究初始油膜厚度对附壁油膜加热蒸发的影响时,其他初始参数为T0 = 400 K,Tg = 900 K,P = 5 MPa,h = 2 500 W/(m2·K)。图 4(a)给出了不同初始厚度的油膜表面温度随时间的变化情况。可以看出在初始阶段厚度对表面温度的影响不大,但随着时间的变化,油膜越薄,油膜表面的温度升高越快。图 4(b)表示了不同厚度的附壁油膜的蒸发率随时间的变化。随着时间的延长,油膜表面温度升高,蒸发率也会增加,同时越薄的油膜蒸发的越快。
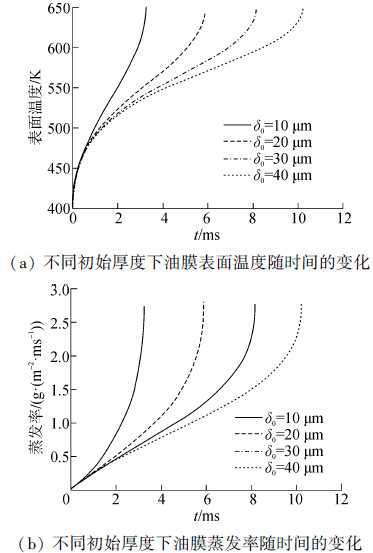
|
| 图4 不同初始厚度下油膜表面温度和蒸发率随时间的变化 Figure 4 Surface temperature and evaporation rate versus time at different initial film thicknesses |
在研究环境温度对附壁油膜加热蒸发的影响时,其他初始参数为:δ0 = 20 μm,T0 = 400 K,P = 5 MPa,h = 2 500 W/(m2·K)。图 5(a)给出了不同环境温度情况下附壁油膜表面温度随时间的变化。可以看出环境温度越高,油膜表面升温越快。当气缸温度比较低时,如Tg = 700 K的情况下,在整个油膜加热蒸发的末尾阶段,油膜与环境气体对流换热所吸收的热量与蒸发所释放的热量达到平衡,因此温度保持恒定,不再升高,直到油膜完全蒸发,而不会出现达到临界温度的快速蒸发阶段。而在环境温度较高的情况下,油膜表面温度会一直升高直至其达到临界温度。
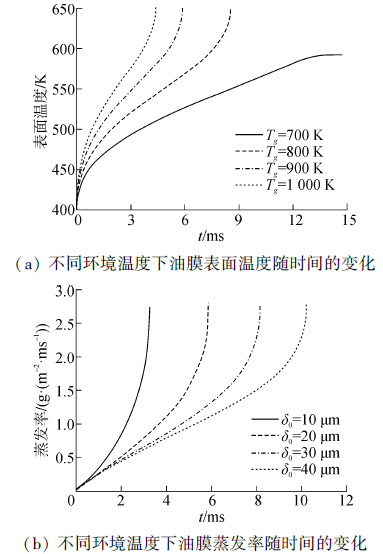
|
| 图5 不同环境温度下油膜表面温度和蒸发率随时间的变化 Figure 5 Surface temperature and evaporation rate versus time at different ambient temperatures |
附壁油膜的蒸发率随时间的变化表现出类似的趋势,如图 5(b)所示。由此可以看出环境温度对蒸发率的影响很大,例如在4 ms左右时,当环境温度从700 K变化到1 000 K,蒸发率大约从0.3 g/(m2·ms)变化到了2 g/(m2·ms),增加了大约6倍。
3.3 环境压力的影响在研究环境压力对附壁油膜加热蒸发的影响时,其他初始参数为:δ0 = 20 μm,T0 = 400 K,Tg = 900 K,h = 2 500 W/(m2·K)。本文所考虑的的环境压力均高于燃料的临界压力。图 6(a)表示了不同环境压力下油膜表面温度随时间的变化情况。可以看出在其他条件一定的情况下,压力对于附壁油膜表面温度的影响很小。但依然可以看出在绝大部分时间内压力越大,油膜表面温度越高,直至温度快达到临界温度时,油膜表面温度趋于相同。然而,蒸发率的变化情况却完全不同,蒸发率随着环境压力的增大而减小,如图 6(b)所示。
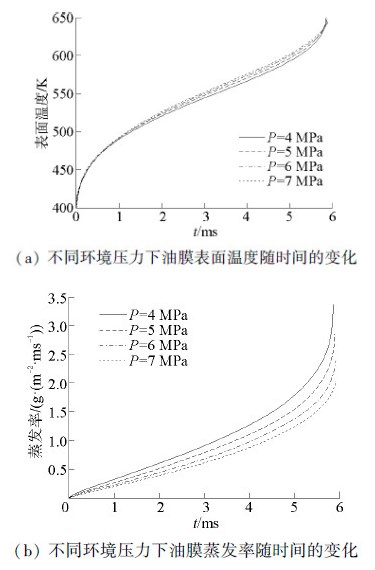
|
| 图6 不同环境压力下油膜表面温度和蒸发率随时间的变化 Figure 6 Surface temperature and evaporation rate versus time at different ambient pressures |
对比环境温度和环境压力对附壁油膜加热蒸发的影响,可以看出环境温度的影响更为显著。这主要是因为在内燃机中压力对对流换热系数的影响十分明显,而当对流换热系数给定为定值时,压力对附壁油膜加热蒸发的影响就会降低。
3.4 对流换热系数的影响在内燃机中影响对流换热系数的因素有很多,因此为了简化计算,本文中的对流换热系数取的都是定值,在该节中单独讨论对流换热系数的影响。其他初始参数选定为:δ0 = 20 μm,T0 = 400 K,Tg = 900 K,P = 5 MPa。图 7(a)为在不同的对流换热系数下,附壁油膜表面温度随时间的变化图,可以看出对流换热系数越大,油膜表面温度升高越快,但这个差距随着对流换热系数的增大而减小。图 7(b)给出对流换热系数对蒸发率的影响,可以看出对流换热系数对蒸发率的影响十分显著,例如在4 ms时,当对流换热系数从1 500 W/(m2·K)到3 000 W/(m2·K)时,蒸发率大约从0.3 g/(m2·ms)变化到1.8 g/(m2·ms)。因此提高气缸内对流换热系数可以有效促进附壁油膜的蒸发。图 7(c)为不同对流换热系数下油膜厚度随时间的变化图。尽管对流换热系数不同,但在计算停止时,即油膜表面温度达到临界温度时,油膜厚度却基本相同。

|
| 图7 不同对流换热系数下油膜表面温度,蒸发率和厚度随时间变化 Figure 7 Surface temperature, evaporation rate, and film thickness versus time at different convective rates |
本文建立了油膜蒸发速率模型,并在此基础上建立了一维非稳态油膜蒸发传热数学模型,运用解析方法计算和预测内燃机中附壁油膜的加热和蒸发问题。分别讨论了初始油膜厚度,环境温度和环境压力以及对流换热系数对油膜加热和蒸发的影响。通过分析得出如下结论:
1) 附壁油膜的加热蒸发过程大致可以分为3个阶段,即初始表面迅速加热阶段,稳定加热蒸发阶段和末尾阶段。在较高的环境温度下,末尾阶段油膜温度会迅速升高直至达到临界温度;在较低的环境温度下,末尾阶段温度保持恒定,附壁油膜吸收的热量与蒸发释放的热量达到平衡,直至油膜完全蒸发。
2) 不同初始厚度的附壁油膜在加热蒸发的初始阶段差别不大,但随着时间的变化,越薄的油膜表面温度升高越快,蒸发速率越大。
3) 环境温度对附壁油膜的影响很大,环境温度越高,油膜表面升温越快,蒸发所需要的时间越短。
4) 不同的环境压力对油膜表面温度的影响很小,但对蒸发速率的影响比较明显,环境压力越高,蒸发速率越小。
5) 增加对流换热系数可以有效的提高附壁油膜表面温度,促进油膜蒸发。
| [1] | PANÃO M R O, MOREIRA A L N. Interpreting the influence of fuel spray impact on mixture preparation for HCCI combustion with port-fuel injection[J]. Proceedings of the combustion institute, 2007, 31(2): 2205–2213. |
| [2] | JIANG X, SIAMAS G A, JAGUS K, et al. Physical modelling and advanced simulations of gas-liquid two-phase jet flows in atomization and sprays[J]. Progress in energy and combustion science, 2010, 36(2): 131–167. |
| [3] | ANDREASSI L, UBERTINI S, ALLOCCA L. Experimental and numerical analysis of high pressure diesel spray–wall interaction[J]. International journal of multiphase flow, 2007, 33(7): 742–765. |
| [4] | STANTON D W, RUTLAND C J. Multi-dimensional modeling of thin liquid films and spray-wall interactions resulting from impinging sprays[J]. International journal of heat and mass transfer, 1998, 41(20): 3037–3054. |
| [5] | HONG K, LEE S H, RYOU H S. Modelling of wall films formed by impinging diesel sprays. SAE Technical Paper 2001-01-3228[R]. SAE, 2001. |
| [6] |
胡宗杰, 李理光, 于水. 燃料油膜蒸发的热重分析法研究[J].
科学通报, 2006, 51(17): 2150–2157.
HU Zongjie, LI Liguang, YU Shui. Thermogravimetric analysis of fuel film evaporation[J]. Chinese science bulletin, 2006, 51(17): 2150–2157. |
| [7] |
李韬, 邓康耀, 程用胜. 壁面温度对喷射油膜附壁厚度的影响[J].
内燃机工程, 2010, 31(3): 67–70.
LI Tao, DENG Kangyao, CHENG Yongsheng. Quantitative measurement of the influence of temperature of surface on spray film thickness with laser induced fluorescence technique[J]. Chinese internal combustion engine engineering, 2010, 31(3): 67–70. |
| [8] | PARK S W, LEE C S. Macroscopic and microscopic characteristics of a fuel spray impinged on the wall[J]. Experiments in fluids, 2004, 37(5): 745–762. |
| [9] |
马宗正, 程勇, 纪少波, 等. 汽油机起动工况附壁油膜挥发过程的计算分析[J].
燃烧科学与技术, 2011, 16(6): 503–507.
MA Zongzheng, CHENG Yong, JI Shaobo, et al. Study on wall film evaporation of gasoline engine during start[J]. Journal of combustion science and technology, 2011, 16(6): 503–507. |
| [10] | LIU Hong, LEE C F. Numerical study on wall film formation and evaporation. SAE Technical Paper 2014-01-1112[R]. SAE, 2014. |
| [11] | O'ROURKE P J, AMSDEN A A. A particle numerical model for wall film dynamics in port-injected engines. SAE Technical Paper 961961[R]. SAE, 1996. |
| [12] | NABER J, FARRELL P V. Hydrodynamics of droplet impingement on a heated surface. SAE Technical Paper 930919[R]. SAE, 1993. |
| [13] | JIA Li, FANG Zhaohong. Advanced heat transfer[M].2nd ed. Beijing: Higher Education Press,2008 . |
| [14] | KAYS W M, CRAWFORD M E, WEIGAND B. Convective heat and mass transfer[M].4th ed. India: Tata McGraw-Hill Education,2012 . |
| [15] | ABRAMZON B, SAZHIN S. Convective vaporization of a fuel droplet with thermal radiation absorption[J]. Fuel, 2006, 85(1): 32–46. |



