2. Marine Engineering College, Dalian Maritime University, Dalian 116026, China
涡轮入口温度较高,为防止动叶叶片受热膨胀后与机匣发生摩擦,叶片顶部与机匣之间通常会留有一定间隙,叶顶附近气流在压力面和吸力面压差作用下,以较高速度通过该间隙,并在流出间隙之后与主流掺混而造成较大的流动损失,研究表明,由叶尖间隙引起的损失已经占到涡轮端区损失的一半以上[1]。而对于间隙流动,普遍认为受4种因素影响:叶片压力面与吸力面间的压差、端壁附面层、叶片与机匣间的相对运动及叶尖间隙尺寸[2]。实际工作中,涡轮叶片顶部的泄漏流体总是从叶片压力面流向吸力面:当机匣与叶片相对静止时,间隙流动主要受压力面和吸力面之间压差的驱动,而当机匣与叶片相对运动时,间隙流动还要受机匣附近黏性附面层剪切应力的影响,黏性剪切力及间隙内的径向速度梯度改变了叶顶区的流场结构。
涡轮转子叶片与机匣间的相对运动显著影响间隙流动特性,而控制间隙流动是提高涡轮性能的有效手段之一,为此,国内外学者围绕涡轮动叶与机匣间相对运动开展了大量的研究工作,也获得了许多有益的结果:Graham[3]发现当机匣速度不同时,间隙流动轨迹发生不规则运动,说明转动引起的黏性刮削作用会影响间隙流动;Yaras[4]和Luo[5]认为机匣相对运动会导致间隙泄漏流量降低,泄漏涡向吸力面靠近,强度减弱,但通道涡增强;Xiao[6]发现机匣和叶顶的相对运动造成叶顶区域流场的复杂程度显著增加并导致损失上升;McCarter[7]认为相对运动使得叶片吸力面附近存在一个低压区,很有可能还存在刮削涡;Tallmall[8, 9]采用数值方法研究了间隙高度、机匣相对转动对间隙流动的影响,认为相对运动能增强近壁面区二次流;Srinivasan[10]认为机匣与叶片的相对转动减小了叶片压力面和吸力面的静压差,相同的间隙高度可使通过间隙的流量下降9%;Yang[11]发现端壁相对运动使叶顶间隙前缘附近的泄漏流量降低,却增加了尾缘附近的泄漏量;Acharya[12]的研究表明,机匣与叶片的相对运动显著影响涡轮叶顶的传热和气动性能;牛茂升[13]认为叶片转动对涡轮间隙流动有阻塞作用,且转速下降会加剧动叶出口截面气流过偏/偏转不足现象。
以上研究一定程度上揭示了端壁相对运动对涡轮间隙流动影响的规律,为进一步采取主动或被动措施控制间隙流动,降低流动损失,提高涡轮性能奠定了基础。超声速膨胀器是结合超声速膨胀喷管、常规轴流涡轮以及旋转冲压压缩转子结构设计方法而出现的一种新型膨胀做功系统,就其功能而言实质上是一种特殊结构形式的超声速涡轮,与常规涡轮相比,超声速膨胀器不仅可以减少气流在膨胀系统中的流动损失,而且结构简单紧凑、体积小、功率重量比大、效率高,更重要的是超声速膨胀器可以满足切向来流的进气条件,此外,还能实现切向或轴向排气。在小型船舶动力、小型发电燃气轮机、涡轮泵和分布式供能用微小型燃气轮机中有着令人期待的应用前景。笔者前期已对无间隙超声速膨胀器进行了相关研究[14, 15, 16],获得了膨胀型面的造型方法,三维流道内部的主要流动特性及影响超声速膨胀器性能的主要几何参数,实际工作中,超声速膨胀器隔板与机匣之间留有间隙,端壁相对运动对超声速膨胀器间隙流动和整体性能都将产生影响,基于此,本文就隔板与机匣相对运动对超声速膨胀器间隙流动的影响进行了数值研究。
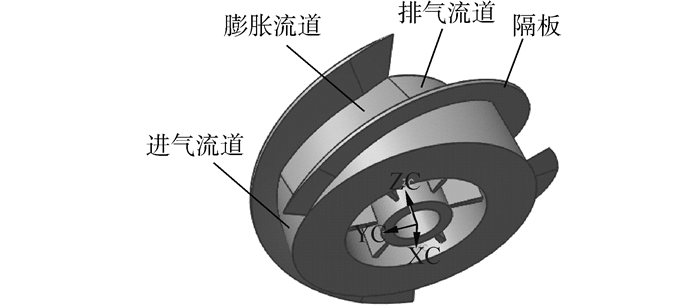
1 计算模型与数值方法 1.1 计算模型文献[14]给出了超声速膨胀器(图 1)的设计方法。超声速膨胀器包含3个流道,为节省资源并提高计算速度,本文仅对一个三维流道的流场进行数值计算,三维流道几何参数:初始膨胀角为24°、进口高度比0.17、圆弧半径喉部高度比0.5、流道长高比6、出进口面积比4、隔板安装角26°[14],隔板顶部与机匣之间的间隙高度为1.5%h0(h0为喉部高度)。分别就隔板与机匣相对静止,30%、60%、90%以及100%相对速度时超声速膨胀器间隙流动特性开展数值研究。
|
| 图1 超声速膨胀器结构 Figure 1 Structure of the supersonic expander |
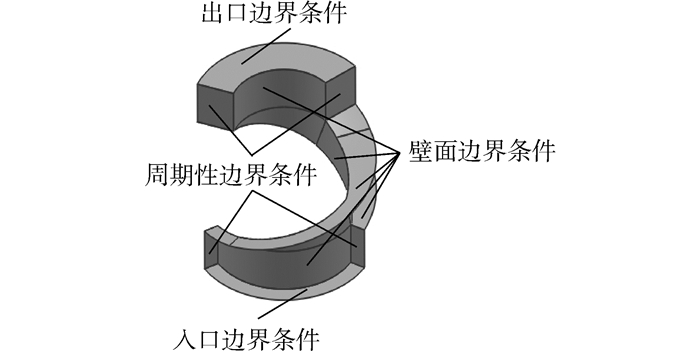
采用Fluent软件对超声速膨胀器的三维流道流场进行数值仿真,控制方程为三维定常雷诺平均N-S方程,湍流模型为标准k-ε两方程模型。计算中选用隐式耦合求解算法,方程对流项采用二阶迎风格式离散。 对于边界条件,给定进口绝对总压、静压和总温。三维流道上壁面、进出口延伸段上壁面设定为绝对静止的绝热壁面,而三维流道下壁面、侧壁面(吸、压力面)和进出口延伸段下壁面设置为与流体一起转动的绝热壁面;进出口延伸段与三维流道吸、压力面相接侧壁面设置为周期性边界条件(图 2)。超声速膨胀器三维流道设计工况计算条件为:转速nd=30 000 r/min,进口绝对总压p0*=1 013 250 Pa,进口静压p0=917 713 Pa,进口总温T0*=1 200 K。
|
| 图2 计算域与边界条件 Figure 2 Computational domain and boundary conditions |
采用的三维流道膨胀比、损失系数及等熵效率公式如下
| $ \pi _1^{\rm{*}}{\rm{ = }}p_0^{\rm{*}}/p_1^{\rm{*}} $ | (1) |
| $ {Y_R} = \frac{{{p_0}{{^*}_{,rel}} - {p_1}{{^*}_{,rel}}}}{{{p_1}{{^*}_{,rel}} - {p_1}}} $ | (2) |
| $ {\eta _T}^{\rm{*}}{\rm{ = }}\frac{{\pi _1^{\rm{*}}\frac{{k{\rm{ - }}1}}{k} \bullet (1 - \frac{{{T_1}^*}}{{{T_0}^*}})}}{{{\pi ^*}\frac{{k - 1}}{k} - 1}} $ | (3) |
式中: p0*、p1*、p0*,rel、p1,rel*、p1、T0*、T1*、k分别为进出口绝对和相对总压、出口静压、进出口总温和比热比。
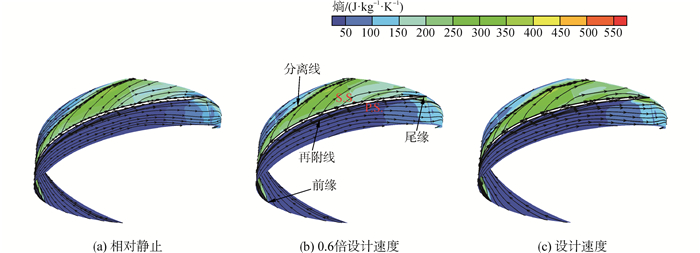
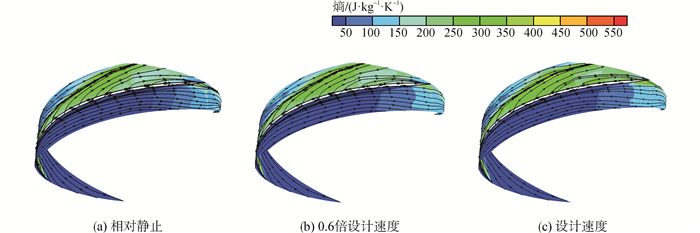
2 计算结果与分析 2.1 间隙内熵和流线分布图 3、4给出了间隙内S1流面的熵和流线分布图,可以看出,沿流向除尾缘外压力面附近熵值始终维持在较低值,而吸力面熵值较高且影响范围不断扩大;随机匣与隔板之间相对速度的增加,分离线明显向吸力面靠近,压、吸力面近出口区域的熵值有所增加;比较而言,间隙中截面受端壁相对运动的影响更明显,熵值更高,分离线和再附线离隔板也更近。
|
| 图3 近隔板顶部S1流面熵和流线分布 Figure 3 Entropy and streamlines near to the strake wall tip inside the clearance |
|
| 图4 间隙中分面熵和流线分布 Figure 4 Entropy and streamlines at the mid-gap |
机匣与隔板相对静止时,气流在压、吸力面压差作用下从压力面侧经间隙泄漏到吸力面侧,沿流向吸卷附面层和主流而发展壮大成泄漏涡,泄漏涡涡核主要由隔板前缘气流形成,并在形成之后向流道中央发展,所导致的掺混损失严重,因此,吸力面侧熵值高,高熵影响范围沿流向不断扩大,而压力面侧熵值低,仅尾缘由于泄漏流体回流造成熵值增加。从图 3(a)和4(a)还可看出,环绕分离线区域的熵值较高,且分离线右侧气流熵值更高一些,这是因为,右侧气流不仅受机匣附近黏性流体的剪切应力,还存在泄漏流体、主流和端壁附面层的掺混,附面层低能流体的潜流和摩擦。流道中、后部的泄漏流体已摆脱泄漏涡的卷吸,在剪切应力作用下靠近吸力面向出口运动。
随机匣与隔板相对速度的增加,泄漏涡横向运动削弱,分离线向隔板吸力面靠近,但间隙区域的熵值却是增加的。这是因为,机匣与隔板相对速度较大时,端壁附面层黏性剪切力增大,其方向与间隙流动方向相反,因此,泄漏流体的横向运动受到抑制;与此同时,黏性剪切力的增加促使泄漏流、主流、附面层之间的相互作用增强,所导致的掺混损失相应增加,特别是隔板尾缘区域,由于剪切应力的增加,泄漏流体从吸力面侧到压力面侧的回流现象更明显,流动损失更大,熵值更高。
间隙中截面受机匣与隔板相对运动的影响更显著,分离线和再附线均向隔板靠近,特别是吸力面侧,仅前缘附近泄漏流体参与泄漏涡的形成,隔板中、后部泄漏流体完全摆脱泄漏涡的卷吸,靠近吸力面向出口运动,随相对速度的增加,尾缘附近有更多气流从吸力面侧回流至压力面侧。
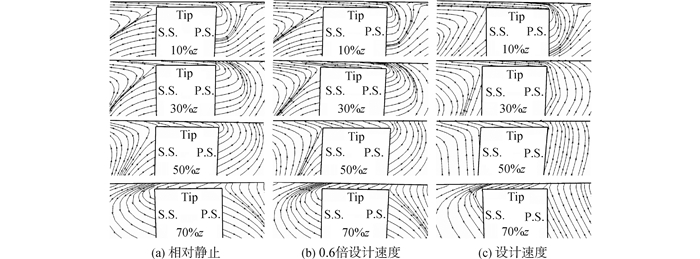
图 5给出了间隙内的流线分布,可以看出,间隙内流线几乎与隔板顶部平行,吸力面与机匣角区气流的运动出现分支,一支在泄漏流作用下发生折转,另一支靠近吸力面运动,压力面与机匣角区气流的运动也出现分界,其中,近隔板顶部区域气流在压、吸力面压差作用下通过间隙泄漏到吸力面侧,另一部分气流从压力面侧向相邻隔板吸力面运动(图 5 10%z);流道中、后部的泄漏流动更强,压力面角区气流几乎都越过间隙形成间隙泄漏流,吸力面角区气流被泄漏涡卷吸,促进泄漏涡壮大,受径向压力梯度影响,间隙内气流斜向左上方流出间隙(图 5 30%z和50%z);斜激波之后,三维流道内压力场改变,隔板尾缘间隙内气流的运动明显变化,一方面,泄漏流流出间隙,并斜向右下方卷曲,另一方面,吸力面侧气流经间隙流回到压力面侧(图 5 70%z)。
|
| 图5 隔板顶部间隙内流线 Figure 5 Streamlines near the tip of the strake wall inside clearance |
从图 5还可看出,随机匣与隔板相对速度的增加,黏性剪切力变大,吸力面角区气流一致向左折转,泄漏流吸卷更多附面层,气流之间的掺混更加严重,损失相应增加;间隙内不存在复杂的三维流动,部分气流在径向力作用下向左上方运动并贴附于机匣内表面。
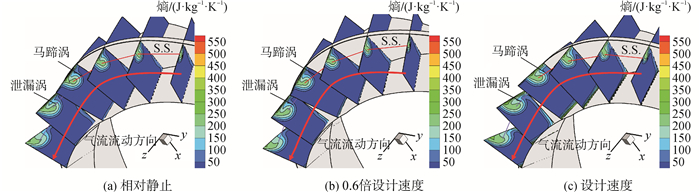
2.2 三维流道内部流动特性图 6给出了不同S3流面熵等值线,可以看出,沿流向马蹄涡吸力面分支尺度变大,强度增加,泄漏流的挤压作用促使其远离吸力面向下端壁发展,并在流道中、后部破碎,破碎之后的马蹄涡与泄漏流掺混;泄漏流吸卷附面层和主流并在流道后部形成泄漏涡,泄漏涡尺度较大,形成之后向流道中央发展;三维流道中的损失主要来源于泄漏损失,马蹄涡、泄漏涡和主流之间的掺混损失,环壁面低能流体迁移、摩擦、掺混所导致的损失。
|
| 图6 沿流向不同S3流面熵等值线 Figure 6 Distribution of entropy on different S3 surfaces |
机匣与隔板相对静止时,气流在横向压差作用下自压力面侧向吸力面侧泄漏,泄漏流横向运动较强。对比隔板顶部附近S1流面和间隙中分面可知(图 3(a)和4(a)),间隙中分面的分离线更靠近吸力面,说明机匣与隔板相对静止虽然降低了黏性剪切力的作用,但端壁的壁面效应对间隙流动却存在影响。
机匣与隔板相对运动,将有更多气流从压力面侧泄漏到吸力面侧(图 6(a)~(c)),泄漏涡强度增加,但横向运动受到抑制。这与传统涡轮的研究结果不完全相同,Yara[4]、Srinivasan[10]、牛茂升[17]以及王大磊[18]的研究都表明机匣相对运动降低了间隙泄漏流流量,削弱了泄漏涡强度;此外,牛茂升[17]和王大磊[18]的研究还表明,机匣相对转动使得叶片前缘吸力面气流克服横向压差进入间隙,从而阻塞泄漏流。而图 3和4则表明,机匣相对运动,导致泄漏流动严重,泄漏损失增加,但泄漏涡横向运动得到抑制;从图 5可以看出,机匣相对运动,促使更多气流越过间隙泄漏到吸力面侧。分析原因,主要有两方面:一是随机匣与隔板相对速度的增加,顶部区域的径向压差变大(图 7),气流沿隔板自下而上的潜流运动加强,有限时间内将有更多气流越过间隙;二是对比传统涡轮叶片,超声速膨胀器隔板较薄,顶部间隙的横向尺寸较小,剪切应力对泄漏流的抑制作用有限。
|
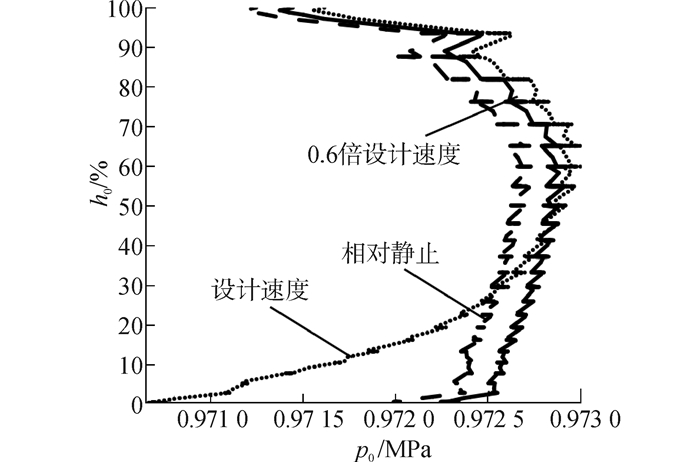
| 图7 进口静压沿径向分布 Figure 7 Distribution of static pressure at inlet in the radial direction |
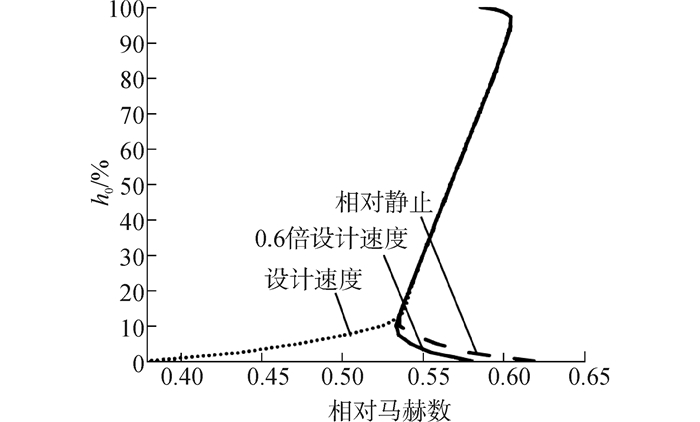
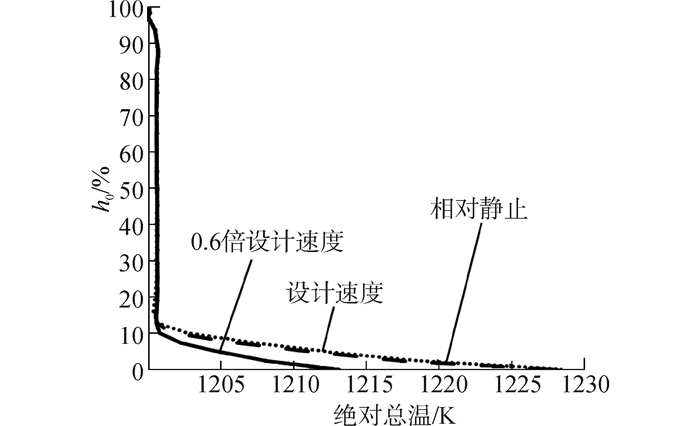
图 6还说明,机匣与隔板的相对运动,导致附面层损失的增加,特别是二者相对速度达到设计速度之后,下端壁和吸力面的熵值显著增加,流动损失很大。从图 7~9可知,机匣与隔板相对速度较大时,入口近下端壁气流静压低、速度低,而总温高,即下端壁附近是低能流体汇聚区,沿流向低能流体不断积累,低能流体之间以及与壁面的摩擦损失大,因此,下端壁熵值高;此外,径向压差变大(图 7),气流沿壁面的迁移运动增强,由此而导致的损失增加,吸力面熵值较高。
|
| 图8 进口相对马赫数沿径向分布 Figure 8 Distribution of relative Mach number contour at inlet in the radial direction |
|
| 图9 进口绝对总温沿径向分布 Figure 9 Distribution of total temperature at inlet in the radial direction |
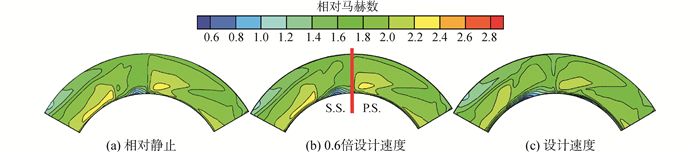
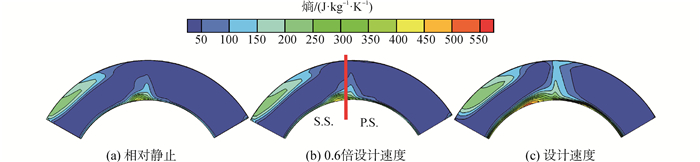
图 10和11给出了出口相对马赫数和熵分布云图,可以看出,出口主要存在两个高速区,一是压力面与下端壁相接角区,二是远离吸力面的下端壁;低速区主要位于吸力面与下端壁相接角区以及流道中央上端壁附近;随机匣与隔板相对速度增加,气流最高速度降低,高速区影响范围缩减,而低速区扩大,特别是上端壁附近的低速区,范围扩大的同时向吸力面靠近。 2.3机匣与隔板相对速度大时,入口下端壁附近气流静压低,速度也低(图 7和8),导致气流不能充分膨胀,加速性变差,因此,三维流道内气流最高速度降低,高速影响范围缩减。入口处下端壁附近气流速度低,低能流体沿流向集聚的同时在横向压差作用下向吸力面与下端壁相接角区运动,出口斜激波打在吸力面上,导致附面层分离,分离后的附面层沿节距方向运动,在离吸力面不远的下端壁形成一个较大的低速气流团。机匣与隔板相对速度的增加,促使更多泄漏流体到达吸力面侧,泄漏涡增强,但其横向运动受到黏性剪切力的抑制,为此,上端壁低速区范围扩大,但其空间位置向吸力面迁移;出口损失增加,熵值较高,其中,泄漏损失、端壁损失、附面层分离和掺混损失都有所增加。
|
| 图10 出口相对马赫数等值线图 Figure 10 Relative Mach number isoline maps at outlet |
|
| 图11 出口熵等值线 Figure 11 Entropy isoline maps at outlet |
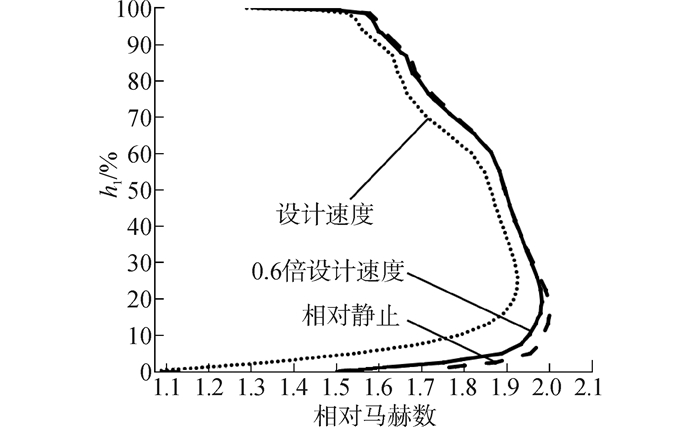
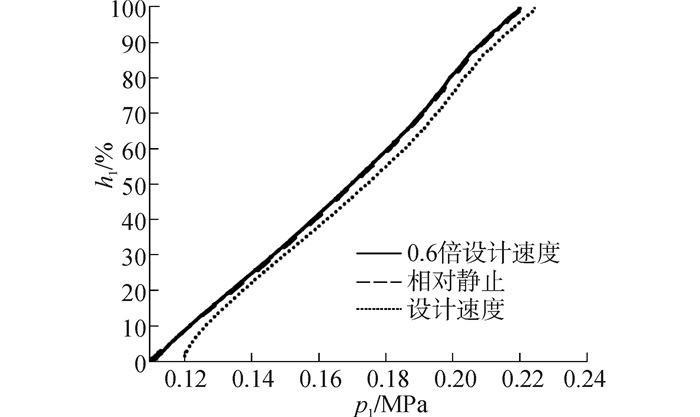
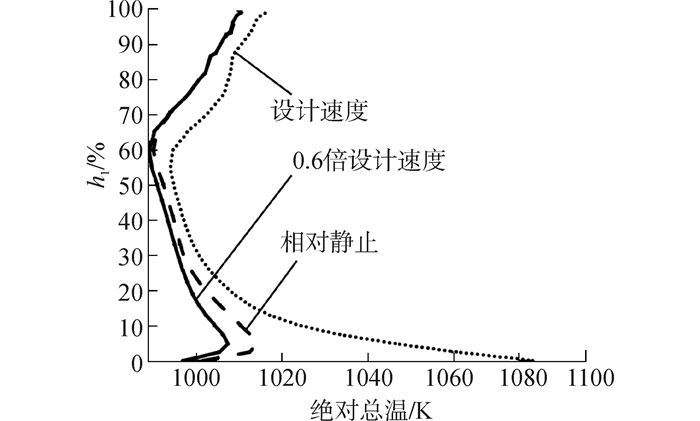
从图 12~14给出的出口气动参数沿径向的分布可以看出,10%h1~20%h1相对隔板高度范围内的气流速度最高;20%h1~60%h1范围内的气流速度较稳定;60%h1相对隔板高度之后,随相对高度增加,气流速度迅速降低,而总温较高,这说明三维流道下半平面内气流的加速性最好,泄漏涡的影响范围扩展到60%h1相对隔板高度。当机匣与隔板相对速度达到设计速度,沿径向出口相对马赫数降低,总温上升,特别是近下端壁区域,气流速度迅速降低,总温很高。
|
| 图12 出口相对马赫数沿径向分布 Figure 12 Distribution of relative Mach number contour at outlet in the radial direction |
|
| 图13 出口静压沿径向分布 Figure 13 Distribution of static pressure at outlet in the radial direction |
|
| 图14 出口绝对总温沿径向分布 Figure 14 Distribution of total temperature at outlet in the radial direction |
表 1给出了超声速膨胀器的主要性能参数,可以看出,机匣与隔板的相对运动导致超声速膨胀器出口平均绝对马赫数降低、膨胀比上升、损失系数增加,效率下降。其原因是,二者之间的相对运动造成入口下端壁附近气流速度低、静压低,而超声速膨胀器主要依靠下端壁向外的扩张来实现气流的膨胀加速,因此,三维流道内气流的加速性变差,出口速度低。此外,下端壁低能流体沿流向的集聚,斜激波与附面层的相互作用,吸力面附面层迁移以及隔板顶部的泄漏流动都相应增强,导致超声速膨胀器内部总的流动损失增加,损失系数增加,效率下降。
| 相对速度 | 出口平均绝对马赫数 | 静压比 | 膨胀比 | 等熵效率 | 损失系数 |
| 静止 | 1.262 | 5.378 | 2.145 | 0.853 | 0.134 |
| 0.3 | 1.260 | 5.397 | 2.156 | 0.851 | 0.137 |
| 0.6 | 1.256 | 5.404 | 2.165 | 0.847 | 0.142 |
| 0.9 | 1.250 | 5.388 | 2.172 | 0.843 | 0.146 |
| 1 | 1.213 | 5.259 | 2.217 | 0.799 | 0.174 |
本文采用数值方法对超声速膨胀器的三维流场进行了数值研究,揭示了隔板与机匣相对运动对超声速膨胀器隔板顶部区域、三维流道内部及出口气动参数影响的规律。通过本文研究,可得到以下结论:
1) 泄漏流与主流、角区附面层掺混所导致的损失是超声速膨胀器间隙区域流动损失的主要来源,吸力面靠近分离线右侧区域的流动损失最大,压力面附近除尾缘外流动损失均较低;同常规涡轮相比,超声速膨胀器间隙内的流动结构相对简单。
2) 机匣与隔板相对静止降低了黏性剪切力的作用,但端壁的壁面效应对间隙流动却存在影响;端壁相对运动削弱了泄漏涡的横向运动,分离线向吸力面靠近,与常规涡轮不同的是,泄漏流量却是增加的,泄漏涡增强,由此导致的流动损失上升。
3) 随机匣与隔板相对速度的增加,三维流道内气流最高速度降低,高速影响范围缩减,而低速区扩大,特别是上端壁附近的低速区,范围扩大的同时向吸力面靠近。此外,端壁和吸力面低能流体所导致的损失增加。
4)端壁相对运动导致超声速膨胀器出口平均绝对马赫数降低、膨胀比上升、损失系数增加,效率下降。
| [1] | GVMMER V, GOLLER M, SWOBODA M. Numerical investigation of end wall boundary layer removal on highly loaded axial compressor blade rows[J]. Journal of turbomachinery, 2008, 130(1): 011015. |
| [2] |
杨策, 马朝臣, 王延生, 等. 透平机械叶尖间隙流场研究的进展[J].
力学进展, 2001, 31(1): 70–83.
YANG Ce, MA Chaochen, WANG Yansheng, et al. A review of studies on turbomachinery tip gap leakage flow[J]. Advances in mechanics, 2001, 31(1): 70–83. |
| [3] | GRAHAM J A H. Investigation of a tip clearance cascade in a water analogy rig[J]. Journal of engineering for gas turbines and power, 1986, 108(1): 38–46. |
| [4] | YARAS M I, SJOLANDER S A. Prediction of tip-leakage losses in axial turbines[J]. Journal of turbomachinery, 1992, 114(1): 204–210. |
| [5] | LUO J, LAKSHMINARAYANA B. Three-dimensional Navier-Stokes analysis of turbine rotor; tip-leakage flowfield[C]//Proceedings of ASME Turbo Expo 1997: the International Gas Turbine and Aeroengine Congress and Exhibition. Orlando, 1997. |
| [6] | XIAO Xinwen. Investigation of tip clearance flow physics in axial flow turbine rotors[D]. Pennsylvania: The Pennsylvania State University, 2001. |
| [7] | MCCARTER A A, ASSISTANT G, XIAO Xinwen, et al. Tip clearance effects in a turbine rotor: part Ⅱ-velocity field and flow physics[J]. Journal of turbomachinery, 2001, 123(2): 305–313. |
| [8] | TALLMAN J, LAKSHMINARAYANA B. Numerical simulation of tip leakage flows in axial flow turbines, with emphasis on flow physics: partⅠ-effect of tip clearance height[J]. Journal of turbomachinery, 2000, 123(2): 314–323. |
| [9] | TALLMAN J, LAKSHMINARAYANA B. Numerical simulation of tip leakage flows in axial flow turbines, with emphasis on flow physics: partⅡ-effect of outer casing relative motion[J]. Journal of turbomachinery, 2000, 123(2): 314–333. |
| [10] | SRINIVASAN V, GOLDSTEIN R J. Effect of endwall motion on blade tip heat transfer[J]. Journal of turbomachinery, 2003, 125(2): 267–273. |
| [11] | YANG Dianliang, YU Xiaobing, FENG Zhenping. Investigation of leakage flow and heat transfer in a gas turbine blade tip with emphasis on the effect of rotation[J]. Journal of turbomachinery, 2010, 132(4): 041010. |
| [12] | ACHARYA S, MOREAUX L. Numerical study of the flow past a turbine blade tip: effect of relative motion between blade and shroud[J]. Journal of turbomachinery, 2013, 136(3): 031015. |
| [13] |
牛茂升, 臧述升. 叶片转动对涡轮间隙内部流动影响的数值研究[J].
力学学报, 2009, 41(5): 628–634.
NIU Maosheng, ZANG Shusheng. Simulation of effects of blade rotation on tip clearacne flow in axial turbines[J]. Chinese journal of theoretical and applied mechanics, 2009, 41(5): 628–634. |
| [14] |
钟兢军, 黄振宇, 杨凌, 等. 超声速膨胀器设计及其内部流动研究[J].
工程热物理学报, 2015, 36(1): 60–66.
ZHONG Jingjun, HUANG Zhenyu, YANG Ling, et al. Research on design and internal flow of supersonic expander[J]. Journal of engineering thermophysics, 2015, 36(1): 60–66. |
| [15] | HUANG Zhenyu, ZHONG Jingjun, YANG Ling, et al. Research on the structure design and flow field of supersonic expander[C]//Proceedings of ASME Turbo Expo 2014: Turbine Technical Conference and Exposition. Düsseldorf, 2014. |
| [16] |
钟兢军, 黄振宇, 杨凌, 等. 膨胀型面造型方式对超声速膨胀器流场及性能的影响[J].
中国电机工程学报, 2014, 34(35): 6329–6337.
ZHONG Jingjun, HUANG Zhenyu, YANG Ling, et al. Influence of different expansion surface shapes on the flow field and performance of a supersonic expander[J]. Proceedings of the CSEE, 2014, 34(35): 6329–6337. |
| [17] |
牛茂升, 臧述升. 机匣相对转动对涡轮叶顶间隙流动的影响[J].
空气动力学学报, 2009, 27(5): 597–601.
NIU Maosheng, ZANG Shusheng. Effects of endwall relative motion on tip clearance flow in turbine rotors[J]. Acta aerodynamica sinica, 2009, 27(5): 597–601. |
| [18] | 王大磊. 跨音速高压涡轮转子叶尖间隙泄漏流动及控制方法研究[D]. 北京: 清华大学, 2012. WANG Dalei. Research on tip leakage flow and tip desensitization of a transonic high turbine[D]. Beijing: Tsinghua University, 2012. |



