随着近代石油危机的出现,为达到节能减排的目的,风力助航船的研究与推广极有可能会成为未来航运业竞相发展的一种新趋势。然而,目前对于风帆助航船舶的研究多集中于风帆类型、机桨帆配合操纵分析及风帆助航船舶的节能分析,少有研究将重点着眼于风帆助航船舶的运动控制上。这主要是由于风帆助航船舶是一个具有强干扰和模型不确定性的非线性时变系统[1],其模型建立及控制较为困难。近年来,随着世界经济发展,小型帆船的出现使学者们对帆船运动控制重视程度日益提高,许多相关文献在近年来陆续发表。 杨承恩[1]以神经网络的控制方法对小型帆船进行自适应控制,并与PID控制进行了比较。 XIAO[2]采用反演方法对帆船进行了航向控制。葛艳[3]针对帆船的非线性提出了一种基于Sugeno模糊模型的控制方法,成功对舵角与帆角进行了控制。这些帆船控制方法为风帆助航船舶运动控制的研究提供了参考。
由于风帆助航船舶运动数学模型具有非线性、不确定性,且受外界风浪流扰动等特点,因而很难用数学模型精确描述。滑模控制作为一种具有强鲁棒性的非线性控制方法,能够用于尝试解决此类非线性问题。目前,滑模控制器有多种设计方法,如直接对模型设计非线性滑模控制器[4],或是对模型线性化处理后设计滑模控制器[5],有些学者则着眼于滑模面的设计,如采用反步法[6-7]或构造多层滑模的方法[8-10]设计控制器。有些学者还结合模糊控制[11]或神经网络控制[12-13]来逼近系统不确定函数。然而上述方法或是处理方法复杂,或是对系统模型的准确性有一定程度的依赖,很难用于处理如风帆助航船舶这类复杂非线性系统。为了解决上述问题,可以借鉴HUANG[14]所采用的递归滑模法,但这种方法需要对模型控制增益进行线性化处理,不能直接用于船舶非线性模型。卜仁祥、边信黔等人[15-16]采用非线性迭代滑模法分别对水面船舶、水下机器人进行了航向、航迹跟踪控制,但该控制器中滑模参数是固定不变的,无法使控制器参数在不同环境下获得最优值,控制器缺乏自适应性。
本文将针对风帆助航船舶运动非线性系统,引入模糊逻辑对滑模参数进行自适应调节,提出一种基于滑模面反馈的模糊自适应非线性迭代滑模控制方法。该控制方法无需对模型进行线性化处理或对模型的不确定项及干扰进行估计,且对抖振有着很好的抑制效果。 最后,以“文竹海”号76000DWT散货船为目标,设计风帆助航船舶运动的模糊自适应迭代滑模控制器,在风浪等干扰环境下进行控制仿真,并将仿真结果与PID控制、迭代滑模控制进行对比分析。
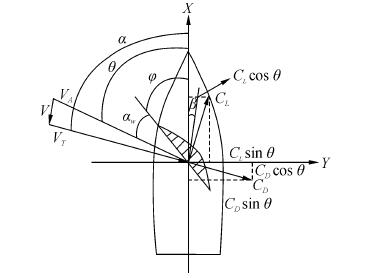
1 风帆助航船舶运动数学模型风帆助航船舶的风帆受力情况如图 1所示,该图以船舶重心为原点建立直角坐标系,定义船首方向为x轴正方向,纵轴线右侧为y轴正方向,其中,设VT为真风风速,α为真风与航向的夹角,VA为相对风速,θ为相对风向角,αW为几何攻角,φ为转帆角,β为横漂角,CL与CD为升、阻力系数。
|
| 图1 风帆受力示意图 Figure 1 Sailing force schematic diagram |
根据风帆受力的分析,可得
| $ \left\{ \begin{array}{l} {F_L} = \frac{1}{2}\rho S{V_A}^2{C_L}\\ {F_D} = \frac{1}{2}\rho S{V_A}^2{C_D}\\ {X_S} = {F_L}\sin \theta - {F_D}\cos \theta \\ {Y_S} = {F_L}\cos \theta + {F_D}\sin \theta \\ {N_S} = {C_M}\frac{1}{2}\rho S{V_A}^2 \cdot {L_{XS}}\\ {L_S} = {Y_S} \cdot {L_{ZS}} \end{array} \right. $ | (1) |
式中:XS为帆船前进方向受力,YS为横漂方向受力,NS为艏摇力矩,LS为横摇力矩,ρ为空气密度,S为帆的面积,LXS为帆的弦长,LZS为帆的重心到船重心在z轴方向上的距离,CM为转矩系数,N为帆的个数。在此公式中,假设风角右舷为正,左舷为负。 由于风帆控制不是重点,因而假设风帆攻角αw时刻处于最佳攻角状态,即获得风帆最大推力状态。针对风帆助航船舶模型,基于MMG分离模型思想,结合式(1)可将其运动惯性数学模型描述为:
| $ \left\{ {\begin{array}{*{20}{l}} {\left( {m + {m_x}} \right)\dot u; - \left( {m + {m_y}} \right)vr = }\\ {\;\;\;\;\;\;{X_H} + {X_P} + {X_R} + {X_{{\rm{wind}}}} + {X_{{\rm{wave}}}} + {X_S}}\\ {\left( {m + {m_y}} \right)\dot v + \left( {m + {m_x}} \right)ur = }\\ {\;\;\;\;\;\;{Y_H} + {Y_P} + {Y_R} + {Y_{wind}} + {Y_{wave}} + {Y_S}}\\ {\left( {{I_{zz}} + {I_{zz}}} \right)\dot r = {N_H} + {N_P} + {N_R} + {N_{{\rm{wind}}}} + {N_{wave}} + {N_S}}\\ {\left( {{I_{{\rm{xx}}}}{\rm{ + }}{{\rm{J}}_{{\rm{xx}}}}} \right)\dot p = {L_H} + {L_R} + + {L_{wave}} + {L_{wind}} + {L_S}} \end{array}} \right. $ | (2) |
式中:X表示船前进向受力,Y表示垂直于船前进方向受力,N表示艏摇力矩,L表示横摇力矩,下角标H表示裸船体,P表示螺旋桨,R表示舵,wave表示波浪,wind表示风,u为纵荡速度,v为横荡速度,r为首摇角速度、p为横摇角速度,S表示风帆,mx为附体坐标系下x轴的附加水质量,my为附体坐标系下y轴的附加水质量,Jzz为附体坐标系下z轴的附加转动惯量,Jxx为附体坐标系下x轴的附加转动惯量,Ixx为附体坐标系下的x轴的转动惯量,Izz为 附体坐标系下的y轴的转动惯量。
根据船舶物理特性可知,在船舶实际操作过程中,由于受到控制能量的限制,即使航向偏差较大,转艏角速度r也不能太大,而在航向偏差较小时,为保证稳定时间和控制品质,转艏角速度需要随航向偏差的减小逐渐减小。综上可得如下约束条件:
| $ \left\{ \begin{array}{l} \left| r \right| \le {r_{\max }}\\ \left| \delta \right| \le {\delta _{\max }} \end{array} \right. $ | (3) |
式中:rmax为船舶最大转艏角速度。常规大型船舶满舵旋回通常需要5~10 min,最大转艏角速度为0.01~0.02 rad/s;δmax为船舶最大舵角,常规船舶为35°。
2 风帆助航船舶运动控制器设计 2.1 迭代滑模控制器的设计根据式(2)所建立的模型,为实现风帆助航船舶运动控制,可将其航向控制问题描述为:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot \psi = r}\\ {\dot r = \left( {{N_H} + {N_p} + {N_R} + {N_{wind}} + {N_{wave}} + {N_S}} \right) \cdot }\\ {\;\;\;\;\;\;\;\;\;{{\left( {{I_{zz}} + {J_{zz}}} \right)}^{ - 1}} = f\left( {r,\delta ,t} \right) + d\left( {\psi ,t} \right)}\\ {y = \psi } \end{array}} \right. $ | (4) |
假设f(r,δ,t)为对δ存在连续偏导数的光滑未知连续函数,d(Ψ,t)为未知外界扰动(风、浪、风帆等干扰)。由于式(4)中的干扰项会使系统非线性与时变性增强,因而会使船舶运动控制更加困难。虽然经过线性化处理后依然可建立控制器,但这样会忽略部分非线性环节,使得控制准确性降低。为解决上述问题,将船舶运动控制问题化为标量零阶系统的镇定控制问题。以船舶实际航向Ψ跟踪设定航向Ψd为控制目标,设计非线性迭代滑动模态:
| $ \left\{ {\begin{array}{*{20}{l}} {{s_1}\left( {{\psi _e}} \right) = {k_1}\tanh \left( {{k_0}{\psi _e}} \right) + {{\dot \psi }_e}}\\ {{s_2}\left( {{s_1}} \right) = {k_3}\tanh \left( {{k_2}{s_1}} \right) + {{\dot s}_1}} \end{array}} \right. $ | (5) |
式中:ki∈R+(i=0,1,2,3),Ψe=Ψ-Ψd为航向的跟踪误差,$ \tanh \left( x \right) = \frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}} $为严格有界性的双曲正切非线性函数。根据式(5)可知,当s1→0,有Ψe→-k1tanh(k0Ψe),当航向误差Ψe较大时,以接近固定速率(即k1)收敛,当Ψe较小时以指数规律收敛,k0为压缩或拉伸坐标而设置,与k1共同决定相平面原点处的滑模斜率。通过滑模迭代设计,系统控制目标转化为对s2的镇定控制。为了保证系统在s2→0时,得到s1→0及Ψe→0,式(5)应满足k3≥k1。
为避免对未知函数f(r,δ,t)、d(Ψ,t)的估计,利用滑模面s2的反馈来计算控制舵角的变化率[15],得到
| $ \dot \delta = - {k_d}{s_2} - \varepsilon {\rm{sgn}}\left( {{s_2}} \right) $ | (6) |
式中kd,ε∈R+。
为证明式(5)中航向跟踪误差Ψe是渐近收敛的,根据Lyapunov稳定性理论构造Lyapunov函数V并求导可得:
| $ V = \frac{1}{2}{s_2}^2 $ | (7) |
| $ V = {s_2}{\dot s_2} = {s_2}\frac{{\partial {s_2}}}{{\partial \delta }}\dot \delta $ | (8) |
其中,s2的展开式为
| $ {s_2} = {k_3}\tanh \left( {{k_2}{s_1}} \right) + \frac{{{k_1}{k_0}{\psi _e}}}{{{{\cosh }^2}\left( {{k_0}{\psi _e}} \right)}} + {\bar \psi _e} $ | (9) |
结合风帆助航船舶数学模型(2)可以发现,式(8)中仅Ψe对δ求导后不为零,且Ψe项中仅有NR项与输入δ有关,可表示为:
| $ {N_R} = h\left( x \right)\cos \delta \sin {\alpha _R} $ | (10) |
式中:αR为有效冲角,大小与舵角输入δ有关且符号相同,h(x)为一个恒正的函数。综上可知NR对δ求导在δ∈(-35,35)是恒大于零的。因此式(9)对δ求导可得
| $ \frac{{\partial {s_2}}}{{\partial \delta }} = \frac{{\partial {N_R}}}{{\partial \delta }} \ge 0 $ | (11) |
结合式(8)可知V的符号取决于s2与δ两项,因此结合式(6)可得
| $ {s_2}\dot \delta = - {k_d}{\left( {{s_2}} \right)^2} - \varepsilon \left| {{s_2}} \right| \le 0 $ | (12) |
综合式(8)、(11)、(12)即可得
| $ V = {s_2}{\dot s_2} = {s_2}\frac{{\partial {s_2}}}{{\partial \delta }}\dot \delta \le 0 $ | (13) |
由Lyapunov稳定性定理可知,在控制率(6)的作用下,系统(4)的航向跟踪误差Ψe是渐近稳定的。
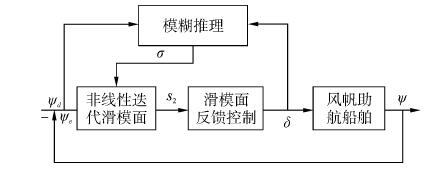
2.2 模糊自适应迭代滑模控制器的设计前面所设计的迭代滑模控制器无需对系统的不确定项和扰动等进行估计。在不同外界环境和工况下,控制器滑模参数若能自适应地调整,则系统控制性能将得到提升。为此,对滑模参数进行优化重点考虑以下两点:首先,船舶在实际航行时,除非遇到紧急状况,否则禁止使用满舵,这主要是由于船舶在满舵情况下容易产生大幅度横倾,不仅会使船员身体不适,更会增大倾覆的危险性。其次,由式(5)可知,所设计系统的控制收敛速率会随着参数k0~k3的变化而改变,为了使船舶尽快到达设定航向,控制器的滑模参数应随航向跟踪误差的大小而改变。若在航向跟踪误差较大时,可以适当加快控制速率;而当舵角过大时,则应适当减小控制速率。基于上述分析,设计出如图 2所示的风帆助航船舶运动模糊自适应迭代滑模控制结构图。
|
| 图2 风帆助航船舶运动的模糊自适应迭代滑模控制结构图 Figure 2 FAISMC control structure for sail-assisted ship motion |
图 2中对控制器滑模参数做以下处理:
| $ {\hat k_i} = {k_i}\left( {1 + \sigma } \right)\left( {i = 0,1,2,3} \right) $ | (14) |
通过调节参数σ得到参数ki的调节值ki,达到对控制器滑模参数优化目的。其中模糊推理系统输入为航向误差Ψe与控制舵角δ,输出为调节参数σ,设计的模糊规则如表 1所示。
| δ | NB | NS | Z | PS | PB |
| NB | NB | NB | NB | NB | NB |
| NS | PS | PS | PB | PS | PS |
| Z | PB | PS | Z | PS | PB |
| PS | PS | PS | PB | PS | PS |
| PB | NB | NB | NB | NB | NB |
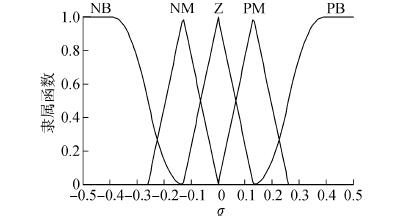
基于表 1的模糊规则,使用图 3所示三角型、Z型、S型相结合的隶属度函数,其取值如式(15):
|
| 图3 输出量σ的隶属函数 Figure 3 Membership function of the output variable σ |
| $ \left\{ \begin{array}{l} {\psi _e} = \left\{ {NB\left( { - 5.0,- 0.3} \right),NS\left( { - 0.6,0} \right),} \right.\\ \left. {Z\left( { - 0.3,0.3} \right),PM\left( {0,0.6} \right),PB\left( {0.3,5.0} \right)} \right\}\\ \delta = \left\{ {NB\left( { - 35,- 8} \right),NS\left( { - 16,0} \right),Z\left( { - 8,8} \right),} \right.\\ \left. {PM\left( {0,16,PB\left( {8,35} \right)} \right.} \right\}\\ \sigma = \left\{ {NB\left( { - 0.5,- 0.13} \right),NS\left( { - 0.26,0} \right),} \right.\\ \left. {Z\left( { - 0.13,0.13} \right),PM\left( {0,0.26} \right),PB\left( {0.13,0.5} \right)} \right\} \end{array} \right. $ | (15) |
采用重心法解模糊化后可得
| $ \left\{ \begin{array}{l} \sigma = \frac{{\sum\limits_{l = 1}^M {{u_i} \cdot {\mu _{FRj}}} }}{{\sum\limits_{l = 1}^M {{\mu _{FRj}}} }}\\ {\mu _{FRj}} = {\mu _\beta }\left( {{\psi _e}} \right) \cdot {\mu _\beta }\left( \delta \right) \end{array} \right. $ | (16) |
式中:M为模糊规则数,ui为输出模糊集合元素,β表示PB、PS、Z、NS、NB,μFRj为第j条规则下精确输入的隶属函数。 经模糊推理与清晰化后可得控制器优化后的滑动模态为
| $ \left\{ \begin{array}{*{35}{l}} {{{\hat{s}}}_{1}}\left( {{\psi }_{e}} \right)={{{\hat{k}}}_{1}}\tanh \left( {{{\hat{k}}}_{0}}{{\psi }_{e}} \right)+{{{\dot{\psi }}}_{e}} \\ {{{\hat{s}}}_{2}}\left( {{{\hat{s}}}_{1}} \right)={{{\hat{k}}}_{3}}\tanh \left( {{{\hat{k}}}_{2}}{{{\hat{s}}}_{1}} \right)+{{{\dot{\hat{s}}}}_{1}} \\ \end{array} \right. $ | (17) |
同时,滑模面反馈控制率转换为
| $ \dot{\hat{\delta }}=-{{k}_{s}}{{\hat{s}}_{2}}-\varepsilon \text{sgn}\left( {{{\hat{s}}}_{2}} \right) $ | (18) |
结合式(18)可知,通过控制滑模面反馈即可调节舵机的输入舵角。在航向跟踪误差较大时,控制器参数增大,控制器速率增加。当舵角过大时,控制器参数减小,控制速率减小,输入舵角减小。经过以上过程即可实现控制器参数的优化。
3 仿真研究以“文竹海”号76000DWT远洋散货船为对象建立风帆助航船舶模型并设计控制器。目标船舶与风帆参数如表 2所示。
| 船舶主要参数 | 数值 |
| 垂线间间长LPP/m | 217 |
| 型宽B/m | 32.26 |
| 型深D/m | 19.6 |
| 设计吃水T/m | 14.4 |
| 方形系数Cb | 0.76 |
| 排水量Δt/DWT | 76 000 |
| 风帆面积S/m2 | 720 |
| 风帆个数 | 4 |
| 拱度比 | 0.14 |
| 展弦比 | 1.5 |
仿真过程中假设流力、流向在行驶过程中为定值,选用风级在4~8级风之间,同时假设风帆角时刻处于最佳攻角状态(即风帆最大推力状态)。
3.1 无风作用时的控制仿真设风帆助航船舶重载低速稳定运行,起始主机转速91 r/min、船速13 kn,设定航向为15°,分别使用滑模迭代控制器、模糊滑模迭代控制器、PID控制器对风帆助航船舶进行船舶运动控制仿真。设定k0~k3的初始值分别为0.004 3、6、0.025、8,ks=100,ε=0.001,PID参数为kp=2.3,kd=76.8。
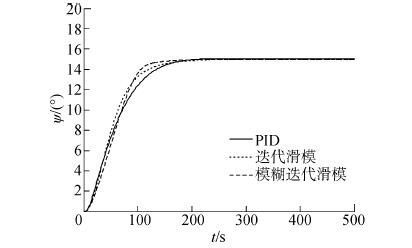
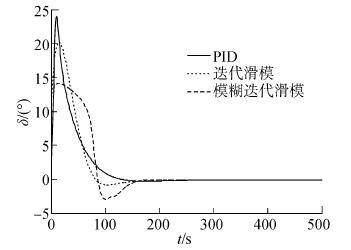
图 4~6为风帆助航船舶在无风作用时(即不起帆,相当于普通船舶)航向、舵角和参数变化趋势。由图 4可知,3种控制器控制速率基本相同,目标船舶在200 s时基本达到设定航向。但3种控制器在到达设定航向前,舵角的变化趋势有所差异。采用PID控制时舵角最大值为24°,采用迭代滑模控制时最大舵角为20°,采用模糊迭代滑模控制时舵角保持在15°以下,符合实际要求。
|
| 图4 航向曲线(无风作用) Figure 4 The course angel curve (no wind) |
|
| 图5 舵角曲线(无风作用) Figure 5 The rudder angle curve (without wind) |
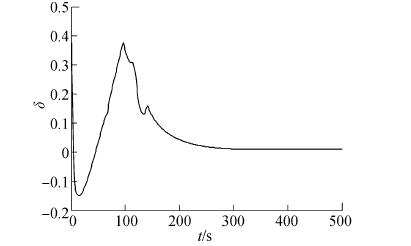
图 6为模糊逻辑输出σ的变化趋势图,由于起始命令舵角很大,σ将先减小使控制器控制速率下降,随着船舶运动逐渐趋于平稳,σ逐渐增加以恢复并加快控制器控制速率。当偏航角接近设定航向时,σ将会减小,使控制器在下一次命令到来时能够快速的调节舵角。
|
| 图6 参数σ曲线(无风作用) Figure 6 The parameter σ curve (without wind) |
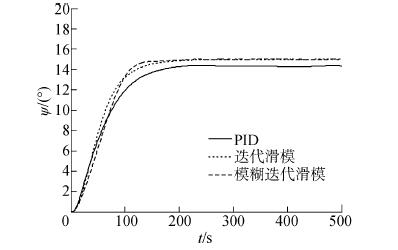
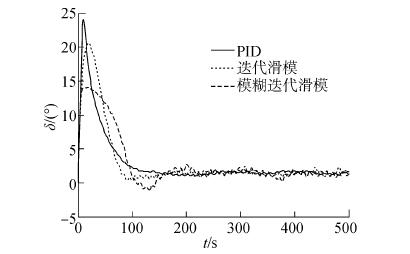
假设在风速为10 m/s,风向130°的来风作用下,只考虑波浪的规则波对船舶运动的影响,控制参数和3.1节中相同,3种控制器的控制效果如图 7~9所示,可看出控制效果具有明显差异。采用PID控制时船舶无法精确到达设定航向,而采用模糊迭代控制与迭代控制时可准确到达设定航向。在有风作用后采用迭代滑模控制时的舵角最大值增加到20°以上,采用模糊迭代滑模控制时的舵角依然可以保持在15°以下。模糊逻辑输出σ与无风作用时的变化趋势图基本相同。
|
| 图7 航向曲线(有风作用,设定航向15°) Figure 7 The course angel curve (with wind, set course 15°) |
|
| 图8 舵角曲线(有风作用,设定航向15°) Figure 8 The rudder angle curve (with wind, set course 15°) |
为证明控制器的自适应性,得到控制器对风帆助航船舶在不同设定航向下的控制效果,设定航向为30°,分别使用滑模迭代控制器与模糊滑模迭代控制器对风帆助航船舶进行控制仿真,可得图 10~12曲线图。
|
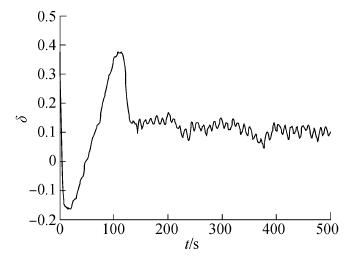
| 图9 参数σ曲线(有风作用,设定航向15°) Figure 9 The parameter σ curve (with wind, set course 15°) |
|
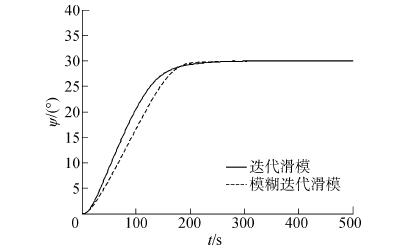
| 图10 航向曲线(有风作用,设定航向30°) Figure 10 The course angel curve (with wind, set course 30°) |
|
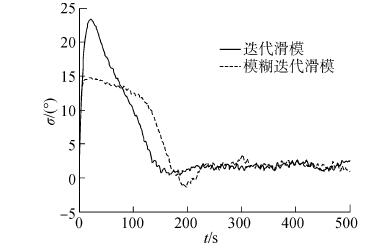
| 图11 舵角曲线(有风作用,设定航向30°) Figure 11 The rudder angle curve (with wind, set course 30°) |
|
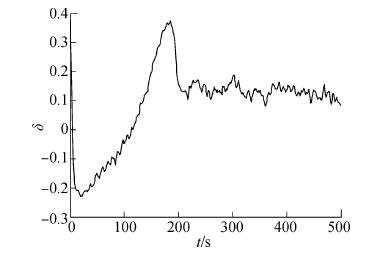
| 图12 参数σ曲线(有风作用,设定航向30°) Figure 12 The parameter σ curve (with wind, set course 30°) |
由图 10所示的偏航角变化情况可知,两种控制器的控制速率与控制效果基本相同,均可在300 s之前到达设定航向。但相较于设定航向为15°时,舵角变化更为剧烈,最大舵角接近25°,而采用模糊迭代滑模控制时舵角可以保持在15°以下。这主要是由于相较于之前设定航向为15°的时候,系数σ在前100 s为避免舵角过大而下降了更多,从而保证了船舶运动过程中舵角不会过大。
4 结论针对风帆助航船舶这一具有强干扰和模型不确定性的非线性时变系统,设计了一种结合滑模面反馈的模糊自适应非线性迭代滑模控制器并证明其稳定性。以“文竹海”号76000DWT远洋散货船为研究对象分别设计PID、迭代滑模、模糊迭代滑模控制器。由仿真结果对比分析可知:
1) 相较于PID控制器,迭代滑模和模糊迭代滑模控制器在拥有更好的鲁棒性的同时,可以更加准确的对此类非线性系统进行控制。
2) 使用PID与迭代滑模控制器时舵角略大,难以满足实际要求。采用模糊迭代滑模控制器能够在保证控制速率的前提下使舵角保持在合理范围以内,更加符合实际要求。
3) 滑模面反馈控制参数ks和ε的取值大小对控制效果也有较大影响,下一步研究工作可考虑这两项参数的优化问题。
| [1] |
杨承恩, 毕英君. 用神经网络控制器对小型帆船的航向控制[J].
中国造船, 2004, 45(1): 25–32.
YANG Cheng'en, BI Yingjun. Application of a neural network adaptive autopilot for a yacht[J]. Shipbuilding of China, 2004, 45(1): 25–32. |
| [2] | XIAO L, JOUFFROY J. Modeling and nonlinear heading control of sailing yachts[J]. IEEE journal of oceanic engineering, 2014, 39(2): 256–268. |
| [3] |
葛艳, 孟庆春, 魏振刚, 等. 基于Sugeno模糊模型的帆船控制方法研究[J].
控制与决策, 2004, 19(6): 659–662.
GE Yan, MENG Qingchun, WEI Zhengang, et al. Research on sailboat control method based on Sugeno fuzzy model[J]. Control and decision, 2004, 19(6): 659–662. |
| [4] | CHENG J, YI J, ZHAO D. Design of a sliding mode controller for trajectory tracking problem of marine vessels[J]. IET control theory & applications, 2007, 1(1): 233–237. |
| [5] | ZHANG Rongjun, CHEN Yaobin, SUN Zengqi, et al. Path control of a surface ship in restricted waters using sliding mode[J]. IEEE transactions on control systems technology, 2000, 8(4): 722–732. |
| [6] |
朱齐丹, 于瑞亭, 夏桂华, 等. 风浪流干扰及参数不确定欠驱动船舶航迹跟踪的滑模鲁棒控制[J].
控制理论与应用, 2012, 29(7): 959–964.
ZHU Qidan, YU Ruiting, XIA Guihua, et al. Sliding-mode robust tracking control for underactuated surface vessels with parameter uncertainties and external disturbances[J]. Control theory & applications, 2012, 29(7): 959–964. |
| [7] |
王岩, 朱齐丹, 孟浩, 等. 欠驱动船舶航迹跟踪指令滤波滑模鲁棒控制[J].
电机与控制学报, 2013, 17(5): 110–118.
WANG Yan, ZHU Qidan, MENG Hao, et al. Command filter sliding mode robust tracking control of underactuated surface vessels[J]. Electric machines and control, 2013, 17(5): 110–118. |
| [8] |
孟威, 郭晨, 孙富春, 等. 欠驱动水面船舶的非线性滑模轨迹跟踪控制[J].
哈尔滨工程大学学报, 2012, 33(5): 585–589.
MENG Wei, GUO Chen, SUN Fuchun, et al. Nonlinear sliding mode tracking control of underatuated surface vessels[J]. Journal of Harbin engineering university, 2012, 33(5): 585–589. |
| [9] | YU R, ZHU Q, XIA G, et al. Sliding mode tracking control of an underactuated surface vessel[J]. IET control theory & applications, 2012, 6(3): 461–466. |
| [10] | FAHIMI F. Sliding-mode formation control for underactuated surface vessels[J]. IEEE Transactions on robotics, 2007, 23(3): 617–622. |
| [11] |
刘文江, 隋青美, 周风余, 等. 基于自适应模糊滑模控制的船舶航向控制器设计[J].
信息与控制, 2012, 41(2): 136–141.
LIU Wenjiang, SUI Qingmei, ZHOU Fengyu, et al. Controller design based on adaptive fuzzy sliding mode control for Ship course[J]. Information and control, 2012, 41(2): 136–141. |
| [12] | LIN C M, LI H Y. Adaptive dynamic sliding-mode fuzzy CMAC for voice coil motor using asymmetric gaussian membership function[J]. IEEE transactions on industrial electronics, 2014, 61(10): 5662–5671. |
| [13] | ZHANG Lijun, JIA Heming, QI Xue. NNFFC-adaptive output feedback trajectory tracking control for a surface ship at high speed[J]. Ocean engineering, 2011, 38(13): 1430–1438. |
| [14] | HUANG Zhengyu, EDWARDS R M, LEE K Y. Fuzzy-adapted recursive sliding-mode controller design for a nuclear power plant control[J]. IEEE transactions on nuclear science, 2004, 51(1): 256–266. |
| [15] |
卜仁祥, 刘正江, 李铁山. 迭代滑模增量反馈及在船舶航向控制中的应用[J].
哈尔滨工程大学学报, 2007, 28(3): 268–272.
BU Renxiang, LIU Zhengjiang, LI Tieshan. Iterative sliding mode based increment feedback control and its application to ship autopilot[J]. Journal of Harbin engineering university, 2007, 28(3): 268–272. |
| [16] |
边信黔, 程相勤, 贾鹤鸣, 等. 基于迭代滑模增量反馈的欠驱动AUV地形跟踪控制[J].
控制与决策, 2011, 26(2): 289–292.
BIAN Xinqian, CHENG Xiangqin, JIA Heming, et al. A bottom-following controller for underactuated AUV based on iterative sliding and increment feedback[J]. Control and decision, 2011, 26(2): 289–292. |



