正弦信号的频率估计问题是信号处理领域的一个基本问题,其在雷达、声呐、探测、无线通信以及语音识别等领域被广泛关注和研究[1, 2, 3, 4] 。极大似然估计法(maximum likelihood,ML)算法能够达到克拉美罗限,但是需要进行大量计算[2, 3],在工程中难以实现。为寻找计算量合适的次优算法,研究者进行了很多探索[3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22],焦点集中在两个方面:估计的精度和算法实现所需的计算量。最大似然估计是最优估计,其方差接近克拉美罗限(CRLB)[1, 2],但计算量大无法满足实时处理的要求[5]。Quinn、 Candan等[6, 16, 17]利用FFT系数进行插值计算。Rife、Aboutanios等[1, 18, 19, 20]利用迭代估计频率。为了提高估计性能采用相位校正[21, 22]技术,能够在插值算法中改善算法精度。而迭代法的性能则一定程度上依赖于初值的选取[5, 21]。文献[5]指出当初值落在频率真值5倍克拉美罗限均方根范围之内,迭代法方可获得高性能。设计出新的高精度直接估计法,既可为迭代提供准确初值,也可直接作为频率估计器,具备理论和应用的价值[21]。
利用正弦信号线性(linear prediction,LP)性质及自相关函数,研究者提出了多种算法,如改进协方差(modified covariance,MC)算法[13]、Pisarenko谐波分解法(PHD算法)等 [8]。PHD算法具备实现步骤简单、计算量少等优点,SO等[9, 10]提出了众多改进算法,从改进自相关函数设计的角度,减少估计误差。Rim等[11]则考虑利用更多自相关信息,包括高阶自相关等来进行算法改进。曹燕[4]利用Rim算法作为初值,利用泰勒展开式进行频率细化,获得了更好的精度。本文将利用高阶自相关函数在提高估计精度上的优势[14]与PHD算法的派生形式[12],进行新估计算法的设计,寻找合适的直接估计算法。
1 基于线性(LP)性质的估计方法 1.1 MC估计法
单一频率实正弦信号模型可表示为
xn=sn+qn,n=1,2,…,N
(1)
s(n)=αcos (ω0n+)
(2)
噪声q(n)为零均值,方差为σq2的高斯白噪声,信号的幅值为α,频率为ω0∈(0,π),相位∈[0,2π)。
在无噪声的情况下,利用正弦信号的LP性质可以得到
2cos kω0sn-k=sn+sn-2k
(3)
e(n)=x(n)-2cos $\varpi $0x(n-1)+x(n-2)
(4)
$$\eqalign{
& \hat \omega _0^{{\text{MC}}} = \arg \mathop {\min }\limits_{{{\hat \omega }_0}} \left\{ {\sum\limits_{n = 3}^N {2(n)} } \right\} = \cr
& {\cos ^{ - 1}}\left( {\frac{{\sum\limits_{n = 3}^N {x(n - 1)(x(x(n) + x(n - 2))} }}{{2\sum\limits_{n = 3}^N {{x^2}(n - 1)} }}} \right) \cr} $$
(5)
此方法被也就是改进协方差(modified covariance,MC)算法[13]。
1.2 Rim估计法当噪声存在时,MC算法是一个有偏的方法[15]。为了改进MC算法的估计精度,不少文献开展了研究[9, 11]。其中Rim提出基于自相关的频率估计算法[11]。
无噪理想情况下,对式(1)给出的信号模型,定义基于时间平均的自相关函数:
$$\eqalign{
& {r_k} = \frac{1}{{N - k}}\sum\limits_{n = 1}^{N - k} {x(n)} x(n + k) = \frac{{{\alpha ^2}}}{2}\cos (k{\omega _0}) + \cr
& \frac{1}{{N - k}}(\frac{{{\alpha ^2}}}{2}\sum\limits_{n = 1}^{N - k} {\cos } ((2n + k){\omega _0} + 2\Phi )) + \cr
& \sum\limits_{n = 1}^{N - k} {\left[{q(n)s(n + k) + q(n + k)s(n) + q(n)q(n + k)} \right]} \cr} $$
(6)
当N足够大时,式(6)中第二项趋于零,对自相关求数学期望为
$$E({r_k}) \approx \frac{{{\alpha ^2}}}{2}\cos ({\omega _0}k) + {\sigma ^2}{\sigma _{k,0}}$$
(7)
$${r_k} \approx \frac{{{\alpha ^2}}}{2}\cos ({\omega _0}k)$$
(8)
自相关信号的频率与原信号频率相同,即原信号的频率估计问题转化为自相关信号的频率估计问题。同样利用LP性质可得rk+rk+2≈2cos (ω0)rk+1,则对q>p>1,观察序列:
$$\sum\limits_{k = p}^q {{r_{k + 1}}({r_k} + } {r_{k + 2}}) \approx 2\cos ({\omega _0})\sum\limits_{k = p}^q {} r_{_{k + 1}}^2$$
(9)
$$\hat \omega _0^{{\text{Rim}}} = {\cos ^{ - 1}}\left( {\frac{{\sum\limits_{k = p}^q {{r_{k + 1}}({r_k} + {r_{k + 2}}} }}{{2\sum\limits_{k = p}^q {r_{k + 1}^2} }}} \right)$$
(10)
对Rim算法的性能进行了进一步分析表明,Rim算法在中高信噪比下表现较好。但是由于算法需要进行多个自相关函数计算,因此计算量较大[7]。
2 基于高阶自相关的频率估计方法从基于自相关的频率估计误差分析,自相关阶数越高,性能越好[14]。文献[12]对PHD算法的派生形式进行了研究,提出基于方程求根形式的PHD算法表达。本文算法引入高阶自相关系数,利用LP性质推广PHD派生形式。推导出基于高阶自相关的估计算法。
自相关函数定义由式(6)得到,同时由式(8)可以得到
$$\left\{ {\matrix
{{r_k} \approx \frac{{{\alpha ^2}}}{2}\cos ({\omega _0}k)} \\
{{r_{k + 1}} \approx \frac{{{\alpha ^2}}}{2}\cos ({\omega _0}k + 1)} \\
} \right.$$
(11)
4r2cos3${\hat \omega }$0-2r3cos2${\hat \omega }$0-3r2cos${\hat \omega }$0+r3=0
(12)
${\hat \omega }$0,i=cos-1γi,i=1,2,3
(13)
上述过程都利用了高阶的自相关函数,会带来频率模糊问题。文献[11]和文献[18]提出利用与PHD估计值最近的估计值作为算法的估计值。
从i个${\hat \omega }$0,i中选择最接近真实的频率i*的方法为
$${i^*} = \mathop {\arg \min }\limits_{i \in \left\{ {1,2,3\} } \right.} \left| {{{\hat \omega }_0} - \hat \omega _{\text{0}}^{{\text{phd}}}} \right|$$
(14)
最终,由式(13)、(14)得到本文给出本文算法。注意到,计算${\hat \omega }$0phd需要的r2已经计算出,不需额外计算自相关函数。带入PHD估计式只需比较一次即可。额外的计算负担为4次乘法、2次加法、一次开方和一次比较。相较Rim算法需要计算自相关和多次连加、乘,大大减少了计算量。对比算法计算量统计表1所示。
| 方法 | 加 | 乘 | 除 | 开方 | cos-1 |
| ML | 5N-2 | 5N+9 | 1 | 0 | 0 |
| MC | 3N-8 | 2N-3 | 1 | 0 | 1 |
| PHD | 2N-1 | 2N+3 | 1 | 1 | 1 |
| RPHD | 3N-3 | 2N+5 | 1 | 1 | 1 |
| RIM | (q-p+1)(N+3-(p+q)/2)-2 | (q-p+1)(N+3-(p+q)/2) | 1 | 0 | 1 |
| 本文算法 | 2N+7 | 2N+30 | 3 | 3 | 1 |
第2节提出了利用高阶自相关的估计算法并进行了计算量比较。在本节中,通过理论分析,推导出估计频率${\hat \omega }$0的方差。
由式(12)定义三阶多项式:
f(T)=4r2T3-2r3T2-3r2T+r3
(15)
式(15)的根即对应频率的估计值T*=cos ($_{{\omega _0}}^ \gg $),利用Taylor展开将f(T*)在T=cos (ω0)一阶展开。
$$\eqalign{
& 0 = f({T^*}) \approx (T) + ({T^*} - T)f'(T)\left| {_{T = COS({\omega _0})}} \right. \Rightarrow \cr
& {({T^*} - T)^2} \approx \frac{{{f^2}(T)}}{{{{\left[{f'(T)} \right]}^2}}}\left| {_{T = COS({\omega _0})}} \right| \Rightarrow \cr
& \operatorname{var} ({T^*}) = {\text{E}}\left\{ {{{\left( {{T^*} - T} \right)}^2}} \right\} \approx {\left. {\frac{{{\text{E}}\left\{ {{f^2}(t)} \right\}}}{{{{\left[{f'(T)} \right]}^2}}}} \right|_{T = COS({\omega _0})}} \cr} $$
(16)
$$\eqalign{
& \operatorname{var} ({T^*}) = {\text{E}}\left\{ {(\cos ({\omega _0}) - \cos {{({{\mathop \omega \limits^ \gg }_0})}^2}} \right\} = \cr
& {\text{E}}\left\{ {4{{\sin }^2}\left( {\frac{{{\omega _0} + {{\mathop \omega \limits^ \gg }_0}}}{2}} \right){{\sin }^2}\left( {\frac{{{\omega _0} - {{\mathop \omega \limits^ \gg }_0}}}{2}} \right)} \right\} \approx \cr
& 4{\sin ^2}({\omega _0}) \cdot \frac{{{\text{E}}\left\{ {{{({\omega _0} - {{\mathop \omega \limits^ \gg }_0})}^2}} \right\}}}{4} \Rightarrow \cr
& \operatorname{var} ({\mathop \omega \limits^ \gg _0}) \approx \frac{{\operatorname{var} ({T^*})}}{{{{\sin }^2}({\omega _0})}} \cr} $$
(17)
利用式(6)进行期望计算,为计算式(16),可以从式(15)得到
E(f2(T))=cos2(3ω0)·E(r22)+cos2(2ω0)·E(r32)-2E(r32r)·cos(2ω0)cos(3ω0)
(18)
E(f′(T))=2E(r3)·sin(2ω0)-3E(r2)·sin(3ω0)
(19)
$$\eqalign{
& E({r_2}) = \frac{1}{{N - 2}}\left\{ {\sum\limits_{n = 1}^{N - 2} {x(n)x(n + 2)} } \right\} = \cr
& \frac{{{\alpha ^2}}}{2}\cos (2{\omega _0}) + \frac{1}{{N - 2}}(\frac{{{\alpha ^2}}}{2}\sum\limits_{n = 1}^{N - 2} {cos((2n + 2){\omega _0} + 2\Phi )} \cr} $$
(20)
$$\eqalign{
& {\text{E}}({r_3}) = \frac{1}{{N - 3}}{\text{E}}\left\{ {\sum\limits_{n = 1}^{N - 3} {x(n)x(n + 3)} } \right\} = \cr
& \frac{{{\alpha ^2}}}{2}\cos (3{\omega _0}) + \frac{1}{{N - 3}}(\frac{{{\alpha ^2}}}{2}\sum\limits_{n = 1}^{N - 3} {cos((2n + 3){\omega _0} + 2\Phi )} \cr} $$
(21)
$$\eqalign{
& E\left( {r_2^2} \right) = \frac{{{\sigma ^4}}}{{N - 2}} + \cr
& \frac{{{\alpha ^4}{{\left( {\left( {N - 2} \right)\cos \left( {2{\omega _0}} \right) + \sum\limits_{n = 1}^{n - 1} {\cos \left( {\left( {2n + 2} \right){\omega _0} + 2\phi } \right)} } \right)}^2}}}{{4{{\left( {N - 2} \right)}^2}}} + \cr
& \frac{{{\alpha ^2}{\sigma ^2}\left( {N - 2} \right) + \sum\limits_{n = 1}^{N - 2} {\cos \left( {2n{\omega _0} + 2\phi } \right)} }}{{2{{\left( {N - 2} \right)}^2}}} + \cr
& \frac{{{\alpha ^2}{\sigma ^2}\left( {\left( {N - 4} \right)\cos \left( {4{\omega _0}} \right) + \sum\limits_{n = 1}^{N - 4} {\cos \left( {\left( {2n + 4} \right){\omega _0} + 2\phi } \right)} } \right)}}{{{{\left( {N - 2} \right)}^2}}} \cr
& \frac{{{\alpha ^2}{\sigma ^2}\left( {\left( {N - 2} \right) + \sum\limits_{n = 1}^{N - 2} {\cos \left( {\left( {2n + 4} \right){\omega _0} + 2\phi } \right)} } \right)}}{{2{{\left( {N - 2} \right)}^2}}} \cr} $$
(22)
$$\eqalign{
& {\text{E}}(r_3^2) = \frac{{{\sigma ^4}}}{{N - 3}} + \cr
& \frac{{{\alpha ^4}((N - 3)\cos (3{\omega _0}) + \sum\limits_{n = 1}^{N - 3} {\cos ((2n + 3){\omega _0} + 2\Phi ){)^2}} }}{{4{{(N - 3)}^2}}} + \cr
& \frac{{{\alpha ^2}{\sigma ^2}((N - 3) + \sum\limits_{n = 1}^{N - 3} {\cos (2n} {\omega _0} + 2\Phi ))}}{{2{{(N - 3)}^2}}} + \cr
& \frac{{{\alpha ^2}{\sigma ^2}((N - 6)cos(6{\omega _0}) + \sum\limits_{n = 1}^{N - 6} {\cos ((2n} + 6){\omega _0} + 2\Phi ))}}{{{{(N - 3)}^2}}} + \cr
& \frac{{{\alpha ^2}{\sigma ^2}((N - 3) + \sum\limits_{n = 1}^{N - 3} {\cos ((2n} + 6){\omega _0} + 2\Phi ))}}{{2{{(N - 3)}^2}}} \cr} $$
(23)
$$\eqalign{
& E({r_2}{r_3}) = \cr
& \frac{{{\alpha ^4}((N - 2)\cos (2{\omega _0}) + \mathop \Sigma \limits_{n = 1}^{N - 2} \cos ((2n + 2){\omega _0} + 2\Phi ))}}{{4(N - 2)(N - 3)}} \cdot \cr
& \frac{{((N - 3)\cos (3{\omega _0}) + \mathop \Sigma \limits_{n = 1}^{N - 3} \cos ((2n + 3){\omega _0} + 2\Phi ))}}{{4(N - 2)(N - 3)}} + \cr
& \frac{{{\alpha ^2}{\sigma ^2}((N - 3)\cos ({\omega _0}) + \mathop \Sigma \limits_{n = 1}^{N - 3} \cos ((2n + 1){\omega _0} + 2\Phi ))}}{{2(N - 2)(N - 3)}} + \cr
& \frac{{{\alpha ^2}{\sigma ^2}((N - 5)\cos (5{\omega _0}) + \mathop \Sigma \limits_{n = 1}^{N - 5} \cos ((2n + 5){\omega _0} + 2\Phi ))}}{{(N - 2)(N - 3)}} + \cr
& \frac{{{\alpha ^2}{\sigma ^2}((N - 3)\cos ({\omega _0}) + \mathop \Sigma \limits_{n = 1}^{N - 3} \cos ((2n + 5){\omega _0} + 2\Phi ))}}{{2(N - 2)(N - 3)}} \cr} $$
(24)
将结果代入式(18)、(19),通过略去高次项进行近似,得到方差的精确理论估计:
$$\eqalign{
& {\text{var}}(\mathop {{\omega _0}}\limits^ \gg ) \approx \frac{{{{\cos }^2}(3{\omega _0}) + {{\cos }^2}(2{\omega _0})}}{{SN{R^2}(N - 2)\Delta }} + \cr
& \frac{{2{{\cos }^2}(3{\omega _0})}}{{SNR(N - 2)\Delta }} + \frac{{2{{\cos }^2}(2{\omega _0})}}{{SNR(N - 3)\Delta }} + \cr
& \frac{{2(N - 6)cos(6{\omega _0})co{s^2}(3{\omega _0})}}{{SNR{{(N - 2)}^2}\Delta }} + \cr
& \frac{{2(N - 6)cos(6{\omega _0})co{s^2}(3{\omega _0})}}{{SNR{{(N - 3)}^2}\Delta }} - \cr
& \frac{{4cos{\omega _0}cos(2{\omega _0})cos(3{\omega _0})}}{{SNR(N - 2)\Delta }} - \cr
& \frac{{4cos(2{\omega _0})cos(3{\omega _0})cos(5{\omega _0})(N - 5)}}{{SNR(N - 2)(N - 3)\Delta }} \cr
& \Delta = ((2\cos (3{\omega _0})\sin (2{\omega _0}) - \cr
& 3\cos (2{\omega _0})\sin (3{\omega _0}))sin{\omega _0}{)^2} \cr} $$
(25)
当N值较大时,式(25)的后几项可以进行进一步的简化得到:
$${\mathop{\rm var}} (\mathop {{\omega _0}}\limits^ \gg ) \approx {{{{\cos }^2}(3{\omega _0}) + {{\cos }^2}(2{\omega _0})} \over {SN{R^2}(N - 2)\Delta }}$$
(26)
其结构更加清楚简洁,当然,准确程度受到相应的限制。通过图像可以清楚的对比理论误差式(25)、(26)与估计算法的数值试验的近似程度。
图1显示精确误差公式在SNR=10 dB,N=200时能够较好的匹配试验结果。但注意到式(26)在对式(25)近似时,要求合适的SNR与N值。在对SNR与N取不同值时发现理论误差公式(26)在较大的SNR与较小N值情况下,近似效果较差。
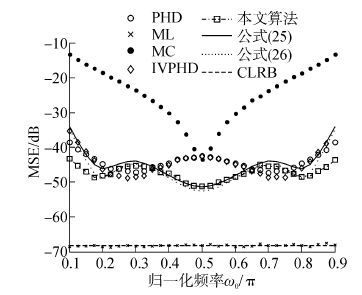
|
| 图1 SNR=10 dB,N=200时均方误差 Fig.1 MSE vs ω0 / π , SNR = 20 dB, N = 200 |
图2,图3,图4分别显示增大SNR、长度 N不变,SNR不变、N减小,SNR增大同时N减小三种情况下理论误差公式与试验情况的对比图。
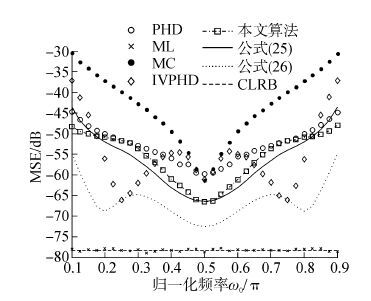
|
| 图2 SNR=20 dB,N=200时均方误差 Fig.2 MSE vsω0/π,SNR=20 dB,N=200 |
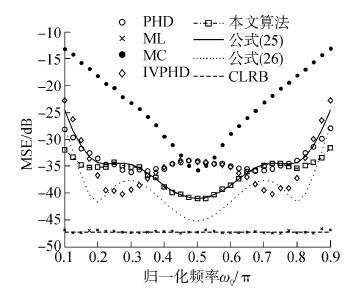
|
| 图3 SNR=10 dB,N=40时均方误差 Fig.3 MSE vsω0/π,SNR=10 dB,N=40 |
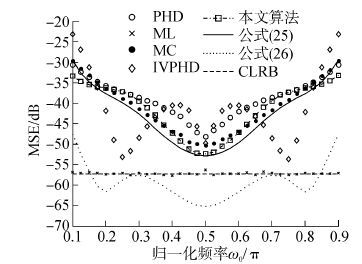
|
| 图4 SNR=20 dB,N=40时均方误差 Fig.4 MSE vsω0/π,SNR=20 dB,N=40 |
通过表2,清楚的看到式(25)与式(26)的近似程度差别。虽然式(25)结构繁琐,但能够更好的逼近估计误差。在相对低SNR与高数据长度N情况下则能够用式(26)近似。相对于SNR变化,式(26)对于数据长度N变化更加敏感,这与理论分析相吻合。
| SNR=10 dB | SNR=20 dB | |
| N=200 | 好(图1) | 较差(图2) |
| N=40 | 差(图3) | 非常差(图4) |
利用计算机对本文提出的估计算法进行模拟。 并将算法与PHD算法[8]、ML算法[3]、MC算法[13]、IVPHD(improved PHD)算法[9] 、RPHD(reformed PHD)算法[10]、Rim算法[11]进行比较。最后,与CRLB限[2]进行对比。
本文中实信号CRLB限定义为:${\sigma _{{\omega _0}}} = \frac{{12}}{{{\text{SNR}} \cdot N \cdot ({N^2} - 1)}}$ 。其中${\text{SNR}} = \frac{{{\alpha ^2}}}{{2\sigma _q^2}}$,信号的幅值α=2。全部计算都利用Monte Carlo方法进行1000次计算,取平均值。
图5的比较结果显示本文提出的算法明显优于各种PHD算法及其改进IVPHD,RPHD算法等。特别的,在区间(0.35π,0.65π),最大领先10 dB。注意到在图2,图3,图4中,IVPHD体现出过大的波动性,并且在区间(0.35π,0.65π)内明显差与本文算法(并且差于其他算法),并在区间外呈现大幅震荡的结果,算法稳定性较差。并且,与计算量最大的Rim算法相比,算法总体上优于Rim算法,特别在区间ω0≤0.2π 和ω0≥0.8π有5 dB以上的优势,并且算法的稳定性很好。
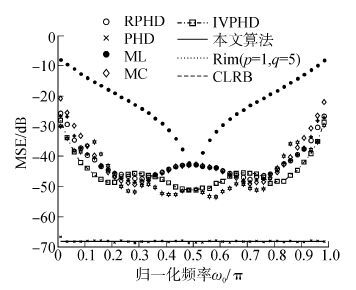
|
| 图5 SNR=20 dB 、 N=200时各算法MSE Fig.5 MSE vsω0/π,SNR=20 dB,N=200 |
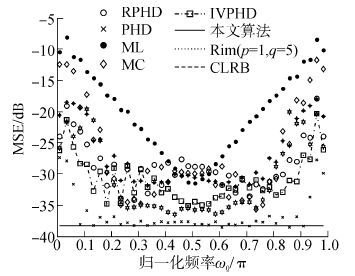
|
| 图6 SNR=10 dB 、 N=20时各算法MSE Fig.6 MSE vsω0/π,SNR=10 dB & N=20 |
图7显示本文提出的两种算法,与其他6种算法,在ω0=0.825π,N=20,=0 情况下,MSE 随SNR 变化情况。结果显示算法体现出优势。本文提出的算法全面优于MC、PHD、IVPHD、RPHD,Rim算法。特别是在SNR>10 dB情况下,算法能够接近于CLRB界,相差小于1 dB ,体现了计算量和计算精度很好的综合。
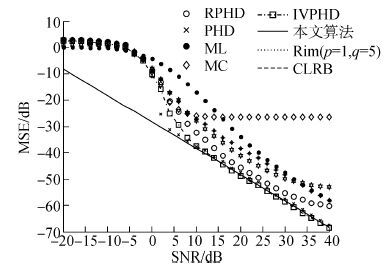
|
| 图7 ω0=0.85π,N=20时各算法MSE Fig.7 MSE vs SNR atω0=0.85π,N=20 |
本文对正弦信号频率估计问题进行研究,通过理论分析和推导,利用正弦信号的LP性质及高阶自相关函数的特点,提出基于高阶自相关的新估计算法:
1)对算法进行计算复杂度比较,相较其他算法,本文算法在计算量上的消耗较小。适用于实时情况;
2)利用泰勒展开式对算法的方差进行理论推导,给出本文算法的估计误差的精确和粗略2种闭合表达式。精确公式能够在各种条件下更准确逼近估计误差。但在N值较大情况下,结构简单的粗略形式表达满足精度要求;
3)对算法的仿真结果表明,本文算法精度性能上优于与之对比的算法,特别是在数据序列较小和中高信噪比情况下能够逼近理论界CRLB。本文提出的估计算法能够综合平衡计算精度和计算量,既能单独作为估计算法,以较小计算量满足精度需求。同时,也能作为频率估计迭代算法的合适初值,进一步提高频率估计算法的性能。
| [1] | RIFE D, BOORSTYN R R. Single tone parameter estimation from discrete-time observations[J]. IEEE transactions on information theory, 1974, 20(5): 591-598. |
| [2] | KAY S M. Fundamentals of statistical signal processing: estimation theory [M]. Prentice Hall: Englewood Cliffs, NJ, 1993: 56-57. |
| [3] | KENEFIC R J, NUTTALL A H. Maximum likelihood estimation of the parameters of a tone using real discrete data[J]. IEEE journal of oceanic engineering, 1987, 12(1): 279-280. |
| [4] | CAO Yan, WEI Gang, CHEN Fangjiong. A closed-form expanded autocorrelation method for frequency estimation of a sinusoid[J]. Signal processing, 2012, 92(4): 885-892. |
| [5] | ABATZOGLOU T J. A Fast maximum likelihood algorithm for frequency estimation of a sinusoid based on newton's method[J]. IEEE transactions on acoustics, speech and signal processing, 1985, 33(1): 77-89. |
| [6] | QUINN B G. Recent advances in rapid frequency estimation[J]. Digital signal processing, 2009, 19(6): 942-948. |
| [7] | CAO Yan, WEI Gang, CHEN Fangjiong. An exact analysis of Modified Covariance frequency estimation algorithm based on correlation of single-tone[J]. Signal processing, 2012, 92(11): 2785-2790. |
| [8] | PISARENKO V F. The retrieval of harmonics from a covariance function[J]. Geophysical journal international, 1973, 33(3): 347-366. |
| [9] | LUI K W K, SO H C. Improved variant of pisarenko harmonic decomposition for single sinusoidal frequency estimation[J]. IEICE transactions on fundamentals of electronics, communications and computer sciences, 2007, E90-A(11): 2604-2607. |
| [10] | SO H C, CHAN K W. Reformulation of pisarenko harmonic decomposition method for single-tone frequency estimation[J]. IEEE transactions on signal processing, 2004, 52(4): 1128-1135. |
| [11] | ELASMI-KSIBI R, BESBES H, LÓPEZ-VALCARCE R, et al. Frequency estimation of real-valued single-tone in colored noise using multiple autocorrelation lags[J]. Signal processing, 2010, 90(7): 2303-2307. |
| [12] | XIAO Y, TADOKORO Y. On pisarenko and constrained yule-walker estimators of tone frequency[J]. IEICE transactions on fundamentals of electronics, communications and computer sciences, 1994, E77-A(8): 1404-1406. |
| [13] | FERTIG L B, MCCLELLAN J H. Instantaneous frequency estimation using linear prediction with comparisons to the DESAs[J]. IEEE signal processing letters, 1996, 3(2): 54-56. |
| [14] | ELASMI-KSIBI R, LÓPEZ-VALCARCE R, BESBES H, et al. A family of real single-tone frequency estimators using higher-order sample covariance lags[C]//2008 16th European Signal Processing Conference. Lausanne, 2008: 956-959. |
| [15] | 黄超, 索继东, 于亮. 扩展自相关的正弦信号频率估计算法[J]. 信号处理, 2014, 30(10): 1229-1233. HUANG Chao, SUO Jidong, YU Liang. Expanded autocorrelation method for frequency estimation of a sinusoid[J]. Journal of signal processing, 2014, 30(10): 1229-1233. |
| [16] | CANDAN C. A method for fine resolution frequency estimation from three dft samples[J]. IEEE signal processing letters, 2011, 18(6): 351-354. |
| [17] | CANDAN C. Analysis and further improvement of fine resolution frequency estimation method from three dft samples[J]. IEEE signal processing letters, 2013, 20(9): 913-916. |
| [18] | ABOUTANIOS E. A modified dichotomous search frequency estimator[J]. IEEE signal processing letters, 2004, 11(2): 186-188. |
| [19] | ABOUTANIOS E, MULGREW B. Iterative frequency estimation by interpolation on fourier coefficients[J]. IEEE transactions on signal processing, 2005, 53(4): 1237-1242. |
| [20] | LIAO J R, CHEN C M. Analysis and reduction of estimation bias for an iterative frequency estimator of complex sinusoid[C]//2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Vancouver, BC, 2013: 6138-6142. |
| [21] | 黄翔东, 孟天伟, 丁道贤, 等. 前后向子分段相位差频率估计法[J]. 物理学报, 2014, 63(21): 214304-1-214304-7. HUANG Xiangdong, MENG Tianwei, DING Daoxian, et al. A novel phase difference frequency estimator based on forward and backward sub-segmenting [J]. Acta physica sinica, 2014, 63(21): 214304-1-214304-7. |
| [22] | LIAO J R, CHEN C M. Phase correction of discrete fourier transform coefficients to reduce frequency estimation bias of single tone complex sinusoid[J]. Signal processing, 2014, 94: 108-117. |



