2. School of Mechanical and Automotive Engineering, Fujian University of Technology, Fuzhou 350118, China
TBM刀盘作为掘进机的核心部件,起着破岩和支撑掌子面的功能[1]。刀盘系统设计既要考虑高承载能力,又要考虑高可靠性、高安全性及长寿命的设计要求,需根据地质报告进行面向地质适应性的非标定制设计。合理的刀盘设计对提高掘进效率、延长刀盘、刀具及主轴承寿命,减轻整机振动,降低噪音等具有重要作用。因此,有必要在设计阶段就对TBM刀盘系统的振动特性进行分析,提出结构参数的设计依据。
目前,国内外学者对TBM刀盘系统设计的相关研究还非常有限。谭青等[2, 3]采用离散元法模拟滚刀侵入岩体的过程,得到不同切深下比能耗与刀间距的规律,确定常见切深下的最优刀间距。韩美东等[4]采用有限元法对刀盘掘进过程进行动态仿真,得到不同岩层下保证刀盘动力稳定性的推进速度临界值,为提升TBM的地质适应性和施工安全性提供参考。Huo等[5, 6]基于ADAMS软件平台对刀盘系统的运动学及动力学特性进行了仿真和分析,为系统的动态优化设计提供参考。Li等[7]建立刀盘驱动系统的广义非线性时变动态模型,将方程线性化后,用状态空间理论求解系统的动态响应,并分析系统参数对响应的影响。Sun等[8, 9]基于集中质量法提出考虑多种复杂因素影响的分体式刀盘系统整体耦合动力学理论及仿真模型,初步研究了刀盘在空间多点冲击载荷和内部激励作用下的振动响应及参数影响分析。而在利用固有特性分析及系统模态能量方面,主要集中在齿轮传动系统领域,如Guo等[10, 11, 12]国内外学者建立不同类型的齿轮系统动力学理论及仿真模型,通过求解系统模态特征方程,分析模态能量分布规律及不同振动模式下固有频率对物理参数的灵敏度,判断各阶模态影响最大的系统参数,探讨模态跃迁现象。
综上所述,由于技术保密等原因,目前国内外很少见到关于TBM刀盘结构振动特性的报道,也尚无有关刀盘系统模态能量分布的文献。因此,本文在已有TBM刀盘系统多自由度耦合动力学模型的基础上[8],基于实际工程参数,通过求解系统自由振动特征方程,得到各阶固有频率和振型,提取各构件的模态动能和应变能分布,进一步区分各阶模态振型,并分析敏感参数对低阶固有频率的影响。
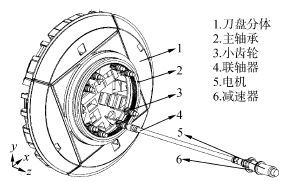
1 动力学建模TBM刀盘系统主要由刀盘、主轴承、驱动齿轮、减速器及电机等几大部分组成,减速器和电机固定在主梁上,通过联轴器联接小齿轮,整体结构组成如图1所示,图中仅绘出一个电机驱动系统。刀盘实际工作时,8个对称布置的变频电机经过行星齿轮减速器后,将扭矩通过联轴器传至小齿轮,小齿轮同时沿顺时针方向驱动大齿圈,而大齿圈、传力环及刀盘法兰采用螺栓固定,进而带动刀盘旋转。
|
| 图1 TBM刀盘系统组成 Fig.1 Components of TBM cutterhead system |
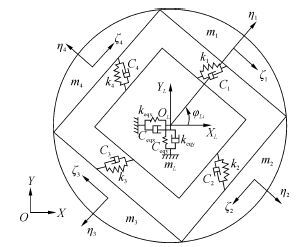
基于集中参数质量法建立TBM分体式刀盘系统多自由度耦合动力学模型,其中刀盘分体弯扭耦合动力学模型如图2所示,其余自由度模型详见参考文献[8],同时动力学微分方程也在该文献中。
|
| 图2 刀盘系统弯扭耦合动力学模型 Fig.2 Bend-torsion coupled dynamic model of cutterhead system |
对刀盘系统进行自由模态分析,采用平均刚度代替时变刚度,得到与之对应的特征值问题为
$$(\bar K - \omega _i^2M){\varphi _i} = 0$$
(1)
基于辽西北供水工程项目硬岩刀盘系统的设计参数,刀盘直径8.53 m,其他参数大小见文献[13]。
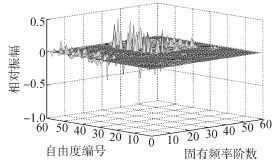
得到前15阶固有频率大小见文献[13],同时将模态振型正规化后,可以确定与各阶固有频率对应的振型,如图3所示,其中自由度编号1~59分别对应刀盘系统各构件的自由度。
|
| 图3 刀盘系统各阶振型 Fig.3 Vibration modes of the cutterheader system |
由模态分析结果可知,刀盘系统振动主要集中在中间阶模态,低阶和高阶相对振幅较小;前15阶振型主要是电机和小齿轮的纯扭转振动、刀盘和大齿圈平移倾覆耦合振动,且纯扭转振型对应的频率为57 Hz,大于小齿轮的转频(1.16 Hz)和啮合频率(16.24 Hz)等内部激励频率,理论上不会发生共振。
2.2 模态能量为进一步研究系统模态振型,本文提出基于模态能量的方法区分各阶振型及分析参数对固有频率的影响。通过研究各构件在各阶模态下的动能和应变能可分别了解构件的振动剧烈程度及变形程度,同时间接反应各参数对固有频率的敏感程度。
2.2.1 模态动能分析
对于第n阶模态动能,系统的总动能等于各个构件的质量和转动惯量动能之和:
$${E_n} = \frac{1}{2}\omega _n^2\varphi _n^TM{\varphi _n} = \sum\limits_{s = i,L,r,d,p} {E_s^n} + \sum\limits_{s = L,r,p,m} {E_t^n} $$
(2)
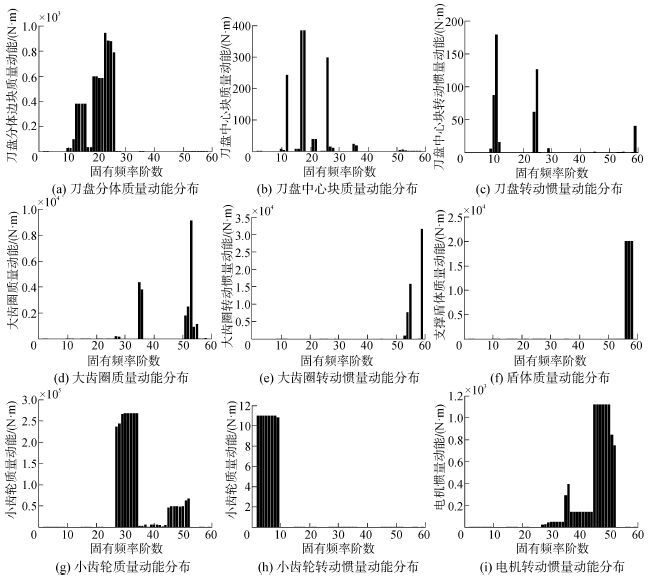
将各阶固有频率及振型矢量代入Es和Et的计算公式,得到各构件的模态动能分布如图4所示。
|
| 图4 各构件模态动能 Fig.4 Mode kinetic energy of each component |
对于第n阶模态应变能,总应变能等于各构件的支撑应变能、扭转应变能及啮合应变能之和:
$$\eqalign{
& {U_n}_t = \frac{1}{2}\varphi _n^T\bar K{\varphi _n} = U_i^n + U_L^n + U_r^n + U_d^n + \cr
& + U_{Lr}^n + \sum\limits_{j = 1}^8 ( U_{pj}^n + U_{prj}^n + U_{mj}^n) \cr} $$
(3)
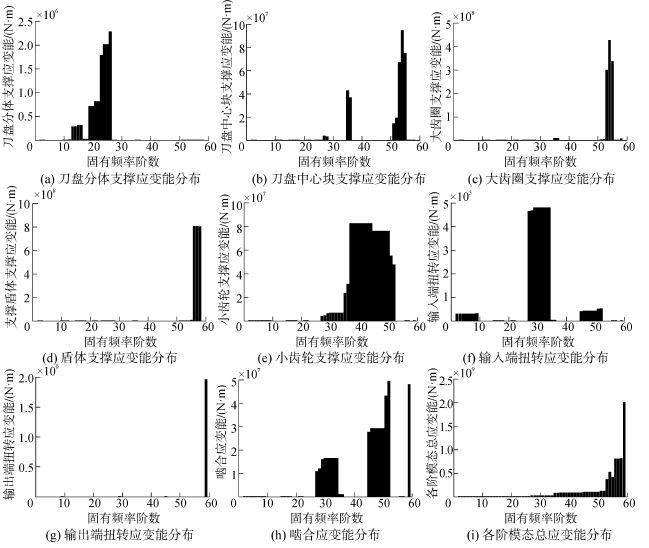
通过计算,同样可分别得到各构件的振动模态应变能分布如图5所示。
|
| 图5 各构件模态应变能 Fig.5 Mode strain energy of each component |
基于上述模态能量分布规律,可将影响刀盘系统各阶固有频率的敏感参数总结如表1所示。
| 模态阶数 | 质量参数 | 转动惯量参数 | 刚度参数 |
| 2~10 | 小齿轮 | 输入端 | |
| 11~25 | 刀盘 | 刀盘 | 刀盘分体 |
| 26~35 | 小齿轮 | 输入端 | |
| 36~50 | 电机 | 小齿轮啮合刚度 | |
| 51~59 | 盾体、大齿圈 | 大齿圈 | 刀盘中心块、盾体、大齿圈、输出端 |
从表1结果可以看出,刀盘系统前10阶模态能量主要集中在输入端的扭转应变能和小齿轮的转动惯量动能,说明低阶固有振型表现为小齿轮纯扭转模态,同时也表明低阶频率主要受输入端扭转刚度和小齿轮转动惯量的影响;刀盘的质量、转动惯量动能及支撑应变能主要集中在第11~25阶等中低阶固有振型中,而大齿圈、盾体及电机等其余模态能量则集中在中高阶固有振型中;系统模态总动能集中在中间阶模态,与振型分析的结果一致,而总应变能随模态阶数的增大而增大,说明高频振动时系统变形较大。
3 参数对固有频率的影响通常低阶固有频率对系统的动态特性影响最大,由刀盘系统模态能量分布规律可知,可定性判断影响刀盘系统低阶固有频率的主要是小齿轮的转动惯量及输入端的扭转刚度这两个参数。为此,本节着重定量分析这两个参数对低阶频率的影响,依次在原始方案50%的范围内增加及减小参数大小,基于数值计算,分析参数变化对固有频率的影响,得到结果如图6和图7所示,图中横坐标表示各参数的相对变化量,即0点为原方案参数值,-0.5和0.5分别表示参数值为原方案的0.5倍和1.5倍。
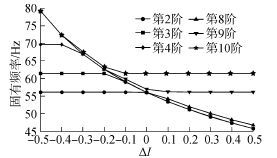
|
| 图6 小齿轮转动惯量对固有频率的影响 Fig.6 The influence of pinion inertia to natural frequencies |
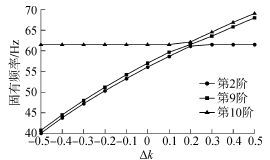
|
| 图7 输入端扭转刚度对固有频率的影响 Fig.7 The influence of input terminal torsional stiffness to natural frequencies |
由图6可知,当小齿轮转动惯量取原始方案的1.1倍时,能够使得系统避开参数的敏感区域(频率曲线交错区),振动特性较为稳定,且第9阶固有频率能保持在56 Hz左右,保证低阶固有频率值较高,不易发生共振。由图7可知,当输入端扭转刚度取原始方案的1.3倍时,第2阶固有频率(基频)能稳定在62 Hz左右,使得系统参数的匹配性能良好。
4 结论1) 刀盘系统振动主要集中在中间阶模态,低阶和高阶相对振幅较小,且低阶固有振型主要是电机、小齿轮纯扭转振动模态及刀盘和大齿圈平移倾覆耦合振动模态,纯扭转振型对应的固有频率为57 Hz,大于内部激励频率,理论上不会发生共振。
2) 从模态能量的角度区分刀盘系统振型及分析参数的影响规律,小齿轮转动惯量和输入端扭转刚度对第2~10阶固有频率影响最大,而刀盘分体质量及支撑刚度主要影响第11~20阶固有频率,其余构件的结构参数则影响中高阶固有频率。
3) 小齿轮转动惯量取原始方案的1.1倍,输入端扭转刚度取原始方案的1.3倍,能够使得系统避开参数敏感区域,振动特性较为稳定,且低阶频率值较高。设计时可采取缩短输入端连接轴长度及采用空心轴结构,均有助于改善系统动态特性,为后继系统参数匹配及优化奠定理论基础。
在以上结论的基础上,下一步将进一步分析刀盘系统输入端结构设计参数对振动特性的影响,为设计参数的选取提供参考。
| [1] | 水利部科技推广中心. 全断面岩石掘进机[M]. 北京: 石油工业出版社, 2005: 1-3. Promotion Center for Science & Technology Achievements of Ministry of Water Resources. Full face rock tunnel boring machine [M]. Beijing: Petroleum Industry Press, 2005: 1-3. |
| [2] | 谭青, 易念恩, 夏毅敏, 等. TBM滚刀破岩动态特性与最优刀间距研究[J]. 岩石力学与工程学报, 2012, 31(12): 2453-2464. TAN Qing, YI Nianen, XIA Yimin, et al. Research on rock dynamic fragmentation characteristics by TBM cutters and cutter spacing optimization [J]. Chinese journal of rock mechanics and engineering, 2012, 31(12): 2453-2464. |
| [3] | XIA Yimin, OUYANG Tao, ZHANG Xinming, et al. Mechanical model of breaking rock and force characteristic of disc cutter [J]. Journal of Central South university, 2012, 19(7): 1846-1852. |
| [4] | 韩美东, 蔡宗熙, 曲传咏. 基于动力稳定性的全断面岩石隧道掘进机刀盘临界推进速度研究[J]. 机械工程学报, 2014, 50(21): 1-7. HAN Meidong, CAI Zongxi, QU Chuanyong. Study on the critical driving speed of the tunnel boring machine cutterhead based on the dynamic stability [J]. Journal of mechanical engineering, 2014, 50(21): 1-7. |
| [5] | HUO Junzhou, OUYANG Xiangyu, ZHANG Xu, et al. The Influence of front support on vibration behaviors of TBM cutterhead under impact heavy loads [J]. Applied mechanics and materials, 2014, 541/542: 641-644. |
| [6] | ZHU Lida, SU Pengcheng, LI Gang, et al. Dynamic analysis of cutter head system in tunnel boring machine [J]. Advanced materials research, 2011, 186: 51-55. |
| [7] | LI Xianhong, YU Haibin, YUAN Mingzhe, et al. Dynamic modeling and analysis of shield TBM cutterhead driving system [J]. Journal of dynamic systems measurement and control, 2010, 132(4): 044504. |
| [8] | SUN Wei, LING Jingxiu, HUO Junzhou, et al. Dynamic characteristics study with multidegree-of-freedom coupling in TBM cutterhead system based on complex factors [J]. Mathematical problems in engineering, 2013, 2013: 635809. |
| [9] | 霍军周, 欧阳湘宇, 王亚杰, 等. 重载冲击激励下TBM刀盘振动特性的影响因素分析[J]. 哈尔滨工程大学学报, 2015, 36(4): 555-559. HUO Junzhou, OUYANG Xiangyu, WANG Yajie, et al. Analysis of influencing factors of vibration behaviors of TBM cutterhead under heavy impact loads [J]. Journal of Harbin Engineering University, 2015, 36(4): 555-559. |
| [10] | GUO Yichao, PARKER R G. Sensitivity of general compound planetary gear natural frequencies and vibration modes to model parameters [J]. Journal of vibration and acoustics, 2010, 132(1): 011006(1)-011006(13). |
| [11] | 冯海生, 王黎钦, 郑德志, 等. 柔性齿轮-柔性转子-滑动轴承系统动特性分析[J]. 哈尔滨工程大学学报, 2015, 36(3): 384-388. FENG Haisheng, WANG Liqin, ZHENG Dezhi, et al. Analysis of the dynamic characteristics of flexible gear-flexible rotor-journal bearing system [J]. Journal of Harbin Engineering University, 2015, 36(3): 384-388. |
| [12] | 段福海, 胡青春, 谢存禧. 钢/塑料齿轮组合行星传动的固有特性分析[J]. 中国机械工程, 2008, 19(20): 2423-2427. DUAN Fuhai, HU Qingchun, XIE Cunxi. Natural modes of Steel/plastic compound planetary gear sets [J]. China mechanical engineering, 2008, 19(20): 2423-2427. |
| [13] | 凌静秀, 孙伟, 霍军周, 等. TBM刀盘系统多自由度耦合固有特性及敏感度[J]. 东北大学学报:自然科学版, 2015, 36(4): 546-550.LING Jingxiu, SUN Wei, HUO Junzhou, et al. Natural characteristics and sensitivity of TBM cutterhead system with multi-degree-of-freedom coupling [J]. Journal of Northeastern University: natural science, 2015, 36(4): 546-550. |



