2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
由于通信网络节点发送功率和水声信道带宽的限制[1, 2, 3, 4],基于水声通信网络的点对点远距离稳健数据交互面临着极大的挑战,有效的路由协议是水声通信网络信息交互性能的关键。串型路由ALOHA协议[5]在复杂的水声通信网络中也取得了广泛的应用,深入研究ALOHA协议在串型路由水声通信网络中的网络性能具有重要意义。纯ALOHA协议由于缺少避碰机制,其最大吞吐量仅为0.184[6]。针对ALOHA协议改进的协议有很多,如N. Chirdchoo等提出了碰撞避免Aloha(Aloha-CA)和预先通知Aloha(Aloha-AN)[7]等,在一定程度上提高了网络吞吐量。但针对现有水声通信装备性能及水声信道参数约束下串型路由ALOHA协议的最优网络性能参数配置的理论研究尚无深入研究。本文通过建立串型路由水声通信网络模型,研究ALOHA协议在串型水声通信网络的交付率、吞吐量及端对端时延等网络性能测度,推导出获取最佳网络性能的网络参数配置,从而为ALOHA协议在串型路由水声通信网路中的应用提供理论支撑。
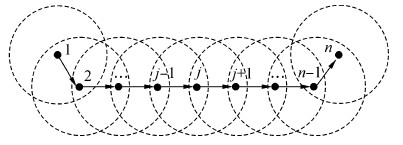
1 水声通信网络串型路由模型由n个通信节点构成的串型水下通信网络 (如图 1所示),其中第1个节点(编号为1)和最后一个节点(编号为n)为水面节点,中间为水下节点(编号从2~n-1)。相邻节点间距离相等,仅节点1产生数据流采用固定间隔发送数据模式,水下节点仅负责转发,将上一跳节点的数据转发给下一跳节点,节点n为目的节点负责接收。
|
| 图 1 串型路由水声通信网络模型 Fig. 1 A model of string underwater sensor networks |
对于任意节点j(1 < j < n)的覆盖范围内仅包括节点j-1和节点j+1,节点1的覆盖范围内仅包括节点2,节点n的覆盖范围内仅包括节点n-1。
在该模型下,在水声信道环境较好的情况下,在节点2处会导致数据包丢失的原因如下:1)节点1发送的前后2个数据包的间隙小于数据包的发送时延,造成节点2转发节点1的前一个数据包时,节点1发出的后一个数据包已经到达,此时由于节点2处于发送状态无法接收。2)节点1发送的数据包与节点3转发的数据包在节点2处发生碰撞。
2 最优网络性能测度作如下假设:
1)所有数据包长度相同,数据包调制/解调所需时间用Td表示,归一化为1;
2)节点之间的平均传播时延为τ,归一化后为α=τ/Td;
3)节点1发送数据包按固定间隔产生,前后2个数据包之间的时间间隙为Tinterval,归一化后为β=Tinterval/Td;
4)网络运行时间为Tsim。
2.1 碰撞规律碰撞规律定理:节点1发送的第k个数据包经过节点2、节点3转发后再次到达节点2,如果节点1发送的第j个数据包(j>k),与第k个数据包在节点2处没有发生碰撞,那么这2个数据包也不会在后续的节点处发生碰撞。
证明:
第k个数据包的发送时间是(k-1)β+(k-1)经过节点2、节点3转发后再次到达节点2,被节点2接收的时间区间为
| $\begin{array}{*{20}{c}} {\left( {k - 1} \right)\beta + \left( {k - 1} \right) + 2 + 3\alpha }\\ {\left( {k - 1} \right)\beta + \left( {k - 1} \right) + 3 + 3\alpha } \end{array}$ | (1) |
第j个数据包发送时间是(j-1)β+(j-1),节点2接收第j个数据包的时间区间为
| $\begin{array}{*{20}{c}} {\left( {j - 1} \right)\beta + \left( {j - 1} \right) + \alpha }\\ {\left( {j - 1} \right)\beta + \left( {j - 1} \right) + 1 + \alpha } \end{array}$ | (2) |
结合式(1)、(2)可得第k个数据包与第j个数据包碰撞的充要条件:
| $\begin{array}{*{20}{c}} {\left( {j - 1} \right)\beta + j - 1 + \alpha < \left( {k - 1} \right)\beta + k + 3\alpha + 1 < }\\ {\left( {j - 1} \right)\beta + j + \alpha } \end{array}$ |
或
| $\begin{array}{*{20}{c}} {\left( {j - 1} \right)\beta + j - 1 + \alpha < \left( {k - 1} \right)\beta + k + 3\alpha + 2 < }\\ {\left( {j - 1} \right)\beta + j + \alpha } \end{array}$ |
推导后可得
| $\frac{{2\alpha - j + k + 1}}{{j - k}} < \beta < \frac{{2\alpha - j + k + 3}}{{j - k}}$ | (3) |
那么第k个数据包与第j个数据包不碰撞的充要条件为
| $\beta \ge \frac{{2\alpha - j + k + 3}}{{j - k}}或\beta \le \frac{{2\alpha - j + k + 1}}{{j - k}}$ | (4) |
同理可得:如果节点1发送的第j个数据包(j>k),与第k个数据包在节点2处没有发生碰撞,则第j个数据包到达节点3的时间区间为
| $\begin{array}{*{20}{c}} {\left( {j - 1} \right)\beta + \left( {j - 1} \right) + 1 + 2\alpha }\\ {\left( {j - 1} \right)\beta + \left( {j - 1} \right) + 2 + 2\alpha } \end{array}$ | (5) |
第k个数据包的发送时间是(k-1)β+(k-1)经过节点2、节点3、节点4转发后再次到达节点3的时间区间为
| $\begin{array}{*{20}{c}} {\left( {k - 1} \right)\beta + \left( {k - 1} \right) + 3 + 4\alpha }\\ {\left( {k - 1} \right)\beta + \left( {k - 1} \right) + 4 + 4\alpha } \end{array}$ | (6) |
同上,得到第k个数据包与第j个数据包在节点3处不碰撞的充要条件为
| $\beta > \frac{{2\alpha - j + k + 3}}{{j - k}}或\beta < \frac{{2\alpha - j + k + 1}}{{j - k}}$ | (7) |
式(4)、(7)完全相同,即如果第k个数据包与第j个数据包在节点2处不碰撞,那么第k个数据包与第j个数据包在节点3处不碰撞。以此类推,第k个数据包与第j个数据包在后续节点处均不会发生碰撞,从而命题结论得证。
碰撞规律推论:数据包的碰撞仅仅会发生在节点2处。
2.2 网络交付率网络的交付率是串型路由水声通信网络关注的重要指标,若相邻节点链路的交付率为Pj→j+1,则串型网络的整体交付率P表达式为
| $P = \prod\limits_{j = 1}^{n - 1} {{P_{j \to j + 1}}} $ | (8) |
根据推论可知当j≥2时,Pj→j+1=1,则串型网络的整体交付率P表达式为
| $P = {P_{1 \to 2}}$ | (9) |
网络吞吐量与交付率关系表达式如下
| ${\rm{TP = }}P\frac{{N{L_d}}}{{{T_{{\rm{sim}}}}}}$ | (10) |
式中:Ld表示数据包的大小,N=$\frac{{{T_{{\rm{sim}}}}/{T_d}}}{{\beta + 1}}$表示发送的数据包的数量。
令$\rho = \frac{{{L_d}}}{{{T_d}}}$,将式(9)代入式(10)得
| ${\rm{TP = }}\rho \frac{{{P_{1 \to 2}}}}{{\beta + 1}}$ | (11) |
当0≤β < 1时,节点1发送的2个数据包之间的间隙小于数据包的发送时间,导致在节点3发数据包的信号到达节点2时会和节点1发出的数据包中的1个或者连续2个发生碰撞。
若节点3转发的数据包为第1个包,根据式(4)可知,节点1发出的第j个数据包与节点3转发的数据包在节点2处碰撞的条件为
| $\frac{{2\alpha - j + 2}}{{j - 1}} < \beta < \frac{{2\alpha - j + 4}}{{j - 1}}$ | (12) |
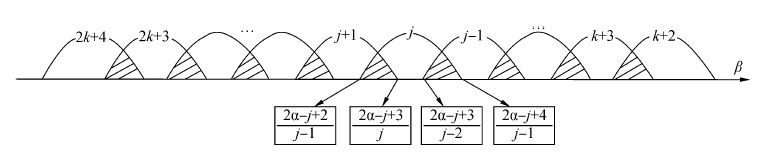
当α∈[k,k+0.5),k是大于或等于0的整数,则节点1发出的第k+2个数据包至第个2(k+2)个数据包,一共涉及k+3个数据包中的1个或者连续2个数据包会与节点3转发的数据包在节点2处碰撞。根据β取值的不同,碰撞的点也不一样,图 2是0≤β < 1时的碰撞规律示意图。
|
| 图 2 当0≤β < 1时的碰撞规律示意图 Fig. 2 Regular patterns of data packets collisions where 0≤β < 1 |
设j是自然数,且j∈[k+2,2(k+2)]。
1)若j是偶数。
当$j = k + 2,\frac{{2\alpha - j + 3}}{j} < \beta < \frac{{2\alpha - j + 4}}{{j - 1}}$且0≤β < 1。节点3转发的节点1的第1个数据包仅与节点1发出的第j个数据包发生碰撞;节点1发出的第2个数据包在0≤β < 1时,节点2处处于发送状态,节点2收不到,数据包丢弃失;节点3转发节点1的第3个数据包仅与节点1发出的第j+3个数据包发生碰撞;以此类推,网络吞吐量可归纳为$\frac{\rho }{{\beta + 1}} \cdot \frac{1}{2}$。
假设2α=2k+ε,(0≤ε < 1),有
| $\begin{array}{*{20}{c}} {0 \le \frac{{2\alpha - j + 3}}{j} = \frac{{2k + \varepsilon - k - 2 + 3}}{{k + 2}} = \frac{{k + \varepsilon + 1}}{{k + 2}} < 1,}\\ {\frac{{2\alpha - j + 4}}{{j - 1}} = \frac{{k + \varepsilon + 2}}{{k + 2}} > 1,而0 \le \beta < 1} \end{array}$ |
据此,确定β的区间范围是$\frac{{2\alpha - j + 3}}{j} < \beta < 1$。
若$2k + 4 > j > k + 2,\frac{{2\alpha - j + 3}}{j}\; < \beta < \frac{{2\alpha - j + 3}}{{j - 2}}$,仅与节点1发出的第j个数据包均发生碰撞,此时网络吞吐量归纳为$\frac{\rho }{{\beta + 1}} \cdot \frac{1}{2}$。
若$2k + 4 > j > k + 2,\frac{{2\alpha - j + 2}}{{j - 1}}\; <\beta <\frac{{2\alpha - j + 3}}{j}$,与节点1发出的第j个数据包以及j+1个数据包均发生碰撞,此时网络吞吐量归纳为$\frac{\rho }{{\beta + 1}} \cdot \frac{j}{{4j - 2}}$。
若j=2k+4,则节点3发出的数据包仅与节点1发出的第j个数据包数据包发生碰撞是不可能的。原因是节点1的第j=2k+4个数据包与节点3的数据包发生碰撞的β区间为
| $\frac{{2\alpha - j + 2}}{{j - 1}} < \beta < \frac{{2\alpha - j + 3}}{{j - 2}}$ |
左侧为
| $\frac{{2\alpha - j + 2}}{{j - 1}} = \frac{{2k + \varepsilon - 2k - 4 + 2}}{{2k + 3}} = \frac{{\varepsilon - 2}}{{2k + 3}} < 0$ |
右侧为
| $\frac{{2\alpha - j + 3}}{{j - 1}} = \frac{{2k + \varepsilon - 2k - 4 + 3}}{{2k + 2}} = \frac{{\varepsilon - 1}}{{2k + 2}} < 0$ |
这与0≤β < 1矛盾,因此,j=2k+4时,节点3的数据包是不可能仅与节点1发出的第j个数据包发生碰撞的。
2)若j是奇数。
若j=k+2,则$\frac{{2\alpha - j + 3}}{j} < \beta < 1 $,仅与节点1发出的第j个数据包发生碰撞,此时网络吞吐量归纳为$\frac{\rho }{{\beta + 1}} \cdot \frac{{j - 1}}{{2j}}$。
若$2k + 4 > j > k + 2,\frac{{2\alpha - j + 3}}{j}\; < \beta < \frac{{2\alpha - j + 3}}{{j - 2}}$时,仅与节点1发出的第j个数据包发生碰撞,此时网络吞吐量归纳为$\frac{\rho }{{\beta + 1}} \cdot \frac{{j - 1}}{{2j}}$。
若$2k + 2 > j > k + 2,\frac{{2\alpha - j + 2}}{{j - 1}}\; < \beta < \frac{{2\alpha - j + 3}}{j}$时,则与节点1发出的第j个数据包以及第j+1个数据包均发生碰撞,此时网络吞吐量归纳为$\frac{\rho }{{\beta + 1}} \cdot \frac{1}{4}$。
若$j = 2k + 3,\frac{{2\alpha - j + 2}}{{j - 1}} < \beta < \frac{{2\alpha - j + 4}}{j}$时,则与节点1发出的第j个数据包以及第j+1个数据包均发生碰撞。此时的网络吞吐量可归纳为:$\frac{\rho }{{\beta + 1}} \cdot \frac{1}{4}$。
此时,$\frac{{2\alpha - j + 2}}{{j - 1}} = \frac{{\varepsilon - 1}}{{2k + 2}} < 0$,因此,β的区间进一步确定为$0 \le \beta < \frac{{2\alpha - j + 3}}{j}$。
综上,将上述0≤β < 1,α∈[k,k+0.5)且α>0时的吞吐量表达式如下
| ${\rm{TP = }}\left\{ \begin{array}{l} \frac{\rho }{{\beta + 1}} \cdot \frac{1}{4},\;\;\left( {0 \le \beta < \frac{{2\alpha - j + 3}}{j},j = 2k + 3} \right),与第j、j + 1个碰\\ \frac{\rho }{{\beta + 1}} \cdot \frac{1}{4},\left( {\frac{{2\alpha - j + 2}}{{j - 1}} < \beta < \frac{{2\alpha - j + 3}}{j},j \in \left( {k + 2,2k + 2} \right)且j为奇} \right),与第j、j + 1个碰\\ \frac{\rho }{{\beta + 1}} \cdot \frac{j}{{4j - 2}},\left( {\frac{{2\alpha - j + 2}}{{j - 1}} < \beta < \frac{{2\alpha - j + 3}}{j},j \in \left( {k + 2,2k + 4} \right)且j为偶} \right),与第j、j + 1个碰\\ \frac{\rho }{{\beta + 1}} \cdot \frac{{j - 1}}{{2j}},\left( {\frac{{2\alpha - j + 3}}{j} < \beta < \frac{{2\alpha - j + 3}}{{j - 2}},j \in \left( {k + 2,2k + 4} \right)且j为奇} \right),与第j个碰\\ \frac{\rho }{{\beta + 1}} \cdot \frac{1}{2},\left( {\frac{{2\alpha - j + 3}}{j} < \beta < \frac{{2\alpha - j + 3}}{{j - 2}},j \in \left( {k + 2,2k + 4} \right)且j为偶} \right),与第j个碰\\ \frac{\rho }{{\beta + 1}} \cdot \frac{1}{4},\left( {\frac{{2\alpha - j + 3}}{j} < \beta < 1,\;j = k + 2AAAjBBB} \right),与第j个碰\\ \frac{\rho }{{\beta + 1}} \cdot \frac{1}{2},\left( {\frac{{2\alpha - j + 3}}{j} < \beta < 1,\;j = k + 2AAAjBBB} \right),与第j个碰 \end{array} \right.$ | (13) |
同样,当α∈[k-0.5,k),k是自然数。则节点1发出的第k+2个数据包至第2(k+2)-1个数据包中的1个或连续2个与节点3转发的数据包在节点2处碰撞。设j是自然数,且j∈[k+2,2(k+2)-1],则吞吐量表达式如下
| ${\rm{TP = }}\left\{ \begin{array}{l} \frac{\rho }{{\beta + 1}} \cdot \frac{j}{{4j - 2}},\;\;\left( {0 \le \beta < \frac{{2\alpha - j + 3}}{j},j = 2k + 2} \right),与第j、j + 1个包碰\\ \frac{\rho }{{\beta + 1}} \cdot \frac{1}{4},\left( {\frac{{2\alpha - j + 2}}{{j - 1}} < \beta < \frac{{2\alpha - j + 3}}{j},j \in \left( {k + 2,2k + 2} \right)且j为奇} \right),与第j、j + 1个包碰\\ \frac{\rho }{{\beta + 1}} \cdot \frac{j}{{4j - 2}},\left( {\frac{{2\alpha - j + 2}}{{j - 1}} < \beta < \frac{{2\alpha - j + 3}}{j},j \in \left( {k + 2,2k + 2} \right)且j为偶} \right),与第j、j + 1个包碰\\ \frac{\rho }{{\beta + 1}} \cdot \frac{{j - 1}}{{2j}},\left( {\frac{{2\alpha - j + 3}}{j} < \beta < \frac{{2\alpha - j + 3}}{{j - 2}},j \in \left( {k + 2,2k + 3} \right)且j为奇} \right),与第j个包碰\\ \frac{\rho }{{\beta + 1}} \cdot \frac{1}{2},\left( {\frac{{2\alpha - j + 3}}{j} < \beta < \frac{{2\alpha - j + 3}}{{j - 2}},j \in \left( {k + 2,2k + 3} \right)且j为偶} \right),与第j个包碰\\ \frac{\rho }{{\beta + 1}} \cdot \frac{{j - 1}}{{2j}},\left( {\frac{{2\alpha - j + 3}}{j} < \beta < 1,\;j = k + 2且j为奇} \right),与第j个包碰\\ \frac{\rho }{{\beta + 1}} \cdot \frac{1}{2},\left( {\frac{{2\alpha - j + 3}}{j} < \beta < 1,\;j = k + 2且j为偶} \right),与第j个包碰 \end{array} \right.$ | (14) |
当α∈[k-0.5,k+0.5),k是自然数。则节点1发出的第2~k+2个共计k+1个数据包中的1个可能会与节点3转发的数据包在节点2处碰撞。
设j是自然数,且j∈[2,k+2]。
若j=k+2,1≤β < $\frac{{2\alpha - j + 4}}{{j - 1}}$,则仅与节点1发出的第j个包碰撞,吞吐量为$\frac{\rho }{{\beta + 1}} \cdot \frac{1}{2}$。
若k+2>j≥2,$\frac{{2\alpha - j + 2}}{{j - 1}} < \beta < \frac{{2\alpha - j + 4}}{{j - 1}}$,与节点1发出的第j个包碰撞,吞吐量为$\frac{\rho }{{\beta + 1}} \cdot \frac{1}{2}$。
若k+2>j>2,$\frac{{2\alpha - j + 3}}{j} \le \beta \le \frac{{2\alpha - j + 2}}{{j - 1}}$或$\frac{{2\alpha - j + 4}}{{j - 1}} \le \beta \le \frac{{2\alpha - j + 3}}{{j - 2}}$,则节点3转发的数据包不会与节点1发出的任何数据包碰撞,吞吐量为$\frac{\rho }{{\beta + 1}}$。
若j=2,则β≥2α+2时,则节点3转发的数据包不会与节点1发出的任何数据包碰撞,吞吐量等于$\frac{\rho }{{\beta + 1}}$。
综上,将上述β≥1,α∈[k-0.5,k+0.5)时的吞吐量表达式总结如下
| ${\rm{TP = }}\left\{ \begin{array}{l} \frac{\rho }{{\beta + 1}} \cdot \frac{1}{2},\;\;\left( {1 \le \beta < \frac{{2\alpha - j + 4}}{{j - 1}},j = k + 2} \right),与第j个包碰\\ \frac{\rho }{{\beta + 1}} \cdot \frac{1}{2},\left( {\frac{{2\alpha - j + 2}}{{j - 1}} < \beta < \frac{{2\alpha - j + 4}}{{j - 1}},j \in \left( {2,k + 2} \right)} \right),与第j个包碰\\ \frac{\rho }{{\beta + 1}},\left( {\frac{{2\alpha - j + 3}}{j} \le \beta \le \frac{{2\alpha - j + 2}}{{j - 1}}或\frac{{2\alpha - j + 4}}{{j - 1}} \le \beta \le \frac{{2\alpha - j + 3}}{{j - 2}}且j \in \left( {2,k + 2} \right)} \right),无碰撞\\ \frac{\rho }{{\beta + 1}},\left( {\beta \ge 2\alpha + 2,j = 2} \right),无碰撞 \end{array} \right.$ | (15) |

|
| 图 3 β≥1时的碰撞规律示意图 Fig. 3 Regular patterns of data packets collisions where β≥1 |
|
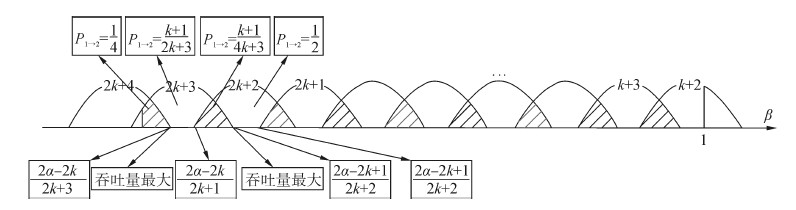
| 图 4 β∈[0,1),α∈[k,k+0.5)最大吞吐量原理图 Fig. 4 The maximum throughput whereβ∈[0,1),α∈[k,k+0.5) |
1)当β∈[0,1)时的最大网络吞吐量分析。
①β∈[0,1),α∈[k,k+0.5)时。
根据式(13),在β∈[0,1),α∈[k,k+0.5)区域内,节点碰撞被分为4种碰撞类型,节点3与第奇数个包、与第偶数个包以及与以奇数开头的连续2个包碰撞、与以偶数开头的连续2个包碰撞。各种类型碰撞的吞吐量结果不同,在相应的区间上随着β的增大,其吞吐量不断减小,因此对应各个碰撞类型的吞吐量最大值在相应区间最左侧的点处。
设与以奇数开头的连续2个包碰撞的吞吐量最大值为TP1,则
| ${\rm{T}}{{\rm{P}}_1}{\rm{ = }}\rho \frac{{{P_{1 \to 2}}}}{{\beta + 1}} = \frac{\rho }{4}$ | (16) |
设与第奇数个包碰撞的最大吞吐量为TP2,则
| ${\rm{T}}{{\rm{P}}_2}{\rm{ = }}\rho \frac{{k + 1}}{{2\alpha + 3}}$ | (17) |
设与以偶数开头的连续2个包碰撞的吞吐量最大值为TP3,则
| ${\rm{T}}{{\rm{P}}_3}{\rm{ = }}\rho \frac{{\left( {k + 1} \right)\left( {2k + 1} \right)}}{{\left( {2\alpha + 1} \right)\left( {4k + 3} \right)}}$ | (18) |
设与第偶数个包碰撞的吞吐量最大值为TP4,则
| ${\rm{T}}{{\rm{P}}_4}{\rm{ = }}\rho \frac{{k + 1}}{{2\alpha + 3}}$ | (19) |
比较式(16)~(19)可知:TP2=TP4>TP1,TP2=TP4>TP3。
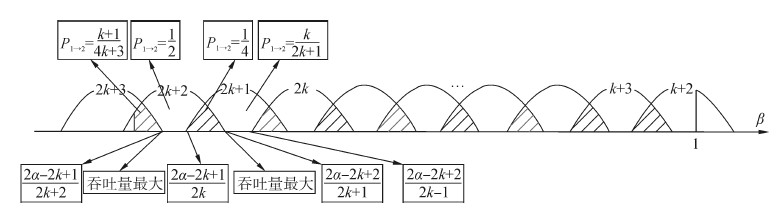
②β∈[0,1),α∈[k-0.5,k)时。
|
| 图 5 β∈[0,1),α∈[k-0.5,k)时最大吞吐量原理图 Fig. 5 The maximum throughput where β∈[0,1),α∈[k-0.5,k) |
根据式(14),当β∈[0,1),α∈[k-0.5,k),节点碰撞分为4种类型。即:节点3与第奇数个包、与第偶数个包、与以奇数开头的连续2个包、与以偶数开头的连续2个包碰撞。各种类型的吞吐量在相应的区间上随着β的增大而减小,因此对应各种碰撞类型的最大吞吐量在相应区间最左侧的点处。
设与以偶数开头的连续2个包碰撞的最大吞吐量为TP5,则
| ${\rm{T}}{{\rm{P}}_5}{\rm{ = }}\rho \frac{{k + 1}}{{4k + 3}}$ | (20) |
设与第偶数个包碰撞的最大吞吐量为TP6,则
| ${\rm{T}}{{\rm{P}}_6}{\rm{ = }}\rho \frac{{k + 1}}{{2\alpha + 3}}$ | (21) |
设与以奇数开头的连续2个包碰撞的最大吞吐量为TP7,则
| ${\rm{T}}{{\rm{P}}_7}{\rm{ = }}\rho \frac{k}{{4\alpha + 2}}$ | (22) |
设与第奇数个包碰撞的最大吞吐量为TP8,则
| ${\rm{T}}{{\rm{P}}_8}{\rm{ = }}\rho \frac{k}{{2\alpha + 3}}$ | (23) |
比较式(20)~(23)有
| ${\rm{T}}{{\rm{P}}_6} > {\rm{max}}\left\{ {{\rm{T}}{{\rm{P}}_5},{\rm{T}}{{\rm{P}}_7},{\rm{T}}{{\rm{P}}_8}} \right\}$ |
综上所述,当β∈[0,1)时,吞吐量的最大值是节点3转发的包仅与节点1发出的第2k+3(最大奇数)个或第2k+2(最大偶数)个数据包碰撞的时候达到,其中2个包之间的间隙β取对应区间的最小值。
|
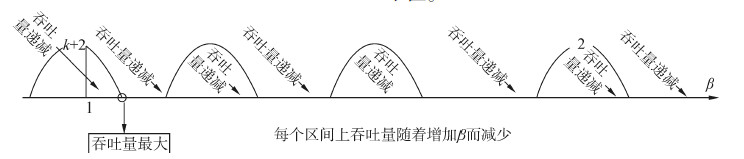
| 图 6 β∈[1,+$\infty $)时最大吞吐量原理图 Fig. 6 The maximum throughput whereβ∈[1,+$\infty $) |
2)β∈[1,+$\infty $)时的最大网络吞吐量分析。
根据式(15),当β∈[1,$\infty $),α∈[k-0.5,k+0.5)时,节点3与其中一个包碰撞和没有碰撞两种情况,得到吞吐量结果不同,在相应的区间上随着β的增大,其吞吐量不断减小,因此碰撞时吞吐量最大值在β=1处取得,不碰撞时最大吞吐量在相应区间最左侧的点处。
设碰撞的最大吞吐量为TP9,则
| ${\rm{T}}{{\rm{P}}_9}{\rm{ = }}\frac{\rho }{4}$ | (24) |
设不碰撞的最大吞吐量为TP10,则
| ${\rm{T}}{{\rm{P}}_{10}}{\rm{ = }}\rho \frac{{k + 1}}{{2\alpha + 3}}$ | (25) |
比较式(24)、(25)可知:TP10>TP9。
综合式(17)、(19)、(21)、(25),可得以下重要结论。即在给定α的条件下,网络的最大吞吐量为
| ${\rm{T}}{{\rm{P}}_{\max }}{\rm{ = }}\rho \frac{{k + 1}}{{2\alpha + 3}}$ | (26) |
若$\alpha \in \left[{k - 0.5,k} \right]$,β在$\frac{{2\alpha - 2k + 1}}{{2k + 2}}$、$\frac{{2\alpha - k + 2}}{{k + 2}}$两处,网络吞吐量达到最大值TPmax;若α∈[k,k+0.5),β在$\frac{{2\alpha - 2k}}{{2k + 3}}$、$\frac{{2\alpha - 2k + 1}}{{2k + 2}}$、$\frac{{2\alpha - k + 2}}{{k + 1}}$三处,网络吞吐量达到最大值TPmax。
3 仿真实验分析 3.1 实验参数配置仿真采用NS3仿真软件进行仿真,仿真参数配置为:节点数量7个,相邻节点距离为5 000 m,声速1 500 m/s,数据包长度为2 048 bit,发送速率为1 024 bit/s,仿真时间为3 600 s。
3.2 仿真结果及分析仿真不断改变数据包间隙β(即网络负载),仿真结果与理论计算结果对比如图 7~9所示。
|
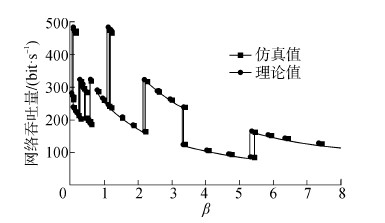
| 图 7 网络吞吐量随数据包发送间隙β变化曲线 Fig. 7 Throughput as the delivering interval β between data packets is varied |
|
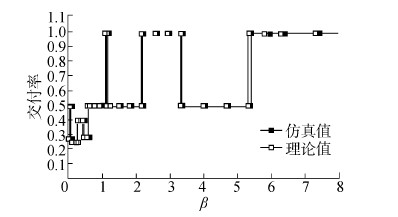
| 图 8 交付率随数据包发送间隙β变化曲线 Fig. 8 Delivery rate as the delivering intervalβbetween data packets is varied |
|
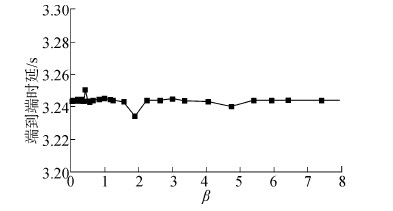
| 图 9 端到端时延随数据包发送间隙β变化曲线 Fig. 9 End-to-end delay as the delivering interval β between data packets is varied |
1)吞吐量分析
仿真值比理论值稍滞后一点,原因是由于处理时延非常小,在吞吐量理论分析时没有考虑数据包的处理时延造成的偏移。从图 7可以看出,实验结果存在2个吞吐量最大值的点,一个在其数据包发送间隙0~1区间上,另一个在大于1的区间上,与理论分析一致。
2)交付率分析
交付率的仿真值和理论值一致,由于理论分析时没有考虑数据包的处理时延造成的存在仿真值比理论值稍滞后一点。图中存在三段交付率为1的区间,其数据包发送间隙β均大于1。很显然,β值较小的区间其吞吐量更大。
3)网络时延分析
从图 9可以看出,网络时延基本保持在32.4 s左右,很稳定,原因是发送时延、数据处理时延以及传播时延基本是固定不变的。
4)综合分析
综合对比图 7、8可知,在0≤β < 1区间上取得吞吐量最大值的点,所在区间的交付为0.5,也就是说,节点1发送的数据包有一半丢失了,尽管吞吐量较大,但节点消耗的能量较多。在β≥1区间上取得吞吐量最大值的点,所在区间恰好是三段交付率为1的区间的第一段,与0≤β < 1区间上的取得吞吐量最大值的点比较,2个点吞吐量一样大,但此处交付率为1,没有造成包的丢失,能耗较小。上述2个点端到端时延基本没有区别。
因此,综合交付率、时延以及吞吐量来看,在β≥1区间上取得吞吐量最大值的点是网络综合性能最佳点,仿真试验结果与理论推导的最优值$\beta = \frac{{2\alpha - k + 2}}{{k + 1}}$,即TPmax$= \rho \frac{{k + 1}}{{2\alpha + 3}}$吻合。
4 结束语目前ALOHA协议在功能较为单一水声通信网络中应用广泛,但其实际的最优性能与节点布放以及通信装备的参数有着密切的关系,本文基于水声通信网络的3种性能评价指标(即数据交付率、吞吐量以及端对端时延),推导了串型路由条件下获取最佳网络综合性能的参数配置条件,仿真实验验证了本文的理论分析结论,该理论分析为该协议的实际应用提供有力的指导依据。
| [1] |
周密, 崔勇, 徐兴福, 等. 水声传感网MAC协议综述[J]. 计算机科学, 2011, 38(9): 5-10, 17. ZHOU Mi, CUI Yong, XU Xingfu, et al. Survey of the MAC protocols on underwater acoustic sensor network[J]. Computer science, 2011, 38(9): 5-10, 17. |
| [2] | DOMINGO M C. Overview of channel models for underwater wireless communication networks[J]. Physical communication, 2008, 1(3): 163-182. |
| [3] | NASRI N, KACHOURI A, ANDRIEUX L, et al. Design considerations for wireless underwater communication transceiver[C]//Proceedings of the 2nd international conference on signals, circuits and systems (SCS). Monastir: IEEE, 2008: 1-5. |
| [4] | CATIPOVIC J A. Performance limitations in underwater acoustic telemetry[J]. IEEE journal of oceanic engineering, 1990, 15(3): 205-216. |
| [5] | ROBERTS L G. ALOHA packet system with and without slots and capture[J]. ACM SIGCOMM computer communication review, 1975, 5(2): 28-42. |
| [6] | BERTSEKAS D P, GALLAGER R. Data networks[M]. 2nd ed. New Jersey: Prentice hall, 1992. |
| [7] | CHIRDCHOO N, SOH W S, CHUA K C. Aloha-based MAC protocols with collision avoidance for underwater acoustic networks[C]//Proceedings of the 26th IEEE international conference on computer communications. Anchorage, AK, USA: IEEE, 2007. |



