在LTE系统中,均衡算法的设计原则要同时考虑到系统较大时算法的复杂度和在非理想信道估计下的算法性能。线性检测算法[1, 2],算法复杂度简单,但是系统性能随着信噪比的增加提升缓慢。非线性判决反馈均衡[3, 4, 5, 6]的提出解决了这个问题,算法通过反馈信号信息能进一步消除残留码间干扰,然而系统性能依赖于判决反馈滤波器的阶数,阶数越高,性能越好,但系统复杂度也随之提高。非线性串行/并行干扰消除算法[7, 8, 9],在上一次迭代过程中重建信号出现偏差,会对下次迭代带来影响,会造成不同程度的误差传播,系统性能提升有限。信道编码与均衡算法相结合的最大后验概率(maximum a posterior probability,MAP)均衡算法[10]性能最好,但是复杂度较高,在实际中无法实现。基于MMSE准则的软干扰消除均衡算法[11],虽然该算法相比于MAP算法性能有所降低[12],但算法的复杂度相比于MAP算法要低,性能也是最为接近MAP算法。该算法随着天线数量和调制方式的大小增加,算法的复杂度也是随之增加。同时上述算法都没有考虑天线间干扰的问题,使得性能提升受限。为了减少天线间的干扰问题,人们提出基于预编码矩阵的软输入软输出MMSE(soft-input soft-output MMSE based on precoding,SISO MMSE BOP)均衡算法[13],但算法复杂度与文献[11]相同,复杂度相对较高。
因此,针对多天线的天线干扰、多径干扰和迭代过程中误差传播的问题,本文提出一种低复杂度的基于预编码矩阵的混合迭代均衡算法。通过预编码矩阵可以解决天线间干扰问题,提高算法第1次迭代性能较准确。使系统性能提升。通过分析和仿真不同信道环境结果证明,本文算法性能提升显著。
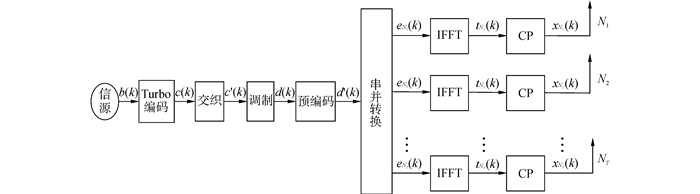
1 系统模型 1.1 发射机模型基于预编码的迭代均衡算法模型如图 1所示。
|
| 图 1 基于预编码的迭代均衡算法发射模 Fig. 1 Iterative equalization algorithm based on precoding transmitter model |
信源产生K个信息比特b(k)=[b(1),b(2),…,b(K)],随后信息比特通过turbo编码得到长度为N信息序列c(k),则编码器传输速率为r=K/N。编码器输出c(k)经过随机交织器得到c'(k),之后c'(k)经过QPSK调制得到复数数据序列d(k),对复数序列d(k)进行预编码处理得到d'(k),这里的预编码与文献[14]中的线性预编码不同,这里预编码矩阵的目的是将发射信号扩展到所有天线的每一个子载波上。而后经过串并转化为NT个天线的数据eNt(k)。其中d'(k)=Fd(k),F预编码矩阵,且F为酉矩阵FHF=I,预编码矩阵可以选用傅里叶变换矩阵和Hadamerd矩阵,在本文中选用傅里叶变换矩阵。NR为接收天线数。将eNt(k)作M点的IFFT变换得到时域信号tNt(k):
| ${{t}_{{{N}_{t}}}}\left( k \right)=\sum\limits_{i=0}^{M-1}{{{e}_{{{N}_{t}}}}\left( k \right)\exp \left( \text{j2 }\!\!\pi\!\!\text{ ik}/M \right)/\sqrt{M}}$ | (1) |
时域信号tNt(k)加循环前缀(cyclic prefix,CP),得到发送信号xNt(k)送入信道。
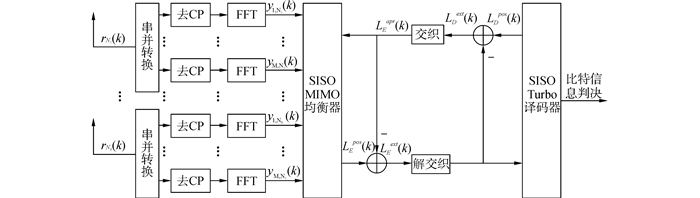
1.2 接收机模型接收机模型如图 2所示,第Nr根接收天线上的接收信号为rNr(k):
| ${{r}_{{{N}_{r}}}}\left( k \right)=\sum\limits_{l=0}^{L-1}{h\left( l \right)x\left( k-l \right)+n\left( k \right)}$ | (2) |
|
| 图 2 基于线性预编码的迭代均衡算法接收机模型 Fig. 2 Iterative equalization algorithm based on linear precoding receiver model |
图 2中展示了均衡器通过计算后验概率LEpos(k)并且与上一次迭代得到的先验信息LEapr(k)作差运算得到外信息LEext(k),进一步通过解交织作为SISO turbo译码器的先验信息LDapr(k)。Turbo译码器首先根据输入信息LDapr(k)计算后验概率LDpos(k),之后通过LDpos(k)与LDapr(k)取差运算得到SISO MIMO均衡器的外信息LDext(k),外信息通过交织得到均衡器的先验信息,LEapr(k)为均衡器重建干扰信号提供数据信息,从此完成一次迭代。
2 基于预编码矩阵的混合迭代均衡算法 2.1 第1次迭代过程解决天线间干扰问题,预编码矩阵是一种较好的选择。根据文献[12],基于预编码矩阵的SISO MMSE均衡算法的发送信号x(k)估计值$\hat x$(k)为
| $\begin{align} & \hat{x}\left( k \right)=v\left( k \right){{A}^{H}}{{R}^{-1}} \\ & \left( y\left( k \right)-A\text{E}\left[ x\left( k \right) \right]+\text{E}\left[ x\left( k \right) \right] \right) \\ \end{align}$ | (3) |
因此,本文在第1次迭代过程中引入MMSE-SQRD算法,通过信道重建和排序优先检测信噪比较大的符号,为下次迭代提供较为准确的初值。
在不影响似然比计算的情况下,式(3)可以写为
| $\begin{align} & \hat{x}\left( k \right)=v\left( k \right){{\left( {{A}^{\text{H}}}Av\left( k \right)+{{\sigma }^{2}}I \right)}^{-1}}{{A}^{H}} \\ & \left( y\left( k \right)-A\mu \left( k \right) \right)+\mu \left( k \right) \\ \end{align}$ | (4) |
| $\mu \left( k \right)=\sum\limits_{x\in \mathbb{Z}}{xP\left( x\left( k \right)=x|L_{E}^{apr}\left( k \right) \right)}$ | (5) |
| $v\left( k \right)=\sum\limits_{x\in \mathbb{Z}}{{{\left| x \right|}^{2}}P\left( x\left( k \right)=x|L_{E}^{apr}\left( k \right) \right)}-{{\left| \mu \left( k \right) \right|}^{2}}$ | (6) |
| $\begin{align} & P\left( x\left( k \right)x|L_{E}^{apr}\left( k \right) \right)= \\ & \prod\limits_{j=1}^{Mc}{\frac{\exp \left( \left( 1-2{{c}^{j}} \right)L_{E}^{apr}\left( k \right)/2 \right)}{\sum{_{\lambda =1,-1}\exp \left( L_{E}^{apr}\left( k \right)/2 \right)}}} \\ \end{align}$ | (7) |
根据文献[13]给出了MMSE-SRQD检测算法,对信道矩阵和接收信号向量重新定义为
| $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{A}=\left[ \begin{align} & A \\ & {{\sigma }_{n}}{{v}^{-\frac{1}{2}}}\left( k \right) \\ \end{align} \right]$ | (8) |
| $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y}\left( k \right)=\left[ \begin{align} & y\left( k \right) \\ & {{\sigma }_{n}}{{v}^{-\frac{1}{2}}}\left( k \right)\mu \left( k \right) \\ \end{align} \right]$ | (9) |
| $\hat{x}\left( k \right)={{\left( {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{A}}}^{H}}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{A} \right)}^{-1}}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{A}}^{H}}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y}\left( k \right)$ | (10) |
对矩阵$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{A} $进行QR分解得到
| $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{A} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{Q} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{R} = \left[ \begin{gathered} {Q_1} \hfill \\ {Q_2} \hfill \\ \end{gathered} \right]\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{R} = \left[ \begin{gathered} {Q_1}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{R} \hfill \\ {Q_2}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{R} \hfill \\ \end{gathered} \right]$ | (11) |
利用式(10)、(11),式(4)可以写为
| $\begin{align} & \hat{x}\left( k \right)={{R}^{-1}}\left( k \right) \\ & \left( {{Q}_{1}}^{H}\left( k \right)y\left( k \right)+\sigma {{Q}_{2}}^{H}\left( k \right){{v}^{\frac{-1}{2}}}\left( k \right)\mu \left( k \right) \right) \\ \end{align}$ | (12) |
在不影响计算的情况下,让R(k)$\hat{x}$(k)表示为$\tilde{x}$(k),利用$\tilde{x}$(k)=Q1H(k)y(k)+σQ2H(k)·${{v}^{\frac{-1}{2}}}$(k)μ(k)与Q1H(k)Ax(k)+σQ2H(k)·${{v}^{\frac{-1}{2}}}$(k)μ(k)+Q1H(k)n(k)相等,Q1H(k)A+σ·Q2H(k)${{v}^{\frac{-1}{2}}}$(k)=R(k),则式(12)可写为
| $\begin{align} & \hat{x}\left( k \right)=R\left( k \right)x\left( k \right)-\sigma Q_{2}^{H}\left( k \right){{v}^{\frac{-1}{2}}}\left( k \right) \\ & \left( x\left( k \right)-\mu \left( k \right) \right)+Q_{1}^{H}\left( k \right)n\left( k \right) \\ \end{align}$ | (13) |
提取$\tilde{x}$i(k),可以得到
| $\begin{align} & {{{\tilde{x}}}_{i}}\left( k \right)=\sum\limits_{j-i}^{{{N}_{T}}}{{{r}_{ij}}\left( k \right){{x}_{j}}\left( k \right)}-\sum\limits_{j=1}^{i}{\sigma {{q}_{2,ij}}\left( k \right){{v}_{j}}^{\frac{-1}{2}}\left( k \right)} \\ & \left( {{x}_{j}}\left( k \right)-{{\mu }_{j}}\left( k \right) \right)+\sum\limits_{j=1}^{{{N}_{R}}}{{{q}_{1,ij}}\left( k \right){{n}_{j}}\left( k \right)} \\ \end{align}$ | (14) |
利用MMSE-SQRD算法进行软干扰消除,可以得到
| ${{\overset{\gg }{\mathop{x}}\,}_{i}}\left( k \right)={{\tilde{x}}_{i}}\left( k \right)-\sum\limits_{j=i+1}^{{{N}_{T}}}{{{r}_{ij}}\left( k \right)}\mu _{j}^{p}\left( k \right)$ | (15) |
| $\begin{align} & \overset{\gg }{\mathop{{{x}_{i}}}}\,\left( k \right)={{\left( {{r}_{ii}}\left( k \right)-\sigma {{q}_{2,ij}}\left( k \right)v_{i}^{\frac{-1}{2}}\left( k \right) \right)}^{-1}} \\ & \left( {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tilde{y}}}}_{i}}\left( k \right)-\sum\limits_{j=i+1}^{{{N}_{T}}}{{{r}_{ij}}\left( k \right)\mu _{j}^{p}\left( k \right)-{{r}_{ii}}\left( k \right)q_{2,ii}^{2}\left( k \right){{\mu }_{i}}\left( {} \right)} \right) \\ \end{align}$ | (16) |
为了计算信号${{\overset{\gg }{\mathop{x}}\,}_{i}}$(k)的似然值,需要计算出估计信号的方差,则估计信号方差ν${{\overset{\gg }{\mathop{x}}\,}_{i}}$(k)为
| $\begin{align} & {{v}_{\overset{\gg }{\mathop{{{x}_{i}}}}\,}}_{\left( k \right)}=r_{_{ii}}^{-2}\left( k \right)\left( ^{1}-q_{_{2,ii}}^{2}\left( k \right) \right)- \\ & 2\left( {{\sigma }^{2}}\left( 1-q_{_{2,ii}}^{2}\left( k \right) \right)+\sum\limits_{j=i+1}^{{{N}_{T}}}{{{\left| {{r}_{ij}}\left( k \right) \right|}^{2}}v_{j}^{p}\left( k \right)} \right) \\ \end{align}$ | (17) |
| $\mu _{j}^{p}\left( k \right)=\sum\limits_{x\in \mathbb{Z}}{xP\left( {{x}_{j}}\left( k \right)=x|L_{E,j}^{pos}\left( k \right) \right)}$ | (18) |
| $\begin{align} & v_{j}^{p}\left( k \right)=\sum\limits_{x\in \mathbb{Z}}{{{\left| x \right|}^{2}}P\left( {{x}_{j}}\left( k \right)=x|L_{E,j}^{pos}\left( k \right) \right)}- \\ & {{\left| \mu _{j}^{p}\left( k \right) \right|}^{2}} \\ \end{align}$ | (19) |
| $\begin{align} & P\left( x\left( k \right)=x|L_{E}^{pos}\left( k \right) \right)= \\ & \prod\limits_{j=1}^{Mc}{\frac{\exp \left( \left( 1-2{{c}^{j}} \right)L_{E}^{pos}\left( k \right)/2 \right)}{\sum{_{\lambda =1,-1}\exp \left( L_{E}^{pos}\left( k \right)/2 \right)}}} \\ \end{align}$ | (20) |
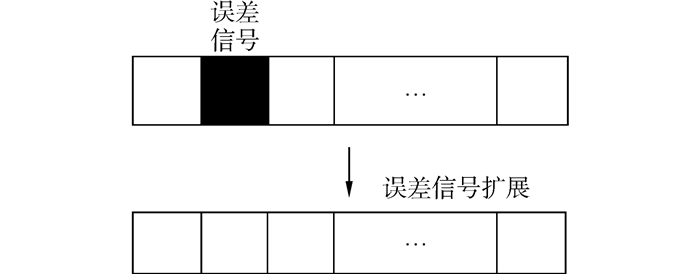
根据ν${{\overset{\gg }{\mathop{x}}\,}_{i}}$(k),利用λi=2Re(${{\overset{\gg }{\mathop{x}}\,}_{i}}$(k))/(ν${{\overset{\gg }{\mathop{x}}\,}_{i}}$(k))计算出估计信号${{\overset{\gg }{\mathop{x}}\,}_{i}}$(k)(k)实部的似然值,同理,可得到虚部的似然值,输出似然值通过预编码矩阵进行扩展[16],目的是减少误差传播,从而为第2次迭代提供更加准确的信息,扩展原理如图 3所示。第1次迭代通过把SISO MMSE BOP并行迭代均衡算法改写为串行迭代均衡,使得第1次迭代输出值较为精确,进而提升系统的性能。
|
| 图 3 误差信号扩展过程 Fig. 3 Error extension process |
在第2次及之后的迭代过程中,采用SISO MMSE BOP并行迭代均衡算法。为了计算估计值的似然值,需要计算式(3)中估计值$\hat{x}$(k)的方差。提取估计值$\hat{x}$i(k),可以得到
| $\begin{align} & {{{\hat{x}}}_{i}}\left( k \right)=\rho _{i}^{-1}e_{i}^{T}{{\left( {{A}^{H}}Av\left( k \right)+{{\sigma }^{2}}I \right)}^{-1}}{{A}^{H}}\cdot \\ & \left( y\left( k \right)-A\mu \left( k \right) \right)+{{\mu }_{i}}\left( k \right) \\ \end{align}$ | (21) |
| ${{v}_{{{{\hat{x}}}_{i}}}}\left( k \right)=\rho _{i}^{-1}\left( k \right)-{{v}_{i}}\left( k \right)$ | (22) |
为了验证本文算法效果,仿真过程采用(7,5) turbo编码,编码速率为1/2。数据载波数为300,FFT变换点数为512,数据符号数为14个符号,系统带宽为10 MHz,载波频率间隔为15 kHz,带宽为10 MHz,调制方式为QPSK,turbo译码为LOG-MAP译码,发送天数为4天线,接收天线为4天线。本文假设在理想信道估计下,信道选用LTE标准常见的步行扩展信道中文名称(extended pedestrian A,EPA),信道和车辆扩展信道中文名称(extended vehicular A,EVA)信道模型[15]。
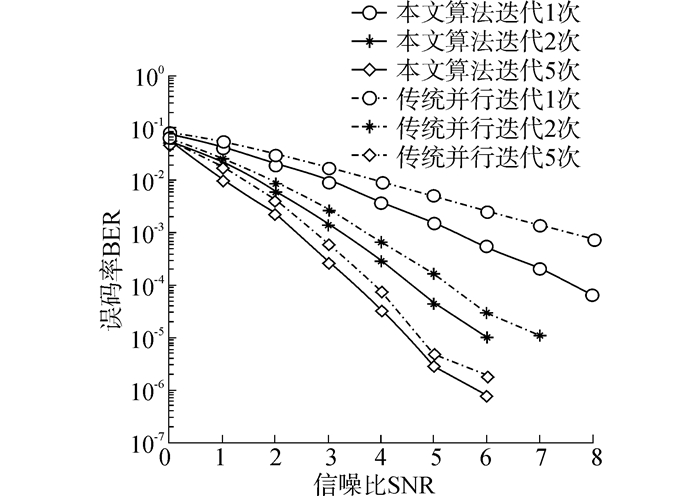
图 4为4发4收情况下,不同迭代次数中,本文基于预编码矩阵的混合迭代均衡算法与SISO MMSE BOP算法的误码率的性能对比。由图 4可知,本文算法随着迭代次数的增加,性能明显提升。这是因为一方面通过预编码的处理减少了天线之间的干扰,使得发射信号扩展到每根天线的所有子载波,降低了信道对载波间正交性的破坏,改善了误码率。另一方面是因为本文在接收端采用MMSE-SRQD算法对信道矩阵重建并排序,对信噪比最大的符号优先检测,使得第1次均衡结果相比于对比算法更为准确,所以在迭代过程中本文算法误差相比于对比算法的误差较小,误差对均衡的影响更小,使本文算法性能更好。5次迭代之后本文算法相比于对比算法,则带来了0.5 dB左右的增益。
|
| 图 4 4发4收时本文算法与SISO MMSE BOP在EPA信道中的性能比 Fig. 4 Performance comparison of proposed algorithm and SISO MMSE BOP for 4 transmitters and 4 receivers in EPA channel |
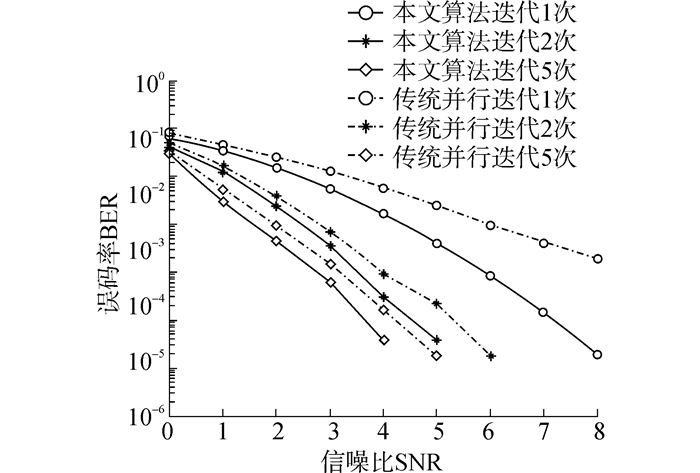
图 5为4发4收情景下,在不同迭代次数下,本文基于预编码矩阵的混合迭代均衡算法与SISO MMSE BOP算法的误码率的性能对比。由图 5可知,采用本文算法总体性能优越于传统算法,这是因为通过预编码的处理减少了天线之间的干扰,使得发射信号扩展到每根天线的所有子载波,降低了信道对载波间正交性的破坏,改善了误码率。经过一次迭代,误码率在10-3时,本文算法相比于传统算法性能提升1.8 dB左右,本文算法随着迭代次数的增加,性能随之提升并收敛。五次迭代之后本文算法相比于对比算法,则带来了0.7 dB左右的增益,这是由于通过预编码的处理使得错误信号扩展到整个帧上,减少了重建信号的错误率,继续提升了系统的性能。
|
| 图 5 4发4收时本文算法与SISO MMSE BOP在EVA信道中的性能对比 Fig. 5 Performance comparison of proposed algorithm and SISO MMSE BOP for 4 transmitters and 4 receivers in EVA channel |
本文算法的复杂度主要包括两个部分,第1次迭代引入的MMSE-SQRD算法复杂度与第二步以及之后算法SISO MMSE BOP的复杂度。MMSE-SQRD算法复杂度为O(NT3+NT2NR),该算法对传输信号软干扰消除需要O(NTNR),计算后验概率和先验概率需要O(Mc2Mc),计算均衡器最大后验概率似然值LEpos(k)与译码器输出最大后验概率似然值LDpos(k)需要O(Mc2Mc),其中Mc表示调制方式星座集的大小,本文采用QPSK调制Mc=2,则本文算法经过一次迭代需要总的复杂度为O(NT3+NT2NR+NTMc2Mc)。根据文献[16],对比算法一次迭代复杂度为O(NT2NR+NTNR3+NTMc2Mc)。综合以上可得知,当天线数目为NR≥NT时,本文算法运算复杂度相对较低。
为了证明本文算法复杂度更低,本文给出更为详细的复杂度比较。本文算法在第1次引入MMSE-SQRD算法,第2次及第2次之后与SISO MMSE BOP均衡算法相同。文中发射天线和接收天线相同,都配置为n。文中算法与对比算法在软调制和软解调都是相同的,所以在分析复杂度时不考虑这方面的影响。本文提出的算法,在第1次迭代时采用MMSE-SQRD算法,在频域需要4n3+n2/2+n/2次浮点计算,在计算$\tilde{x}$(k)需要3n2+n+3次浮点计算,之后计算符号估计值$\overset{\gg }{\mathop{x}}\,$(k)及其方差要求3n2/2+29n/2+1次浮点计算,则第1次迭代的运算量为3个部分的和,即总共需要4n3+5n2+16n+4次浮点计算。根据文献[18]传统算法一次迭代需要7n4/3+3n3+5n2次浮点运算,通过分析可以得出,当天线数目n≥3,本文算法复杂度相比于对比算法复杂度要低,减少了算法的运算复杂度。
5 结论针对MIMO-OFDM系统存在天线间干扰和多径干扰,本文提出一种低复杂度的基于预编码矩阵的混合迭代均衡算法。
1) 一方面利用预编码对发射端数据进行预处理,减少部分子载波深衰落对扩展前原始发射信号的影响,另一方面在接收端利用预编码对误差信号进行扩展,减少误差传播。通过实验证明了本文算法的有效性。
2) 在接收端,引入MMSE-SQRD算法,一方面充分利用信道信息,另一方面通过引入MMSE-SQRD算法有效的减少了对比算法的复杂度,通过公式和分析证明本文算法的优越性。
在4发4收的情景下,误码率在10-5时,5次迭代后本文算法性能相比于现有算法改善约为0.7 dB左右。
| [1] | LUNTTILA T, LINDHOLM J, PAJUKOSKI K, et al. EUTRAN uplink performance[C]//Proceedings of the 2nd international symposium on wireless pervasive computing. San Juan: IEEE, 2007: 515-519. |
| [2] | GERSTACKER W H, NICKEL P, OBERNOSTERER F, et al. Trellis-based receivers for SC-FDMA transmission over MIMO ISI channels[C]//Proceedings of IEEE international conference on communications (ICC'08). Beijing: IEEE, 2008: 4526-4531. |
| [3] | ZHANG Chao, WANG Zhaocheng, YANG Zhixing, et al. Frequency domain decision feedback equalization for uplink SC-FDMA[J]. IEEE transactions on broadcasting, 2010, 56(2): 253-257. |
| [4] | FICKERS J, GHAZISAEIDI A, SALSI M, et al. Decision-feedback equalization of bandwidth-constrained N-WDM coherent optical communication systems[J]. Journal of lightwave technology, 2013, 31(10): 1529-1537. |
| [5] | HUANG G, NIX A, ARMOUR S. Decision feedback equalization in SC-FDMA[C]//Proceedings of the IEEE 19th international personal, indoor and mobile radio communications. Cannes: IEEE, 2008: 1-5. |
| [6] |
陈强, 杨霄鹏, 达新宇. 一种快速收敛的航空信道载波恢复判决反馈盲均衡算法[J]. 中南大学学报:自然科学版, 2013, 44(9): 3707-3712. CHEN Qiang, YANG Xiaopeng, DA Xinyu, et al. A fast super-exponential Iteration Decision Feedback blind equalization algorithm for carrier recovery of aeronautical channel[J]. Journal of central south university: science and technology, 2013, 44(9): 3707-3712. |
| [7] | LOPEZ S M, DIEHM F, VISOZ R, et al. Measurement and prediction of turbo-SIC receiver performance for LTE[C]//Proceedings of IEEE 76th vehicular technology conference. Quebec City, QC: IEEE, 2012: 1-5. |
| [8] | LIN Huajiong, TANG Youxi, GUAN Lu, et al. Ordered Successive Interference Cancellation (OSIC) in V-BLAST systems with asynchronous transmission mode[J]. Wireless personal communications, 2011, 60(2): 263-275. |
| [9] | KHALIGHI M A, BOUTROS J J, HELARD J F. Data-aided channel estimation for turbo-PIC MIMO detectors[J]. IEEE communications letters, 2006, 10(5): 350-352. |
| [10] | DOUILLARD C, JEZEQUEL M, BERROU C, et al. Iterative correction of intersymbol interference: Turbo-equalization[J]. European transactions on telecommunications, 1995, 6(5): 507-511. |
| [11] | LU B, YUE Guosen, WANG Xiaodong. Performance analysis and design optimization of LDPC-coded MIMO OFDM systems[J]. IEEE transactions on signal processing, 2004, 52(2): 348-361. |
| [12] | XU Chongbin, WANG Hao, LIN Xiaokang. Precoding for OFDM systems with imperfect channel state information at the transmitter[J]. IEICE transactions on communications, 2011, E94-B(6): 1770-1773. |
| [13] | WUBBEN D, BOHNKE R. MMSE extension of V-BLAST based on sorted QR decomposition[C] //Proceedings of the IEEE 58th vehicular technology conference.Orlando, FL, USA: IEEE, 2003: 508-512. |
| [14] |
莫韬甫, 邵士海, 刘田, 等. 异步MIMO-OFDM中基于预处理矩阵的迭代检测算法[J]. 电子与信息学报, 2012, 34(4): 795-801. MO Taofu, SHAO Shihai, LIU Tian, et al. Pre-processing matrix based iterative detection algorithm in asynchronous MIMO-OFDM[J]. Journal of electronics & information technology, 2012, 34(4): 795-801. |
| [15] | 3GPP TS 36.104 V8.4.0 (2008-12). Evolved universal terrestrial radio access (EUTRA)[Z]. Base Station (BS) radio transmission and reception, 2005: 6-9. |
| [16] | MATACHE A, JONES C, WESEL R. Reduced complexity MIMO detectors for LDPC coded systems[C] //Proceedings of IEEE military communications conference.Monterey, CA, USA: IEEE, 2004: 1073-1079. |



