2. Shantui Construction Machinery Co., Ltd., Jining 272073, China
液力变矩器的开发设计主要是叶栅系统的设计,叶栅设计得是否合理会直接影响液力变矩器的最高效率、能容、启动转矩比等特性。通常,叶栅的设计分3步进行:计算叶片角度,通过保角变换法或环量分配法计算叶片骨线,通过保角变换法等方法对叶片进行加厚。实践证明,对于双涡轮液力变矩器而言,第一涡轮和泵轮叶片形态较短,厚度变化较为剧烈,因此其叶片厚度变化规律对变矩器性能的影响较大。但是,传统的叶片加厚方法多依赖经验设计,较多采用等倾角射影法,其设计过程复杂且坐标转换过程存在失真,往往设计出来的叶片与理论结果偏差较大,容易造成双涡轮液力变矩器的理论效率与实际效率偏差较大。
近年来,随着三维CAD技术和加工制造技术的发展,液力变矩器的叶片三维设计方法得到快速发展:王键等[1]将叶片分成多个翼面层分别设计,完成了叶片三维成型,但是由于仍然采用等倾角射影法,因此仍需要调整各翼面的相对位置;袁彩云等[2]采用反求设计得出铸造叶片的形状,可以通过调整关键点位置来改变形态,但是得出的规律对于不同型号的液力变矩器不能适用;D. L. Robinette等[3]建立了一种评价液力变矩器仿形设计的方法,可以预测不同直径液力变矩器叶片入口的空穴现象,为液力变矩器仿型设计提供支持;刘冀察等[4, 5]将儒科夫斯基翼型和NACA翼型运用到液力变矩器的设计中,由于仍然采用的是翼型提供的骨线,且仍需通过等倾角射影法展开到平面进行设计,因此仍然没能够得到广泛的运用。
三维设计方法能够实现自动化、快速化设计,因此,仍然是液力变矩器叶片的主流设计方法。本文探讨了叶片法向加厚法,利用叶片的形态特征和常见的翼型函数形式,探索叶片流线的参数化表达方法,为叶片的自动设计探索新途径。
1 符合NACA翼型特征的叶片厚度函数液力变矩器的叶片是空间扭曲的,对于铸造叶片,一般采用变厚度叶片,大量的研究表明,其叶片形态应具有入口处较厚,出口处较薄,呈流线型的特征,以减少液流损失。传统的保角变换法设计出的叶片会出现狭长和扭曲现象。为解决此问题,本文改变传统的厚度设计方法,基于NACA翼型的特征提出了新的叶片厚度空间设计方法。
NACA翼型系列族谱是由美国国家航空委员会在经过大量的风洞试验之后发布的,该翼型系列通过公式确定叶型的骨线和厚度的分布函数。NACA 4位翼型函数是由4位数字决定的一系列翼型形状,其中前两位数字表示骨线的扭曲程度,后两位表示叶片最大厚度,本设计中变矩器的骨线是由环量分配法得到,所以只要利用后两位决定的厚度函数即可,例如翼型0015,其厚度分配规律如下(其厚度形态如图 1所示):
| $\begin{array}{l} {{y'}_t} = t'c/0.2\left( {0.2969\sqrt {x'/c} - 0.1260x'/c - } \right.\\ \left. {0.351{{\left( {x'/c} \right)}^2} + 0.0843{{\left( {x'/c} \right)}^3} - 0.1015{{\left( {x'/c} \right)}^4}} \right) \end{array}$ | (1) |
式中:y't是叶片厚度的一半,m;x'为叶片计算点到入口点的弦长,m;t'为叶片入口处到最大厚度值占叶片骨线弦长的比例,%;c为弦长,即叶片骨线的空间长度,m。

|
| 图1 NACA0015翼型 Fig.1 NACA0015 airfoil |
由于该翼型是根据试验结果推导得到,不能简单地直接运用到液力变矩器叶片的设计,因此,需按照液力变矩器的设计要求对该翼型模型的系数进行调整,将该函数整理如下
| ${y_t} = tf\left( x \right)$ | (2) |
| $f\left( x \right) = A\sqrt x + Bx + C{x^2} + D{x^3} + E{x^4}$ | (3) |
定义函数f(x)为叶片某点的厚度占叶片最大厚度的百分比,则0≤f(x)≤1,其中,在厚度为零时f(x)min=0,在最大厚度处f(x)max=1。式中其他参数含义如下:yt为叶片法向厚度,mm;t表示叶片最大厚度,mm;x为叶片计算点到入口点的弧长占总弧长的百分比(叶片距离百分比)(0≤x≤1,入口侧为0,出口处为1);A、B、C、D、E待定系数。
由叶片的形态决定其叶片出口厚度为零,即:
| $f\left( 1 \right) = 0$ | (4) |
翼型函数其他系数的确定,是在将该翼型函数运用到具体模型时,根据叶片的流固耦合要求进行调整,调整的标准是使液流流经叶片间流道时液力损失(冲击、摩擦、扩散等)较小,叶片所受载荷均匀。
由统计资料估算工作轮叶片最大厚度处的叶片距离百分比xi,通常其值变化范围为0.25~0.4,且与工作轮叶片角的极点β=90°相一致,则
| $f\left( {{x_i}} \right) = 1$ | (5) |
且该点导函数值也为0,即
| $f'\left( {{x_i}} \right) = 0$ | (6) |
根据式(4)~(6),再由经验规律给定该翼型函数的入口、出口处斜率,即可确定一组翼型函数。
对各个工作轮分别计算,便可得到各个工作轮的厚度值函数。
2 计算叶片的厚度矢量本文采用的加厚算法是针对液力变矩器叶片中间流面的加厚,因此在加厚前需根据环量分配法得到各叶片的内外环骨线点[6]。然后对由环量分配法得到的内外环线点按弧长等分进行插值。将新得到的等分点按照入口到出口排列,并将得到的内环线点计作S1,即为叶片的内环骨线;将得到的外环线点计作S2,即为叶片的外环骨线。内、外环骨线组成的直纹曲面即为叶片的中间流面。
通常,为了方便制造时制模和生产,液力变矩器叶片多由直纹曲面构成。直纹曲面是指,采用直母线素几何设计方法得到的导向型叶片型面,即通过2条设计基线上无数个点之间的连线确定曲面形态[7],因此,复杂的曲面设计可简化为两条设计基线的曲线设计。对于某有厚度的叶片设计,可以先转化为叶片工作面和非工作面的设计,再简化为工作面和非工作面上的2个设计基线的设计。
通常,流固耦合的叶片要求内侧和外侧均为光顺的曲面,因此本文在设计加厚时是针对中间流面进行两面加厚,现以外环某点S2i(x,y,z)为例,简述其加厚原理。
如图 2所示,叶片外环需要加厚处坐标为S2i(x,y,z),其相邻点的S2i-1(x,y,z),内环上对应的坐标为S1i(x,y,z),若该点的法向厚度为yt(i),设定加厚后的点坐标为P2i+(x,y,z)和P2i-(x,y,z),令$\frac{{\overrightarrow {{S_{{2_i}}}{P_{{2_i}}}} }}{{\left| {\overrightarrow {{S_{{2_i}}}{P_{{2_i}}}} } \right|}}$为向量$\overrightarrow {{S_{{2_i}}}{P_{{1_i}}}} $和$\overrightarrow {{S_{{2_i}}}{P_{{2_{i - 1}}}}} $组成平面(如图 2中Face)的法向量,用以下方程组可以求解该向量:
| $\left\{ \begin{array}{l} \overrightarrow {{S_{{2_i}}}{P_{{1_i}}}} \cdot \frac{{\overrightarrow {{S_{{2_i}}}{P_{{2_i}}}} }}{{\left| {\overrightarrow {{S_{{2_i}}}{P_{{2_i}}}} } \right|}} = 0\\ \overrightarrow {{S_{{2_i}}}{P_{{2_{i - 1}}}}} \cdot \frac{{\overrightarrow {{S_{{2_i}}}{P_{{2_i}}}} }}{{\left| {\overrightarrow {{S_{{2_i}}}{P_{{2_i}}}} } \right|}} = 0 \end{array} \right.$ | (7) |

|
| 图2 法向加厚算法原理 Fig.2 Normal thickening theory |
由方程(7)可求出2组法向量,2组方向相反,再根据曲线凹凸特性选取一组向量作为工作面向量,另外一组作为非工作面向量:
| $\left\{ \begin{array}{l} \overrightarrow {{S_{{2_i}}}P_{{2_i}}^ + } = k \cdot {y_t}\left( i \right) \cdot \frac{{\overrightarrow {{S_{{2_i}}}{P_{{2_i}}}} }}{{\left| {\overrightarrow {{S_{{2_i}}}{P_{{2_i}}}} } \right|}}\\ \overrightarrow {{S_{{2_i}}}P_{{2_i}}^ - } = \left( {1 - k} \right) \cdot {y_t}\left( i \right) \cdot ( - \frac{{\overrightarrow {{S_{{2_i}}}{P_{{2_i}}}} }}{{\left| {\overrightarrow {{S_{{2_i}}}{P_{{2_i}}}} } \right|}}) \end{array} \right.$ | (8) |
式中:k值为中间流面上某点到工作面的厚度占该点整个厚度的比例,(1-k)为中间流面上某点到非工作面的厚度占该点整个厚度的比例。对于弯曲叶片外侧的点,其厚度比例取值较大,令k=65%;对于弯曲叶片内侧的点,令k=35%。计算出的P1i+和P1i-即为内环加厚后的工作面、非工作面点坐标。
对内环线和外环线上其余的点分别作上述运算,得到加厚后的内环点阵P1+、P1-和外环点阵P2+、P2-。将点阵P1+和P2+用直纹曲面连接,得到叶片工作面;将点阵P1-和P2-用直纹曲面连接,再通过桥接、缝合操作,即可得到成型叶片。
3 双涡轮液力变矩器设计性能的比较将本文提到的叶片厚度设计方法运用在某型号双涡轮液力变矩器的叶片厚度设计上,通过三坐标测量机测量叶片关键部位的参数,再由环量分配法得到叶片中间流面,分别按照本方法和等倾角射影法对叶片骨线进行加厚,得到的叶片模型分别称为法向加厚模型和等倾角射影模型。
3.1 法向加厚模型将式(3)运用到双涡轮液力变矩器上时,需根据该变矩器的特点,确定厚度函数系数。分析该双涡轮液力变矩器的第1涡轮、第2涡轮和导轮中间流线上的液流角度变化(如图 3)可知:第1涡轮和导轮叶片角等于90°的位置靠前,第2涡轮叶片角等于90°的位置靠后,因此可以认为当第1涡轮、第2涡轮和导轮厚度位于极大值点时,叶片距离百分比分别为0.25、0.4和 0.25。

|
| 图3 各轮中间流线叶片角变化 Fig.3 Blade angle changes along design path |
由经验可知,该翼型函数的导函数f'(x)通常是单调递减,且在x∈0.1,1,最大值小于10,最小值大于-4,由此选定入、出口斜率。由此可计算第1涡轮、第2涡轮和导轮翼型函数如下
| $\begin{array}{c} {f_{T1}} = 3.2761\sqrt x - 1.2978x - 7.5095{x^2} + \\ 11.4461{x^3} - 5.9149{x^4} \end{array}$ | (9) |
| $\begin{array}{c} {f_{T2}} = 1.9571\sqrt x + 0.5485x - 3.4931{x^2} + \\ 1.9909{x^3} - 1.0034{x^4} \end{array}$ | (10) |
| $\begin{array}{c} {f_D} = 0.9949\sqrt x + 6.4063x - 23.8720{x^2} + \\ 28.0429{x^3} - 11.5721{x^4} \end{array}$ | (11) |
由式(9)~(11)得到的是该点厚度占最大厚度的比例,因此仍然需要确定叶片的最大厚度值,本文选取泵轮、第1涡轮、第2涡轮和导轮的最大厚度值分别为4.0、12.5、12.5和13.0 mm。
查阅相关资料可知,铸造泵轮的叶片厚度变化通常不大;并且大量仿真结果表明,其厚度变化规律对变矩器性能影响较小。因此,本文近似认为泵轮叶片是等厚度的[8]。
对环量分配法得到的骨线,依据法向加厚算法按照上述厚度分配规律进行加厚,即得到法向加厚模型。
3.2 等倾角射影模型等倾角射影法利用的保角变换原理[12],思路是将叶片内外环流线投影到圆柱体上,再将圆柱体展开成平面图形,然后根据经验的厚度分布规律对展开图进行厚度设计,最后将平面叶片展开到三维坐标系中,得到加厚后的叶片模型。其中,等倾角射影模型的叶片厚度百分比分配规律如表 1所示。
| 叶片距离百分比/% | 每点厚度占最大厚度的百分比/% | |||
| 泵轮 | 1涡轮 | 2涡轮 | 导轮 | |
| 0 | 0 | 0 | 0 | 0 |
| 10 | 80 | 60 | 62 | 60 |
| 20 | 100 | 95 | 93 | 95 |
| 30 | 97 | 100 | 100 | 100 |
| 40 | 86 | 92 | 93 | 92 |
| 50 | 68 | 79 | 80 | 79 |
| 60 | 52 | 63 | 62 | 63 |
| 70 | 38 | 46 | 46 | 46 |
| 80 | 22 | 32 | 29 | 32 |
| 90 | 10 | 18 | 13 | 18 |
| 100 | 0 | 8 | 0 | 8 |
由于泵轮的传统厚度函数也是非均匀变化的,因此设定其最大厚度值为6 mm,其他轮最大厚度均与新模型一致。
将按照此方法得到的模型称为等倾角射影模型。
3.3 模型与仿真结果对比将法向加厚模型和等倾角射影模型的厚度规律进行对比,结果如图 4所示。

|
| 图4 改进的NACA翼型厚度和经验厚度对比 Fig.4 Comparison of adjusted NACA airfoil and traditional thickness |
对比可知,法向厚度模型的入口点厚度函数斜率较大,即入口点出厚度变化剧烈,据此加厚出的叶片入口处较圆,有利于减少入口处冲击损失,法向加厚模型的厚度函数在x=0处斜率为正无穷,使得入口处曲率没有突变,实现光滑连接,进一步降低冲击损失;法向加厚模型的厚度函数斜率变化较为平缓,而等倾角射影模型的厚度函数斜率变化较为剧烈。
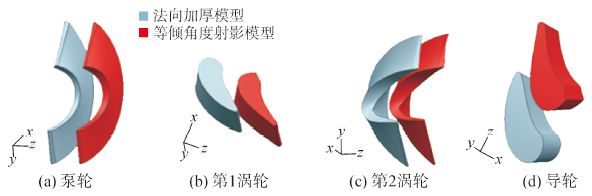
将2种模型的叶片进行对比,如图 5所示进行对比。分析可知,等倾角射影模型的第1涡轮入口处出现厚度变化剧烈点,原因是第1涡轮在将经验厚度函数按照等倾角射影法在中间流线进行平面加厚时,由于缺乏人工手动光顺,因此,反算后叶片在此处出现曲率突变点;导轮入口也是如此。
|
| 图5 2种设计方法设计出的叶片对比 Fig.5 Comparison of blades designed by two methods |
由图 5还能看出,等倾角射影模型的第2涡轮入口处存在扭曲,该处也是由于入口点平面坐标反算到三维空间时,坐标点发生变形所致。因此,对于大多数骨线来说,按照法向加厚方法更容易得到形态光滑的叶片。
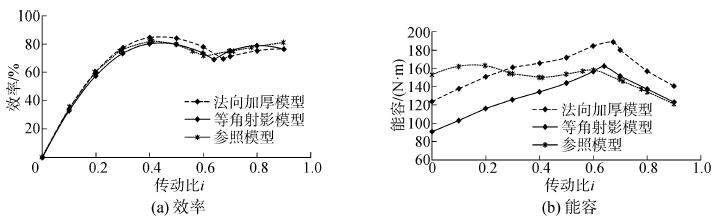
将上述2组模型分别代入计算机流体力学仿真软件(CFD)中来运算,将得到两模型的效率曲线和能容曲线与试验台架试验数据对比,如图 6。
|
| 图6 2个模型效率、能容与台架试验结果对比 Fig.6 Compare of torque & efficiency of two models and bench test results |
图 6中参照模型即为台架试验数据。由图可知,在双涡轮工况转换点前,法向加厚模型在工况转换点之前的最高效率比等倾角射影模型和参照模型的高;法向加厚模型的能容转矩比等倾角射影模型和参考模型的也高出较多。某厂家的整机试验表明,作业时双涡轮液力变矩器处于低转速比的概率较高,故法向加厚法设计出的叶片符合设计要求。
图 6中,某个工作轮的能容转矩的定义为
| ${T_{nri}} = {T_i}/{\left( {{n_B}/1000} \right)^2}$ | (12) |
比较法向加厚模型和等倾角射影模型的三维模型和CFD仿真结果可知,法向加厚方法能够很好的实现叶片加厚,且加厚后的叶片光顺度高,叶片的厚度易于调整。运用符合NACA翼型特征的液力变矩器叶片厚度设计方法对叶片设计是适用的,尤其对于双涡轮液力变矩器的第一涡轮和导轮设计效果比较明显。
4 结论本文基于直纹曲面的特征提出了符合NACA翼型特征的液力变矩器厚度设计方法,适用于已经设计出中间流面空间形态的叶片厚度设计,实质是对三维曲面的直接加厚,该方法能够满足流固耦合作用对液力变矩器叶片的提出的要求。在工程实践中,每一种方法都有其局限性,本方法需要将中间流线沿着直母线向外拓展1~2 mm,这样的调整是为了保证设计得到的叶片与循环圆严格相交,因为设计要求的叶片角度体现在中间流线上,但这种调整不影响中间流线,故不会对结果产生影响。相对于以往变矩器叶片的造型方法,本文方法有如下特点:
1)克服了传统的等角射影法因坐标变换导致叶片连续性差的缺点,使叶片的设计不需要人工调整,可精确地实现叶片加厚,且设计出的叶片形态自然光滑。
2)与参考模型的台架试验结果和等角射影模型的仿真结果比较,法向加厚模型的效率和能容均有提高。
3)现有变矩器叶片厚度设计方法是由三维坐标与二维坐标之间影射间接得出的,本文提出的厚度设计方法从理论上实现了叶片的三维设计,为变矩器翼型自动设计提供了理论支持。
4)符合NACA翼型特征的厚度函数在叶片的入口处斜率为正无穷,故叶片入口钝圆、液流损失小。由于引入NACA翼型特征,使叶片厚度的设计变量由数10个减少到3个。
| [1] | 王健, 葛安林, 雷雨龙, 等. 液力变矩器叶片三维成型法及其性能分析[J]. 吉林大学学报:工学版, 2007, 37(1): 43-47. WANG Jian, GE Anlin, LEI Yulong, et al. Three-dimensional design for hydraulic torque converter blades and its performance analysis[J]. Journal of Jilin university: engineering and technology edition, 2007, 37(1): 43-47. |
| [2] | 袁彩云, 崔亚辉, 王宏江, 等. 基于Pro/E的液力变矩器叶片设计[J]. 机械设计与制造工程, 2014, 43(3): 18-22. YUAN Caiyun, CUI Yahui, WANG Hongjiang, et al. Design on the blades of hydraulic torque converter based on Pro/E[J]. Machine design and manufacturing engineering, 2014, 43(3): 18-22. |
| [3] | ROBINETTE D L, SCHWEITZER J M, MADDOCK D G, et al. Predicting the onset of cavitation in automotive torque converters-part I: Designs with geometric similitude[J]. International journal of rotating machinery, 2008: 803940, doi: 10.1155/2008/803940. |
| [4] | 刘冀察. 儒科夫斯基翼型用于液力变矩器叶型设计的研究[J]. 工程机械, 2003, 34(1): 22-24. LIU Jicha. Theoretical research on blade design method of hydrodynamic torque converter based on Joukowski arfoil[J]. Construction machinery and equipment, 2003, 34(1): 22-24. |
| [5] | 许睿, 宮立强, 于征平, 等. 液力变矩器叶型设计[J]. 工程机械, 2014, 45(3): 41-44. XU Rui, GONG Liqiang, YU Zhengping, et al. Hydraulic torque converter blades design[J]. Construction machinery and equipment, 2014, 45(3): 41-44. |
| [6] | 刘伟辉, 刘春宝, 汪清波, 等. 基于二次函数环量分配的液力变矩器叶片设计方法[J]. 农业机械学报, 2008, 39(8): 145-148. LIU Weihui, LIU Chunbao, WANG Qingbo, et al. Design method of torque converter blade based on quadratic function distribution[J]. Transactions of the Chinese society for agricultural machinery, 2008, 39(8): 145-148. |
| [7] | 王立军, 吴光强, 王欢. 基于叶片角变化规律的液力变矩器改型设计法[J]. 同济大学学报: 自然科学版, 2011, 39(11): 1673-1679. WANG Lijun, WU Guangqiang, WANG huan. Design strategy for modification of torque converters based on variation law of blade angle[J]. Journal of tongji university:natural science, 2011, 39(11): 1673-1679. |
| [8] | 褚亚旭. 基于CFD的液力变矩器设计方法的理论与实验研究[D]. 长春: 吉林大学, 2006: 100-105. ZHU Yaxu. Theoretical and experimental research on design method of hydrodynamic torque converter based on CFD[D]. Changchun: Jilin University, 2006: 100-105. |
| [9] | 魏巍,闫清东.液力变矩器泵轮叶片优化设计研究[J].系统仿真学报,2008,20(23):6549-6553.WEI Wei, YAN Qingdong. Study on optimization design of pump vanes in hydrodynamic torque converter[J].Journal of system simulation,2008,20(23):6549-6553. |
| [10] | 刘悦,马文星,刘春宝, 等.综合式液力变矩器内特性的计算与分析[J].吉林大学学报:工学版,2008,38(1):70-74.LIU Yue, MA Wenxing, LIU Chunbao, et al. Calculation and analysis of internal characteristics of torque converter-coupling[J].Journal of Jilin University:Engineering and Technology Edition,2008,38(1):70-74. |
| [11] | 马文星,刘春宝,雷雨龙, 等.工程机械液力变矩器现代设计方法及应用[J].液压气动与密封,2012(10):71-76.MA Wenxing, LIU Chunbao, LEI Yulong, et al. Modern design methods and application of engineering machinery torque converter[J]. Hydraulics pneumatics & seals,2012(10):71-76. |
| [12] | 朱经昌.液力变矩器的设计与计算[M].北京: 国防工业出版社,1991. |



